Journal of Modern Physics
Vol.06 No.01(2015), Article ID:53592,5 pages
10.4236/jmp.2015.61011
A Quantum Field Theory Description of Separate Electric and Magnetic Effects in Elementary Fermion Epigenetics
Claudio Verzegnassi1,2
1Department of Chemistry, Physics and Environment, University of Udine, Italy
2AMeC (Association for Medicine and Complexity), Trieste, Italy
Email: claudio@ts.infn.it
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 January 2015; accepted 24 January 2015; published 28 January 2015
ABSTRACT
The separate effects that an electric and a magnetic field would have on the total energy and spin of an elementary electron state have been computed in a theoretical quantum field theory framework. It is shown that all the effects in this process, that are defined “fermion epigenetics”, can be expressed in a simple and elegant way in terms of the components of the electron field, called “psinons” in this approach. In the minimal interaction prescription, the electric and the magnetic effects can be separated into the sum of “classical” components reproducing conventional Stark and Zeeman effects, and new components of different type. In the non-relativistic limit, the two residual effects on the energy only depend on the electron intrinsic properties, i.e. its charge and its spin, and on the value of the electric and magnetic potentials. A comparison with the results obtainable in a Pauli formalism approach is discussed and, finally, a very qualitative calculation of the size of possible effects is performed.
Keywords:
Elementary Fermion Epigenetics

1. Introduction
In two previous papers [1] [2] a definition and a description of “fermion epigenetics” have been proposed in the framework of quantum field theory, concentrating the calculation on the case of one electron state. The moti- vations of my definition have been thoroughly elucidated in ref. [1] [2] , to which I refer for a more complete discussion. For the purpose of this paper it will be enough to recall the fact that the starting point was an impressive analogy between the four components of the elementary organic nucleus, the hystones, and the four components of the fermionic field 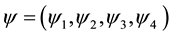 that were called “psinons”. As shown in [1] [2] , all the physical properties of the free electron can be expressed in terms of different combinations of couples of psinons and of their complex conjugate entities.
that were called “psinons”. As shown in [1] [2] , all the physical properties of the free electron can be expressed in terms of different combinations of couples of psinons and of their complex conjugate entities.
In this approach, the process of “magnetic fermion epigenetics” has been described as the result of an interaction between the electron and a classical magnetic field treated in the conventional “minimal interaction” scheme. The main motivation for this search was the idea of proposing possible analogies between the results that we obtained and those of a performable future realistic medical study of magnetic effects on the human organism, that have attracted great interest in recent studies. All the obtained results have been concentrated on the determination of “pure magnetic” effects both in the absence [1] and in the presence [2] of surrounding environment. To simplify the calculations, the analysis was limited to the case of a constant magnetic field whose direction was chosen along the 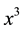 axis. The results that we have obtained, and the associated discussion on the possibility of analogy with a proper medical experiment, have been discussed in [1] [2] .
axis. The results that we have obtained, and the associated discussion on the possibility of analogy with a proper medical experiment, have been discussed in [1] [2] .
The aim of this paper is to generalize the investigation of [1] [2] to the case of a non-constant magnetic and a non-constant electric field, whose effects on the total electron energy and spin will be computed to lowest order in the fields, in the minimal prescription approach. The results will first be given in the general case and then in the constant field case. For the sake of completeness, the various expressions will be compared with those that would have been obtained in the conventional Pauli approach, showing analogies and differences. To conclude, a very qualitative numerical estimate of the electric and magnetic effects for constant fields will be performed. A final discussion on the possible relevance of my calculations will then be given at the end of the paper.
2. Electric and Magnetic Effects on an Elementary Electron State
I shall start this analysis writing the explicit expressions of the total energy, of the spin and of the electric charge of a free electron state. The reason of the choice of the two “intrinsic” electron properties, spin and charge, will become clear in the following part of the paper. I shall choose as basic quantities, as done in [1] [2] , the four complex components of the electron field , i.e.
, i.e.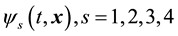 , and retain for them my definition of “psinons”. For the total energy
, and retain for them my definition of “psinons”. For the total energy 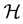 I write:
I write:
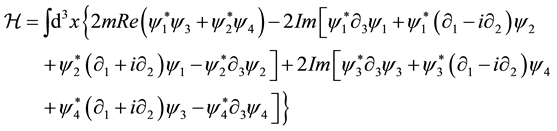 (1)
(1)
For the spin vector 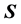 I have:
I have:
 (2)
(2)
where the “spin current” components 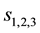 are
are
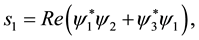 (3)
(3)
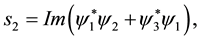 (4)
(4)
 (5)
(5)
The last expression that is needed is that of the electric charge Q. From the conventional definition one obtains
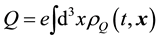 (6)
(6)
where
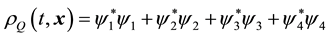 (7)
(7)
and 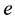 is the electric charge, fixed by the chosen convention, e.g. negative for electrons. The effects on the energy of a classic electromagnetic field, described in the usual way by four potentials
is the electric charge, fixed by the chosen convention, e.g. negative for electrons. The effects on the energy of a classic electromagnetic field, described in the usual way by four potentials 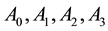 have been now considered. The prescription has been that of the “minimal interaction” approach in which the replacement is used
have been now considered. The prescription has been that of the “minimal interaction” approach in which the replacement is used

Imposing the electron field to satisfy the Dirac equation leads then to the following set of changes of the four psinons, denoted as 




where, 










where 

where 

Here

where

The next term can be written as

where

Equations (13), (16), (18) provide the electric and magnetic effects on the electron energy. The effects have been computed to lowest order in the in the electromagnetic potentials, neglecting components



From this condition one easily finds that the two surviving terms have the following form in the limit


In Equations (21), (22) the expressions of the charge density 



Equations (21), (22) represent the main results that have been obtained. They are valid for general, i.e. non- constant fields. This case can be easily treated replacing in the first term of the magnetic effect equation (22) the magnetic potential potential 

One obtains in this case an overall contribution of the kind 


Returning to the NRL, one sees that the two effects are given by the product of the potentials 

A final point to be discussed is the fact that the formal expressions of the general electric and magnetic effects, computed adopting the minimal interaction formalism and exploiting the Dirac equation, appear perhaps different from what one would expect on the basis of the analogy with the simple Stark and Zeeman effects. In this spirit I have computed the effects that would have been produced in the quantum field theory framework replacing the minimal interaction approach with a Pauli scheme, in which one simply adds to the Lagrangian the interaction term

where 

case. Denoting the effect on the Hamiltonian as

Equation (27) reproduces the effects of conventional Stark and Zeeman type, with the explicit expression for the two currents, that I write for simplicity in a conventional way as


where the 

A possible conclusion is that the minimal interaction scheme produces in the general case the effects that one would expect from the Pauli scheme, plus other terms that are typical of the particular, and firmly respected, approach. In the non-relativistic limit the terms that survive are, though, different from those derivable in the other scheme, since the scalar product with the electron spin which remains is not that of the magnetic field, but is that of the vector potential.
For the completeness of this search, the effects that an electric and a magnetic field would have on the purely intrinsic property of the electron which has been considered here, i.e. its spin, have also been computed. In the scheme that has been followed, the procedure is rather simple and starts form the changes of the spin currents, Equations (3)-(5), that are generated by the modifications of the psinons, Equations (9)-(12). This easily leads to the following results, denoted as usually by 



One sees that the same vector quantities







One final question is that of whether it might be possible to produce, at least qualitatively, an estimate of the two non-relativistic effects. With this purpose I have considered two values of the electric and magnetic fields that have been suggested to us by a dedicated medical equipe [3] . More precisely I have taken the values (for zero frequency fields)


In a super-simplified approach, some “average” values for 








In this qualitative calculation, one sees that the intensity of the scalar and vector potentials are essentially the same. To derive the effect on the energy, one can retain in the defining integrals Equations (21), (22) the average potentials and obtain ( with 



A possible conclusion to be drawn from this very qualitative analysis is that the electric effect appears to be always positive since it is always





3. Conclusions
One clean conclusion that I draw from this analysis is that all the possible changes of the energy of an elementary electron state under the effect of general electric and magnetic fields only depend on two intrinsic property of the electron, i.e. its charge and its spin. I have shown that the considered process can be defined, as in my approach, a “fermion epigenetic” one, since all the visible effects on energy and spin are generated by changes of the four electron “psinons” which recall the analogous chain of effects that are generated in the human organic cells under the action of magnetic fields. A possible relevant conclusion that may be derived is that the size of magnetic and electric effects for realistic values of the fields is comparable and that, in particular, the magnetic effect depends on the space orientation of the magnetic potential A, which is orthogonal to that of the magnetic field.
The possibility that these conclusions might have some relevance for the fascinating medical study of epigenetics is totally based on the belief that there might exist certain analogies between the evolution of the elementary matter components and the evolution of complex living organisms, as stated in a beautiful book written by A. Lima-de-Faria [5] :
“The evolution of living systems is a continuation of that of the physical world”.
This possibility is at the moment being experimentally examined [3] , and I am willing and ready to collaborate with the components of the group.
Acknowledgements
I am deeply indebted with my friend E. Spallucci for his precious suggestions and useful discussions.
References
- Burigana, F., Spallucci, E. and Verzegnassi, C. (2013) Journal of Modern Physics, 4, 1133-1138. http://dx.doi.org/10.4236/jmp.2013.48152
- Spallucci, E. and Verzegnassi, C. (2014) Journal of Modern Physics, 5, 99-102. http://dx.doi.org/10.4236/jmp.2014.53016
- P. Biava, Boffelli, private communication
- G. Giannini, private communication.
- Lima-de-Faria, A. (2003) Evoluzione senza selezione. Nova Scripta Edizioni, Genova.

