Journal of Modern Physics
Vol.5 No.1(2014), Article ID:42263,6 pages DOI:10.4236/jmp.2014.51011
Time-of-Flight Mass Spectrometer with Transaxial Ion Reflector
Almaty University of Power Engineering and Telecommunication, Almaty, Kazakhstan
Email: bimurzaev@mail.ru
Received November 11, 2013; revised December 13, 2013; accepted January 14, 2014
ABSTRACT
Two variants of application of a transaxial mirror with stigmatic spatial time-of-flight focusing in the timeof-flight mass spectrometer have been considered. In the first variant, the transaxial mirror is used as an ion reflector in the ordinary scheme of the time-of-flight mass reflectron. In the second variant, the transaxial mirror simultaneously fulfills the function of the ion reflector and corrector of aberrations caused by the energy spread of ions in the package, formed by the ion source of the mass reflectron. The expressions defining the conditions of stigmatic spatial time-of-flight focusing in the transaxial mirror and the combined system consisting of an ion source and a mirror have been derived. The relationships between geometrical and electrical parameters of threeand four-electrode transaxial mirrors realizing these conditions have been obtained by numerical calculations.
Keywords:Time-Of-Flight (TOF) Mass Reflectron; Transaxial Electrostatic Mirror; Transaxial Ion Reflector; TOF Chromatic Aberration; Stigmatic Spatial-TOF Focusing
1. Introduction
A transaxial mirror is an electrostatic mirror, the field of which has a rotational symmetry, and the optical axis of the mirror is perpendicular to the axis of the rotational symmetry. A transaxial electrostatic mirror can provide high-quality TOF focusing of ions in energy simultaneously with their spatial focusing in two mutually perpendicular planes. Under certain conditions, in this mirror stigmatic spatial-TOF focusing (SSTOF) can be achieved.
The properties of TOF focusing in three-electrode transaxial mirror whose electrodes are plane-parallel plates separated by circular gaps were first studied in [1]. The geometrical and electrical parameters providing conditions of TOF focusing up to the second order under different modes of mirror operation were obtained by numerical calculations. However, the mode of spatial focusing of such a mirror has not been considered, which limits its application as an ion reflector of TOF mass spectrometer.
The aim of the present paper is to determine conditions of SSTOF focusing in transaxial mirrors and to use numerical calculations to study the possibility of using such mirrors in TOF mass spectrometers of high resolution and high sensitivity. Two variants of application of the transaxial mirror with stigmatic spatial TOF focusing in TOF mass spectrometer are considered. In the first variant, the transaxial mirror is used as the ion reflector in the typical scheme of TOF mass reflectron. In the second variant, the transaxial mirror simultaneously fulfills the function of ion reflector and corrector of aberrations caused by energy spread in the ion package formed by the ion source.
It should be noted that TOF chromatic aberration (TOFCA) is the problem of special interest among the problems of TOF focusing of beams of charged particles. This is explained by the fact that in the electron-optical systems with direct optical axis TOF geometric aberrations are reduced effectively by diaphragming. In this case TOFCA remains unchanged and imposes principal limitations on the quality of TOF focusing. Therefore we will further consider only these aberrations.
2. A Transaxial Ion Reflector
2.1. Conditions of Time-of-Flight Focusing
Let us introduce a rectangular coordinate system , the axis
, the axis 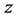 of which is aligned with the optical axis of the mirror, the plane
of which is aligned with the optical axis of the mirror, the plane ![]() coincides with its mean plane (horizontal plane), and the plane
coincides with its mean plane (horizontal plane), and the plane  coincides with the plane perpendicular to the mean plane (vertical plane).
coincides with the plane perpendicular to the mean plane (vertical plane).
According to [2], the time-of-flight of an ion of charge ![]() and mass
and mass![]() , moving along the optical axis of the mirror
, moving along the optical axis of the mirror ![]() from the initial plane
from the initial plane  to an arbitrary plane
to an arbitrary plane , taking into account values up to the third order of smallness can be written as
, taking into account values up to the third order of smallness can be written as
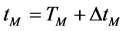 . (1)
. (1)
Here
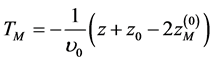 (2)
(2)
is the time-of-flight of the central particle,
 . (3)
. (3)
is the total TOFCA of the mirror, ![]() is the initial energy spread of ions,
is the initial energy spread of ions, 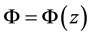 is the axial distribution of the electrostatic potential,
is the axial distribution of the electrostatic potential, 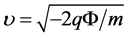 is the speed of the central particle, and
is the speed of the central particle, and
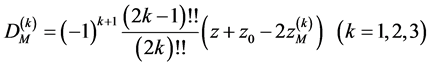 (4)
(4)
is the TOFCA coefficient of order![]() , where the quantities
, where the quantities  and
and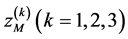 , determining the position of the effective plane of the mirror reflection and its reference planes of TOF focusing of order
, determining the position of the effective plane of the mirror reflection and its reference planes of TOF focusing of order![]() , respectively, are functions only of
, respectively, are functions only of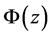 . Let us consider the particle moving along the axis
. Let us consider the particle moving along the axis ![]() with
with ![]() as the central particle. Here and below the subscript “0” denotes the values in the initial plane
as the central particle. Here and below the subscript “0” denotes the values in the initial plane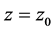 .
.
As it can be seen from (4), the condition of TOF focusing of ions by energy of order 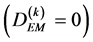
![]() is written as
is written as
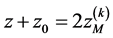 , (5)
, (5)
which means that TOF focusing is achieved when the plane  (the ground plane) and
(the ground plane) and 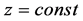 (the TOF image plane) are located symmetrically with respect to the plane
(the TOF image plane) are located symmetrically with respect to the plane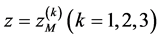 .
.
The plane  is called the main plane of TOF focusing of the mirror [3]. Taking (5) into account, let us rewrite (2) as
is called the main plane of TOF focusing of the mirror [3]. Taking (5) into account, let us rewrite (2) as
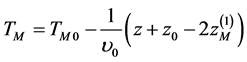 , (6)
, (6)
where
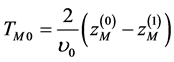 (7)
(7)
is the time interval between the moments of intersection of plane  by ions before and after reflection by the mirror. This time period is called the time interval of mirror focusing. The dependence of the time period of mirror focusing on its mass determines the value of its TOF mass dispersion
by ions before and after reflection by the mirror. This time period is called the time interval of mirror focusing. The dependence of the time period of mirror focusing on its mass determines the value of its TOF mass dispersion
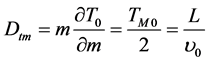 , (8)
, (8)
where
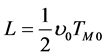 . (9)
. (9)
is the effective drift distance of the mirror.
If the condition
 (10)
(10)
is fulfilled simultaneously with (5), all TOFCA coefficients are equal to zero , i.e. the TOF focusing in energy up to third order is realized.
, i.e. the TOF focusing in energy up to third order is realized.
2.2. Conditions of Spatial Focusing
According to [2], locations of mutually conjugate planes  (the ground plane) and
(the ground plane) and  (image plane) are determined by the equation
(image plane) are determined by the equation
 . (11)
. (11)
Here 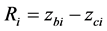 is the radius of the mirror curvature,
is the radius of the mirror curvature,  and
and  are
are ![]() coordinates of the center of the mirror curvature and its vertex, and the subscript
coordinates of the center of the mirror curvature and its vertex, and the subscript ![]() denotes the values in two mutually perpendicular planes
denotes the values in two mutually perpendicular planes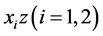 , respectively.
, respectively.
When the centers of mirror curvature in two mutually perpendicular planes coincide or the center of curvature in the mean plane of the mirror coincides with its vertex in the plane perpendicular to the mean plane, i.e. if
 or
or , (12)
, (12)
stigmatic spatial focusing (SSF) is realized in the transaxial mirror.
2.3. Conditions of Spatial-TOF Focusing
Solving the system of equations (5) and (11) we find the spatial-TOF condition for the mirror:
 . (13)
. (13)
The condition (13) determines the position of mutually conjugate planes 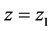 and
and , for which spatial and TOF focusing are fulfilled simultaneously. For the electrostatic mirror with the given field distribution on its axis, there is only one pair of mutually conjugate planes that satisfy this condition [3].
, for which spatial and TOF focusing are fulfilled simultaneously. For the electrostatic mirror with the given field distribution on its axis, there is only one pair of mutually conjugate planes that satisfy this condition [3].
As it is seen from (13), if the condition
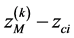 or
or  (14)
(14)
is fulfilled, spatial and TOF images of the object are formed in the same plane , i.e. spatial-TOF is fulfilled.
, i.e. spatial-TOF is fulfilled.
If conditions (5), (10) and (12) - (14) are fulfilled simultaneously, in the transaxial mirror the stigmatic spatial-TOF focusing (SSTOF) is realized.
2.4. Characteristics of a Three-Electrode Transaxial Mirror
In this section we used numerical calculations to determine the SSTOF conditions up to the second order in the three-electrode transaxial mirror (Figure 1). Each electrode of the mirror is a pair of parallel plates positioned symmetrically with respect to the median plane of the mirror.
Slits between the electrodes are cut along the arcs of concentric circles with the common centers of curvature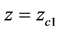 , radii
, radii![]() , where
, where ![]() is the coordinate
is the coordinate ![]() of the middle of the
of the middle of the ![]() - th gap
- th gap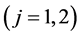 . Two modes of realization of SSF (12) conditions simultaneously with the TOF focusing of ions in energy up to the second order
. Two modes of realization of SSF (12) conditions simultaneously with the TOF focusing of ions in energy up to the second order  in such a mirror are considered. In the first mode SSTOF is achieved by superposition of the center of curvature in two mutually perpendicular planes, i.e. provided
in such a mirror are considered. In the first mode SSTOF is achieved by superposition of the center of curvature in two mutually perpendicular planes, i.e. provided .
.
In the second mode SSTOF is obtained by superposition of the center of curvature of the mirror in the mean plane 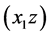 and its vertex in the perpendicular plane
and its vertex in the perpendicular plane , i.e. provided
, i.e. provided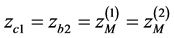 . The trajectories (T) in the vertical plane
. The trajectories (T) in the vertical plane 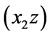 for these modes are shown in Figures 2 and 3. As it can be seen from these figures, when the trajectories pass through the center of curvature of the mirror their direct and inverse branches are the same, and when trajectories pass through its vertex their direct and inverse branches are symmetrical with respect to the optical axis of the mirror [3].
for these modes are shown in Figures 2 and 3. As it can be seen from these figures, when the trajectories pass through the center of curvature of the mirror their direct and inverse branches are the same, and when trajectories pass through its vertex their direct and inverse branches are symmetrical with respect to the optical axis of the mirror [3].
The relations between geometrical and electrical parameters of the mirror defining the SSTOF conditions in the first and second modes are shown in Tables 1 and 2, respectively. Here 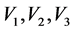 are the potentials of the first, second and third electrodes,
are the potentials of the first, second and third electrodes,  is the width of the second (middle) electrode,
is the width of the second (middle) electrode, ![]() is the distance between the electrode plates,
is the distance between the electrode plates, 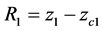 is the radius of the first circle. The values of geometric parameters are given
is the radius of the first circle. The values of geometric parameters are given

Figure 1. A scheme of a three-electrode transaxial mirror.
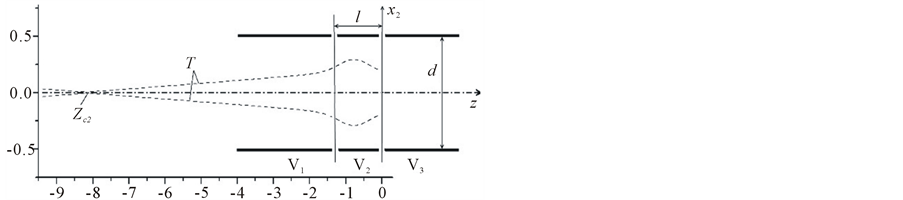
Figure 2. A course of the trajectories in the three-electrode transaxsial mirror![]() .
.

Figure 3. A course of the trajectories in the three-electrode transaxsial mirror![]() .
.
in units of![]() , the electrical values—in units of potential
, the electrical values—in units of potential . The origin of coordinates is located in the middle of the gap between the second and third electrodes.
. The origin of coordinates is located in the middle of the gap between the second and third electrodes.
As it seen from the above data, the effective drift distance of the mirror![]() , hence, its TOF mass dispersion (8) in the second mode is two-three times higher than in the first mode. Moreover, the second mode has a higher capacity.
, hence, its TOF mass dispersion (8) in the second mode is two-three times higher than in the first mode. Moreover, the second mode has a higher capacity.
2.5. Characteristics of a Four-Electrode Transaxial Mirror
In this section, the four-electrode transaxial mirror, the second and the third (middle) electrode of which have the same width, are considered. Due to higher variety of the field distribution, in such a mirror it is possible to get SSTOF of higher quality.
Using numerical calculations we obtained the relationships between geometric and electrical parameters of the mirror that determine the conditions of TOF focusing up to the third order  simultaneously with SSF
simultaneously with SSF , i.e. conditions
, i.e. conditions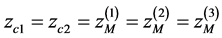 .
.
The results of calculations are presented in table 3, where  are the potentials of the first, second, third and fourth electrodes,
are the potentials of the first, second, third and fourth electrodes, 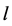 is the width of the second and third (middle) electrodes,
is the width of the second and third (middle) electrodes, ![]() ,
, ![]() ,
, ![]() and
and ![]() have the same meaning as in the previous modes. The origin of coordinates is located in the middle of the gap between the third and fourth electrodes.
have the same meaning as in the previous modes. The origin of coordinates is located in the middle of the gap between the third and fourth electrodes.
3. A Transaxial Corrector of Aberrations
3.1. Conditions of Compensation of the Energy Spread in the Ion Package Formed by the Ion Source
Let us consider the ion source consisting of the ionization region and the accelerating gap. Moving in the ion source, any ion with the initial energy 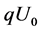 will increase its own energy up to [4]:
will increase its own energy up to [4]:
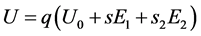 . (15)
. (15)
Here 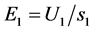 is the electric field strength in the ionization region of width
is the electric field strength in the ionization region of width![]() , produced by the pushing-out pulse
, produced by the pushing-out pulse ,
, 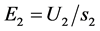 is the field strength in the accelerating gap of width
is the field strength in the accelerating gap of width  produced by the accelerating potential difference
produced by the accelerating potential difference![]() ,
, ![]() is the path traveled by the ion in the field of the pushing-out pulse. At the outlet of the ion source, ions have different energies due to the two factors: 1) different initial ion energies
is the path traveled by the ion in the field of the pushing-out pulse. At the outlet of the ion source, ions have different energies due to the two factors: 1) different initial ion energies 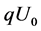 caused by thermal scattering, 2) different paths
caused by thermal scattering, 2) different paths ![]()
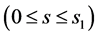 . Therefore, we can rewrite (15) in the form
. Therefore, we can rewrite (15) in the form
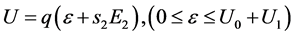 , (16)
, (16)
where ![]() is the energy spread of ions in the package formed by the ion source.
is the energy spread of ions in the package formed by the ion source.
Taking into account (16) the time-of-flight of an ion in the ion source can be written as
 . (17)
. (17)
By simple transformations (17) can be represented in the form
 , (18)
, (18)
where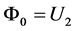 .
.
Expanding by powers of the small value 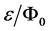 (relative energy spread), and limiting by the order of smallness of not lower than the third order, we can write (18) in the form
(relative energy spread), and limiting by the order of smallness of not lower than the third order, we can write (18) in the form
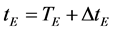 , (19)
, (19)
where
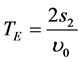 (20)
(20)
is time-of-flight of the central  ion,
ion,  is the total TOFCA of the ion source determined by the equation
is the total TOFCA of the ion source determined by the equation

(21)
As it is seen from (21), under the condition
 (22)
(22)
the term of the series proportional to , which makes the greatest contribution to the total TOFCA of the ion source, vanishes. The remaining part of aberrations of the ion source can be compensated by aberrations of the electrostatic mirror equal in magnitude and opposite in sign.
, which makes the greatest contribution to the total TOFCA of the ion source, vanishes. The remaining part of aberrations of the ion source can be compensated by aberrations of the electrostatic mirror equal in magnitude and opposite in sign.
In the combined system consisting of the ion source and the electrostatic mirror, the total time-of-flight of the ion (in case the end of the accelerating interval of the ion source coincides with the initial plane  of the mirror) taking into account (1) - (4) and (19) - (22) can be written as
of the mirror) taking into account (1) - (4) and (19) - (22) can be written as
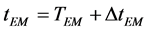 , (23)
, (23)
where
 , (24)
, (24)
 . (25)
. (25)
Here
 (26)
(26)
is the TOFCA coefficient of the combined system of order![]() ,
,
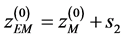 , (27)
, (27)
 . (28)
. (28)
From (26) it follows that in the combined system the condition of the k-th order of TOF focusing of ions in energy  is determined as
is determined as
 , (29)
, (29)
which means that TOF focusing is achieved when the plane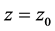 , coinciding with the end of the second accelerating gap, and plane
, coinciding with the end of the second accelerating gap, and plane 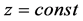 where the ions are recorded, are located symmetrically relative to the plane
where the ions are recorded, are located symmetrically relative to the plane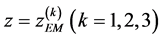 .
.
By analogy with the mirror let us call the plane 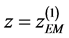 the main plane of TOF focusing of the combined system. Taking into account (29) we can rewrite (24) in the form
the main plane of TOF focusing of the combined system. Taking into account (29) we can rewrite (24) in the form
 , (30)
, (30)
where
 (31)
(31)
is the time interval of focusing of the combined system.
TOF dispersion in mass and the effective drift distance of the combined system are determined by formulas similar to (8) - (9).
3.2. TOF Mass-Reflectron with Transaxial Corrector of Aberrations
As an example calculations for TOF mass reflectron have been made, where the role of aberration corrector is played by the four-electrode transaxial mirror with two middle electrodes of the same width (Figure 4). The origin of coordinates is located in the middle of the gap between the third and fourth electrodes. The results of calculations are presented in Table4
Potentials on the second , third
, third  and fourth
and fourth  electrodes of the mirror, the width of its middle electrode
electrodes of the mirror, the width of its middle electrode , coordinates
, coordinates ![]() of the center of curvature of the mirror
of the center of curvature of the mirror ![]() and the effective drift distance
and the effective drift distance ![]() were calculated for different values of width
were calculated for different values of width  of the accelerating gap of the ion source for the condition
of the accelerating gap of the ion source for the condition
 . (32)
. (32)
When this condition is fulfilled in the plane  coinciding with the plane
coinciding with the plane , in the combined system TOF focusing up to the third order and stigmatic spatial focusing are achieved simultaneously.
, in the combined system TOF focusing up to the third order and stigmatic spatial focusing are achieved simultaneously.
In this case, the resolution of mass reflectron
 , (33)
, (33)
will be limited only by the aberrations of the fourth and higher orders
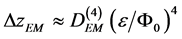 , (34)
, (34)
where  is the width of the packet of ions in the detector plane,
is the width of the packet of ions in the detector plane, 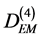 is the 4-th order TOFCA coefficient.
is the 4-th order TOFCA coefficient.
It should be noted that in the conventional scheme of mass reflectron the resolution is limited by the ion packet width in the primary time focus [5]:
 , (35)
, (35)
where  is the focus distance of the ion source.
is the focus distance of the ion source.

Figure 4. TOF mass reflectron with transaxial corrector of aberrations.
It follows that, other things being equal, in this mass reflectron the width of the ion packet in the detector plane is significantly (by an order or more) smaller than the width of the ion packet in the primary focus of the conventional mass-reflectron. This effect is caused by the compression of the initial width of the ion package by the mirror.
4. Conclusions
Application of the transaxial mirror as the ion deflector of the mass reflectron has certain advantages. The transaxial mirror has a smaller size in the direction perpendicular to its mean plane than that of the rotationallysymmetric mirror. Moreover, it does not have aberrations of oblique beams typical of the mirror with rotational symmetry and caused by the large angle of inclination of trajectories to the optical axis of the mirror.
The use of transaxial mirror as a corrector of the initial energy spread in the ion package formed by an ion source opens a new direction in the TOF mass spectrometry.
This research was supported by grant number No. 055/GF3 under the program of the Ministry of Education and Science of the Republic of Kazakhstan.
REFERENCES
- S. B. Bimurzaev, K. N. Temirbekova and E. M. Yakushev, Soviet/Radiotekhnika i Elektronika, Vol. 43, 1998, pp. 331-335.
- S. B. Bimurzaev, R. S. Bimurzaeva and B. T. Sarkeev, Soviet/Radiotekhnika i Elektronika, Vol. 36, 1991, pp. 2186-2195.
- E. M. Yakushev, Advances in Imaging and Electron Physics, Vol. 178, 2013, pp. 147-247. http://dx.doi.org/10.1016/B978-0-12-407701-0.00003-0
- W. C. Wiley and I. H. McLaren, Review of Scientific Instruments, Vol. 26, 1955, pp. 1150-1157. http://dx.doi.org/10.1063/1.1715212
- B. A. Mamyrin, V. I. Karataev, D. V. Shmikk and V. A. Zagulin, Soviet/Journal of Experimental and Theoretical Physics, Vol. 64, 1973, pp. 82-89.



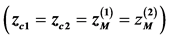 .
.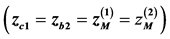 .
.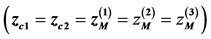 .
. .
.