Journal of Modern Physics
Vol.4 No.11(2013), Article ID:40053,6 pages DOI:10.4236/jmp.2013.411186
Gravitational Force between the Black Hole & Light Particle in AGN
1University Department of Physics, Tilka Manjhi Bhagalpur University, Bhagalpur, India
2Department of Physics, Marwari College, Tilka Manjhi Bhagalpur University, Bhagalpur, India
3Department of Education, Sunderwati Mahila College, Bhagalpur, India
4Department of Physics, Bhagalpur College of Engineering, Bhagalpur, India
5Department of Physics, G. L. A. College, Daltanganj, India
Email: *dipomahto@hotmail.com
Copyright © 2013 Md Shams Nadeem et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 10, 2013; revised September 12, 2013; accepted October 11, 2013
Keywords: Gravitational Force; Event Horizon; Singularity and AGN
ABSTRACT
In this research paper, we have used the formula for gravitational force acting between the black hole and light particle passing near the radius of event horizon of black holes (Mahto et al. 2013) to calculate their values for different test of black holes existing in Active Galactic Nuclei (AGN) and compared with that of the black holes in XRBs.
1. Introduction
Isaac Newton proposed universal law of gravitation in 1687 which stated that every particle in the universe exerts a force on every particle along the line joining their centres. The magnitude of the force is directly proportional to the product of the masses of the two particles, and inversely proportional to the square of the distance between them [1].
In 1915, Albert Einstein demonstrated better theory of gravitation on the basis of general relativity, which has overcome the limitations of Newton’s law of universal gravitation [2,3].
In 1997, L. Lerner discussed the problem of the deflection of light in a medium with varying refractive index applied to the motion of light in a weak Schwarzschild gravitational field [3,4].
In 2002, Ph. M. Kanarev calculated the gravitational radius of a black hole using the frame of the space-mattertime unity that took into account the wavelength of the electromagnetic radiation [5].
In 2013, Dipo Mahto et al. derived the formula for gravitational force acting between the black hole and light particle passing near the radius of event horizon of black holes and calculated their values of different test black holes existing in XRBs [3].
In the present work, we have used the formula for gravitational force acting between the black hole and light particle passing near the radius of event horizon of black holes as proposed by Dipo Mahto et al. (2013) and calculated their values of different test of black holes existing in Active Galactic Nuclei (AGN). We have also compared this work with that of the black holes existing in X-ray binaries (XRBs).
2. Theoretical Discussion
2.1. Black Hole and Singularity
After the death of a red giant star by super nova explosion, the black hole has been formed and its whole mass is squeezed into a single point. At this point, both space and time stop and its gravity becomes so enough and abnormal that nothing can escape from it.
The point at the center of a black hole is called a singularity. Within a certain distance of the singularity, the gravitational pull is so strong that nothing—not even light—can escape. That distance is called the event horizon. The event horizon is not a physical boundary but the point-of-no-return for anything that crosses it. When people talk about the size of a black hole, they are referring to the size of the event horizon. The more mass the singularity has, the larger the event horizon [6].
2.2. Formula for the Gravitational Force Acting between the Black Hole and Light Particle
Dipo Mahto et al. derived the formula for gravitational force acting between black hole and the light particles on the basis of Newton’s universal laws of gravitation (F = Gm1m2/r2) using Einstein’s mass-energy equivalence relation (E = mc2), quantum theory of radiation (E = hν) and Schwarzschild radius for Non-spinning and spinning black holes as given by the following equations [3].
 (1)
(1)
(for Non-spinning black holes)
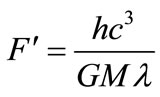 (2)
(2)
(for spinning black holes)
where 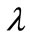 be the wavelength of radiation, i.e. electromagnetic wave, specially visible wave, because electromagnetic radiation with a wavelength between approximately 400 nm and 700 nm is directly detected by the human eye and perceived as visible light. Since the invisibility of black holes occurs due to the presence of visible waves. A light adapted eye generally has maximum sensitivity at around 555 nm, in the green region of the optical spectrum [3]. Due to this reason, we have used
be the wavelength of radiation, i.e. electromagnetic wave, specially visible wave, because electromagnetic radiation with a wavelength between approximately 400 nm and 700 nm is directly detected by the human eye and perceived as visible light. Since the invisibility of black holes occurs due to the presence of visible waves. A light adapted eye generally has maximum sensitivity at around 555 nm, in the green region of the optical spectrum [3]. Due to this reason, we have used  in calculations.
in calculations.
The Equntions (1) and (2) represent the gravitational force acting on light particle due to non-spinning and spinning black holes.
The importance and significance of the three fundamental constants of nature—the speed of light (c), Planck’s constant (h) and Newton’s gravitational constant (G) can seen in the research paper [3].
In this new conception, space time was no longer a spectator of events but itself a dynamical participant that changed in response to the amount of matter present. It was no longer flat and Euclidean but curved in much the same way as the surface of the earth is round and curved. This curvature of space time is, according to Einstein, the origin of gravity [7].
For convenience, we shall use G = h = c = 1, in our research work, then Equations (1) and (2) are transformed as [3]
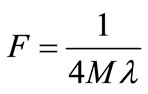 (3)
(3)
and
 (4)
(4)
with the help of equation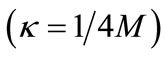 , the Equations (3) and (4) can be expressed in terms of surface gravity as given below.
, the Equations (3) and (4) can be expressed in terms of surface gravity as given below.
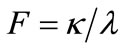 (5)
(5)
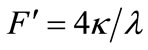 (6)
(6)
The term M and 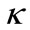 stand for the mass and surface gravity of black holes respectively. The role of surface gravity
stand for the mass and surface gravity of black holes respectively. The role of surface gravity 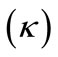 may be seen in the research paper [3,7,8].
may be seen in the research paper [3,7,8].
The surface gravity  of a black hole is constant on horizon. Hence for the region of event horizon of black holes, Equations (5) and (6) can be written as
of a black hole is constant on horizon. Hence for the region of event horizon of black holes, Equations (5) and (6) can be written as
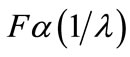 (7)
(7)
The above relation shows that the force of attraction acting between black hole and light particle is inversely proportional to the wavelength of electromagnetic wave coming towards the event horizon of black holes. Hence the electromagnetic radiations of longer wavelengths are attracted much lesser than that of others [3].
2.3. Different Aspects of Surface Gravity
Let us now consider Reissner-Nordstrom geometry, describing a static electrically charged black hole with the following line element.
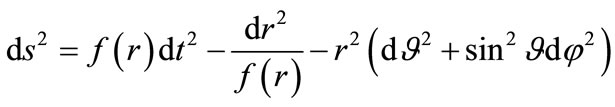 (8)
(8)
where
 (9)
(9)
and
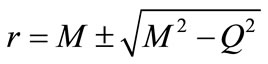 (10)
(10)
here the parameter r denotes two possible horizon called outer and inner horizons for sign (+) and (−) respectively [3,8,9].
The Equation (9) representing the space time describes a black hole, i.e. there is a horizon, when M > Q. For M < Q there is no horizon and the space-time has a naked singularity. The case M = Q is called an external black hole. For , the temperature reduces to the Schwarzschild result. However, as
, the temperature reduces to the Schwarzschild result. However, as 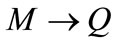 the surface gravity
the surface gravity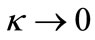 , with
, with  for M = Q. Therefore, the temperature vanishes for an external black hole [3,10].
for M = Q. Therefore, the temperature vanishes for an external black hole [3,10].
The above explanation shows that the gravitational force acting between a static electrically charged black hole and light particle is zero in the case of  as
as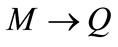 .
.
Equation (6) holds for spinning black holes, hence surface gravity  in this case is given by the Kerr solution [11].
in this case is given by the Kerr solution [11].
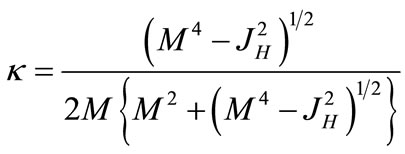 (11)
(11)
For maximally spinning black holes, JH = M2, the surface gravity 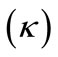 from equation is given by [3].
from equation is given by [3].
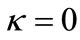 (12)
(12)
For Reissner-Nordstrom black holes, the temperature is still given by following eqn
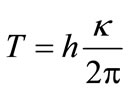 (13)
(13)
This means that for maximally spinning black holes, the surface gravity becomes to zero and temperature should vanish in the case of a static electrically charged black hole.
3. Data in Support of Mass of Black Holes in AGN
There are two categories of Black holes classified on the basis of their masses clearly very distinct from each other, with very different masses M ~ 5 20 Mʘ for stellar— mass Black holes in X-ray binaries and M ~ 106 - 109.5 Mʘ for super massive black holes in Galactic Nuclei [8,12] and masses in the range 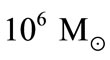 to
to  have been estimated by this means in about 20 galaxies [12]. The most viable scenario for modeling of active galactic nuclei includes a super massive black hole with the mass
have been estimated by this means in about 20 galaxies [12]. The most viable scenario for modeling of active galactic nuclei includes a super massive black hole with the mass  accreting the galaxian matter from its vicinity [13]. At the distance of the Virgo cluster, 15 Mpc, the sphere of influence of a
accreting the galaxian matter from its vicinity [13]. At the distance of the Virgo cluster, 15 Mpc, the sphere of influence of a  super-massive black holes (SBH) would shrink to a projected radius of 0.07, not only well beyond the reach of any ground based telescope, beyond even HST capabilities [14]. Assuming an isotropic, spherically symmetric system, Sargent et al. detected a central dark mass
super-massive black holes (SBH) would shrink to a projected radius of 0.07, not only well beyond the reach of any ground based telescope, beyond even HST capabilities [14]. Assuming an isotropic, spherically symmetric system, Sargent et al. detected a central dark mass 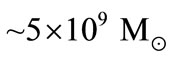 within the inner 110 pc of M87 [15].
within the inner 110 pc of M87 [15].
Assuming the disk is Keplerian, Greenhill and Gwinn estimated the mass enclosed within 0.65 pc to be 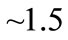
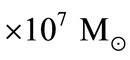 . Although the NGC 1068 observations provide only par
. Although the NGC 1068 observations provide only par 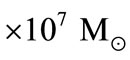 tial evidence for the presence of a massive black hole, they do give us perhaps the clearest picture of the centre of an AGN [14].
tial evidence for the presence of a massive black hole, they do give us perhaps the clearest picture of the centre of an AGN [14].
A kinematical study of NGC4261 followed in 1996, claiming a 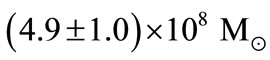 [16]. In NGC 4041, acquiescent Shc spiral, Marconi et al. (2003) remark that the systematic blue shift of the disk relative to systemic velocity might be evidence that the disk is kinematically decoupled. They conclude that only an upper limit of
[16]. In NGC 4041, acquiescent Shc spiral, Marconi et al. (2003) remark that the systematic blue shift of the disk relative to systemic velocity might be evidence that the disk is kinematically decoupled. They conclude that only an upper limit of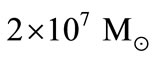 , can be put on the central mass. Cappellari et al. (2002) conclude that non-gravitational motions might indeed be present in the case of IC 1459, for which the ionized gas shows no indication of rotation in the inner 1”. IC 1459 is the only galaxy for which a SBH mass estimate exists based both on gas and stellar kinematics. Three-integral models applied to the stellar kinematics produce
, can be put on the central mass. Cappellari et al. (2002) conclude that non-gravitational motions might indeed be present in the case of IC 1459, for which the ionized gas shows no indication of rotation in the inner 1”. IC 1459 is the only galaxy for which a SBH mass estimate exists based both on gas and stellar kinematics. Three-integral models applied to the stellar kinematics produce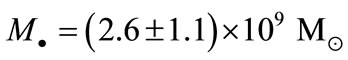 , while the gas kinematics produces estimates between a few
, while the gas kinematics produces estimates between a few 
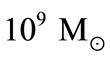 , depending on the assumptions made regarding nature of the gas velocity dispersion [14].
, depending on the assumptions made regarding nature of the gas velocity dispersion [14].
With the important exception of the Balbus-Hawley (1998) instability, the major developments in recent years have been observational or at least strongly motivated by observations. Masses of “central dark object” have been estimated in about forty cases, using stellar dynamics, emission lines of orbiting gas and, most accurately, using water masers. They range from 
 and, in many cases, the compactness is sufficient to rule out star clusters with confidence [17].
and, in many cases, the compactness is sufficient to rule out star clusters with confidence [17].
Most detected SBHs are in the 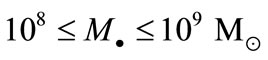 range, there are no detections below 106 Mʘ (the “building block” range) or above
range, there are no detections below 106 Mʘ (the “building block” range) or above 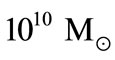 (the brightest quasar range), and even the
(the brightest quasar range), and even the  range is very poorly sampled [14].
range is very poorly sampled [14].
On the basis of the data mentioned above, we have calculated the gravitational force between black holes and light particles in AGN for different test non-spinning and spinning black holes listed in the Tables 1 and 2 respectively.
4. Result and Discussion
In this paper, we have used a formula for gravitational force  for non-spinning black holes and
for non-spinning black holes and  for spinning black holes acting between the black hole and light particle passing near the radius of event horizon of black holes to calculate the values of different test black holes existing in Active Galactic Nuclei (AGN). To discuss the nature of gravitational force acting between the black hole and light particle passing near the radius of event horizon with the wavelength, graphs have been plotted between:
for spinning black holes acting between the black hole and light particle passing near the radius of event horizon of black holes to calculate the values of different test black holes existing in Active Galactic Nuclei (AGN). To discuss the nature of gravitational force acting between the black hole and light particle passing near the radius of event horizon with the wavelength, graphs have been plotted between:
1) The radius of the event horizon  of different test non-spinning black holes and their corresponding values of gravitational force acting between the black hole and light particle passing near the radius of event horizon of black holes in AGN (Figure 1).
of different test non-spinning black holes and their corresponding values of gravitational force acting between the black hole and light particle passing near the radius of event horizon of black holes in AGN (Figure 1).
2) The the radius of event horizon 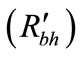 of different test spinning black holes and their corresponding values of gravitational force acting between the black hole and light particle passing near the radius of event horizon of black holes in AGN (Figure 2).
of different test spinning black holes and their corresponding values of gravitational force acting between the black hole and light particle passing near the radius of event horizon of black holes in AGN (Figure 2).
In the Tables 1 and 2, the gravitational forces acting between different test black holes and light particle have been calculated for given values of the wavelength 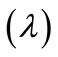 and mass of different black holes ranging from 1 × 106 Mʘ to
and mass of different black holes ranging from 1 × 106 Mʘ to  in the case of non-spinning and spinning black holes with the help of Equations (3) and (4)
in the case of non-spinning and spinning black holes with the help of Equations (3) and (4)


Table 1. Gravitational force between non-spinning black holes & light particles in AGN.


Table 2. Gravitational force between spinning black holes & light particles in AGN.

Figure 1. The graph plotted between the radius of event horizon and gravitational force between different test non-spinning black holes & light particles in AGN.

Figure 2. The graph plotted between the radius of event horizon and gravitational force between different test spinning black holes & light particles in AGN.
respectively.
From Figures 1 and 2 and Tables 1 and 2, it is clear that initially the gravitational force acting between the black holes and light particle decreases rapidly with increase the radius of the event horizon from 0.0295 × 1011 m to 0.2655 × 1011 m ( to
to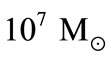 ) for non-spinning and 0.01475 × 1011 m to 0.1327 × 1011 m (
) for non-spinning and 0.01475 × 1011 m to 0.1327 × 1011 m ( to
to ) for spinning black holes and then decreases gradually for a given wavelength of radiation.
) for spinning black holes and then decreases gradually for a given wavelength of radiation.
From the data available in the Tables 1 and 2, it is also clear that the spinning black hole of the same mass has more gravitational force than that of non-spinning black holes for the same frequency/wavelength of radiation in AGN. In this case, the nature of graph differs slightly to that of the graph plotted for XRBs (Mahto et al. 2013). This is due higher successive difference in the mass of black holes to that of the mass of black holes in XRBs. In the both cases either for non-spinning or spinning black holes in AGN, the nature of graph is similar showing that most of the characteristics of both of black holes are the same. Equations (3) and (4) also justify the above facts. Equations (5) and (6) shows that the light particle (light wave) of shorter wavelength has attracted more than that of longer wavelength for constant surface gravity in XRBs as well as AGN.
5. Conclusions
In course of the present research work, we have concluded that most of the characteristics of non-spinning or spinning black holes in Active Galactic Nuclei (AGN) are the same to that of cases of X-ray binaries (XRBs), but differing in some sense.
1) The gravitational force acting between the black holes and light particle decreases rapidly with increasing the radius of the event horizon, whereas in the case of XRBs, the gravitational force acting between the black holes and light particle decreases slowly with increasing the radius of the event horizon.
2) The spinning black hole of the same mass has more gravitational force than that of non-spinning black holes in XRBs as well as AGN.
3) For the both cases of XRBs and AGN, the light particle (light wave) of shorter wavelength has attracted more than that of longer wavelength for constant surface gravity.
REFERENCES
- I. Newton, “The Principia (The Mathematical Principles of Natural Knowledge),” 1667.
- P. G. Bergmann, “Introduction to the Theory of Relativity,” Prentice-Hall of India, New Delhi, 1969.
- D. Mahto, M. S. Nadeem, M. Ram and K. Vineeta, Journal of Gravity, Vol. 2013, 2013, Article ID: 222676. http://dx.doi.org/10.1155/2013/232676
- L. Lerner, American Journal of Physics, Vol. 65, 1997, pp. 1194-1196.
- Ph. M. Kanarev, Journal of Theoretics, Vol. 4, 2002, pp. 1-7.
- C. Miller, “Black Holes and Neutron Stars,” 17 September 2003.
- A. Dabholkar, Current Science, Vol. 89, 2005, p. 25.
- D. Mahto, V. Prakash, U. Prasad, B. K. Singh and K. M. Singh, Astrophysics and Space Science, Vol. 343, 2012, pp. 153-159. http://dx.doi.org/10.1007/s10509-012-1219-y
- K. Nozari and B. Fazlpour, Acta Physica Polonica B, Vol. 39, 2008, pp. 1364, 1367, 1372.
- J. Transchen, “An Introduction to Black Hole Evaporation,” 2000. arXiv: gr-qc/0010055V1.
- J. M. Bardeen, B. Carter and S. W. Hawking, Communications in Mathematical Physics, Vol. 31, 1973, pp. 161- 170.
- R. Narayan, “Black Holes in Astrophysics,” 2005. arXiv: gr-qc/0506078v1.
- G. Madejski, “Black Holes in Active Galactic Nuclei,” SLAC-PUB-9702, 2003.
- L. Ferrarese and H. Ford, Space Science Reviews, Vol. 116, 2055, pp. 523-624. http://dx.doi.org/10.1007/s11214-005-3947-6
- W. L. W. Sargent, et al., The Astrophysical Journal, Vol. 221, 1978, p. 731. ttp://dx.doi.org/10.1086/156077
- L. Ferrarese, H. C. Ford and W. Jaffe, The Astrophysical Journal, Vol. 470, 1996, p. 444. http://dx.doi.org/10.1086/177876
- R. D. Blandford, Astrophysics and Space Science, Vol. 261, 1999, pp. 245-252. http://dx.doi.org/10.1023/A:1002093710287
NOTES
*Corresponding author.

