Journal of Modern Physics
 Vol.4 No.2(2013), Article ID:28314,4 pages DOI:10.4236/jmp.2013.42031

Impacts of Opinion Propagation on Social Balance*

Songlin Zhang1,2, Lixue Chen1, Dong Hu1, Yuefei Guo3

1School of Computer Science, Southwest Petroleum University, Chengdu, China

2Department of Computer Engineering, Sichuan College of Architectural Technology, Deyang, China

3Department of Electrical Engineering and Automation, Shanxi Polytechnic College, Taiyuan, China

Email: songlin_zhang@yeah.net

Received November 23, 2012; revised December 25, 2012; accepted January 3, 2013

Keywords: Opinion Diffusion; Relationship Evolution; Social Balance; Complex Network; Coevolution

ABSTRACT

In social networks, opinions diffusion often leads to relationships evolution. Then changes of relationships result in the change of balance degree of social system. We simulate the opinion diffusion on Barabási & Albert (BA) network and Watts & Strogatz (WS) network to study the effects of the two types of networks, dynamical parameters and structural parameters on the balance degree of system. We employ the spectral analysis to quantify the balance degree of system before and after opinion propagation. The result reveals that it is very similar effect of BA networks and WS networks on it. However, it is opposite effects between dynamical parameters and structural parameters. The balance degree of system is proportional to the two dynamical factors 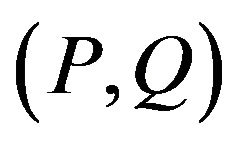at initial state and always inversely proportional to the two structural factors 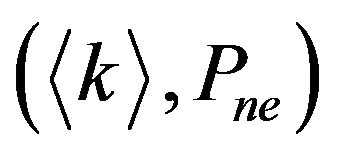at initial and convergence state.

1. Introduction

In a community, opinion propagation always impacts interpersonal relationships in some degree. It has been a challenge for researchers to figure out the rule and the characteristic about the impact by opinion propagation in different social structure. The network approach has contributed significantly to our understanding of the structure, function, and response of various complex systems, from genetic transcriptions to human societies [1,2]. In the case of human social systems, this approach was introduced by social scientists and they established important concepts and tools to study them [3,4].

In 1998 and 1999, Watts and Strogatz [5], Barabási and Albert [6] successively discovery the properties of small-world and scale-free, which many natural and artificial complex networks have. Based on the discovery, more and more researchers were attracted to use the Barabási & Albert (BA) networks and Watts & Strogatz (WS) networks to simulate the social networks [7,8]. While many opinion models have been introduced to simulate the process of opinion diffusion on complex networks: the Sznajd model [9], the voter model [10,11], the majority rule model [12,13], the social impact model [14], the bounded-confidence model [15], to name a few.

More researches focus on the changes of opinion by propagation than the changes of social relationship. In this paper, we quantify the changes of relationship affected by opinion diffusion on BA and WS networks in combination of two classes of parameters (dynamical parameters, structural parameters).

We employ the Heider theory [16] of structural balance (i.e., social balance) to evaluate social relationship. Let us firstly recall the notion of structural balance [16]. Suppose we have three entities (individual or agents): A, B, and C; each pair of distinct entities has an edge labeled + that denotes a positive sentiment or—that indicates a negative sentiment (all pair-wise relationships will be symmetric in our discussion: the sentiment that A displays to B is precisely the sentiment that B holds to A).

Clearly, a triad (3-cycle) with all three edges positive can be considered stable or balanced. Heider [16,17] also postulates the triad with exactly odd negative edge to be unbalanced and the unbalance triad trends to be balance. A network is balanced if each constituent triad is balanced [16-18]. An ostensibly more general definition of balanced network is that every cycle in the network is balanced. Cartwright et al. [19] extended and generalized the balance theory from 3-circle to n-circle (n ≥ 3). They postulates that n-circle with odd negative edge is also unbalanced.

Cartwright et al. [19] gave a basic method to measure the balance degree of the whole network: calculating the faction of unbalance circle. Later, Jérôme Kunegis et al. [20] suggested the spectral analysis method and Giuseppe Facchetti et al. [21] presented the energy function method. In this study, we use the spectral analysis method to calculate the smallest eigenvalue to measure the balance degree of the whole network. The smaller the smallest eigenvalue is, the more stable the whole social system is and the more harmonious the social relationships are, vice versa.

2. The Model

Let us consider opinion synchronous diffusion1 on BA and SW networks.

2.1. Opinion Model

Each of N vertices denotes an individual and each of M links denotes a relationship between two individuals in the network. We consider Oi possible opinions of which every individual must hold one and two relationships (called +1 and −1) denote positive sentiment (friends) and negative sentiment (enmities), according to balance theory. Opinion model in this study is the majorityfriends-rule model extending the majority-rule model [12, 13]. It assumes that individuals preferentially follow the friends instead of following the crowd (the majority-rule2) in their opinion update. In each step, every vertex has the same opportunity to update its opinion or relations by the flowing rules.

1) Majority friends’ preference (MFP): with probability P, the focal individual accepts the specific opinion held by a majority of its friends (i.e., the opinion is the one or one of that has the largest supporter among the friends). If the specific opinion is more than one, random one of them is chosen. We call this process Q action.

2) Cognitive consistence (CC) [22]: with probability 1-P, the focal individual updates (keeps or flips) its relationship. It will keep the sign of edge if the focal pair is cognitive consistence: holding the same opinion with positive (+1) relation or different opinions with the negative (−1) relation. On the country, an edge will flip the sign if the focal pair is cognitive inconsistence: the same opinion hold by focal pair individual with negative (−1) relation or conversely. When flipping is activated, with likelihood Q, the focal individual will flip all of links to neighbors, or with likelihood 1-Q, it will flip random one of links to neighbors. We call these processes Q action and 1-Q action.

Repeating above steps, the system will converge to consensus state. The consensus state has two sub-states: one is opinion consensus sub-state; another is relation consensus sub-state. They respectively represents that all opinions and all relations currently hold by all individuals do not change over time. After reaching the two substates, the system can only reach consensus state. It also claims that the coevolution between opinions and relations has been completed.

2.2. Parameters

The two networks (BA WS) which have same parameters and scopes of parameters. The total number (N) of vertices and the initial number 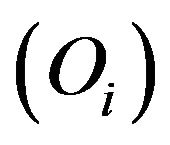of opinions are fixed. The type of variable has two: structural parameters and dynamical parameters. Structural parameters include average degree 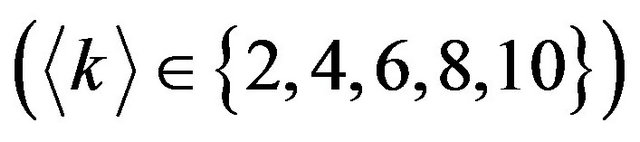and proportion of negative edge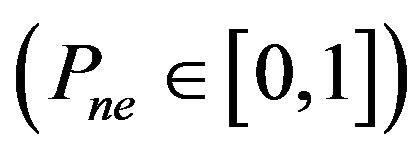. Dynamical parameters is the probability of opinions propagation 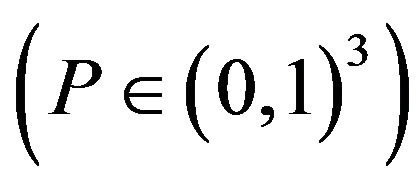and the likelihood of relations evolution.

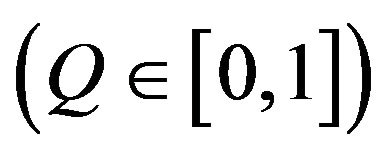3. Numerical Results

In this section, we study effects of the two kinds of parameters on the balance degree of networks in initial state and convergence state.

3.1. Initial State

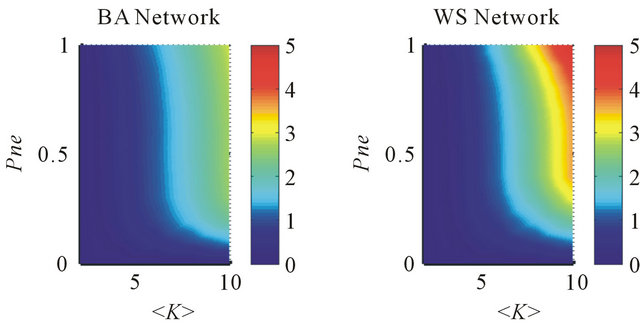
As it shown in Figure 1, the effect of 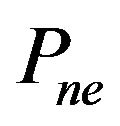and on the balance degree of networks is consistent: the balance degree decreases with their increasing. It suggests structural parameters are negative factors to the stability of networks. The difference between them is that the effects of 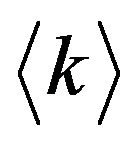is stronger than that of 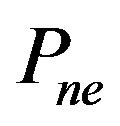in the same rate of increasing. Figure 1 also shows that the effects on the

(a)                             (b)

Figure 1. The effects of structural parameters variations on the balance degree of BA and WS network in initial state. The right color bar indicates the value of the smallest eigenvalue of networks. The color of data point which is closer to blue/red implies the smallest eigenvalue is smaller/bigger (i.e., the balance degree of relations in networks is smaller/bigger).

balance degree between BA and WS networks are a little difference: BA network is generally more stable than WS network under the same conditions.

3.2. Convergence State

Generally, the balance degree of the two networks is proportional to dynamical parameters (Figures 2(a) and (b)), but inversely proportional to structural parameters (Figures 2(c) and (d)).

With the increasing of dynamical parameters, the probability of eliminating inconsistence will also increase and the system will trend to balance. To dynamical parameters, P is the major and Q is the minor because P is apparently greater impact on the balance degree of networks than Q. P value become the bigger, positive edges probabilistically exit the more in networks, leading to the more balance circles in networks. So the balance degree of system will enhance. It may be reflect that relations will be more harmonious in social networks when positive relations are more and more.

With the increase of Q value, the balance degree of system will increase in trend, but not in strict. There are two reasons to explain it. One is that Q and 1-Q action happen in the conditional probability of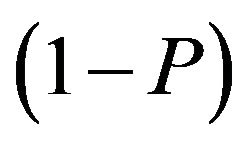. So occurrence probability of Q and 1-Q action is usually smaller than P action (as Equation (1)).

(1)

The other is that though Q and 1-Q action both eliminated discordant state, the results of them maybe increase positive edges or negative edges. Except when is

Figure 2. The effects of dynamical parameters (P, Q) and structural parameters variations on the balance degree of BA and WS network in converge state. The indication of color is same as Figure 1.

close to 1, the probability of increasing positive edges is bigger than that of negative edges in the edges evolving way of CC rule, for there is always much more opinion consensus than no consensus in networks when opinion propagating by MFP rule. So it is more advantage to the balance of system than unbalance of it in probability.

However, the effects of structural parameters are contrary to that of dynamical parameters: the balance degree of system drops down when structural parameters rise. The reason of the two structural parameters is respectively that: the rising of results in increasing of negative edges and circles in networks, finally leads to decreasing of the balance degree of system. In the same way, the increasing of leads to the worse of the balance degree of system.

4. Conclusion

In this paper, we simulate the coevolution of opinions and relations on BA and WS networks by MFP and CC rule, trying to study the effects of two kinds of parameter (dynamic structure) and two types of networks (BA WS) on the system balance. It is found that the effect of two kinds of parameter on the system degree is opposite and that of two types of networks is similar.

5. Acknowledgements

Songlin Zhang acknowledges the support from Graduate Innovation Foundation of Southwest Petroleum University, GIFSB0707.

REFERENCES

  1. M. E. J. Newman, A.-L. Barabási and D. J. Watts, “The Structure and Dynamics of Networks,” Princeton Univer-sity Press, Princeton, 2006.
  2. G. Caldarelli, “Scale-Free Networks: Complex Webs in Nature and Technology,” Oxford University Press, Oxford, 2007. doi:10.1093/acprof:oso/9780199211517.001.0001
  3. M. Granovetter, “Economic Action and Social Structure: The Problem of Embeddedness,” American Journal of Sociology, Vol. 91, No. 3, 1985, pp. 481-510. doi:10.1086/228311
  4. S. Wasserman and K. Faust, “Social Network Analysis: Methods and Applications,” Cambridge University Press, Cambridge, 1994. doi:10.1017/CBO9780511815478
  5. D. J. Watts and S. H. Strogatz, “Collective Dynamic of Small World Network,” Nature, Vol. 393, No. 6684, 1998, pp. 440-442. doi:10.1038/30918
  6. A.-L. Barabási and R. Albert, “Emergence of Scaling in Network,” Science, Vol. 286, No. 5439, 1999, pp. 509- 512. doi:10.1126/science.286.5439.509
  7. G. Palla, A.-L. Barabasi and T. Vicsek, “Quantifying Social Group Evolution,” Nature, Vol. 446, No. 7136, 2007, pp. 664-667. doi:10.1038/nature05670
  8. A. Srinivasan, “Local Balancing Influences Global Structure in Social Networks,” Proceedings of the National Acadamic Science of the USA, Vol. 108, 2011, pp. 1751- 1752. doi:10.1073/pnas.1018901108
  9. K. Sznajd-Weron and J. Sznajd, “Opinion Evolution in Closed Community,” International Journal of Modern Physics C, Vol. 11, No. 6, 2000, p. 1157. doi:10.1142/S0129183100000936
  10. T. M. Liggett, “Stochastic Interacting Systems: Contact, Voter, and Exclusion Processes,” Springer, Berlin, 1999.
  11. R. Lambiotte and S. Redner, “Dynamics of Non-Conservative Voters,” Europhysics Letters, Vol. 82, No. 1, 2008, Article ID: 18007. doi:10.1209/0295-5075/82/18007
  12. S. Galam, “Minority Opinion Spreading in Random Geometry,” The European Physical Journal B, Vol. 25, No. 4, 2002, pp. 403-406. doi:10.1140/epjb/e20020045
  13. P. L. Krapivsky and S. Redner, “Dynamics of Majority Rule in Two-State Interacting Spin Systems,” Physical Review Letters, Vol. 90, No. 23, 2003, Article ID: 238701. doi:10.1103/PhysRevLett.90.238701
  14. B. Latane, “The Psychology of Social Impact,” American Psychologist, Vol. 36, No. 4, 1981, pp. 343-356. doi:10.1037/0003-066X.36.4.343
  15. R. Hegselmann and U. Krause, “Opinion Dynamics and Bounded Confidence Models, Analysis and Simulation,” Journal of Artificial Societies and Social Simulation, Vol. 5, No. 3, 2002, p. 3.
  16. F. Heider, “Attitudes and Cognitive Organization,” The Journal of Psychology, Vol. 21, No. 1, 1946, pp. 107-112.
  17. F. Heider, “The Psychology of Interpersonal Relations,” Wiley, New York, 1982.
  18. S. Wasserman and K. Faust, “Social Network Analysis: Methods and Applications,” Cambridge University Press, New York, 1994.
  19. D. Cartwright, F. Harary and R. Norman, “Structural Models: An Introduction to the Theory of Directed Graphs,” Wiley, New York, 1965.
  20. J. Kunegis, et al., “Spectral Analysis of Signed Graphs for Clustering, Prediction and Visualization: Siam Conference on Data Mining,” 2010.
  21. G. Facchetti, G. Iacono and C. Altafini, “Computing Global Structural Balance in Large-Scale Signed Social Networks,” Proceedings of the National Academy of Sciences of the USA, Vol. 108, No. 52, 2011, pp. 20953-20958. doi:10.1073/pnas.1109521108
  22. L. Festinger, “A Theory of Cognitive Dissonance,” Stanford University Press, Palo Alto, 1957.

NOTES

*Competing interests: The authors have no competing interests to declare.

1Synchronous diffusion: each vertex updates opinion at the same time in order to ensure diffusion independent of the sequence of vertex.

2Synchronous diffusion by majority preference rule finally leads to a trivial absorb state that all of vertices holding the same opinion. So we employ majority friends’ preference in this study.

Journal Menu >>