Journal of Modern Physics
Vol.3 No.9(2012), Article ID:22673,15 pages DOI:10.4236/jmp.2012.39126
Relativity Theory and Paraquantum Logic—Part I: The Time and Space in the Paraquantum Logical Model
1Group of Applied Paraconsistent Logic-Santa Cecília University, Santos, Brazil
2Institute for Advanced Studies of the University of São Paulo Cidade Universitária, São Paulo, Brazil
Email: inacio@unisanta.br
Received July 8, 2012; revised August 18, 2012; accepted August 28, 2012
Keywords: Paraconsistent Logic; Paraquantum Logic; Classical Physic; Relativity Theory; Quantum Mechanics
ABSTRACT
From fundamental concepts of the Paraconsistent Annotated Logic with annotation of two values (PAL2v), whose main feature is to be capable of treating contradictory information, was created the Paraquantum Logic (PQL). The studies of the PQL are based on propagation of Paraquantum logical states ψ in a representative Lattice of four vertices. Based in interpretations that consider resulting information of measurements in physical systems, are found two Paraquantum factors: the Paraquantum Gamma Factor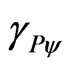 , that has his action in the measurements of Observable Variables in the Physical world and the Paraquantum Factor of quantization hψ, which has his action in the Paraquantum World represented by the PQL Lattice. Correlation between
, that has his action in the measurements of Observable Variables in the Physical world and the Paraquantum Factor of quantization hψ, which has his action in the Paraquantum World represented by the PQL Lattice. Correlation between  and hψ produces paraquantum equations for computation of the physical quantities in real physical systems. In this work we present a study of application of the PQL in resolution of phenomena of physical systems that involve concepts of the Relativity Theory. Initially the time t is considered like an Observable Variable and the paraquantum analysis is done with the same conditions assumed in the relativity theory for the study of the time dilatation. After the time considerations, paraquantum equations are involved with the space-time and velocity creating conditions for a relativistic/paraquantum analysis. In the part II of this work a new approaches of the relativistic phenomena in the Paraquantum Logical Model will show the correlation of these effects with the Newtonian universe and with quantum mechanics.
and hψ produces paraquantum equations for computation of the physical quantities in real physical systems. In this work we present a study of application of the PQL in resolution of phenomena of physical systems that involve concepts of the Relativity Theory. Initially the time t is considered like an Observable Variable and the paraquantum analysis is done with the same conditions assumed in the relativity theory for the study of the time dilatation. After the time considerations, paraquantum equations are involved with the space-time and velocity creating conditions for a relativistic/paraquantum analysis. In the part II of this work a new approaches of the relativistic phenomena in the Paraquantum Logical Model will show the correlation of these effects with the Newtonian universe and with quantum mechanics.
1. Introduction
A Paraconsistent Logic (PL) is a non-classical logic which revokes the principle of non-Contradiction and admits the treatment of contradictory information in its theoretical structure [1-3]. The Paraconsistent Annotated Logics with annotation of two values (PAL2v) is a class of Paraconsistent Logics particularly represented through a Lattice of four vertices (see [4]).
Under certain conditions the results obtained from the LPA2v model changed through leaps or unexpected variations [5]. With that it is verified that the application of its foundations presents results strongly connected to the ones found in modeling of phenomena studied in quantum mechanics (see [5-7]). Because of this behavior, with fundamental concepts of the Paraconsistent Annotated Logic with annotation of two values (PAL2v), was created the Paraquantum Logic (PQL). Through the paraquantum equations we investigate the effects of balancing of energies and the quantization and transience properties of the Paraquantum Logical Model in real Physical Systems [5,8,9].
We can obtain through the PAL2v a representation of how the annotations or evidences express the knowledge about a certain proposition P [4]. This is done through a lattice on the real plane with pairs 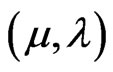 which are the annotations. If P is a basic formula then:
which are the annotations. If P is a basic formula then:
 where ~ is the logic negation of P and μ,
where ~ is the logic negation of P and μ,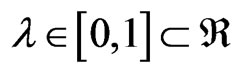 . Considering that μ is the favorable degree of evidence and λ is unfavorable degree of evidence, then the symbol
. Considering that μ is the favorable degree of evidence and λ is unfavorable degree of evidence, then the symbol 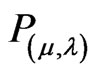 can be read in the following way:
can be read in the following way:
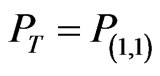 → The annotation
→ The annotation 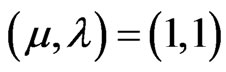 assigns intuitive reading that P is Inconsistent;
assigns intuitive reading that P is Inconsistent;
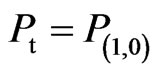 → The annotation
→ The annotation 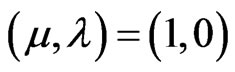 assigns intuitive reading that P is True;
assigns intuitive reading that P is True;
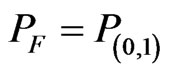 → The annotation
→ The annotation 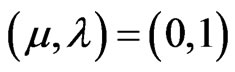 assigns intuitive reading that P is False;
assigns intuitive reading that P is False;
 → The annotation
→ The annotation 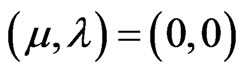 assigns intuitive reading that P is Indeterminate.
assigns intuitive reading that P is Indeterminate.
In the internal point of the lattice which is equidistant from all four vertices, we have the following interpretation: 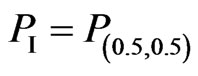 → The annotation
→ The annotation  assigns intuitive reading that P is undefined.
assigns intuitive reading that P is undefined.
With the values of x and y that vary between 0 and 1 and being considered in an Unitary Square on the Cartesian Plane (USCP) we can get linear transformations for a Lattice k of analogous values to the associated Lattice τ of the PAL2v [4,5]. The obtained final transformation is:
 (1)
(1)
According to the language of the PAL2v, we have:
 → is the favorable Evidence Degree;
→ is the favorable Evidence Degree;
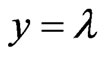 → is the unfavorable Evidence Degree.
→ is the unfavorable Evidence Degree.
The first coordinate of the transformation (1) is called Certainty Degree (DC) and is obtained by:
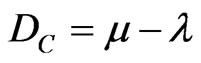 . (2)
. (2)
The second coordinate of the transformation (1) is called Contradiction Degree 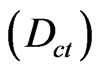 and is obtained by:
and is obtained by:
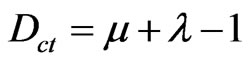 . (3)
. (3)
The second coordinate is a real number in the closed interval . The y-axis of the Lattice τ is called “axis of the contradiction degrees”. From (1)-(3) we can represent a Paraconsistent logical state (eτ) into Lattice τ of the PAL2v [4,5], such that:
. The y-axis of the Lattice τ is called “axis of the contradiction degrees”. From (1)-(3) we can represent a Paraconsistent logical state (eτ) into Lattice τ of the PAL2v [4,5], such that:
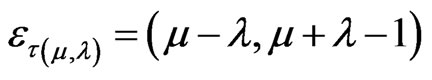 or
or where:
where: 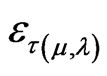 is the Paraconsistent logical state.
is the Paraconsistent logical state.
DC is the Certainty Degree obtained from the evidence Degrees μ and λ.
Dct is the Contradiction Degree obtained from the evidence Degrees μ and λ.
Figure 1 shows sequences for obtaining the Lattice of Paraconsistent Annotated Logic with values.
1.1. The Paraquantum Logic (PQL)
With base in the concepts of the LPA2v the foundations of the denominated Paraquantum Logic (PQL) are considered (see [4,5]).
Initially it is verified that the Equations (2) and (3) can be expressed in terms of μ and λ obtaining:
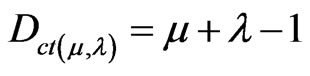 . (4)
. (4)
Then, a Paraquantum logical state ψ is created on the lattice of the PQL as the tuple formed by the Certainty degree (DC) and the Contradiction degree (Dct) [4],
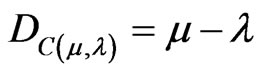 . (5)
. (5)
Both values depend on the measurements perfomed on the Observable Variables in the physical environment which are represented by μ and λ [5,8,9].
A Paraquantum function  is defined as the Paraquantum logical state y:
is defined as the Paraquantum logical state y:
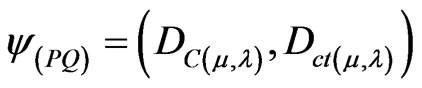 .
.
For each measurement performed in the physical world of μ and λ, we obtain a unique duple 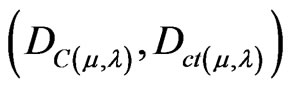
which represents a unique Paraquantum logical state ψ which is a point of the lattice of the PQL [5,8].
On the vertical y-axis of contradictory degrees, the two extreme real Paraquantum logical states are:
1) The contradictory extreme Paraquantum logical state which represents Inconsistency T:
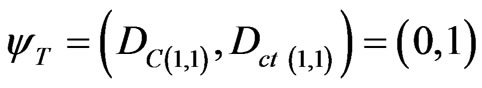 ;
;
2) The contradictory extreme Paraquantum logical

Figure 1. Sequences of linear transformations for obtaining the Lattice of Paraconsistent logic with values.
state which represents Undetermination ^:
 .
.
On the horizontal x-axis of certainty degrees, the two extreme real Paraquantum logical states are:
1) The real extreme Paraquantum logical state which represents Veracity t:

2) The real extreme Paraquantum logical state which represents Falsity F:
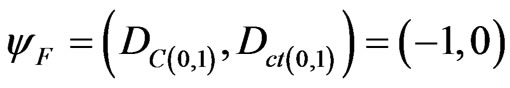
A Vector of State 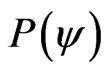 will have origin in one of the two vertexes that compose the horizontal axis of the certainty degrees and its extremity will be in the point formed for the pair indicated by the Paraquantum function
will have origin in one of the two vertexes that compose the horizontal axis of the certainty degrees and its extremity will be in the point formed for the pair indicated by the Paraquantum function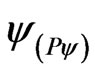 .
.
If the Certainty Degree is negative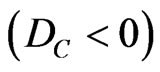 , then the Vector of State
, then the Vector of State 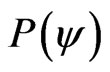 will be on the lattice vertex which is the extreme Paraquantum logical state False:
will be on the lattice vertex which is the extreme Paraquantum logical state False: 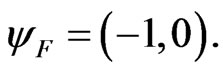
If the Certainty Degree is positive , then the Vector of State
, then the Vector of State 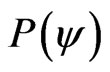 will be on the lattice vertex which is the extreme Paraquantum logical state True:
will be on the lattice vertex which is the extreme Paraquantum logical state True: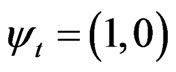 .
.
If the certainty degree is nil , then there is an undefined Paraquantum logical state
, then there is an undefined Paraquantum logical state 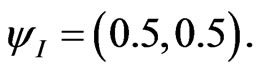
The Vector of State  will always be the vector addition of its two component vectors:
will always be the vector addition of its two component vectors:
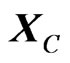 Vector with same direction as the axis of the certainty degrees (horizontal) whose module is the complement of the intensity of the certainty degree:
Vector with same direction as the axis of the certainty degrees (horizontal) whose module is the complement of the intensity of the certainty degree: 
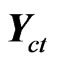 Vector with same direction as the axis of the contradiction degrees (vertical) whose module is the contradiction degree:
Vector with same direction as the axis of the contradiction degrees (vertical) whose module is the contradiction degree: 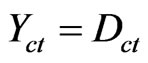
Given a current Paraquantum logical state ψcur defined by the duple 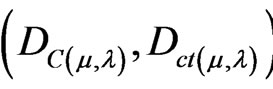 then we compute the module of a Vector of State
then we compute the module of a Vector of State 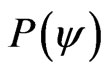 as follows:
as follows:
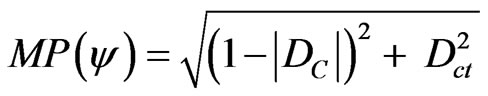 (6)
(6)
where: Dct = Contradiction Degree computed by (4).
DC = Certainty Degree computed by (5).
Using (6) which is for computing the module of a Vector of State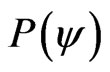 , we have:
, we have:
1) For DC > 0 the real Certainty Degree is computed by:
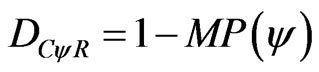 (7)
(7)
Therefore:
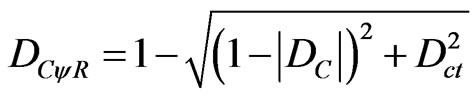 (8)
(8)
where:  = real Certainty Degree;
= real Certainty Degree;
Dct = Contradiction Degree computed by (4);
DC = Certainty Degree computed by (5).
2) For DC < 0, the real Certainty Degree is computed by:
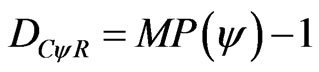 (9)
(9)
Therefore:
 (10)
(10)
3) For DC = 0, then the real Certainty Degree is nil:

The intensity of the real Paraquantum logical state is computed by:
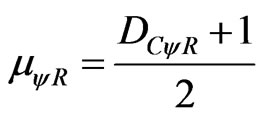 (11)
(11)
The inclination angle ay of the Vector of State which is the angle formed by the Vector of State 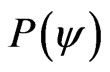 and the x-axis of the certainty degrees is computed by:
and the x-axis of the certainty degrees is computed by:
 (12)
(12)
1.2. Uncertainty Paraquantum Region
When the module of the Vector of State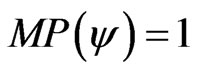 , this vector will represent the maximal fundamental superposed Paraquantum logical states
, this vector will represent the maximal fundamental superposed Paraquantum logical states 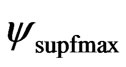 which has real certainty degrees zero. The maximum Contradiction Degree for this condition is when the Vector of State
which has real certainty degrees zero. The maximum Contradiction Degree for this condition is when the Vector of State 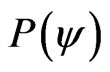 forms an angle of 45˚ with the horizontal axis of certainty degrees.
forms an angle of 45˚ with the horizontal axis of certainty degrees.
The unbalanced contradictory Paraquantum logical state ψctru is the one located on the lattice of states of the PQL where there is a condition of opposite signs between the Certainty Degree (DC) and the real Certainty Degree ( ) [5,8].
) [5,8].
When the module of the Vector of State is of larger value than the unit , means that the Paraquantum logical state ψ are in an uncertainty region.
, means that the Paraquantum logical state ψ are in an uncertainty region.
1.3. The Paraquantum Factor of Quantization hψ
The propagation of the superposed Paraquantum logical states 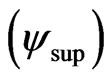 through the lattice of the PQL happens due to the continuous measurements performed on the Observable Variables in the physical world.
through the lattice of the PQL happens due to the continuous measurements performed on the Observable Variables in the physical world.
When the superposed Paraquantum logical state ysup propagates on the lattice of the PQL a value of quantizetion for each equilibrium point is established. This point is the value of the contradiction degree of the Paraquantum logical state of quantization 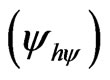 [5] such that:
[5] such that:
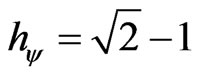 (13)
(13)
where:  is the Paraquantum Factor of quantization.
is the Paraquantum Factor of quantization.
The factor 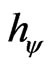 quantifies the levels of energy through the equilibrium points where the Paraquantum logical state of quantization
quantifies the levels of energy through the equilibrium points where the Paraquantum logical state of quantization , defined by the limits of propagation throughout the uncertainty of the PQL, is located [5,7,8].
, defined by the limits of propagation throughout the uncertainty of the PQL, is located [5,7,8].
1.4. The Propagation of the Paraquantum Logical State ψ
Since the Paraquantum analysis deals with favorable and unfavorable evidence degrees 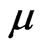 and
and 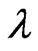 of the measurements performed on the physical world, these variations affect the behavior and propagation of the superposed Paraquantum logical states
of the measurements performed on the physical world, these variations affect the behavior and propagation of the superposed Paraquantum logical states  on the lattice of the PQL. In a process of propagation of Paraquantum logical state
on the lattice of the PQL. In a process of propagation of Paraquantum logical state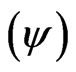 , we have that in the instant that the superposed Paraquantum logical state
, we have that in the instant that the superposed Paraquantum logical state 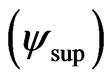 reaches the representative points of the limiting factors of the uncertainty region of the PQL, the Certainty Degree
reaches the representative points of the limiting factors of the uncertainty region of the PQL, the Certainty Degree  remains zero but the real Certainty Degree
remains zero but the real Certainty Degree 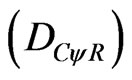 will be increased or decreased from zero and this difference corresponds to the effect called of the Paraquantum Leap [5,8]. Since the propagation exists, then we have to take into account the factor related to the Paraquantum Leaps which will be added to or subtracted from the Paraquantum Factor of quantization [5] such that:
will be increased or decreased from zero and this difference corresponds to the effect called of the Paraquantum Leap [5,8]. Since the propagation exists, then we have to take into account the factor related to the Paraquantum Leaps which will be added to or subtracted from the Paraquantum Factor of quantization [5] such that:
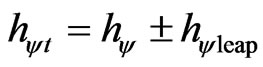 (14)
(14)
Figure 2(a) shows representing a Paraquantum logical state ψ on the Paraquantum lattice of states (PQL Lattice)
on the point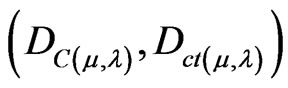 . Figure 2(b) shows the effect of the Paraquantum Leap in the quantization of values when the Superposed Paraquantum Logical states
. Figure 2(b) shows the effect of the Paraquantum Leap in the quantization of values when the Superposed Paraquantum Logical states 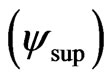 reach the point where the Paraquantum Logical state of Quantization
reach the point where the Paraquantum Logical state of Quantization 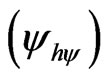 on the PQL Lattice.
on the PQL Lattice.
Where, from Figure 2(b) we can make the calculations:
 (15)
(15)
So, the Paraquantum Factor of quantization in its complete or total form which acts on the quantities is:
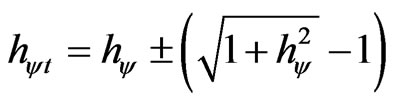 (16)
(16)
1.5. Newton Gamma Factor
Comparisons and analogies between the International unit Systems and the British System result in a proportionality factor 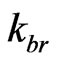 related to the British system [8,10].
related to the British system [8,10].
Given the importance of the Factor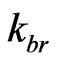 , which will be largely used in the equations of the PQL, its value is called Newton Gamma Factor whose symbol is
, which will be largely used in the equations of the PQL, its value is called Newton Gamma Factor whose symbol is . Therefore, in order to apply classical logics in the Paraquantum Logical model [8,10-12], the Newton Gamma Factor is
. Therefore, in order to apply classical logics in the Paraquantum Logical model [8,10-12], the Newton Gamma Factor is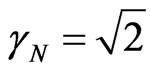 .
.
1.6. Paraquantum Gamma Factor 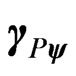
For an expansion process of the PQL Lattice where we
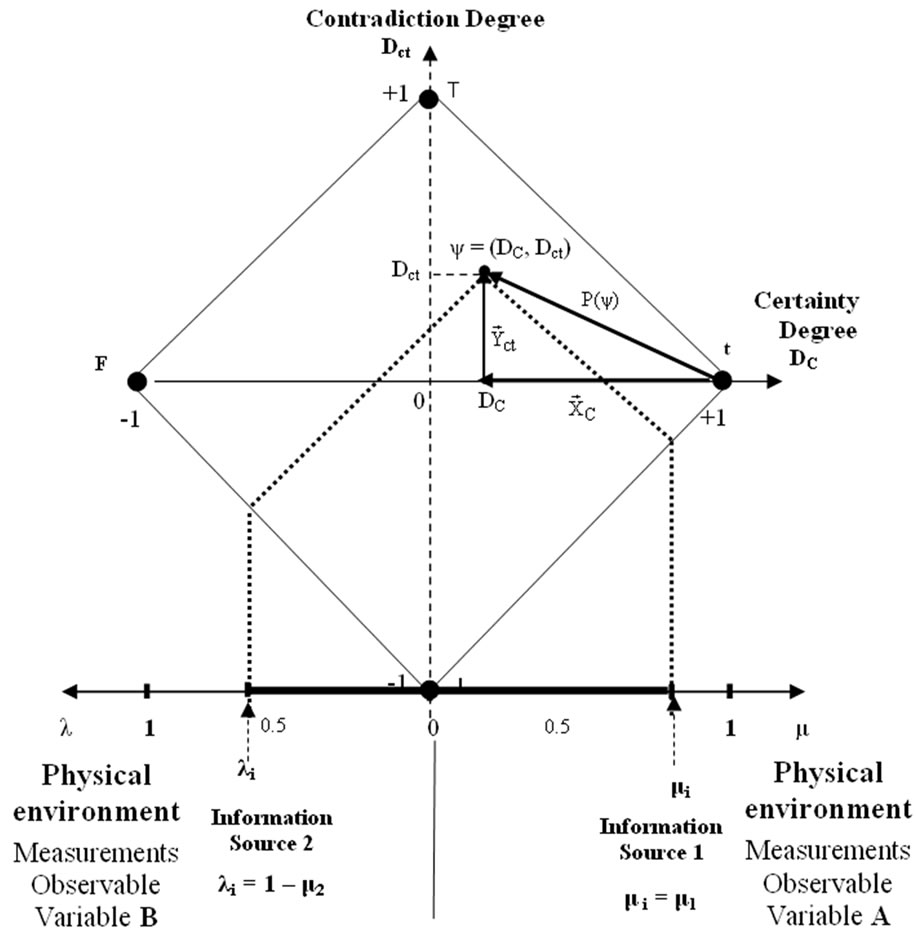
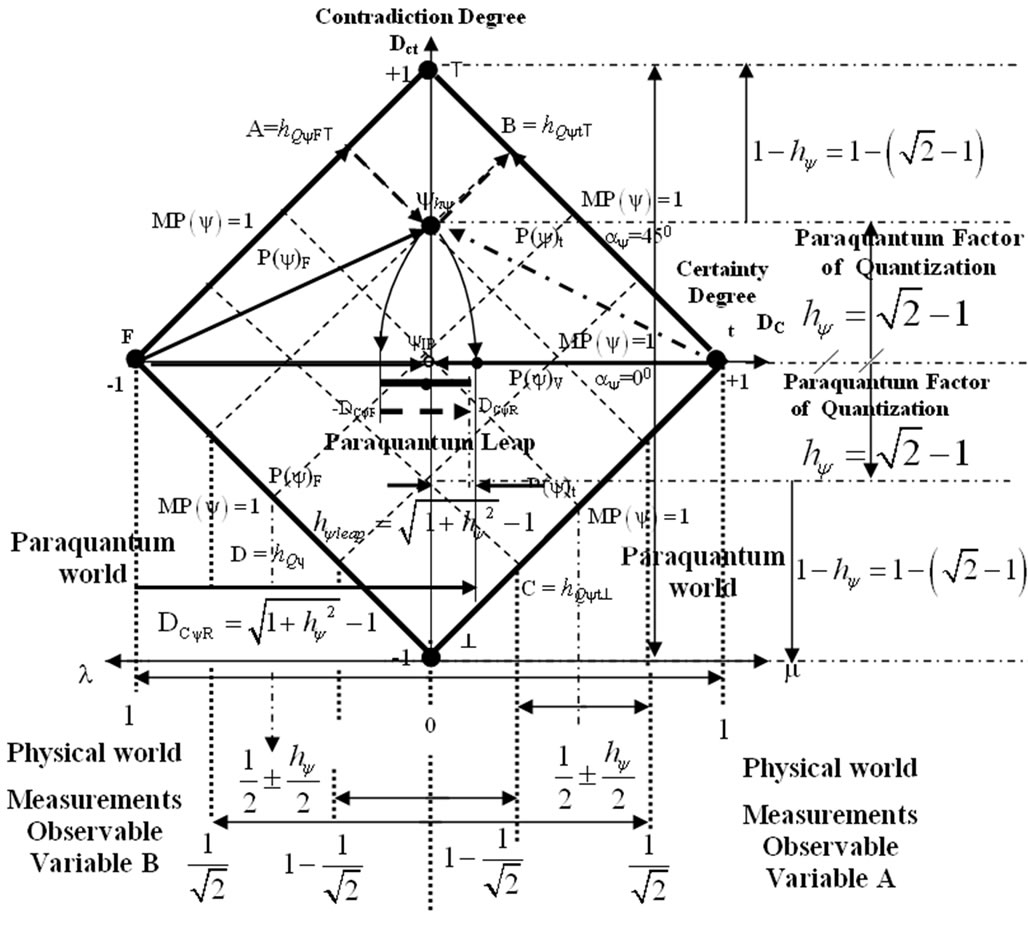
Figure 2. (a) Paraquantum logical state (ψ) into the paraquantum lattice on the point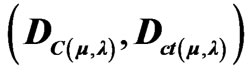 ; (b) The paraquantum factor of quantization hy related to the evidence degrees obtained in the measurements of the observable variables in the physical world.
; (b) The paraquantum factor of quantization hy related to the evidence degrees obtained in the measurements of the observable variables in the physical world.
consider quantizations based in consecutive applications of inversed values of the Newton Gamma Factor we can identify the Lorentz Factor  in the infinite Power Series of the binomial expansion [8,10].
in the infinite Power Series of the binomial expansion [8,10].
In the paraquantum analysis [8] related to the series obtained from consecutively applying the Newton Gamma Factor 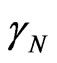 we define a correlation value called Paraquantum Gamma Factor
we define a correlation value called Paraquantum Gamma Factor 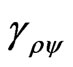 such that:
such that:
 (17)
(17)
where:  is the Newton Gamma Factor:
is the Newton Gamma Factor: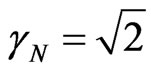 ,
,
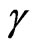 is the Lorentz factor which is:
is the Lorentz factor which is: 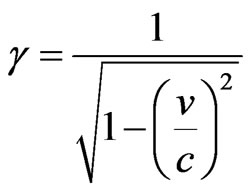
Using the Paraquantum Gamma Factor 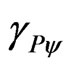 allows the computations, which correlate values of Observable Variables to the values related to quantization through the Paraquantum Factor of quantization hψ [5,8,9].
allows the computations, which correlate values of Observable Variables to the values related to quantization through the Paraquantum Factor of quantization hψ [5,8,9].
2. The Study of the Time Flow in the Paraquantum Analysis
In the Paraquantum analysis applied to Physical Systems, time must be considered as an Observable Variable whose measurements must be inserted in a Universe of Discourse (or Interval of Interest) from where the Evidence Degree (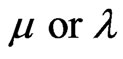 ) is extracted from. However, for the analysis in the Paraquantum Logical Model, when compared to other fundamental physical quantities, time has interesting features. Among these, measurements of the Observable Variable time have the following properties:
) is extracted from. However, for the analysis in the Paraquantum Logical Model, when compared to other fundamental physical quantities, time has interesting features. Among these, measurements of the Observable Variable time have the following properties:
1) Its value always increases and never decreases which make time to be a flow of positive values;
2) Its value is never stable, therefore, is never constant;
3) Measurements are mandatorily quantized due to its fluidity feature.
The Measured Time t Considered as an Observable Variable
The study of time as an Observable Variable in paraquantum analysis can be done from the same conditions assumed in the relativity theory for the study of the time dilatation [10,13].
First, we consider the classical example from the relativity theory where an observer O’ at rest on the referential S’ at a distance L from a mirror, according to Figure 3(a). The observer sends a light pulse through Transmitter E and measures the time interval 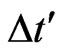 between the emission instant and the return instant of the pulse reflected by the mirror M. Since light travels with velocity c, we can compute this time interval by:
between the emission instant and the return instant of the pulse reflected by the mirror M. Since light travels with velocity c, we can compute this time interval by:
 .
.
We now consider both events: one is the transmission of the light pulse by E and the other is its return to the point where observer O’ is but now observed from other referential S. In this second condition of the referential S, according to Figure 3(b), observer O’ and mirror M are moving to the right with scalar velocity v whose value is a fraction of the velocity of light c in vacuum. For the observer at referential S, both events now happen in different places, such that:
Event 1 → Emission of light pulse by E in X1;
Event 2 → Return to the observer O’ in X2.
According to the figures, the space traveled by the light pulse is larger for referential S than for referential S’. This new condition arises because, since v was brought up, for the observer at referential S there is the horizontal distance 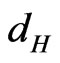 such that:
such that:

where:  is the measured time interval at referential S.
is the measured time interval at referential S.
According to the relativity theory [10,13], the value of the velocity of light in vacuum is a constant c, with
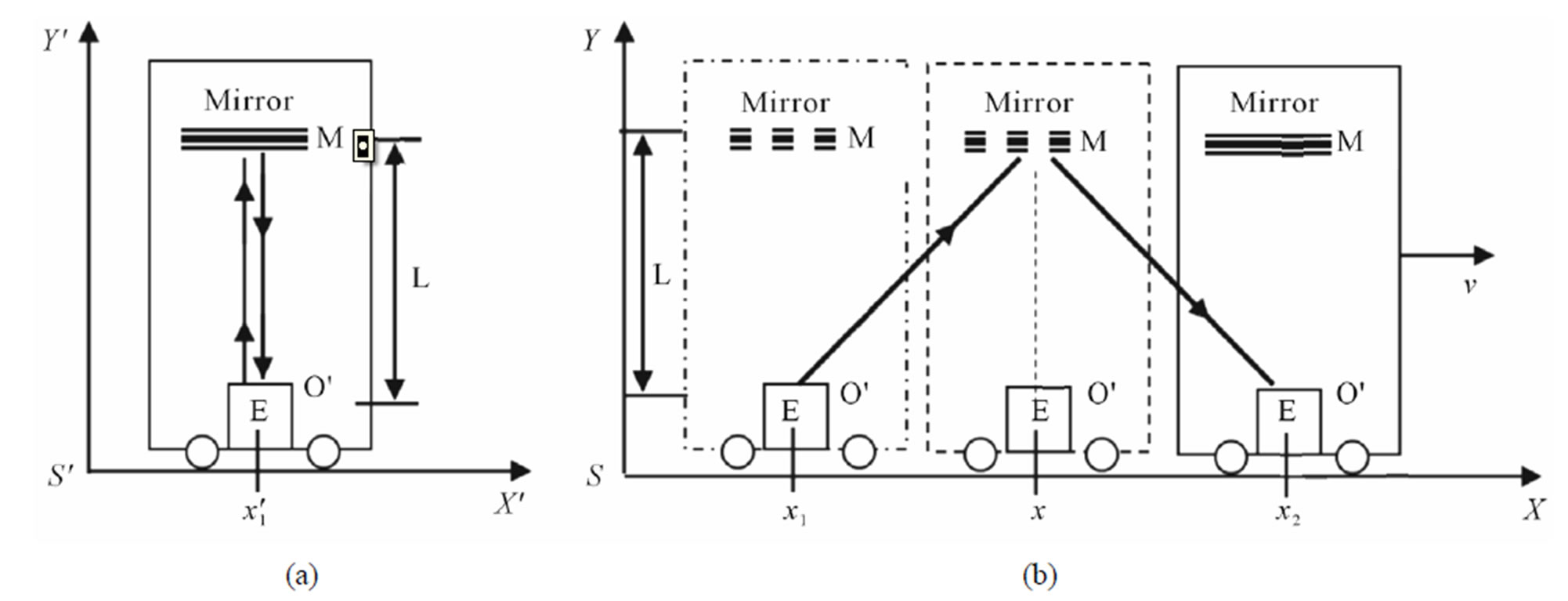
Figure 3. Analysis of the observable variable time (Similar analysis to the study of the time dilatation in the restricted relativity theory).
respect to the referential S as well as with respect to the referential S’. Since the space traveled with respect to the referential S is longer, then when compared to the time passed with respect to S’, the time spent for the light pulse emitted by E to hit the mirror M and to return to the observer O’ is also longer. It is seen on Figure 3(b) that the course of the light pulse observed from the referential S generates a rectangle triangle of vertices EX1 - EX - M. We can use the Theorem of Pythagoras on this rectangle triangle to analyze the situation [10,13]:
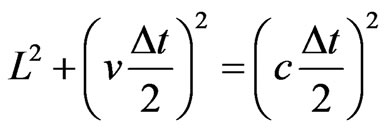 →
→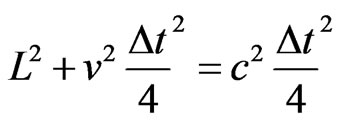 .
.
Isolating L2:
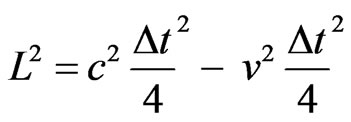 →
→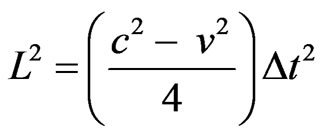
→ →
→
→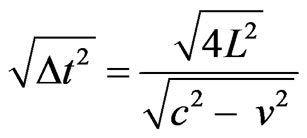 →
→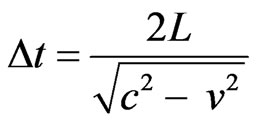 .
.
We do:
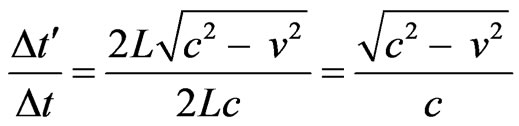
→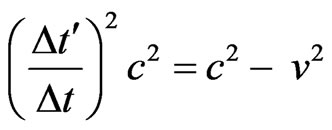 →
→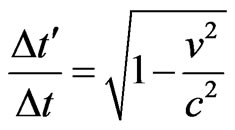 .
.
By inverting, we obtain:
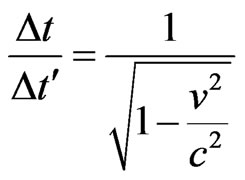 , (18)
, (18)
where:  = Variation of the total time with respect with the referential S.
= Variation of the total time with respect with the referential S.
 = Variation of time with respect to the referential S’ when measured at the referential S.
= Variation of time with respect to the referential S’ when measured at the referential S.
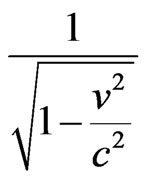 = Factor of time variation—Factor of Lorentz
= Factor of time variation—Factor of Lorentz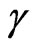 .
.
The last expression from Equation (18) indicates the relation of the variation of measured time or local time at the referential S when this one is unitary with the time measured at the referential S’. So, we can establish a quantitative relation between the time measured at the unitary value ( ) and the Factor of Lorentz
) and the Factor of Lorentz 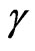 that acts on the amount of time when this one is related to the velocity v of the body being considered. In quantitative terms it means that to each unitary variation of the quantity of time measured at S (
that acts on the amount of time when this one is related to the velocity v of the body being considered. In quantitative terms it means that to each unitary variation of the quantity of time measured at S (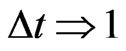 ), there is a decrease of the value of variation of measure time
), there is a decrease of the value of variation of measure time 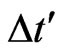 related to the body which has velocity v. We call
related to the body which has velocity v. We call 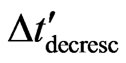 the decreased variation of time and we have:
the decreased variation of time and we have:
 or
or .
.
Considering the example for null velocity,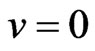 : we have →
: we have →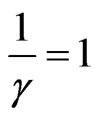 →
→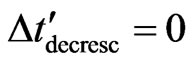 . And for velocity value:
. And for velocity value: 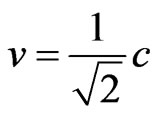 we obtain →
we obtain →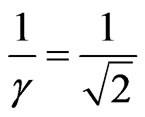 →
→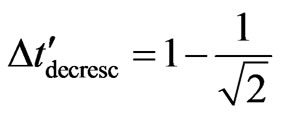 .
.
Being time featured with a flow that always increases, when it is considered as one of the Observable Variables from where the Evidence Degree (μ) is extracted, it shows this property in quantitative terms. We can formulate the following:
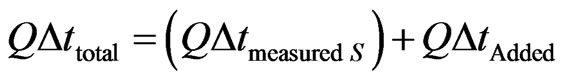 (19)
(19)
where: 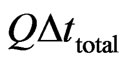 = Quantity of total time measured at the referential S;
= Quantity of total time measured at the referential S;
 = Quantity of time measured at the referential S with v = 0;
= Quantity of time measured at the referential S with v = 0;
 = Quantity of time measured and added to the referential S due to relativistic effects.
= Quantity of time measured and added to the referential S due to relativistic effects.
Therefore, for the observer at the referential S, the quantity of the time variation that decreases in  will be the same quantity of variation that will be increased to the time measured at the referential S. So, in each unit of time measured at S, there will be a corresponding value to the time fraction
will be the same quantity of variation that will be increased to the time measured at the referential S. So, in each unit of time measured at S, there will be a corresponding value to the time fraction  that will be added.
that will be added.
This quantity that will be added to the quantity of time measured at the referential S is given by:
 or
or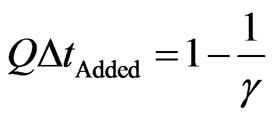 . (20)
. (20)
Equation (20) indicates that when measured at the referential S, the quantity of time added will be the complement of the inverse value of the Factor of Lorentz.
Considering the example for null velocity:
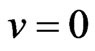 →
→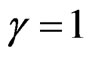 →
→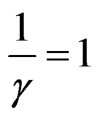 →
→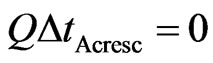 .
.
Equation (20) can be rewritten by isolating the added quantity of time, such that:
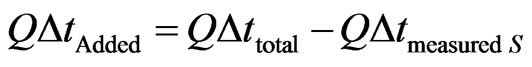 (21)
(21)
In the paraquantum analysis, the value of the quantity of time is considered to be normalized and therefore represents the unit of time measurement in a Universe of Discourse (or Interval of Interest). So, we can equate (20) and (21) such that:
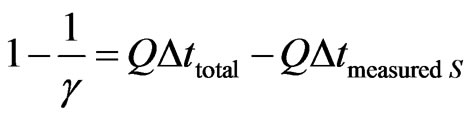 (22)
(22)
Doing so, for the variation of the quantity of total time to be unitary, the quantity of the variation of time measured at the referential of the Universe of Discourse is considered in the paraquantum analysis together with the inverse value of the Factor of Lorentz.
In the Equation (22) the following implication exists:
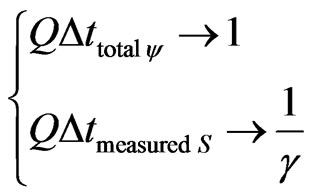
In these conditions were Quantity of total time is unitary, the Quantity of time measured at the referential of the Universe of Discourse of the paraquantum analysis is:
 (23)
(23)
where:  = Quantity of time measured at the referential of the Universe of Discourse of the paraquantum analysis.
= Quantity of time measured at the referential of the Universe of Discourse of the paraquantum analysis.
We observe that in the physical world the time quantization in the paraquantum analysis is related to inverse value of the Lorentz Factor.
3. The Time and the Paraquantum Logic
Considering the formalism of a Paraconsistent logic with annotation of two values (PAL2v) [4,5,8], the concept of Paraquantum logical state 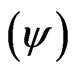 on a system in a given instant t can only be represented by the Paraquantum logical entanglement of the two Evidence Degrees
on a system in a given instant t can only be represented by the Paraquantum logical entanglement of the two Evidence Degrees 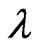 and
and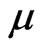 , which are obtained from measurements of the Observable Variables on the physical environment. So, in the language of the Paraquantum Logics, the entanglement between the favorable Evidence Degree (μ) and de unfavorable Evidence Degree (λ) produces the representtation of a final Paraquantum logical state
, which are obtained from measurements of the Observable Variables on the physical environment. So, in the language of the Paraquantum Logics, the entanglement between the favorable Evidence Degree (μ) and de unfavorable Evidence Degree (λ) produces the representtation of a final Paraquantum logical state 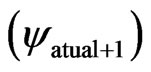 visualized through the Intensity Degree of the Real Paraquantum logical state
visualized through the Intensity Degree of the Real Paraquantum logical state 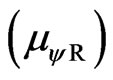 (Equation (11)).
(Equation (11)).
Considering the time as a Variable Observable the Equations (4) and (5) are now dependent of the time measurement, therefore, they become:
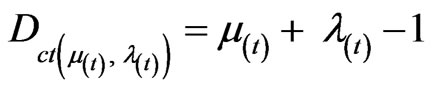 (24)
(24)
 (25)
(25)
And the Paraquantum logical state (y):

We can verify that the time has action directly in the measurements of the Observable Variables of the physiccal world. The variation of the time makes the values of the measurements in the Observable Variables modify and, as consequence, appear a propagation of the Paraquantum logical state through the PQL Lattice.
3.1. The Action of the Paraquantum Time Flow in the Physical Systems
We can study the flow of the Paraquantum time, having in mind that, according to the fundamental laws of physics [10-12], in the analysis of acceleration there are two related physical quantities: one is time and the other is the velocity v, whose value is contained in the attenuation Lorentz factor 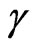 in the relativity theory. Since, in the paraquantum analysis, there is the need of two evidence degrees to form the annotation (which are extracted from the physical quantities considered as Observable Variables), then, for a dynamical process, where the condition of acceleration is valid, there will be the need to extract the Evidence Degree from the Observable Variable time. As it is done in the other physical quantities, the extraction of the Evidence Degree for the Observable Variable time will produce a normalized value in the closed real interval [0,1]. For the unitary value of the quantity of total time at the referential of the Universe of Discourse of the paraquantum analysis, the Evidence Degree of the Observable Variable time must be a fraction of unitary Quantity of total time. Since the Observable Variable time has the feature of being a flow that never stops and always increases, for its measured value to be contained in the closed real interval [0,1], then from Equation (22):
in the relativity theory. Since, in the paraquantum analysis, there is the need of two evidence degrees to form the annotation (which are extracted from the physical quantities considered as Observable Variables), then, for a dynamical process, where the condition of acceleration is valid, there will be the need to extract the Evidence Degree from the Observable Variable time. As it is done in the other physical quantities, the extraction of the Evidence Degree for the Observable Variable time will produce a normalized value in the closed real interval [0,1]. For the unitary value of the quantity of total time at the referential of the Universe of Discourse of the paraquantum analysis, the Evidence Degree of the Observable Variable time must be a fraction of unitary Quantity of total time. Since the Observable Variable time has the feature of being a flow that never stops and always increases, for its measured value to be contained in the closed real interval [0,1], then from Equation (22):
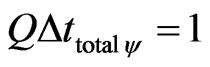 → Universe of Discourse is unitary and from Equation (23):
→ Universe of Discourse is unitary and from Equation (23): 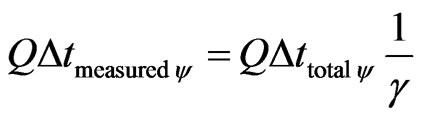
We can consider the time measured at the referential of the Universe of Discourse of the paraquantum analysis in Equation (21) the favorable Evidence Degree of the Variable Observable time (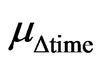 ):
):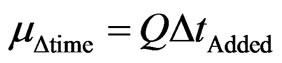
 (26)
(26)
So, the greater the value of the Factor of Lorentz  is, the closer to the unity the favorable Evidence Degree extracted from the Observable Variable time is.
is, the closer to the unity the favorable Evidence Degree extracted from the Observable Variable time is.
Similarly, with the same procedure, we can from Equation (23) write the equation of the unfavorable Evidence Degree depending on the Factor of Lorentz, which will be computed by the complement of the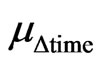 :
:
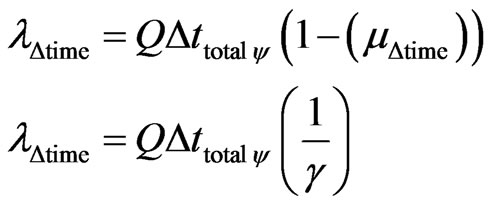 (27)
(27)
So, the greater the Factor of Lorentz  is, the closer to zero is the unfavorable Evidence Degree extracted from the Observable Variable time that is.
is, the closer to zero is the unfavorable Evidence Degree extracted from the Observable Variable time that is.
3.2. The Lorentz Factor in the Quantization of the Paraquantum Time
According to the concepts of the PQL [5,8,9] we observe the correlation among the values extracted from the Observable Variables of the physical environment, in the form of Evidence Degrees, that leads to an equilibrium situation, defined by a paraquantum logical value established by the Paraquantum Factor of quantization hψ. So, there must be an adaptation for using the Factor of Lorentz in the equilibrium condition of the Paraquantum Logical Model. For the existence of the correlation, we must compute the Factor of Lorentz 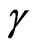 considering that for the equilibrium condition, the value corresponding to the Contradiction Degree on the vertical axis of the PQL Lattice is the Paraquantum Factor of quantization
considering that for the equilibrium condition, the value corresponding to the Contradiction Degree on the vertical axis of the PQL Lattice is the Paraquantum Factor of quantization . This procedure is done by starting with the value of the favorable Evidence Degree extracted from the Observable Variable time with the dependency of the Factor of Lorentz for the equilibrium condition.
. This procedure is done by starting with the value of the favorable Evidence Degree extracted from the Observable Variable time with the dependency of the Factor of Lorentz for the equilibrium condition.
The involved values in the equilibrium condition can be represented on the equation of the Contradiction Degree (4) such that: 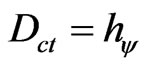 Comparing:
Comparing:
 →
→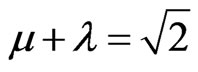
For equilibrium point on the contradiction degrees y-axis: . Therefore:
. Therefore: 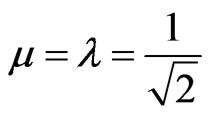
The unfavorable Evidence Degree and the Lorentz Factor when being affected of the paraquantum inverse value, such that on Equation (27): 
Through this equation, we can obtain the Factor of Lorentz for this equilibrium condition:
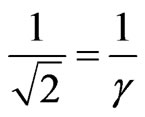 →
→
If in the study of Relativity Theory the velocity v is the Observable Variable for extraction of favorable Evidence Degree (μ), then the time can be used as Observable Variable for extraction of the unfavorable Evidence Degree (λ).
The value of velocity v related to the value of the speed of light c in the vacuum in the equilibrium condition, can be obtained from the value of the Factor of Lorentz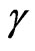 , such that:
, such that: . From the equality considered at the equilibrium condition, we have:
. From the equality considered at the equilibrium condition, we have:
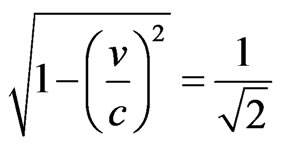 →
→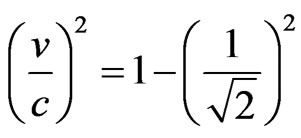 →
→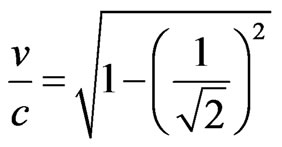 →
→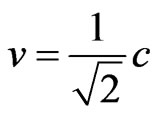 .
.
Therefore, paraquantum analysis applied in the relativity theory the favorable Evidence Degree extracted from the Observable Variable velocity v related to the speed of Light c in the vacuum, in the equilibrium condition, is:
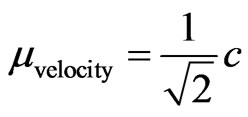
And the unfavorable Evidence Degree is: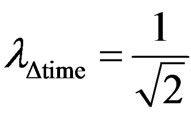 .
.
3.3. Adjust of the Lorentz Factor in the Paraquantum Time
For the corresponding values of the Evidence Degrees extracted from the equilibrium condition [5,8,9], the analysis on the PQL Lattice indicates on the vertical y-axis of the contradiction degrees the Paraquantum Factor of quantization hψ, such that: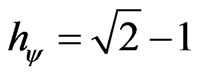 .
.
We can consider that a certain X paraquantum value is the responsible for establishing the connection between the values obtained from the time measure by the analysis of the restricted relativity theory and the quantization on the PQL Lattice. Through the equation of the Lorentz Factor, we observe that this can not be less than 1, therefore, this means that there is a certain paraquantum inversed value  acting on the Factor of Lorentz
acting on the Factor of Lorentz . This inverse paraquantum value adjusts the Evidence Degrees to
. This inverse paraquantum value adjusts the Evidence Degrees to , which means that, at each measurement of the equilibrium condition, the quantization is done by the Paraquantum Factor of quantization
, which means that, at each measurement of the equilibrium condition, the quantization is done by the Paraquantum Factor of quantization 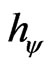 represented on the vertical y-axis of the contradiction degrees of the PQL Lattice. From Equation (27) the action of the inverse value
represented on the vertical y-axis of the contradiction degrees of the PQL Lattice. From Equation (27) the action of the inverse value 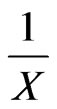 is:
is:
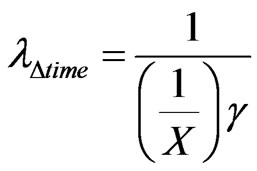 →
→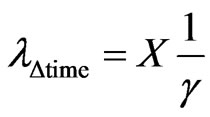
The Contradiction Degree in the equilibrium point by Equation (4) is:
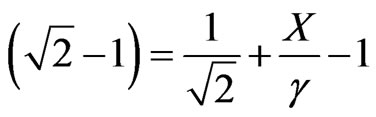 →
→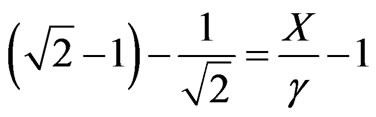
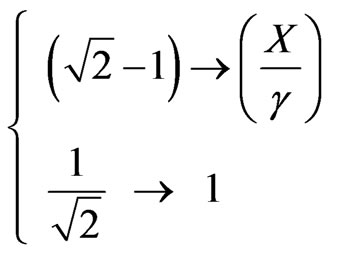 →
→ →
→
Since: 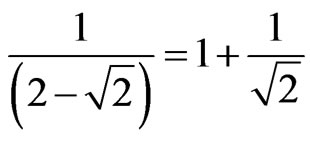 → where we get the X value by:
→ where we get the X value by: 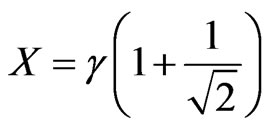 →
→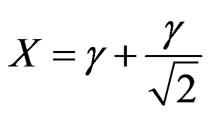 .
.
Including the Newton Gamma Factor, such that:
 →
→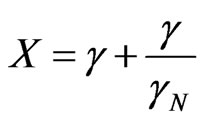 .
.
Do: 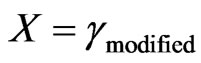 → then
→ then  is the modified Factor of Lorentz by action of Paraquantum inverse value X in the equilibrium condition. We observe that for the unitary Factor of Lorenz (
is the modified Factor of Lorentz by action of Paraquantum inverse value X in the equilibrium condition. We observe that for the unitary Factor of Lorenz ( ), the modified Factor of Lorentz is:
), the modified Factor of Lorentz is: .
.
For adjusting at the equilibrium condition, we subtract the unit and call the new resulting value of Paraquantum Gamma Factor, such that:
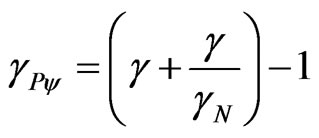 (28)
(28)
For the unitary Factor of Lorentz, therefore null velocity or close to null, as in the Newtonian universe, the resulting Paraquantum Gamma Factor is:
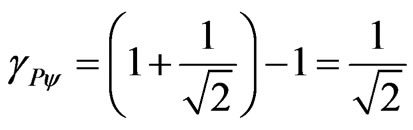
When the Paraquantum Gamma Factor is unitary, the Factor of Lorentz will be computed as follows:
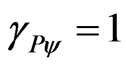 →
→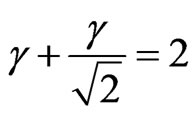 →
→ →
→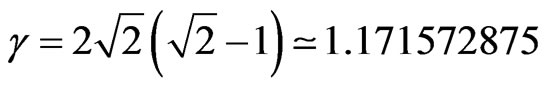
The value of velocity v related to the value of the speed of light c in the vacuum in this condition, can be obtained from the value of the Factor of Lorentz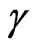 , such that:
, such that: .
.
The Paraquantum Gamma Factor of Equation (17) is the same one that appears on Equation (28) and its goal is to correlate the values of measurements in the physical world with the logical states in the paraquantum world.
4. The Space-Time in Paraquantum Logic Analysis
If the time will be the only physical largeness to be considered in the analysis, then it would not be a Paraquantum analysis, but classic. This happens because it will not have contradiction. For example considers the Equations (26) and (27) in the Contradiction Degree with 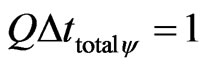 computed by Equation (4):
computed by Equation (4):
 ;
;
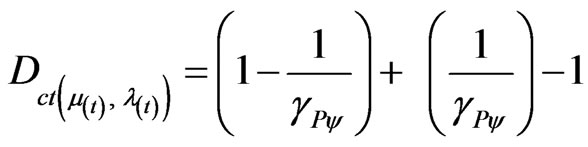 ;
;
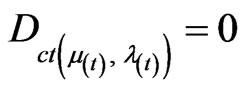 .
.
The Certainty Degree computed by Equation (5) is:
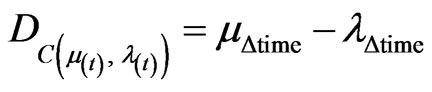 ;
;
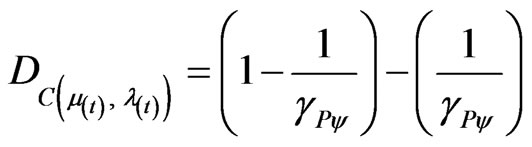 ;
;
 ;
;
 .
.
And the Paraquantum logical state (y) of the time is:
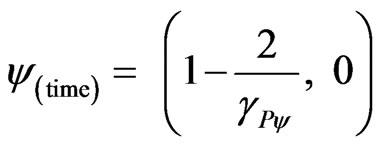 .
.
If the analysis is done using the Lorentz factor equal to 1, then, in accordance with the Equation (28), the value of Paraquantum Gamma Factor is less than 1.
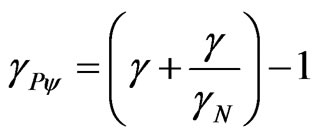 →
→ .
.
This condition of Paraquantum Gamma Factor less than 1 removes in the Equations (26) and (27) the normalization status of evidence degrees:
 and
and 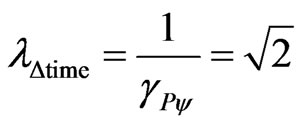
Therefore, 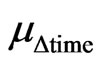 and
and  are incompatible with the fundamentals of Paraconsistent Logic (PAL2v). Thusthe values of the Certainty degree
are incompatible with the fundamentals of Paraconsistent Logic (PAL2v). Thusthe values of the Certainty degree 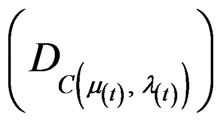 and of the intensity of the real Paraquantum logical state (
and of the intensity of the real Paraquantum logical state ( ) will only be valid if:
) will only be valid if: .
.
This characteristic of the time, when considered as Observable Variable, demonstrates the natural action of his always to act in the sense of expanding the Lattice.
In the representation of the time the characteristic inversely proportional is regarded as a flow, which starts from its maximum unitary value.
For the real world the values of evidence degrees of time related to the Lorentz factor in the relativity theory can be calculated by Equations (4) (5) (11) (26) and (27) for various values of velocity v, as shown in Table 1.
It is verified that for a single source of information, the value of the Degree of Contradiction will always be null, independently of Paraquantum Gamma Factor value. Therefore, using only a single source of information (space or time) the equilibrium point of the Paraquantum logical state (ψ), that is established in the y-axis of the contradiction degrees for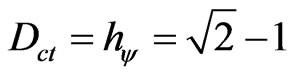 , does not exist.
, does not exist.
4.1. The Space/Time as Source of Information for Extraction of the Evidence Degree
In Physical Systems Analysis the value of velocity (vmeasured)

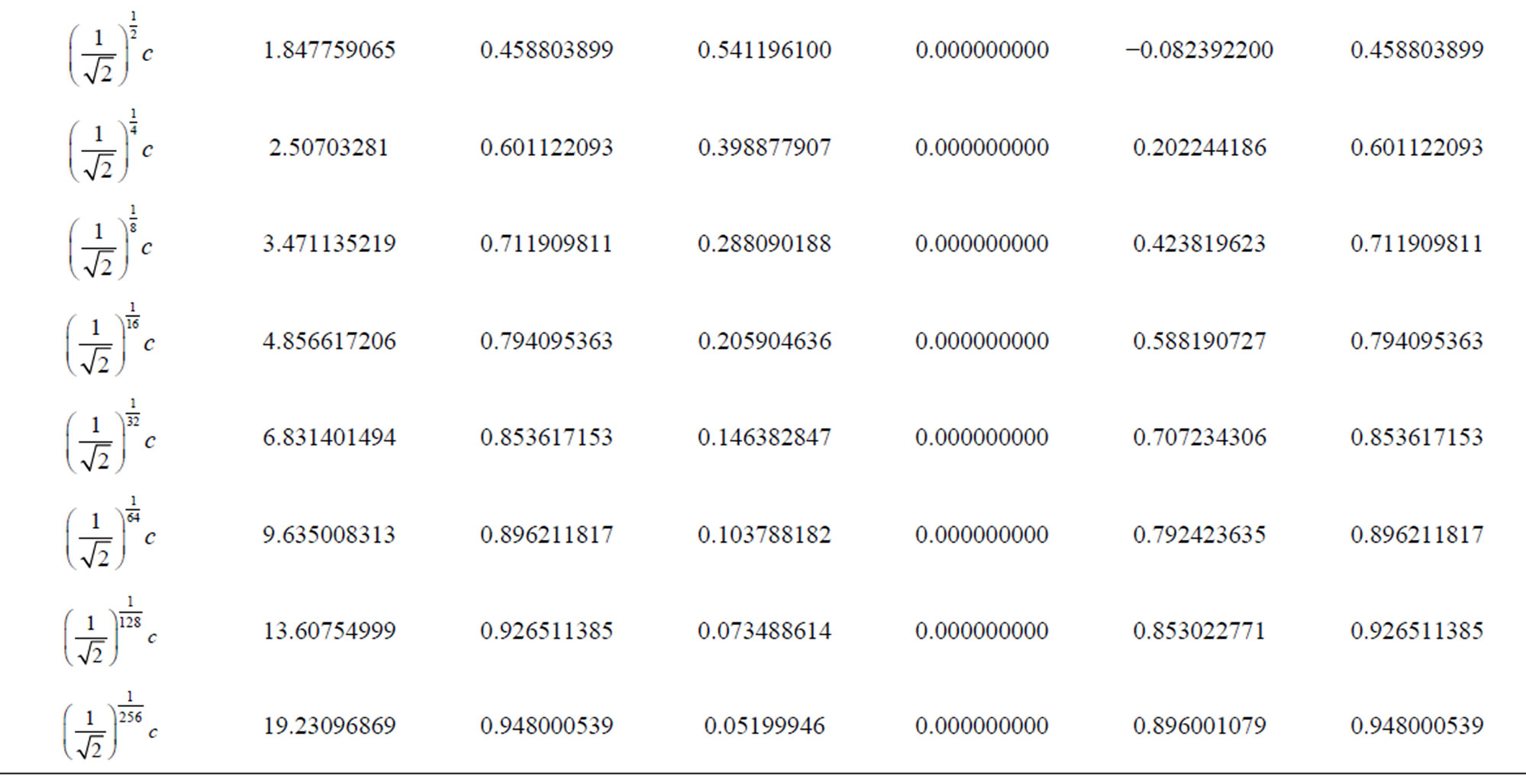
Table 1. Results of the evidence degree of the time for different velocity values using the paraquantum relativity equations.
can also be represented by the measured space  divided by the measured time
divided by the measured time .
.

Based in Equation (23) the variation of measured time 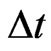 is considered by the following equality:
is considered by the following equality:
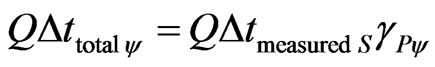
For the paraquantum analysis this equality means that the total amount of time variation , which defines the universe of discourse as unitary, is controlled by the Paraquantum Gamma Factor.
, which defines the universe of discourse as unitary, is controlled by the Paraquantum Gamma Factor.
For the condition of velocity, the relationship between the values of unfavorable Evidence Degree of the space (which doesn’t have the influence of Paraquantum Gamma Factor in their measurements) and of the time (which has the influence of Paraquantum Gamma Factor in their measurements) is:
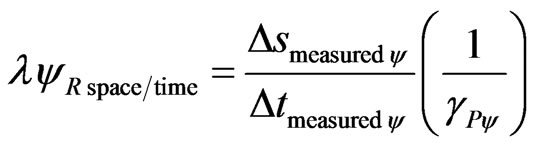 (29)
(29)
When the analysis is made in the universe of the relativity theory the velocity is always related to the speed of the light in the vacuum c. Therefore, in this condition the factor of Lorentz 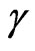 demonstrates that a correlation of the velocity
demonstrates that a correlation of the velocity 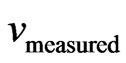 and the mathematical reason between the space and the time exists.
and the mathematical reason between the space and the time exists.
For the existence of correlation in paraquantum analysis, we must compute the value of the Paraquantum Gamma Factor 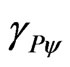 considering that, for the equilibrium condition its value is relates to the Contradiction Degree on the vertical y-axis of the PQL Lattice, which is the Paraquantum Factor of quantization
considering that, for the equilibrium condition its value is relates to the Contradiction Degree on the vertical y-axis of the PQL Lattice, which is the Paraquantum Factor of quantization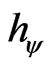 .
.
 (30)
(30)
For the velocity of studied body equal to  the Factor of Lorentz is equal to
the Factor of Lorentz is equal to 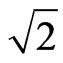 and through Equation (28) we find the resulting Paraquantum Gamma Factor of same value. In this way, considering the Equation (28) it is verified that, for relativistic universe, when:
and through Equation (28) we find the resulting Paraquantum Gamma Factor of same value. In this way, considering the Equation (28) it is verified that, for relativistic universe, when:
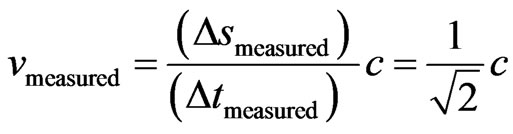 →
→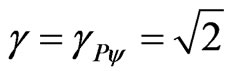
Therefore, it is verified that in to equilibrium point there are no changes of values in the universe of relativeity theory, that uses 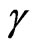 and the Newtonian universe that uses
and the Newtonian universe that uses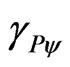 .
.
Considering the Equation (27) the unfavorable Evidence Degree that is result of division of space by time is:
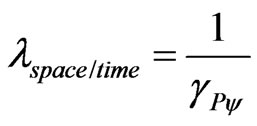
As in the equilibrium point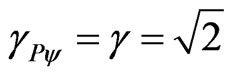 , then for relativistic universe:
, then for relativistic universe: .
.
It is verified that this condition the space/time is regarded as a single source of information. In this way, to the paraquantum analysis means that the unfavorable Evidence Degree extracted from Observable Variable space/time is being controlled by the inverse value of the Lorentz Factor or, only in the equilibrium point, by Paraquantum Gamma Factor. As in relativistic universe the velocity v is related at speed of light in the vacuum c, and as c is the maximum velocity value, then the favorable Evidence Degree is extracted of the velocity value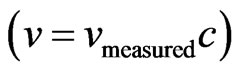 , written as:
, written as:

For the space/time Paraquantum Logical state (ψ) the Contradiction Degree is computed by Equation (4), were:
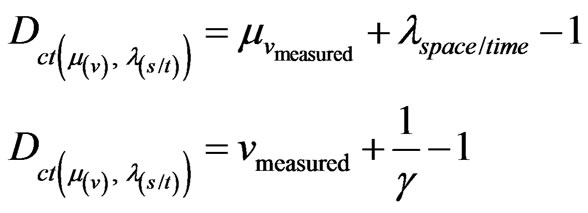 (31)
(31)
And the Certainty Degree is computed by Equation (5), were:
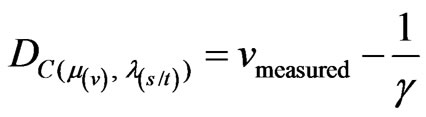 (32)
(32)
Considering that for the universe of relativity theory the unfavorable Evidence Degree is extracted of the Variable Observable space/time and the space/time is a single source of information, being the other source of information the velocity v, then:
When: 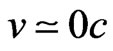 →
→ 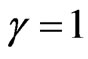
For paraquantum analysis:
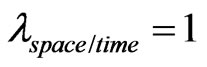 and
and 
From Equation (31):
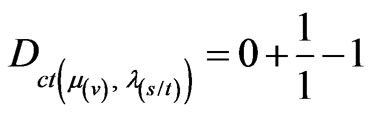 →
→
From Equation (32):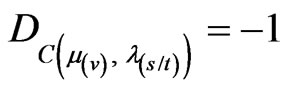 .
.
If the Paraquantum Gamma Factor be used → 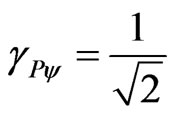
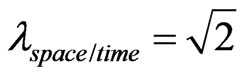 and
and 
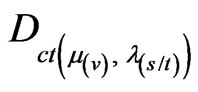 and
and  not exist in paraquantum analysis because
not exist in paraquantum analysis because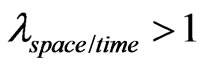 .
.
When:  →
→ 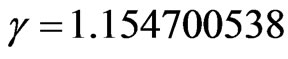
 and
and 
From Equation (31):
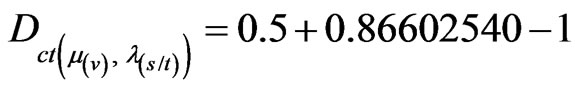
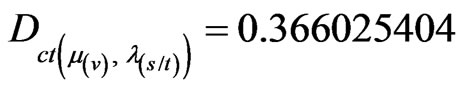
From Equation (32): 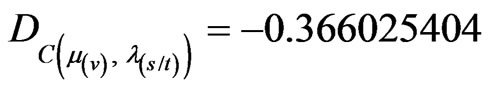
If the Paraquantum Gamma Factor be used → 
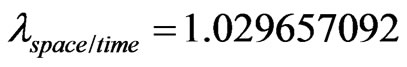 and
and 
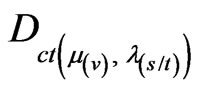 and
and 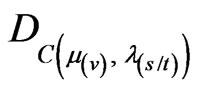 not exist in paraquantum analysis because
not exist in paraquantum analysis because .
.
When:  →
→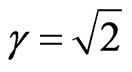 Equilibrium point
Equilibrium point
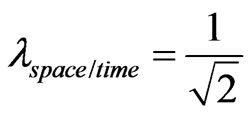 and
and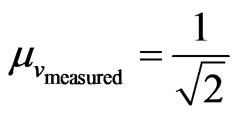 .
.
From Equation (31):
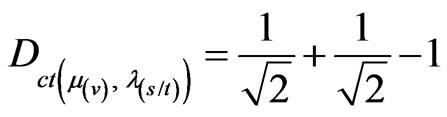
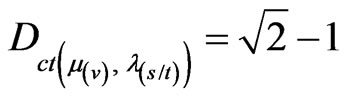
From Equation (32):
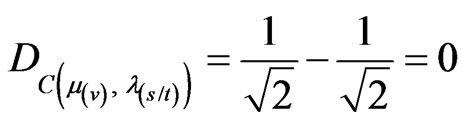 .
.
If the Paraquantum Gamma Factor be used → 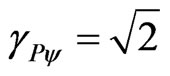
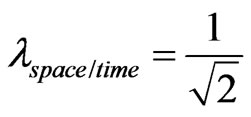 and
and .
.
From Equation (31):
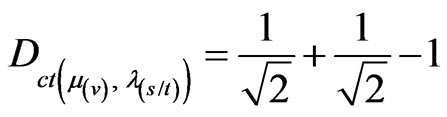
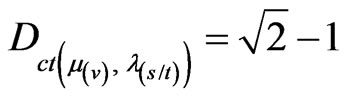 →
→ exist in paraquantum analysis because
exist in paraquantum analysis because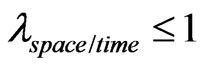 .
.
Table 2 shows results of the Evidence degree values of the Observable Variable space/time for the same values of the Observable Variable velocity considered in the relativity theory.
These results show that exist in paraquantum analysis applied in the theory of relativity a single point of correlation.
4.2. The Equilibrium Point in Paraquantum Analysis
According to the results in Table 2 presented by paraquantum/relativistic analysis verifies that exist an equilibrium point in the PQL Lattice. The equilibrium point that relates to application of Paraquantum Logic in the various areas of physics, including the theory of relativity, is located on the axis of the degree of contradiction and it has the following characteristics:
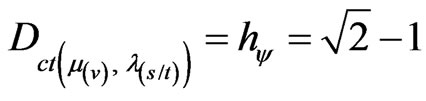
With: 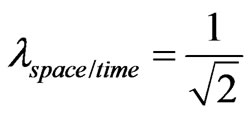 and
and 
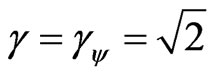 and
and 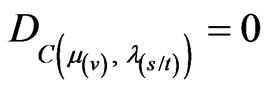
At this point of equilibrium is located into PQL Lattice the Paraquantum Factor of quantization  exactly where we can use either the Paraquantum Gamma Factor
exactly where we can use either the Paraquantum Gamma Factor 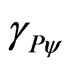 as also the Lorentz Factor
as also the Lorentz Factor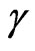 . However, the Certainty degree (DC) can only reach their maximum value when the velocity (v) reaches the value c of the speed of light in a vacuum.
. However, the Certainty degree (DC) can only reach their maximum value when the velocity (v) reaches the value c of the speed of light in a vacuum.
Figure 4 shows the representation of evidences degrees and the action of the time flow in the paraquantum analysis considered in the relativity theory.
The Paraquantum logical state (ψ) propagates in the PQL Lattice as the values of the Degree of contradiction and degrees of certainty of Table 2. In the Paraquantum analysis applied to theory of relativity the Observable Variable space/time suffer indirectly the action of the Lorentz Factor that acts in time. It is seen that this way the modification in the Lorentz Factor value causes the Paraquantum logical state 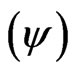 stay out of equilibrium point and include a value of Certainty Degree in the results. With the increase in the value of the velocity will happen changes in the Lorentz Factor and the Paraquantum logical state
stay out of equilibrium point and include a value of Certainty Degree in the results. With the increase in the value of the velocity will happen changes in the Lorentz Factor and the Paraquantum logical state 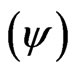 is directed to the maximum Certainty degree (DC).
is directed to the maximum Certainty degree (DC).
4.3. Discussion
The Evidence degree values of the Observable Variable space/time and the Observable Variable velocity are in the Relativy theory, so, are dependent of the Lorentz factor. For the paraquantum analysis of the Physical Systems in the Newtonian universe the space as Variable Observable, and the time as Variable Observable, are considered separately. The equations of paraquantum velocity, acceleration, space, work and energy are extracted from Newton’s laws and in paraquantum analysis consider calculation always in equilibrium point located in the vertical y-axis of the PQL Lattice.
However, in the Newtonian universe the velocity in

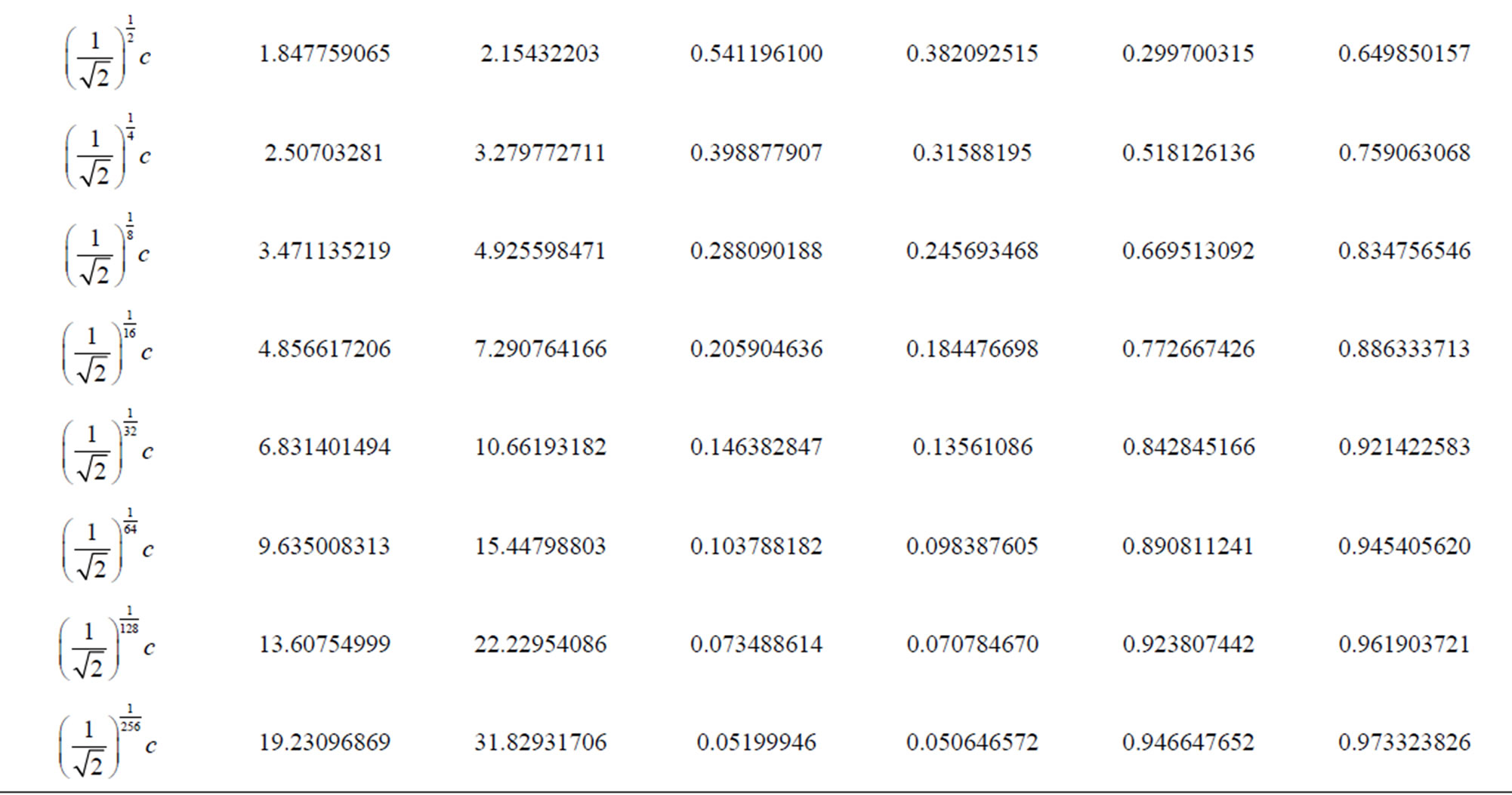
Table 2. Results of the evidence degree extracted of the observable variable space/time and the observable variable velocity in the analisys of paraquantum/relativity.
these equations is not related to the speed of light in a vacuum c, but obtained by dividing the space and time, where only time suffers the action of Paraquantum Gamma Factor. This manner, in the Newtonian universe the Evidence Degree of Observable Variable velocity is extracted of two source of information the space and the time. As, for these equations the velocity that is related to the speed of light in vacuum is equal to zero, then the Lorentz factor is unitary (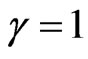 ). This causes the value of the Paraquantum Gamma Factor, which acts in these equations extracted in the Newtonian universe, is always the inverse of the factor of Newton:
). This causes the value of the Paraquantum Gamma Factor, which acts in these equations extracted in the Newtonian universe, is always the inverse of the factor of Newton: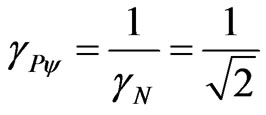 .
.
This value in the Physical world marks the variations of uncertainties that happen within the PQL lattice in quantization form of the axis of contradiction degrees by modifying the intensity of the Paraquantum logical State. This quantization can be expressed in the form of representation of energy, as it was studied in [14] and [15] to calculate energy levels in hydrogen atom.
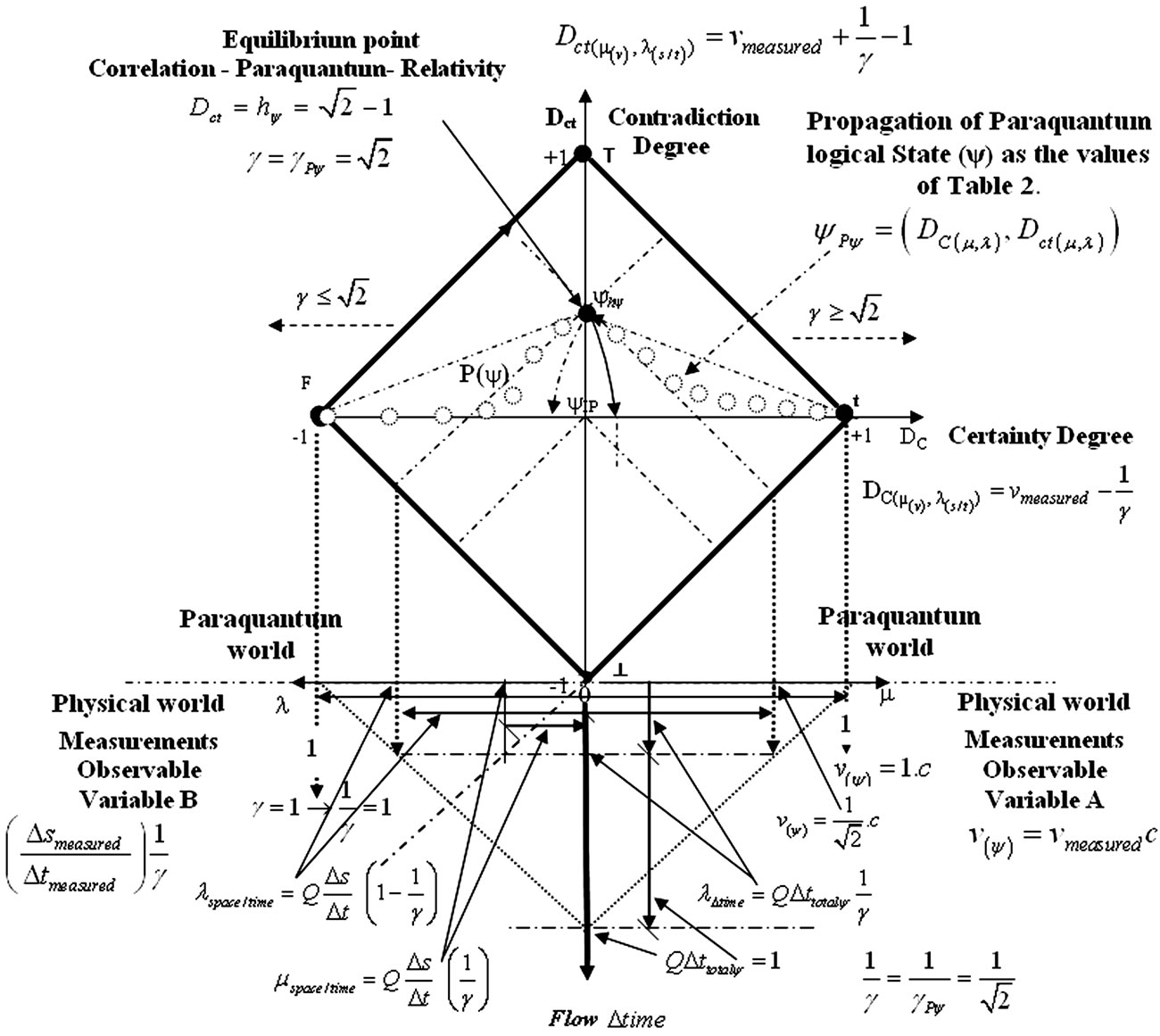
Figure 4. Representation of evidences degrees and the action of the time flow in the paraquantum analysis considered in relativity theory. Propagation of paraquantum logical State (ψ) as the DC and Dct values of Table 2.
The effects related to energy in the Newtonian universe, in the universe of the theory of relativity and in quantum mechanics, can be represented in a single Lattice of the Paraquantum logic. In the part II of this work we will study these phenomena.
5. Conclusions
In this paper we presented a study of physical phenomena that correlates the concepts of the Theory of the Relativity and foundations of the Paraquantum logic (PQL). Through the originated Equations of the Paraquantum Logical Model we did analogies with relativistic effects where we verified the relation between the Factor of Lorentz γ and the Paraquantum Gamma Factor . The effects of these factors were studied in detail and we observed that the Paraquantum Gamma Factor
. The effects of these factors were studied in detail and we observed that the Paraquantum Gamma Factor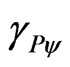 , which aggregates the phenomena found in the theory of relativity and in the Newtonian universe, promotes the connection among the physical universes through the correlation with the Paraquantum Factor of quantization
, which aggregates the phenomena found in the theory of relativity and in the Newtonian universe, promotes the connection among the physical universes through the correlation with the Paraquantum Factor of quantization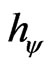 . Through the paraquantum equations we can consider time as an Observable Variable and thus extract degrees of evidence for the analysis. It was studied by paraquantum analysis as is the action of the time in the theory of relativity which can only be considered as a single factor of space/time. We studied as time, space and velocity can be correlated in relativistic and Newtonian world via the equilibrium point in Paraquantum Logic Model. As demonstrated in this work, the results are easy to view through of the PQL lattices and shows with clarity the behavior of physical quantities.
. Through the paraquantum equations we can consider time as an Observable Variable and thus extract degrees of evidence for the analysis. It was studied by paraquantum analysis as is the action of the time in the theory of relativity which can only be considered as a single factor of space/time. We studied as time, space and velocity can be correlated in relativistic and Newtonian world via the equilibrium point in Paraquantum Logic Model. As demonstrated in this work, the results are easy to view through of the PQL lattices and shows with clarity the behavior of physical quantities.
In part II of this work we will show the energy study with the Paraquantum Logic in three main areas of physical science. The paraquantum equations used in these areas have good possibilities for the foundations of unified calculation for Physical Science.
REFERENCES
- N. C. A. Da Costa and D. Marconi, “An Overview of Paraconsistent Logic in the 80’s,” The Journal of NonClassical Logic, Vol. 6, No. 1, 1989, pp. 5-31.
- N. C. A. Da Costa, “On the Theory of Inconsistent Formal Systems,” Notre Dame Journal of Formal Logic, Vol. 15, No. 4, 1974, pp. 497-510. doi:10.1305/ndjfl/1093891487
- S. Jas’kowski, “Propositional Calculus for Contradictory Deductive Systems,” Studia Logica, Vol. 24, No. 1, 1969, pp. 143-157. doi:10.1007/BF02134311
- J. I. Da Silva Filho, G. Lambert-Torres and J. M. Abe “Uncertainty Treatment Using Paraconsistent Logic—Introducing Paraconsistent Artificial Neural Networks,” IOS Press, Amsterdam, 2010.
- J. I. Da Silva Filho, “Paraconsistent Annotated Logic in analysis of Physical Systems: Introducing the Paraquantum Factor of Quantization hψ,” Journal of Modern Physics, Vol. 2, No. 11, 2011, pp. 1397-1409.
- C. A. Fuchs and A. Peres, “Quantum Theory Needs no ‘Interpretation’,” Physics Today, Vol. 53, No. 3, 2000, pp. 70-71. doi:10.1063/1.883004
- D. Krause and O. Bueno, “Scientific Theories, Models, and the Semantic Approach,” Principia, Vol. 11 No. 2, 2007, pp. 187-201.
- J. I. Da Silva Filho, “Analysis of Physical Systems with Paraconsistent Annotated Logic: Introducing the Paraquantum Gamma Factor γψ,” Journal of Modern Physics, Vol. 2, No. 12, 2011, pp. 1455-1469.
- J. I. Da Silva Filho, “Study of the Interactions between Particles Based in Paraquantum Logic,” Journal of Modern Physics, Vol. 3, No. 5, 2012, pp. 362-376. doi:10.4236/jmp.2012.35051
- Pl. A. Tipler and R. A. Llewellyn, “Modern Physics,” 5th Edition, W. H. Freeman and Company, New York, 2007.
- J. P. Mckelvey and H. Grotch, “Physics for Science and Engineering,” Harper and Row Publisher Inc, New York, London, 1978.
- Pl. A. Tipler, “Physics,” Worth Publishers Inc, New York, 1976.
- A. Einstein, “Relativity the Special and the General Theory,” Methuen & Co. Ltd., London, 1955.
- J. I. Da Silva Filho, “Analysis of the Spectral Line Emissions of the Hydrogen Atom with Paraquantum,” Journal of Modern Physics, Vol. 3, No. 3, 2012, pp. 233-254.
- J. I. Da Silva Filho, “An Introductory Study of the Hydrogen Atom with Paraquantum Logic,” Journal of Modern Physics, Vol. 3, No. 4, 2012, pp. 312-333.

