Journal of Modern Physics
Vol.3 No.7(2012), Article ID:21093,12 pages DOI:10.4236/jmp.2012.3780
Features of Malus Law in the Region of X-Ray Radiation
Department of Physics, Samara State University, Samara, Russia
Email: volobuev@samaramail.ru
Received April 19, 2012; revised May 18, 2012; accepted June 2, 2012
Keywords: Malus law; X-ray radiation; intermediate state of electron; effective section of interaction; formula of Klein-Nishina; X-ray laser
ABSTRACT
The light propagation through system a polarizer-analyzer is investigated on the basis of quantum conceptions about the nature of light. It is shown, that Malus law based on principles of classical electrodynamics not completely takes into account all effects which can occur at the light propagation through system a polarizer-analyzer. The phenomenon of possible change of frequency of light in particular drops out, for example in the region of X-ray radiation. The deduction of Malus law based on quantum principles is given. For comparison the differential effective section of interaction of a photon and electron with take into account of rotation of a plane of polarization of a photon in Compton’s effect is found.
1. Introduction
Malus law has experimentally been established by French physicist E. L. Malus in 1810. He tried to explain it on the basis of the corpuscular theory of light of Newton. This law allows calculate propagation of light through system a polarizer-analyzer, Figure 1. It easily explained on the basis of the wave nature of light [1].
If to rotate the analyzer A about the axis concerning polarizer P the intensity of light I leaving the analyzer will submit to the law:
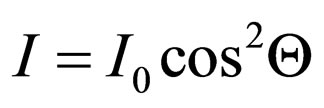 , (1)
, (1)
where —intensity of linearly polarized light falling on the analyzer,
—intensity of linearly polarized light falling on the analyzer, —an angle between planes of polarization of light falling on the analyzer and past through it. Last formula represents the contents of Malus law.
—an angle between planes of polarization of light falling on the analyzer and past through it. Last formula represents the contents of Malus law.
The purpose of article is the finding of Malus law on the basis of quantum representations about the nature of light, the physical analysis of an opportunity and validity of the given approach.
2. Interaction of Quantums of Electromagnetic Radiation with Electrons
The physical phenomenon reflected by Malus law in quantum representation, concerns to the big group of the phenomena of interaction of quantums of electromagnetic radiation with electrons. Absorption by substance of quantums of electromagnetic radiation basically result in the following processes: quantums can be absorbed
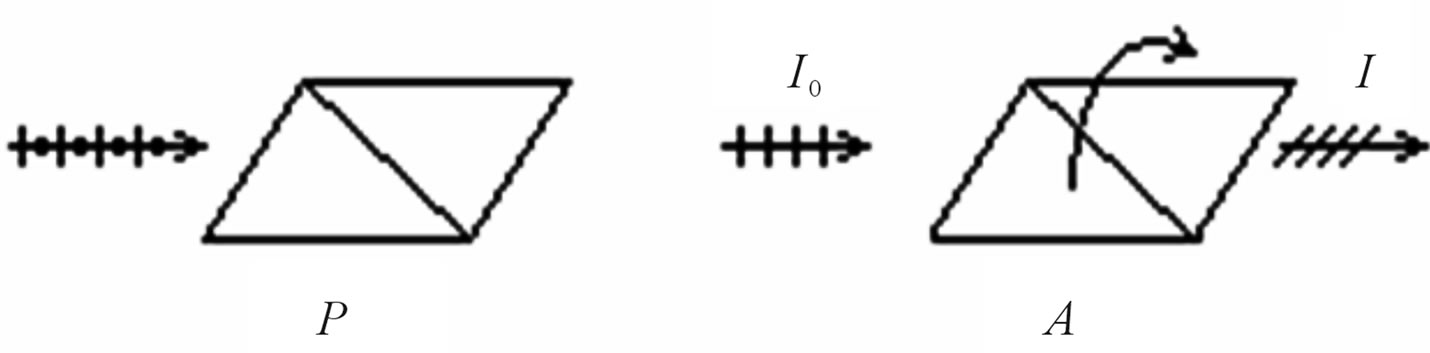
Figure 1. Passage of light through system a polarizer-analyzer.
without occurrence secondary electrons when all energy of quantums is transferred fonons-quantums of mechanical waves in a crystal lattice, and the impulse is transferred all crystal lattice of substance [2], at an internal photoeffect [3], Compton’s effect [4] and combinational scattering [5].
Latter two effects are accompanied by occurrence secondary, i.e. reradiated quantums with changed frequency, in comparison with falling on electron, and absorption of part energy of a falling photon. In [6] it is shown, that interaction of the polarized quantum of light with non-polarized electron can lead to turn of a plane of polarization reradiated quantum, and to change of frequency of secondary quantum in comparison primary quantum. From the point of view of Malus law, the phenomenon of turn of a plane of polarization reradiated quantum in comparison primary one enables this quantum to pass through the analyzer because separation of quantum as against an electromagnetic wave is considered impossible. A photo effect and Compton’s effect are inherent to, basically, for quantums high energy. At combinational scattering on connected electrons in the field of seen light also there is a change of frequency of light. At this form of interaction the absorption of a part of a falling on photon energy by substance is observed.
3. Physical Essence of a Problem
At passage of light through the analyzer there is an interaction of photons with connected electrons in a crystal lattice of substance of the analyzer.
Interaction of electromagnetic radiation with connected electrons of atoms or ions of a crystal lattice is complex and multiple physical processes. Therefore we shall consider the elementary physical phenomenon— interaction of electromagnetic radiation with free or poorly connected initially motionless electrons at which the increase in length of wave reradiated quantum can be observed. If energy of falling radiation is great enough, for example, X-ray radiation the connection electrons in atoms it is possible to neglect and assume that electrons cooperate with radiation, as free particles [7].
Taking into account, that quantum of light or a photon elementary, i.e. indivisible a particle of an electromagnetic field, direct division of quantum is impossible. However such division is present at Compton’s effect (so usually name interaction of quantum with motionless free electron), but it occurs by means of other elementary particle of substance-electron.
Taking into account far incomplete representations, both about the nature of quantum, and about the nature of electron, in modern physics it was necessary to enter concept about “intermediate states” systems a photon-electron during their interaction. These intermediate states it is enough unusual. They are characterized, first, by an opportunity negative electron energy, and second, infringement of the law of energy conservation.
Whether have intermediate states any physical sense or are only mathematical reception for calculation? This question till now has not found the answer. There is no also an answer to a question, whether used mathematical receptions are at the given physical preconditions, i.e. at use of concept of an intermediate state, correct enough?
For more detailed analysis of the set questions we shall consider transition of an initial state of system a photon-electron  to its final state
to its final state  . In this case S (start) means an initial state of system F (finish)-its final state.
. In this case S (start) means an initial state of system F (finish)-its final state.
Parameters of system a photon-electron in an initial state: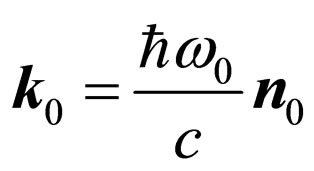 —a vector of an impulse of a photon in an initial state, where
—a vector of an impulse of a photon in an initial state, where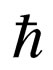 —Planck’s reduced constant,
—Planck’s reduced constant, —cyclic frequency of an initial photon, c—speed of light in vacuum,
—cyclic frequency of an initial photon, c—speed of light in vacuum,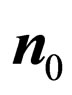 —an unit vector in a direction of radiation of an initial photon;
—an unit vector in a direction of radiation of an initial photon;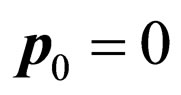 —an impulse immovable electron in an initial state;
—an impulse immovable electron in an initial state; —energy of a photon in an initial state;
—energy of a photon in an initial state; —energy immovable electron in an initial state,
—energy immovable electron in an initial state,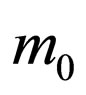 —its rest mass.
—its rest mass.
Parameters of system a photon-electron in a final state:
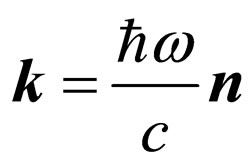 —a vector of an impulse of a photon in a final state,
—a vector of an impulse of a photon in a final state, —cyclic frequency of a final photon,
—cyclic frequency of a final photon,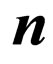 —a unit vector in a direction of radiation of a final photon;
—a unit vector in a direction of radiation of a final photon;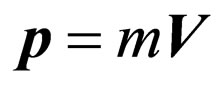 —an impulse of electron in a final state,
—an impulse of electron in a final state,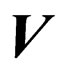 —its speed,
—its speed,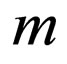 —its relativistic mass;
—its relativistic mass;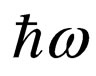 —energy of a photon in a final state;
—energy of a photon in a final state; —energy of electron in a final state, р—the module of an impulse of electron in a final state.
—energy of electron in a final state, р—the module of an impulse of electron in a final state.
Transition of system a photon-electron from a state  in a state
in a state 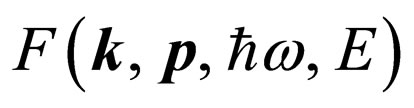 is possible under the following schemes [6,8,9].
is possible under the following schemes [6,8,9].
At first the electron absorbs a photon and transit in an intermediate state with energy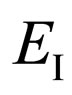 . In this state in system there are no photons. Electron in this case gets an impulse
. In this state in system there are no photons. Electron in this case gets an impulse 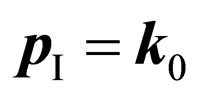 which is equal to an impulse of the absorbed photon. Then electron emit a photon with an impulse
which is equal to an impulse of the absorbed photon. Then electron emit a photon with an impulse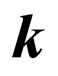 , getting energy Е and an impulse р.
, getting energy Е and an impulse р.
The scheme of transition is shown with the help so-called diagrams of Feynman on Figure 2. The straight lines designate movement of electron, wavy-photons. The dotted line specifies that real movement of electron in this case is absent.
The most unpleasant in this scheme, that it cannot be realized. First of all, it is experimentally established, that there is no time interval between acts of absorption and emission of a photon [10]. There is no instant equality energy or impulses electron and the falling quantum.
However, there are more serious another objection against the scheme on the Figure 2. The law of conservation of an impulse at absorption of a photon by electron in the scalar form looks like 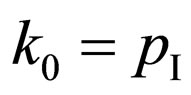 or
or 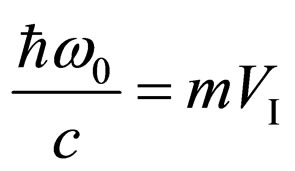 , where
, where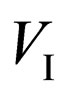 —speed of electron in an intermediate state, m—its relativistic mass. The law of conservation of energy can be written down as:
—speed of electron in an intermediate state, m—its relativistic mass. The law of conservation of energy can be written down as:
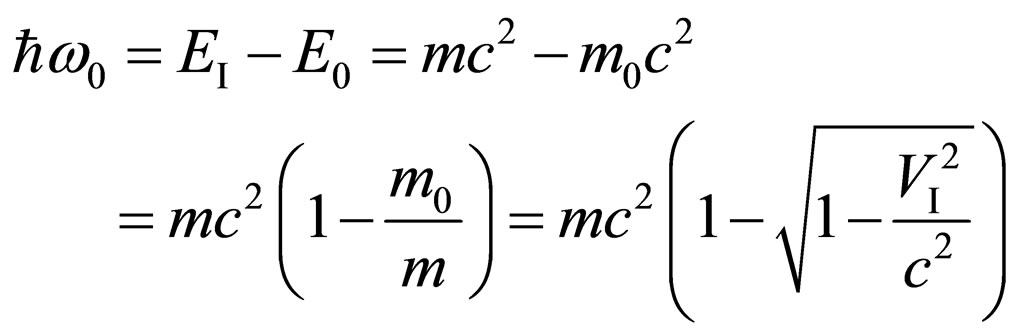 .
.
Having divided the law of conservation of energy on the law of conservation of an impulse, we receive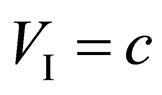 , that, naturally, it is impossible. Hence, one of two laws is not carried out. Usually there are assume, that the law of conservation of energy [5,8] is not carried out. It results also to non-execution of the law of conservation of energy and at radiation of a photon k since as a whole at transition of system a photon-electron from a state
, that, naturally, it is impossible. Hence, one of two laws is not carried out. Usually there are assume, that the law of conservation of energy [5,8] is not carried out. It results also to non-execution of the law of conservation of energy and at radiation of a photon k since as a whole at transition of system a photon-electron from a state 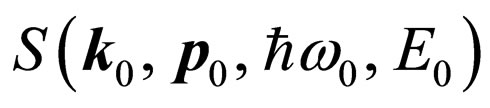 to a state
to a state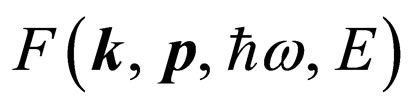 , laws of conservation of energy and an impulse should be carried out. We shall note also, that energy of electron in an intermediate state, formally, taking into account
, laws of conservation of energy and an impulse should be carried out. We shall note also, that energy of electron in an intermediate state, formally, taking into account
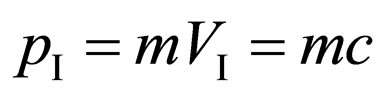 , satisfies to a condition
, satisfies to a condition
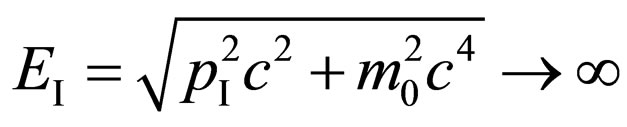 , since at
, since at 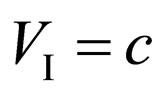 the mass
the mass
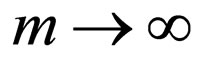 .
.
With the purpose of overcoming the given difficulty, is consisting that free electron cannot absorb the quantum of light, in system the photon-electron is added, at the given stage of development of physics, actually the third substance, namely, vacuum. We shall not stop on the theory of vacuum, its assume structure, we shall note only, that the surplus part of energy of electron  is transferred for a while to vacuum. Hence, the law of conservation of energy at interaction of a photon and electron looks like
is transferred for a while to vacuum. Hence, the law of conservation of energy at interaction of a photon and electron looks like 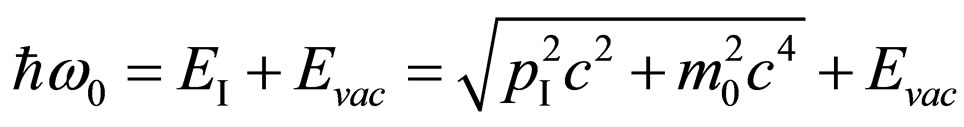 . Then energy of vacuum return in system a photon-electron, translating it in a state
. Then energy of vacuum return in system a photon-electron, translating it in a state . If to accept energy of vacuum
. If to accept energy of vacuum 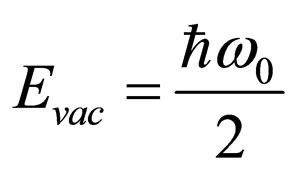 (so-called energy of electromagnetic vacuum) the impulse of electron in an intermediate state (under condition of
(so-called energy of electromagnetic vacuum) the impulse of electron in an intermediate state (under condition of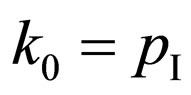 ) becomes equal to imaginary expression
) becomes equal to imaginary expression , that is inadmissible.
, that is inadmissible.
It is possible to assume energy of vacuum  where in this case n—the whole number is more than unit. In this case energy of electron
where in this case n—the whole number is more than unit. In this case energy of electron 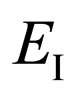 in an intermediate state to become zero (at
in an intermediate state to become zero (at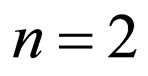 ) or negative (at
) or negative (at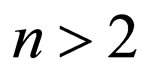 )
)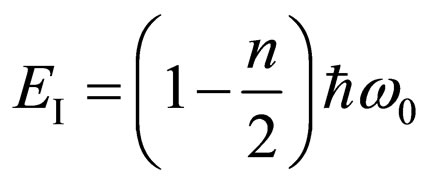 .
.
Usually, negative energy of electron in an intermediate state formally connected with an opportunity of a sign a minus before a root in expression for energy 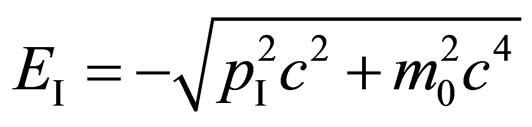 [8].
[8].
4. Quantum Deduction of Malus Law
Quantum deduction of the Malus law we shall begin with the analysis of interaction of photons and electron in the analyzer. Thus we use approximation of free electrons [7]. At a deduction we shall not pay attention on physical nonsense, which were discussed earlier.
Research of processes of transition of electron in an intermediate state 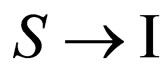 rather simple because linear of the Hamilton’s operator concerning value
rather simple because linear of the Hamilton’s operator concerning value 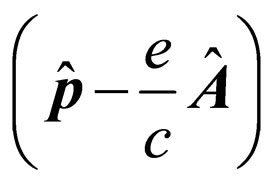 [5].
[5].
At use Coulomb’s calibrations of potentials, we have:
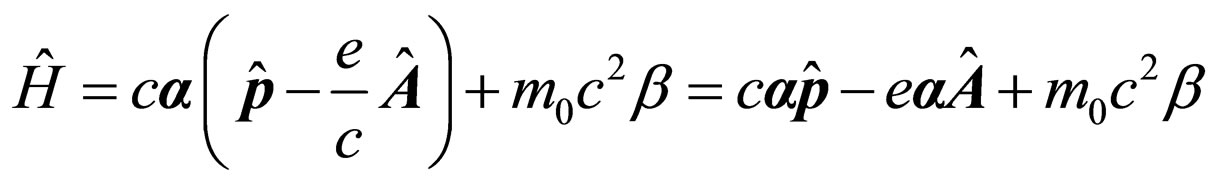 , (2)
, (2)
where A is a vector-potential of a photon, е—a charge of electron, a—so-called a matrix vector (a vector, which coordinate projections-square matrixes of 4-th order, with components 0, ±1, ±i), b—a square matrix of 4-th order with components 0, ±1 [5].
All factors of matrix vector a is four-vectors, at which fourth component is imaginary [5]. Energy of interaction the photon-electron characterizes only the second addend (2). In (2) it is supposed, that the vector-potential of a photon is periodic function of coordinates  ,
,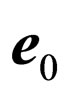 —a unit vector of polarization of an initial photon, V—some normalizing volume. Therefore it is possible to write down:
—a unit vector of polarization of an initial photon, V—some normalizing volume. Therefore it is possible to write down:
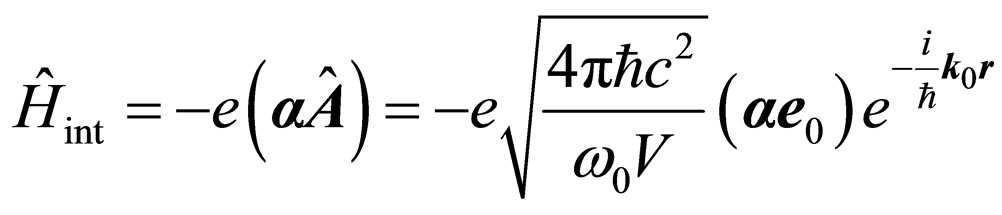 . (3)
. (3)
The matrix element of transition of the electron states  looks like:
looks like:
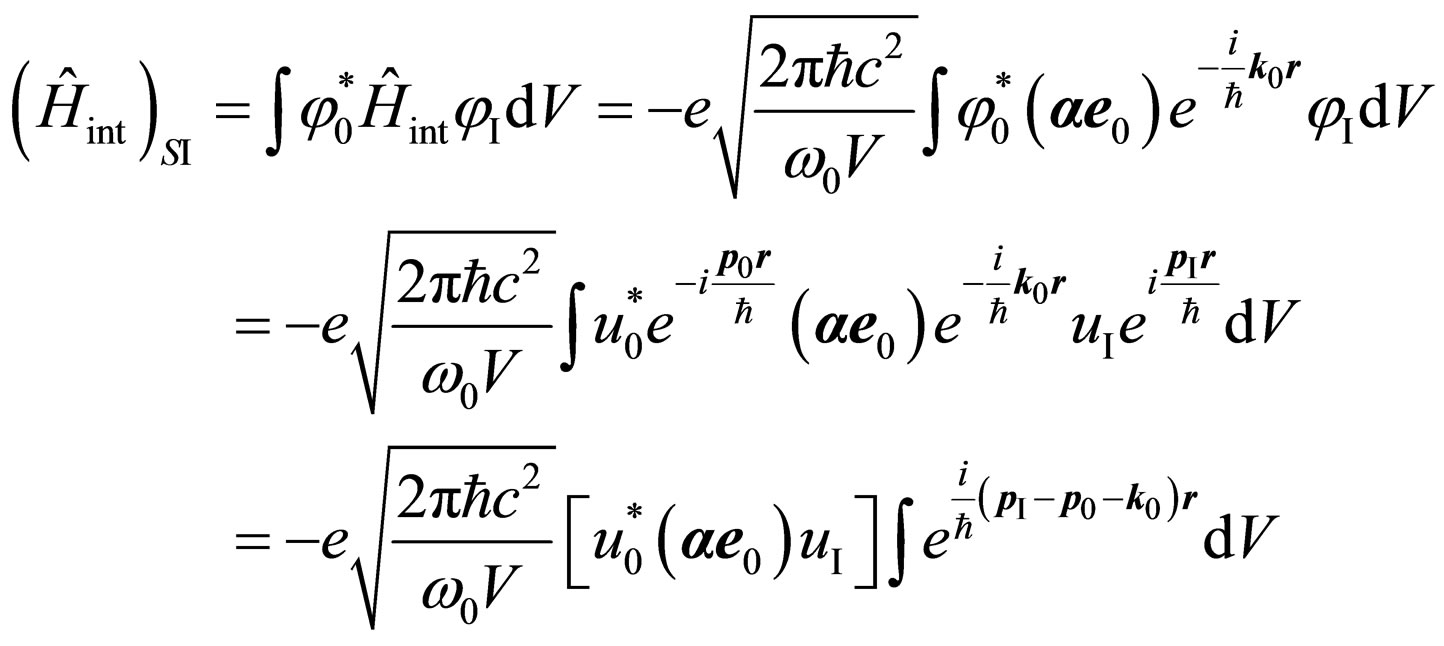 , (4)
, (4)
where 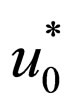 is the conjugate amplitude of wave function
is the conjugate amplitude of wave function 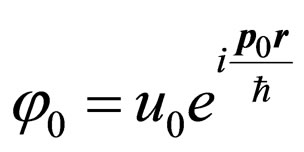 in an initial condition of the electron, r—its radius-vector. After absorption of a photon we believe, that position of the electron has not changed,
in an initial condition of the electron, r—its radius-vector. After absorption of a photon we believe, that position of the electron has not changed, 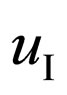 is amplitude of wave function
is amplitude of wave function 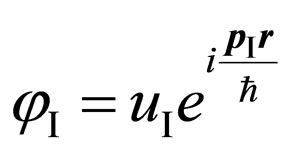 in an intermediate state.
in an intermediate state.
Taking into account the law of conservation of an impulse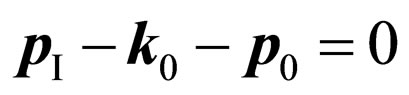 , we have
, we have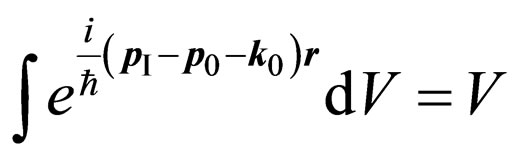 .
.
Believing normalizing volume , we shall find a matrix element of transition
, we shall find a matrix element of transition :
:
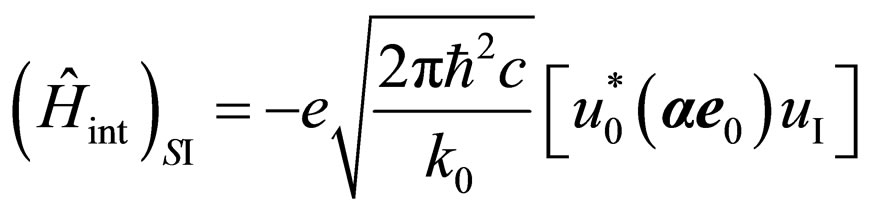 . (5)
. (5)
The received expression corresponds, for example, [8].
Let’s consider process of radiation of a photon k in the scheme on Figure 2, i.e. in process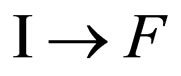 .
.
Similar previous the transformations allow to receive a matrix element of transition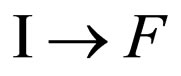 :
:
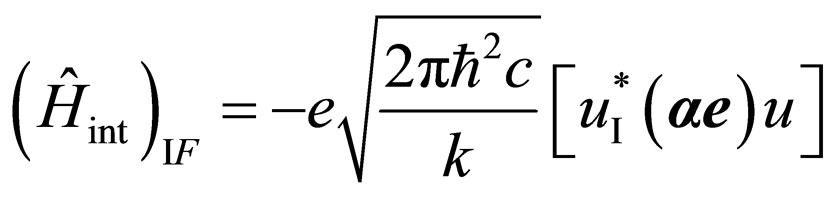 , (6)
, (6)
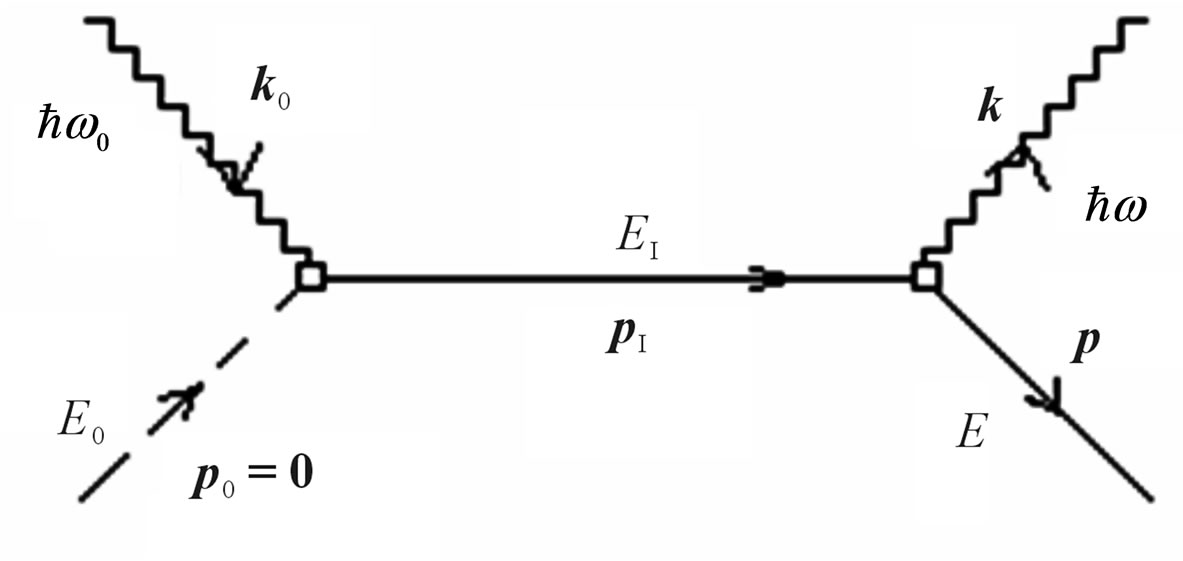
Figure 2. Diagram of Feynman of the first type for interaction of a photon and the electron.
where  is the conjugate amplitude of wave function of the electron in an intermediate state, u—amplitude of wave function of the electron in a final condition,
is the conjugate amplitude of wave function of the electron in an intermediate state, u—amplitude of wave function of the electron in a final condition, —a unit vector of polarization of a final photon.
—a unit vector of polarization of a final photon.
For the full description of transition  of system a photon-electron, it is necessary to consider one more formal variant of process which can be represented diagram of Feynman shown on Figure 3.
of system a photon-electron, it is necessary to consider one more formal variant of process which can be represented diagram of Feynman shown on Figure 3.
According to the considered scheme of transition, Figure 3, motionless ( ) electron having energy
) electron having energy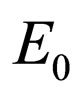 , all over again radiates the quantum an impulse k and energy
, all over again radiates the quantum an impulse k and energy 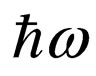 and passes in an intermediate state II. Then the electron absorbs initial quantum with an impulse
and passes in an intermediate state II. Then the electron absorbs initial quantum with an impulse 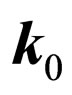 and energy
and energy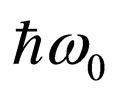 , getting an impulse р and energy Е.
, getting an impulse р and energy Е.
The matrix element of transition  with radiation of a photon looks like:
with radiation of a photon looks like:
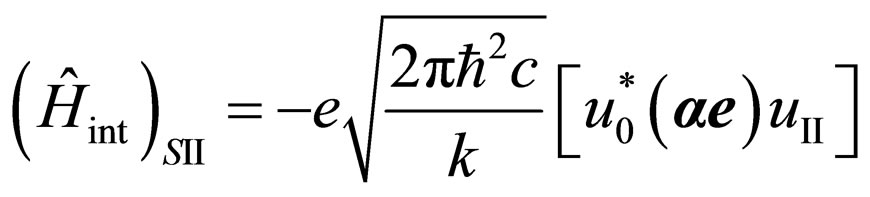 , (7)
, (7)
and the matrix element of transition  with absorption of a photon looks like:
with absorption of a photon looks like:
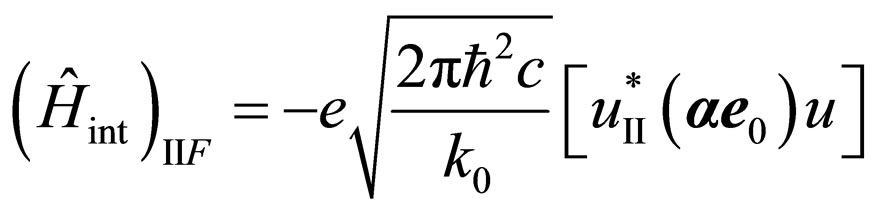 , (8)
, (8)
where 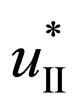 and
and 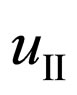 is the conjugate and primary amplitudes of wave function of the electron in an intermediate state.
is the conjugate and primary amplitudes of wave function of the electron in an intermediate state.
The compound matrix element determining full probability of transition  looks like [5]:
looks like [5]:
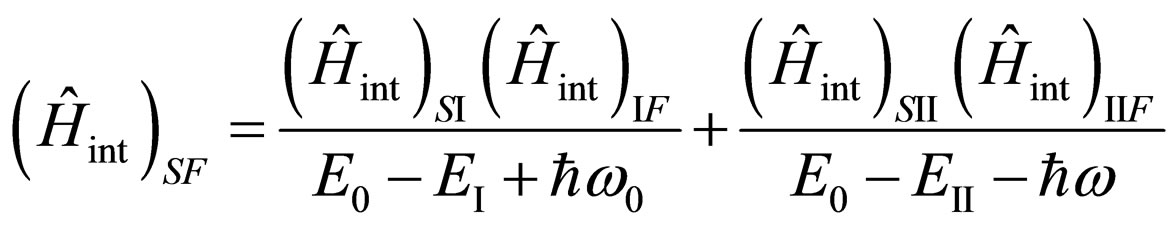 . (9)
. (9)
Let’s substitute in (9) formulas (5)-(8):
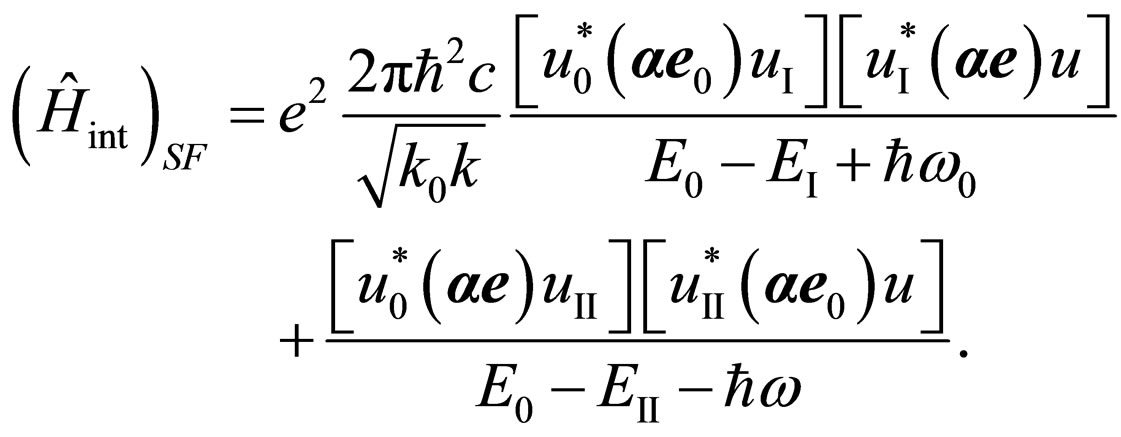 (10)
(10)
The probability of transition  is in unit of time proportional to a square of a corresponding matrix element [5]:
is in unit of time proportional to a square of a corresponding matrix element [5]:
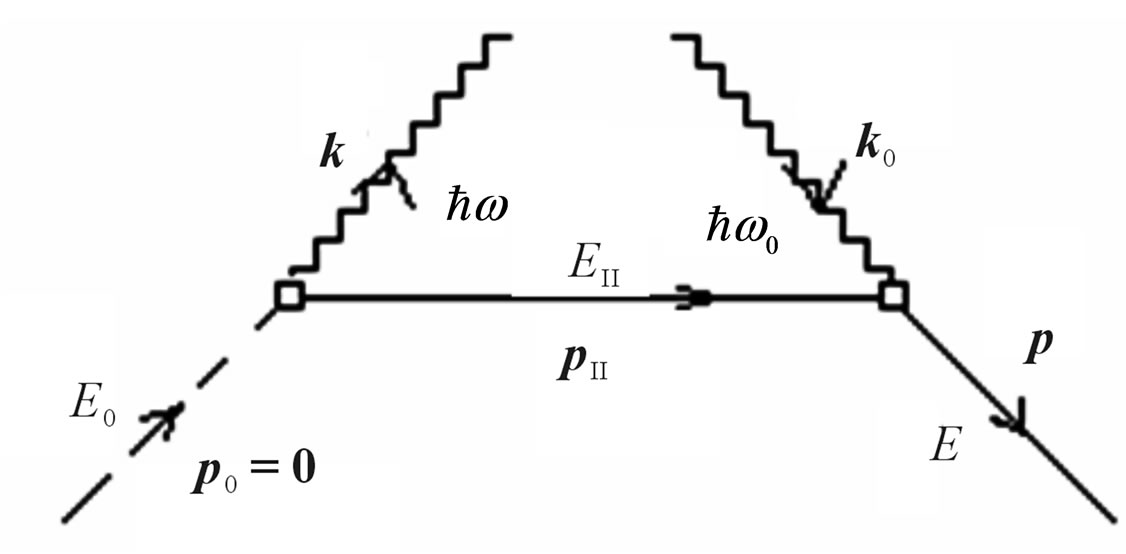
Figure 3. Diagram Feynman of the second type for interaction of a photon and the electron.
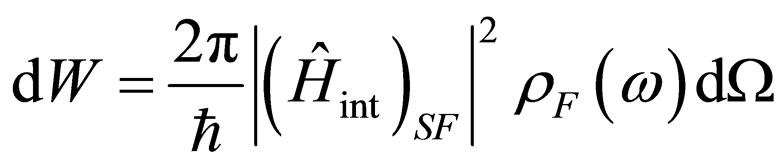 , (11)
, (11)
where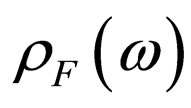 —number of final state of system the photon-electron, contained in a unit interval of energy of a final state [8],
—number of final state of system the photon-electron, contained in a unit interval of energy of a final state [8],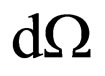 —a solid angle describing a direction of a start of reradiated photon.
—a solid angle describing a direction of a start of reradiated photon.
The number of final states reradiated photon contained in an interval of photon energy corresponding an impulse interval  is equal
is equal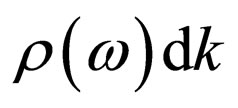 , where
, where 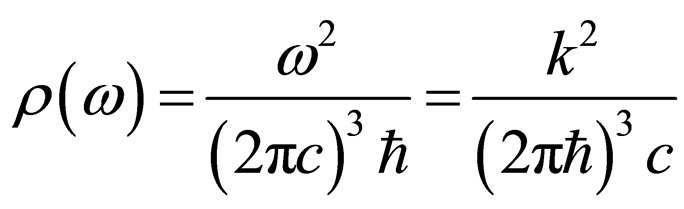 —number of states of the photons contained in a unit interval of their energy [5]. Naturally, the number of states of photons will define number of states of all system:
—number of states of the photons contained in a unit interval of their energy [5]. Naturally, the number of states of photons will define number of states of all system:
 , (12)
, (12)
where 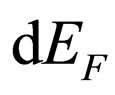 is an energy interval of a final state of the system, corresponding to an impulse interval of photons
is an energy interval of a final state of the system, corresponding to an impulse interval of photons  ,
,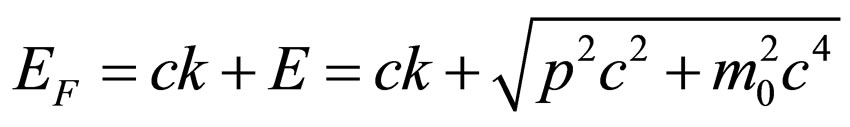 .
.
Hence:
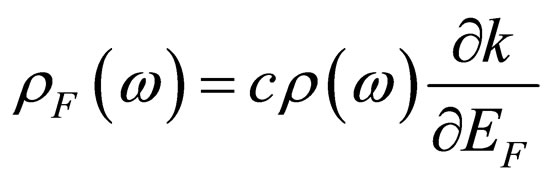 . (13)
. (13)
Substituting (13) in (11), we shall find probability of transition  in unit of time:
in unit of time:
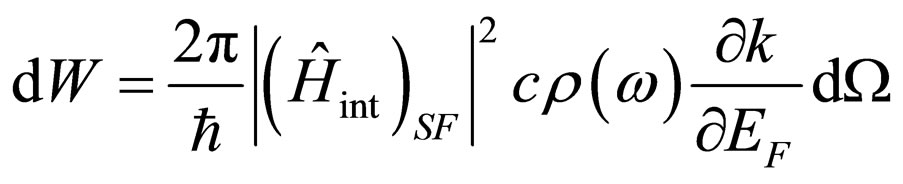 . (14)
. (14)
For finding of differential effective section of process, we shall divide probability of transition in unit of time into numerical density of a flux of falling quantums [5]. One quantum is absorbed, therefore we assume, that in normalizing volume V there is only one quantum. Intensity in this case is equal . Therefore the numerical density of a flux of photons under condition
. Therefore the numerical density of a flux of photons under condition 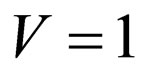 , is equal
, is equal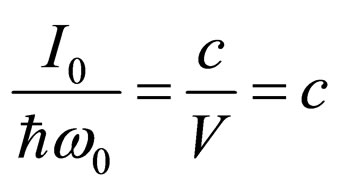 . Hence, differential effective section of process:
. Hence, differential effective section of process:
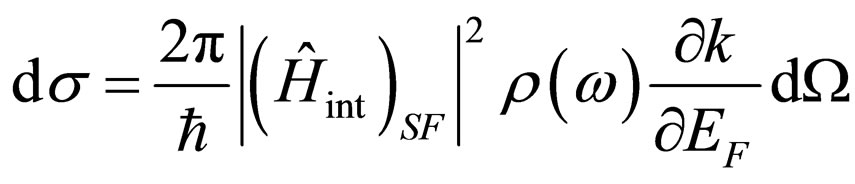 . (15)
. (15)
Further substituting (10) in (15), with the account 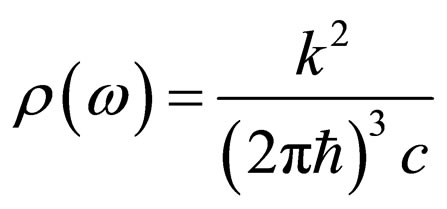 , we shall find:
, we shall find:
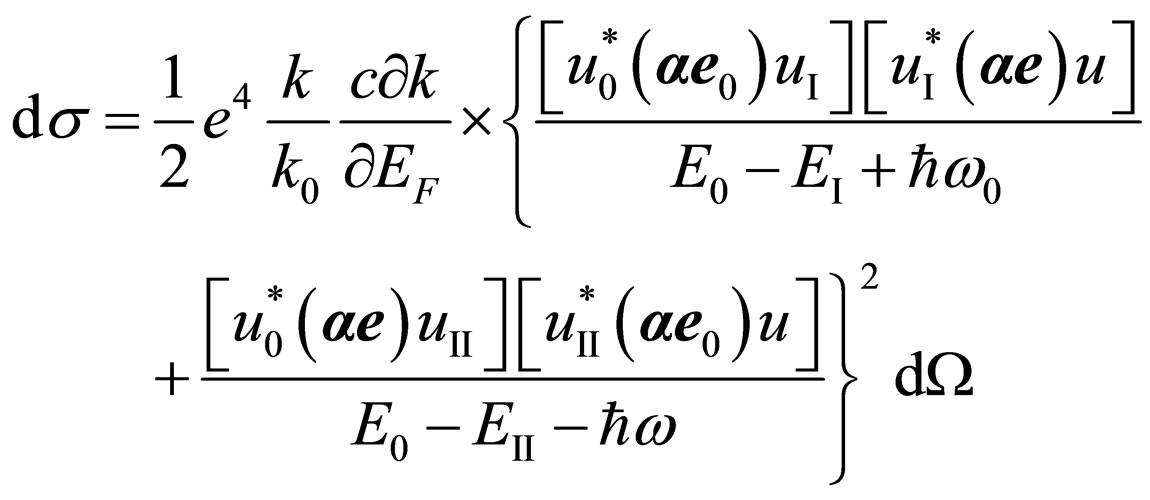 . (16)
. (16)
Factor 1/2 in (16) is consequence of averaging of differential effective section of interaction the photon-electron on spin states of the electron in its initial state [5]. It is similarly, for example, averaging of differential effective section of scattering of the non-polarized wave on a vector of polarization of an electromagnetic wave at the deduction of the Thomson’s formula [7].
Let’s find matrix elements in the formula (16). We shall consider the first addend in brackets. We shall multiply numerator and a denominator in it on 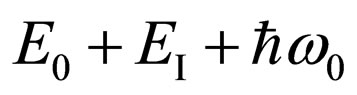 . In result we shall receive:
. In result we shall receive:
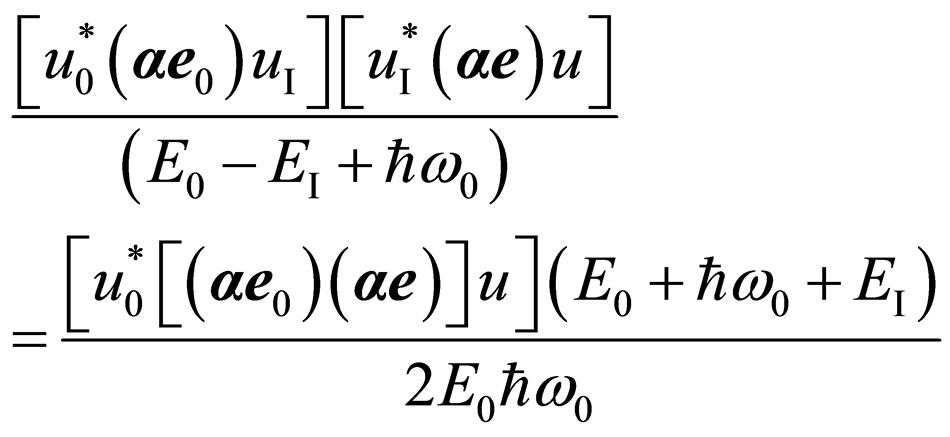 . (17)
. (17)
In numerator the known formula
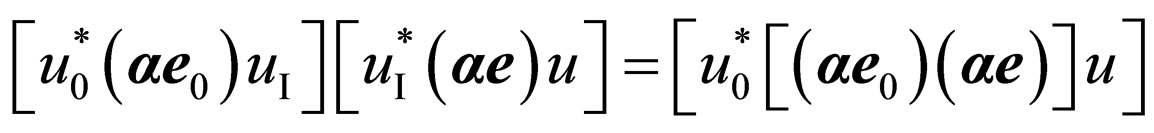 is used, and also
is used, and also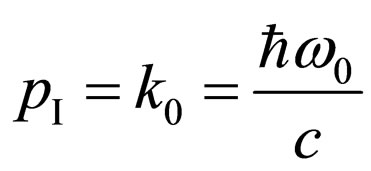 .
.
Similarly, multiplication of numerator and a denominator on  with the account
with the account 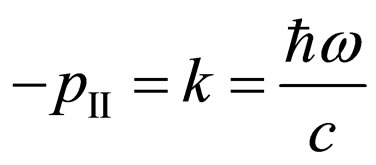 , will transform the second addend (16).
, will transform the second addend (16).
Hence, the formula (16) gets a form:
 (18)
(18)
In intermediate states with energy 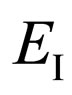 and
and  the electron is a free particle on which the electromagnetic field does not influence, therefore the amplitude of its wave function satisfies to Dirac’s equation [5]:
the electron is a free particle on which the electromagnetic field does not influence, therefore the amplitude of its wave function satisfies to Dirac’s equation [5]:
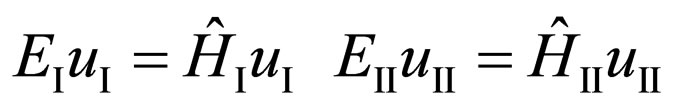 , (19)
, (19)
where Hamilton’s operators follow from the formula (2) at 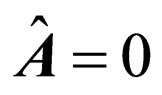 since in intermediate states there are no photons:
since in intermediate states there are no photons:
 , (20)
, (20)
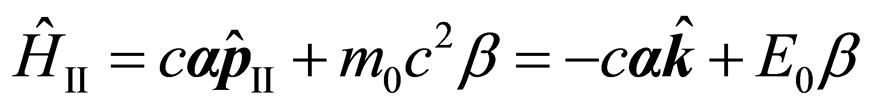 , (21)
, (21)
where it is taken into account , Figure 2, and
, Figure 2, and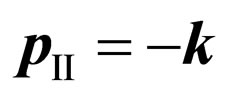 , Figure 3. Hence, it is possible to assume
, Figure 3. Hence, it is possible to assume 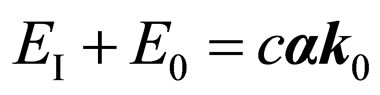 and
and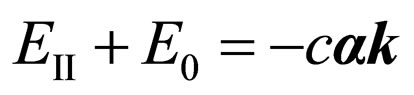 , where
, where —an initial level of reading of energy equal to initial energy of the motionless electron. Components of a matrix
—an initial level of reading of energy equal to initial energy of the motionless electron. Components of a matrix . It is used
. It is used , since initial and intermediate energy in additional factors
, since initial and intermediate energy in additional factors 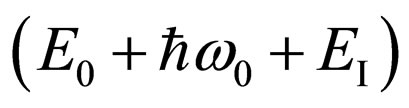 and
and 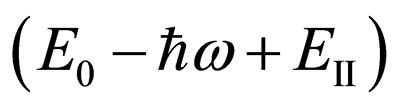 it is summarized. Substituting these values in (18), we shall find:
it is summarized. Substituting these values in (18), we shall find:
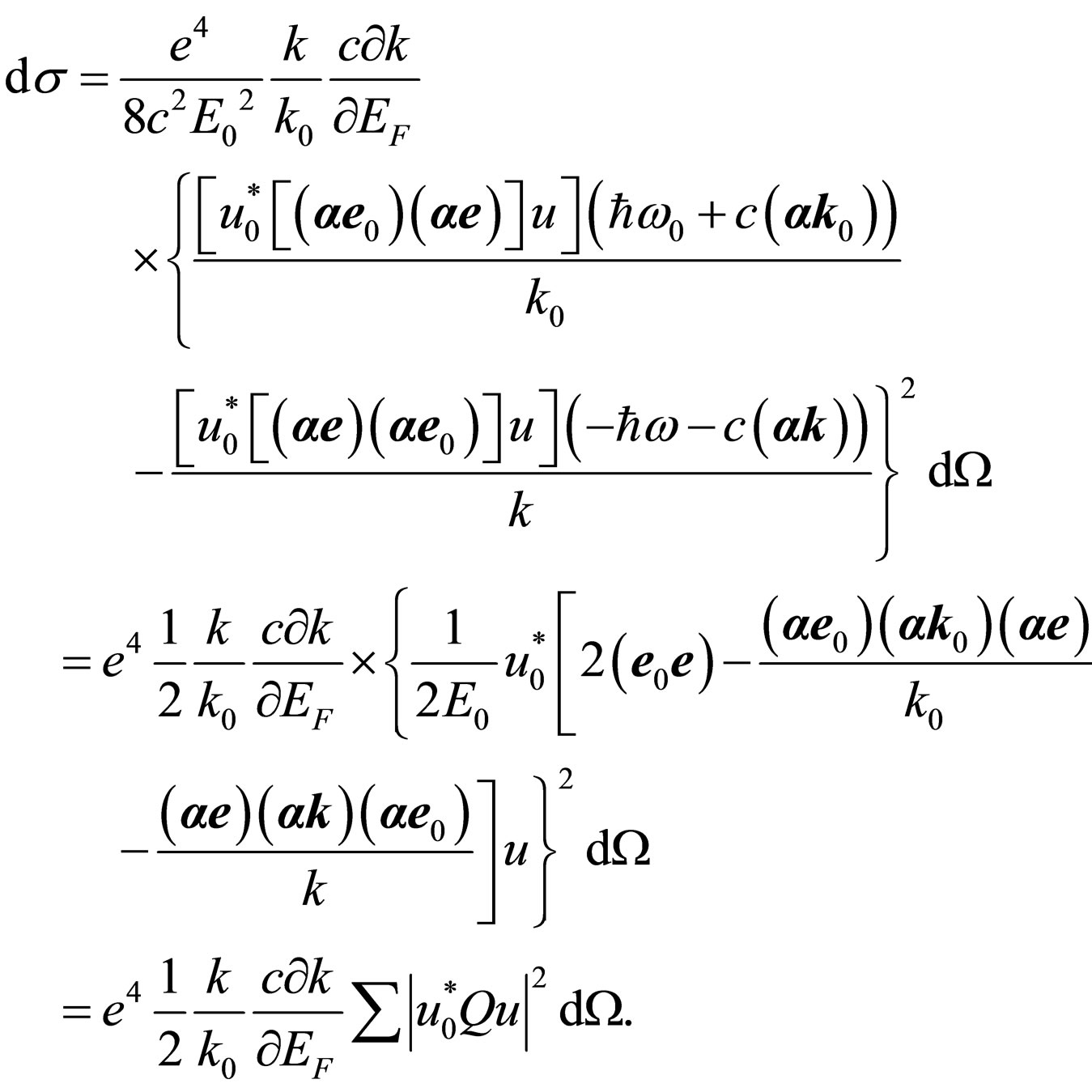 (22)
(22)
where it is designated:
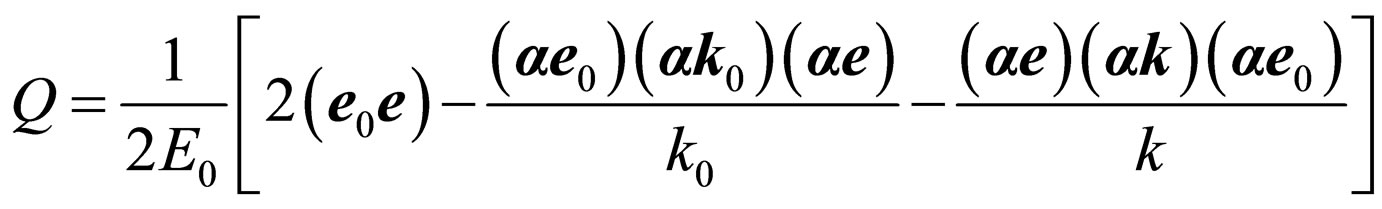 . (23)
. (23)
Known rules of work with a matrix vector [5,8] are used. Property of a matrix vector  is used. Besides the following properties of action of a matrix vector on mutually perpendicular vectors
is used. Besides the following properties of action of a matrix vector on mutually perpendicular vectors ,
, 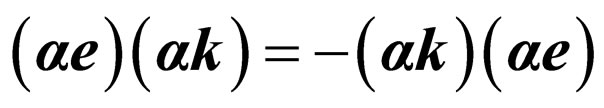 , and also an opportunity of cyclic rearrangement of factors are used. In the further transformations ratio
, and also an opportunity of cyclic rearrangement of factors are used. In the further transformations ratio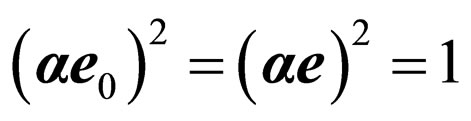 ,
,  ,
, 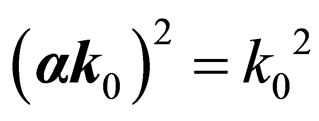 also will be necessary.
also will be necessary.
Summation in (22) is carried out on two spin, real states of the electron with positive energy. For distribution of summation on 4 states of the electron (2 spin and 2 signs on energy) are entered so-called the projective operator (at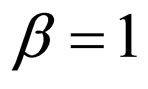 ) [5]:
) [5]:
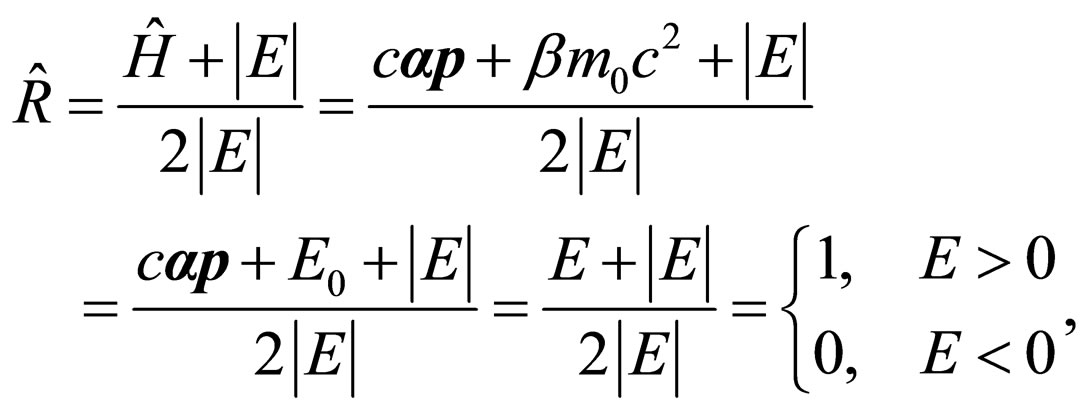 (24)
(24)
where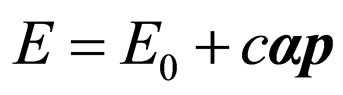 .
.
At use of the projective operator a states with negative energy of the contribution to a total sum do not bring. Hence, expression (22) can be written down as [5]:
 (25)
(25)
where
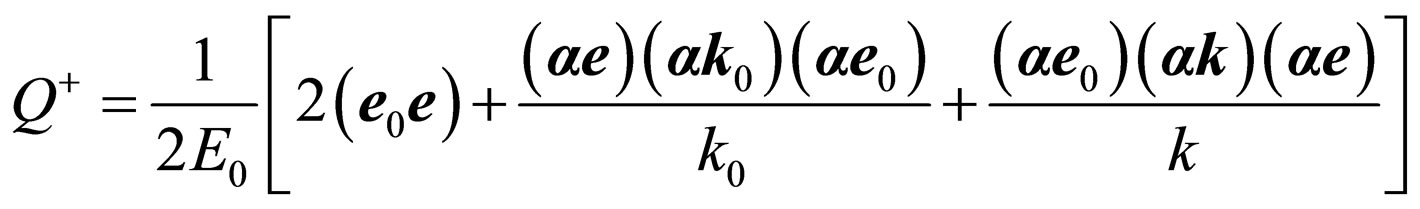
is the conjugate operator as result replacement of sequence factors of the matrix operator in (23) on return and change of a sign before addends with matrix vector a [6]. The projective operator  because the initial impulse of the electron is equal to zero
because the initial impulse of the electron is equal to zero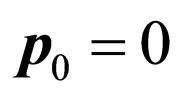 .
.
The projective operator of the free electron, according to a form of the Hamilton’s operator (2) in Dirac’s equation (at  and
and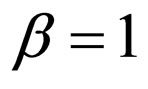 ) in a final state, taking into account
) in a final state, taking into account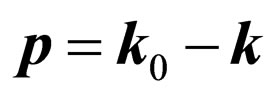 , is equal:
, is equal:
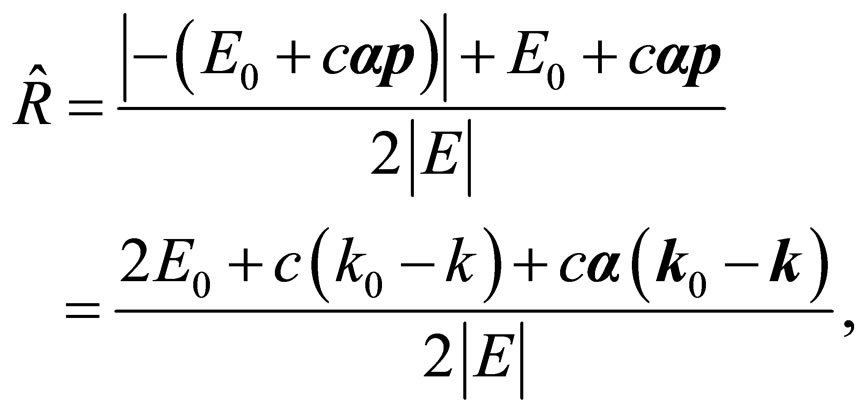 (26)
(26)
where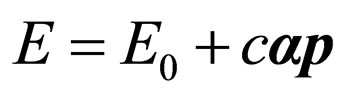 .
.
Substituting (23) and (26) in (25), we shall find:
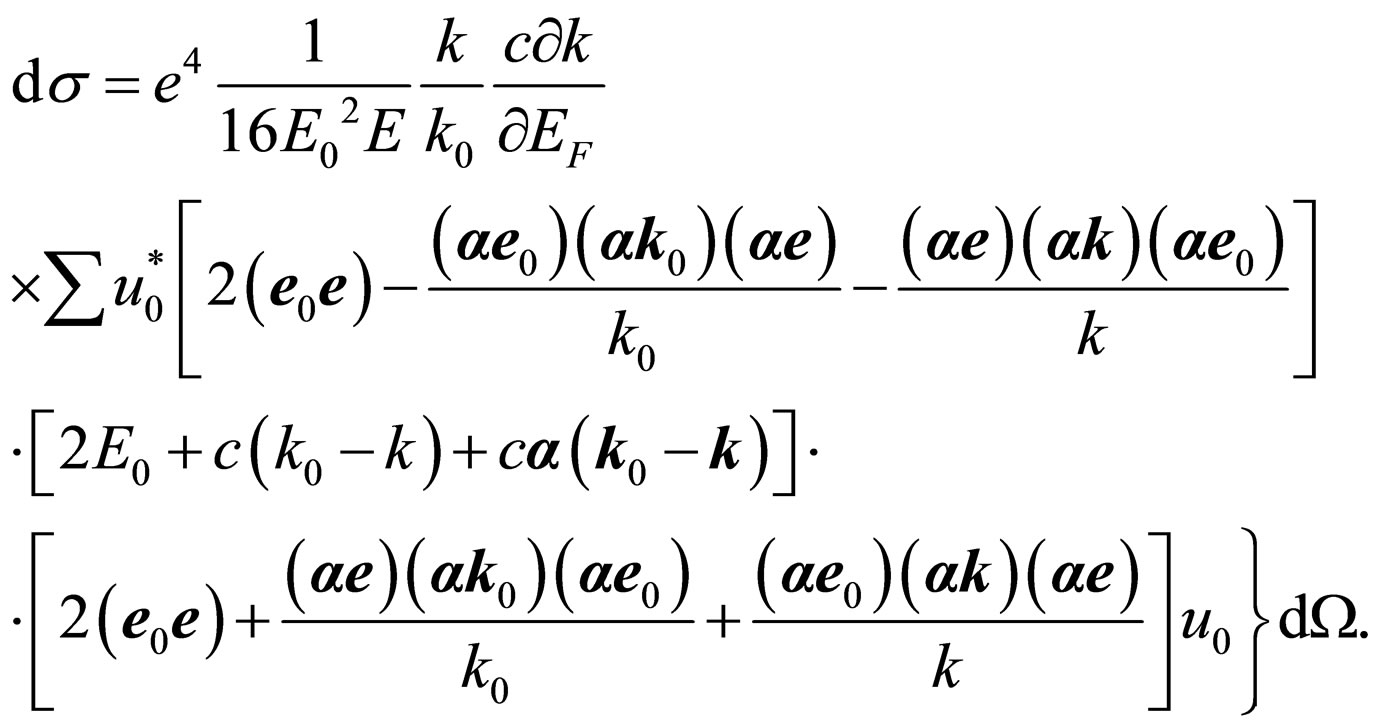 (27)
(27)
For calculation of expression under symbol of the sum we shall take advantage of a rule spur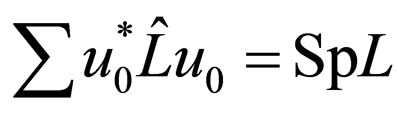 for example [5], where
for example [5], where  -some matrix operator.
-some matrix operator.
After multiplication of brackets, we use the ratio following from properties of a matrix vector: an opportunity of reverse rearrangement of factors with a and 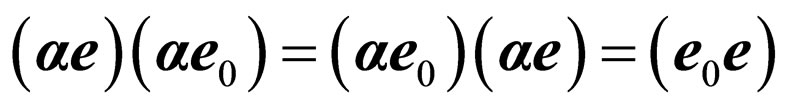 . In result we have:
. In result we have:
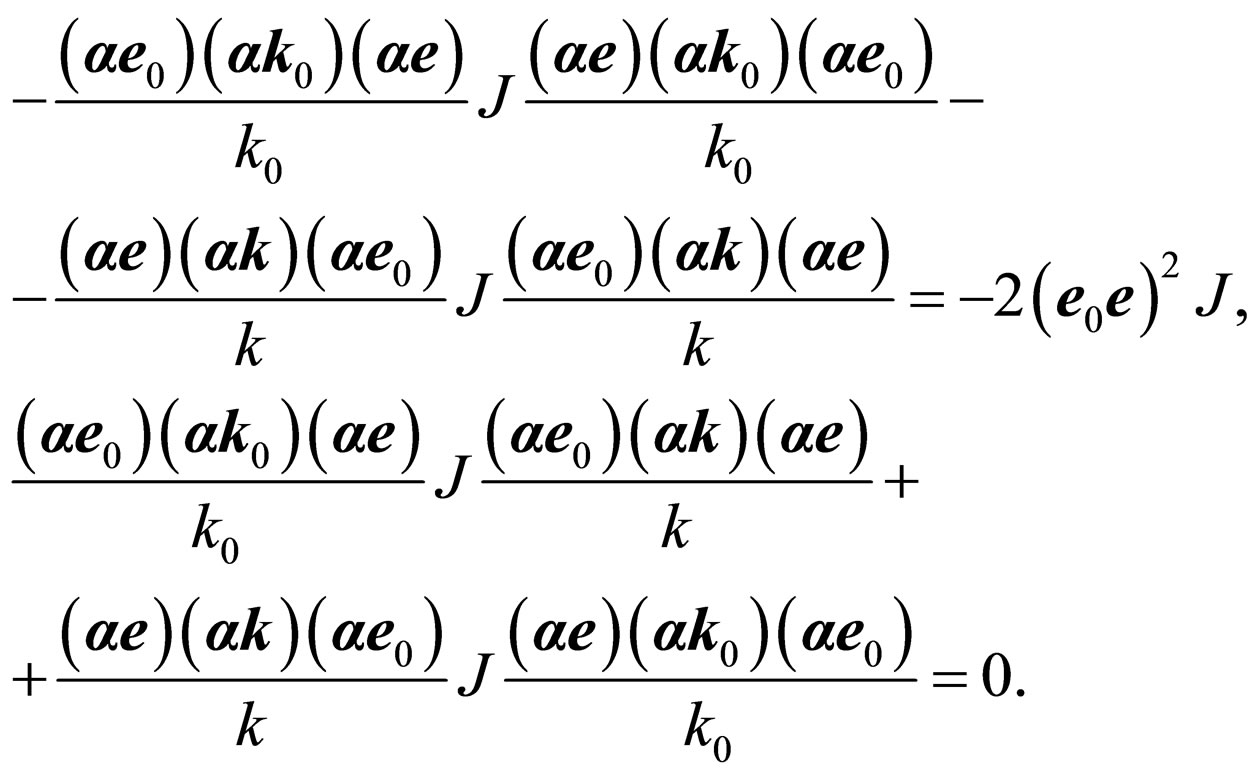
Carrying out simple, but bulky transformations, we use rules of work with spurs [11]: if b and c some vectorsand  is a matrix vector, that
is a matrix vector, that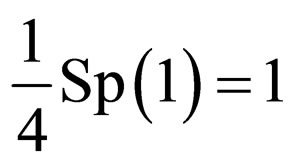 ,
, 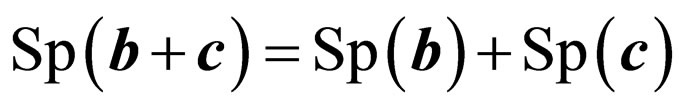 ,
, 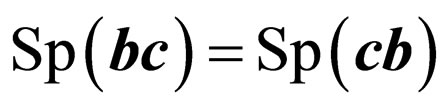 ,
, 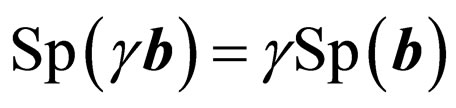 , where g-some algebraic function
, where g-some algebraic function 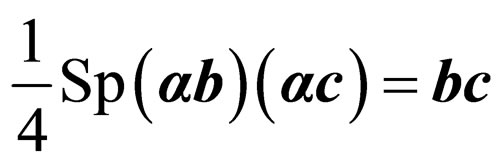 . Besides spur of addend with odd number of the factors containing a matrix vector it is equal to zero. Thus (27) it will be transformed:
. Besides spur of addend with odd number of the factors containing a matrix vector it is equal to zero. Thus (27) it will be transformed:
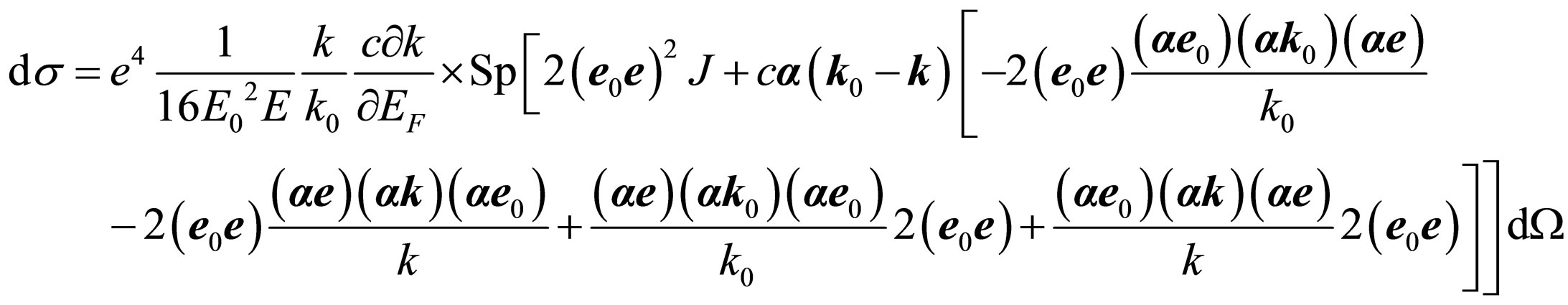
where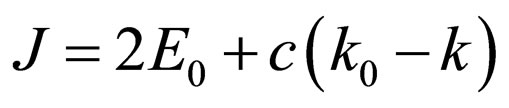 .
.
Taking into account, that the order of factors with a matrix vector under a symbol of spur it is possible to replace on reverse or to rearrange cyclically, and also linearity of a matrix vector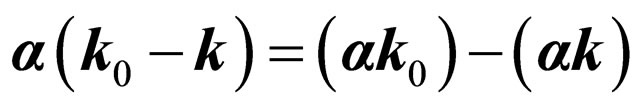 , we shall lead multiplication:
, we shall lead multiplication:
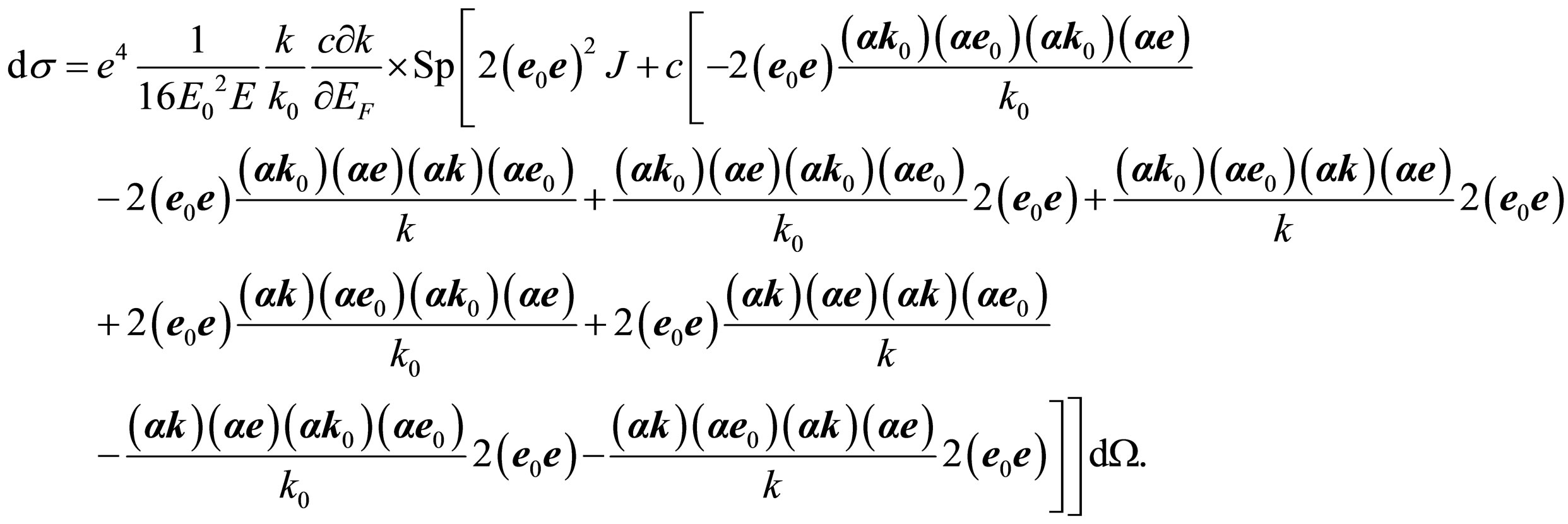
Then, allocating in everyone two addends in internal square brackets a scalar factor 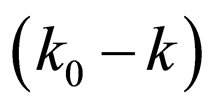 and taking out it of these brackets, we find:
and taking out it of these brackets, we find:
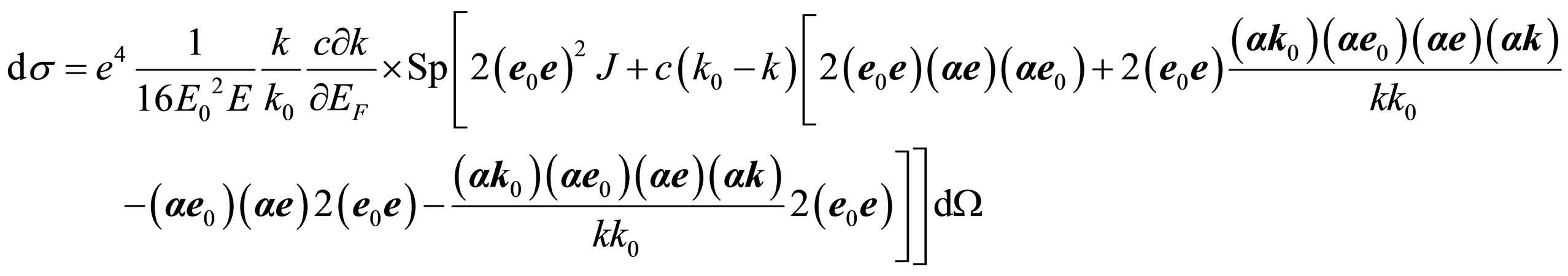 (28)
(28)
Expression in internal square brackets is equally zero. We shall note, that the given result excludes the vector form of impulses of the photons, falling  and reradiate
and reradiate 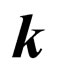 from the further consideration. It is possible to tell, that zero value of internal square brackets in (28) specifies an opportunity and validity of Malus law from the point of view of quantum electrodynamics. Hence, despite of some, existing now, the ambiguity of the physical preconditions discussed earlier, the mathematical base of quantum electrodynamics, at least, at a considered level, adequately describes physical laws, in particular Malus law. All further deduction is defined by absence of angular scattering of photons. Thus:
from the further consideration. It is possible to tell, that zero value of internal square brackets in (28) specifies an opportunity and validity of Malus law from the point of view of quantum electrodynamics. Hence, despite of some, existing now, the ambiguity of the physical preconditions discussed earlier, the mathematical base of quantum electrodynamics, at least, at a considered level, adequately describes physical laws, in particular Malus law. All further deduction is defined by absence of angular scattering of photons. Thus:
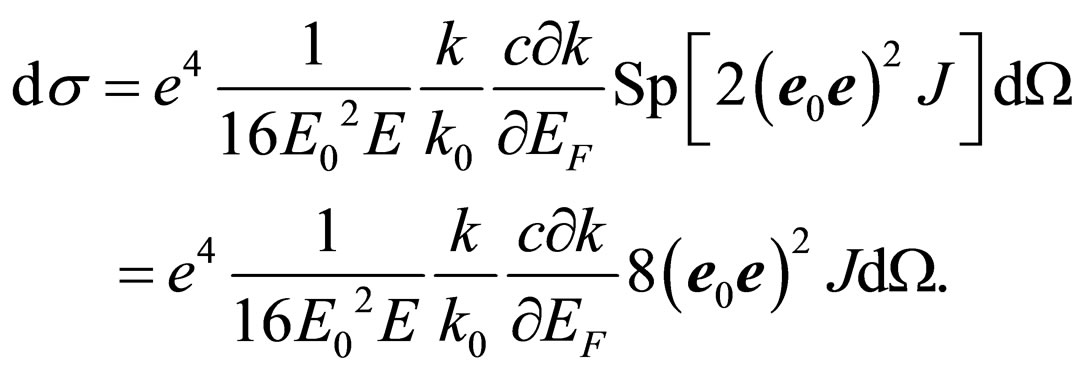 (29)
(29)
Let’s find a derivative 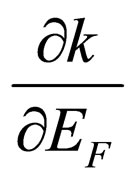 at absence of angular scattering of a photon. Energy of system the photonelectron in a final state is equal:
at absence of angular scattering of a photon. Energy of system the photonelectron in a final state is equal:
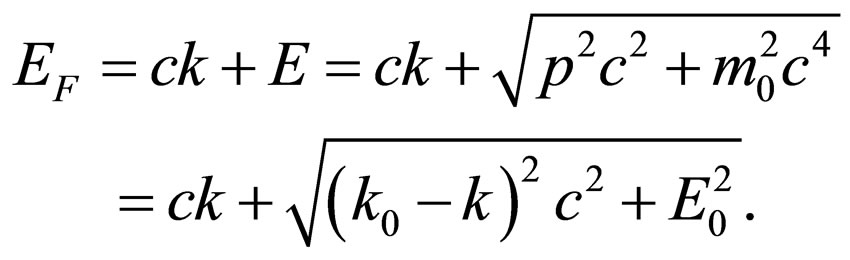
Derivative of this expression is:
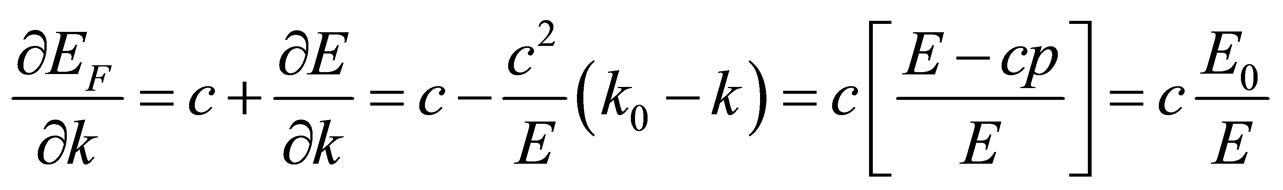 .
.
The law of energy conservation is used as  .
.
Substituting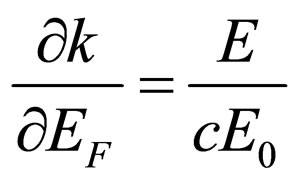 , we shall find:
, we shall find:
 . (30)
. (30)
Using  and
and 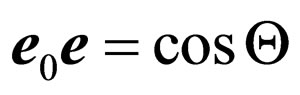 where Q is an angle of turn of polarization plane of quantum after interaction with the electron, we shall receive:
where Q is an angle of turn of polarization plane of quantum after interaction with the electron, we shall receive:
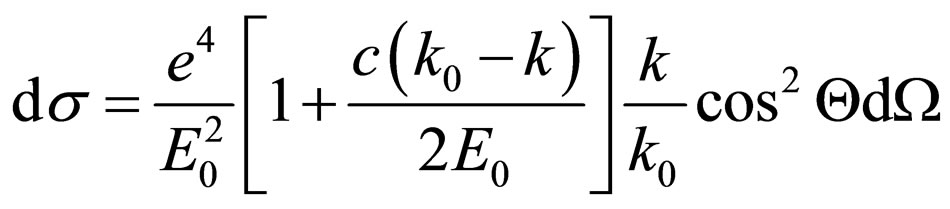 . (31)
. (31)
For the further transformation of the formula (31) it is convenient to enter so-called classical radius of the electron 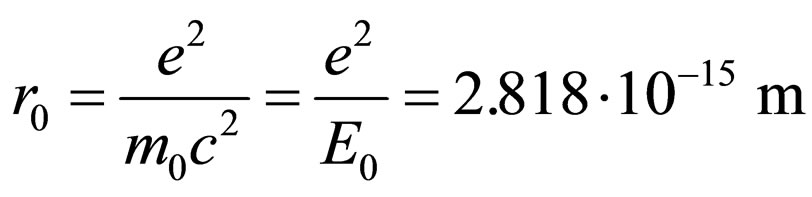 [7]. In result we have:
[7]. In result we have:
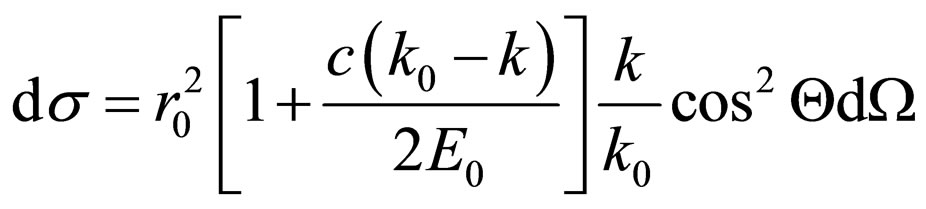 . (32)
. (32)
Using determination of effective section of interaction 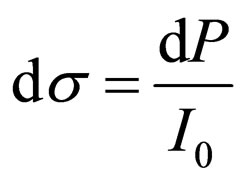 where
where  is energy flux of radiation in a solid angle
is energy flux of radiation in a solid angle 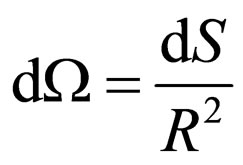 [7], we shall transform the formula (32):
[7], we shall transform the formula (32):
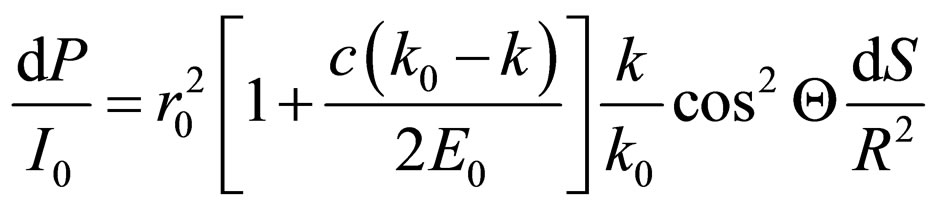 . (33)
. (33)
The solid angle 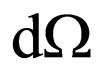 cuts out on sphere of arbitrary radius R the area dS. Taking into account, that intensity of light after interaction with the electron
cuts out on sphere of arbitrary radius R the area dS. Taking into account, that intensity of light after interaction with the electron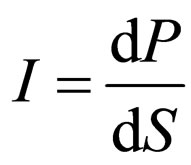 , and also, accepting arbitrary radius equal to classical radius of the electron with which there was an interaction of quantum
, and also, accepting arbitrary radius equal to classical radius of the electron with which there was an interaction of quantum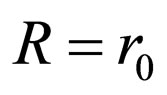 , we receive a quantum variant of Malus law:
, we receive a quantum variant of Malus law:
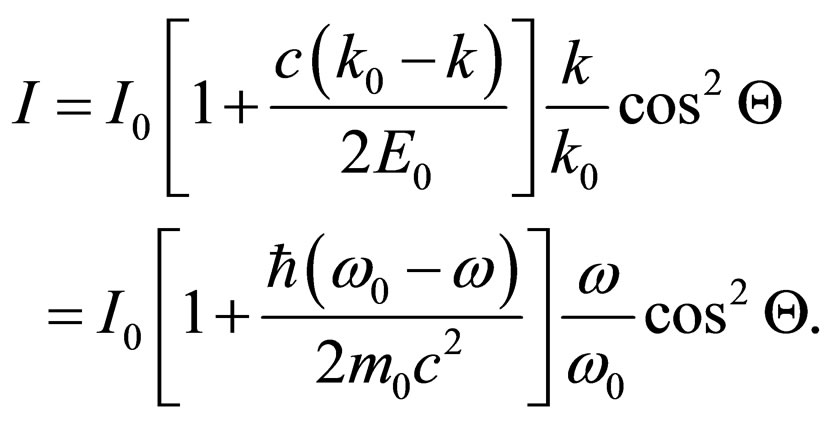 (34)
(34)
If at interaction of quantum with the electron its frequency does not vary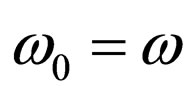 , we receive Malus law (1) in the classical form.
, we receive Malus law (1) in the classical form.
The formula (34) is received as a result of strict mathematical transformations physical problems of a deduction have been discussed earlier. In a basis of a deduction (34) there are lay the method of small perturbations [5], therefore the formula (34) is essentially inexact. Its form specifies expansion into a series of some function dependent on frequency of photons.
Change of reradiated photon frequency appreciable influences on intensity of light which has left the analyzer if the second addend in square brackets (34) makes approximately 10% from unit. Under condition of 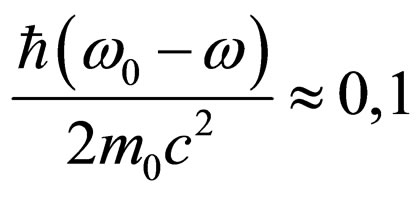 a difference of waves lengths falling on the electron and reradiated a photon it is possible to find from a ratio
a difference of waves lengths falling on the electron and reradiated a photon it is possible to find from a ratio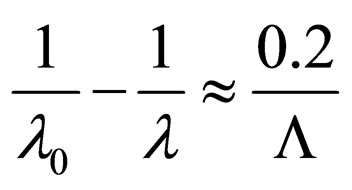 , where
, where 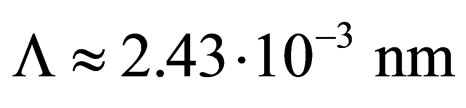 is Compton’s length of a wave. Thus, appreciable influence of change of a photon frequency at passage of light through the analyzer begins only in the region of rigid X-ray radiation.
is Compton’s length of a wave. Thus, appreciable influence of change of a photon frequency at passage of light through the analyzer begins only in the region of rigid X-ray radiation.
Let’s transform (34) to a form:
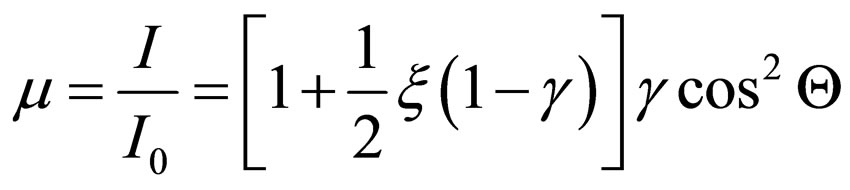
where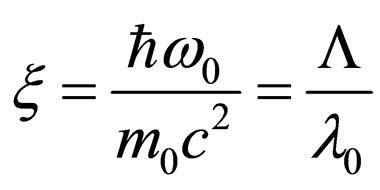 , a value
, a value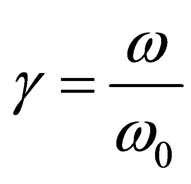 . Naturally
. Naturally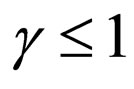 since the part of energy of a photon will be transformed to energy of movement of the electron.
since the part of energy of a photon will be transformed to energy of movement of the electron.
Let’s assume, that the electron interact with a photon which Compton’s lengths of a wave. Hence, 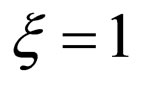 and
and 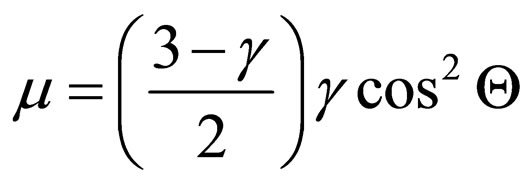 . On Figure 4 calculation of dependence
. On Figure 4 calculation of dependence 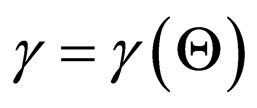 is shown at
is shown at 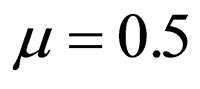 and
and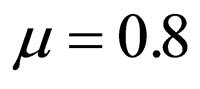 .
.
From Figure 4 it is visible, that at direct reradiated a photon on the electron, there is a proportional dependence between energy reradiated a photon and a angle of
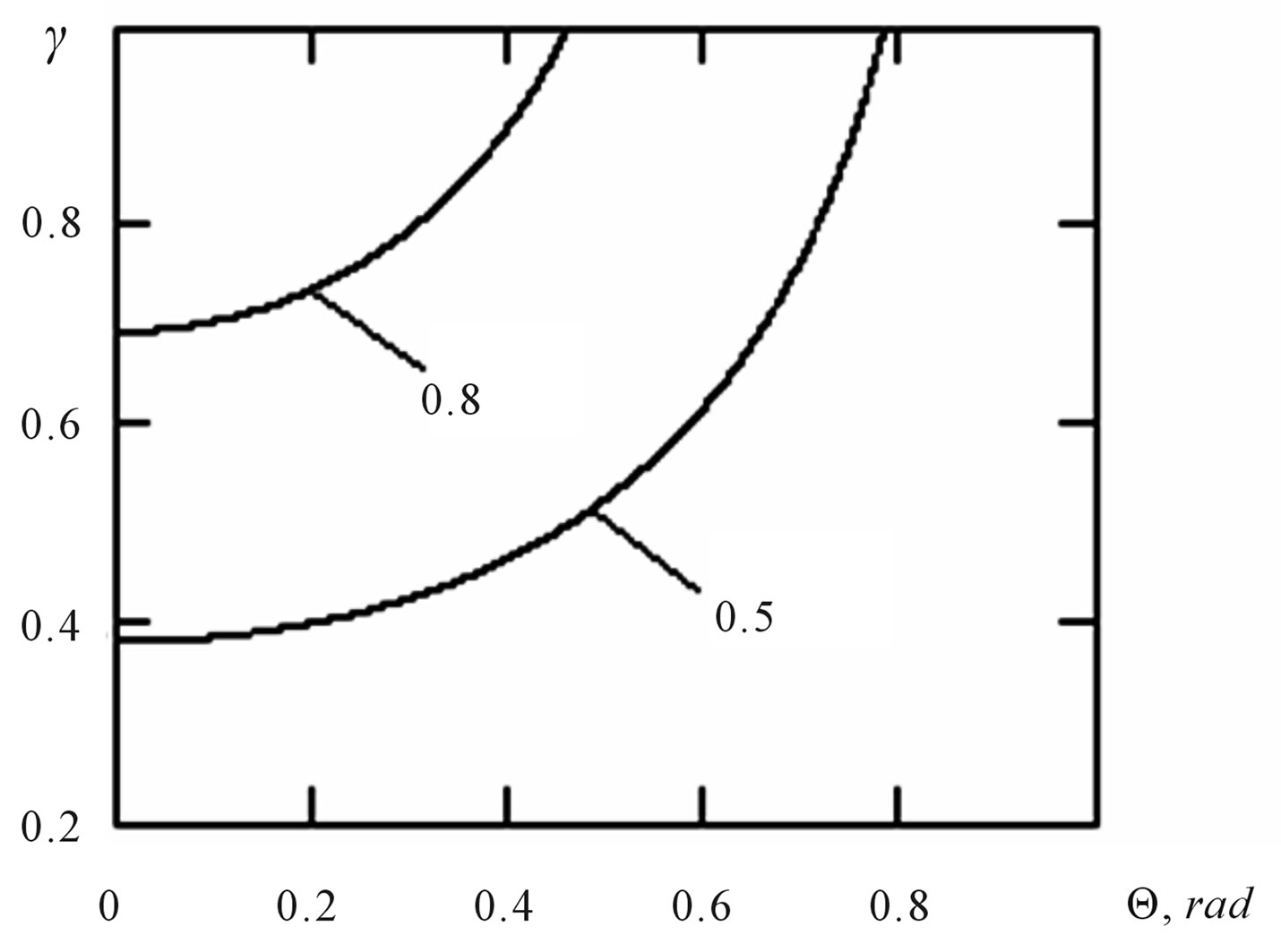
Figure 4. Dependence of relative change of frequency reradiated photon from an angle on its of turn of polarization plane.
turn of its polarization plane.
5. Formula of Klein-Nishina
During a deduction of the formula (34) we did not take into account angular scattering of light, i.e. a deviation of a photon from an initial direction after interaction with the electron.
Formula of Klein-Nishina [6] allows to calculate differential effective section of scattering of quantums for the electron depending on a angle of scattering q:
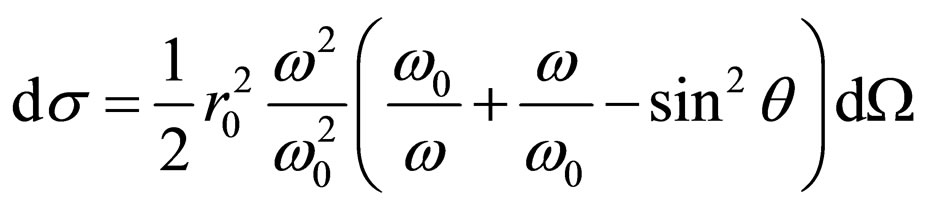 . (35)
. (35)
Experiments well confirm the formula (35) [12].
It is possible to find also the similar formula expressed through an angle of turn of a polarization plane of photon Q at interaction with the electron. Frequently this formula also frequently name of Klein-Nishina [8]. For comparison with a deduction of the formula of Malus law (34) we shall consider a deduction of the formula of Klein-Nishina in more detail.
Expression in internal square brackets (28) has result equal to zero in connection with the following circumstance. Found differential effective section (28) generally determines probability of turn of a polarization plane of a photon on some angle  at scattering of a photon on the electron. The internal square bracket characterizes similarity of probability of turn of a polarization plane of a photon, as an angle
at scattering of a photon on the electron. The internal square bracket characterizes similarity of probability of turn of a polarization plane of a photon, as an angle  and on an angle
and on an angle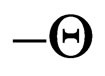 , also identical probability of scattering of a photon on angle
, also identical probability of scattering of a photon on angle 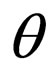 and on an angle
and on an angle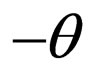 .
.
If to equate expression in internal square brackets to zero we come to dependence (32). For reception of differential effective section of a photon and the electron interaction which taking into account both turn of a polarization plane of a photon, and its scattering on some angle is necessary to use some physical preconditions (condition).
In internal square brackets (28) there are two types of addends. The first and the third addends depend only on an angle of turn of a polarization plane of a photon. The second and the fourth addends depend as on an angle of turn of a polarization plane of a photon, and from an angle of scattering of a photon, and, hence, characterize change of its impulse.
We use the strict mathematical formula 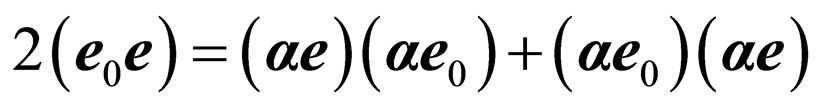 for transformations to the first and the second addends. Both addends in the used formula are equal and characterize only turn of a polarization plane on angle
for transformations to the first and the second addends. Both addends in the used formula are equal and characterize only turn of a polarization plane on angle  and
and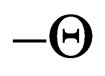 . Equality addends is defined by property
. Equality addends is defined by property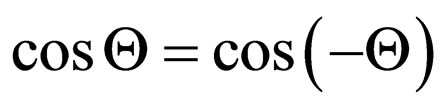 . Therefore for the account of turn of a polarization plane of a photon only in one direction it is used physical (but not strictly mathematical) a condition
. Therefore for the account of turn of a polarization plane of a photon only in one direction it is used physical (but not strictly mathematical) a condition .
.
In result we shall find:
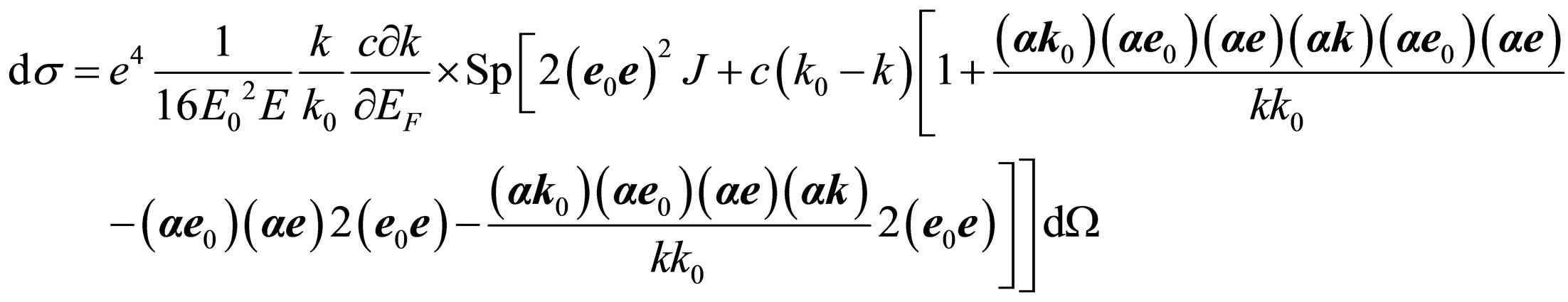
The given formula has been found in [8]. Further, summation the second and the fourth addends, with use of the full formula
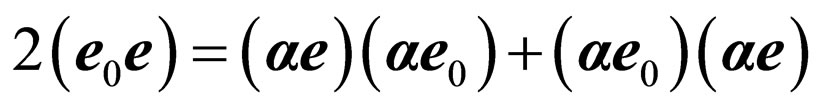
(further transformations have strictly mathematical character), we shall receive:
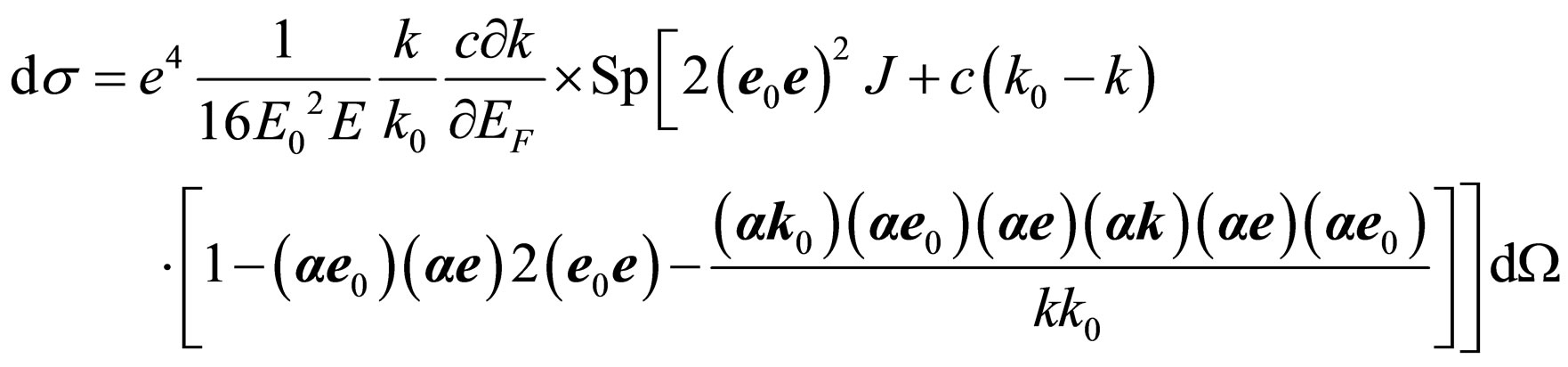 (36)
(36)
The formula (36) can be received, proceeding from (28), easier. The second addend in the internal square brackets (28), antisymmetrical to the fourth it is liquidated, i.e. we assume the unidirectional turn of a polarization plane and scattering of a photon. In the first and the fourth addends it is used a physical condition , that again, with the account
, that again, with the account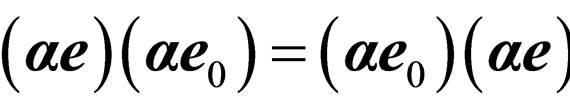 , results to (36). The physical condition
, results to (36). The physical condition  allows to keep also the general normalization of probabilities of a photon’s scattering at ignoring in the formula (28) its scattering in one of the sides.
allows to keep also the general normalization of probabilities of a photon’s scattering at ignoring in the formula (28) its scattering in one of the sides.
Using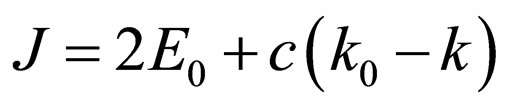 , from (36) we shall find:
, from (36) we shall find:
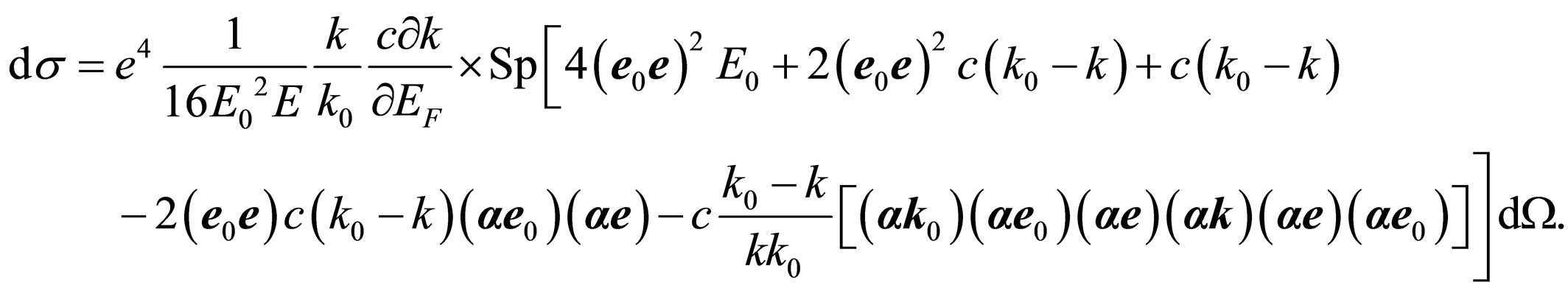
Further taking into account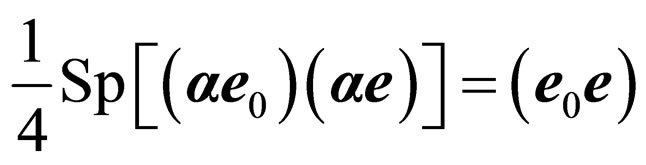 , we have:
, we have:
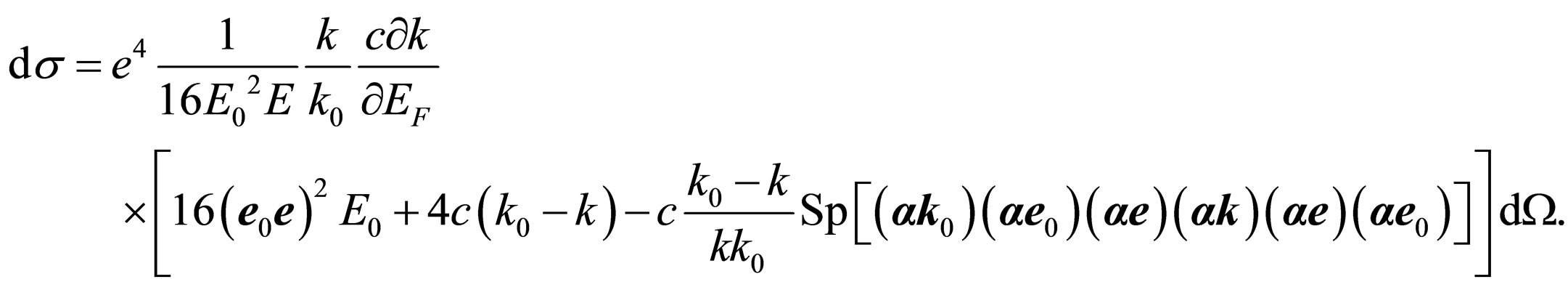
Taking into account (at use of cyclic transposition and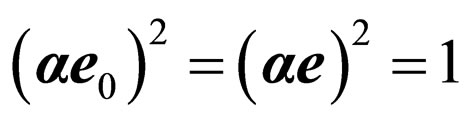 ), that
), that
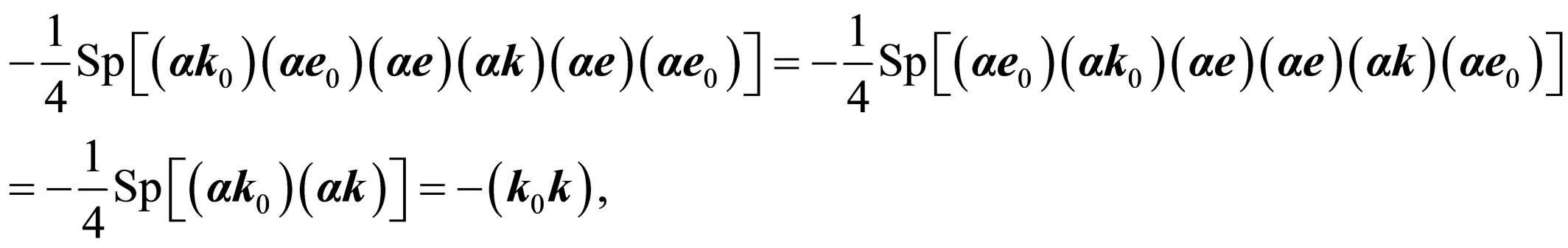
we receive:
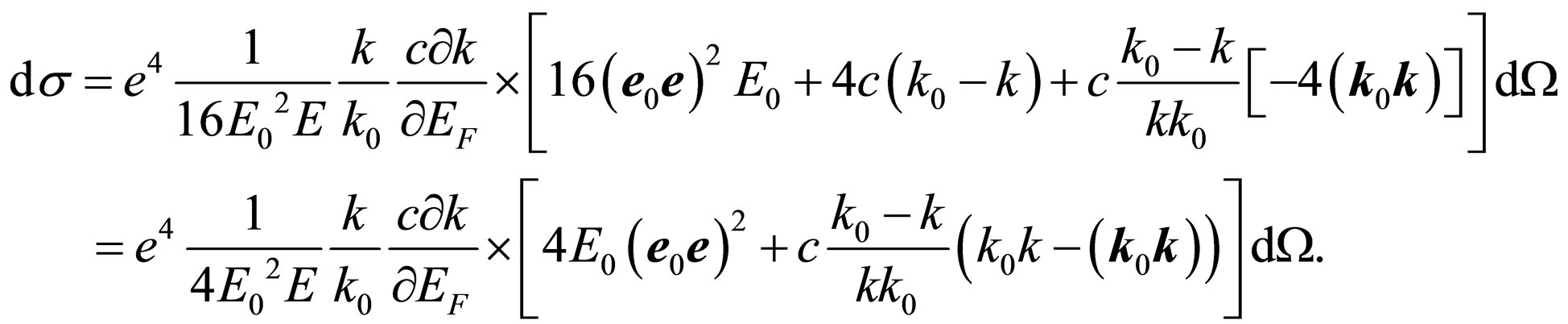 (37)
(37)
Further we use the formula of change of a photon frequency at Compton’s effect [12]:
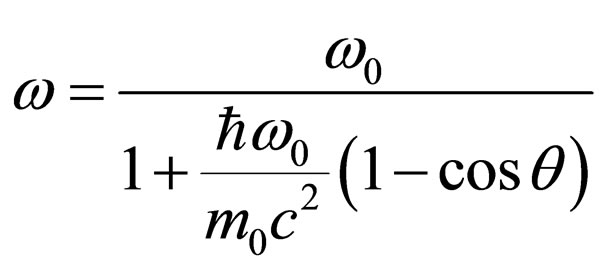 , (38)
, (38)
where q is an angle of a deviation of a secondary photon from an initial direction.
Transition to an impulse of photons, we have:
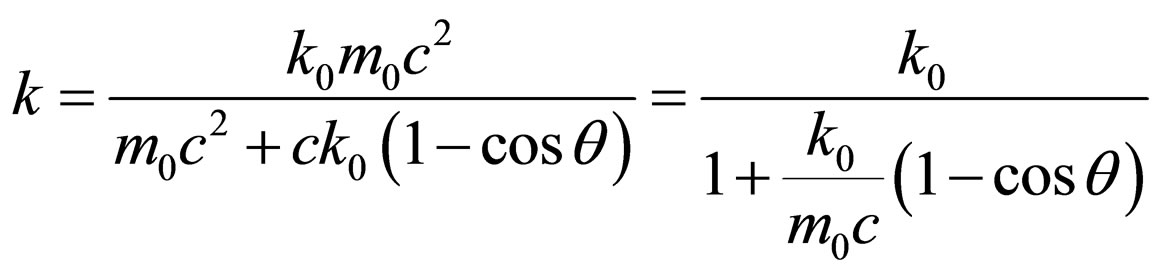 .
.
After simple transformations, we shall find:
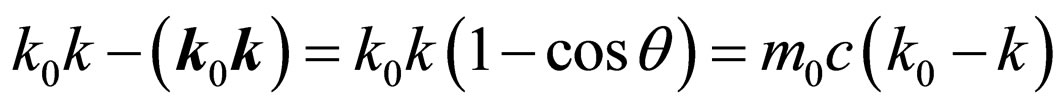 . (39)
. (39)
Hence, the formula (37) receives a form:
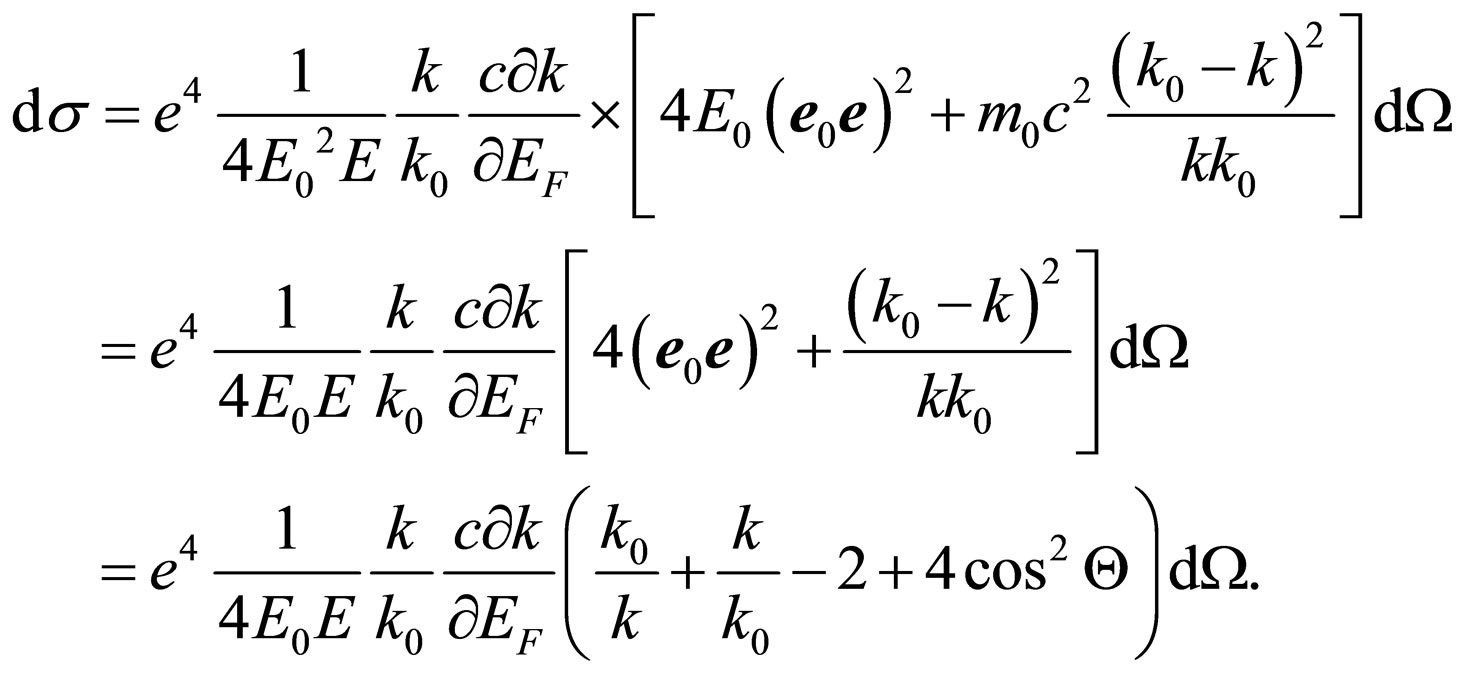 (40)
(40)
Let’s find a derivative 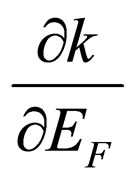 at an opportunity of angular scattering of a photon. Energy of system the photon-electron a final state is equal:
at an opportunity of angular scattering of a photon. Energy of system the photon-electron a final state is equal:
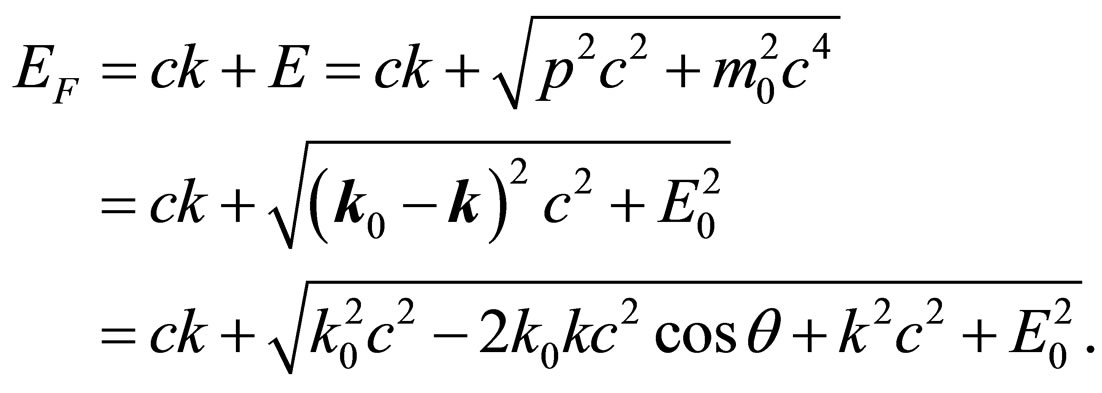
Derivative of this expression:
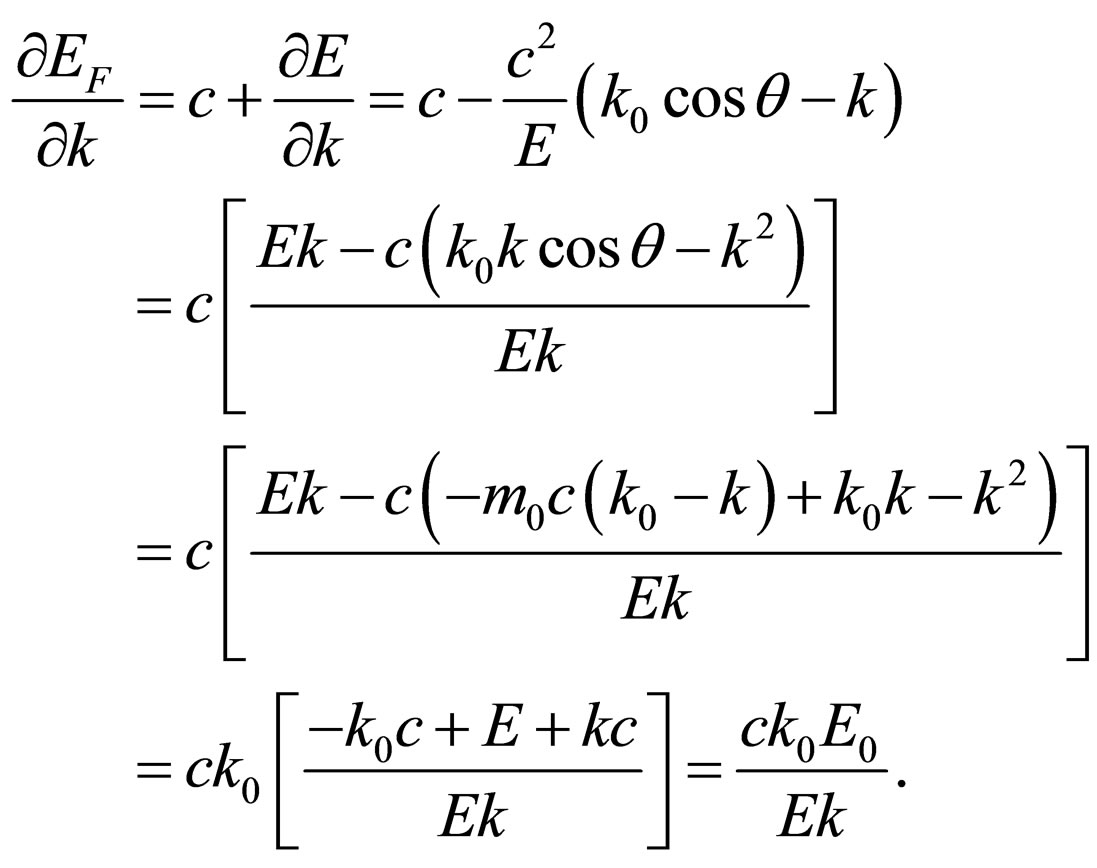
At the deduction the formula (39) and the law of energy conservation 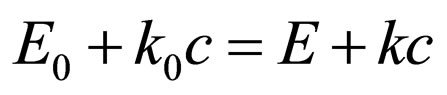 is used.
is used.
Substituting in (40) , we shall find:
, we shall find:
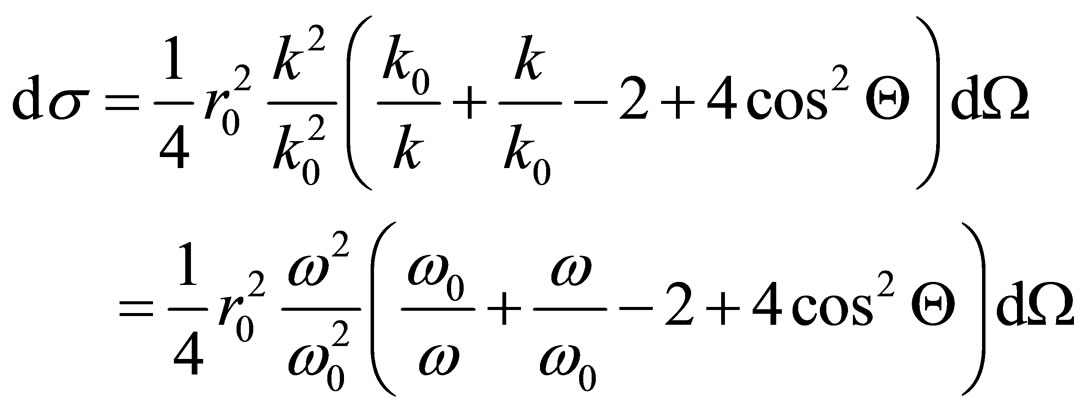 . (41)
. (41)
Let’s note that the formula (41) is deduced with use of the formula (38), i.e. at existence of angular scattering of a photon. therefore it characterizes basically compton’s effect.
6. Physical Reason of Variation of the Photon Frequency after Its Direct Reradiated on the Electron
For an explanation of the physical reason of variation of a photon frequency of after its direct, without change of a direction reradiated on the electron, we shall consider in more detail the formula (28) for differential effective section of interaction of a photon and the electron. The second addend in external square brackets (28) appeared equal to zero. Keeping formally this addend, we shall lead some transformations (28).
Using rules of work with spurs [5]:
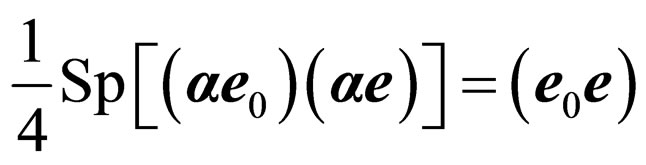 and
and
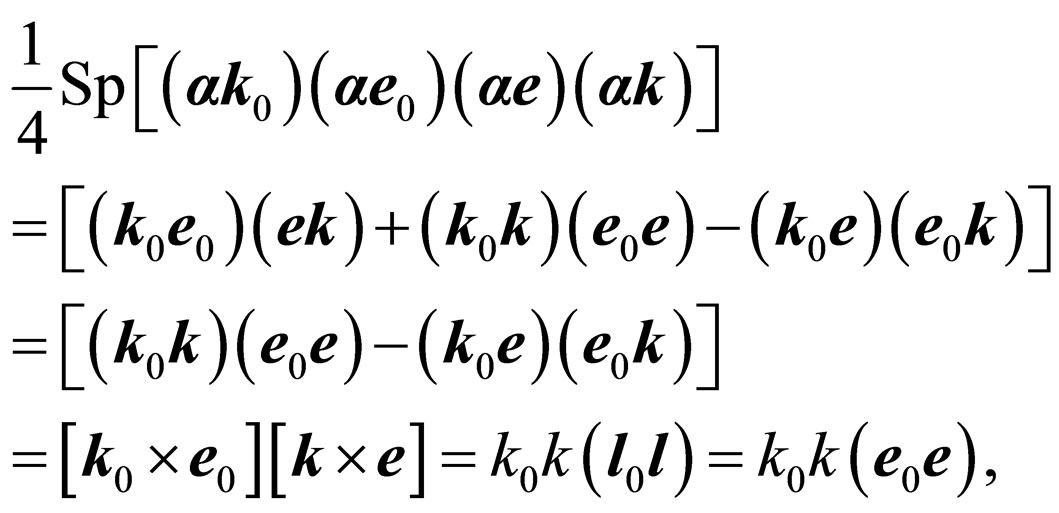
and also the formula of vector algebra [7] where 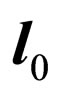 and
and 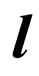 -unit vectors, we shall find:
-unit vectors, we shall find:
 (42)
(42)
It is used, also, that at direct reradiated of photons a derivative in Malus law is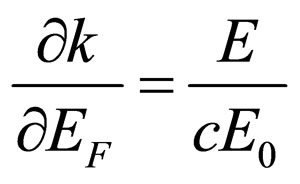 . Besides it is taken into account, as
. Besides it is taken into account, as 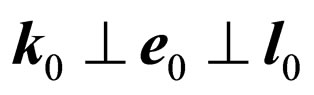 and
and 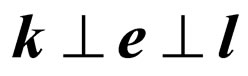 is the right three of vectors. Turn of a plane of polarization of photons is carried out around of vectors of an impulse
is the right three of vectors. Turn of a plane of polarization of photons is carried out around of vectors of an impulse  and
and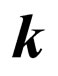 , therefore
, therefore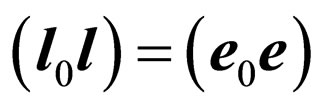 .
.
Substituting in (42) size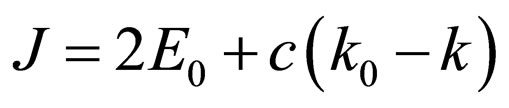 , we shall find:
, we shall find:
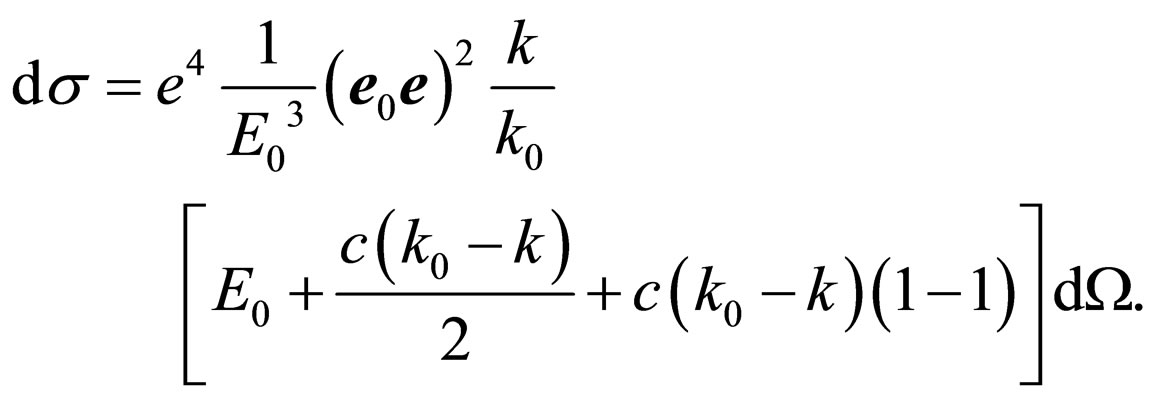 (43)
(43)
Transit from an impulses of photons to their frequencies, we receive:
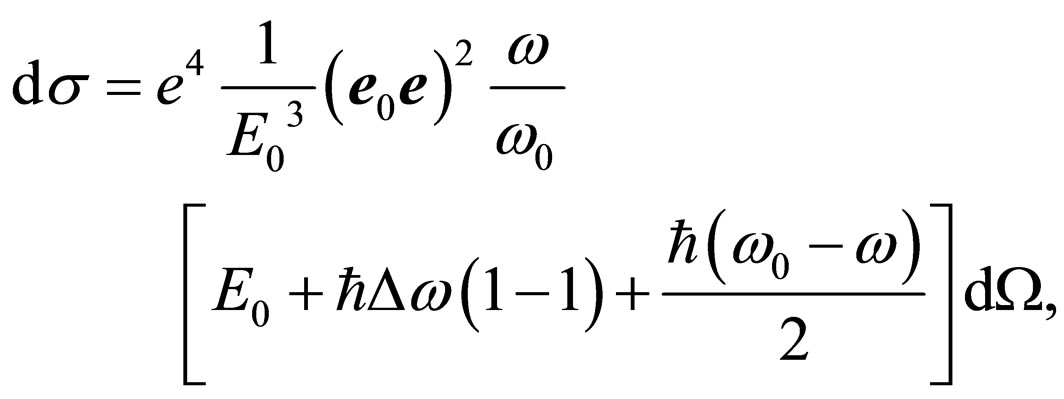 (44)
(44)
where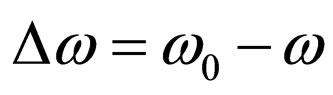 .
.
The formula (44) allows to draw a conclusion, that the electron is not in a motionless state before interaction with a photon. Its energy varies in limits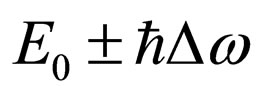 . This fluctuation in free space can occur only due to influence on the electron of vacuum energy. For example, it is similar due to influence of vacuum energy on orbital electrons in atom there is a thin structure of Lamb’s spectrum [5]. Rather conditionally fluctuations of the electron energy are shown on Figure 5.
. This fluctuation in free space can occur only due to influence on the electron of vacuum energy. For example, it is similar due to influence of vacuum energy on orbital electrons in atom there is a thin structure of Lamb’s spectrum [5]. Rather conditionally fluctuations of the electron energy are shown on Figure 5.
After absorption of a photon with energy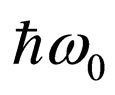 , and transition of the electron to the intermediate state
, and transition of the electron to the intermediate state , the oscillating electron then, according to the diagram on
, the oscillating electron then, according to the diagram on
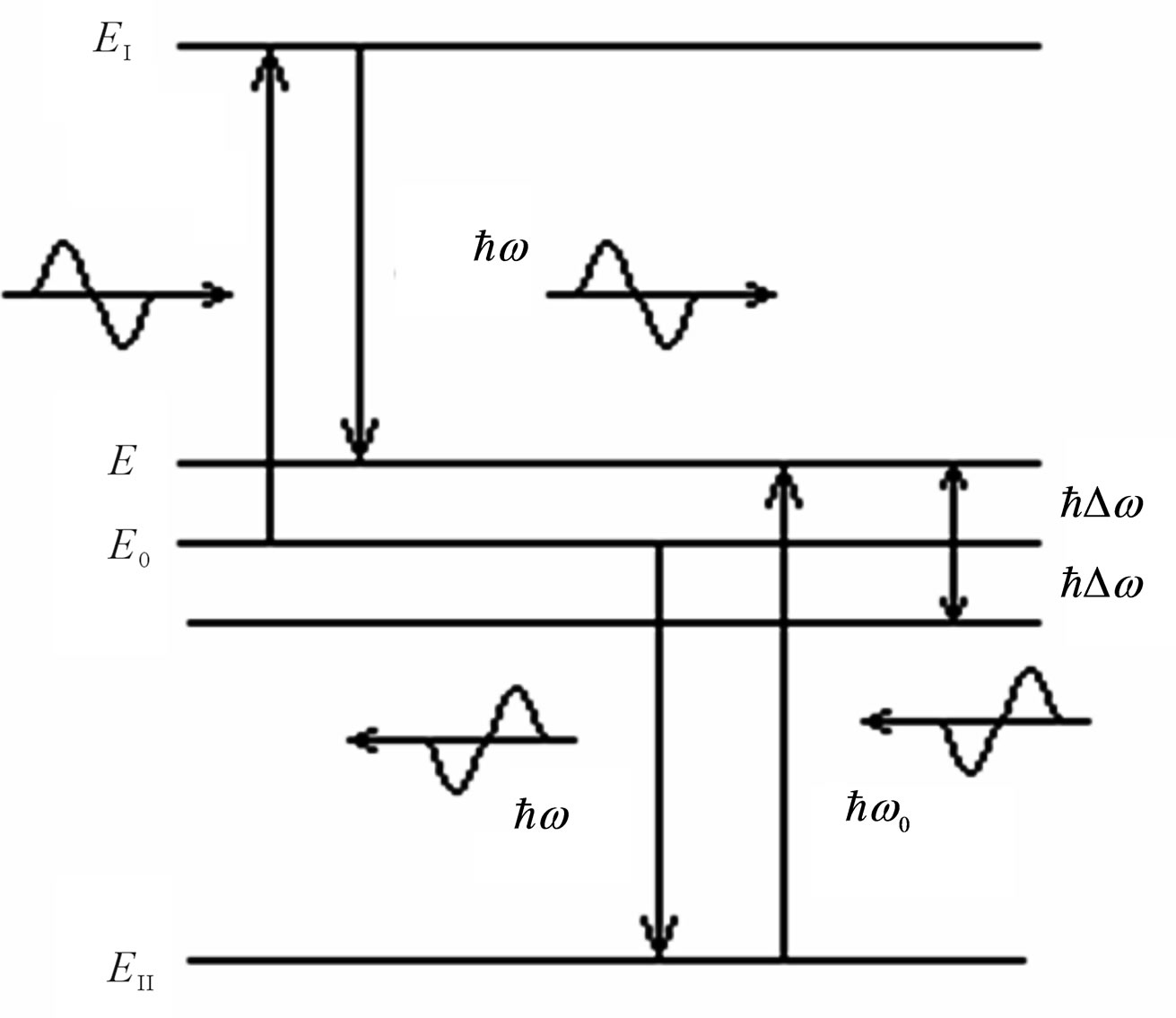
Figure 5. The scheme of energy transitions of the electron at its interaction with a photon.
Figure 2, transit to a final state with energy E. Thus the photon is radiated by energy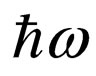 . The second variant, in conformity about Figure 3, consists that the electron at first radiates a photon
. The second variant, in conformity about Figure 3, consists that the electron at first radiates a photon 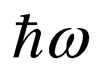 and transit to an intermediate state
and transit to an intermediate state . After that the electron absorbs a photon energy
. After that the electron absorbs a photon energy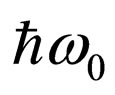 , transit to final state E. Levels of intermediate states on Figure 5 are shown conditionally for presentation. Apparently, these states cannot be placed on a linear scale of energy.
, transit to final state E. Levels of intermediate states on Figure 5 are shown conditionally for presentation. Apparently, these states cannot be placed on a linear scale of energy.
Transition of the electron after interaction with a photon on a level of energy Е is defined by performance of the conservation law of energy before and after interaction of a photon with the electron. Whether transition of the electron to a level , to this question experiment is possible can answer only. However existence of the combinational scattering [13] at interaction of an electromagnetic wave with oscillating charged structures of atoms and molecules allows to assume, that the level
, to this question experiment is possible can answer only. However existence of the combinational scattering [13] at interaction of an electromagnetic wave with oscillating charged structures of atoms and molecules allows to assume, that the level 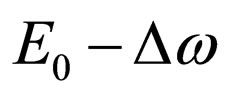 can be important at interaction of a photon with the electron.
can be important at interaction of a photon with the electron.
7. Conclusions
It is shown, that, despite of some ambiguity of physical preconditions existing now, the mathematical base of quantum electrodynamics, at least, at a considered level, adequately describes physical laws, in particular Malus law.
The used Malus law (1) based on principles of classical electrodynamics not completely takes into account all effects which can occur at passage of light through system a polarizer-analyzer. The phenomenon of possible change of light frequency in particular drops out, especial at high frequency, for example in the region of X-ray radiation.
Malus law based on principles of quantum electrodynamics (34), allows to estimate influence of change of light frequency on intensity of passage of light through system a polarizer-the analyzer. This effect is necessary taking into account, for example, by development of X-ray lasers.
Variation of a photon frequency at its direct reradiated, without change of a direction, on the electron occurs due to interaction of the electron with energy of vacuum.
The formula for differential effective section of scattering of a photon on the electron (41) has narrower range of use (connected only with Compton’s effect), than the formula (32) resulting to Malus law for X-ray radiation (34).
REFERENCES
- A. N. Matveev, “Optics,” Higher School, Moscow, 1985.
- N. Ashkroft and N. Mermin, “Physics of a Solid Body,” Vol. 2, World, Moscow, 1979, p. 109.
- A. N. Volobuev and E. S. Petrov, “Angular Distribution of Photoelectrons during Irradiation of Metal Surface by Electromagnetic Wave,” Journal of Modern Physics, Vol. 2, No. 8, 2011, pp. 780-786. doi:10.4236/jmp.2011.28091
- A. N. Volobuev and E. S. Petrov, “Influence of Characteristics of Substance on Parameters of Interaction of Photons High Energy with Free Electrons,” Journal of Modern Physics, Vol. 2, No. 1, 2011, pp. 1443-1449. doi:10.4236/jmp.2011.212178
- V. G. Levich, J. A. Vdovin and V. A. Mjamlin, “Course of theoretical physics,” Vol. 2, Fizmatgiz, Moscow, 1962.
- V. B. Berestetsky, E. M. Lifshits and L. P. Pitaevsky, “Quantum Electrodynamics,” Science, Moscow, 1989.
- V. G. Levich, “Course of Theoretical Physics,” Vol. 1. Fizmatgiz, Moscow, 1962.
- V. Gajtler, “Quantum Theory of Radiation,” Lit, Moscow, 1956.
- A. M. Prokhorov, “Physical Encyclopedia Dictionary,” Soviet Encyclopedia, Moscow, 1983.
- R. Kidd, J. Ardini and A. Anton, “Compton Effect as a Duble Doppler Shift,” American Journal of Physics, Vol. 53, No. 7, 1985, p. 641. doi:10.1119/1.14274
- G. Korn and T. Korn, “Directory on Mathematics,” The Science, Moscow, 1968, p. 350.
- M. A. Blohin, “Physics of X-Rays,” Gostehizdat, Moscow, 1957, pp. 293-300.
- M. M. Sushchinsky, “Compelled Scattering of Light,” Science, Moscow, 1985, p. 46.

