Journal of Modern Physics
Vol. 2 No. 10 (2011) , Article ID: 8056 , 6 pages DOI:10.4236/jmp.2011.210145
On Two-Dimensional Above-Barrier Penetration and Sub-Barrier Tunneling for Non-Relativistic Particles and Photons
Institute for Nuclear Research of NASU, Kiev, Ukraine
E-mail: olkhovsky@mail.ru, romanyukmariya@ukr.net
Received July 27, 2011; revised September 1, 2011; accepted September 11, 2011
Keywords: Two-Dimensional (2D) Penetration and Tunneling, Quasi-Monochromatic Approximation, Propagating Plane Waves, Evanescent and Anti-Evanescent Waves
ABSTRACT
We study the two-dimensional above-barrier penetration and the sub-barrier tunneling of non-relativistic particles and photons, described in the quasi-monochromatic approximation by simple plane waves. Our scheme represents the motion from the left free-motion zero-potential region to the right zero-potential region through the intermediate region with a one-dimensional rectangular potential barrier along the axis, normal to the both parallel interfaces between all three regions, and with the zero potential along the axis, parallel to the those interfaces. We have firstly obtained the analytical expressions for the infinite series of multiple internal and external reflections and also of multiple transmitted waves of particles and photons, with equal shifts between them along the interfaces for the above-barrier penetration and with various shifts between them in the case of the sub-barrier tunneling. Finally the Hartman and Fletcher effect for any transmitted wave is established.
1. Introduction
The one-dimensional (1-D) non-relativistic-particle and photon penetration and tunneling through a potential barrier had been studied in many papers in the stationary and non-stationary descriptions (for instance, in [1-6]; see also a lot of the relevant refs therein). However, there are not very much papers with analysis of multiple internal reflections during tunneling (see, for instance, [7-11] for 1-D tunneling and [12] for 3-D tunneling). Here we shall study the simple geometrical 2-D scheme, described by the two-dimensional (2-D) time-independent Schrödinger equation
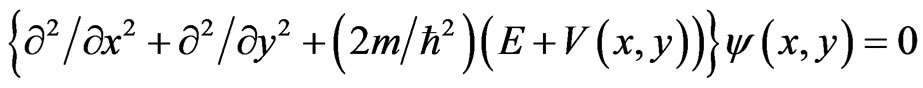 (1)
(1)
for non-relativistic particles in the quasi-monochromatic (and initially stationary) approximation, where 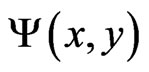 is the stationary wave function for a particle, m is its mass, ħ is Planck’s constant divided by 2π,
is the stationary wave function for a particle, m is its mass, ħ is Planck’s constant divided by 2π, 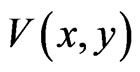 is its potential (barrier), and E is its total energy. The space regions I, II and III are defined as the regions with zero potentials
is its potential (barrier), and E is its total energy. The space regions I, II and III are defined as the regions with zero potentials  (I for
(I for ,
, 
 and III for
and III for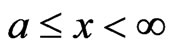 ,
,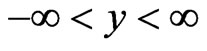 ) and the space region III contains the barrier
) and the space region III contains the barrier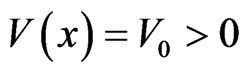 ,
, 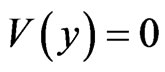 (
(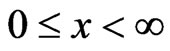 ,
,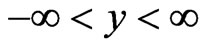 ), all three regions being infinite along the y - axis (parallel to the interfaces between I and II and also between II and III), and due to the translation symmetry the
), all three regions being infinite along the y - axis (parallel to the interfaces between I and II and also between II and III), and due to the translation symmetry the 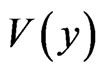 has the same y— dependence in all three regions ( permanently zero potential
has the same y— dependence in all three regions ( permanently zero potential 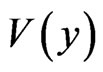 along the y-axis). We neglect the boundary effects in the regions with large
along the y-axis). We neglect the boundary effects in the regions with large 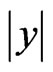 due to the infiniteness of all three regions along the y axis. Then, using the particle-photon similarity, established in [3-5,13], we study the behavior of photons, propagating in isotropic glass media I and III, penetrating or tunneling through the isotropic air layer II. Further we briefly discuss an alternative too much simplified approach from [14], presented without rigorous verification and neglecting multiple internal reflections.
due to the infiniteness of all three regions along the y axis. Then, using the particle-photon similarity, established in [3-5,13], we study the behavior of photons, propagating in isotropic glass media I and III, penetrating or tunneling through the isotropic air layer II. Further we briefly discuss an alternative too much simplified approach from [14], presented without rigorous verification and neglecting multiple internal reflections.
2. The Scheme of 2-D Non-Relativistic-Particle Penetration and Tunneling through a Barrier, Considering Multiple Internal Reflections along the x-Axis
In the simple 2-D geometrical schemes (Figures 1-3) all plane waves in regions I and III are represented, in a usual way for stationary pictures, by straight lines with arrows1. At the bottom of Figure 1, the initial 2-D plane wave  (where
(where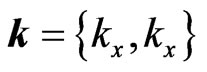 ,
,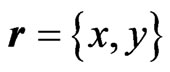 ,
, 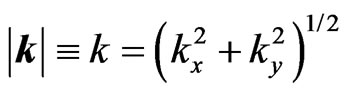 ,
, 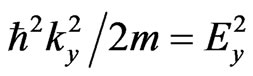
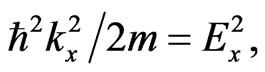 where
where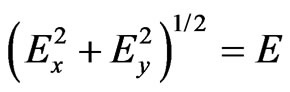 is the total and at the same time kinetic particle energy in I and III ) describes in I the free particle moving towards point (
is the total and at the same time kinetic particle energy in I and III ) describes in I the free particle moving towards point (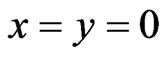 ).
).
Firstly we analyze the above-barrier penetration with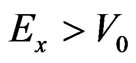 .
.
At point (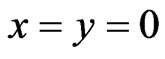 ) the first reflected plane wave
) the first reflected plane wave
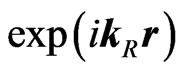
![]() (where
(where ![]() is the amplitude of the firstly externally reflected wave from the left interface into I,
is the amplitude of the firstly externally reflected wave from the left interface into I,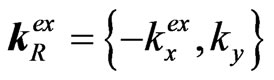 ) and the firstly penetrated (into II) plane wave
) and the firstly penetrated (into II) plane wave 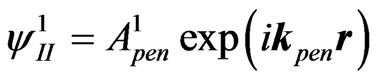 (where
(where![]() is the amplitude of the firstly penetrated wave,
is the amplitude of the firstly penetrated wave,  ,
,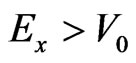 ) appear. Further, at the first exit point (x = a, y = Dy), Dy being the first shift upwards in II due to the motion with ky along the y axis, the firstly transmitted plane wave
) appear. Further, at the first exit point (x = a, y = Dy), Dy being the first shift upwards in II due to the motion with ky along the y axis, the firstly transmitted plane wave
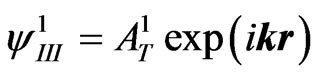 (where
(where 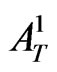 is the amplitude of the firstly transmitted (into II) wave) and the firstly internally reflected wave
is the amplitude of the firstly transmitted (into II) wave) and the firstly internally reflected wave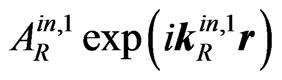 (where
(where![]() is the amplitude of the firstly internally reflected (into II) wave,
is the amplitude of the firstly internally reflected (into II) wave, ) appear. Here Dy can be evidently evaluated as
) appear. Here Dy can be evidently evaluated as
 (2a)
(2a)
or
 (2b)
(2b)
where 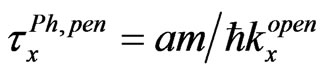 is the phase time2 of particle moving with the velocity
is the phase time2 of particle moving with the velocity 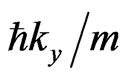 along the distance a (i.e., the time for a quasi-monochromatic particle to transfer the interval from x = 0 to x = a along the x axis inside II evaluated in the stationary-phase approximation).
along the distance a (i.e., the time for a quasi-monochromatic particle to transfer the interval from x = 0 to x = a along the x axis inside II evaluated in the stationary-phase approximation).
Successively, at point ( ,
, ) the second penetrated (into II) wave, or the second internally re-
) the second penetrated (into II) wave, or the second internally re-
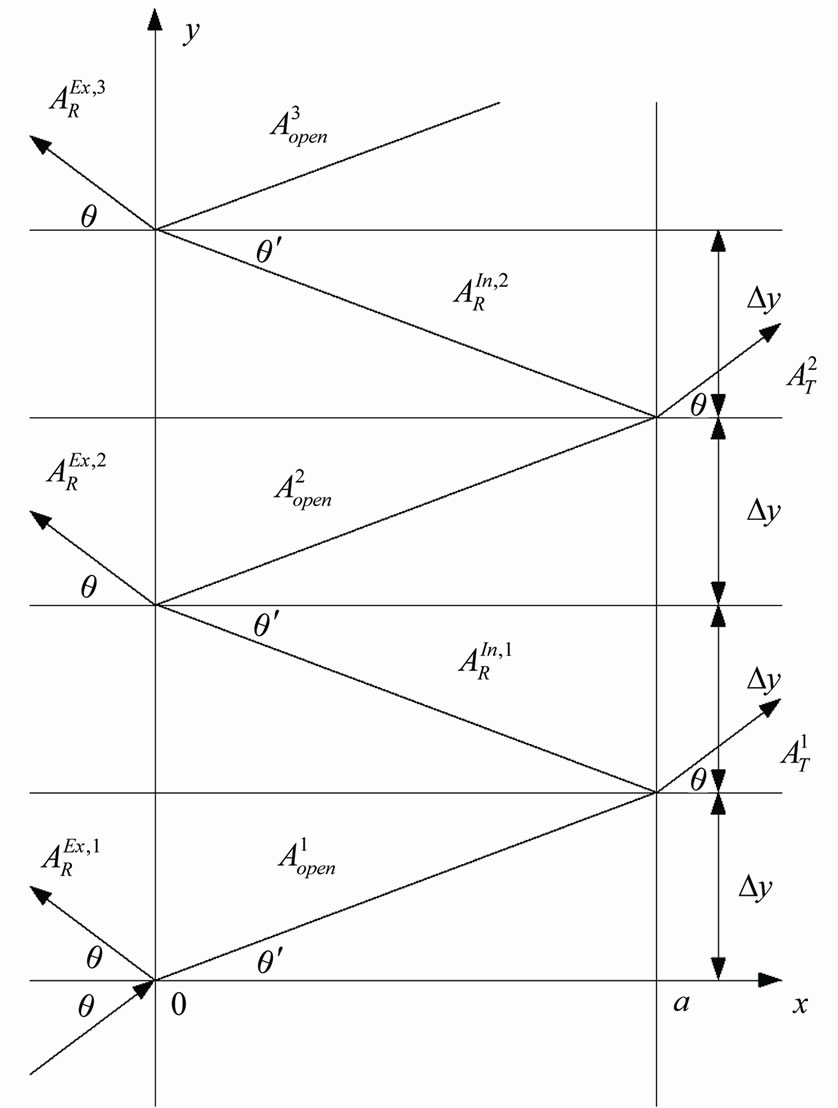
Figure 1. A schematic representation of multiple 2D reflections, above-barrier penetrations and transitions of a nonrelativistic particle.
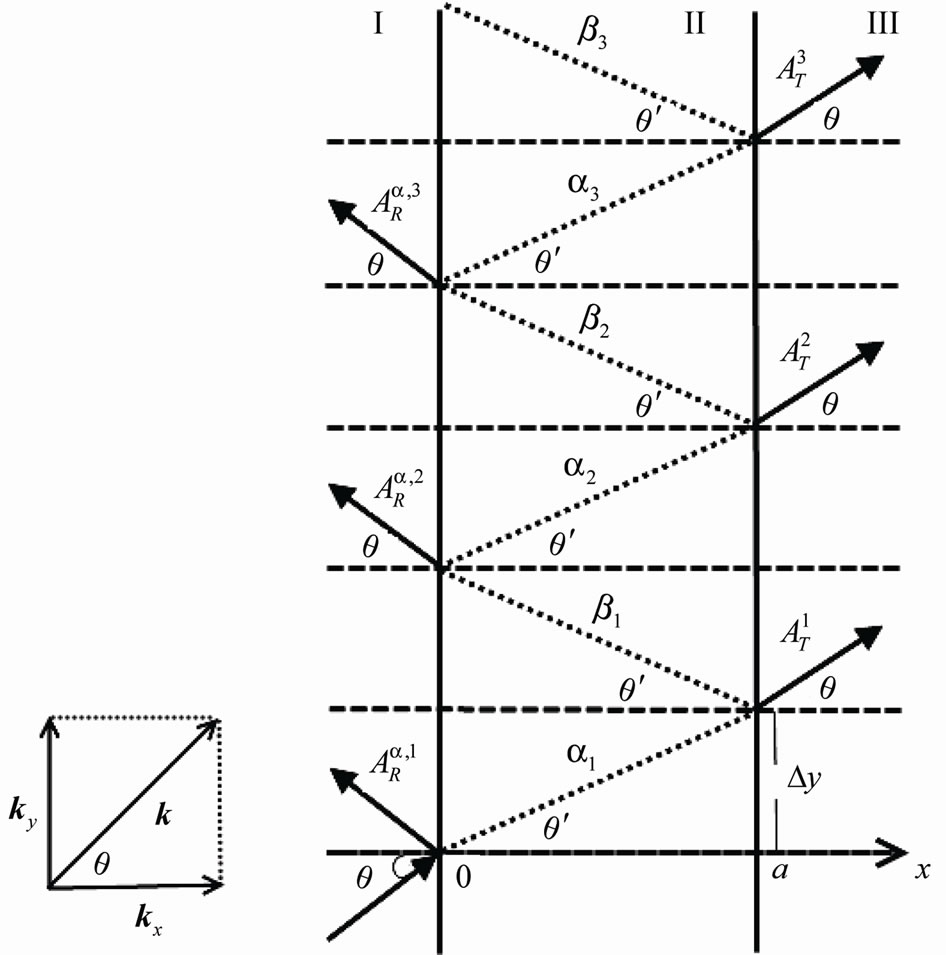
Figure 2. A schematic representation of multiple 2D reflections, sub-barrier tunneling and transitions of a non-relativistic particle.
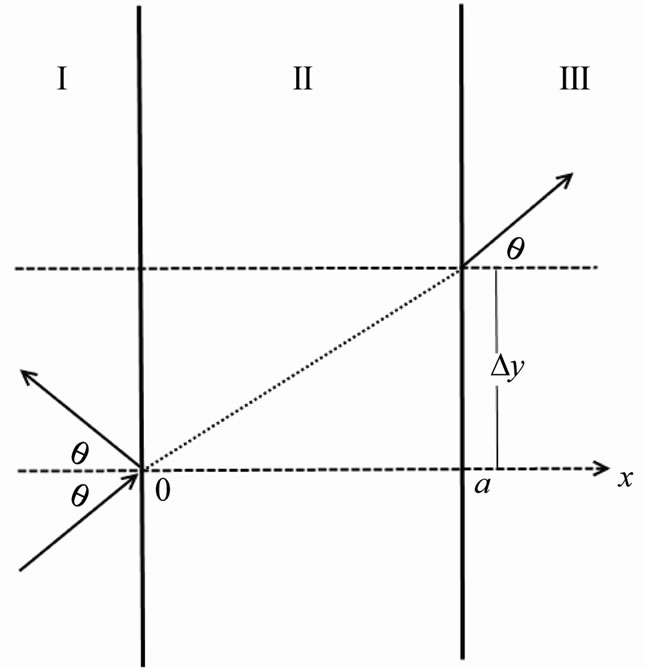
Figure 3. A schematic representation of the alternative 2D tunneling with one transmitted and one reflected propagating waves.
flected (from the left interface II) wave 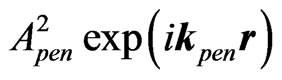 (where
(where 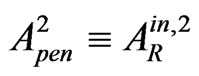 is the amplitude of the second penetrated (into II) wave, or, which is the same, of the second internally reflected (from the left interface into II) wave) and the second externally reflected (into I) wave
is the amplitude of the second penetrated (into II) wave, or, which is the same, of the second internally reflected (from the left interface into II) wave) and the second externally reflected (into I) wave 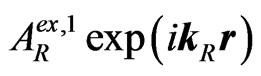 (where
(where![]() is the amplitude of the second externally reflected (into I) wave) appears. And so on (it can be continued up to any n-th externally reflected (into I) wave
is the amplitude of the second externally reflected (into I) wave) appears. And so on (it can be continued up to any n-th externally reflected (into I) wave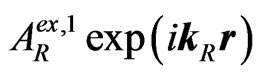 ,
,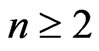 ).
).
From the matching conditions of the waves and their first derivatives 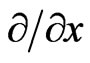 at points (
at points (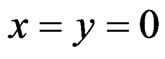 ), (
), (![]() ,
,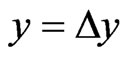 ), (
), ( ,
, ), (
), (![]() ,
,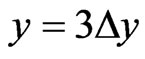 ),
), , we obtain, considering that we can neglect the plane waves
, we obtain, considering that we can neglect the plane waves 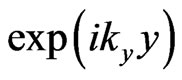 due to the translation symmetry in the both interfaces, that
due to the translation symmetry in the both interfaces, that
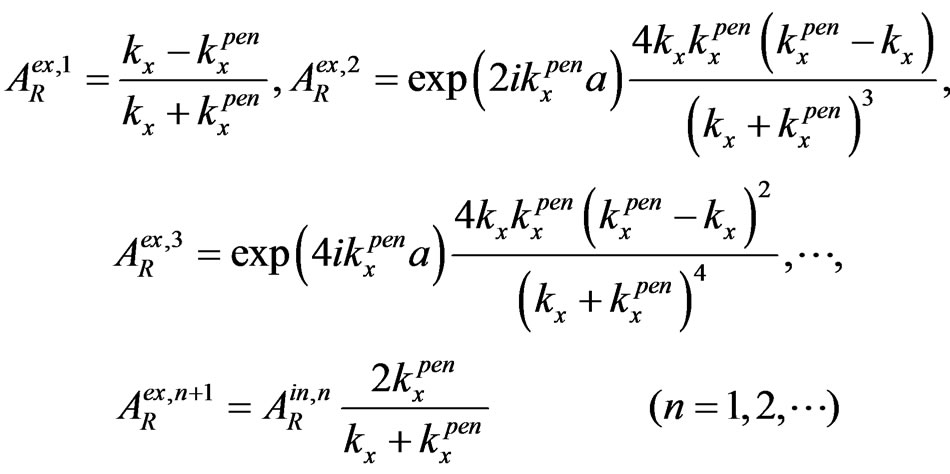 (3)
(3)
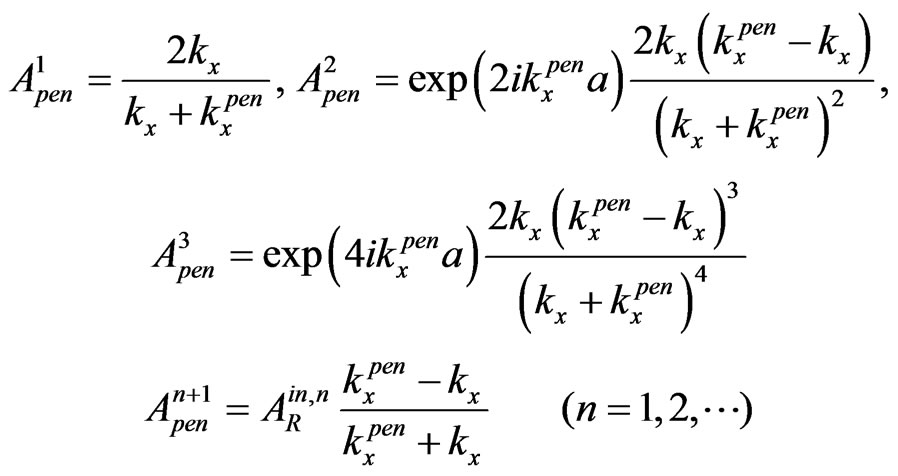 (4)
(4)
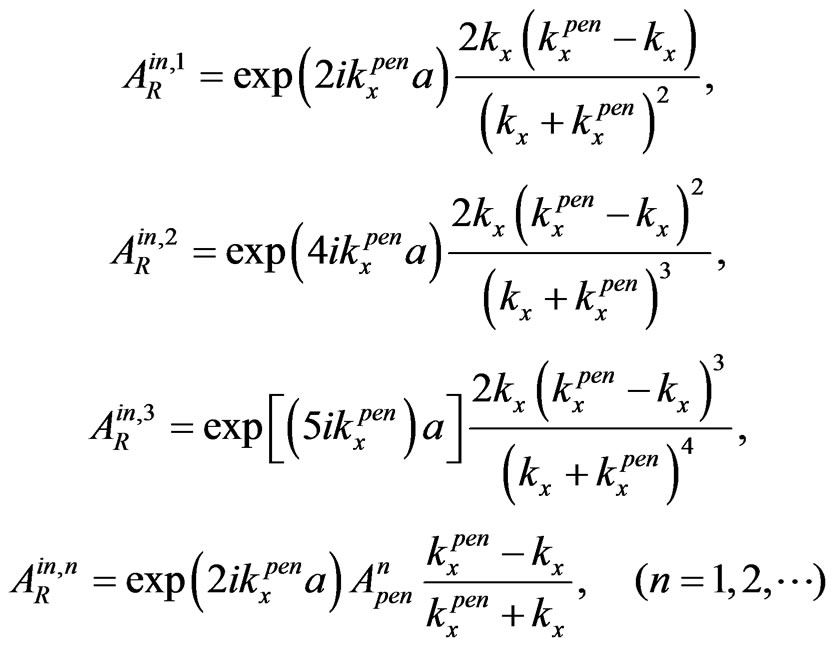 (5)
(5)
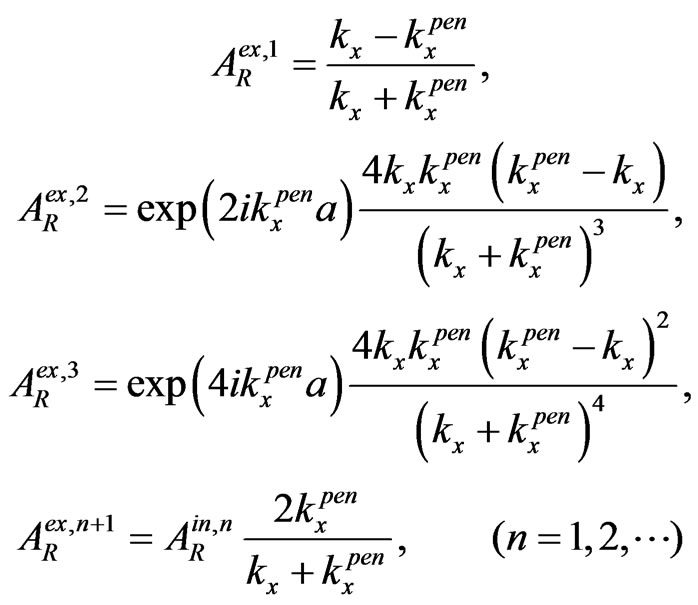 (6)
(6)
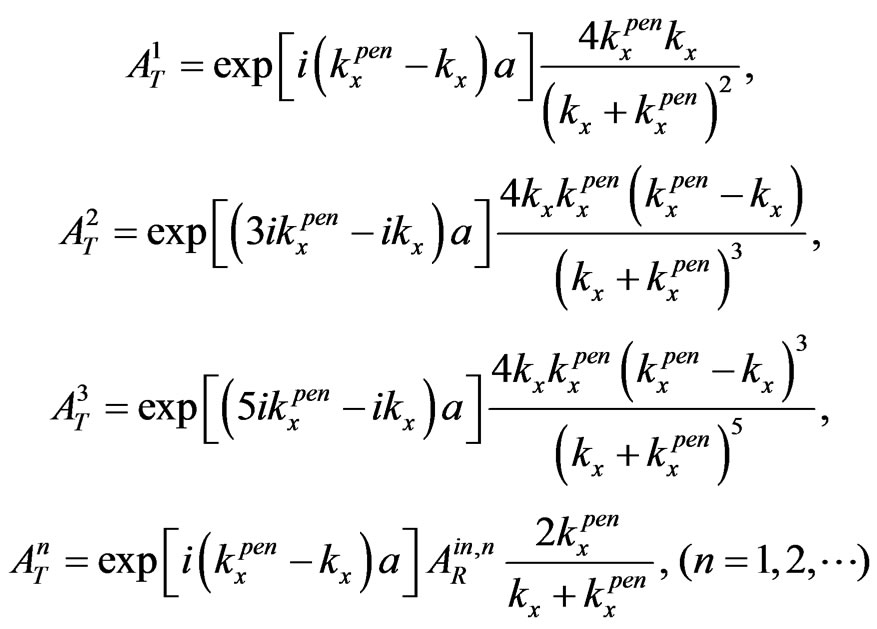 (7)
(7)
For , when
, when 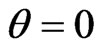 (see Figure 1) and the initial plane wave is normal to the first interface and
(see Figure 1) and the initial plane wave is normal to the first interface and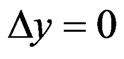 , we see that
, we see that
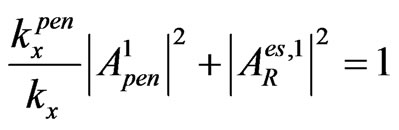
and
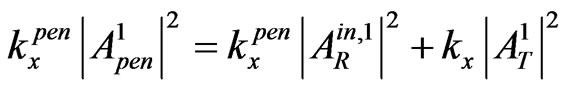
due to the flux conservation in the first passing through points ( ) and (
) and (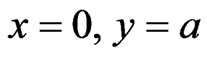 ). By the way, here we have evidently generalized (practically repeated) the introducing of multiple internal reflections from [10,11] for our simple scheme of 2-D penetration. And in the case of 1-D penetration (namely when
). By the way, here we have evidently generalized (practically repeated) the introducing of multiple internal reflections from [10,11] for our simple scheme of 2-D penetration. And in the case of 1-D penetration (namely when 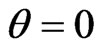 (see Figure 1) and the initial plane wave is normal to the first interface and
(see Figure 1) and the initial plane wave is normal to the first interface and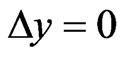 ) all the expressions, including the last expressions
) all the expressions, including the last expressions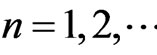 , in (3)-(7) are coincident with the relevant 1D expressions in [11], where had been presented the direct time approach to the penetration and tunneling with the multiple internal reflections.
, in (3)-(7) are coincident with the relevant 1D expressions in [11], where had been presented the direct time approach to the penetration and tunneling with the multiple internal reflections.
Now let analyze the sub-barrier tunneling with Ex < V0. We assume that the angle q is sufficiently large
(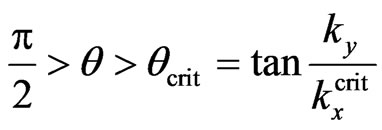 , where
, where  is defined by equality
is defined by equality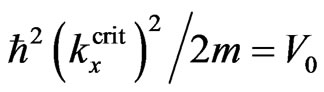 ), so that
), so that 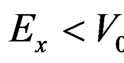 and
and 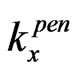 is imaginary, i.e.
is imaginary, i.e.  with
with 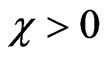 and
and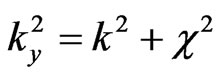 . So, in this case we have the under-barrier tunneling. In this case, instead of the above-barrier penetration, which is described by formulas (3)-(7), in order to describe the sub-barrier tunneling, we have to insert c instead
. So, in this case we have the under-barrier tunneling. In this case, instead of the above-barrier penetration, which is described by formulas (3)-(7), in order to describe the sub-barrier tunneling, we have to insert c instead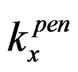 , utilizing relation
, utilizing relation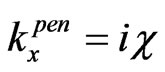 . So, instead of the propagating in II waves
. So, instead of the propagating in II waves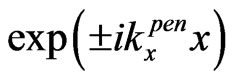 , we have the evanescent and anti-evanescent waves
, we have the evanescent and anti-evanescent waves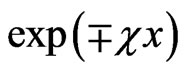 , and instead of the amplitudes
, and instead of the amplitudes ![]() and
and 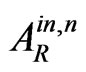 of the propagating waves
of the propagating waves 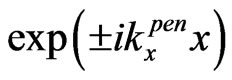 we have the coefficients
we have the coefficients 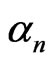 and
and
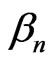 the evanescent and anti-evanescent waves
the evanescent and anti-evanescent waves 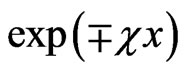 , respectively. The correspondent scheme is represented by Figure 2. Thus, for such case, we exploit a simple analytic continuation from real (over-barrier) wave numbers to imaginary (sub-barrier) wave numbers, strictly following the first method from [11]. And they obtained results, similar to (3)-(7) after the substitutions
, respectively. The correspondent scheme is represented by Figure 2. Thus, for such case, we exploit a simple analytic continuation from real (over-barrier) wave numbers to imaginary (sub-barrier) wave numbers, strictly following the first method from [11]. And they obtained results, similar to (3)-(7) after the substitutions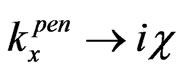 ,
, 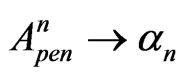 ,
, 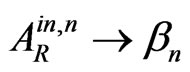 , do coincide with the similar 1D results in [11]. Namely the same results will be obtained, if one uses the Fourier expansion over the virtual momentum space or the instant on approach (these two methods are also presented in [11]).
, do coincide with the similar 1D results in [11]. Namely the same results will be obtained, if one uses the Fourier expansion over the virtual momentum space or the instant on approach (these two methods are also presented in [11]).
And instead of the shift Dy along the y axis, defined for the above-barrier penetration by Equations (2a) and (2b) and represented in Figure 1, we have to use, somewhat similarly to (2b), the relations
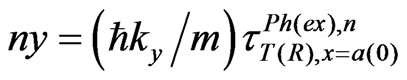 (2c)
(2c)
where
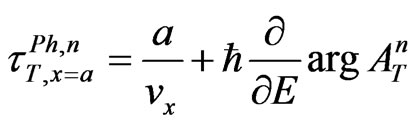
 (8)
(8)
and
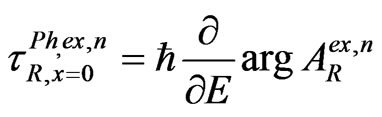
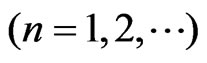 (9)
(9)
are the phase times (i.e., times for quasi-monochromatic particle evaluated in the stationary-phase approximation —see, for instance, [1,3] and refs therein) of the n-th step for sub-barrier tunneling through the point x = a and of the n-th step for the external reflection from the first barrier wall in the point x = 0, respectively. Of course, the shifts ![]() with the different values of
with the different values of 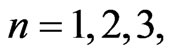 are different (slightly numerically growing for the growing numbers n, but always being proportional to
are different (slightly numerically growing for the growing numbers n, but always being proportional to 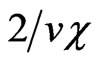 in the limit
in the limit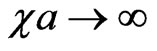 ), and also the transmitted and externally reflected waves are quickly damping with the final vanishing, due to presence of the evanescent-wave factors
), and also the transmitted and externally reflected waves are quickly damping with the final vanishing, due to presence of the evanescent-wave factors 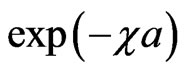 of the growing order in the expressions for
of the growing order in the expressions for 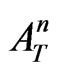 and
and 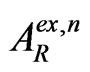 with the growing number n.
with the growing number n.
In [14], without strict theoretical verification and with the disregard of multiple internal reflections and transitions, it was used for the kx-component inside the region II the only one usual linear combination of evanescent and anti-evanescent waves  and for the ky-component inside the region II only one propagating wave
and for the ky-component inside the region II only one propagating wave , and it was obtained the following expression for the only one shift along y axis at the second interface (between II and III)
, and it was obtained the following expression for the only one shift along y axis at the second interface (between II and III)
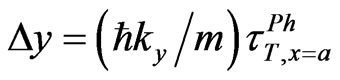 (2d)
(2d)
which is represented in Figure 2, where
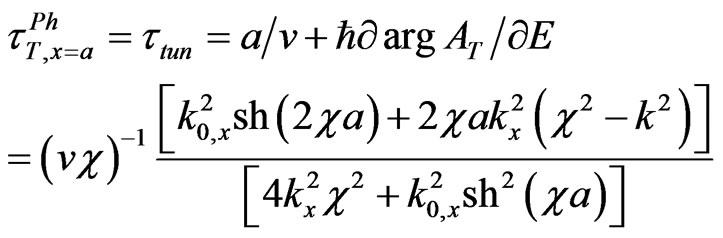 (10)
(10)
where
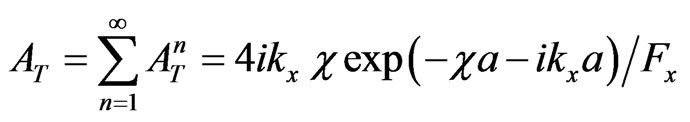 ,
,
 ,
,
 ,
,
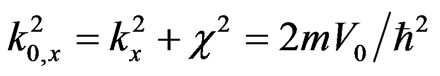 .
.
And, consequently, here one obtains the only one transmitted (into region III) 2D propagating wave 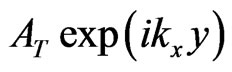
 which moves in a parallel way to the incident wave.
which moves in a parallel way to the incident wave.
So, here we compare two different approaches for 2-D sub-barrier non-relativistic-particle tunneling. Our approach, which generalizes [11], is represented by Figure 2 with an infinite series of multiple internal reflections and transmitted waves and by formulas (3)-(7), with the substitutions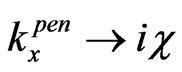 ,
,  ,
, 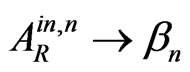 , and also by shifts (2c). The second one follows [14] and is represented by the Figure 3 with one shifted line of tunneling and one transmitted wave, moving in a parallel way to the incident wave, and also with one reflected wave, with the complete disregard of multiple internal reflections and transmitted waves. But both approaches indicate to the non-local behavior of the sub-barrier tunneling,which brings to the Hartman-Fletcher effect for tunneling phase time in the limit
, and also by shifts (2c). The second one follows [14] and is represented by the Figure 3 with one shifted line of tunneling and one transmitted wave, moving in a parallel way to the incident wave, and also with one reflected wave, with the complete disregard of multiple internal reflections and transmitted waves. But both approaches indicate to the non-local behavior of the sub-barrier tunneling,which brings to the Hartman-Fletcher effect for tunneling phase time in the limit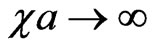 . This effect consists in the independence of the tunneling phase time from the barrier width (see, for instance, reviews [1,3]): precisely this time is equal to 2/vc for any phase time (8) and (9),
. This effect consists in the independence of the tunneling phase time from the barrier width (see, for instance, reviews [1,3]): precisely this time is equal to 2/vc for any phase time (8) and (9),  , as well as for the general tunneling time (10) in the both approaches.
, as well as for the general tunneling time (10) in the both approaches.
Of course, it remains to confirm experimentally which of the approaches will be real for the sub-barrier tunneling. Up to now only our approach is verified by several methods, described in [11], and confirmed by the preliminary (apparently without the real data processing) experimental observations, published in [15,16].
3. The Scheme of 2D Photon Penetration and Tunneling through a Barrier, Considering Multiple Internal Reflections along the x-Axis
Now, starting from the strict particle-photon similarity, formulated in [2,4,5,13] (see also revelant refs therein), we can extend the established in the previous section 2 (for particles) results for the case of photon 2-D penetration and tunneling. One can see that Figures 1-3 can be also applied for photons, propagating in isotropic glass media I and III, penetrating or tunneling through the isotropic air layer II. In this case the quantity
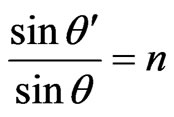 (11)
(11)
is the index of light refraction in the glass (taking the index of light refraction in the air as 1), and Figure 1 describes the penetration through layer II for the angles lesser than the critical angle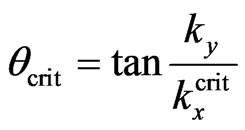 , i.e., the angle of the total internal reflection for the incident photons of the s-polarized (i.e., polarized perpendicularly to the x-y pane of the incidence) light.
, i.e., the angle of the total internal reflection for the incident photons of the s-polarized (i.e., polarized perpendicularly to the x-y pane of the incidence) light.
As to the light, Figures 2 and 3 can in this relation describe the frustrated total internal reflection (FTIR) of the s-polarized light tunneling through the layer II for the incident angles q > qcrit (frustrated-in the sense of the partial transmission through the layer II into the glass media III). They describe it differently, really in accordance with the cardinally different approaches: either by the extension of the 2D non-relativistic-particle tunneling with multiple internal reflections presented above here and also earlier in a slightly different form for light in [11], or by the extension of the 2D non-relativistic particle and photon tunneling presented in [14], respectively. We expect that future precise and accurate experiments for both non-relativistic particles and photons can establish which of the both pictures will be observed really for the sub-barrier penetration, as it was earlier analyzed in [15,16] (as a preliminary).
4. Conclusions and Perspectives
1) Starting from the theoretical analysis, elaborated in [5] for 1-D tunneling, and also from the preliminary (at least in the data processing) 2-D photonic experimental papers [15,16], we have firstly theoretically developed an approach, resulting by infinite multiple penetrating (or tunneling) waves and by infinite internally (and externally) reflected waves in the simple but realistic geomentrical 2-D scheme, described by Figures 1, 2 and formulas (2)-(10).
2) But if one starts from the physical analysis, described in [14], then an alternative approach with only one transmitted wave and only one reflected wave will be obtained in the both 1-D and 2-D schemes. It is namely because that the authors of [14] had completely neglected multiple internal reflections and also multiple transmissions.
3) For the concluding analysis of such cardinal divergence between these two approaches it will be instructive to undertake decisive thorough and precise experiments for a clear description of the above-barrier penetration and sub-barrier tunneling.
4) And also it will be rather interesting to research experimentally the possibility of the photon superluminal group velocities in the parallel transmitted and externally reflected parallel propagation lines connected with the Hartman and Fletcher effect during the sub-barrier tunneling, generalizing the results of 1-D photon tunneling, described in reviews [1,3] (including refs to the experimental results).
5) In the future we intend to present additionally the results of the numerical study of 2D Gaussian wave packets incident to the first interface normally and at the angle q to the axis, normal to the interface.
5. Acknowledgements
We are thankful for the stimulating discussions to Prof. E. Recami, Prof. R. Mignani and Doctoressa V. Petrillo and to Dr. S. A. Maydanyuk for the useful discussions.
REFERENCES
- V. S. Olkhovsky and E. Recami, “Recent Developments in the Time Analysis of Tunnelling Processes,” Physics Reports, Vol. 219, No. 6, 1992, pp. 339-356. doi:10.1016/0370-1573(92)90015-R
- R. Landauer and M. Martin, “Barrier Interaction Time in Tunneling,” Reviews of Modern Physics, Vol. 66, No. 1, 1994, pp. 217-228. doi:10.1103/RevModPhys.66.217
- V. S. Olkhovsky, E. Recami and J. Jakiel, “Unified Time Analysis of Photon and Particle Tunnelling,” Physics Reports, Vol. 398, No. 3, 2004, pp. 133-178. doi:10.1016/j.physrep.2004.06.001
- V. S. Olkhovsky and A. Agresti, “Developments in Time Analysis of Tunnelling Processes,” In: D. Mugnai, A. Ranfagni and L. S. Schulman, Eds., Procееdings of the Adriatico Research Conference on Tunneling and Its Implications, Trieste, 30 July-2 August 1996, World Scientific, Singapore, 1997, pp. 327-355.
- V. S. Olkhovsky, “Time Analysis of Tunnelling of Particles and Photons,” Physics of the Alive, Vol. 5, No. 1, 1997, pp. 23-41.
- V. S. Olkhovsky, V. Petrillo and A. K. Zaichenko, “Decrease of the Tunneling Time and Violation of the Hartman Effect for Large Barriers,” Physical Review, Vol. A70, No. 1, 2004, pp. 034103-1-4.
- J. H. Fermor, “Quantum-Mechanical Tunneling,” American Journal of Physics, Vol. 34, No. 12, 1966, pp. 1168- 1170. doi:10.1119/1.1972543
- K. W. McVoy, L. Heller and M. Bolsterli, “Optical Analysis of Potential Well Resonances,” Reviews of Modern Physics, Vol. 39, 1967, pp. 245-258. doi:10.1103/RevModPhys.39.245
- A. Anderson, “Multiple Scattering Approach to OneDimensional Potential Problems,” American Journal of Physics, Vol. 57, No. 3, 1989, pp. 230-235. doi:10.1119/1.16095
- S. P. Maydanyuk, V. S. Olkhovsky and A. K. Zaichenko, “Multiple Internal Reflections Method in the Description of Tunnelling Evolution of Nonrelativistic Particles and Photons,” Journal of Physical Studies (Ukraine), Vol. 6, No. 1, 2002, pp. 24-39.
- F. Cardone, R. Mignani, S. P. Maidanyuk and V. S. Olkhovsky, “Multiple Internal Reflections during Particle and Photon Tunneling,” Foundations of Physics Letters, Vol. 19, No. 5, 2006, pp. 441-457. doi:10.1007/s10702-006-0903-y
- V. S. Olkhovsky, M. V. Romanyuk, “Particle Tunneling and Scattering in a Three-Dimensional Potential with a Hard Core and an External Potential Barrier,” Nuclear Physics and Atomic Energy (Ukraine), Vol. 10, No. 3, 2009, pp. 273-281.
- R. Y. Chiao, P. G. Kwiat and A. M. Steinberg, “Analogies between Electron and Photon Tunneling: A Proposed Experiment to Measure Photon Tunneling Times,” Physica B, Vol. 175, 1991, pp. 257-262. doi:10.1016/0921-4526(91)90724-S
- A. M. Steinberg and R. Y. Chiao, “Tunneling Delay Times in One and Two Dimensions,” Physical Review, Vol. A, No. 49, 1994, pp.3283-3285.
- C. K. Carniglia and L. Mandel, “Phase-Shift Measurement of Evanescent Electromagnetic Waves,” Journal of the Optical Society of America, Vol. 61, No. 8, 1971, pp. 1035-1043. doi:10.1364/JOSA.61.001035
- S. Zhu, A. W. Yu, D. Hawley and R. Roy, “Frustrated total Internal Reflection: A Demonstration and Review,” American Journal of Physics, Vol. 54, No. 7, 1986, pp. 601-606. doi:10.1119/1.14514
NOTES
1Then we assume, as one does usually assume in the approximation of the stationary picture, that the straight line represents the axis of the moving quasi-monochromatic wave packet, neglecting its transversal dimensions which are unessential in the initial approximation.
2The definition of phase time see, for instance, [1,3] (and correspondent refs therein).

