Journal of Modern Physics
Vol.3 No.1(2012), Article ID:17104,6 pages DOI:10.4236/jmp.2012.31011
Phase Shift between Supersymmetric Partner Potentials
Department of Physics, St. Paul’s Cathedral Mission College, Raja Rammohan Roy Sarani, Kolkata, India
Email: smahapatra99@gmail.com
Received July 23, 2011; revised September 6, 2011; accepted October 15, 2011
Keywords: phase shift; supersymmetry; shape invariant potential
ABSTRACT
The relationship between phase shifts produced by two supersymmetric (SUSY) partner potentials has been examined critically. Phase shifts produced by two SUSY partner potentials bear a simple relation irrespective of being shape invariant potential (SIP) or not (non-SIP). In general, the phase shift cannot be obtained algebraically, even for standard SIPs except the Coulomb potential.
1. Introduction
Supersymmetric quantum mechanics (SSQM) was introduced by Witten [1], Coopper and Freedman [2] as a simple model for testing supersymmetric field theories which were introduced by Gel’fand and Likhtman [3] for a unified description of the fundamental interaction in nature. The study of SSQM has since been of great interest, as it provided an insight into the factorization of the Hamiltonian and introduction of partner Hamiltonians having wholly or partially identical energy spectrum. It also explained analytical solvability of potentials, whose partner potentials have the same shape, introducing the concept of shape invarince. From a given Hamiltonian (H1), a partner Hamiltonian (H2) is usually obtained by deleting the ground state of H1, the rest of the spectrum of H1 being identical with the spectrum of H2 [4]. The partner Hamiltonian H2 can also be obtained by adding an energy level below the ground state of H1 or by matching the spectrum of H2 identical to that of H1 (isospectral Hamiltonians) [5]. We will focus our attention to the first class of partner Hamiltonians. An elegant and exhaustive review of the procedure and its consequences can be found in Ref. [4]. The principal result is the energy degeneracy, viz., 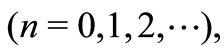
 where
where 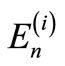 is the energy of the n-th excited (bound) state of
is the energy of the n-th excited (bound) state of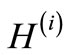 . The bound state eigen function
. The bound state eigen function 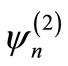 of
of 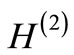 can be obtained by applying an operator
can be obtained by applying an operator 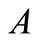 on the eigen function
on the eigen function 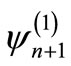 of
of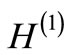 , viz.,
, viz.,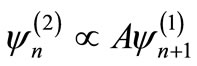 . The operator
. The operator 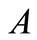 destroys a node of an eigen function of
destroys a node of an eigen function of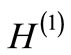 . This procedure can also be extended to the scattering (unbound) states. From the asymptotic form of the scattering wave function, one can then find a relation between the phase shifts produced by the two partner potentials [5]. If the potential
. This procedure can also be extended to the scattering (unbound) states. From the asymptotic form of the scattering wave function, one can then find a relation between the phase shifts produced by the two partner potentials [5]. If the potential 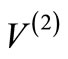 of the partner Hamiltonian
of the partner Hamiltonian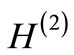 has the same functional shape (but with different parameters) as that of the potential
has the same functional shape (but with different parameters) as that of the potential 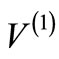 of the original Hamiltonian
of the original Hamiltonian , then the potential is said to be a “shape invariant potential (SIP)”. It can be shown that the entire bound state energy spectrum and corresponding energy eigen functions of
, then the potential is said to be a “shape invariant potential (SIP)”. It can be shown that the entire bound state energy spectrum and corresponding energy eigen functions of  can be obtained algebraically if
can be obtained algebraically if 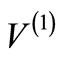 is shape invariant [4]. However, shape invariance is not a prerequisite for obtaining the partner potential
is shape invariant [4]. However, shape invariance is not a prerequisite for obtaining the partner potential 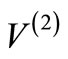 from any starting potential
from any starting potential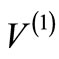 . The partner potential can be constructed, if the ground state wave function of the original potential is known, even if the corresponding Hamiltonian is not solvable analytically. Hence for any given potential
. The partner potential can be constructed, if the ground state wave function of the original potential is known, even if the corresponding Hamiltonian is not solvable analytically. Hence for any given potential , one can construct the partner potential
, one can construct the partner potential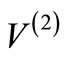 , according to a clear prescription (to be outlined in Section 2), such that
, according to a clear prescription (to be outlined in Section 2), such that  has the same energy spectrum as
has the same energy spectrum as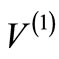 , except that the ground state of
, except that the ground state of 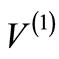 will be absent in the spectrum of
will be absent in the spectrum of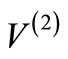 . Then extending the procedure to scattering states, one can show that the phase shifts produced by
. Then extending the procedure to scattering states, one can show that the phase shifts produced by  and
and 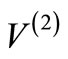 bear a simple relation [5], which will also be outlined in Section 2. Since this procedure is valid for any potential
bear a simple relation [5], which will also be outlined in Section 2. Since this procedure is valid for any potential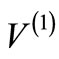 , the relationship between the phase shifts produced by
, the relationship between the phase shifts produced by 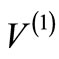 and
and 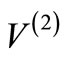 should also hold whether or not
should also hold whether or not 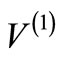 is shape invariant. Likewise, energy degeneracy
is shape invariant. Likewise, energy degeneracy 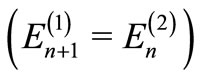 and relation between
and relation between 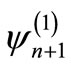 and
and  should also hold even if
should also hold even if  is not shape invariant. In Reference [5], it was shown analytically that the phase shift relation holds for the Coulomb potential, which is well known to be shape invariant. In connection with that derivation, to be outlined in Section 2.2, it was shown that if the original potential
is not shape invariant. In Reference [5], it was shown analytically that the phase shift relation holds for the Coulomb potential, which is well known to be shape invariant. In connection with that derivation, to be outlined in Section 2.2, it was shown that if the original potential  is taken with an orbital angular momentum l, then the phase shift of the partner potential corresponds to angular momentum
is taken with an orbital angular momentum l, then the phase shift of the partner potential corresponds to angular momentum . For the Coulomb potential (an SIP), the partner of
. For the Coulomb potential (an SIP), the partner of 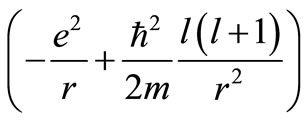 is
is
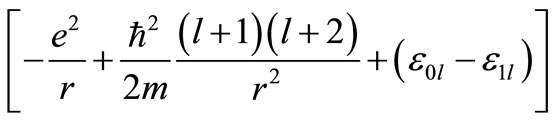
where 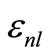 is the energy of the eigen state with radial and orbital quantum numbers n and l respectively. In this case the partner potential has an explicit orbital angular momentum
is the energy of the eigen state with radial and orbital quantum numbers n and l respectively. In this case the partner potential has an explicit orbital angular momentum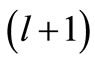 . It is important to note that the orbital angular momentum
. It is important to note that the orbital angular momentum  becomes the shape invariance parameter, and it changes to
becomes the shape invariance parameter, and it changes to 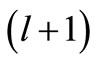 by the condition of shape invariance
by the condition of shape invariance
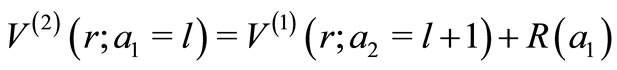
with
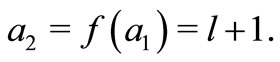 (1)
(1)
Consequently, the phase shifts associated with 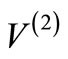 corresponds to orbital angular momentum
corresponds to orbital angular momentum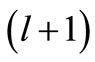 . On the other hand, for a non-SIP, there is no shape invariance condition, Equation (1). Hence
. On the other hand, for a non-SIP, there is no shape invariance condition, Equation (1). Hence 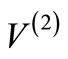 is not explicitly associated with orbital angular momentum
is not explicitly associated with orbital angular momentum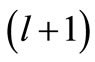 . It is actually associated with orbital angular moentum l, but its
. It is actually associated with orbital angular moentum l, but its  behavior is
behavior is  (as will be shown in Section 2.2). This may cause a serious pitfall in assigning orbital angular momentum for the partner potential
(as will be shown in Section 2.2). This may cause a serious pitfall in assigning orbital angular momentum for the partner potential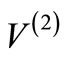 : if an explicit
: if an explicit 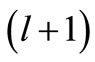 is taken for
is taken for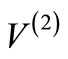 , it will give wrong results. Instead, one should include l in
, it will give wrong results. Instead, one should include l in  only and then calculate its partner
only and then calculate its partner , without additional inclusion of any l. We wish to stress this point in this paper, to avoid a possible pitfall.
, without additional inclusion of any l. We wish to stress this point in this paper, to avoid a possible pitfall.
In the present work, we critically examine the relationship between phase shifts produced by the two partner potentials for both SIP and non-SIP. We find that the difference between the phase shifts produced by 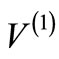 and
and 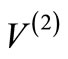 for both SIP and non-SIP do not obey the SSQM predicted relation, if
for both SIP and non-SIP do not obey the SSQM predicted relation, if 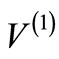 and its supersymmetric partner
and its supersymmetric partner  are taken with l and
are taken with l and  respectively, whereas it is obeyed when both
respectively, whereas it is obeyed when both 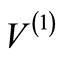 and
and 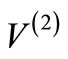 are taken with the same l. Thus, unless the parameter involved in the shape invariance relation, Equation (1), change automatically from l to
are taken with the same l. Thus, unless the parameter involved in the shape invariance relation, Equation (1), change automatically from l to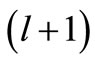 , one should not change l for the partner.
, one should not change l for the partner.
The paper is organized as follows. In Section 2, we briefly recapitulate the basic relations between energies, eigen functions and phase shifts of the partner potentials. We also indicate how the partner potential can be constructed for any potential, if its ground state wave function is known. In Section 3, results will be presented for the finite square well potential, which is a non-SIP, along with the Pöschl-Teller potential (SIP). The difference of their phase shifts will be compared with the expectations from SSQM. In Section 4, we draw our conclusions.
2. Partner Potentials: Relations between Their Observables
2.1. Energy Degeneracy and Shape Invariance
In this sub-section, we present an outline of energy degeneracy associated with partner potentials, following the review article of Cooper, Khare and Sukhatme [4]. Consider a spherically symmetric potential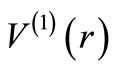 . The energy scale is so chosen that the ground state of orbital angular momentum l in this potential has zero energy. We assume that
. The energy scale is so chosen that the ground state of orbital angular momentum l in this potential has zero energy. We assume that  goes slower than
goes slower than  for
for 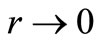 and approaches a constant value
and approaches a constant value 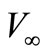 for
for . Then the Schrödinger equation for the ground state of orbital angular momentum l in this potential is
. Then the Schrödinger equation for the ground state of orbital angular momentum l in this potential is
 (2)
(2)
where,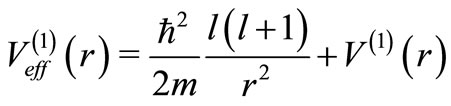 . Then one can obtain
. Then one can obtain 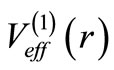 as
as
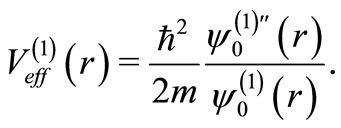 (3)
(3)
Define a “super potential”  through
through
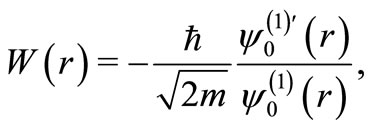 (4)
(4)
so that
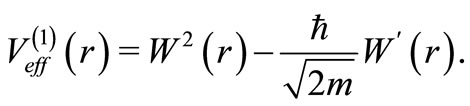 (5)
(5)
Define a partner potential
 (6)
(6)
and the corresponding Hamiltonian
 (7)
(7)
The supersymmetric partner of 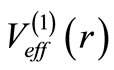 is
is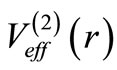 . Defining the operators A and
. Defining the operators A and  as
as
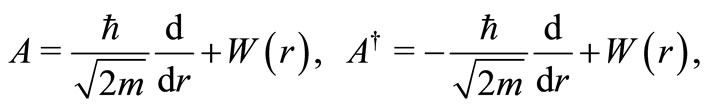 (8)
(8)
one sees that
 (9)
(9)
The eigenvalue equations satisfied by these Hamiltonians are
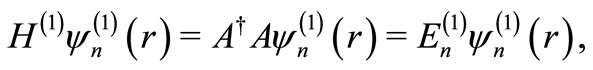
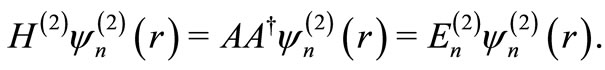 (10)
(10)
Then one can easily see that (energies are expressed in the scale in which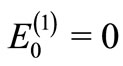 ) [4]
) [4]
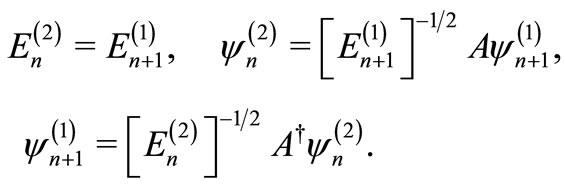 (11)
(11)
This shows that 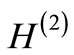 has the same spectrum as that of
has the same spectrum as that of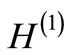 , except that there is no state in
, except that there is no state in 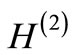 corresponding to the ground state of
corresponding to the ground state of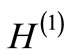 .
.
If 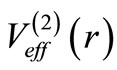 has the same functional shape as that of
has the same functional shape as that of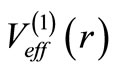 , but have different parameters, then the potential is said to be a shape invariant potential (SIP). The parameters of the partner are obtained as a simple mathematical function of the original parameters of
, but have different parameters, then the potential is said to be a shape invariant potential (SIP). The parameters of the partner are obtained as a simple mathematical function of the original parameters of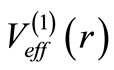 . Then it is easily seen that the entire energy spectrum is obtained algebraically [4].
. Then it is easily seen that the entire energy spectrum is obtained algebraically [4].
From Equations (4)-(6), we have
 (12)
(12)
This shows that the 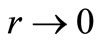 behavior of
behavior of 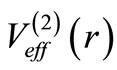 corresponds to angular momentum l + 1, since for
corresponds to angular momentum l + 1, since for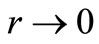 ,
, goes as
goes as . Both the potentials
. Both the potentials 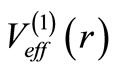 and
and 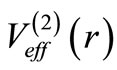 approach the same value
approach the same value  in the limit
in the limit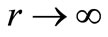 .
.
From Equations (4) and (8), we have
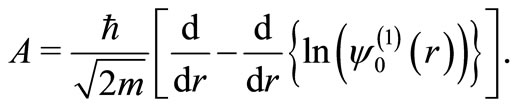 (13)
(13)
The operator A takes an eigenfunction of 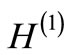 into an eigenfunction of
into an eigenfunction of 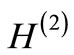 (including those corresponding to continuous eigenvalues).
(including those corresponding to continuous eigenvalues).
2.2. Relation between the Phase Shifts Produced by the Partner Potentials
For scattering states, energy should be in the continuum. In the energy scale chosen so far,  and
and . Now we change our energy scale by shifting it by
. Now we change our energy scale by shifting it by  such that each one of
such that each one of 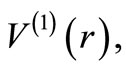
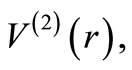
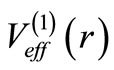 and
and 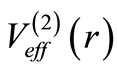 vanish in the limit
vanish in the limit . Energies of the bound states are expressed as
. Energies of the bound states are expressed as
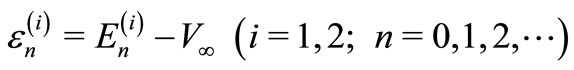 (14)
(14)
We consider scattering states 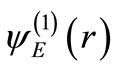 and
and 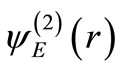 corresponding to energy
corresponding to energy 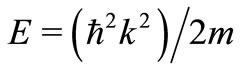 (
(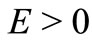 ) in the potentials
) in the potentials 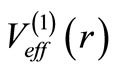 and
and 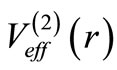 respectively. These states are connected by the operator A
respectively. These states are connected by the operator A
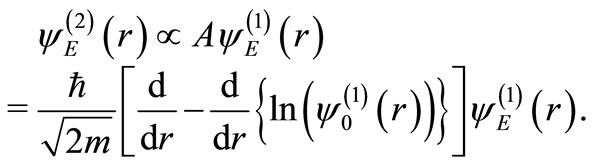 (15)
(15)
To calculate phase shifts, we need the asymptotic forms of these wave functions. For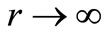 ,
,
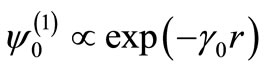 where
where
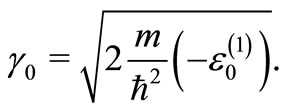 (16)
(16)
Hence we have
 (17)
(17)
The asymptotic form of 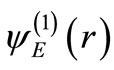 is
is
 (18)
(18)
where 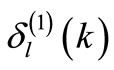 is the phase shift produced by
is the phase shift produced by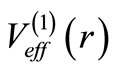 , corresponding to orbital angular momentum l and energy
, corresponding to orbital angular momentum l and energy . Substituting it in Equation (17), we have
. Substituting it in Equation (17), we have
 (19)
(19)
where
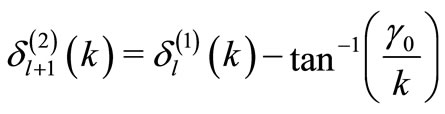 (20)
(20)
is the phase shift produced by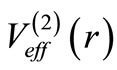 , corresponding to energy
, corresponding to energy . Note that the
. Note that the 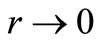 behavior of the partner potential corresponds to orbital angular momentum
behavior of the partner potential corresponds to orbital angular momentum 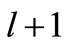 [see the discussion following Equation (12)], which justifies the subscript
[see the discussion following Equation (12)], which justifies the subscript 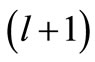 of
of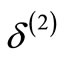 . Note also that
. Note also that  is the phase shift produced by
is the phase shift produced by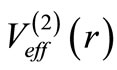 , which is the supersymmetric partner of
, which is the supersymmetric partner of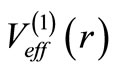 , and not of the potential [
, and not of the potential [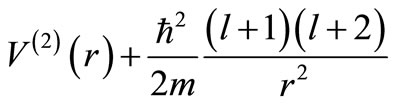 ] (where
] (where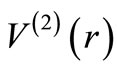 is the supersymmetric partner of
is the supersymmetric partner of ), even though
), even though 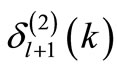 corresponds to the phase shift of the
corresponds to the phase shift of the 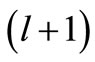 -th partial wave. Thus it will be wrong to take the phase shift of the explicit
-th partial wave. Thus it will be wrong to take the phase shift of the explicit 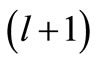 -th partial wave of
-th partial wave of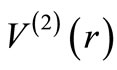 , unless l is the shape invariance parameter of Equation (1), such that
, unless l is the shape invariance parameter of Equation (1), such that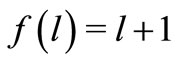 . For a shape invariant potential, for which Equation (1) holds,
. For a shape invariant potential, for which Equation (1) holds, 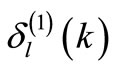 and
and 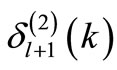 correspond to the same functional form of the potential. Hence in this case, use of Equation (20) permits the derivation of an algebraic expression for the phase shift. This is true only for the Coulomb potential [5,7]. In the above derivation, we have not assumed the shape invariance property [4]. Hence, Equation (20) should hold equally well for both SIP and non-SIP.
correspond to the same functional form of the potential. Hence in this case, use of Equation (20) permits the derivation of an algebraic expression for the phase shift. This is true only for the Coulomb potential [5,7]. In the above derivation, we have not assumed the shape invariance property [4]. Hence, Equation (20) should hold equally well for both SIP and non-SIP.
3. Results
3.1. Application to a Square Well Potential
As a simple application, we consider the 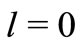 partial wave in a square well potential having the form
partial wave in a square well potential having the form
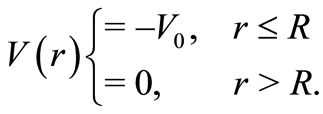
Note that the finite square well potential, although solvable semi-analytically, is not an SIP. A bound state in this potential is obtained using the continuity of the wave function and its first derivative at . This gives a transcendental equation for the binding energy
. This gives a transcendental equation for the binding energy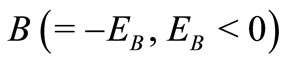 :
:
 (21)
(21)
where
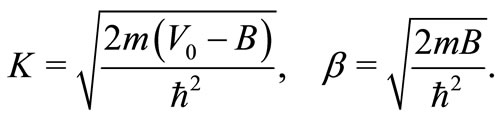
The numerical solution of Equation (21) with the largest possible value of 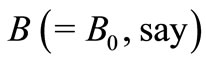 gives binding energy of the ground state. Corresponding to this value of
gives binding energy of the ground state. Corresponding to this value of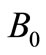 , we can get the ground state wave function
, we can get the ground state wave function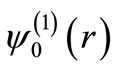 . Then the superpotential for the square well is given by Equation (3) as
. Then the superpotential for the square well is given by Equation (3) as
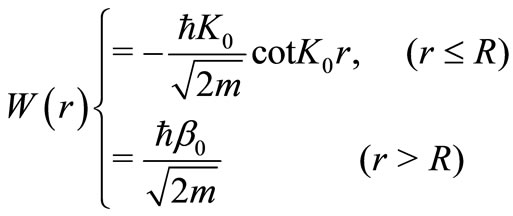 (22)
(22)
where 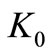 and
and 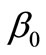 are values of K and
are values of K and 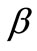 respectively, with B replaced by
respectively, with B replaced by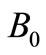 . Substitution of
. Substitution of 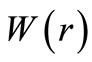 in Equation (5) reproduces
in Equation (5) reproduces 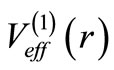 (for
(for ) and Equation (6) gives
) and Equation (6) gives
 (23)
(23)
3.2. Numerical Calculation of the Phase Shift
For the potential 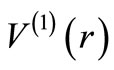 (with
(with 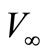 subtracted, so that
subtracted, so that 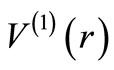 vanishes asymptotically) the radial Schrödinger equation for the l-th partial wave takes the form
vanishes asymptotically) the radial Schrödinger equation for the l-th partial wave takes the form
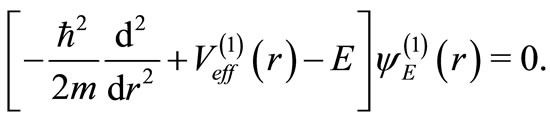 (24)
(24)
The asymptotic solution is given by Equation (18). We integrate Equation (24) numerically using the RungaKutta algorithm from 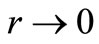 (subject to
(subject to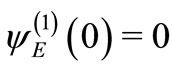 ) to two large values of r (say R1 and R2) to obtain
) to two large values of r (say R1 and R2) to obtain 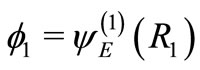 and
and . Then
. Then
 (25)
(25)
For calculation of , we follow the above procedure, replacing
, we follow the above procedure, replacing  by
by 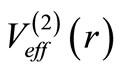 in Equaiton (24).
in Equaiton (24).
The partner potential is calculated using Equations (2), (4) and (6). No explicit l-dependent term is inserted in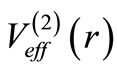 .
.
3.3. Numerical Results
We choose dimensionless units:  and take
and take 
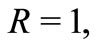 which support two bound states for
which support two bound states for 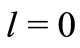 in this square well potential. Numerical solution of Equation (21) gives the binding energies of the ground and first excited state as B0 = 42.374903 and B1 = 20.714111 respectively. The partner potential is calculated from Equation (23), using the numerical value of
in this square well potential. Numerical solution of Equation (21) gives the binding energies of the ground and first excited state as B0 = 42.374903 and B1 = 20.714111 respectively. The partner potential is calculated from Equation (23), using the numerical value of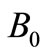 . Since
. Since 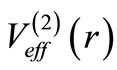 is no more analytically solvable, we solve the corresponding Schrödinger equation numerically by RungaKutta algorithm with appropriate boundary conditions for
is no more analytically solvable, we solve the corresponding Schrödinger equation numerically by RungaKutta algorithm with appropriate boundary conditions for 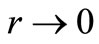 and
and . We checked that this potential supports only one bound state, whose binding energy is
. We checked that this potential supports only one bound state, whose binding energy is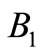 , to within numerical error. Furthermore, the calculated eigenfunction agrees with the second of Equation (11), within numerical errors. We also solved Equation (2) by the Runga-Kutta algorithm and verified that the energies and wave functions of the ground and excited states were reproduced correctly within numerical errors. These indicate the accuracy of the numerical procedure. Finally we obtained
, to within numerical error. Furthermore, the calculated eigenfunction agrees with the second of Equation (11), within numerical errors. We also solved Equation (2) by the Runga-Kutta algorithm and verified that the energies and wave functions of the ground and excited states were reproduced correctly within numerical errors. These indicate the accuracy of the numerical procedure. Finally we obtained  and
and 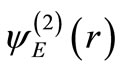 in the range
in the range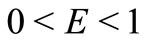 , by the Runga-Kutta algorithm, subject to
, by the Runga-Kutta algorithm, subject to . Phase shifts were calculated using Equation (25). Calculated phase shifts satisfy the supersymmetric relation Equation (20), within estimated numerical errors, when
. Phase shifts were calculated using Equation (25). Calculated phase shifts satisfy the supersymmetric relation Equation (20), within estimated numerical errors, when 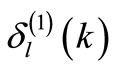 and
and 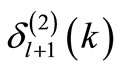 are obtained from the solutions of the Schrödinger equation with
are obtained from the solutions of the Schrödinger equation with  and
and 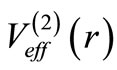 respectively. We have verified that the relationship Equation (20) is not valid between the phase shifts produced by
respectively. We have verified that the relationship Equation (20) is not valid between the phase shifts produced by  and
and
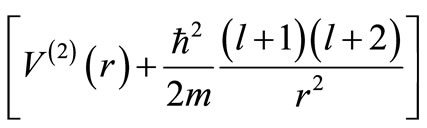 .
.
We again stress that for the  effective potential
effective potential 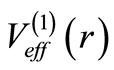
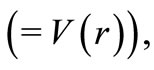 the partner potential
the partner potential 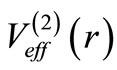 is given by Equation (23), without any additional l-dependence. As a further check, we verified these relations by a numerical calculation for the Pöschl-Teller potential [4], which is an SIP. Thus the phase shift relation is valid whether the potential is an SIP or not, when
is given by Equation (23), without any additional l-dependence. As a further check, we verified these relations by a numerical calculation for the Pöschl-Teller potential [4], which is an SIP. Thus the phase shift relation is valid whether the potential is an SIP or not, when 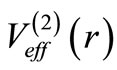 is obtained as the supersymmetric partner of
is obtained as the supersymmetric partner of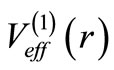 , with no change in the l value, even though it may appear from Equation (20) that the phase shift for the partner potential should be for the
, with no change in the l value, even though it may appear from Equation (20) that the phase shift for the partner potential should be for the 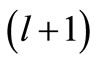 -th partial wave. The calculated results are presented in tables 1 and 2 for the square well and Pöschl-Teller potentials, respectively.
-th partial wave. The calculated results are presented in tables 1 and 2 for the square well and Pöschl-Teller potentials, respectively.
4. Conclusion
In this work, we have critically examined the relationship between phase shifts produced by two supersymmetric (SUSY) partner potentials. A simple analytic reation, Equation (20), holds for both SIP and non-SIP, which relates the phase shift produced by the l-th partial wave of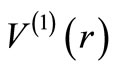 , i.e. by the potential
, i.e. by the potential

and that by its SUSY partner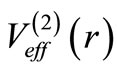 . The latter phase shift corresponds to the
. The latter phase shift corresponds to the  -th partial wave. However, there is no relation between phase shifts produced by
-th partial wave. However, there is no relation between phase shifts produced by
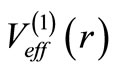 and
and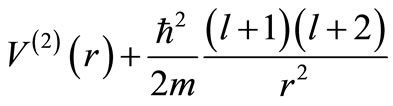 ,
,
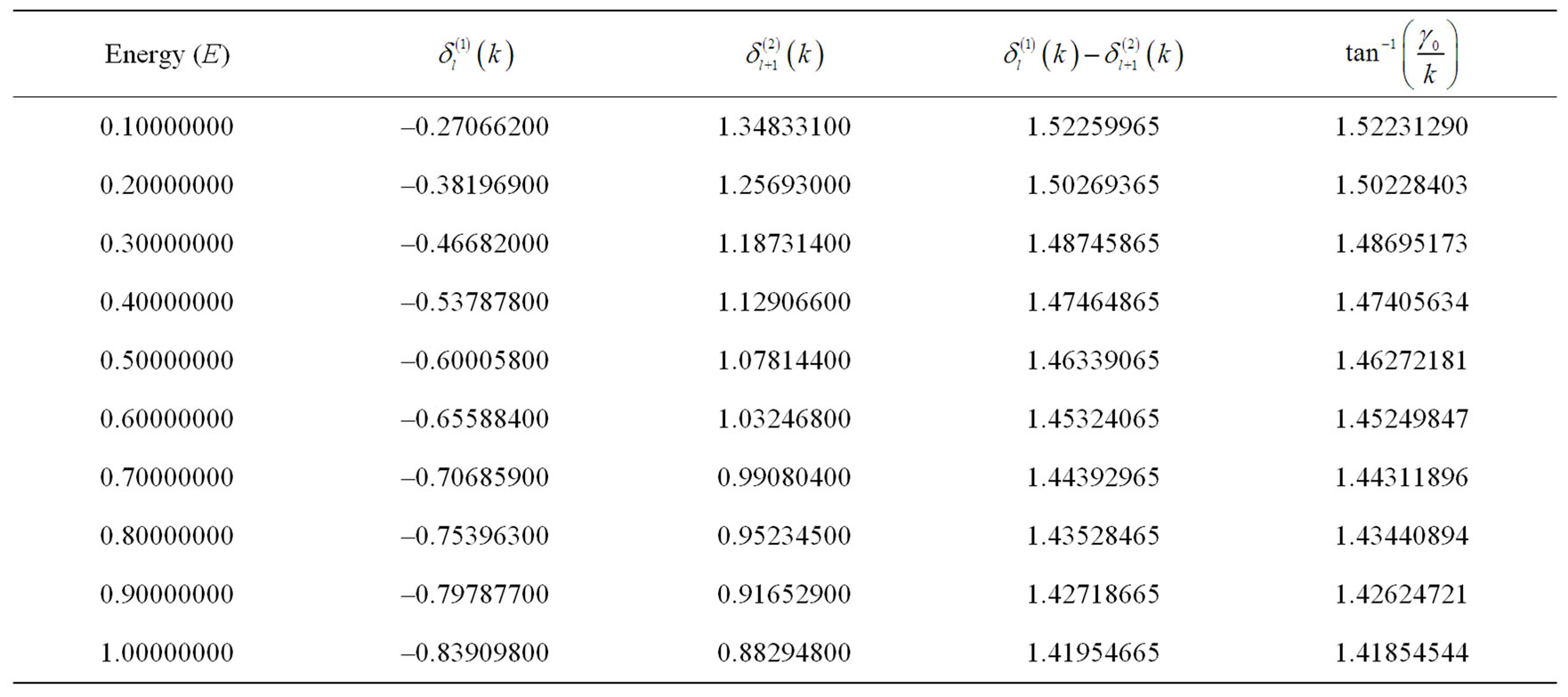
Table 1. Results of our calculation for the square well potential. 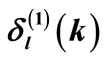 and
and 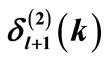 stand for the phase shifts produced by the potentials
stand for the phase shifts produced by the potentials 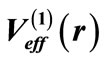 and
and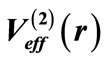 , respectively.
, respectively.
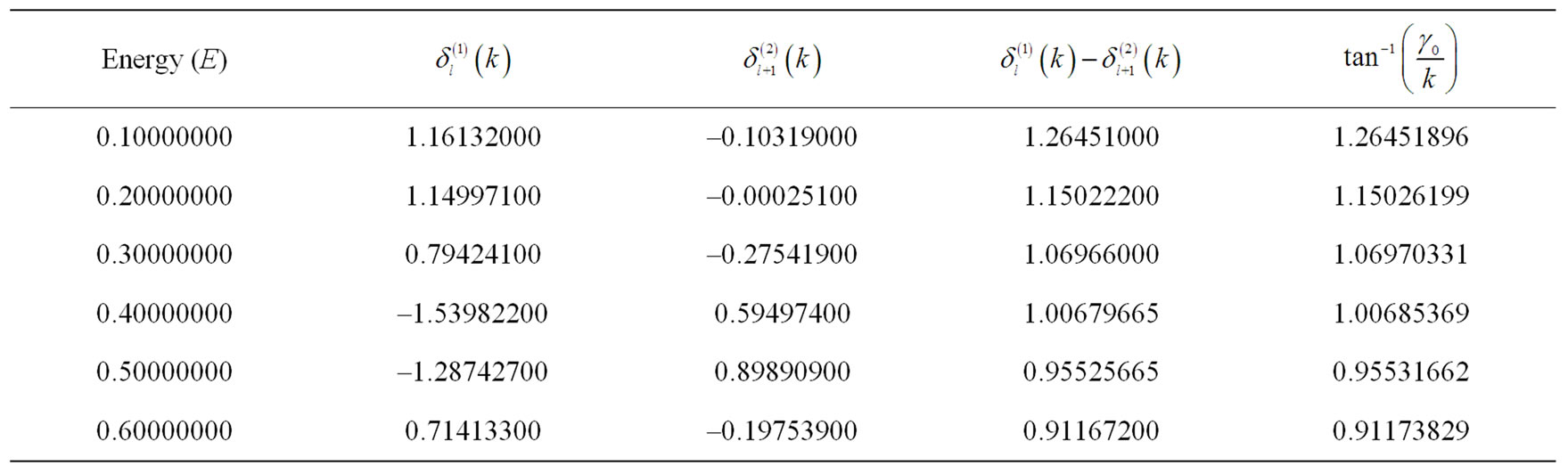
Table 2. Results of our calculation for the Pöschl-Teller potential. 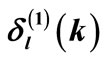 and
and  stand for the phase shifts produced by the potentials
stand for the phase shifts produced by the potentials 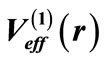 and
and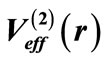 , respectively.
, respectively.
where 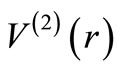 is the SUSY partner of
is the SUSY partner of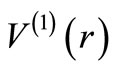 . It would be wrong to take
. It would be wrong to take 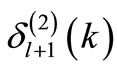 to be the phase shift produced by the
to be the phase shift produced by the 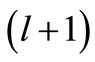 -th partial wave in
-th partial wave in . Our numerical calculation of the phase shifts produced by a non-SIP as well as an SIP confirm this. It would be of great interest, if the phase shift could be obtained algebraically. This would be possible, if
. Our numerical calculation of the phase shifts produced by a non-SIP as well as an SIP confirm this. It would be of great interest, if the phase shift could be obtained algebraically. This would be possible, if 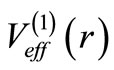 were shape invariant. But, even if
were shape invariant. But, even if 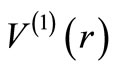 is shape invariant, i.e.
is shape invariant, i.e.  and
and 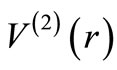 have same mathematical shapes, in general
have same mathematical shapes, in general  is not shape invariant. Thus, in general the phase shift cannot be obtained algebraically, even for standard SIPs. Since Equation (20) relates
is not shape invariant. Thus, in general the phase shift cannot be obtained algebraically, even for standard SIPs. Since Equation (20) relates 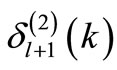 with
with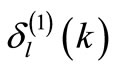 , an algebraic derivation of the phase shift is possible if
, an algebraic derivation of the phase shift is possible if 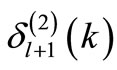 and
and  relate to potentials which have the same mathematical shape. This is possible, if SUSY partner of
relate to potentials which have the same mathematical shape. This is possible, if SUSY partner of  explicitly corresponds to the
explicitly corresponds to the 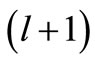 partial wave, i.e. l is the shape invariance parameter of Equation (1) and
partial wave, i.e. l is the shape invariance parameter of Equation (1) and . Such a restrictive condition is valid only for the Coulomb potential [4], only for which analytic expression for the phase shift is possible [5-7].
. Such a restrictive condition is valid only for the Coulomb potential [4], only for which analytic expression for the phase shift is possible [5-7].
5. Acknowledgements
The author wishes to thank Prof. T. K. Das for his helpful discussions and suggestions.
REFERENCES
- E. Witten, “Dynamical Breaking of Supersymmetry,” Nuclear Physics B, Vol. 188, No. 3, 1981, pp. 513-554. doi:10.1016/0550-3213(81)90006-7
- F. Cooper and B. Freedman, “Aspects of Supersymmetric Quantum Mechanics,” Annals of Physics, Vol. 146, No. 2, 1983, pp. 262-288. doi:10.1016/0003-4916(83)90034-9
- Y. A. Gel’fand and E. P. Likhtman, “Extension of the Algebra of Poincare Group Generators and Violation of P Invariance,” JETP Letters, Vol. 13, 1971, p. 323.
- F. Cooper, A. Khare and U. Sukhatme, “Supersymmetry and Quantum Mechanics,” Physics Reports, Vol. 251, No. 5-6, 1995, pp. 267-385. doi:10.1016/0370-1573(94)00080-M
- C. V. Sukumar, “Supersymmetric Quantum Mechanics and the Inverse Scattering Method,” Journal of Physics A, Vol. 18, No. 15, 1985, p. 2937. doi:10.1088/0305-4470/18/15/021
- J. J. Sakurai, “Modern Quantum Mechanics,” AddisonWesley, Boston, 2000.
- S. Mahapatra and T. K. Das, “On the Algebraic Derivation of Phase Shifts for Shape Invariant Potentials,” Modern Physics Letters A, Vol. 26, No. 23, 2011, pp. 1753-1761. doi:10.1142/S0217732311036061

