Journal of Modern Physics
Vol. 2 No. 7 (2011) , Article ID: 5791 , 5 pages DOI:10.4236/jmp.2011.27084
2D J–INEPT NMR Spectroscopy for CDn Groups: A Theorsssical Study
Ondokuz Mayıs University, Samsun, Turkey
E-mail: Gencten@omu.edu.tr, Isaka@omu.edu.tr
Received March 15, 2011; revised May 13, 2011; accepted June 1, 2011
Keywords: NMR, 2D J-INEPT, Product Operator Formalism, CDn Groups
ABSTRACT
2D J-INEPT NMR experiment is a combination of heteronusclear 2D J-Resolved and INEPT experiments. In this study, 2D J-INEPT experiment was analytically investigated by using product operator theory for weakly coupled ISn (I = 1/2, S = 1; n = 1, 2, 3) spin systems. The obtained theoretical results represent the FID values of CD, CD2 and CD3 groups. In order to make Fourier transform of the obtained FID values, a Maple program is used and then simulated spectra for of 2D J-INEPT experiment are obtained for CD, CD2 and CD3 groups. It is found that 2D J-INEPT is a useful experiment for both polarisation transfer and 2D J-resolved spectral assignment for CDn groups in complex molecules.
1. Introduction
Polarization transfer from high natural abundance nucleus to low natural abundance nucleus is widely used for heteronuclear weakly coupled spin systems in liquid–state NMR experiments [1-3]. The most common examples for the polarization transfer experiments are Distortionless Enhancement by Polarization Transfer (DEPT) and Insensitive Nuclei Enhanced by Polarization Transfer (INEPT). They both are used to increase sensitive enhancement of 13C spectra from spin-1/2 or spin-1 nucleus [4,5]. In order to resolve the chemical shift and spin-spin coupling parameters along the two different axes heteronuclear 2D J-Resolved NMR spectroscopy is used. Sometimes, spectral assignments of 2D J-Resolved NMR spectra become too difficult due to complex overlapping spectra. In order to overcome this problem, 2D J-INEPT experiment [6], which is the combination of 2D J-Resolved and INEPT NMR experiments, can be used.
As NMR is a quantum mechanical phenomenon, the product operator theory as a quantum mechanical method is widely used for the analytical description of multipulse NMR experiments on weakly coupled spin systems in liquids having spin- and spin-1 nuclei [7-18]. Analytical description of polarization transfer in INEPT experiment using product operator formalism has been presented for IS and IS2 (I = 1/2 and S = 1) spin systems [12]. So far, the product operator description of 2D J-INEPT NMR experiment is not investigated for heteronuclear weakly coupled ISn (I = 1/2; S = 1; n = 1, 2, 3) spin systems.
and spin-1 nuclei [7-18]. Analytical description of polarization transfer in INEPT experiment using product operator formalism has been presented for IS and IS2 (I = 1/2 and S = 1) spin systems [12]. So far, the product operator description of 2D J-INEPT NMR experiment is not investigated for heteronuclear weakly coupled ISn (I = 1/2; S = 1; n = 1, 2, 3) spin systems.
In this study, by using product operator formalism, analytical description of 2D J-INEPT NMR experiment is presented for heteronuclear weakly coupled ISn (I = 1/2; S = 1; n = 1, 2, 3) spin systems. Then, using the obtained theoretical results and a Maple program, the simulated spectra of the experiment are obtained for CD, CD2 and CD3 groups. Simulated spectra of 2D J-INEPT NMR spectroscopy are explained in detail for CDn groups. It is shown that this experiment can be used for the polarization transfer and J-resolved spectral assignment of CDn groups in complex molecules.
2. Theory
The product operator theory is the expansion of the density matrix operator in terms of matrix representation of angular momentum operators for individual spins. For IS (I = 1/2, S = 1) spin system, four Cartesian spin angular momentum operators for I = 1/2; EI, Ix, Iy, Iz and nine Cartesian spin angular momentum operators for S=1; ESSx, Sy, Sz, 
 ,
, 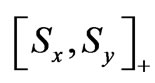
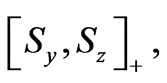 ,
,
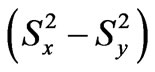 can be easily found [19]. So,
can be easily found [19]. So,  product operators are obtained with direct products of these angular momentum operators for IS (I = 1/2, S = 1) spin system.
product operators are obtained with direct products of these angular momentum operators for IS (I = 1/2, S = 1) spin system.
Time dependency of the density matrix is given by [11]
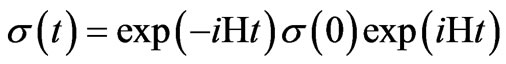 (1)
(1)
where H is the total Hamiltonian which consists of radio frequency (r.f.) pulse, chemical shift and spin-spin coupling Hamiltonians and s(0) is the density matrix at t = 0. After employing the Hausdorff formula [11]
 (2)
(2)
evolutions of product operators under the r.f. pulse, chemical shift and spin-spin coupling Hamiltonians can easily be obtained [7,11,13,16]. A complete product operator theory for IS (I = 1/2, S = 1) spin system and its application to some NMR experiments are presented elsewhere [16-18].
At any time during the experiment, the ensemble averaged expectation value of the spin angular momentum, e.g. for Iy, is
 (3)
(3)
where 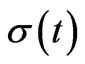 is the density matrix operator calculated from Eq. (6) at any time. As
is the density matrix operator calculated from Eq. (6) at any time. As 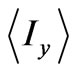 is proportional to the magnitude of the y-magnetization, it represents the signal detected on y-axis. So, in order to estimate the free induction decay (FID) signal of a multiple-pulse NMR experiment, density matrix operator should be obtained at the end of the experiment.
is proportional to the magnitude of the y-magnetization, it represents the signal detected on y-axis. So, in order to estimate the free induction decay (FID) signal of a multiple-pulse NMR experiment, density matrix operator should be obtained at the end of the experiment.
3. Results and Discussion
In this study, the product operator formalism is used for the analytical description of 2D J-INEPT NMR experiment. Pulse sequence of 2D J-INEPT, shown in Figure 1, is used [6]. The density matrix operator at each stage of the experiment is labelled with numbers. 13C is treated as spin I and D (2H) as spin S. For the analytical descriptions of the experiment, we have written a computer program in Mathematica which is very flexible for the implementation and the evolutions of the product operators under the Hamiltonians [20].
3.1. IS Spin System
 is the density matrix operator at thermal equilibrium for IS spin system. Evolutions of density matrix operator for each labelled point are obtained:
is the density matrix operator at thermal equilibrium for IS spin system. Evolutions of density matrix operator for each labelled point are obtained:
 (4)
(4)
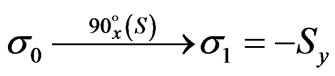 (5)
(5)
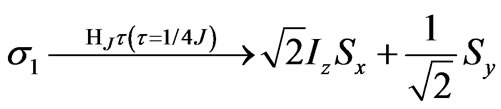 (6)
(6)
 (7)
(7)
 (8)
(8)
At the end of the experiment we obtain
 (9)
(9)
In Equation (9), 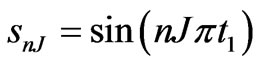 ,
,  ,
, 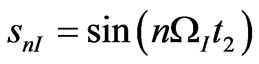 and
and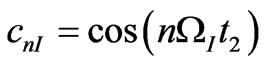 . In density matrix operator theory, only the last term of Equation (9) contributes to the signal as acquisition is taken along y-axes. It is necessary to obtain the
. In density matrix operator theory, only the last term of Equation (9) contributes to the signal as acquisition is taken along y-axes. It is necessary to obtain the  values of observable product operators indicated by O. For ISn (I = 1/2, S = 1; n = 1, 2, 3) spin systems,
values of observable product operators indicated by O. For ISn (I = 1/2, S = 1; n = 1, 2, 3) spin systems,  values of all the observable product operators can be found elsewhere [16].
values of all the observable product operators can be found elsewhere [16].
Using 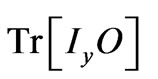 values and making trigonometric
values and making trigonometric
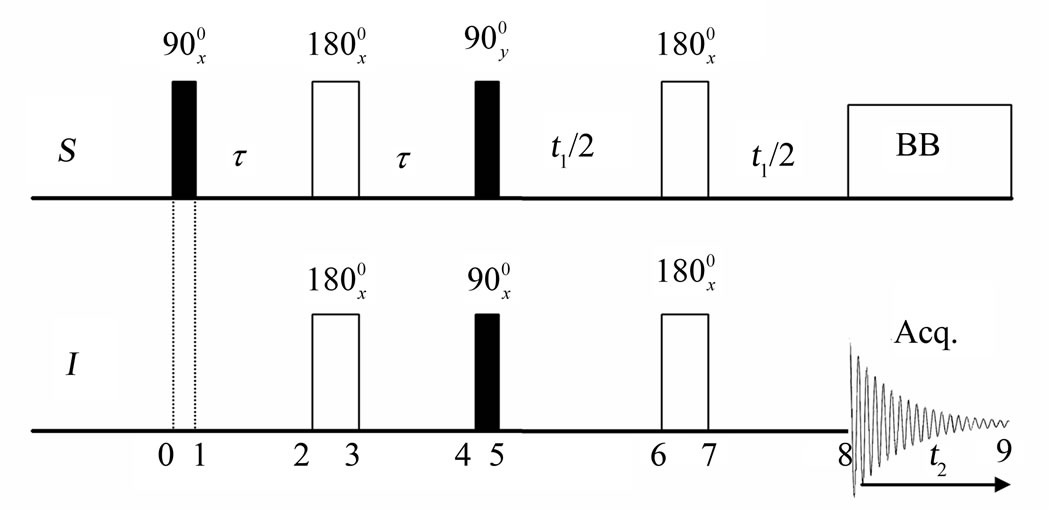
Figure 1. Pulse sequence of 2D J-INEPT NMR experiment. Optimum t value is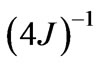 . BB: Broad band decoupling [6].
. BB: Broad band decoupling [6].
expansions,
 (10)
(10)
is obtained. This equation shows that the spin–spin coupling information appears on F1 axis and represents two coherences for I nucleus with phase of . Therefore, they give doublets signals with opposite direction and no signal for central peak. The signals coordinate are
. Therefore, they give doublets signals with opposite direction and no signal for central peak. The signals coordinate are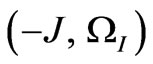 ,
,  and
and 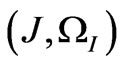 with intensity distribution of –1:0:1, respectively.
with intensity distribution of –1:0:1, respectively.
3.2. IS2 Spin System
For IS2 spin system, 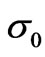 is the density matrix operator at thermal equilibrium:
is the density matrix operator at thermal equilibrium:
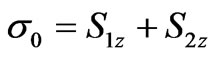 (11)
(11)
The density matrix operator at the end of the experiment is
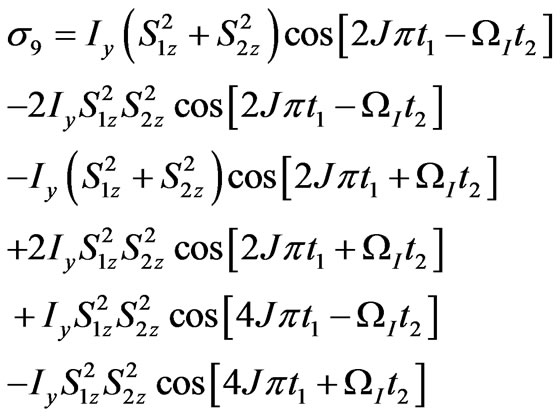 (12)
(12)
Using 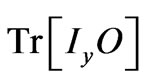 values;
values;
 (13)
(13)
is obtained. This equation represents five signals at the coordinates of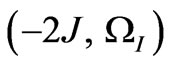 ,
,  ,
,  ,
,  and
and  with the relative intensities of –2:–2:0:2:2, respectively.
with the relative intensities of –2:–2:0:2:2, respectively.
3.3. IS3 Spin System
For IS3 spin system, applying the same procedure
 (14)
(14)
is obtained. As seen in this equation, there exist seven signals at ,
, ,
,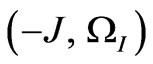 ,
, 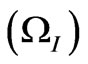 ,
,  ,
, 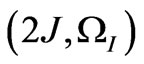 and
and  coordinates with the relative intensities of –3:–6:–6:0:6:6:3, respectively.
coordinates with the relative intensities of –3:–6:–6:0:6:6:3, respectively.
3.4. Simulated Spectra
A computer program was written by Kanters et. al. for product operator description of NMR experiments and for the simulations of FID signals [21,22]. This is called Product Operator Formalism (POF.M) using Maple. In this study, in order to obtain the simulated spectra of the FID results, POF.M program is implemented for this experiment.  values obtained for IS, IS2 and IS3 spin systems are given in Eqs. (10), (13) and (14), respectively. They represent the FID signals of 2D J-INEPT NMR spectroscopy for CDn groups. By using
values obtained for IS, IS2 and IS3 spin systems are given in Eqs. (10), (13) and (14), respectively. They represent the FID signals of 2D J-INEPT NMR spectroscopy for CDn groups. By using  values, simulated spectra of this experiment are obtained and they are given in Figures 2-4 for CD, CD2 and CD3 groups, respectively. In simulated
values, simulated spectra of this experiment are obtained and they are given in Figures 2-4 for CD, CD2 and CD3 groups, respectively. In simulated

Figure 2. Simulated spectrum of 2D J-INEPT NMR experiment for CD group.

Figure 3. Simulated spectrum of 2D J–INEPT NMR experiment for CD2 group.

Figure 4. Simulated spectrum of 2D J-INEPT NMR experiment for CD3 group.
spectra, 13C chemical shift values of CD, CD2 and CD3 groups were assumed to be 75 ppm, 50 ppm and 25 ppm, respectively. Spin-spin coupling constants between 13C and 2D nuclei for all CD, CD2 and CD3 groups were taken as 25 Hz. It can be seen from the theoretical results and the simulated spectra that 2D J-INEPT NMR experiment can be used to identify CD, CD2 and CD3 groups from each other and also to determine spin-spin coupling constant between 13C and 2D nuclei in CDn groups.
4. Conclusions
In this study, by using product operator theory, analytical description of 2D J-INEPT NMR experiment is presented for CDn groups. The obtained theoretical results represent the FID values of CDn groups. Then, in order to obtain the simulated spectra for CD, CD2 and CD3 groups, the Fourier transforms of the FID values are performed in Maple. Simulated spectra of 2D J-INEPT NMR spectroscopy are explained in detail for CDn groups. It is shown that, by using 2D J-INEPT NMR experiment, CDn groups can be identified from each other and 1J(C,D) coupling constants can be determined in deuterated complex molecules.
REFERENCES
- J. M. Bulsing, W. M. Brooks, J. Field. and D. M. Doddrell, “Polarization Transfer via an Intermediate Multiple-quantum State of Maximum Order,” Journal of Magnetic Resonance, Vol. 56, No. 1, 1984, pp. 167-173.
- J. M. Bulsing, W. M. Brooks, J. Field and D. M. Doddrell, “Reverse Polarization Transfer through Maximum Order Multiple-Quantum Coherence. A Reverse POMMIE Sequence,” Chemical Physics Letters, Vol. 104, No. 2-3 1984, pp. 229-234. doi:10.1016/0009-2614(84)80201-8
- J. M. Bulsing and D. M. Doddrell, “Multiple-Quantum Polarization-Transfer Coherence Pathways in Liquids,” Journal of Magnetic Resonance, Vol. 61, No. 2, 1985, pp. 197-219.
- D. M. Doddrell, D. T. Pegg and M. R. Bendall, “Distortionless Enhancement of NMR Signals by Polarization Transfer,” Journal of Magnetic Resonance, Vol. 48, No. 2, 1982, pp. 323-327.
- G. A. Morris and R. J. Freeman, “Enhancement off Nuclear Magnetic-Resonance Signals by Polarization Transfer,” Journal of the American Chemical Society, Vol. 101, No. 3, 1979, pp. 760-762.
- “Enhancement of Signals with Polarization Transfer via: INEPT.” http:www.chem.queensu.ca/facilities/NMR/nmr/webcourse/inept.htm
- W. Sfrensen, G. W. Eich, M. H. Levitt, G. Bodenhausen and R. R. Ernst, “Product Operator Formalism for the Description of Pulse NMR Experiments,” Progress in NMR Spectroscopy, Vol. 16, 1983, pp. 163-192.
- F. J. M. Van de Ven and C. W. Hilbers, “A Simple Formalism for the Description of Multiple-Pulse Experiments. Application to a Weakly Coupled 2-Spin (I = 1/2) System,” Journal of Magnetic Resonance, Vol. 54, No. 3, 1983, pp. 512-520.
- K. J. Packer and K. M. Wright, “The Use of Single-Spin Operator Basis Sets in the NMR Spectroscpy of Scalar-Coupled Spin Systems,” Molecular Physics, Vol. 50, No. 4, 1983, pp. 797-813. doi:10.1080/00268978300102691
- J. Shriver, “Product Operators and Coherence Transfer In Multiple-Pulse NMR Experiments,” Concepts in Magnetic Resonance, Vol. 4, No. 1, 1992, pp. 1-33. doi:10.1002/cmr.1820040102
- N. Chandrakumar and S. Subramanian, “Modern Techniques in High Resolution FT NMR,” Springer, New York, 1987.
- N. Chandrakumar, “Polarization Transfer between Spin 1 and Spin 1/2 Nuclei,” Journal of Magnetic Resonance, Vol. 60, No. 1, 1984, pp. 28-36.
- R. R. Ernst, G. Bodenhausen and A. Wokaum, “Principles of Nuclear Magnetic Resonance in One and Two Dimentions,” Clarendon Press, Oxford, 1987.
- A. Gençten and F. Köksal, “A Product Operator Description of 2D-J Resolved NMR Spectroscopy for ISn Sspin System (I = 1/2, S = 1),” Spectroscopy Letters, Vol. 30, No. 1, 1997, pp. 71-78. doi:10.1080/00387019708002590
- A. Gençten, Ö. Tezel and A. Köroğlu, “A Theoretical Application of SEMUT NMR Spectroscopy to Deuterated compounds,” Applied Magnetic Resonance, Vol. 20, No. 1-2, 2001, pp. 265-273.
- A. Gençten and İ. Şaka, “A Complete Product Operator Theory for IS (I = (1)/(2), S = 1) Spin System and Application to DEPT-HMQC NMR Experiment,” Molecular Physics, Vol. 104, No. 18, 2006, pp. 2983-2989. doi:10.1080/00268970600909197
- İ. Şaka and A. Gençten, “A Theoretical Application of MAXY NMR for CDn Groups,” Verlag der Zeitchrift Naturforsch, Vol. 62a, No. 5-6, 2007, pp. 259-264.
- İ. Şaka, “Analytical Descriptions of DEPT NMR Spectroscopy for ISn (I = 1, S = 1; n = 1, 2, 3, 4) Spin Systems,” Brazilian Journal of Physics, Vol. 38, No. 3A, 2008, pp. 323-328.
- P. Allard and T. Härd, “A Complete Hermitian Operator Basis Set for Any Spin Quantum Number,” Journal of Magnetic Resonance, Vol. 153, No. 1, 2001, pp. 15-23. doi:10.1006/jmre.2001.2416
- S. Wolfram, “The Mathematica Book 3rd Edition,” Wolfram Media/Cambridge University Press, New York, 1996.
- R. P. F. Kanters, B. W. Char and A. W. Addison, “A Computer Algebra Appilcation for the Description of NMR Experiments Using the Product-operator Formalism,” Journal of Magnetic Resonance A, Vol. 101, No. 1, 1993, pp. 23-29. doi:10.1006/jmra.1993.1003
- R. P. F. Kanters, “Product Operator Formalism Using Maple.” 1993. http://oncampus.richmond.edu/~rkanters/POF/.

