ABSTRACT

The boundary value problem with a spectral parameter in the boundary conditions for a polynomial pencil of the Sturm-Liouville operator is investigated. Using the properties of the transformation operators for such operators, the asymptotic formulas for eigenvalues of the boundary value problem are obtained.

Keywords:

Sturm-Liouville Equation, Boundary Value Problem, Transformation Operator, Spectral Theory of Differential Operators, Asymptotic Formulas, Fractional Derivative, Eigenvalue, Eigenfunction, Polynomial Pencil

1. Introduction

In this paper the boundary value problem, generated on the finite interval by equation

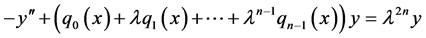(1)

and the boundary conditions

(2)

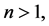
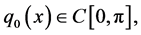
is considered. Here we assume that 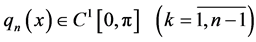are complex valued functions; is a complex parameter and

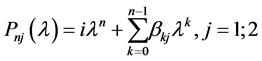
with the given constants.

It is known that the Sturm-Liouville problems play an important role in solving many problems in mathematical physics. There has been a growing interest in Sturm- Liouville problems with spectral parameter in boundary conditions in recent years and there are a lot of articles on this subject in the literature. For more detailed analysis we refer to the papers [1] - [9] and the references therein. In the case 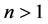the simple boundary value problem for the Equation (1) with conditions 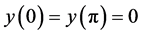is investigated in [10] (also see [11] ).

Note that many of these investigations are based on some integral representations for the fundamental solutions of the Sturm-Liouville equation called transformation operators. The transformation operators for Sturm-Liouville equation and quadratic pencil of the Sturm-Liouville equation are constructed and studied in [12] [13] and [14] [15] respectively, while the corresponding operators for the pencil (1) are investigated in [10] [16] .

In this paper using the properties of transformation operators, the considering boundary value problem is investigated and asymptotic formula for the eigenvalues is obtained.

We studied in [10] , the solutions 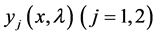of the Equation (1) satisfying the initial conditions

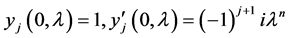
and it is proved that in the sectors of complex plane

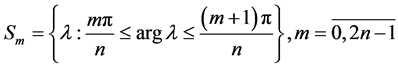
the solutions have the following integral representations:

(3)

where, 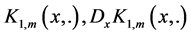and,

belong to and respectively. Moreover, if denotes Riemann-Liouville fractional derivative of order (see [17] ) with respect to t, i.e.

then for all the functions and belong to and respectively. Furthermore, the following equalities are valid:

(4)

(5)

where

(6)

2. Asymptotic Formulas for the Solutions and Eigenvalues

By and we denote the solutions of the Equation (1) with initial conditions

(7)

Using integral representations (3) and formulae (4), (5), it is easy to show that for each

(8)

(9)

(10)

(11)

Let us consider the boundary problem (1), (2). Denote by the characteristic function of this problem. Then

(12)

Zeros of the function we’ll call eigenvalues of the problem (1), (2). Let be the solution of the Equation (1) with initial conditions

(13)

It is clear that

(14)

and

(15)

From formulae (8)-(11) we find that

(16)

(17)

Then for we can write the asymptotic formula

(18)

where and are constants. From this we conclude that there exists the constant such that

(19)

for all, where

(20)

From (20) we have that for sufficiently large positive integer there are a finite number of zeros of in the circle. In other words, the total number of zeros of in is equal to the total number of zeros of the function Moreover, there exists a positive number such that on the circle the estimation

(21)

satisfies. Hence, from (28), (30) and the equality

(22)

according to Rouche’s theorem we conclude that and have the same number of zeros in the circle for sufficiently large. Using a simple asymptotic estimations (see [2] ), we obtain that zeros having sufficiently large module of the func-

tion lie near rays and so the eigenvalues of the problem (1),

(2) consist of series. Solving the equation asymptotically we find the following asymptotic formula for series of eigenvalues of the problem (1), (2):

(23)

where

Theorem 2. Boundary value problem (1), (2) has a countable number of eigenvalues. The eigenvalues having sufficiently large module are placed near the rays

, and series of these satisfy the asymptotic formula (23).

Cite this paper

Adiloglu Nabiev, A. (2016) On a Boundary Value Problem for a Polynomial Pencil of the Sturm-Liouville Equation with Spectral Parameter in Boundary Conditions. Applied Mathematics, 7, 2418-2423. http://dx.doi.org/10.4236/am.2016.718190

References