Applied Mathematics
Vol.07 No.17(2016), Article ID:72194,17 pages
10.4236/am.2016.717176
The Compound Indexing of Human Self-Similar Behavioural Patterns
Petr Kloucek1, Pavel Zakharov2, Armin von Gunten1
1CAMPsyN, Old Age Psychiatry Service, Lausanne University Hospital, Lausanne, Switzerland
2Biovotion AG, Zurich, Switzerland

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 7, 2016; Accepted: November 20, 2016; Published: November 23, 2016
ABSTRACT
Applications of a constitutive framework providing compound complexity analysis and indexing of coarse-grained self-similar time series representing behavioural data are presented. A notion of behavioural entropy and hysteresis is introduced as two different forms of compound measures. These measures provide clinically applicable complexity analysis of behavioural patterns yielding scalar characterisation of time- varying behaviours registered over an extended period of time. The behavioural data are obtained using body attached sensors providing non-invasive readings of heart rate, skin blood perfusion, blood oxygenation, skin temperature, movement and steps frequency. The results using compound measures of behavioural patterns of fifteen healthy individuals are presented. The application of the compound measures is shown to correlate with complexity analysis. The correlation is demonstrated using two healthy subjects compared against a control group. This indicates a possibility to use these measures in place of fractional dimensions to provide a finer characterisation of behavioural patterns observed using sensory data acquired over a long period of time.
Keywords:
Behavioural Complexity, Physiological and Behavioural Surrogate Data, Behavioural Entropy, Behavioural Hysteresis, Seld-Similar Normally Distributed Precesses, Non-Integer Hausdorff-Besicovitch Dimension, Hurst Exponent

1. Introduction
Behaviours encompass both normal and pathological patterns characterised by short- time instances of transitional clinical presentations. Such types of transitions are usually accompanied by self-similar behavioural patterns re-organisation. Underlying complexity of observable data can be registered using external sensors attached to, say, an arm or torso with a posteriori computer assisted indexing.
For the sake of terminological simplicity and the purpose of this paper we use the term “behavioural” in a very broad sense. We use this term to encapsulate both physiological and behavioural variables. An example of physiological variable is, e.g., heart rate. An example of behavioural variable is, e.g., steps frequency. In other words, we view behavioural variables as pronunciations. Also, we consider the term variable to be interchangeable with the term measurable observable [1] . We assume that variables considered are independent of order at which they are consecutively sensed during a short time span on order of seconds.
Complexity analysis of behavioural patterns allows for indexing of behavioural states. It may be a way of reducing complex data to a vector characterising both a given disorder, and/or a patient suffering from this disorder. This approach is neither available in clinical settings nor, to the best of our knowledge, in research in the area of mental disorders except for partial approaches in the field of psychotherapy [2] .
If a time series possesses a self-similar structure the non-integer Hausdorff-Besico- vitch dimension can be assigned to it [3] [4] [5] . This dimension is an indicator of complexity. It is often computed using the Hurst exponent. The loss of self-similarity in some of the measurable variables or a change of the non-integer Hausdorff-Besicovitch dimension of these variables, might be an essential part of a definition of behaviours, including altered behaviours.
We use the term surrogate data to denote variables that can be recorded in a non- invasive way using suitable external wearable sensors. The adjective surrogate is used to indicate that we are not dealing with EEG based scans but with macroscopic coarse- grained smoother data collected using skin attached sensors1.
We collect simultaneously the following surrogate data time series: heart rate, blood oxygenation, skin blood perfusion, skin temperature, movement and step frequency.
The aim of the presented communication is to introduce a constitutive notion of behavioural entropy and behavioural hysteresis and their application to compounded indexing of fractional behavioural patterns. The approximate self-similarity of human behavioural data is verified by the presented variational principle providing a robust mechanism to establish approximate self-similarity of finite noisy patterns.
The presented method and its applications can be implemented in clinical environments. Ultimately, health practitioners may be able to use this approach to gauge behavioural states using just a small number of significant numerical indices, each referring to one set of sensory surrogate data.
Thermodynamic temperature may serve as an example to illustrate our approach. Temperature is a scalar measure of kinetic energy of micro-scale fluctuations that have to be observed over a period of time. The analogy is that we are proposing a characterisation of surrogate data fluctuations over longer periods of time followed up by a subsequent complexity analysis yielding algebraic characterisations of a chosen behavioural variable.
Fractional-like data and their analysis has been used in a variety of fields since its introduction by B. Mandelbrot including applications in medicine, bioinformatics with its recent implementations in clinical controlled environments. There is a vast amount of literature related to fractional dimensionality and complexity of natural structures.
Fundamentals of description and analysis of bounded topological objects with complex boundaries or time series having non-integer dimensionality including general appications in medicine can be learned about in, e.g., [4] [6] [7] [8] [9] . The most of clinically applications of complexity indexing pertain to Heart Rate Variability based on the EEG scans, c.f., [10] [11] [12] [13] [14] . A more complex overview of the bioinformatics and biomedical fields can be found in books such as [8] [15] [16] [17] . Certain aspects of a fractional analysis of time series are patented [18] . There is only a limited literature on other behavioural variables we use, e.g., perfusion, skin temperature and poster and gaits, some of them using wavelets analysis [19] [20] [21] .
The notion of entropy has been used in physics, materials science as well as biology and bioinformatics [22] [23] [24] [25] . We introduce an alternative notion and definition of this important quantity. Our approach is similar in its core to the approach reported in [26] and [27] .
We note that the presented concept of constitutive behavioural indexing stems and follows upon concepts of geometrically nonlinear materials science that is based on phase transitions, notion of criticality and evidence of multiple equilibrium atomic structures. For this reason we include references to some basic introductory text as well as more recent publications such as [28] [29] [30] [31] .
2. Structure of the Communication
The presented communication introduces signed behavioural entropy and behavioural hysteresis based on the behavioural data segmentation and its subsequent complexity analysis using the Hurst exponent. The notion of behavioural entropy and hysteresis are, to the best of our knowledge, novel. In addition we present fractional analyses of compounded surrogate sensory data that are important for multi-dimensional indicators applicable to diagnoses of altered states. The reported self-similarities of body attached sensory behavioural data is also novel to the best of our knowledge. We note that just a single behavioural index is insufficient when constitutive diagnoses of altered states are needed for clinical practices.
We present an example of indexing of two healthy subjects from the point of view of the entropy and hysteresis indices out of fifteen healthy subjects representing a sample of about twenty six days of data collection.
In addition we present a variational principle2 to evaluate an approximate self-simil- arity based on noisy finite data that we use prior to posterior estimates of the Hurst exponent using allometric power law, maximum likelihood fractional Brownian process parameters, and the distributional measure based on the introduced variational principle.
We describe the sensory surrogate data in Section 3. The constitutive measures in terms of behavioural entropy and hysteresis are introduced in Section 4. We present a sample of constitutive indexing of the two healthy subjects out of fifteen subjects in Section 5. The self-similarity verification procedure and the subsequent computations of the Hurst exponent are presented at Section 8.
3. Macroscopic Behavioural Data
We implement four hierarchically structured layers of sensing technologies. These layers encompass 1) micro-electronics-based wearable sensors, 2) communication with a data collection device, 3) mathematics-based data processing, 4) a projection of complexity indexing onto multidimensional Euclidian product spaces.
The first two layers refer to a wearable attach-and-forget Vital Signs Monitor (VSM) capable of motion-tolerant monitoring of human vital signs without interfering with the person’s activities. The third and the forth layers deal with the detection of self- similarity of surrogate measurables that can be uniquely characterized by their scaling properties. VSM provides measurements of heart rate (HR), blood oxygenation (SpO2), skin blood perfusion, skin temperature, movement indicator and steps frequency [32] . Monitoring results in the time series. VSM performs quasi-continuous measurements and sends data every thirty seconds to a smartphone via Bluetooth communication while attached on an upper arm.
Multi-wavelength monitoring in combination with short source-detector distance through an optical sensor allows for more stable heart-rate detection. Combination of optical and acceleration signals using signal processing algorithms provides separation of arterial pulsation signal from motion artefacts. More information about the sensor design can be found in [33] .
The approach is illustrated using the combination of step frequency and heart rate in two healthy subjects as an example in place of all available combinations.
3.1. Sensory Variables
3.1.1. Heart Rate
Heart rate is estimated by means of a motion-compensating algorithm from pulse-in- duced variations of optical reflection from skin under the VSM. Intensity of light diffusely reflected from the skin changes with blood flow and volume during the cardiac cycle. VSM is measuring heart rate by following these variations and by compensating for effects of motion.
3.1.2. Skin Blood Perfusion
Skin perfusion allows oxygen delivery to the skin and thermoregulation of the body in order to facilitate heat dissipation the amount of blood in the skin can be increased to more than 5% of the total blood volume. Besides internal or environmental temperature, changes in perfusion can be triggered by a blood pressure, blood oxygenation, heart rate, posture, physical activity, external pressure, metabolic status, or psychological stress to name a few [32] .
3.1.3. Blood Oxygenation
The device is using reflected red and infrared light supported by motion-compensating algorithms to estimate the ratio of haemoglobin molecules in arterial blood. The blood oxygenation as measured by SpO2 is expected to be above 95% for healthy subject.
Blood oxygenation significantly contributes to both the acute control of local blood flow and its long-term control. The frequency of the acute time scale of the blood flow, and, consequently, of the blood oxygenation, ranges from seconds in the blood flow increase mode to minutes in the decrease mode, [34] . The long-term control is on order of hours. The presence of two different time scales, the acute and the long-term, is a possible signature of self-similar scalability.
3.1.4. Skin Temperature
Skin temperature is lower than measurements taken at body cavities. It’s peak values lag behind by about three hours compared to the mouth or cavity based peak readings, [20] . Since skin temperature is taken at the surface that forms an interface between environment and body it is an acceptable measure of heat transfer. Skin temperature is measured by VSM on the surface in proximity of the optical sensor.
3.1.5. Movement and Steps Frequency
Movement indicator is a parameter characterising instantaneous activity of a human subject. The measurements are performed with 3-axis VSM accelerometer. The indicator is given by an energy of variations of low-passed filtered differentials of accelerometer measurements. Steps frequency is inversely proportional to speed of motion. The movement indicator and the steps frequency are uncorrelated and represent different parameters.
4. Compound Measures
It is quite common to find biological structures and patterns such as sub-cellular membranes for which the measurements of the length of their boundaries increase with observational resolution. Mathematically, it is possible to construct curves such that any two points will be infinitely distant using standard definition of length [15] . Commonly, such structures are referred to as fractals.
The behavioural indices are given by the Hurst exponents corresponding to some approximately self-similar and normally distributed surrogate data given by discrete time series with fractional-like structures.
The notion of the behavioural state implicitly requires invariance in the sense of statistically reproducible behavioural indices arising from repeated distinct realisations of data acquisitions under similar conditions.
The introduction of the Behavioural Entropy and Hysteresis addresses the need to obtain a clinically applicable a single number characterisation of the structural, behavioural, complexity of time segmented surrogate data as the structural complexity changes with time. In particular, the entropy is designed to characterise a pathway to a behavioural equilibrium that is reflected by its sign.
Both the entropy and hysteresis combine information that include complexity indices, frequencies, projection of time varying complexity measures as well as variances of surrogate data, etc., we decide to call them collectively compound measures of behavioural states.
4.1. Behavioural Entropy
Entropy in classical thermodynamics as well as in its Boltzman’s statistical version is a measure of the number of possible configurations. Another interpretation of entropy is given by Shannon’s version of the classical Gibbs definition [29] to measure the averaged number of bits needed specify an arbitrary word of certain length [35] . An application of the entropy in psychiatric setting is reported in [25] .
We define the behavioural entropy by

The quantity H denotes the complexity index of acquired self-similar surrogate data given by the Hurst exponent,  denotes a jump of an enclosed quantity, i.e.,
denotes a jump of an enclosed quantity, i.e., 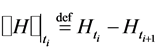 ,
,  are time equidistant points at which the function
are time equidistant points at which the function 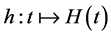 has a finite jump. The behavioural entropy reflects the sign and the magnitude of the discontinuities of time evolution of the Hurst exponent.
has a finite jump. The behavioural entropy reflects the sign and the magnitude of the discontinuities of time evolution of the Hurst exponent.
Behavioural entropy, S, is constructed to measure of the ability of a given living organism to react to internal and/or external constraints.
The above definition of entropy implies that entropy is negative if more changes are in the direction of lesser complexity of behavioural surrogates and positive otherwise. In other words, the positivity of the entropy indicates a tendency to achieve high reactivity, and its negativity relates to a tendency to achieve a low reactivity.
The higher complexity corresponds to the Hurst exponent closer to zero, and the lower complexity corresponds to the Hurst exponent smaller than one but close to it. If the behavioural entropy is zero at some time span then the complexity of the segmented surrogates is, at least locally, constant. Thus a living organism ceases to function if its entropy, computed with some , is zero and the Hurst exponent is equal to one for an arbitrarily small period of time. Constant entropy and the Hurst exponent smaller than one for an arbiltrarilly small time span implies significant lack of responsiveness. Non-zero values, both negative and positive, are measures of responsiveness.
, is zero and the Hurst exponent is equal to one for an arbitrarily small period of time. Constant entropy and the Hurst exponent smaller than one for an arbiltrarilly small time span implies significant lack of responsiveness. Non-zero values, both negative and positive, are measures of responsiveness.
Classical statement of the Second Law of Thermodynamics for isolated systems states that the time variation of thermodynamic entropy must increase yielding thus increased levels of disorder or, more closer to our interpretation, increased level of informational complexity.
The behavioural entropy increases and it is positive if some behavioural surrogates temporarily lower their Hurst exponents yielding thus higher complexity, i.e., higher behavioural disorder. The behavioural entropy as well as the classical entropy can attain negative values [36] [37] [38] .
4.2. Behavioural Hysteresis
It is argued that “one observes scale invariance near a critical point” [39] . Critical points can be viewed as states where the behavioural complexity indices abruptly change. Criticality is closely related to phase transitions [28] [31] [40] .
Phase transitions are intimitaly connected with hysteresis [29] . We find that a typical example of a behavioural hysteresis pertaining to healthy subjects in Heart Rate Complexity × Heart Rate Variance product space as time progresses from low activity to high activity and to low activity in the end of fifteen hours of sensing.
Hysteresis is thus a pathway connecting different complexity indices in certain multi- dimensional Euclidian spaces during cycling of high-to-low activities as time progresses. In general, this should be nearly a closed curve with, consequently, well defined area.
If it were possible to obtain identical time-reversed trajectories in this space the area enclosing the beging and the end of the cycled activities the hysteresis area would be zero. This is impossible though due to biological processes. Hence the area enclosed by the hysteresis loop should be always positive.
Hypothetically, the behavioural hysteresis can be attributed to diminishing availability of resources or to some bio-thermodynamical processes controlling energy distribution. We can consider as a possible example the amount of residual milk acid in muscles during a high activity. Collectively, these processes yield long-range surrogate data dependence that is pronounced in lower complexity indices as long as the surrogate data can/could be considered self-similar and normally distributed. Hence, we can hypothesise that during consequent time cycling among high and low behavioural states the complexity of self-similar surrogates data cannot increase.
We observe a hysteresis given by some computed complexity indices versus the variance of the surrogates over a suitable time span. This implies that the considered indices must be generated by non-linear processes for otherwise they could not exhibit hysteresis. Since we observe the behavioural hysteresis in certain surrogate data it seems plausible to hypothesise that physiological networks operate in such a way that they can perform sudden change of functionality patters.
5. Indexing of Healthy Subjects
5.1. Surrogate Data Segmentation
The complexity scaling properties of the surrogate data are changing in time. Self-si- milarity can be lost or its scaling properties can change. These discontinuities may indicate changes in behavioural patterns pertaining to changes of feedback control of the central nervous system and its convergence in response to internal and/or to external stimuli. We use a clustering approach based on the discontinuities of the Hurst exponent applying uniform, and finest possible, data segmentation to address the observation that the scaling properties can change during long-time data acquisition time spans. An example is given by Figure 1.
5.2. Segmented Behavioural Patterns Complexities
Table 1 and Table 2 display surrogate data complexity indexing of a highly trained subject and a healthy individual, respectively. The former subject is also younger. The baseline Hurst exponents are based on the mean of behavioural indexing of fifteen subjects yielding twenty one data sets3. The behavioural complexity baselines are 0.78, 0.52, 0.57, 0.48 (low pass filtered), 0.73 and 0.33 for heart rate, blood oxygenation, skin blood perfusion, skin temperature, relative movement and steps frequency, respectively, at high activity period of four hours at thirty seconds stroboscopic time resolution4. The repeated data acquisition exhibited a reasonable level of consistency with small standard deviation and the data spread of about 0.15 allowing to determine the Hurst exponent based on nineteen surrogate data sets5. The spread is computed as the difference between the clusters of maximum and minimum values of the control group.
The first observation is that the surrogate data reported do exhibit self-similar structures most of the time. Exceptions are, e.g., the steps frequency during sleep or perfusion during low activity periods.
The second observation made is that a highly trained subject (Table 1) outperforms
Figure 1. Heart rate data segmentation. The step function (blue piece-wise constant function) correlates only with the time axis. It represents values of the Hurst exponents computed from data points corresponding to about fifteen hours segmented to two hours time intervals.
Table 1. The table summarises about fifteen hours of surrogate data segmented and indexed in two hours time intervals. The presented indices correspond to a highly trained subject. The Hurst exponents are estimated using allometric power law, maximum likelihood and a distributional distance. Each method yields different estimates. This is the reason we report a range rather than single value of the Hurst exponent. All the reported values are on or below 0.1 using a distributional distance. N/A is reported if the distributional error estimate of the self-similarity exceeds 0.1. LPF stands for Low Pass Filter applied when the original data do not provide consistency with respect to self-similarity. The last column of this table indicates individual subjective evaluations of activities.
Table 2. The table provides indexing of a healthy subject obtained using fifteen hours of data acquisition. Some surrogate data seems to be quite different from individual subjective evaluation.
the control group at perceived high activity periods considering the upper bounds of the heart rate. Running indices exhibits negative to neutral correlation and, consequently, a short range dependence of heart rate and steps frequency. The skin blood oxygenation and movement behavioural indices shown are within the spread of the control group but with higher regularity of surrogate data. Perfusion and skin temperature exhibit lower complexity, i.e., longer range correlation compared to the control group.
These analyses suggest that during high physical activity periods a well trained subject exhibits a complex heart rate index. The rest of the surrogate data are positively correlated with smaller complexity of the surrogates compared to the control group.
The second healthy subject exhibits lower complexity with respect to the control group except for steps frequency (Table 2). This could indicate that this subject’s reaction to change of either external or internal demands falls short in terms of adequate responsivenesses.
5.3. Behavioural Entropy Based Results
Comparing the two data sets presented by Table 1 and Table 2, c.f., Figure 2, we obtain heart rate entropy of −0.34 for the first subject, and −0.10 for the second subject, respectively. Following the definition and the underlying interpretation of entropy we observe that both subjects overall move to a lower complexity state that is expressed by the negative signs during the consecutive fifteen hours of data acquisition.
Moreover, the first subject, a highly trained individual, has three times the heart rate entropy compared to the second healthy subject considering absolute values. Higher positive behavioural entropy is likely to indicate higher capability to deal with stimuli and to reach a lower complexity of a behavioural equilibrium.
5.4. Hysteresis Based Results
The cycling between high-low activity periods may represent a recuperation process, e.g., from “fatigue”, when the loop evolves towards the starting point. We compute the recuperation from fatigue as the area enclosed by the hysteresis loop in the complexity- variance Euclidian space projection of surrogate data.
Figure 3 visualizes the behavioural hystereses of the two subjects discussed in Section 5.2.
Figure 2. The plot represents complexity indexing of about fifteen hours of surrogate data for heart rate of a healthy subject summarised by Table 2. The green line indicates the overall index, the orange line depicts the difference between date and night complexity, while the blue line provides indexing in two hours intervals. Both night/day and the fine-grained complexity analysis shows that heart rate complexity decreases during low activity periods. The low activity time span is defined as six pm to midnight.
Figure 3. Behavioural hysteresis loops comparing highly trained and a healthy subjects. The areas enclosed by the loops are interpreted as behavioural fatigue. The red loop corresponds to a highly trained individual, the blue loop corresponds to a healthy individual. The complexity-variance Euclidian representation shows clear distinction between the two individuals.
The hysteresis dimensionless area of the former is 668.36 while that of the other healthy individual is 1011.44. This might indicate that highly trained individuals have significantly quicker recuperation times during a typical day rutines than less trained individuals.
Behavioural complexity indexing of the two healthy subjects shows an association between behavioural entropy and hysteresis. There are more upward changes of the behavioural entropy in both cases suggesting that both subjects tend to reach an overall equilibrium state corresponding to a lower complexity state. A smaller hysteresis area as observed in the more trained individual indicates a higher efficiency to reach a low complexity state.
6. Clinically Relevant Summaries
6.1. Surrogate Data Projections
We represent surrogate data by constructing maps from the space of behaviours to the space of complexity indices. This representation allows to track time evolution of behavioural patterns with respect to different vital signes in multi-dimension Euclidian spaces that can be partitioned into identifiable behaviour regions.
We present such maps yielding a graphical representation of the data summarised by Table 1 and Table 2 at Figure 4. This graph shows the projection of the data onto the blood oxygenation and steps frequency versus the heart rate. The regions which we denote, somewhat tentatively, as “high activity” and “stress” regions are speculative. Nevertheless they do conform to a general understanding of these characterisations. The high activity region is characterised in our interpretation by a low Hurst exponent.
Figure 4. The graphical Euclidian representation corresponds to data given by Table 1 and Table 2. The blue dots and their approximate convexifiction are drawn from Table 2. The red ones correspond to Table 1. The graphical representation shows a clear distinction between highly trained (red) and a healthy individual (blue) with respect to stress and work load. This visualised by the shift to higher Hurst exponent indicating lower complexity of behavioural readings for the highly trained individual. The data analysed were recorded during a typical day for both subjects. The numbers refer to sequential order of the two hours periods into which the fifteen hours of recordings are split correspondingly to segmentation such as shown at Figure 1.
This means that the surrogate data, projected onto blood oxygenation/heart rate, exhibit a high level of complexity. The stress region can be characterised by a low complexity of motion and a higher complexity of heart rate.
The introduction of the index spaces is necessary to dissect a proper or impaired contribution of various subsystems to the overall behaviour [41] [42] .
6.2. Compound Indexing
The compound indexing is provided by the behavioural entropy and hysteresis as a characterisation of human subjects capabalities to react to various stimuli and to recover from fatigue, respectively.
Table 3 provides compound measures of the data given by Table 1 and Table 2. The results presented by this table are compatible with the observations discussed in Section 5.2. The important aspect of the presented approach is in its capability to provide a “single number” characterisation of behavioural states with time varying behavioural patterns.
7. Conclusions
The data collected using human healthy subjects show that some of the externally collected data using body attached sensors possess self-similarity at some periods of time.
This property allows complexity analysis using non-integer Hausdorff-Besicovich dimension and related mathematical tools. The compound measures in terms of behavioural entropy and hysteresis yield indexing of surrogate data providing a single digit characterisations of behavioural states in a way that thermometer based measurements are used. We think this approach may prove useful in clinical settings for diagnostic and follow-up purposes.
The introduction of behavioural entropy and hysteresis provides characterisations of time-extended and time-varying analyses of surrogate data. The behavioural indexing or, equivalently, the complexity analysis of the acquired surrogate data, shows that phenotypic change can be dynamically monitored.
Contributions
PK provided the mathematical framework based on the use of fractional dimension to characterise behavioural complexity, Cassiopee computational ecosystem as well as all the computational results. He also introduced the notion of constitutive definitions of behavioural entropy and hysteresis.
PZ delivered time series based on the human raw data acquired during the experimental part of the project using the VSM biosensor.
Table 3. The table summarises the results based on the data presented at Table 1 and Table 2. The table exemplifies differences between the two subjects from the point of view their efficiency to achieve low complexity behavioural equilibria. The lower the signed entropy as well as the size of area of the hysteresis loop are better from the behavioural point of view. The behavioural entropy and hysteresis were computed using fifteen hours of surrogate data acquisitions. The negative sign of the entropy indicate a path to a low complexity equilibrium. The area of the hysteresis indicates the efficiency to recover from behavioural fatigue to achieve the equilibria structures indicated by the behavioural entropy.
AvG led the experimental part of the project. In addition, he established a link among some of the human sensory data acquired and the interpretation of the results using behavioural entropy and hysteresis. He fundamentally contributed to the link between mathematics and the need for objective measures of human behaviours.
Ethics Statement
We declare that 1) the study was carried out in accordance with the Declaration of Helsinki and CIOM, 2) all subjects gave their written informed consent. The presented research includes observational research only with no video or participation by the authors of this study. Consequently, this communication is exempt from an Institutional Review Board review. We refer to Code of Federal Regulations of the United States of America, Part 46, Protection of Human Subjects, Revised on January 15, 2009.
Acknowledgements
The authors were supported in part by Biovotion, AG, that provided the sensors and access to the raw sensory data. The raw data were processed by the Cassiopee computational ecosystem created by one of the authors. Our activities were supported in part by the Service Universitaire de Psychiatrie de l’Age Avancé that is part of Centre hospitalier universitaire vaudois and University of Lausanne, Switzerland. We would like to express our gratitude to all participants taking part in the study reported in this communication.
Cite this paper
Kloucek, P., Zakharov, P. and von Gunten, A. (2016) The Compound Indexing of Human Self-Similar Behavioural Patterns. Applied Mathematics, 7, 2212-2228. http://dx.doi.org/10.4236/am.2016.717176
References
- 1. Weyl, H. (1949) Philosophy of Mathematics and Natural Science. Chapter Quantum Physics and Causality, Appendix C. Princeton University Press, Princeton.
- 2. Tschacher, W., Schiepek, G. and Brunner, E.J. (1992) Self-Organization and Clinical Psychology: Empirical Approaches to Synergetics in Psychology. Springer Series in Synergetics, Springer-Verlag, New York.
https://doi.org/10.1007/978-3-642-77534-5 - 3. Van Ness, M. (1968) Fractional Brownian Motions, Fractional Noise and Application. SIAM Review, 10, 422-437.
https://doi.org/10.1137/1010093 - 4. Peitgen, H.-O., Jürgens, H. and Saupe, D. (1992) Chaos and Fractals. Springer-Verlag, New York.
https://doi.org/10.1007/978-1-4757-4740-9 - 5. Mo¨rters, P. and Peres, Y. (2010) Brownian Motion. Cambridge Series in Statistical and Probabilistic Mathematics, Cambridge University Press, Cambridge.
- 6. Kaye, B.H. (2008) A Random Walk through Fractal Dimensions. Wiley, Hoboken.
- 7. Gavrilova, M.L., Tan, C.J.K. and Kuijper, A. (2013) Transactions on Computational Science XVIII: Special Issue on Cyberworlds. Lecture Notes in Computer Science, Springer Berlin Heidelberg.
https://doi.org/10.1007/978-3-642-38803-3 - 8. Losa, G.A., Merlini, D., Nonnenmacher, T.F. and Weibel, E.R. (2005) Fractals in Biology and Medicine. Number V. 4 in Mathematics and Biosciences in Interaction. Birkhäuser Basel, Basel.
https://doi.org/10.1007/3-7643-7412-8 - 9. Holden, J.G., Riley, M.A., Gao, J. and Torre, K.M., Eds. (2013) Fractal Analyses: Statistical and Methodological Innovations and Best Practices. Frontiers in Physiology E-Book.
http://www.frontiersin.org/Fractal_Physiology/researchtopics/Fractal_Analyses:_Statistical_and_Methodological_Innovations_and_Best_Practices./555 - 10. Ching, E.S. and Tsang, Y.K. (2007) Multifractality and Scale Invariance in Human Heartbeat Dynamics. Physical Review E, 76, Article ID: 041910.
https://doi.org/10.1103/PhysRevE.76.041910 - 11. Ernst, G. (2013) Heart Rate Variability. Springer, London.
- 12. Cusenza, M., Accardo, A., D’Addio, G. and Corbi, G. (2010) Relationship between Fractal Dimension and Power-Law Exponent of Heart Rate Variability in Normal and Heart Failure Subjects. 2010 Computing in Cardiology, September 2010, 935-938.
- 13. Voss, A., Schulz, S., Schroeder, R., Baumert, M. and Caminal, P. (2009) Methods Derived from Non-Linear Dynamics for Analysing Heart Rate Variability. Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 367, 277-296.
https://doi.org/10.1098/rsta.2008.0232 - 14. Ivanov, P.C., Amaral, L.A., Goldberger, A.L., Havlin, S., Rosenblum, M.G., Struzik, Z.R. and Stanley, H.E. (1999) Multifractality in Human Heartbeat Dynamics. Nature, 399, 461-465.
https://doi.org/10.1038/20924 - 15. Murray, J.D. (2002) Mathematical Biology, An Introduction, Volume Interdisciplinary Applied Mathematics. Springer-Verlag, Berlin.
- 16. Bronzino, J.D. and Peterson, D.R. (2014) Biomedical Signals, Imaging, and Informatics. The Biomedical Engineering Handbook, 4th Edition, CRC Press, Boca Raton.
- 17. Najarian, K. and Splinter, R. (2016) Biomedical Signal and Image Processing. 2nd Edition. CRC Press, Boca Raton.
- 18. Vo-Dinh, T. and Sadana, A. (2002) Fractal Analysis of time Varying Data. US Patent No. 6,422,998.
- 19. Häfner, H.-M., Bräuer, K., Eichner, M., Koch, I., Heinle, H., Röcken, M. and Strlin, A. (2007) Wavelet Analysis of Skin Perfusion in Healthy Volunteers. Microcirculation, 14, 137-144.
https://doi.org/10.1080/10739680601131234 - 20. Kelly, G. (2006) Body Temperature Variability (Part 1): A Review of the History of Body Temperature and Its Variability Due to Site Selection, Biological Rhythms, Fitness, and Aging. Alternative Medicine Review, 11, 278-293.
- 21. Van Marken Lichtenbelt, W.D., Daanen, H.A.M., Fronczek, R., Raymann, J.E.M., Severens, M.W. and Van Someren, E.J.W. (2006) Evaluation of Wireless Determination of Skin Temperature Using iButtons. Physiology & Behavior, 88, 489-497.
https://doi.org/10.1016/j.physbeh.2006.04.026 - 22. Hong, S.L., Bodfish, J.W. and Newell, K.M. (2006) Power-Law Scaling for Macroscopic Entropy and Microscopic Complexity: Evidence from Human Movement and Posture. Chaos, 16, Article ID: 013135.
https://doi.org/10.1063/1.2186765 - 23. Liu, P.Y., Iranmanesh, A., Keenan, D.M., Pincus, S.M. and Veldhuis, J.D. (2007) A Noninvasive Measure of Negative-Feedback Strength, Approximate Entropy, Unmasks Strong Diurnal Variations in the Regularity of LH Secretion. American Journal of Physiology-Endocrinology and Metabolism, 293, E1409-E1415.
https://doi.org/10.1152/ajpendo.00365.2007 - 24. Pincus, S. (1995) Approximate Entropy (ApEn) as a Complexity Measure. Chaos, 5, 110-117.
https://doi.org/10.1063/1.166092 - 25. Pincus, S.M. (2006) Approximate Entropy as a Measure of Irregularity for Psychiatric Serial Metrics. Bipolar Disorders, 8, 430-440.
https://doi.org/10.1111/j.1399-5618.2006.00375.x - 26. Shi, Y., Nguyen, M.H., Blitz, P., French, B., Fisk, S., De La Torre, O, Smailagic, A., Siewiorek, D.P., Al Absi, M., Ertin, E., Kamarck, T. and Kumar, S. (2010) Personalized Stress Detection from Physiological Measurements. International Symposium on Quality of Life Technology Proceedings, Las Vegas, 28-29 June 2010, 71-75.
- 27. Wijsman, J., Grundlehner, B., Liu, H., Hermens, H. and Penders, J. (2011) Towards Mental Stress Detection Using Wearable Physiological Sensors. 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, 30 August-3 September 2011, 1798-1801.
https://doi.org/10.1109/IEMBS.2011.6090512 - 28. Stanley, H.E. (1971) Introduction to Phase Transitions and Critical Phenomena. International Series of Monographs on Physics, Oxford University Press, Oxford.
- 29. Ericksen, J.L. (1998) Introduction to the Thermodynamics of Solids. Springer, Berlin.
- 30. Kloucek, P. and Luskin, M. (1994) The Computations of the Dynamics of the Martensitic Deformation. Continuum Mechanics and Thermodynamics, 6, 209-240.
https://doi.org/10.1007/BF01135254 - 31. Cox, D.D., Hardt, R.M. and Kloucek, P. (2008) Convergence of Gibbs Measures Associated with Simulated Annealing. SIAM Journal on Mathematical Analysis, 39, 1472-1496.
https://doi.org/10.1137/060657169 - 32. Caduff, A., Talary, M.S. and Zakharov, P. (2010) Cutaneous Blood Perfusion as a Perturbing Factor for Noninvasive Glucose Monitoring. Diabetes Technology & Therapeutics, 12 1-9.
https://doi.org/10.1089/dia.2009.0095 - 33. Caduff, A., Talary, M.S. and Zakharov, P. (2009) A Wearable Diffuse Reflectance Sensor for Continuous Monitoring of Cutaneous Blood Content. Physics in Medicine & Biology, 17, 5301-5320.
- 34. Guyton, A.C. and Hall, J.E. (2010) Textbook of Medical Physiology. Guyton Physiology. Elsevier Health Sciences, Amsterdam.
- 35. Kurths, J., Voss, A., Saparin, P., Witt, A., Kleiner, H.J. and Wessel, N. (1995) Quantitative Analysis of Heart Rate Variability. Chaos, 5, 88-94.
https://doi.org/10.1063/1.166090 - 36. Schrodinger, E. (1944) What Is Life? Cambridge University Press, Cambridge.
- 37. Brillouin, L. (1962) Science and Information Theory. 2nd Edition, Academic Press, New York.
- 38. Penrose, O. (1970) Foundations of Statistic Mechanics: A Deductive Approach. Pergamon Press, Oxford.
- 39. Proekt, A., Banavar, J.R., Maritan, A. and Pfaff, D.W. (2012) Scale Invariance in the Dynamics of Spontaneous Behavior. Proceedings of the National Academy of Sciences of the United States of America, 109, 10564-10569.
https://doi.org/10.1073/pnas.1206894109 - 40. Salje, E.K. (1993) Phase Transitions in Ferroelastic and Co-Elastic Crystals. Cambridge Topics in Mineral Physics and Chemistr, Cambridge University Press, Cambridge.
- 41. Hassabis, D. and Maguire, E.A. (2009) The Construction System of the Brain. Philosophical Transactions of the Royal Society B: Biological Sciences, 364, 1263-1271.
https://doi.org/10.1098/rstb.2008.0296 - 42. Zeithamova, D. and Preston, A.R. (2010) Flexible Memories: Differential Roles for Medial Temporal Lobe and Prefrontal Cortex in Cross-Episode Binding. The Journal of Neuroscience, 30, 14676-14684.
https://doi.org/10.1523/JNEUROSCI.3250-10.2010 - 43. Gloter, A. and Hoffmann, M. (2007) Estimation of the Hurst Parameter from Discrete Noisy Data. Annals of Statistics, 35, 1947-1974.
https://doi.org/10.1214/009053607000000316 - 44. Cox, D.R. (1984) Long-Range Dependence: A Review. In: David, H.A. and David, H.T., Eds., Statistics: An Appraisal, Iowa State University Press, Ames, 55-74.
Appendix
Estimates of an Approximate Self-Similarity and the Hurst Exponent
The presented estimates of the behavioural indices are tested to verify their self-simi- larity using a distributional distance. The Hurst exponent estimates are obtained using allometric power law, maximum likelihood fractional Brownian process parameters identification, and a distributional measure.
The verification of the self-similarity is a crucial step for otherwise the subsequent computing of the scaling parameters, such as the Hurst exponent, would be questionable, [43] .
Following [44] , we could consider a discrete-time stochastic process 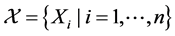 to be self-similar with the Hurst exponent H if
to be self-similar with the Hurst exponent H if
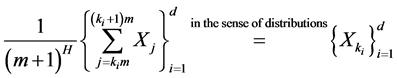 (1)
(1)
holds for an unique 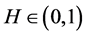 for all d-tuples
for all d-tuples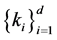 , where d and m obey
, where d and m obey 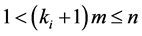 , and
, and


Instead, we compare the probability density of surrogate data directly to the density of a fractional Brownian function. The reason is that dealing with a limited amount of somewhat noisy data with varying frequencies does not produce reliable estimates of the self-similarity using (1).
Let 




applied to 


Here, p denotes the number of bins applied to histogram of the approximate probability density. The points


.
NOTES
1The adjective surrogate is also used to refer to synthetics data in fractal dynamical systems literature. We decided to use this term as is often used in the non-smooth optimisation where it refers to solving a smoother problem having the same extrema instead. We see the analogy in that we deal with smoother macroscopic data provided by behavioural pronunciations as opposed to microscopic EEG-like data.
2Section 8 can be initially skipped.
3Some of the subjects were indexed repeatedly.
4The single number is obtained as the average of the clustered surrogates to eliminate outliers.










