Received 29 September 2015; accepted 22 November 2015; published 25 November 2015

ABSTRACT

In this paper, we establish asymptotically optimal simultaneous confidence bands for the copula function based on the local linear kernel estimator proposed by Chen and Huang [1] . For this, we prove under smoothness conditions on the derivatives of the copula a uniform in bandwidth law of the iterated logarithm for the maximal deviation of this estimator from its expectation. We also show that the bias term converges uniformly to zero with a precise rate. The performance of these bands is illustrated by a simulation study. An application based on pseudo-panel data is also provided for modeling the dependence structure of Senegalese households’ expense data in 2001 and 2006.

Keywords:

Copula Function, Kernel Estimation, Local Linear Estimator, Uniform in Bandwidth Consistency, Simultaneous Confidence Bands

1. Introduction

Let us consider a random vector 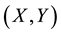with joint cumulative distribution function H and marginal distribution functions F and G. The Sklar’s theorem (see [2] ) says that there exists a bivariate distribution function C on 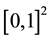with uniform margins such that

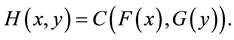
The function C is called a copula associated with the random vector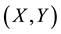. If the marginal distribution functions F and G of H are continuous, then the copula C is unique and is defined as

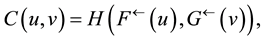
where 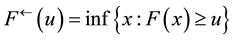and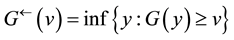, , are the generalized inverses of F and G respectively.

From these facts, estimating bivariate distribution function can be achieved in two steps: 1) estimating the margins F and G; 2) estimating the copula C.

In this paper, we are dealing with nonparametric copula estimation. We consider a copula function C with uniform margins U and V defined on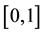. Then, we can write

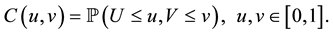
The aim of this paper is to construct asymptotic optimal confidence bands, for the copula C, from the local linear kernel estimator proposed by Chen and Huang [1] . Our approach, based on modern functional theory of empirical processes, allows the use of data-driven bandwidths for this estimator, and is largely inspired by the works of Mason [3] and Deheuvels and Mason [13] .

There are two main methods for estimating copula functions: parametric and nonparametric methods. The Maximum likelihood estimation method (MLE) and the moment method are popular parametric approaches. It happens that one may use a nonparametric approach like the MLE-method and, at the same time, estimates margins by using parametric methods. Such an approach is called a semi-parametric estimation method (see [4] ). A popular nonparametric method is the kernel smoothing. Scaillet and Fermanian [5] presented the kernel smoothing method to estimate bivariate copulas for time series. Genest and Rivest [6] gave a nonparametric empirical distribution method to estimate bivariate Archimedean copulas.

A pure nonparametric estimation of copulas treats both the copula and the margins in a parameter-free way and thus offers the greatest generality. Nonparametric estimation of copulas goes back to Deheuvels [7] who proposed an estimator based on a multivariate empirical distribution function and on its empirical marginals. Weak convergence studies of this estimator can be found in Fermanian et al. [8] . Gijbels and Mielniczuk [9] proposed a kernel estimator for a bivariate copula density. Another approach of kernel estimation is to directly estimate a copula function as explored in [5] . Chen and Huang [1] proposed a new bivariate kernel copula estimator by using local linear kernels and a simple mathematical correction that removes the boundary bias. They also derived the bias and the variance of their estimator, which reveal that the kernel smoothing produces a second order reduction in both the variance and mean square error as compared with the unsmoothed empirical estimator of Deheuvels [7] .

Omelka, Gijbels and Veraverbeke [10] proposed improved shrinked versions of the estimators of Gijbels and Mielniczuk [9] and Chen and Huang [1] . They have done this shrinkage by including a weight function that removes the corner bias problem. They also established weak convergence for all newly-proposed estimators.

In parallel, powerful technologies have been developed for density and distribution function kernel estimation. We refer to Mason [3] , Dony [11] , Einmahl and Mason [12] , Deheuvels and Mason [13] . In this paper, we’ll apply these recent methods to kernel-type estimators of copulas. The existence of kernel-type function estimators should lead to nonparametric estimation by confidence bands, as shown in [13] , where general asymptotic simultaneous confidence bands are established for the density and the regression function curves. Furthermore, to our knowledge, there is not yet such type of results in nonparametric estimation of copulas. This motivated us to extend such technologies to kernel estimation of copulas by providing asymptotic simultaneous optimal confidence bands.

Let 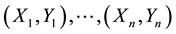be an independent and identically distributed sample of the bivariate random vector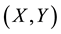, with continuous marginal cumulative distribution function F and G. To construct their estimator, Chen and Huang proceed in two steps. In the first step, they estimate margins by

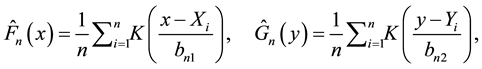
where 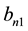and 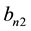are some bandwidths and K is the integral of a symmetric bounded kernel function k supported on. In the second step, the pseudo-observations and are used to estimate the joint distribution function of the unobserved and, which gives the estimate of the

unknown copula C. To prevent boundary bias, Chen and Huang suggested using a local linear version of the kernel k given by

where for; and is a bandwidth. Finally, the local linear kernel estimator of the copula C is defined as

(1)

where The subscript h in is a variable bandwidth which may depend either on the sample data or the location.

Our best achievement is the construction of asymptotic confidence bands from a uniform in bandwidth law of the iterated logarithm (LIL) for the maximal deviation of the local linear estimator (1), and the uniform convergence of the bias to zero with the same speed of convergence.

The paper is organized as follows. In Section 2, we expose our main results in Theorems 1, 2 and 3. Simulation studies and applications to real data sets are also made in this section to illustrate these results. In Section 3, we report the proofs of our assertions. The paper is ended by Appendix in which we postpone some technical results and numerical computations.

2. Main Results and Applications

2.1. Main Results

Here, we state our theoretical results. Theorem 1 gives a uniform in bandwidth LIL for the maximal deviation of the estimator (1). Theorem 2 handles the bias, while Theorem 3 provides asymptotic optimal simultaneous confidence bands for the copula function.

Theorem 1. Suppose that the copula function has bounded first order partial derivatives on. Then for any sequence of positive constants satisfying, , and for some, we have almost surely

(2)

where is a positive constant such that and.

Remark 1. Theorem 1 represents a uniform in bandwidth law of the iterated logarithm for the maximal deviation of the estimator (1). As in [15] we may use it, in its probability version, to construct simultaneous asymptotic confidence bands from the estimator (1). In this purpose, we must ensure before hand that the bias term converges uniformly to 0, with the same rate, as. But this requires that the copula function admits bounded second-order partial derivatives on the unit square.

Theorem 2. Suppose that the copula function admits bounded second-order partial derivatives on. Then for any sequence of positive constants satisfying, and for some, we have almost surely,

(3)

Because a number of copula families do not possess bounded second-order partial derivatives, the application of these results is limited by a corner bias problem. To overcome this difficulty and apply these results to a wide family of copulas, we adopt the shrinkage method of Omelka et al. [10] , by taking a local data-driven bandwidth satisfying the following condition:

(H₁)

where is a sequence of positive constants converging to 0, and is a real-valued function defined by

(4)

For such a bandwidth, the local linear kernel estimator can be rewritten as

(5)

By condition (H₁), (5) is equivalent for large enough to

(6)

This latter estimator (6) is exactly the improved shrinked version proposed by Omelka et al. [10] . It enables us to keep the bias bounded on the borders of the unit square and then to remove the problem of possible unboundedness of the second order partial derivatives of the copula function C. To set up asymptotic optimal simultaneous confidence bands for the copula C, we need the following additional condition:

(H₂)

If conditions (H₁) and (H₂) hold, then we can infer from Theorem 1 that

This is still equivalent to

(7)

To make use of (7) for forming confidence bands, we must ensure that the bandwidth is chosen in such a way that the bias of the estimator (5) may be neglected, in the sense that

(8)

This would be the case if condition H₂) holds and.

Theorem 3. Suppose that the assumptions of Theorem 1 and Theorem 2 hold. Then for any local data-driven bandwidth satisfying (H₁) and (H₂), and any, one has, as,

(9)

and,

(10)

where, , and.

Remark 2. Whenever (9) and (10) hold jointly for each, we will say that the intervals

(11)

provide asymptotic simultaneous optimal confidence bands (at an asymptotic confidence level of 100%) for the copula function So, with a probability near to 100%, we can write for all

(12)

2.2. Simulations and Data-Driven Applications

2.2.1. Simulations

We make some simulation studies to evaluate the performance of our asymptotic confidence bands. To this end, we compute the confidence bands given in (11) for some classical parametric copulas, and check for whether the true copula is lying in these bands. For simplicity, we consider for example two families of copulas: Frank and Clayton, defined respectively as follows:

(13)

and

(14)

We fix values for the parameter, and generate n pairs of data:, respectively from the two copulas by using the conditional sampling method. The steps for drawing from a bi-variate copula C are:

・ step 1: Generate two values u and v from,

・ step 2: Set,

・ step 3: Compute, where.

Then and are random observations drawn from the copula C. To compute the estimator, we take and given by formula (4), with, so that conditions (H₁)

and (H₂) are fulfilled. That is the case for The function is obtained by integrating the the local linear kernel function defined in the introduction, where k is the Epanechnikov kernel density defined as. Finally for any, we compute the confidence interval (11) by taking.

In Figure 1, we represent the confidence bands and the Frank copula, while Figure 2 represents the confidence bands and the Clayton copula. One can see that the true curves of the two parametric copulas are well contained in the bands.

We can also remark some simulitudes between Figure 1 and Figure 2. This seems normal because of the closeness of the values of used for the Frank and clayton copulas. Indeed, we made several simulations with other values for and observed every time that the representations of both copulas were rather similar for enough closed values of like 2, 3, 4, 5 and different for values of taken away enough like 2 and 25. But in any case the copula function lies in our nonparametric bands.

As we cannot visualize all the information in the above figures, we provide in Appendix some numerical computations to best appreciate the performance of our bands. To this end, we generate 10 couples of random numbers uniformly distributed in and compute, for each of them and for each of the considered copulas, the lower bound, the upper bound and the true value of the copula for different values of. These computations are given in Appendix (see, Table A1 and Table A2). In Table A1 represents the Clayton copula calculated from (14), for. and are respectively the lower and upper bounds of our proposed confidence intervals obtained from (11) by taking

. Similarly Table A2 summarizes the Frank copula for. We can see that all the values of are contained in their respective confidence intervals. This shows the performance of our bands. The negative values observed for the lower bounds in the tables are normal because the values of estimator

may be less than the quantity. Since copulas are positive valued, one may replace the negative values by zero without affecting the performance of the bands.

2.2.2. Data-Driven Applications

In this subsection, we apply our theoretical results to select graphically, among various copula families, the one that best fits sample data. Towards this end, we shall represent in a same 2-dimensional graphic the confidence bands established in Theorem 3 and the curves corresponding to the different copulas considered. To illustrate this, we use data expenses of Senegalese households, available in databases managed by the National Agency of Statistics and Demography (ANSD) of the Republic of Senegal (www.ansd.sn). The data were obtained from two sample surveys: ESAM2 (Senegalese Survey of Households, 2nd edition, 2001-2002) and ESPS (Monitoring Survey of Poverty in Senegal, 2005-2006). Because of the not availability of recent data, we deal with the pseudo-panel data utilized in [17] , which consist of two series of observations of size extracted from the surveys of 2001 and 2006.

Instead of smoothing these observations denoted by, we deal with pseudo-observations

to define the kernel estimator of the true copula. Here, and are empirical cumulative distribution functions associated respectively with the samples and.

This application is limited to Archimedean copulas. We will consider for example three parametric families of copulas: Frank, Gumbel and Clayton. Our aim is to find graphically, using our confidence bands, the family that best fits these pseudo-panel data. The unknown parameter, for each family, is estimated by inversion of Kendall’s tau (). For this, we first calculate the empirical Kendall’s tau (we find), and then we deduce from it the values of the parameter for each family (see Table 1 below).

is the Debye function of order 1 defined as:.

Figure 3 shows that the Clayton family seems more adequate to fit our pseudo-panel data. That is, the dependence modeling for these Senegalese households expense data is more satisfactory with the Clayton family than for the other two copulas.

We now apply the maximum likelihood method for fitting copulas and compare it with our graphical method described in Figure 3. For this, it suffices to compute (see Table 2 below), for each of the three copulas, the log-likelihood function defined as

where, and. The copula that best fits the data is that, which has the greatest log-likelihood.

From Table 2, we can see that the maximum likelihood method also leads to the Clayton family as the best copula for fitting our data. So we recommend it to model the dependence structure of the Senegalese households expense data in the years 2001 and 2006.

2.3. Concluding Remarks

This paper presented a nonparametric method to estimate the copula function by providing asymptotic confidence bands based on the local linear kernel estimator. The results are applied to select graphically the best copula function that fits the dependence structure of the Senegalese households pseudo-panel data.

In perspective, similar results can be obtained with other kernel-type estimators of copula function like the mirror-reflection and transformation estimators.

3. Proofs

In this section, we first expose technical details allowing us to use the methodology of Mason [3] described in Proposition 1 and Corollary 1 that are necessary to prove our results. In the second step we give successively the proofs of the theorems stated in Section 2.

We begin by decomposing the difference, as follows:

The probabilistic term

is called the deviation of the estimator from its expectation. We’ll study its behavior by making use of the methodology described in [3] . The other term that we denote

is the so-called bias of the estimator. It is deterministic and its behavior will depend upon the smoothness conditions on the copula C and the bandwidth h.

Recall the estimator proposed by Deheuvels in [7] , which is defined as

where and are the empirical cumulative distribution functions of the marginals F and G. This estimator is asymptotically equivalent (up to a term) with the estimator based directly on Sklar’s Theorem given by

with the empirical joint distribution function of. Then the empirical copula process is defined as

To study the behavior of the deviation, we introduce the following notation. Let

be the uniform bivariate empirical distribution function based on a sample of i.i.d random variables uniformly distributed on. Define the following empirical process

Then one can observe that

(15)

For all, define

where g belongs to a class of measurable functions defined as

Since is an unbiased estimator for, one can observe that

To make use of Mason’s Theorem in [3] , the class of functions must verify the following four conditions:

(G.i)

(G.ii)There exists some constant such that for all,

(F.i) satisfies the uniform entropy condition, i.e.,.

(F.ii) is a point wise measurable class, i.e. there exists a countable sub-class of such that for all, there exits such that.

The checking of these conditions constitutes the proof of the following proposition which will be done in Appendix.

Proposition 1. Suppose that the copula function C has bounded first order partial derivatives on. Assuming (G.i), (G.ii), (F.i) and (F.ii), we have for with probability one

where is a positive constant.

Corollary 1. Under the assumptions of Proposition 1, for any sequence of constants satisfying, one has with probability one

Proof. (Corollary 1)

First, observe that the condition yields

(16)

Next, by the monotonicity of the function on, one can write for n large enough, and hence,

(17)

Combining this and Proposition 1, we obtain

Thus the Corollary 1 follows from (16).

Proof. (Theorem 1)

The proof is based upon an approximation of the empirical copula process by a Kiefer process (see [14] , p. 100). Let be a 3-parameters Wiener process defined on. Then the Gaussian process is called a 3-parameters Kiefer process defined on .

By Theorem 3.2 in [14] , for, there exists a sequence of Gaussian processes such that

where

This yields

(18)

By the works of Wichura on the iterated law of logarithm (see [15] ), one has

(19)

which readily implies

Since and are asymptotically equivalent in view of (15), one obtains

The proof is then finished by applying Corollary 1 which yields

(20)

Thus, there exists a constant, with, such that

(21)

Proof. (Theorem 2)

For all, one has

and

with and. We can easily show that

Hence

By continuity of F and G, we have for n large enough,

and

Thus,

By applying a 2-order Taylor expansion and taking account of the symmetry of the kernels and i.e.,

we obtain, by Fubini, that for all,

Since the second order partial derivatives are assumed to be bounded, then we can infer that

and hence,

(22)

Proof. (Theorem 3)

From (8), we can infer that for any given and, there exists such that for all,

That is

(23)

On the other hand we deduce from (7) that for all,

Case 1. If

then (23) becomes

Thus, for any given and all large n, we can write

(24)

Case 2. If

then, analogously to Case 1, we can infer from (23) that, for any given and all large n,

(25)

Letting tends to 0, it follows from (24) and (25) that

(26)

or

(27)

Now, by observing that

we can write, for any, with probability tending to 1,

and

That is, (9) and (10) hold.

Acknowledgements

The authors are very grateful to anonymous referees for their valuable comments and suggestions.

Cite this paper

DiamBâ,Cheikh TidianeSeck,Gane SambLô, (2015) Asymptotic Confidence Bands for Copulas Based on the Local Linear Kernel Estimator. Applied Mathematics,06,2077-2095. doi: 10.4236/am.2015.612183

References

Appendix

1. Proof of Proposition 1

Proof. It suffices to check the conditions (G.i), (G.ii), (F.i) and (F.ii) given in Section 3.

Checking for (G.i). For and, one has

Then,

This implies

Checking for (G.ii).

We have to show that

where is a constant. Recall that and. Then, we can write

Now we express A and B as integrals of the copula function.

Since because takes its values in [0, 1] as a distribution function, we observing that . Then we can write

We can also notice that

Thus

For n enough large, we have by continuity of F and G,

and

By splitting the integrals, we obtain after simple calculus that

All these six terms can be bounded up by applying Taylor expansion. Precisely, we have

From this, we can conclude that

and

with

Checking for (F.i). We have to check that satisfies the uniform entropy condition.

Consider the following classes of functions:

.

It is clear that by applying the lemmas 2.6.15 and 2.6.18 in van der Vaart and Wellner (see [16] , p. 146-147), the sets are all VC-subgraph classes. Thus, by taking the function as a measurable envelope function for (indeed), we can infer from Theorem 2.6.7 in [16] that satisfies the uniform entropy condition. Since and have the same structure, we can conclude that satisfies this property too. That is,

Checking for (F.ii).

Define the class of functions

It’s clear that is countable and. Let

and, for,

where and.

Let and define

and

Then, one can easily see that and.

This implies, for all large m, that and, which are equivalent to

and

By right-continuity of, we obtain

and conclude that is pointwise measurable class.

2. Numerical Computations