Received 7 April 2015; accepted 22 September 2015; published 25 September 2015

ABSTRACT

A delayed HIV/AIDS epidemic model with treatment and vertical transmission is investigated. The model allows some infected individuals to move from the symptomatic phase to the asymptomatic phase; next generation of infected individuals may be infected and it will take them some time to get maturity and infect others. Mathematical analysis shows that the global dynamics of the spread of the HIV/AIDS are completely determined by the basic reproduction number R₀ for our model. If R₀ < 1 then disease free equilibrium is globally asymptotically stable, whereas the unique infected equilibrium is globally asymptotically stable if R₀ > 1.

Keywords:

HIV/AIDS Epidemic Model, Vertical Transmission, Basic Reproduction Number, Time Delay

1. Introduction

Mathematical models play an important role in the study of the transmission dynamics of HIV/AIDS, and in some sense, delay models give better compatibility with reality, as they capture the dynamics from the time of infection to the infectiousness. Some HIV/AIDS models are introduced in [1] -[5] . In recent years, a few studies of vertical transmission have been conducted to describe the effects of various epidemiological and demographical factors [6] - [8] , and some models considered vertical transmission with time delay [9] [10] . Some specific HIV models with imperfect vaccine were introduced in [11] - [13] .

In [1] , L. Cai and X. Li studied local and global stability of the equilibria of a SIJA model with treatment:

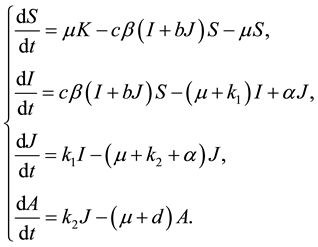(1)

In model (1), it is assumed that some individuals with the symptomatic phases J can be transformed into asymptomatic individuals I after treatment and they get the result that when 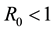the disease free equilibrium is globally asymptotically stable and if 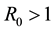the endemic equilibrium is globally asymptotically stable.

In [9] , Ram Naresh et al. considered the following SIA model with vertical transmission:

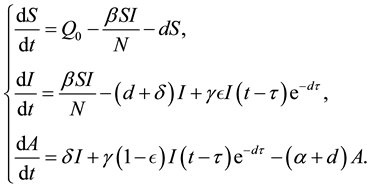(2)

Here, the authors assume that a fraction of newborns, who sustain treatment, join the infective class while others, who do not sustain treatment, join the AIDS class after getting sexual maturity. The infectives through vertical transmission at any time t are given by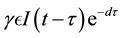. The authors proved the local and global stability of disease free equilibrium and endemic equilibrium under some conditions. Inspired by these works, we consider an HIV/AIDS model with vertical transmission and with time delay.

The organization of the paper is as follows. In the next section we present the model with delay. Section 3 presents the basic properties of the model. In Section 4, we analyze local and global stability of equilibrium points. In the last section, we present a brief conclusion.

2. Mathematical Model

We propose an HIV/AIDS model which incorporates time delay during which a newly born infected child attains sexual maturity and becomes infectious. In this model, the sexually mature population is divided into four subclasses: the susceptibles (S), the asymptomatic infectives (I), the symptomatic infectives (J) and full-blown AIDS group (A). The number of total population is denoted by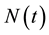, for any time t. We assume that the susceptibles become HIV infected via sexual contacts with infectives. It is also assumed that all newborns are infected at birth. It is reasonable to assume that full-blown AIDS patients are sexually inactive and symptomatic stage patients feel uncomfortable (some may know they are AIDS) and the possibility of producing children is small, so can be taken negligible. We also assume that a fraction of infected newborns, who sustain treatment, joins the asymptomatic infective class while others, who do not sustain treatment, joins AIDS class after getting sexual maturity. The infectives through vertical transmission at any time t is given by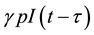, because those who are infected at time 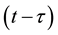becomes infectoius (asymptomatic stage infectious) at time t, if they do not develop to AIDS patient by that time. The fraction of infectives which became AIDS patient during the period of getting sexual maturity, if they survive to the maturity, joins to the AIDS class. However, for the model to be biologically reasonable, it may be more realistic to assume that not all those infected will survive after 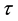time units, and this claim support the introduction of the survival term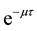. Thus, in our model the term 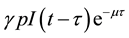also represents the introduction of infectives through vertical transmission. If the birth rate of newborns 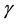equals to zero, then our model will back to the model (1).

With the above considerations and assumptions, the spread of the disease is assumed to be governed by the following model:

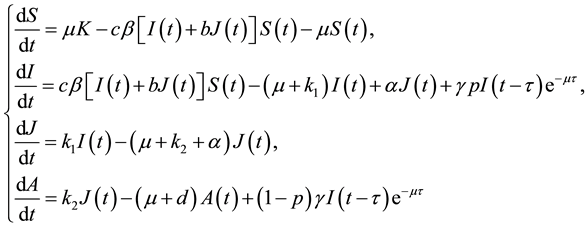(3)

where 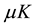is the recruitment rate of the population, is the death rate. c is the average number of contacts of an individual per unit of time. and are the probability of disease transmission per contact by an infective in the first stage and in the second stage, respectively. and are transfer rate from the asymptomatic phase I to the symptomatic phase J and from the symptomatic phase to the AIDS cases, respectively. is transformation rate from the symptomatic phase J to asymptomatic phase I. d is the disease-related death rate of the AIDS cases. is the birth rate of infected newborns, p is the fraction of infected newborns joining the asymptomatic infective class after getting sexual maturity and remaining part of the infected newborns joins the AIDS class after getting sexual maturity. It is also assumed that all the parameters of the model are non-negative. Based on it’s biological meaning, we always assume that.

3. Basic Properties

For model (2), let the initial condition be, , , for all, with. Then, it is clear that the solution of the model (3) remain positive for all time.

Let, then

which gives,

Define

This implies that if all solutions of model (3) starting in are bounded and eventually enter the attracting set.

It is reasonable to assume that the general death rate is greater than the birth rate of infected newborns, that is. In some models, death rate equal to birth rate. However, in this model, is smaller than birth rate. Below we assume.

Since the variable A of model (3) does not appear in the first three equation, in the subsequent analysis, we only consider the submodel:

(4)

Model (4) always has a disease-free equilibrium. Further we define the basic reproduction number as follows.

By straightforward computation, when model (4) has the unique positive equilibrium, where

4. Stability Analysis

First we will study the local and global stability of disease free equilibrium.

The variational matrix of model (4) is given by

Theorem 4.1. If, the disease free equilibrium is locally asymptotically stable.

Proof. The Jacobian matrix corresponding to model (4) about as follows,

where,.

The characteristic equation of this matrix is given by, where I is the unit matrix.

(5)

where

Clearly, one root of this equation is. So we consider the following equation.

(6)

If, the equation becomes

Since

when, notice that,. Hence the roots of this equation have negative real part by the Hurwitz criterion.

If, we assume that is the root of characteristic Equation (6), then satisfies

Separating the real and imaginary parts, we have

Eliminating by squaring and adding above the two equation, we get that

Let, then this equation becomes

(7)

Through simple computation, we can found that all the coefficients of this equation is positive, so Equation (7) have no solution, it implies that Equation (6) have not the root like. Hence all roots of (6) have negative real part.

We are now in a position to investigate the global stability of the disease-free equilibrium.

Theorem 4.2. If, then the infection free equilibrium is globally asymptotically stable.

Proof. Consider the following Lyapunov functional.

Calculating the derivative of L along with the solution of model (4), we have

This implies that when, the equality holds if and only if, the maximal

invariant set of is the singleton. Hence is globally asymptotically stable by the LaSalle invariance principle [14] .

Now, when we will study the local and global stability of.

Theorem 4.3. If, the infected equilibrium is locally asymptotically stable.

Proof. For this purpose, we obtain the Jacobian matrix corresponding to model (4) about as follows,

where, ,.

The characteristic equation of this matrix is

(8)

where

Notice that

Hence

when, the characteristic Equation (8) yields

where

Obviously, and. This implies that when and, is locally asymptotically stable by the Hurwitz criterion.

Now we study the stability behavior of in the case.

We assume that is the root of characteristic equation, then satisfies

Separating the real and imaginary parts, we have

(9)

(10)

Eliminating by squaring and adding (9) and (10), we get the equation determining for as,

where

Substituting in above Equation, we have

(11)

when, through simple computation we can see that, , , in this circumstance (11) has not positive root. So all roots of (8) has negative real part.

Next, we consider the global stability of when.

Theorem 4.4. If, then the infected equilibrium is globally asymptotically stable.

Proof. Firstly, we define a function, ,. Take the Lyapunov functional as follows.

Next calculating the derivative of V along with the solution of model (4), we have

Since, we have

Next,we consider the following variables substitutions by letting,

Then,

Further let

Then, through a straight computation, we have

Since the arithmetic mean is greater than or equal to the geometric mean and function g is a positive function, we have

Thus, in. The equality holds if and only if. That is,. The maximal invariant set of model (4) on the set is the singleton. Thus, the endemic equilibrium is globally asymptotically stable if by LaSalle Invariance Principle [14] .

5. Conclusion

In this paper, we have considered an HIV/AIDS model with treatment, vertical transmission and time delay. Under the assumption that asymptomatic infectives (J) have the symptoms of AIDS, AIDS patients (A) are isolated; hence their probability of producing children is small; and it is neglected. From the local stability of disease free equilibrium, we calculated the basic reproduction number. Further we get the results that when the disease free equilibrium is globally asymptotic stable, and when the endemic equilibrium is globally asymptotic stable.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grants nos. 11261056, 11261058 and 11271312).

Cite this paper

ZohragulOsman,XamxinurAbdurahman, (2015) Stability Analysis of a Delayed HIV/AIDS Epidemic Model with Treatment and Vertical Transmission. Applied Mathematics,06,1781-1789. doi: 10.4236/am.2015.610158

References

NOTES

^*Corresponding author.