Applied Mathematics
Vol.06 No.04(2015), Article ID:56037,12 pages
10.4236/am.2015.64068
Global Attractors and Dimension Estimation of the 2D Generalized MHD System with Extra Force
Zhaoqin Yuan, Liang Guo, Guoguang Lin*
Department of Mathematics, Yunnan University, Kunming, China
Email: yuanzq091@163.com, *gglin@ynu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 March 2015; accepted 26 April 2015; published 29 April 2015
ABSTRACT
In this paper, firstly, some priori estimates are obtained for the existence and uniqueness of solutions of a two dimensional generalized magnetohydrodynamic (MHD) system. Then the existence of the global attractor is proved. Finally, the upper bound estimation of the Hausdorff and fractal dimension of attractor is got.
Keywords:
MHD System, Existence, Global Attractor, Dimension Estimation

1. Introduction
In this paper, we study the following magnetohydrodynamic system:
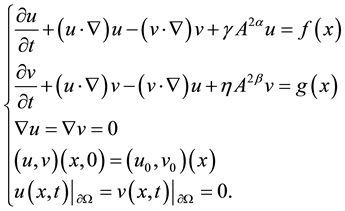 (1.1)
(1.1)
here
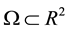 is bounded set,
is bounded set,
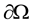 is the bound of
is the bound of , where u is the velocity vector field, v is the magnetic
, where u is the velocity vector field, v is the magnetic
vector field,
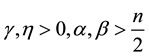 are the kinematic viscosity and diffusivity constants respectively.
are the kinematic viscosity and diffusivity constants respectively.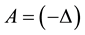 . Let
. Let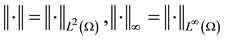 .
.
When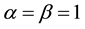 , problem (1.1) reduces to the MHD equations. In particular, if
, problem (1.1) reduces to the MHD equations. In particular, if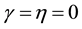 , problem (1.1) becomes the ideal MHD equations. It is therefore reasonable to call (1.1) a system of generalized MHD equations, or simply GMHD. Moreover, it has similar scaling properties and energy estimate as the Navier-Stokes and MHD equations.
, problem (1.1) becomes the ideal MHD equations. It is therefore reasonable to call (1.1) a system of generalized MHD equations, or simply GMHD. Moreover, it has similar scaling properties and energy estimate as the Navier-Stokes and MHD equations.
The solvability of the MHD system was investigated in the beginning of 1960s. In particular in [1] -[4] the global existence of weak solutions and local in time well-posedness was proved for various initial boundary value problems. However, similar to the situation with the Navier-Stokes equations, the problem of the global smooth solvability for the MHD equations is still open.
Analogously to the case of the Navier-Stokes system (see [5] -[8] ) we introduce the concept of suitable weak solutions. We prove the existence of the global attractor (see [9] ) and getting the upper bound estimation of the Hausdorff and fractal dimension of attractor for the MHD system.
2. The Priori Estimate of Solution of Problem (1.1)
Lemma 1. Assume
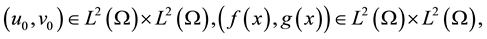 so the smooth solution
so the smooth solution
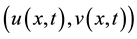 of problem (1.1) satisfies
of problem (1.1) satisfies

Proof. We multiply u with both sides of the first equation of problem (1.1) and obtain
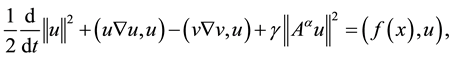 (2.1)
(2.1)
We multiply v with both sides of the second equation of problem (1.1) and obtain
 (2.2)
(2.2)
According to
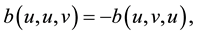 we obtain
we obtain
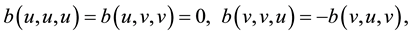 (2.3)
(2.3)
According to (2.1) + (2.2), so we obtain

According to Poincare and Young inequality, we obtain



From (2.5)-(2.7), we obtain
Let
Using the Gronwall’s inequality, the Lemma 1 is proved.
Lemma 2. Under the condition of Lemma 1, and




Proof. For the problem (1.1) multiply the first equation by



According to the Sobolev’s interpolation inequalities,


According to (2.9)-(2.10), we have

Here
In a similar way, we can obtain

Here

Here

Here
According to the Poincare’s inequalities



From (2.12)-(2.17), we have
Here
So
We obtain
Using the Gronwall’s inequality, the Lemma 2 is proved.
3. Global Attractor and Dimension Estimation
Theorem 1. Assume that


exist a unique solution
Proof. By the method of Galerkin and Lemma 1-Lemma 2,we can easily obtain the existence of solutions. Next, we prove the uniqueness of solutions in detail.
Assume





The two above formulae subtract and obtain

For the problem (3.3) multiply the first equation by u with both sides and obtain

For the problem (3.3) multiply the second equation by v with both sides and obtain

According to

According to (3.1) + (3.2), we have

According to Sobolev inequality, when n < 4


According to (3.8)-(3.9),we can get




From (3.10)-(3.13),
Here
So, we have
Let
According to the consistent Gronwall inequality,
So we can get

Theorem 2. [9] Let E be a Banach space, and



1)





2) It exists a bounded absorbing set



3) When

Therefore, the semigroup operators

Theorem 3. Assume




Proof.
1) When

So

2)

From Lemma 2, when

Since



3) So the semigroup operator

In order to estimate the Hausdorff and fractal dimension of the global attractor A of problem (1.1), let problem (1.1) linearize and obtain

Assume




To prove



Theorem 4. Assume









Proof. Meet the initial value problem (3.14) of respectively for








Here


For the problem (3.16) multiply the first equation by



Then

Here
For the problem (3.16) multiply the first equation by



According to the Sobolev’s interpolation inequalities


According to (3.22)-(3.23), we have

In a similar way, we can obtain







So, we can get
Here
According to the Poincare’s inequalities

Let
According to Gronwall’s inequalities, we obtain

Let



So, we can get

Here


For the problem (3.33) multiply the first equation by w1 with both sides and for the problem (3.33) multiply the second equation by w2 with both sides and obtain

According to (3.8)-(3.9), then










According to, we obtain
Here
We obtain
So

Let






Theorem 5. Under the assume of Theorem 3, the global attractor A of problem (1.1) has finite Hausdorff and fractal dimension, and
Here J0 is a minimal positive integer of the following inequality
Proof. By theorem [8] , we need to estimate the lower bound of



According to (3.8)-(3.9), we can get






Under the bounded condition, select




Let
Let
By

So, we can obtain
We have
Therefore


Funding
This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11161057.
References
- Wu, J. (2003) Generalized MHD Equations. Journal of Differential Equations, 195, 284-312. http://dx.doi.org/10.1016/j.jde.2003.07.007
- Tran, C.V., Yu, X. andZhai, Z. (2013) On Global Regularity of 2D Generalized Magnetohydrodynamic Equations. Journal of Differential Equations, 254, 4194-4216. http://dx.doi.org/10.1016/j.jde.2013.02.016
- Mattingly, J.C. and Sinai, Ya.G. (1999) An Elementary Proof of the Existence and Uniqueness Theorem for the Navier- Stokes Equations. Communications in Contemporary Mathematics, 1, 497-516. http://dx.doi.org/10.1142/S0219199799000183
- Ladyzhenskaya, O.A. and Seregin, G.A. (1960) Mathematical Problems of Hydrodynamics and Magnetohydrodynamics of a Viscous Incompressible Fluid. Proceedings of V.A. Steklov Mathematical Institute, 59, 115-173. (In Russian)
- Caffarelli, L., Kohn, R.V. and Nirenberg, L. (1982) Partial Regularity of Suitable Weak Solutions of the Navier-Stokes Equations. Communications on Pure and Applied Mathematics, 35, 771-831. http://dx.doi.org/10.1002/cpa.3160350604
- Vialov, V. (2014) On the Regularity of Weak Solutions to the MHD System near the Boundary. Journal of Mathematical Fluid Mechanics, 16, 745-769. http://dx.doi.org/10.1007/s00021-014-0184-3
- Ladyzhenskaya, O.A. and Seregin, G.A. (1999) On Partial Regularity of Suitable Weak Solutions to the Three- Dimensional Navier-Stokes Equations. Journal of Mathematical Fluid Mechanics, 1, 356-387. http://dx.doi.org/10.1007/s000210050015
- Scheffer, V. (1977) Hausdorff Measure and Navier-Stokes Equations. Communications in Mathematical Physics, 55, 97-112. http://dx.doi.org/10.1007/BF01626512
- Lin, G.G. (2011) Nonlinear Evolution Equations. Yunnan University Press, Kunming.
NOTES
*Corresponding author.






















































