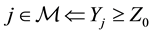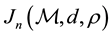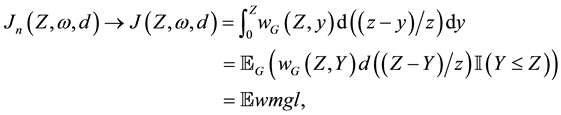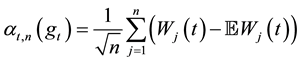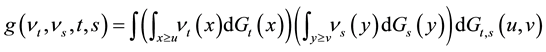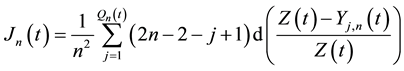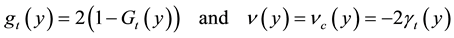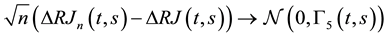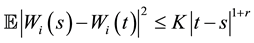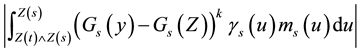Applied Mathematics
Vol.06 No.05(2015), Article ID:56709,16 pages
10.4236/am.2015.65079
Functional Weak Laws for the Weighted Mean Losses or Gains and Applications
Gane Samb Lo1,2, Serigne Touba Sall1,3, Pape Djiby Mergane1
1LERSTAD, Université Gaston Berger de Saint-Louis, Saint-Louis, Sénégal
2LSTA, Université Pierre et Marie Curie, Paris, France
3Ecole Normale Supérieure, Dakar, Sénégal
Email: pdmergane@ufrsat.org
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 February 2015; accepted 24 May 2015; published 27 May 2015
ABSTRACT
In this paper, we show that many risk measures arising in Actuarial Sciences, Finance, Medicine, Welfare analysis, etc. are gathered in classes of Weighted Mean Loss or Gain (WMLG) statistics. Some of them are Upper Threshold Based (UTH) or Lower Threshold Based (LTH). These statistics may be time-dependent when the scene is monitored in the time and depend on specific functions w and d. This paper provides time-dependent and uniformly functional weak asymptotic laws that allow temporal and spatial studies of the risk as well as comparison among statistics in terms of dependence and mutual influence. The results are particularized for usual statistics like the Kakwani and Shorrocks ones that are mainly used in welfare analysis. Data-driven applications based on pseudo-panel data are provided.
Keywords:
Empirical Process, Time Dependent Process, Weak Theory, Risk Measures, Poverty Index, Loss Function, Economic Welfare

1. Introduction and Motivation
In many situations and many areas, we face the double problem of estimating the risk of lying in some marked zone and, at the same time, the cost associated with it. To fix ideas, we may be interessed in estimating the immunocompromised patients number , and the size of the set
, and the size of the set  of infected people, in some population
of infected people, in some population . At the same time, we know that the severity of the infection is measured by the viral load
. At the same time, we know that the severity of the infection is measured by the viral load 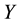 expressed in RNA copies per milliliter of blood plasma. The cost of treatement, for example a course of chemotherapy, heavily depends on the viral load. If one has to treat all the patients, there is a cost to pay for each treatment, which is a cost function
expressed in RNA copies per milliliter of blood plasma. The cost of treatement, for example a course of chemotherapy, heavily depends on the viral load. If one has to treat all the patients, there is a cost to pay for each treatment, which is a cost function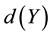 . Facing these two problems at the same time, comparing two different populations or monitoring the evolution of the global situation should be based on the couple
. Facing these two problems at the same time, comparing two different populations or monitoring the evolution of the global situation should be based on the couple 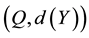 rather than on which is commonly called the HIV/AIDS adult prevalence rate, on what is based international comparison. In order to make a workable statistic, consider a sample of individuals
rather than on which is commonly called the HIV/AIDS adult prevalence rate, on what is based international comparison. In order to make a workable statistic, consider a sample of individuals 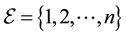 drawn for
drawn for 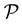 and measure the viral load
and measure the viral load  for each
for each . A general comparative statistic should be of the form
. A general comparative statistic should be of the form
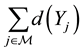
Since comparisons over the time are based on this index, one will be interested in putting more or less emphasis on the more infected or not, in terms of viral load. This is achieved by affecting a weight 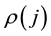 to
to  as a monotone function of the rank
as a monotone function of the rank 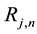 of
of 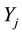 in the sample. For an increasing
in the sample. For an increasing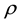 , it is paid more attention to less infected while the contrary holds for a decreasing one. This leads to statistics like
, it is paid more attention to less infected while the contrary holds for a decreasing one. This leads to statistics like
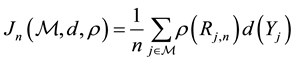
It is also known that the viral load is detectable only above a threshold of value 
and

We may decide to concentrate on the very expansive chemotherapy courses due to financial pressure. In that case, we change the threshold to 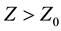
Such statistics are also used in insurance theory. Suppose that one insurance company receives 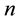




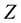

and to choose a distorsion function 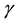

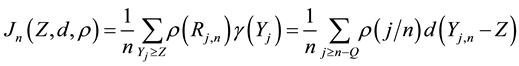
where 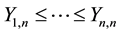


In poor countries, an individual is considered as a poor one when his income 
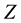

is the total number of poor people in the sample, while 
here depends on the relative poverty gap
may be called a General Poverty Index (GPI). The same form may also be used in medical science when dealing with vitamine (say vitamine D) deficiency. In this case, 
We see from the lines above that (1) is a very general statistic, which works in various fields, with losses or gains dependent on the meaning of the cost function
When we have time-dependent data, over the time 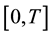


In the case where 

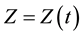
The choice of 
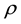
Finally, taking into account various forms of (1) in the literature, the following form of threshold-based weighted mean loss seems to be a general one
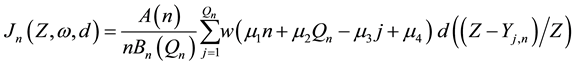
or the following

depending on whether we handle loss (with 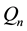
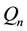

From a mathematical point of view, the asymptotic behaviors of the two forms radically differ although the writing seems symetrical. The reason is that for the first, the random variables used in (4) are bounded and the asymptotic handling is much easier. As for (5), we should face heavy tail problems and further complications may arise.
This paper is aimed at offering a full functional weak theory according to the most recent setting of such theories as stated in [5] . Particularly, we are interested here in the time-dependent investigation of (4), and next the functional weak theory in 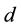

Consider for a while that 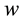

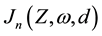
where 
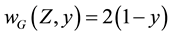


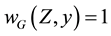
To be able to base statistical tests of such results, we may be interested in finding the asymptotic law of

However, we still need to handle longitidunal data, where the risk situation is analysed over a continuous period of time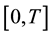

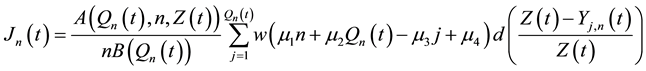
with 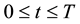

Instead of analysing such UTB WMLG for some specific functions 





This paper is aimed at settling the uniform weak convergence of such statistics, which is the asymptotic theory of the time-dependent poverty measures (6), in the space 
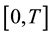
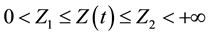
An important application is the statistical estimation of the Relative Mean Loss Variation (RMLV) from time 

by confidence intervals where 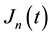


We will need a number of hypotheses towards an adequate frame for our study. These hypotheses may appear severe and numerous, at first sight, but most of them are natural and easy to get. We first need the following shape conditions for the WMLG measures themselves. The letter S in the hypotheses names refers to shape con- ditions.
(HS1) There exist functions 
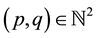


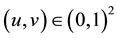



where 
(HS2)
(HS3) There exists a function 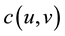




We will require other assumptions depending on the regularity of the functions 


(HR1) The bivariate functions 

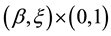


(HR2) For a fixed


(HR3) There exist 



and
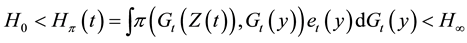
Our final achievement is that, when putting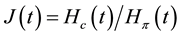
law of 

enables the statistical uniform estimates of 

2. Our Results
Our results will rely on the representation of Theorem [11] , which in turn will need the following assumptions.
(HL1) There exist 

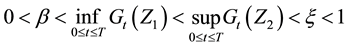
(HL2) The subclass 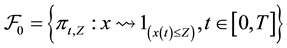

tinuous functions, is a 
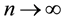
where, for any 
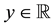










Finally let us denote

(HL3) For any



(HL4) 

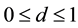

Theorem 1 Suppose that (HS1)-(HS2), (HR1)-(HR3) and (HL1)-(HL4) hold. Put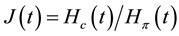

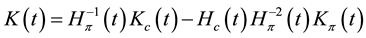

and
Define

and
Then we have, uniformly in

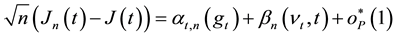
with

and

Suppose that (HS3), (HR1)-(HR3) and (HL1)-(HL4) hold. Then, (10) holds with

This theorem expresses our studied time-dependent statistics as the sum of a functional empirical process and the stochastic process (11). It will be seen, for a fixed time, that 


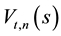
function) and then of empirical process


Now, we use these tools to give first, general laws for the WMLG statistic below and then for the Kakwani class of indices in Section 2.2 and for the Shorrocks-Thon indices in Section 3. We finish by a special study of the absolute and the relative poverty changes in Section 4.
While we deal with the general index and we use the outcomes of Theorem 1, we adopt the following writing:
where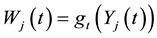








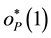

(HT1) For
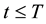


(HT2) For



In order to define our last assumption, we need the following functions:
and

with, by convention, 
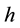
(HT3) If there is a universal constant



We are now able to give our general main result.
Theorem 2 Assume the conditions of Theorem 1 hold and that (HT1)-(HT3) are satisfied. Then the stochastic process 



with
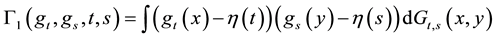


and

with
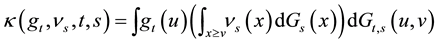
and 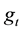


Proof. We have to do three things. First, we show that 
Since the assumptions of Theorem 1 hold, we have the representation (10). Put

First (HT2) and (HT2) yield, for each

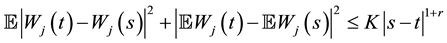
and hence, by repeated use of 

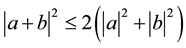

We remind again that 


find in [12] , that 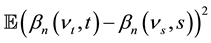

where 






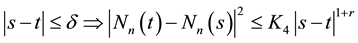
Thus 





and

where the 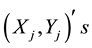






Now let, for each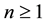





and

Now, let 




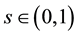
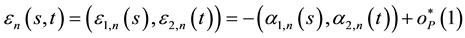
uniformly in



where 





We have

for






But 
pirical processes). Thus putting

in 
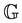
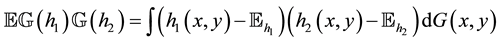
Further, for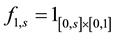


and for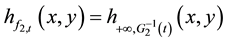
Now, by using the Skorohod-Wichura-Dudley Theorem, we are entitled to suppose that we are on a probability space such that

Now, since the functions 




One easily proves that

is a Gaussian random variable since the second term is a Riemann integral, which is a limit of finite linear com- binations of Gaussian random variables. Thus 




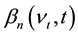

2.1. Special Cases
Since the results are stated in a more general form and may appear very sophisticated, it seems necessary to show how they work for common cases. We apply our results to two key examples in Welfare analysis: the class of Kakwani’s and Shorrocks’ statistics. These two examples are particularly interesting since they put the emphasis on the less deprived individuals within the whole population (with weight


2.2. The Kakwani Case
We are now applying the general results to the Kakwani WMLG statistics of parameter

The way we are using here is to be repeated for any particular index. For instance, the results in [9] and [10] may be rediscovered in this way. In this specific case, we turn the hypotheses (HT1) and (HT2) on 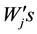


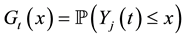


(H0) For



(H1) There exists a positive function 

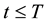

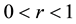

and

(H2) For


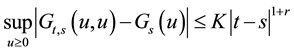
and

(H3) For
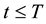

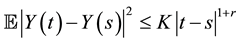
We check, in the Kakwani case, that the representation of Theorem 1 holds with


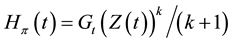

so that
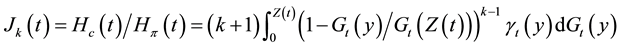
Next

and then
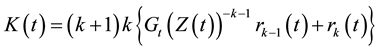
where

For
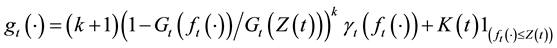
and
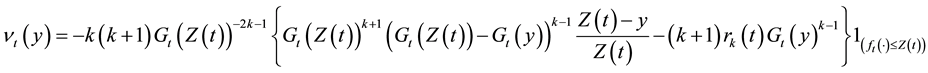
we will get the representation
with
Theorem 3 Let (HL1), (HL3), (HL4), (H0)-(H3) hold. Then 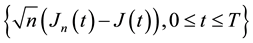


Proof. We begin to remark that (H3) ensures that 
3. The Shorrocks-Thon-Like Case
We apply our results to the Shorrocks-Thon WMLG statistics measures defined by
This is the Thon index. One obtains the Shorrocks one by replacing 
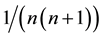

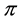

Here again 
under the same hypotheses (HL1)-(HL4) and (H0)-(H3)
4. Estimation of the WLMG Statistic Variation
Although they are very expensive to collect, longitudinal data are highly preferred for adequate estimate of the absolute index variation
periods t and s and the associate relative WMLG variation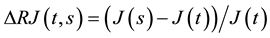
natural estimators are of course 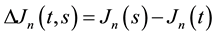
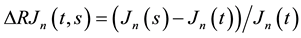
Theorem 4 Under the assumptioms of Theorem 1 or Theorem 2,

where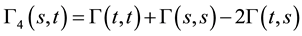
where
with

The proof is straightforward. We also might consider the convergence of 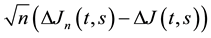
Gaussian process 





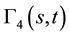
An important application of the second part of this theorem is related to checking the achievement of specific goals. One may, within a national or regional strategy, whish to have some deprivation limited to some extent. For example, the UN has assigned a number of goals, named Millennium Development Goals (MDG), to its members. We are concerned here by one of them. Indeed, it is whished to halve the extreme poverty in the world in year 





where
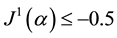
4.1. Datadriven Applications and Variance Computations
We apply our results in Economics and Welfare analysis. Especially, we consider the household surveys in Senegal in 2011 (ESAM II) and in 2006 (EPS) from which we construct pseudo-panel data and apply our results.
4.1.1. Variance Computations for Senegalese Data
We apply our results to Senegalese data. We do not really have longitudinal data. So we have constructed pseudo-panel data of size


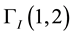
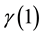


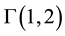
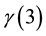
When constructing pseudo-panel data, we get small sizes like 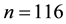

Before we present the outcomes, let us say some words on the packages. We provide different R script files at http://www.ufrsat.org/lerstad/resources/sallmergslo01.zip.
The user should already have his data in two files data1.txt and data2.txt. The first script file named after gamma_mergslo1.dat provides the values of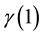

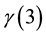

4.1.2. Analysis
First of all, we find that, at an asymptotical level, all our inequality measures and poverty indices used here have decreased. When inspecting the asymptotic variance, we see that for the poverty index, the FGT and the Kakwani classes respectively for
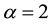


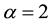
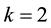
Table 1. Variations of the poverty indices.
5. Conclusion
We obtained asymptotic laws of the UTB WMLG statistics with in mind, among other targets, the uniform estimation of the variation 

References
- Lo, G.S. (2013) The Generalized Poverty Index. Far East Journal of Theoretical Statistics, 42, 1-22. http://pphmj.com/journals/fjst.htm
- Artzner, P., Delbaen, F., Eber, J.M. and Heath, D. (1999) Coherent Measures of Risk. Mathematical Finance, 9, 203- 228. http://dx.doi.org/10.1111/1467-9965.00068
- Sen, A.K. (1976) Poverty: An Ordinal Approach to Measurement. Econometrica, 44, 219-231. http://dx.doi.org/10.2307/1912718
- Zheng, B. (1997) Aggregate Poverty Measures. Journal of Economic Surveys, 11, 123-162. http://dx.doi.org/10.1111/1467-6419.00028
- van der Vaart, A.W. and Wellner, J.A. (1996) Weak Convergence and Empirical Processes With Applications to Statistics. Springer, New York.
- Shorrocks, A.F. (1995) Revisiting the Sen Poverty Index. Econometrica, 63, 1225-1230. http://dx.doi.org/10.2307/2171728
- Thon, D. (1979) On Measuring Poverty. Review of Income and Wealth, 25, 429-440. http://dx.doi.org/10.1111/j.1475-4991.1979.tb00117.x
- Kakwani, N. (1980) On a Class of Poverty Measures. Econometrica, 48, 437-446. http://dx.doi.org/10.2307/1911106
- Sall, S.T. and Lo, G.S. (2009) Uniform Weak Convergence of the Time-Dependent Poverty Measure for Continuous Longitudinal Data. Brazilian Journal of Probability and Statistics, 24, 457-467. http://dx.doi.org/10.1214/08-BJPS101
- Lo, G.S. and Sall, S.T. (2009) Uniform Weak Convergence of Non Randomly Weighted Poverty Measures for Longitudinal Data. 57th ISI Session.
- Lo, G.S. and Sall, S.T. (2010) Asymptotic Representation Theorems for Poverty Indices. Afrika Statistika, 5, 238-244.
- Lo, G.S. (2010) A Simple Note on Some Empirical Stochastic Process as a Tool in Uniform L-Statistics Weak Laws. Afrika Statistika, 5, 245-251.
- Shorack, G.R. and Wellner, J.A. (1986) Empirical Processes with Applications to Statistics. Wiley-Interscience, New York.
Appendix
Put
with
and
We have first to prove that for
Based on the expression of 
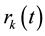

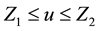
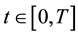

for
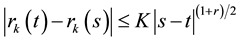
and

This would help to conclude with the 
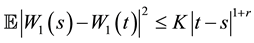
Let us establish (14). We have
where 



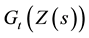


Now we show (15)
ince 

Further

and, since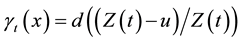
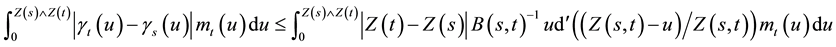
where 
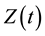


From (24)-(26), we conclude that
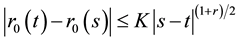
and for

and

with
and
less than
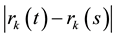


and

By (H2), A is less than 

for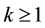

which proves (15). Let us finally prove (16). We have by (H2), for a fixed

for some constant
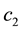
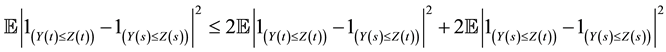
with

and

and then (16) holds.
By putting together (14), (15) and (16) and by repeatedly using the 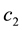
Now we have to establish that

Put

with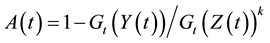

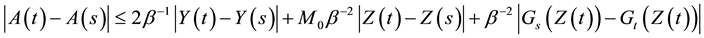
Then by (H0)-(H3) and the 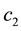
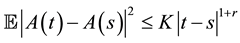
Next

and
with

and
Then by (H2)

and

Next, by putting

where 
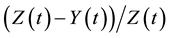


By similar methods, we get

By combining all that precedes, we get (27), which together with (21) establishes by the 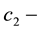

Now we have to prove that

We only sketch this second part. Let us consider


and

By (14),(15) and the decomposition of 

Furthermore

We then get

Then

Now

with

Then
Since 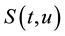
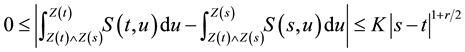
Moreover, one easily shows by the (H0)-(H3), with similar techniques used when handling

Thus
 .
.