Applied Mathematics Vol.06 No.03(2015), Article ID:54970,8 pages
10.4236/am.2015.63052
Fixed Points of Two-Parameter Family of Function
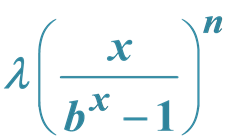
Ming-Gar Lee, Chih-Chang Ho
Department of Applied Mathematics, Chinese Culture University, Taipei, Taiwan
Email: lmj@faculty.pccu.edu.tw
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 27 January 2015; accepted 18 March 2015; published 24 March 2015

ABSTRACT
We establish sufficient conditions of the multiplicity of real fixed points of two-parameter
family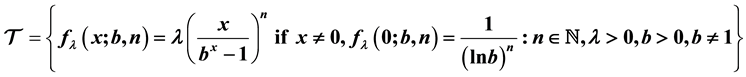 . Moreover, the be-
haviors of these fixed points are studied.
. Moreover, the be-
haviors of these fixed points are studied.
Keywords:
Fixed Points, Attracting Fixed Points, Rationally Indifferent Fixed Points, Repelling Fixed Points

1. Introduction
The introduction of chaos, fractal, and dynamical system could be found in many classical textbooks, such as Scheinerman [1] . A dynamical system has two parts, a state and a function. The second part of a dynamical system is a rule which tell us how the system changes over time. According to the time, we have the discrete and continuous system. The discrete dynamical system, in which we are interested, always does not have an analytical solution. Therefore, the behaviors of fixed points are very important. They play a vital role in the chaos, bifurcation, Julia sets problem in the dynamical system (see [2] [3] ). Those problems have been studied for last thirty years. Using the dynamics of functions near the real fixed points, the dynamics of functions in complex
plane were induced by the following researchers: The dynamics of families of entire
functions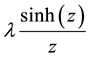 ,
,
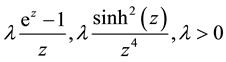 were studied
by Prasad [4] , Kapoor and Prasad [2] , Sajid and Kapoor [5] , respectively. The
dynamics of
were studied
by Prasad [4] , Kapoor and Prasad [2] , Sajid and Kapoor [5] , respectively. The
dynamics of
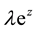 is found in Devaney [6] . Recently, Sajid [7] [8] gave the results about the fixed
points of one parameter family of function
is found in Devaney [6] . Recently, Sajid [7] [8] gave the results about the fixed
points of one parameter family of function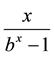 . His work is motivated by the relationship of the function
. His work is motivated by the relationship of the function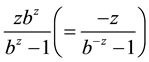 with the well-known generating functions on base b by choosing
with the well-known generating functions on base b by choosing
 and
and
 in the generalized Bernoulli generating function
in the generalized Bernoulli generating function
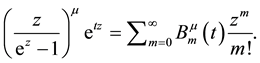 The proofs in [7] and [8] are too
The proofs in [7] and [8] are too
complicated. In this paper, we not only give a simple proof of the work of Sajid [7] , but also generalize his work.
2. Main Results
We will determine the fixed points of
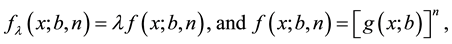 where
where
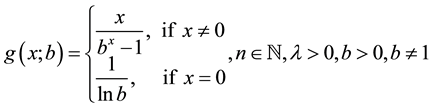 (2-1)
(2-1)
i.e., we will solve the equation
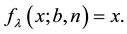 Moreover, we also discuss the multiplicity and the behavior of the fixed points
for two parameters b and n. For simplicity of notation, we denote
Moreover, we also discuss the multiplicity and the behavior of the fixed points
for two parameters b and n. For simplicity of notation, we denote
 and
and
 by
by
 and
and
For
Theorem 1. Let


(1) The function


(2) The unique fixed point








(3) There exists

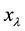






Proof. Suppose that






point of the function



is unique. Moreover, (2-3) easily implies statement (2).
Next, we proved statement (3). It is easy that

and the function



Hence,



Therefore, statement (3) are true by (2-6), (2-7), and (2-8).
The results about

fixed points is similar to the case


Hence, if the integer n is even, then


Suppose that the fixed point of



and



Lemma 2. Let








Proof. Suppose that


Therefore, (2-9) implies that









(2-4) implies that

and
where

Let


Moreover, let


In fact, the graph of



By the algorithm of bisection,







To study the behavior of the fixed points in Theorem 5, we need Lemma 3 and Lemma 4 as follows.
Lemma 3. Suppose that

Then (1)



Proof. The statement (1) is easy. (2-16) implies



Let









Lemma 4. Suppose that




and

Then there is a unique

Moreover, if









Proof. Let





Suppose to the contrary that

There exist


Then

For




Suppose that






Suppose to the contrary that










and there exists the minimum of


Let the minimum occurs at



Finally, suppose that








Suppose to the contrary that









suppose that



Theorem 5. Let


(1) There exists a unique








(2) Let n be fixed. If



(3) Let b be fixed. Then

(4) Suppose









Moreover,

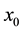






(5) The fixed points

Proof. Let

(1) We want to solve the equation





Because of


By





intersections of














(2) The statement (2) is easy by Lemma 2 and Part (1).
(3) In fact,



(2-1) and (2-4) imply to solve

Let


Lemma 3 and (2-25) imply that

(4) Suppose that









(5) Let


Let

Lemma 3, (2-21) and


Theorem 6. Let


(1) The function




(2) Let










(3) There exists








Proof. The proof of Theorem 6 is similar to that of Theorem 5. We just mention some
key points. The function f is positive, decreasing, and concave upward. Let



Let



Lemma 3 and (2-27) imply that there exists a unique





Theorem 7. Let n be odd. Then
(1)







(2) Let the parameter n be fixed. Then




(3) Let the parameter




a unique number













(4) There exists








Proof. The proof of Theorem 7 is similar to that of Theorem 5. We just also mention
some key points. The function f is decreasing if


downward if












3. Discussion
The Sarkovskii’s theorem said that let the function

of







References
- Scheinerman, E.R. (1996) Invitation to Dynamical System. Prentice-Hall, Upper Saddle River.
- Kapoor, G.P. and Prasad, M.G.P. (1998) Dynamics of
 :
The Julia Set and Bifurcation. Ergodic Theory and Dynamical Systems, 18, 1363-1383.
http://dx.doi.org/10.1017/S0143385798118011
:
The Julia Set and Bifurcation. Ergodic Theory and Dynamical Systems, 18, 1363-1383.
http://dx.doi.org/10.1017/S0143385798118011 - Sajid, M. and Alsuwaiyan, A.S. (2014) Chaotic Behavior in the Real Dynamics of a One Parameter Family of Functions. International Journal of Applied Science and Engineering, 12, 289-301.
- Prasad, M.G.P. (2005) Chaotic Burst in the Dynamics
of
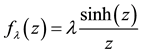 . Regular
and Chaotic Dynamics, 10, 71- 80. . Regular and Chaotic Dynamics, 10, 71- 80. http://dx.doi.org/10.1070/RD2005v010n01ABEH000301
. Regular
and Chaotic Dynamics, 10, 71- 80. . Regular and Chaotic Dynamics, 10, 71- 80. http://dx.doi.org/10.1070/RD2005v010n01ABEH000301 - Sajid, M. and Kapoor, G.P. (2004) Dynamics of a Family of Non-Critically Finite Even Transcendental Meromorphic Functions. Regular and Chaotic Dynamics, 9, 143-162. http://dx.doi.org/10.1070/RD2004v009n02ABEH000272
- Devaney, R.L. (1991) -Dynamics and Bifurcation. International Journal of Bifurcation and chaos, 1, 287-308. http://dx.doi.org/10.1142/S0218127491000221
-
Sajid, M. (2015) On Real Fixed Points of One Parameter Family of Function
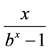 . Tamkang
Journal of Mathematics, 46, 61-65.
. Tamkang
Journal of Mathematics, 46, 61-65. - Sajid, M. (2014) On Fixed Points of One Parameter Family of Function
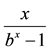 II. International Journal of Mathematical Analysis, 8, 891-894.
II. International Journal of Mathematical Analysis, 8, 891-894.



























