Received 15 January 2015; accepted 2 February 2015; published 5 February 2015

ABSTRACT

One-shot systems such as missiles and extinguishers are placed in storage for a long time and used only once during their lives. Their reliability deteriorates with time even when they are in storage, and their failures are detected only through inspections for their characteristics. Thus, we need to decide an appropriate inspection policy for such systems. In this paper, we deal with a system comprising non-identical units in series, where only minimal repairs are performed when unit failures are detected by periodic inspections. The system is replaced and becomes “as good as new” when the nth failure of the system is detected. Our objective is to find the optimal inspection interval and number of failures before replacement that minimize the expected total system cost per unit of time.

Keywords:

One-Shot System, Maintenance Policy, Minimal Repair, Cost Rate

1. Introduction

Systems such as missiles and extinguishers are used only once during their lives. Once the system is placed in an operational position or a nearby depot, it spends almost its entire life in storage until it is used. Usually, such systems are not moved except for inspections or other special situations. Because of these characteristics, these systems are called one-shot systems or storage systems.

The reliability of a one-shot system decreases with time even if it is placed in storage. Hence, inspections should be carried out at appropriate times to ensure high reliability. Frequent inspections will ensure its high availability, while they sometimes incur a high cost that may not be acceptable to users.

Inspection policy problems for a one-shot system have been studied by numerous researchers. Barlow and Proschan [1] found an optimum inspection policy that minimized the cost rate in the case that a system was perfectly repaired upon failure detection. Ito and other researchers assumed that a system consisted of two and three types of unit [2] -[4] . They formulated the periodic inspection policy for a system requiring high reliability. Yun and other researchers considered the inspection policy for a system with two types of unit, where intrinsic replacement times for one type of unit were predetermined [5] -[7] . They determined the optimum inspection schedule of another type of unit by simulation to meet the goal of reliability.

All the above papers dealt with perfect repairs upon the detection of failures. On the other hand, there is another type of repair action. A minimal repair simply restores a failed unit to the working state. In this case, the hazard rate of the minimally repaired unit is the same as that immediately before the failure. Minimal repairs are useful for a complex one-shot system because they have a much lower cost than perfect repairs or replacements. Nakagawa [8] discussed an inspection policy for the case that the failures of a unit were detected instantly and minimally repaired. As we explained above, failures are not always detected instantly in a one-shot system. Thus, we have to take system down into account to develop a more practical model of a one-shot system.

In this paper, we deal with an inspection policy for a one-shot system that consists of m units in series. The system is not available when at least one unit is out of order. We assume that the system is inspected at periodic time intervals, T, and failures are detected only by inspections. A minimal repair is performed when a failure is detected, and all units in the system are replaced and become “as good as new” when a total of n failures are detected after the last replacement. The system has a predetermined limitation for the number of minimal repairs, N. We minimize the expected cost rate, which is expressed as a function of n and T. In Section 2, we explain the proposed model and derive the cost rate. A numerical example is shown in Section 3.

2. Model Assumptions and Analysis

2.1. Notations & Nomenclature

The following notations and nomenclature are used.

Cost rate: cost per unit time

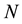: limitation of number of minimal repairs for a system

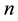: number of failures until replacement, i.e.,.

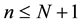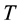: inspection interval

: number of units in a system

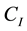: inspection cost of a system

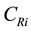: minimal repair cost of unit i

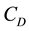: risk (i.e., cost) per unit of time resulting from system down

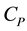: replacement cost of a system

: failure distribution function of a system until first failure

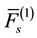: reliability function of a system between th failure and lth failure, which can be given by as the product of reliability function of each unit, where the 0th failure indicates the time that a system is in service.

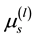: mean operating time of a system between th failure and lth failure

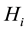: cumulative hazard rate function of unit i

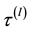: expected total time until detection of lth failure

: expected total cost until detection of lth failure

: ratio of the number of failures of unit i to n

: cost rate function, given by

2.2. Model Assumptions

We consider a one-shot system that is described in the following. Figure 1 shows an example of the process of the proposed model.

1) The system has a series structure of m units (unit 1, unit 2, …, unit m) and the system’s hazard rate increases with time.

2) All the units in the system are inspected periodically and simultaneously.

3) A failure of a unit is detected at the following inspection, and a minimal repair is performed upon the detection. The hazard rate of a failed unit is not changed by the minimal repair.

4) System down incurs some risk, which is the product of the system down probability and the incurred cost. In this paper, we regard the risk as the system down cost per unit of time for simplicity.

5) When a total of n failures are detected since the last replacement, all the units in the system are replaced and the system becomes “as good as new.”

6) Times needed for inspections, minimal repairs, and replacements are negligible.

2.3. Model Analysis

Here we derive the cost rate function of the system. We can regard the time interval between replacements as one cycle because the system is renewed when n failures are detected after the last replacement. The expected cost rate is calculated from the expected cost per cycle and the expected time per cycle.

First, we consider the case that n = 1, which means that the system is replaced when the first failure is detected. In this case, the expected total cost until replacement is obtained as

(1)

where.

Similarly, we can derive as

. (2)

The cost rate function when is

. (3)

The result also can be derived using the results in [1] .

To calculate the cost rate for, we use two approximations for the system parameters. One is used for the mean operating time and the other is used for the number of repairs of each unit. We have found that these approximations are useful in many cases, as shown in the numerical example in Section 3.

1) Mean operating time

The exact mean operating time until the second or a later failure is obtained by applying multiple integrals. It is not easy to calculate these integrals when n becomes large. Thus, we focus on the fact that the probability of detecting multiple failures at one inspection is very small. If we ignore the multiple failures and assume that the first failure of the system occurs at exactly, we express and as

, (4)

. (5)

are also obtained similarly. In other words, we assume that the system operating time between the th failure and the kth failure is exactly. Then, and are given by

, (6)

. (7)

2) Number of failures of unit i

We introduce, which represents the ratio of the number of failures of unit i to n. Ignoring the downtime, the expected number of failures of unit i until a specific time would be calculated theoretically using the cumulative hazard rate function. We also use the cumulative hazard rate function and express as

. (8)

Using these two approximations, we can obtain the expected cost and time until replacement as

, (9)

. (10)

The expected cost rate until replacement, , is given by

. (11)

The larger n and T become, the longer the downtime becomes. However, too small value of n and T incur high replacement and inspection costs per unit of time. Thus, we have to determine the optimum values of n and T that minimize Equation (11).We determine the optimum values of n and T that minimize Equation (11) subject to by the steepest decent method.

3. Numerical Example

We show a numerical example of a missile system. The missile has three units; unit 1 is a blasting case, unit 2 is a guide and control unit, and unit 3 is an engine unit. Calculated results are compared with simulation results and errors are evaluated.

Parameters are given in Table 1, where Wei indicates Weibull distributions whose reliability function is. The unit of time is a day and the unit of cost is 1000 dollars. The optimum solutions and the errors are shown in Table 2. The sample number of the simulation is 1 million, and the error is estimated assuming that the simulation result is correct.

In this case, the optimum value of n is the same in both methods, but the optimum values of T and the minimum cost rate have some errors.

Figure 2 shows the cost rate plotted against n and T. It can be seen that the cost rate function is unimodal with respect to both n and T and the optimal policy can be determined uniquely.

Hence, we describe the tendency of the errors. First, we used the approximation for the mean operating times (Equation (7)). Table 3 shows the errors for the example. The error increases as T or n increases in many cases. When T increases, the probability of detecting multiple failures at inspections increases, but this effect is ignored in Equations (6) and (7). That is why the mean operating time calculated using the approximation is longer than the value computed by simulation in many situations. Next, we also used the approximation for the number of repairs for each unit (Equation (8)). The errors are smaller than those for the mean operating time in many cases. In this example, the errors are about 1%. They also appear to depend on the values of n and T, but the behaviors are complex.

4. Conclusion

We considered a multiple-unit repairable system that is inspected periodically and whose failures are detected at the next inspection. We derived the cost rate function by using two approximations and determined the optimum number of failures until replacement and the inspection interval. We confirmed the effectiveness of our approximate method by a numerical example. Note that the proposed method does not always find the optimal solution. Establishing a search method to find global optimal solutions remains as a future work. Moreover, we assumed that no maintenance was performed before failure. However, in practice, not only repairs but also other preventive maintenance actions are performed for many types of systems. This should be considered when expanding the proposed model.

References