Applied Mathematics
Vol.05 No.21(2014), Article ID:52220,9 pages
10.4236/am.2014.521317
Complex Matter Space and Relativistic Quantum Mechanics
Reza Ahangar
Department of Mathematic, Texas A & M University-Kingsville, Kingsville, TX, USA
Email: reza.ahangar@tamuk.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 October 2014; revised 6 November 2014; accepted 16 November 2014
ABSTRACT
The Special Relativity Theory cannot recognize speed faster than light. New assumption will be imposed that matter has two intrinsic components, 1) mass, and 2) charge, that is M = m + iq. The mass will be measured by real number system and charged by an imaginary unit. This article presents a Complex Matter Space in Relativistic Quantum Mechanics. We are hoping that this approach will help us to present a general view of energy and momentum in Complex Matter Space. The conclusion of this article on Complex Matter Space (CMS) theory will lead help to a better understanding toward the conversion of mass and energy equation, unifying the forces, and unifying relativity and quantum mechanics.
Keywords:
Complex Matter, Complex Mass, Complex Energy and Momentum

1. Introduction to the Complex Matter Space
It is common in mathematics to define an abstract space like metric, Hilbert, or Banach spaces without physical or experimental verifications. In fact logical approach with definitions, some related axioms, and presentation of some examples may be sufficient to accept and apply to practical life problems. But for constructing a theoretical physical space, in addition to the logical and theoretical approach, an experimental or physical justification is needed (see [1] and [2] ).
In 1928, the British Physicist Paul Dirac realized that when electrons are moving very close to the speed of light, special relativity needs to be incorporated which lead to particles with negative mass (see [3] ). The existence of a particle moving faster than light was presented by many authors including, Sudarshan who discussed the physics of complex mass (see [4] ).
During the past decades, various theoretical approaches were presented to unify relativity and quantum mechanics which include complex space-time and axiomatic quantum field theory (see [5] and [6] ).
The content of the paper on “Imaginary Relativity” is a right direction toward Complex Matter Space (CMS) but not sufficient for the unifying forces. The CMS postulates may answer some of the questions in this article’s concluding remarks. This could be a reason for the statement that “the author does not know where the imaginary world is located or what its nature is?” (see [7] ).
We will present postulates that a particle has two components that can be demonstrated in a complex plane as a real component mass (m) and imaginary component charge (q):
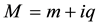 (1.1)
(1.1)
We will show that these assumptions lead us to unify the electromagnetic force and gravitational force.
For example the interaction force between two particles M and M' can be described by
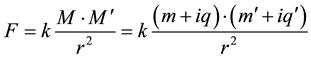 (1.2)
(1.2)
We can observe that, after expansion of (1.2), two terms on the right hand side represent gravitational forces and electromagnetic forces. But two other imaginary components seemed to me not to represent any forces.
Assume that the terminology “matter” in general is an undefined term. In this paper, in addition to the postulates of Special Relativity Theory (SRT), we accept the following new postulates:
The position x(t) and the velocity dx/dt will stay a real number. The speed of light remains a constant real number, c. By this agreement, and contrary to the paper “Imaginary Relativity” by Rezaei, we are not accepting variation of the speed of light or considering it as a complex number. For decades, the discovery of the nature of other forces was a dream. Acceptance of this postulate leads to the necessity to reaffirm the entire physics, Newtonian mechanics, relativity, and quantum mechanics.
The organization of this paper is the following: A new view of complex matter will be presented based on two postulates. We use a geometric interpretation of complex matter to justify new postulates in a complex coordinate plane.
By these new postulates of Mass and Energy we can restructure the relativistic view of complex matter, the Einstein equation of mass-energy. Finally, energy and momentum in Relativistic Quantum Mechanics will be recalculated in the Complex Matter Space.
2. Geometric View of the Complex Matter Using Imaginary Object
Traveling Beyond the Speed of Light: According to the Special Theory of Relativity, we may not be allowed to cross the boundary of the speed of light c in the real world. But if we can pretend that we exist, in the imaginary world then it may be allowed to go faster than light, since our conjugate space will be the real world.
Assume that we are traveling by a rocket which is taking off from the earth to go cruising in space. How much energy is required to accelerate to the speed of light? It would be impossible for a particle to accelerate to a velocity of light c because the speed of light is constant in a vacuum for all inertial observers. What do we observe?
1) Observers in all inertial frames on the earth would measure the same value for c and in fact infinite energies are required to accelerate objects to the speed of light.
2) If we can break the wall of speed of light and travel faster than light, an observer would see things going crazy around―by SRT time dilation the time would freeze around us―mass will approach infinity.
Experiment of Moving the Image of a Light Faster than the Speed of Light: Assume a source of a light located at the epicenter of two spheres (O, c) and (O, R) where OM = R ? c whose radius R is much greater than the speed of light c. This sphere can be real but radius can be astronomically large. To perform this experiment, one can select c = 1 as a unit of the measurement thus R ? 1.
The source of light at the center (O) emitting the light signal in each direction and rotating with the rate of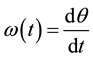 .
.
The light is traveling at the speed of the c and it will take seconds to show the image on the dome. We will measure the linear speed of the image on the dome.
For simplicity two circles of radius c = 1 and R with the images of mapping of A and B on the larger circle is M and N, where their arc-lengths are s and s' respectively.
In Figure 1 the light signal emits from the center (O) and transfers the image of the point A to a point M on the second circle, while the point is moving on the circumference of the first circle. In the following simple approach, we will demonstrate that the image point A is moving faster than the point M on the circumference of the second circle.
We denote T(A) = M and similarly T(B) = N such that length of the arc AB is s and T(s) = S.
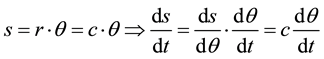
Let us assume that the measure of the angle (AOB) = theta varies with the rate of a fixed real number, for example k = 2, therefore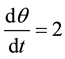 . Substituting in the previous relation implies that
. Substituting in the previous relation implies that
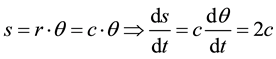
Thus, the image M which is moving on the larger circle (O, R) with the linear speed of 2c is faster than light.
Complex Coordinate in Minkowski Space-Time: Absolute time may be an undefined word and we try to postulate, define, and measure it by its changes, variations, and motions with other physical quantities in space, i.e. physical motion of particles, rotation of the earth around the sun, or clock’s hands on a circle. The unit of time practically is what we perceive about how much the physical objects change position, velocity, energy, or
Figure 1. The light signal is emitting from the center (O) and transfers the image of the point A to the second circle M while the point is moving on the circumference of the first circle and the image is moving faster on the circumference of the second circle.
mass. How do we define one hour, one minute, or one second? They are the measurements of the physical changes that we try to demonstrate by arc-length on a clock using the unit of distance or radians on a circle.
Are they real measurements of time? In the following mathematical argument we introduce  as a unit of time on the imaginary axis. Let us consider a vector
as a unit of time on the imaginary axis. Let us consider a vector 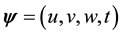 such that
such that
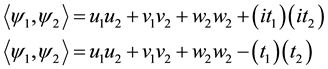 (2.1)
(2.1)
Magnitude of a Vector 4D-Complex Matter Space: We may use the norm in the inner product space as a distance or magnitude of a vector 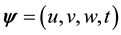
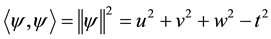
Verifying the CMS Postulate (II): According to time and length dilation in SRT, the value of time and length variation
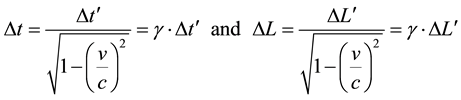 (2.2)
(2.2)
such that
(a) 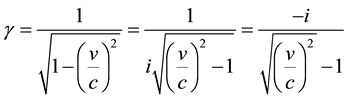 and (b)
and (b)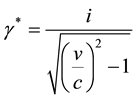 (2.3)
(2.3)
can be interpreted for the velocity v as a real number greater than the speed of light.
This is one indication that time may have an imaginary unit.
Assuming a complex time variation

The relation (2.2) can be expressed by
Case (I): the motion velocity v < c.
The values of


Case (II): the motion velocity v > c: If the particle velocity is faster than the speed of light (v > c) then both 

is a real number. The argument presented in both cases based on the inequality v > c or v < c, demonstrates that the relation in an ordered pairs of real numbers. Thus we cannot select these two numbers in the complex plane.
3. Beyond the Speed Limit of Light and Relativistic Quantum View of the Complex Matter SPACE
Having a new unified presentation of mass and charge in the form of complex matter will bring a new question for us. How do we interpret the principles of Relativistic Quantum Mechanics?
Antimatter: Substance composed of elementary particles having the mass and electric charge of ordinary matter (such as electrons and protons) but for which the charge and related magnetic properties are opposite in sign. The existence of antimatter was predicted by the electron theory of P. A. M. Dirac. In 1932 the positron (antielectron) was detected in cosmic rays, followed by the antiproton and the antineutron detected through the use of particle accelerators. Positrons, antiprotons, and antineutrons, collectively called antiparticles, are the antiparticles of electrons, protons, and neutrons, respectively. When matter and antimatter are in close proximity, annihilation occurs within a fraction of a second, releasing large amounts of energy. The (relativistic) mass of an object measured by an observer in the xyz-frame is given by

By accepting the complex matter Postulate (I), the velocity in (3.1) can be any real or complex number. Mathematically v could be greater than the speed of light, but the mass m would become imaginary. Physically we would have to get to the speed of light first i.e. v = c, which gives us an undefined value for M. So we believe that nothing moves faster than the speed of light because we do not like observables to be imaginary.
A hypothetical particle that is traveling faster-than a light particle is consistent with the special theory of relativity. According to this theory, a free particle has an energy E and a momentum p which form a Lorentz four-vector. The length of this vector is a scalar, having the same value in all inertial reference frames. One writes

Equation (3.2), where c is the speed of light and the parameter m2 is a property of the particle, independent of its momentum and energy. Three cases may be considered: m2 may be positive, zero, or negative. The case m2 > 0 applies for atoms, nuclei, and the macroscopic objects of everyday experience. The positive root m is called the rest-mass. If m2 = 0, the particle is called massless. A few of these are known: the electron neutrino, the muon neutrino, the photon, and the graviton. The name tachyons (after a Greek word for swift) has been given to particles with m2 < 0.
Mayer in 2007, designed the energy momentum in a complex plane very well without acknowledging the idea of complex matter considering the speed of light c = 1 a natural unit (see [8] ). The relation (3.2) can be interpreted by.
Energy in the complex plane: A vector form of the energy is demonstrated with the horizontal component OH = mc2, and vertical component ZH = pc. The state of the energy and its magnitude can be described by


According to postulate (I), Figure 2 and Figure 3 demonstrate that the energy will have the two components of real and imaginary values. The energy for mass-less particles can be observed on the diagram when
where, the magnitude of the complex vector for particle and factor gamma is defined by:

The following steps lead to the effects of complex matter theory on elementary quantum mechanics (see [9] and [10] ).
Figure 2. The state of the complex matter in a complex plane with two components (m, q) and it is denoted by 


Figure 3. Energy in the complex plane: A vector form of the energy demonstrated with the horizontal component OH = mc2, and vertical component ZH = pc. Energy vector 

It is well known that the energy of a photon can be calculated if we assume that light is composed of particles.
The energy is proportional to the density of the photons particles, that is
1) Photon is a complex particle with zero mass. Energy of a package of photon particles is equal to energy of each particle multiply by the number of particles (frequency), that is

Where, h is the Plank constant real number. The momentum can be calculated using.
2) Campton Effect when particle―like is a wave. Momentum of the of the photon wave will be equal to Energy/speed, that is

By considering that velocity is equal to frequency multiplied by the wave length, and 

3) Using de Broglie’s Law we can find the energy of the wave (by 3.6) and replacing the frequency fq is equal to the energy of the mass, that is
Wave length





Consequently:

Let E = mv2/2 and it is clear that

4. Modifying the Einstein’s Equation in Complex Matter Space
Using Postulate (I) let us describe a particle of a Complex Matter Space by a set of points 
We will describe the instantaneous rates of changes of this complex matter by
Complex Matter-Instantaneous Rate of Changes: Given a complex matter in the Equation (3.1) then the instantaneous rate of change satisfies the following relation

Proof: Assuming 

This will conclude the relation (4.1) and also
Energy Equation in Complex Matter Space: The instantaneous rate of change of Energy in Complex Matter Space can be described by

Justification: Let us assume, in the following approach, that the definition of energy and force for the Complex Matter Space is staying the same. Thus;

where, the velocity 


Substitute (4.4) in the relation (4.3)
Simplifying the right hand side concludes

To explain the relativistic energy in Complex Matter Space, we use the trigonometric values in the complex plane (using the relation (3.10) and Figure 3);


When the real part of particle mass is not zero we will derive the energy, mass, and charge in relativistic mechanics.
The complex point E can be described in the following form
Replacing cosine and sine of angle alpha from the previous step, we will get an energy state description

This is a correction of the conclusion presented in a paper by Mayer in 2007 (see [11] ). The relation (4.6) is the state of the energy of a particle with the real rest mass moving faster than light.
5. State of the Momentum in Complex Matter Space
If the charge in wave-like particle is zero, then dividing the real part of energy by real part of momentum will produce the following relations

and we obtain 

Using Figure 2 and the relation (3.10)

The State of the Complex Matter: Using relations (5.2), one can find the value of gamma from (2.2)

State of the Complex Energy: The complex point E can be described in the following state of energy in the complex model 

Thus, from the relation (5.4) one can conclude the real and imaginary components of energy to be

(see [12] ).
The State of the Momentum of Complex Matter: Assume that 
speed 
can be described by

where,

6. Discussions and Conclusion
According to the original postulate, we determine a point in a complex plane by 

with other phenomenon, theories, or experiments.
The existence of a particle traveling faster than light has been presented by many authors including, Sudarshan who discussed the Physics of complex mass (see [12] ).
The idea of negative matter appears in past theories of matter that have now been abandoned (see [13] ). Using the once popular vortex theory of gravity, the possibility of matter with negative gravity was discussed by William Hicks in the 1880s.
In 1928, British physicist Paul A. M. Dirac generalized Einstein’s famous equation E = mc2 by considering negative mass. This hypothesis allowed for the existence of anti-particles in our universe.
These anti-particles are, literally, mirror images of normal or real matter. Each anti-particle has the same mass as its corresponding particle, but the electrical charges are reversed. Examples of antimatter discoveries of the 20th century are: 1) Positrons―Electrons with a positive instead of negative charge; 2) Anti-protons―Protons that have a negative instead of the usual positive charge; 3) Anti-atoms―Pairing together positrons and antiprotons (see [14] ).
Scientists at the European Organization for Nuclear Research, created the first anti-atom. Nine anti-hydrogen atoms were created, each lasting only 40 nanoseconds. As of 1998, CERN researchers were pushing the production of anti-hydrogen atoms to 2000 per hour.
Both particles involved in the interaction process are completely annihilated and create a very huge explosion that occurs when antimatter and matter interact transferring the entire mass of both objects into energy.
It is part of the dream unification theory to build a matter-antimatter reaction engine?
7. Future Research
The quantum states of the particles can be studied in the Complex Matter Space through interactions with other fundamental particles.
The Electromagnetic Interaction, Weak Interaction, and Strong Interaction forces can be considered in the Complex Matter Space. The standard model in quantum state does not consider Gravitation as part of the standard model.
The Complex Matter Space model can include all of the interactions as part of the model including the Weak Forces.
References
- Naber George, L. (1992) The Geometry of Minkowski Spacetime. An Introduction to the Mathematics of Special Theory of Relativity. Dover.
- David, H. and Rensick (with the Assistance of Farrell Edwards and John Merrill) (1970) Fundamentals of Physics. John Wiley & Sons, Inc., Hoboken.
- Dirac, P.A.M. (1928) The Quantum Theory of Electron. Proceedings of the Royal Society A, 117, 610-624.
- Sudarshan, E.C.G. (1970) Physics of Complex Mass Particles. University of Texas, Austin.
- Gerald, K. (2003) Quantum Physics, Relativity, and Complex Space Time: Toward a New Synthesis. (Originally published in 1990 by North-Holland, Amsterdam)
- Richard, F. (1963) The Feynman Lectures on Physics. Vol. III, Addison Wesley, Reading, 1-6.
- Mehran, R. (2010) Imaginary Relativity. Wseas Transaction on Communications, 9.
- Mayer Alexander, F. (2007) Wave Energy in Quantum Mechanics. Journal of Physics, Conference Series, 70, Article ID: 012013. http://iopscience.iop.org/1712-6596/70/1/02013.
- Wall Ernst, L. (1995) The Vortex Theory of the Electron and its de Broglie Waves Pulse. Institute for Basic Research, Palm Harbor. www.gwphysics.com www.tachyonmodel.com
- John, W. and Wojceich, Z. (1983) The Quantum Postulate and the Recent Development of Atomic Theory. In: Quantum Theory and Measurement, Princeton University Press, Princeton, 111.
- Reza, A. (2014) Quantum Complex Matter Space. International Journal of Theoretical and Mathematical Physics, 4, 159-163. http://dx.doi.org/10.1088/1742-6596/70/1/012013
- Zhang, T.X. (2008) Electric Charge as a form of Imaginary Energy. Progress in Physics, 2.
- Sudarshan, E.C.G. (1968) A New Formulation of Relativistic Quantum Theory of Fields with Applications to Particles Traveling Faster Than Light. Proceedings of Nobel Symposium on Elementary Particle Theory.
- Taylor, T.J.R., Zafirots, C.D. and Dubson, M.A. (2004) Modern Physics for Scientists and Engineers. 2nd Edition, Pearson-Printice Hall.












