Received 16 August 2014; revised 14 September 2014; accepted 5 October 2014

ABSTRACT

In this paper, we discuss the B-spline wavelets introduced by Chui and Wang in [1] . The definition for B-spline wavelet packets is proposed along with the corresponding dual wavelet packets. The properties of B-spline wavelet packets are also investigated.

Keywords:

B-Splines, Spline Wavelets, Wavelet Packets

1. Introduction

Spline wavelet is one of the most important wavelets in the wavelet family. In both applications and wavelet theory, the spline wavelets are especially interesting because of their simple structure. All spline wavelets are linear combination of B-splines. Thus, they inherit most of the properties of these basis functions. The simplest example of an orthonormal spline wavelet basis is the Haar basis. The orthonormal cardinal spline wavelets in 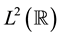were first constructed by Battle [2] and Lemarié [3] . Chui and Wang [4] found the compactly supported spline wavelet bases of 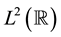and developed the duality principle for the construction of dual wavelet bases [1] [5] .

Wavelets are a fairly simple mathematical tool with a variety of possible applications. If 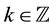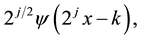is an orthonormal basis of, then 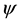is called a wavelet. Usually a wavelet is derived from a given multiresolution analysis of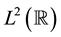. The construction of wavelets has been discussed in a great number of papers. Now, considerable attention has been given to wavelet packet analysis as an important generalization of wavelet analysis. Wavelet packet functions consist of a rich family of building block functions and are localized in time, but offer more flexibility than wavelets in representing different kinds of signals. The main feature of the wavelet transform is to decompose general functions into a set of approximation functions with different scales. Wavelet packet transform is an extension of the wavelet transform. In wavelet transformation signal decomposes into approximation coefficients and detailed coefficients, in which further decomposition takes place only at approximation coefficients whereas in wavelet packet transformation, detailed coefficients are decomposed as well which gives more wavelet coefficients for further analysis.

For a given multiresolution analysis and the corresponding orthonormal wavelet basis of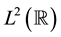, wavelet packets were constructed by Coifman, Meyer and Wickerhauser [6] [7] . This construction is an important generalization of wavelets in the sense that wavelet packets are used to further decompose the wavelet components. There are many orthonormal bases in the wavelet packets. Efficient algorithms for finding the best possible basis do exist. Chui and Li [8] generalized the concept of orthogonal wavelet packets to the case of nonorthogonal wavelet packets. Yang [9] constructed a scale orthogonal multiwavelet packets which were more flexible in applications. Xia and Suter [10] introduced the notion of vector valued wavelets and showed that multiwavelets can be generated from the component functions in vector valued wavelets. In [11] , Chen and Cheng studied compactly supported orthogonal vector valued wavelets and wavelet packets. Other notable generalizations are biorthogonal wavelet packets [12] , non-orthogonal wavelet packets with r-scaling functions [13] .

The outline of the paper is as follows. In, we introduce some notations and recall the concept of B-splines and wavelets. In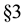, we discuss the B-spline wavelet packets and the corresponding dual wavelet packets.

2. Preliminaries

In this Section, we introduce B-spline wavelets (or simply B-wavelets) and some notions used in this paper.

Every mth order cardinal spline wavelet is a linear combination of the functions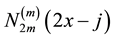. Here the function is the mth order cardinal B-spline. Each wavelet is constructed by spline multiresolution analysis. Let m be any positive integer and let 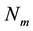denotes the mth order B-spline with knots at the set 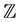of integers such that

The cardinal B-splines 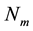are defined recursively by the equations

We use the following convention for the Fourier transform,

The Fourier transform of the scaling function is given by

(1)

For each, we set, and for each, let denotes the -closure of the algebraic span of. Then is said to generate spline multiresolution analysis if the following conditions are satisfied.

1)

2);

3),

4) for each, is a Riesz basis of.

Following Mallat [14] , we consider the orthogonal complementary subspaces that is;

5).

6).

7).

These subspaces, are called the wavelet subspaces of relative to the B-spline. Since and, we have

, (2)

where is some sequence in. Taking the Fourier transform on both sides of (2), we obtain

. (3)

Substituting the value of from (1) into (3), we have

.

This gives

(4)

So, (2) can be written as

,

which is called the two scale relation for cardinal B-splines of order.

Chui and Wang [1] , introduced the following mth order compactly supported spline wavelet or B-wavelet

, (5)

with support that generates and consequently all the wavelet spaces. To verify that is in, we need the spline identity

. (6)

So, substituting (6) into (5), we have the two scale relation

, (7)

where,

. (8)

Let

, (9)

with the corresponding two scale sequence. If is a wavelet, then there exists another called the dual wavelet of such that

. (10)

For the scaling function, we define its dual by

, (11)

such that

. (12)

Now, we have

(13)

Taking the Fourier transform of (13), we have

(14)

where,

(15)

A necessary and sufficient condition for the duality relationship (12) is that and are dual two scale symbols in the sense that

. (16)

A proof of this statement is given in ( [15] , Theorem 5.22). Also from (7) and (9), we have

(17)

where,

(18)

We observe that

(19)

See ( [15] , Section 5.3).

If is an orthogonal scaling function, then

. (20)

We say that is orthogonal (o.n) B-wavelet function associated with orthogonal scaling function if

, (21)

and is an orthonormal basis of, so we have

. (22)

Lemma 1 Let. Then is an orthonormal family if and only if

. (23)

Proof See ([15] , page no. 75].

Theorem 1 Let defined by (13) is an orthonormal scaling function. Assume that whereas and are defined by (15) and (18) respectively. Then is an orthonormal wavelet function associated with if and only if

(24)

Proof Let us suppose that is an orthonormal wavelet function associated with. By Lemma 1 and (21), we have

Again by Lemma 1 and (22), we have

On the other hand, let (24) holds.

Now,

Also,

Thus, and are orthogonal and is an orthonormal wavelet function associated with.

3. B-Spline Wavelet Packets and Their Duals

Following Coifman and Meyer [6] [7] , we introduce two sequences of functions and defined by

(25)

(26)

where

When and, we have

and for and, we have

We call the sequence of B-spline wavelet packets induced by the wavelet and its corresponding scaling function whereas denotes the corresponding sequence of dual wavelet packets. By applying the Fourier transformation on both sides of (25), we have

(27)

where,

(28)

(29)

So, (24) can be written as

(30)

Similarly, taking the Fourier transformation on both sides of (26), we have

(31)

where,

(32)

(33)

Using these conditions we can write

(34)

We are now in a position to investigate the properties of B-spline wavelet packets.

Theorem 2 Let be any orthonormal scaling function and its corresponding family of B-spline wavelet packets. Then for each, we have

(35)

Proof Since satisfies (35) for. We may proceed to prove (35) by induction. Suppose that (35) holds for all, where, a positive integer and. We have

, where denote the largest integer not exceeding. By induction hypothesis and Lemma 1, we have

(36)

By using (27), (30) and (36), we obtain

Hence, by Lemma 1, (35) follows.

Theorem 3 Let be a B-spline wavelet packet with respect to the orthonormal scaling function. Then for every, we have

(37)

Proof By (27), (30) and (36), for we have

For the family of B-spline wavelet packets corresponding to some orthonormal scaling function, consider the family of subspaces

generated by. We observe that

where is the MRA of generated by, and is the sequence of orthogonal complementary (wavelet) subspaces generated by the wavelet. Then the orthogonal decomposition

may be written as

.

A generalization of the above result for other values of can be written as

.

Theorem 4 For the B-spline wavelet packets, the following two scale relation

(38)

holds for all.

Proof In order to prove the two scale relation, we need the following identity, see ([15] , Lemma 7.9)

(39)

Taking the right-hand side of (38), and applying the identity (39), we have

(40)

This completes the proof of the theorem.

Next, we discuss the duality properties between the wavelet packets and.

Lemma 2 For all and,

. (41)

Proof We will prove (41) by induction on. The case is the same as our assumption (12) on the dual scaling functions and. Suppose that (41) holds for all where,

where is a positive integer. Then for, we can write for some,

according to the proof of Theorem 7.24 in [15] . From the Fourier transform formulations of equations (25) and (26) and using (34) we have

Since, it follows from the induction hypothesis that for all, and this is equivalent to

(42)

Thus, we have

This shows that (41) also holds for.

Lemma 3 For all and, and, with,

(43)

Proof By applying the Fourier transform formulations of Equations (25) and (26) and using (42) and (34), we have as in the proof of Lemma 2 that

Cite this paper

SanaKhan,Mohammad KalimuddinAhmad, (2014) A Study on B-Spline Wavelets and Wavelet Packets. Applied Mathematics,05,3001-3010. doi: 10.4236/am.2014.519287

References