Applied Mathematics
Vol.5 No.16(2014), Article
ID:49432,17
pages
DOI:10.4236/am.2014.516243
On Universal Space and Time
Caesar P. Viazminsky1,2, Piere K. Vizminiska3
1Department of Physics, Illinois Institute of Technology, Chicago, USA
2Department of Physics, University of Aleppo, Aleppo, Syria
3Department of Computer Engineering, University of Detroit Mercy, Detroit, USA
Email: kaysarv2@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 July 2014; revised 8 August 2014; accepted 19 August 2014
Abstract
In earlier papers [1] -[4] , it was shown that the consistency of the concept of time with motion requires time and distance to be of the same dimension, and thus measured by the same unit. The arising reduced system of units revealed that mass and energy were only different facets of one entity, and resulted in the well-known mass-energy equivalence formula as a natural consequence. The physical space can be identified with any inertial frame, but when it comes to comparing the results of measurements in two frames, or more, only one frame, say S, can be taken stationary and identified with the physical space, whereas all other inertial frames are moving relative to S. The equivalence of inertial frames as sites of one physical world implies that an intrinsic units system of length, time, mass and charge should be defined in terms of basic constituent physical blocks that have the same identity in all inertial frames. A basic feature of the universal space and time theory (UST) is that the same one time prevails in all inertial frames. The scaling transformations (STs) that relate the geometric distances in two frames, S (s) when chosen the stationary frame, are derived, and applied to explain the Doppler’s effect. The time distance between a moving object in S and an observer depends on its state of motion; and the Euclidean form of the STs is employed to explain arrival of some meta-stable at the earth’s surface despite its short lifetime. The quantitative predicted Doppler’s effect, which is in a striking agreement with the Ives-Stilwell experimental results, coincides with the relativistic prediction for longitudinal motion, but yet predicts a complete absence of a transverse effect at a right angle. In coming parts of this work it will be shown that the UST explains elaborately the drag effect, stellar aberration, and produces naturally the relativistic mechanics. The UST will also be completed through deriving the scaling transformations of the second type, by which the null results of Michelson and Morley experiment, Michelson and Gale experiment, and the Sagnac effect are explained. The current work and our intended future works in UST are new versions containing basic conceptions and visions that didn’t appear in earlier versions [1] -[6] .
Keywords:Reduced System of Units, Intrinsic Units, Universal Time and Distance, Mass-Energy Equivalence

1. Introduction
The UST modifies the Newtonian conceptions of space and time to incorporate observations through light’s signals. While the absolute nature of time is retained, a time distance between an object and an observer that depends on their relative velocity and geometric distance is determined by means of what we call the scaling transformations (ST). Our novel conception of the space and time is characterized by the following:
1) Time durations that are consistent with motion require the former to be measured, in each frame, by spatial displacements intrinsic to light propagation and proportional to it. This defines in addition to the frame-independent (or universal) time durations a constant velocity c of light inside each frame.
2) One arbitrary inertial frame S, to be called universal, is considered stationary and indentified by the physical or absolute space, while all other inertial frames are moving relative to S. The physical space may be corresponded with any other inertial frame s, but this should have no bearing on the transformations that relate geometric distances in S and s regardless of which frame we choose to be stationary.
It follows from 1) that time and geometric length have the same dimension and can be essentially measured by the same unit. The reduced mechanical system of units (RSU) in S contains in addition to the unit of mass a common unit LS (or TS) for time and length, leading naturally to the well-known mass-energy equivalence formula. Being proportional to its geometric length, the time duration of a light trip within S is simply another equivalent measure of its length.
From 2), which allows for identification of the physical space with any inertial frame, several consequences follow:
• All inertial frames (IFs) are equivalent sites for observing one physical world, and consequently the physical laws are the same in all IFs.
• The units of RSU should have identical status in all IFs. This can be fulfilled through constructing them in each frame from the same basic constituents blocks, leading thus to intrinsic or natural units. For instance, the constituent block of length in an inertial frame S is the wavelengths  of the stationary emission of a specific spectral line of some chemical element, and the unit of distance in S is a certain multiple
of the stationary emission of a specific spectral line of some chemical element, and the unit of distance in S is a certain multiple 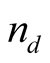 of
of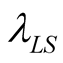 , i.e.
, i.e. 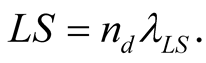 The constituent block of length
The constituent block of length 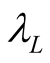 differs from a frame to another, and so does the unit of length
differs from a frame to another, and so does the unit of length  in the corresponding frame.
in the corresponding frame.
• The absolute or physical space in its Newtonian sense as the standard of rest has to be abandoned, but its role as a unique standard for rotations is retained. Moreover, the role of the absolute space in its Maxwellian sense as the carrier of electromagnetic radiation is also retained.
• A light trip follows a universal path that is independent of the frame by which the physical space is identified. However, when observed from the moving frame, the light trip’s path is seen tilted from its path in the stationary frame by the “aberration angle”. This fact will be discussed in the third part of this work.
Based on requirements 1) and 2), and on the implicit assumption regarding the Euclidean nature of the absolute space we determine the relation between the geometric length (whether geometric distance or time) and time length (universal duration) of a light trip in a frame S. Equivalently, we determine the scaling transformations STI between the geometric lengths of a light trip in the frames s, in which the light’s source b is stationary, and S in which b is moving. Explicitly, if the source of light 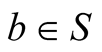 is moving at a constant speed
is moving at a constant speed 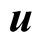 in S, then the STI determines the universal duration t of a light’s trip
in S, then the STI determines the universal duration t of a light’s trip 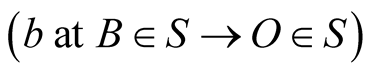 in terms of its geometric length
in terms of its geometric length  Thus t is a function
Thus t is a function 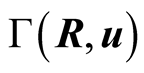 of the position vector of B and the velocity vector of b in S. It is t what is measured for the duration of the latter trip in S and in any other inertial frame. We shall refer to the universal time t as the time length, or time duration, of the latter light’s trip, or the time distance of the moving object b from the observer
of the position vector of B and the velocity vector of b in S. It is t what is measured for the duration of the latter trip in S and in any other inertial frame. We shall refer to the universal time t as the time length, or time duration, of the latter light’s trip, or the time distance of the moving object b from the observer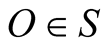 . We shall see that the time length t is generally different from the geometric length
. We shall see that the time length t is generally different from the geometric length 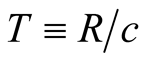 of the trip in S; they are equal however when the source of light is at rest in S.
of the trip in S; they are equal however when the source of light is at rest in S.
As equivalent sites of one physical world, S and s should quantify, employing their intrinsic units of length, the geometric distance 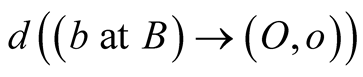 identically. This yields the intrinsic units of length and time in the two frames mapped on each other by the STI.
identically. This yields the intrinsic units of length and time in the two frames mapped on each other by the STI.
The STI is employed to explain the meta-stable particles’ lifetime phenomenon and the Doppler’s effect. It will be shown that while the relativistic longitudinal Doppler’s effect is identical to the prediction of the UST, the two theories are qualitatively distinct when it comes to the transverse Doppler effect. In a second part of this work we shall discuss the universal mechanics, which turns to be almost identical to relativistic mechanics. The direction of a light trip in the moving frame in terms of its direction in the stationary (or universal) one is determined in the third part of this work.
In coming works a second type of scaling transformation (STII) will be derived and applied to explain the drag effect, Sagnac effect, Michelson and Morley experiment, Michelson and Gale experiment.
2. Time Evaluation by Spatial Displacements—Global Time@NolistTemp# Consider an arbitrary inertial frame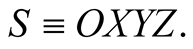 The coordinates system is assumed to be already calibrated using a given unit of length, say LS. The existence of the Cartesian system of coordinates OXYZ in S presupposes the geometry of the space is Euclidean [7] . The geometric distance between two points
The coordinates system is assumed to be already calibrated using a given unit of length, say LS. The existence of the Cartesian system of coordinates OXYZ in S presupposes the geometry of the space is Euclidean [7] . The geometric distance between two points 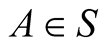 and
and 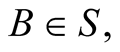 or geometric length of a rod AB stationary in S, refers to the result
or geometric length of a rod AB stationary in S, refers to the result 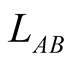 obtained by laying the unit of length LS in S along the rod repeatedly from one end till reaching the other by multiples and fractions of LS. This can be done rationally (or assumed to be already done) and takes no time. In other words, a coordinate system, and accordingly geometric distances in S are already given data. If
obtained by laying the unit of length LS in S along the rod repeatedly from one end till reaching the other by multiples and fractions of LS. This can be done rationally (or assumed to be already done) and takes no time. In other words, a coordinate system, and accordingly geometric distances in S are already given data. If  is the geometric distance of the point B from O, then the dimensionless quantity
is the geometric distance of the point B from O, then the dimensionless quantity  is the radial coordinate of B. The unit of time, though arbitrary, is chosen as the duration, say “second”, between two consecutive ticks (or readings) of identical clocks that run at synchrony with each other. Contemplating in the latter statement, we may be astounded by the fact that we really have defined nothing concerns the world outside the clocks. In order that a unit of time, say a second, bears a meaning as far as motion in S is concerned, it should be correlated to what can happen during “a second” in the world outside the clocks, and more precisely, it should quantify the amount of the spatial displacement intrinsic to some reference physical phenomenon, such as the propagation of light from an arbitrary point in S. A “second” must thus be corresponded with (and actually could be measured by) a certain distance traveled by light within (inside) S during a corresponding period. Time measurements therefore must be reducible to specific types of spatial displacement’s measurements.
is the radial coordinate of B. The unit of time, though arbitrary, is chosen as the duration, say “second”, between two consecutive ticks (or readings) of identical clocks that run at synchrony with each other. Contemplating in the latter statement, we may be astounded by the fact that we really have defined nothing concerns the world outside the clocks. In order that a unit of time, say a second, bears a meaning as far as motion in S is concerned, it should be correlated to what can happen during “a second” in the world outside the clocks, and more precisely, it should quantify the amount of the spatial displacement intrinsic to some reference physical phenomenon, such as the propagation of light from an arbitrary point in S. A “second” must thus be corresponded with (and actually could be measured by) a certain distance traveled by light within (inside) S during a corresponding period. Time measurements therefore must be reducible to specific types of spatial displacement’s measurements.The frame independent entity in the UST, namely “the time”, is defined in terms of spatial displacements and can be measured by length units, which implies that velocity is a dimensionless quantity. Indeed, global timing in an inertial frame S is set up by synchronization with an arbitrary observer 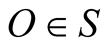 employing light’s signals. The concept of time emerges through envisaging a “linear” correspondence between each instant of time T read by the timer O and the compound event: (the wave front of the pulse that was emitted from O at
employing light’s signals. The concept of time emerges through envisaging a “linear” correspondence between each instant of time T read by the timer O and the compound event: (the wave front of the pulse that was emitted from O at 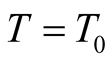 occupies at T, points at equal distances R from O). Through this correspondence, time duration
occupies at T, points at equal distances R from O). Through this correspondence, time duration 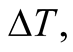 is essentially measured by distance R, i.e.
is essentially measured by distance R, i.e.
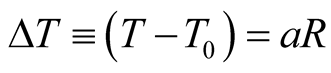 . (2.1)
. (2.1)
The proportionality constant defines a constant velocity c of light by 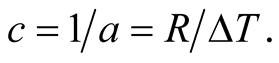 Because of the space is geometrically homogeneous (also physically, and in particular for the propagation of light), time durations defined in this way are independent of the master timer’s position O. The homogeneity of time follows also from the homogeneity of space. The above correspondence is only one step short of synchronization, which is achieved by each S observer at
Because of the space is geometrically homogeneous (also physically, and in particular for the propagation of light), time durations defined in this way are independent of the master timer’s position O. The homogeneity of time follows also from the homogeneity of space. The above correspondence is only one step short of synchronization, which is achieved by each S observer at 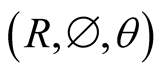 taking note of his distance
taking note of his distance 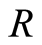 from O and the instant of time
from O and the instant of time 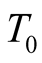 at which the pulse emanated from O, and thus setting his timer at
at which the pulse emanated from O, and thus setting his timer at 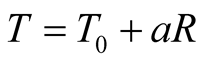 when he receives the pulse. By its way of construction, the global timing is unique up of course to an arbitrary choice of a time unit and of zeroing, i.e., up to a transformation of the form
when he receives the pulse. By its way of construction, the global timing is unique up of course to an arbitrary choice of a time unit and of zeroing, i.e., up to a transformation of the form 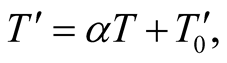 where
where 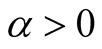 and
and 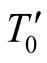 are arbitrary numbers. In UST the global time in S prevails in any other inertial frame s, and timers therefore, have to reflect the facts stated in setting up the global time. Thus every moving timer, if needed, must read the same instant of time read by the S-clock that is contiguous to it. This means, timers which are instruments whose readings is under our disposal, can be manipulated if needed, to conform with light propagation criterion.
are arbitrary numbers. In UST the global time in S prevails in any other inertial frame s, and timers therefore, have to reflect the facts stated in setting up the global time. Thus every moving timer, if needed, must read the same instant of time read by the S-clock that is contiguous to it. This means, timers which are instruments whose readings is under our disposal, can be manipulated if needed, to conform with light propagation criterion.
The 1-1 correspondence expressed by the relation , is additive and homogeneous only for
, is additive and homogeneous only for 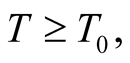 i.e., for
i.e., for 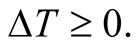 The mapping
The mapping 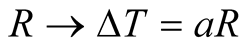 is not linear in the strict mathematical sense because it is defined only for
is not linear in the strict mathematical sense because it is defined only for 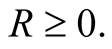 Time intervals in the past may be quantified by
Time intervals in the past may be quantified by 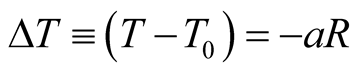 which should be understood as follows: Light that is received by O at
which should be understood as follows: Light that is received by O at  has already taken a duration
has already taken a duration  where R is the distance of its source from O. Thus the instant of time in the past at which light had emanated from a source at a distance R from O and arrived at O at
where R is the distance of its source from O. Thus the instant of time in the past at which light had emanated from a source at a distance R from O and arrived at O at 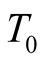 was
was
 (2.2)
(2.2)
The further the location of the event the deeper in the past it happened. All past events 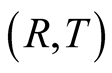 that satisfy the latter relation are detected by the observer O at the same instant
that satisfy the latter relation are detected by the observer O at the same instant 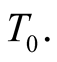 Out of the latter set, subsets which have the same R were simultaneous. If each event
Out of the latter set, subsets which have the same R were simultaneous. If each event 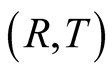 of the set that satisfy (2.2) continues to happen then the same set of events will all be detected at any later instant
of the set that satisfy (2.2) continues to happen then the same set of events will all be detected at any later instant 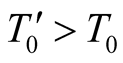 by O. Simultaneous events, corresponding to an instant T, are detected by O at instants
by O. Simultaneous events, corresponding to an instant T, are detected by O at instants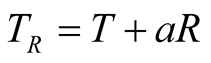 , that depend on R. The latter relation is true whether T refers to an instant in past, present, or future. Two events taking place at
, that depend on R. The latter relation is true whether T refers to an instant in past, present, or future. Two events taking place at 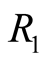 and
and 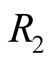 and detectable by O at
and detectable by O at 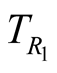 and
and 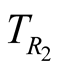 are simultaneous if
are simultaneous if 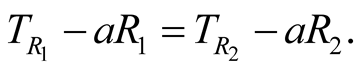
By the latter paragraph, it is justified to imagine a system of synchronized timing that supplements any system of coordinates in S. This means that, in the same way we envisage rationally the assignment of a triplet 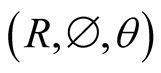 to each point B in S, we can also imagine that a timer can be placed at each point
to each point B in S, we can also imagine that a timer can be placed at each point 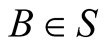 which is synchronized with
which is synchronized with 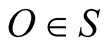 and runs uniformly at the same rate as the master timer, and accordingly at synchrony with all other timers. Thus a global timing in S can be practically established, with the notion of an “instant
and runs uniformly at the same rate as the master timer, and accordingly at synchrony with all other timers. Thus a global timing in S can be practically established, with the notion of an “instant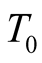 ” has a global meaning in S, in the sense that if an event takes place at
” has a global meaning in S, in the sense that if an event takes place at 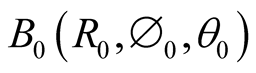 at
at 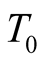 then it will be detected at
then it will be detected at  through a light signal emanating from
through a light signal emanating from 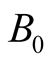 and arriving at B at the instant
and arriving at B at the instant 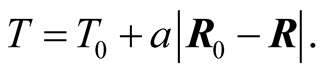 Thus every S observer B assigns to the event of light’s emission the same instant
Thus every S observer B assigns to the event of light’s emission the same instant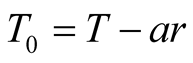 , where r is his spatial separation from
, where r is his spatial separation from 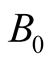 and T is the time read at the clock B when light is received. The concept of time arrow (past, present, and future) has therefore a global meaning in S, and any two or more S observers have the same temporal ordering of all events monitored by them. In particular, the notions of simultaneity and non-simultaneity are well-defined global concepts in S. An inertial frame S endowed with a global time as described above is called a timed (or synchronous) inertial frame. The UST theory maintains the global concepts of simultaneity and accordingly time arrow, as frame independent, or absolute.
and T is the time read at the clock B when light is received. The concept of time arrow (past, present, and future) has therefore a global meaning in S, and any two or more S observers have the same temporal ordering of all events monitored by them. In particular, the notions of simultaneity and non-simultaneity are well-defined global concepts in S. An inertial frame S endowed with a global time as described above is called a timed (or synchronous) inertial frame. The UST theory maintains the global concepts of simultaneity and accordingly time arrow, as frame independent, or absolute.
As far as one observer O is concerned, no synchronization in the real sense is to be done in order an inertial frame becomes timed. In fact, the existence of a coordinate system as well as a timer at O is sufficient to determine the duration of any light’s trip with given ends, whether O was one of the ends or not, provided the spatial coordinates (or radial distance) of each event is messaged instantly to O by a light signal. Also, the duration 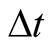 of any event at any point in S, say
of any event at any point in S, say 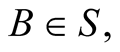 is observed form O to have the same duration. The arbitrary observer O, if he wishes, can replace his timer by a universal one [6] , since his own timer should be equivalent to the universal one. The latter legitimate replacement is applicable to any observer, and hence a universal timer will do for all observers in a coordinated frame S with finite extension.
is observed form O to have the same duration. The arbitrary observer O, if he wishes, can replace his timer by a universal one [6] , since his own timer should be equivalent to the universal one. The latter legitimate replacement is applicable to any observer, and hence a universal timer will do for all observers in a coordinated frame S with finite extension.
In Newton’s mechanics, time and geometric length are independent absolute entities [6] [8] , where distance is measured by a calibrated ruler, and Newton’s global time was assumed to be readable at each point of space. The synchrony of all point-wise timers was partially circumvented through appealing to a universal timer [6] formed by the fixed stars in the firmament, which generalizes the approximately uniform global time set up in the region from which almost all our observations are conducted, namely the earth surface.
Remarks
1) The common perception of a “second” as the duration between two consecutive ticks of a clock becomes identical to our previous conception only if we demand that light travels rectilinearly c meters between each two consecutive ticks. The latter definition conditions the clocks to conform to the reference criterion, which is light propagation. We have thus on one hand the measuring instruments, “the clocks” that can be synchronized and distributed (hypothetically) everywhere in the space, and on the other hand the happenings in the outside world, namely the distance that light travels during the period read by the clocks. Note that the clocks which are indeed indispensable for measuring time, are no more than instruments that can be manipulated to conform to the reference criterion, and their performance should certainly be rejected when they do not. Although only clocks can be used to measure time at one point, time read at various locations should be in accord with light propagation, and so should be each clock.
2) Employing synchronized clocks and a light signal, distance between two points in a timed inertial frame (called optical distance) can be measured and it is certainly equal to the geometric distance as measured by meters or seconds (=c meters), where no light signals and clocks are involved. We shall see however that this equality will be violated when the distance of a moving body from a stationary observer is considered.
3. The Reduced System of Units
Since time durations have to be defined in terms of spatial displacements, geometric lengths and time durations must have the same dimension; both are measured by the same unit. If the unit of time TS in S is defined as the duration taken by light to cross the unit of distance LS (a given rod stationary in S) from one end to another, say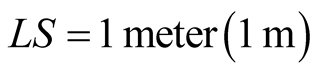 , we may designate the unit of time also by “meter”, to mean the time required by a light’s signal to cross this distance.
, we may designate the unit of time also by “meter”, to mean the time required by a light’s signal to cross this distance.
In terms of a system of units of time, length, and mass
 , (3.1)
, (3.1)
the dimensions of some mechanical observables are listed in the table:
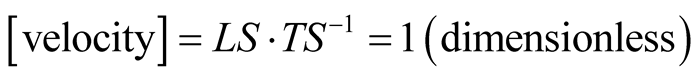
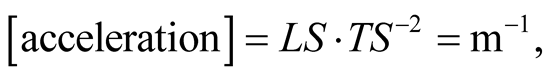
 ,
, 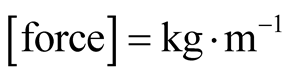

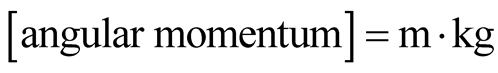 ,
, 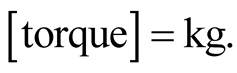
The velocity 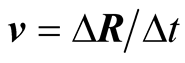 in RSUI is a dimensionless 3-vector, and the speed of light in vacuum is 1 regardless of the chosen unit of length
in RSUI is a dimensionless 3-vector, and the speed of light in vacuum is 1 regardless of the chosen unit of length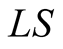 , provided we choose
, provided we choose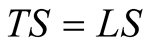 . Mass and energy have the same unit, “kilogram”. In practical applications however, it is convenient to take
. Mass and energy have the same unit, “kilogram”. In practical applications however, it is convenient to take  and adopt a multiple of the unit
and adopt a multiple of the unit 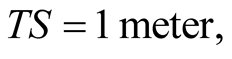 namely, “
namely, “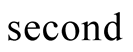 ”. The latter is defined by the period taken by light to travel a distance of
”. The latter is defined by the period taken by light to travel a distance of 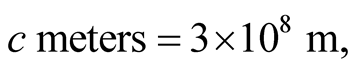 so that,
so that, 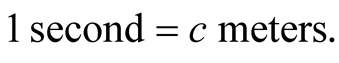 In the reduced system of units
In the reduced system of units
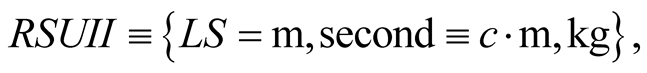 (3.2)
(3.2)
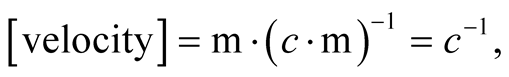
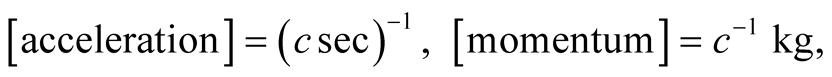
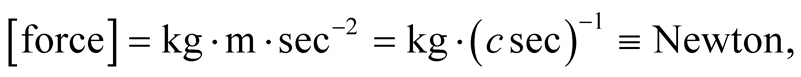
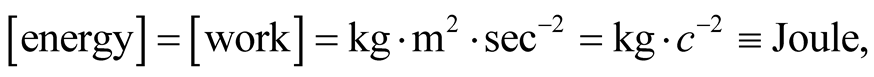
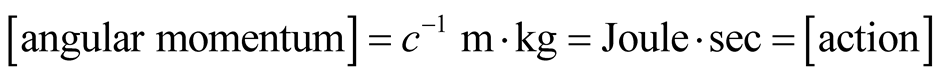

The reduced systems of units, I or II, suggest that observables which are measurable by the same unit are of the same nature, although they may manifest themselves in different facets. Mass and energy for instance are both scalar quantities and both are measurable in RSUI by kg. This means that 1 kg of mass is equal to 1 kg of energy, and that, under suitable circumstances either quantity may be transformed to the other. In the RSUII,
 and
and 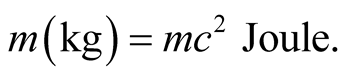
The latter relation holds for any type of energy.
If a vector observable 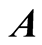 and a scalar observable B are of the same dimension then their squares,
and a scalar observable B are of the same dimension then their squares, 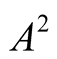 and
and 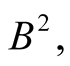 are of the same nature and in principle are transformable to each other.
are of the same nature and in principle are transformable to each other.
It is noted that the reduced system of units I and II are the system MKS with the unit of time is taken as the unit of length itself in RSUI, and defined in terms of the unit of length, with ![]() for RSUII. Symbolically,
for RSUII. Symbolically,
 and
and 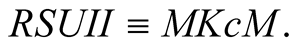
It is clear that time distance or just distance refer essentially to the same thing but using a different unit, which is “second” for the former and “meter” for the latter. The geometric distance between a source of light b that is moving in the timed inertial frame S and an observer 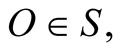 at an instant
at an instant![]() , is the distance between the position
, is the distance between the position 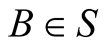 occupied by b at
occupied by b at ![]() and the observer O; it is
and the observer O; it is 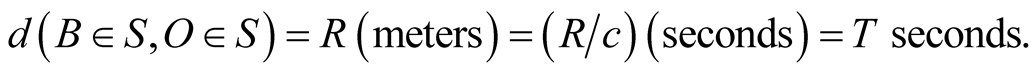 If b emits when at B a pulse of light that arrives
If b emits when at B a pulse of light that arrives 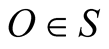 after t seconds, then its time distance (or optical distance) from O , at the emission instant, is
after t seconds, then its time distance (or optical distance) from O , at the emission instant, is 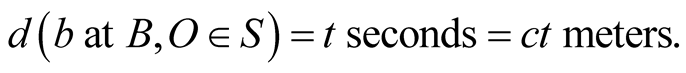 It is clear that the optical distance is identical to the geometric distance in the frame in which the source of light is stationary, otherwise (as we shall see) it is different in general.
It is clear that the optical distance is identical to the geometric distance in the frame in which the source of light is stationary, otherwise (as we shall see) it is different in general.
4. Pullbacks of Inertial Frames
In this section we adhere to the Newtonian absolute length and time, but we extend the traditional conception of inertial frames (IFs) beyond being triads of orthogonal axes translating uniformly with respect to one given inertial frame, or say, with respect to Newton’s absolute space.
A collection of objects all moving at the same velocity u relative to an IF 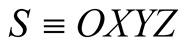 can serve as an IF
can serve as an IF ![]() when other objects’ motions are specified relative to s. This means that s employs 1) the system of intrinsic (or natural) units to measure physical observables and 2) a system of rectangular Cartesian coordinates oxyz to specify positions. Velocity of an object relative to s can always be measured locally as the ratio between the distance ds it travels in s and the corresponding duration dt. Indeed, time and distance in any inertial frame exist and are measurable with no need to endow the frame with a coordinate system. In Newtonian mechanics the set of all IFs partitions the physical world to classes of equivalence with two objects are equivalent if they have the same velocity relative to S, and thus are stationary in some IF.
when other objects’ motions are specified relative to s. This means that s employs 1) the system of intrinsic (or natural) units to measure physical observables and 2) a system of rectangular Cartesian coordinates oxyz to specify positions. Velocity of an object relative to s can always be measured locally as the ratio between the distance ds it travels in s and the corresponding duration dt. Indeed, time and distance in any inertial frame exist and are measurable with no need to endow the frame with a coordinate system. In Newtonian mechanics the set of all IFs partitions the physical world to classes of equivalence with two objects are equivalent if they have the same velocity relative to S, and thus are stationary in some IF.
Let 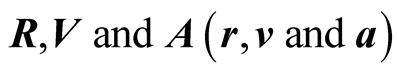 be the position, velocity and acceleration vectors of an object b in S (in s) respectively. In the traditional definition of an IF, the origin o of s is fixed once and for all to coincide with the origin
be the position, velocity and acceleration vectors of an object b in S (in s) respectively. In the traditional definition of an IF, the origin o of s is fixed once and for all to coincide with the origin 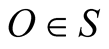 at some instant
at some instant 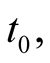 say
say 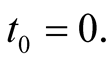 The position and velocity vectors of the object b are related by the Galilean transformations, while the acceleration is the same in both frames [8] -[10] .
The position and velocity vectors of the object b are related by the Galilean transformations, while the acceleration is the same in both frames [8] -[10] .
Pullbacks of an IF: Here the origin of s need not be fixed, but is chosen the s-point (or observer) which at each instant of time, starting from 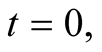 is contiguous to
is contiguous to 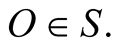 Along the latter choice, and if
Along the latter choice, and if 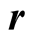 and
and 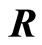 are the position vectors of an s-object relative to s and S respectively, then at each instant of time
are the position vectors of an s-object relative to s and S respectively, then at each instant of time 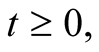 we have
we have
 (4.1)
(4.1)
and
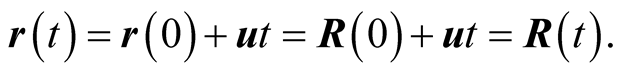 (4.2)
(4.2)
The frame s we have described will be denoted by 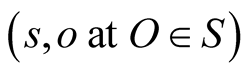 and called the s frame contiguous to the stationary frame S at O, or the pullback of s to
and called the s frame contiguous to the stationary frame S at O, or the pullback of s to 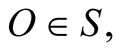 or briefly, the moving frame s. Whenever we talk of a moving inertial frame we shall mean its pullback to a given point in the stationary fame S, and usually,
or briefly, the moving frame s. Whenever we talk of a moving inertial frame we shall mean its pullback to a given point in the stationary fame S, and usually, 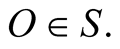 The derivative of the position vector of an s-object in both frames,
The derivative of the position vector of an s-object in both frames,
 (4.3)
(4.3)
is the velocity of s in S, and it is naturally the velocity of an s-object relative to S. Note that  is not the velocity of an s-object in s; for, the latter is zero. If an object b is moving in s at velocity
is not the velocity of an s-object in s; for, the latter is zero. If an object b is moving in s at velocity 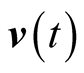 in s then
in s then
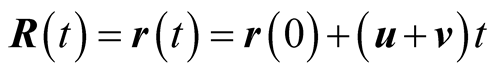 (4.4)
(4.4)
The velocity ![]() is measured locally in s in the sense mentioned earlier. The velocity of b in S is
is measured locally in s in the sense mentioned earlier. The velocity of b in S is
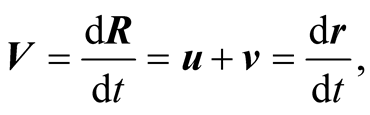 (4.5)
(4.5)
while its velocity ![]() in s is
in s is
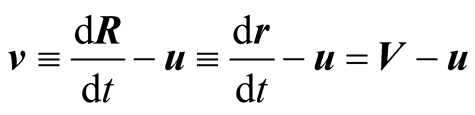 (4.6)
(4.6)
In particular the velocity of an s-object in s is  The acceleration, which is the same in both frames, is still the second derivative of the position vector,
The acceleration, which is the same in both frames, is still the second derivative of the position vector, 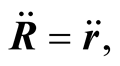 or
or 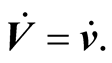
Parallel relations hold between s, when chosen stationary, and the pull back of the moving frame S to ![]()
A visual picture of a pullback frame is the following: A train s passes by a train station S with a specific pole on the pavement  is taken as the origin of S. It is decided to describe the motion in s with respect to the compartment
is taken as the origin of S. It is decided to describe the motion in s with respect to the compartment 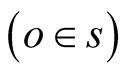 that is currently contiguous to the pole. At each instant of time there is a different compartment passing by the pole, and we may assume the compartments are as tiny as we please. The velocity of an object b in s can be measured relative to any compartment and in particular in the compartment in which b is moving. Although the position vector is the same in both frames, the velocity in
that is currently contiguous to the pole. At each instant of time there is a different compartment passing by the pole, and we may assume the compartments are as tiny as we please. The velocity of an object b in s can be measured relative to any compartment and in particular in the compartment in which b is moving. Although the position vector is the same in both frames, the velocity in  is not simply the time derivative of the position vector; but rather, the latter minus the velocity of s relative to S.
is not simply the time derivative of the position vector; but rather, the latter minus the velocity of s relative to S.
Along the spirit of the Newtonian rational mechanics and its associated concepts of space and time, the above picture ignores, in its Galilean and pullback forms, observations through light signals. However, and as it is shown in the next sections, light signals are inescapable for two basic reasons: 1) they enter in the very definition of the units of distance and time, and 2) all observations involve light signals.
5. Intrinsic Units
Physical entities have intrinsic characteristics that are independent of the IF at which it is realized. These characteristics are manifested in conception, specification, and quantification through measurements in the chosen IF employing given units. Examples of such entities are 1) The characteristics of the stationary emission of electromagnetic radiation of every element or compound. This includes, a priori, the wavelength of each spectral line.
2) The stationary mass of an atom at its ground state.
3) The rate of propagation of light with a particular wavelength. Since this rate is proven to be independent of the wavelength in one IF, it is also so in all IFs.
4) The elementary charge e.
A constituent basic block (or a block unit) of a physical observable is a specified entity by which any given amount of the physical observable can be numerically quantified in a unique manner. We seek here to define intrinsic units of length, time, mass, and charge such that they have the same identity in all IFs. For lucidity we temporarily restrict structuring the intrinsic units to an arbitrary inertial frame S, and thus we omit the index S which is supposed to distinguish these units.
The first step is to determine the constituent basic blocks for such units:
1) The block unit of the geometric distance, or length, is the wavelength of a specific spectral line of the stationary emission of some chemical element chosen and adhered to in all frames. We denote this entity by 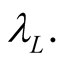
2) Due to the fact that a unit of distance can be used to measure time we may adopt 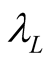 as the block unit of time in S. Or we may rely on clocks to measure time, and thus define the constituent block of time
as the block unit of time in S. Or we may rely on clocks to measure time, and thus define the constituent block of time 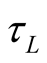 in S by
in S by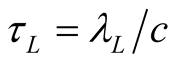 . One can start with the block unit of time
. One can start with the block unit of time 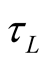 (employing valid clocks) and define the constituent block of length by
(employing valid clocks) and define the constituent block of length by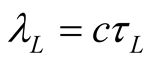 .
.
3) The constituent block of mass is the mass of a stationary 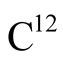 atom at its ground state.
atom at its ground state.
4) The constituent block of charge is the fundamental charge e.
The constituent blocks, which are all in the microcosm, are not practical for direct use. The second step thus is to choose prudently a fixed multiple of the constituent block to define the corresponding unit. Digital quantification of such units by the same number of basic constituent blocks provides intrinsic units with the same meaning and value within every IF.
1). The unit of geometric length or distance, the meter (m), is the length of a certain number 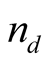 of the specific wavelength of the specific spectral line of the chosen chemical element; it is given in S by
of the specific wavelength of the specific spectral line of the chosen chemical element; it is given in S by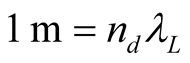 .
.
2) To define the unit of time, the second (s), we resort to the fact that the duration T of the propagation of a light signal is proportional to the distance R it travels, 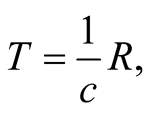 and define
and define 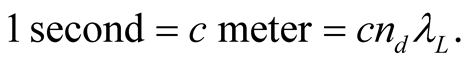 We may write the latter relation as
We may write the latter relation as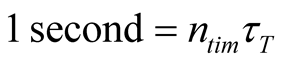 , where
, where 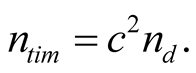 If we choose the second as the unit of length and time then
If we choose the second as the unit of length and time then 
 and
and 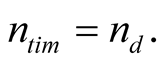
3) The unit of charge, the Coulomb (C), is the charge of a certain number 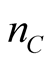 of the elementary charge e,
of the elementary charge e,
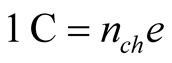 .
.
4) The unit of mass, the kilogram (kg), is a certain number  of the constituent basic block of mass,
of the constituent basic block of mass,
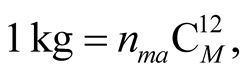 where
where 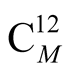 is the mass of the
is the mass of the 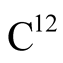 atom at its ground state.
atom at its ground state.
Owing to their definitions, and to the equivalence of inertial frames as sites for describing one physical world, all basic physical blocks in one frame, as well as the intrinsic units derived from them, have the same privilege enjoyed by their corresponding basic blocks in another frame. We shall see however that if s is an IF moving with respect to the IF, S, then units of length, time, and mass in s are not units in S. Explicitly and if we label these units by the frame in which they are set up then the result of measuring these quantities in one frame, say S, will yield in general, 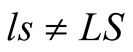 and
and 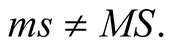 Equivalently,
Equivalently,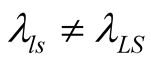 . and
. and .
.
Employing intrinsic units in all IFs, which are equivalent sites for observing one physical world, quantifies physical facts identically in all IFs. The results of any experiment in an IF would be identical to it in any other IF frame provided both experiments are carried out in the same conditions. Moreover, any relation predicting the outcomes of an experiment in one frame, named a law, equally holds in any other inertial frame, and it is valid in one frame to the same degree of its validity in another. It follows that the transformation from an inertial frame to another should map intrinsic units in one frame onto intrinsic units in another. This will result in particular in universal (frame independent) time distances, and in invariant geometric distances, in the sense that, in each frame the geometric length of a light trip is read the same using however the frame’s intrinsic units of length.
6. The Universal Space
Consider the set of all inertial frames. It is clear what is meant by a frame being at motion with respect to another, but the concept of a frame being at rest needs elaboration. To be meaningful, the latter concept requires the existence of an independent entity with respect to which the state of being at rest is referred. This entity corresponds to the space when referred to a frame set up by a force-free observer (i.e. far from matter, or instead at the center of mass of a closed system of objects) that is not rotating relative to the fixed stars. Any given frame S defined by the latter statement is an inertial frame that can be identified by Newton’s absolute space and considered stationary, while the motion of all other inertial frames, or equivalently, the motion of all material objects, are then referred to this “universal frame”. By its definition, there exists only one universal frame at a time.
Since the state of being stationary through identification with the frame of fixed stars can be assigned to any inertial frame (one at a time), the absolute or physical space in its Newtonian sense as the standard of rest has to be abandoned. However, the role of the absolute space in Newtonian sense as a unique standard of rotations, as well as its role in Maxwellian sense as the carrier of electromagnetic radiation, are retained as it will be explained in the sequel.
The spatial site of all material objects, as far as their positions are concerned, enjoys an identity that is independent of the inertial frame by which it is identified (equation (4.1)); it will be called the universal space (We emphasize that we employ in this theory the pullbacks of IFs). The latter fact is manifested in the absoluteness (frame-independence) of the light’s path between any two points in the space. However, the state of motion of material objects depends of course of the choice of the stationary, or universal, frame.
Each member of a set of IFs that have no common measurements can be considered stationary. However, when we compare the results of the same experiment (observation) in different IFs, only one frame can be considered stationary while the other frames are moving.
Absolute Light Trips—Aether’s Role of the Universal Space
If a source of light b has an arbitrary vector velocity ![]() relative to the inertial frame
relative to the inertial frame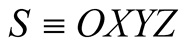 , we may choose without loss of generality the velocity vector in the direction of the X-axis, for we may always rotate the S-axes so that the X-axis is in the direction of
, we may choose without loss of generality the velocity vector in the direction of the X-axis, for we may always rotate the S-axes so that the X-axis is in the direction of 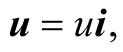 where
where  is the unit vector of the X-axis. Let
is the unit vector of the X-axis. Let ![]() be an inertial frame whose axes are parallel to those of S and moving with respect to S at a constant velocity
be an inertial frame whose axes are parallel to those of S and moving with respect to S at a constant velocity 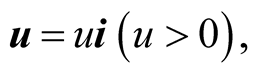 so that the source b is stationary in s. We endow the frames S and s with systems of spherical coordinates
so that the source b is stationary in s. We endow the frames S and s with systems of spherical coordinates  and
and 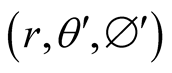 respectively, with
respectively, with 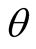
 is the azimuth angle between the X-axis (x-axis) and the radius vector
is the azimuth angle between the X-axis (x-axis) and the radius vector 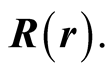 The latitude angles
The latitude angles 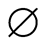 and
and 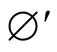 will be suppressed because of the axial symmetry of the motion about the X-axis (figure 1).
will be suppressed because of the axial symmetry of the motion about the X-axis (figure 1).
Assume that the source of light b which is stationary at the point 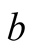 in s emits, when at
in s emits, when at 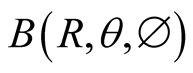 in S, a spherical pulse of light. When light arrives at O, it arrives also to an s-observer whom we choose an origin o of
in S, a spherical pulse of light. When light arrives at O, it arrives also to an s-observer whom we choose an origin o of 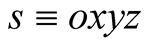 with axes parallel to those of S. Two S and s observers who are contiguous when hit by the pulse are called conjugate observers. Similarly, two sources, each emitting a pulse of light when contiguous, are called conjugate sources.
with axes parallel to those of S. Two S and s observers who are contiguous when hit by the pulse are called conjugate observers. Similarly, two sources, each emitting a pulse of light when contiguous, are called conjugate sources.
The situation we have displayed has the following features:
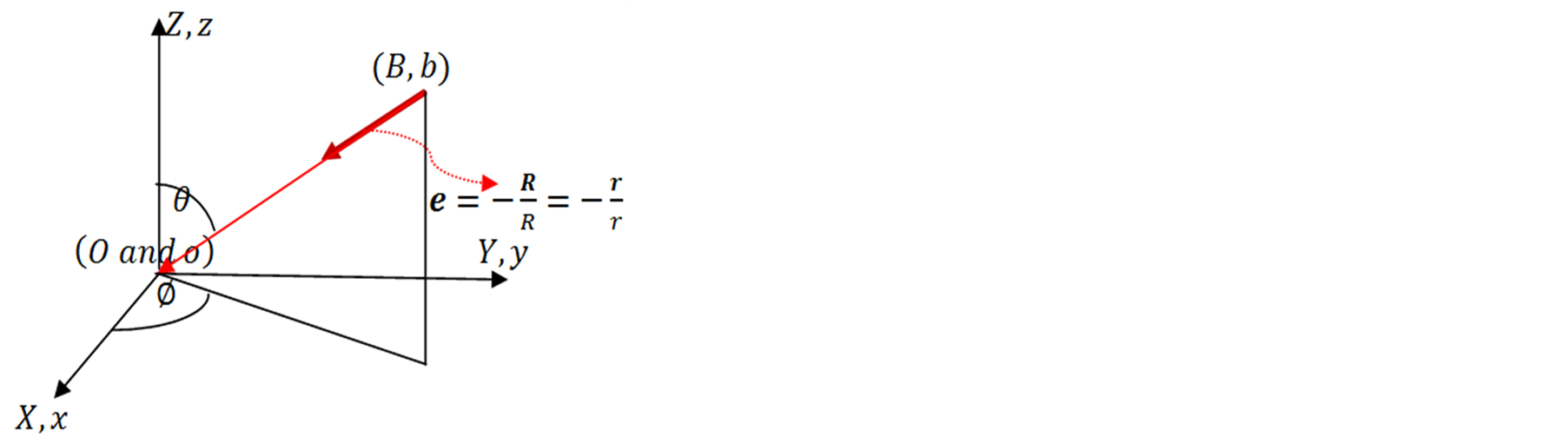
Figure 1. The path of light trip 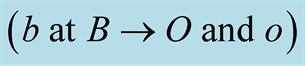 in the universal space whether identified by S or by s.
in the universal space whether identified by S or by s.
1) In a given inertial frame S, a source of light b is moving at a velocity![]() . Or equivalently, in the inertial frame s in which the source is stationary, an inertial observer O attached to a frame S, is moving at velocity
. Or equivalently, in the inertial frame s in which the source is stationary, an inertial observer O attached to a frame S, is moving at velocity 
2) Light is emitted from b when at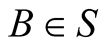 .
.
3) On arriving at 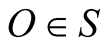 light arrives at the conjugate observer
light arrives at the conjugate observer![]() . While O is already given, o emerges at the instant light arrives at O; it is the s-observer that is contiguous to
. While O is already given, o emerges at the instant light arrives at O; it is the s-observer that is contiguous to 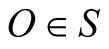 when the pulse hits O (and hence o). But we may equally imagine that when light arrives at
when the pulse hits O (and hence o). But we may equally imagine that when light arrives at ![]() it also arrives at
it also arrives at  and thus
and thus ![]() is already known while
is already known while 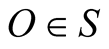 is fixed when light arrives at o.
is fixed when light arrives at o.
The frame S can be considered at rest throughout the light’s trip which starts from (B when occupied by the source b) and ends up at (O and o), while b is moving at velocity 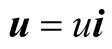 in S. Also the s frame can be claimed the stationary frame during the duration of the trip which starts from the point (b when is at B) and ends up at (o and O), while S is moving at velocity
in S. Also the s frame can be claimed the stationary frame during the duration of the trip which starts from the point (b when is at B) and ends up at (o and O), while S is moving at velocity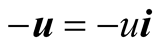 . Since each frame is entitled to claim itself stationary, and thus identifiable with the universal space, while the other is moving, all observers (the S and s observers) accept that light emanated “at the same time” from one and the “same point” in the universal space, whether identified by S or s, and ended at the same time at the same point.
. Since each frame is entitled to claim itself stationary, and thus identifiable with the universal space, while the other is moving, all observers (the S and s observers) accept that light emanated “at the same time” from one and the “same point” in the universal space, whether identified by S or s, and ended at the same time at the same point.
To elaborate, the phrase ( when at
when at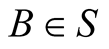 ) defines in each frame a pair composed of a location and an instant of time, or what we shall call a universal point, and denote by (
) defines in each frame a pair composed of a location and an instant of time, or what we shall call a universal point, and denote by ( at
at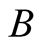 ). Thus a true source of light gives rise to a universal point, which is a frame independent entity that embodies the same instant of time in both frames together with an Sand s-locations that are coincident in the universal space at the instant of contiguity of b and B in a sense which we shall explain (we have already seen that
). Thus a true source of light gives rise to a universal point, which is a frame independent entity that embodies the same instant of time in both frames together with an Sand s-locations that are coincident in the universal space at the instant of contiguity of b and B in a sense which we shall explain (we have already seen that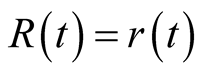 ). Similarly the end point of the pulse in one frame determines a conjugate end in the other frame, and accordingly, another universal point. It follows that all observers concede to the fact that there is one and the same trajectory in the universal space associated with a given light’s trip, which starts from (
). Similarly the end point of the pulse in one frame determines a conjugate end in the other frame, and accordingly, another universal point. It follows that all observers concede to the fact that there is one and the same trajectory in the universal space associated with a given light’s trip, which starts from (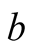 at
at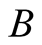 ) and ends at (
) and ends at (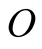 and
and![]() ). In other words, the pulse traces a universal straight path connecting the universal points (b at B) and (O and o), whether S or s is considered stationary and identified by the universal space.
). In other words, the pulse traces a universal straight path connecting the universal points (b at B) and (O and o), whether S or s is considered stationary and identified by the universal space.
Direct consequences of the latter statements are the following:
1) If  are the directional angles of the path in S when considered stationary and
are the directional angles of the path in S when considered stationary and 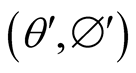 are its directional angles in s when s is considered stationary, then
are its directional angles in s when s is considered stationary, then
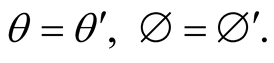 (6.1)
(6.1)
The velocity of the source does not appear in the latter relations. This implies that, had source b was replaced by a source  with another velocity
with another velocity 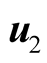 then
then 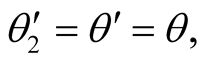
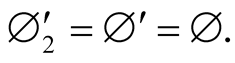
2) The latter result is contained in a more general consequence: The light’s trip possesses universal characters concerning its optical length and direction. This means that associated with a given trip, whose beginning 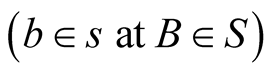 and end
and end 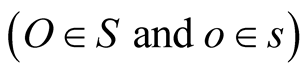 are known, there are one time duration t (optical length ct) and one universal direction in the universal space which can be identified by S or s. The time distance
are known, there are one time duration t (optical length ct) and one universal direction in the universal space which can be identified by S or s. The time distance 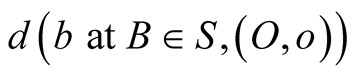 depends on the state of motion of b (i.e. velocity of s relative to S), and hence it is a function
depends on the state of motion of b (i.e. velocity of s relative to S), and hence it is a function  of the position vector of B and the velocity vector of b in S.
of the position vector of B and the velocity vector of b in S.
In a future work we shall determine the direction of the light trip inside the moving frame in terms of its direction in the stationary one.
3) If the universal space is identified with the aether then every inertial frame may be pulled back to coincide with aether, and the Stokes hypothesis of complete drag of the aether by inertial frames [11] is altered to the pullback of the inertial frame so that the moving frame can be considered stationary and identified with the universal space. The aether however, is redundant in the formulation of UST.
7. The Anisotropic Scaling Transformations
Let b be a source of light moving in an inertial frame 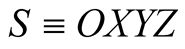 at a constant velocity
at a constant velocity 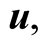 with the X-axis of S is taken along
with the X-axis of S is taken along 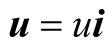
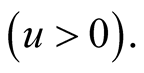 Let s be an inertial frame which is moving relative to S at a constant velocity
Let s be an inertial frame which is moving relative to S at a constant velocity 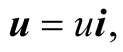 and hence the light’s source b is stationary in s. Now, we set out to determine the transformations which allows for each frame, S or s, to be considered stationary while the other is moving.
and hence the light’s source b is stationary in s. Now, we set out to determine the transformations which allows for each frame, S or s, to be considered stationary while the other is moving.
Assume that when at 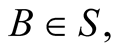 the source b emits a pulse of light. On arriving at the point (or observer)
the source b emits a pulse of light. On arriving at the point (or observer) , the pulse arrives also at its s-conjugate point (or observer)
, the pulse arrives also at its s-conjugate point (or observer) 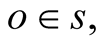 which is contiguous to
which is contiguous to 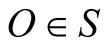 at the moment the pulse hits O (or when the pulse arrives at
at the moment the pulse hits O (or when the pulse arrives at ![]() it also arrives at its S-conjugate
it also arrives at its S-conjugate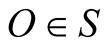 ). We choose now the axes of s such that
). We choose now the axes of s such that 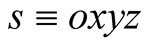 are in standard configuration with
are in standard configuration with . Each of the conjugate observers O and o is entitled to consider his frame stationary relative to the fixed stars and thus identifiable with the universal space while the other frame is moving relative to his own frame. Each observer, O and o, assigns to the pulse’s path the same beginning
. Each of the conjugate observers O and o is entitled to consider his frame stationary relative to the fixed stars and thus identifiable with the universal space while the other frame is moving relative to his own frame. Each observer, O and o, assigns to the pulse’s path the same beginning  and the same end
and the same end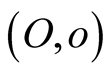 . In other words the pulse follows a universal path connecting the universal points
. In other words the pulse follows a universal path connecting the universal points  and
and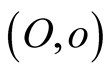 , and the direction of the path is the same when looked at from the stationary frame whether it was S or s. In each frame, when considered stationary, the pulse propagates along a direction determined by a unit vector
, and the direction of the path is the same when looked at from the stationary frame whether it was S or s. In each frame, when considered stationary, the pulse propagates along a direction determined by a unit vector![]() , where
, where
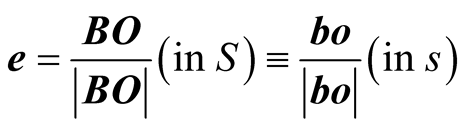 (7.1)
(7.1)
If S is chosen as the stationary frame, then the geometric length 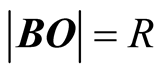 of the trip
of the trip 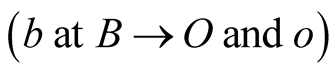 in S is employed to induce corresponding length
in S is employed to induce corresponding length 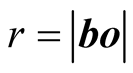 and duration
and duration 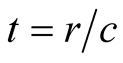 in s such that r and t have the status of geometric length and time in s when s is the stationary frame, in the same way R and T have in S.
in s such that r and t have the status of geometric length and time in s when s is the stationary frame, in the same way R and T have in S.
By the Galilean law of velocity addition, the velocity of the pulse in S is the vector sum of its velocity in s and the velocity ![]() of its emitter. However the pulse emanating from
of its emitter. However the pulse emanating from 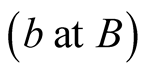 and arriving at O should had been ejected in a direction
and arriving at O should had been ejected in a direction 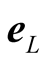 in S (figure 2) such that the resultant velocity
in S (figure 2) such that the resultant velocity 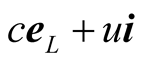 is along the unit vector
is along the unit vector![]() . The duration
. The duration  taken by the pulse to arrive at o (and hence O) is given by the quotient of its displacement vector
taken by the pulse to arrive at o (and hence O) is given by the quotient of its displacement vector 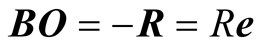 and its velocity
and its velocity 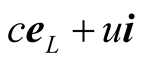 in S, i.e.
in S, i.e.
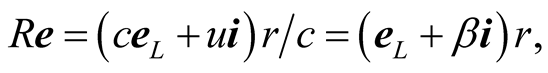 (7.2)
(7.2)
where  Thus the geometric length R of the trip in S, has given rise to the optical length
Thus the geometric length R of the trip in S, has given rise to the optical length 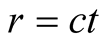 of the trip in S. The length r can be looked on as the geometric length of the trip in s because b is stationary in s, and r therefore must induce for a source B an optical distance
of the trip in S. The length r can be looked on as the geometric length of the trip in s because b is stationary in s, and r therefore must induce for a source B an optical distance 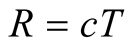 in s which should be identical to its geometric distance R in S. Since B is moving in s at velocity
in s which should be identical to its geometric distance R in S. Since B is moving in s at velocity , the velocity in s of the pulse that emanates from the virtual source B is the sum of its velocity in S and the velocity
, the velocity in s of the pulse that emanates from the virtual source B is the sum of its velocity in S and the velocity 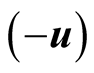 of its emitter. The pulse emanating from B should have then been ejected in a direction
of its emitter. The pulse emanating from B should have then been ejected in a direction 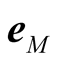 in s (figure 2) such that the resultant velocity
in s (figure 2) such that the resultant velocity 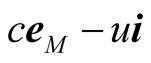 is along
is along ![]() The duration
The duration  taken by the pulse to arrive at O (and hence o) is given by the quotient of the displacement
taken by the pulse to arrive at O (and hence o) is given by the quotient of the displacement 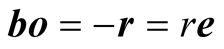 of the pulse as seen in s and its velocity
of the pulse as seen in s and its velocity 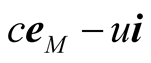 in s, i.e.
in s, i.e.
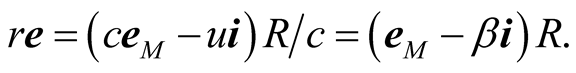 (7.3)
(7.3)
Whether b or B was the source, we start only with one quantity, R if S is the stationary frame, or r if s is the stationary frame (but not both), which is already geometrically measured whereas the other quantity is induced in the other frame by the relations (7.2) and (7.3). It follows that it is sufficient to know the ratio 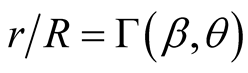 to determine both quantities, regardless of which had been measured geometrically, or equivalently, which frame was considered stationary.
to determine both quantities, regardless of which had been measured geometrically, or equivalently, which frame was considered stationary.
Dividing the equations (7.2) and (7.3) side to side we obtain
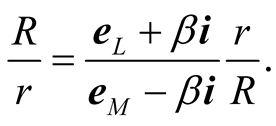 (7.4)
(7.4)
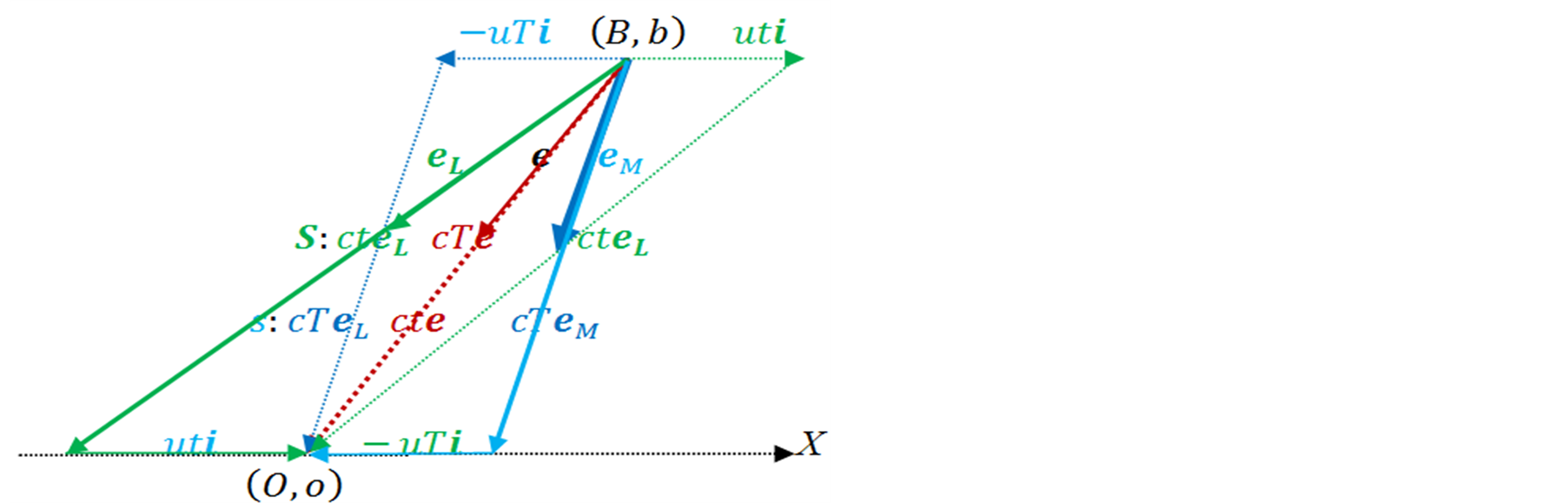
Figure 2. The views of S and s in green and blue respectively.
Or
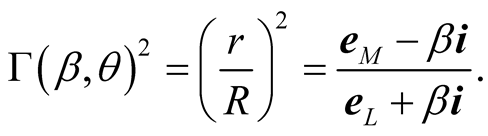 (7.5)
(7.5)
By equations (7.2) and (7.3) the vectors appearing in the numerator and dominator on the right hand-side of the last equation are both along![]() . Setting
. Setting
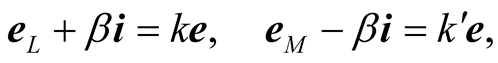 (7.6)
(7.6)
we get
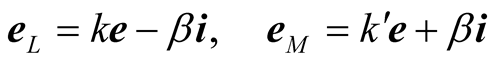 . (7.7)
. (7.7)
Taking the norms of both sides in each equation (7.7) we get
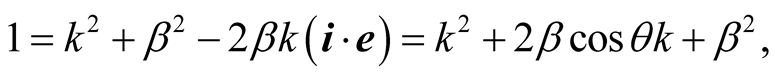
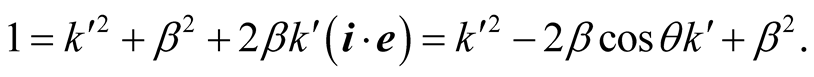
Solving for k and 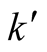 we obtain
we obtain
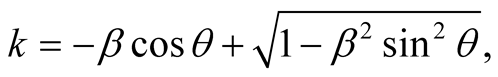
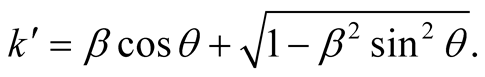
Dividing the latter equations side to side gives
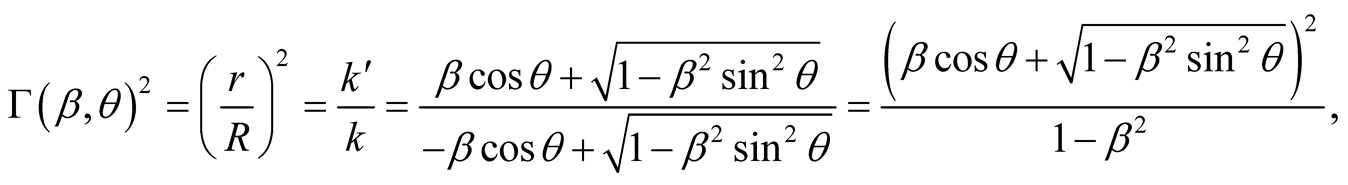
which yields the scaling factor 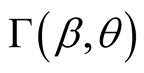 given by
given by
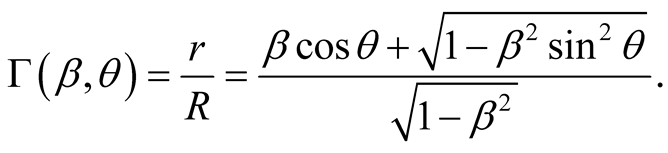 (7.8)
(7.8)
The scaling transformations of the first type (STI) are therefore
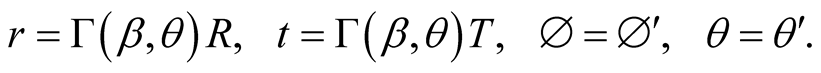 (7.9a)
(7.9a)
These can be written in terms of the angle 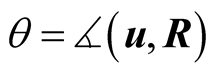 between the velocity of the source b in S and the radius vector as follows:
between the velocity of the source b in S and the radius vector as follows:
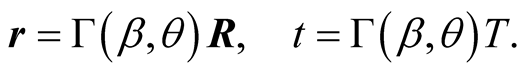 (7.9b)
(7.9b)
Other forms that hold for arbitrary relative orientations of axes of S and s are the following:
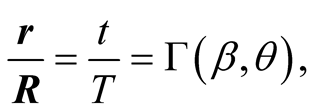 (7.9c)
(7.9c)
 (7.9d)
(7.9d)
supplemented by 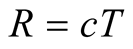 and
and 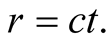
Intercepting a Moving Body by a Light’s Signal
Assume that an instant 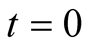 which corresponds to
which corresponds to 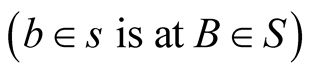 and
and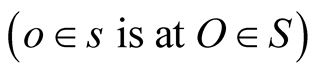 , a spherical pulse emanates from the observer
, a spherical pulse emanates from the observer 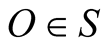 that intercepts the moving object b at a position
that intercepts the moving object b at a position 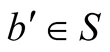 at an instant t. If the geometric distance
at an instant t. If the geometric distance 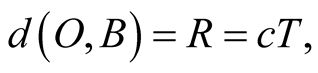 then the pulse arrives at B at an instant T. The trips
then the pulse arrives at B at an instant T. The trips
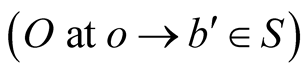 and
and  are viewed in s as
are viewed in s as 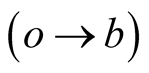 and
and 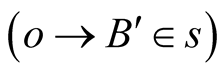 respectively
respectively
(figure 3). In the frame S, the vector sum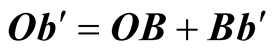 , or
, or 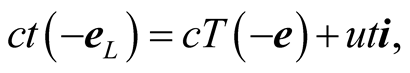 can be written as
can be written as
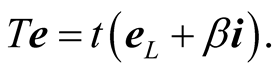 (7.10)
(7.10)
When the frame s is the stationary frame, the vector sum 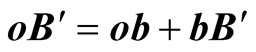 gives
gives
 (7.11)
(7.11)
From the latter two equations we have
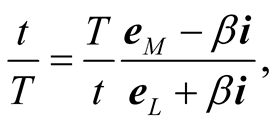 (7.12)
(7.12)
which is the same equation (7.5), and hence the relation between t and T is given again by (7.9).
Note that if the right-hand sides of (7.10) and (7.11) are multiplied with a common factor a, equation (7.12) is again obtained, but the two sides connected at the moving source will change in length in the triangle  The factor a will be determined in part 2 such that each triangle is Euclidian.
The factor a will be determined in part 2 such that each triangle is Euclidian.
Being universal, the time lengths t and T are the same in S and s, with t (T) is equal to the geometric time distance between o and b (between O and B) in s (in S).
Let S be the universal frame, and assume that at the same instant of time  which corresponds to
which corresponds to  two pulses of light are emitted from b and O simultaneously. It follows from the latter identical scaling transformations that the pulse emitted from O arrives at b (which occupies now
two pulses of light are emitted from b and O simultaneously. It follows from the latter identical scaling transformations that the pulse emitted from O arrives at b (which occupies now ) at the time of arrival of the pulse emitted from (b at B) at O.
) at the time of arrival of the pulse emitted from (b at B) at O.
The latter result is a direct consequence of the symmetry of the relationships between the source and observer in the universal space. The symmetries of the scaling transformations will have a systematic study in future works.

Figure 3. The light trips 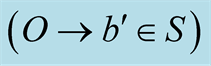 and
and 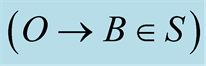 are viewed in s as
are viewed in s as 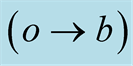 and
and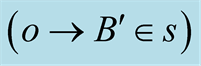 .
.
8. Basic Properties of the Scaling Factor and the STI
It is easily seen that
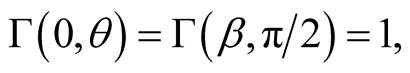 (8.1)
(8.1)
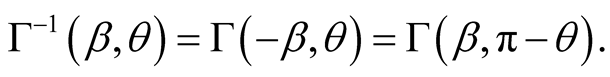 (8.2)
(8.2)
It follows from (8.1) that  only when
only when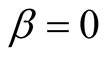 , or
, or 
Since
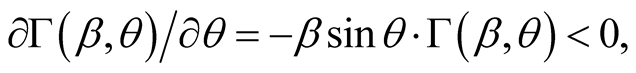 (8.3)
(8.3)
the function 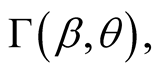 with
with 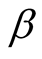 is fixed and positive, is a monotonically decreasing with
is fixed and positive, is a monotonically decreasing with 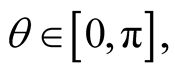 and
and
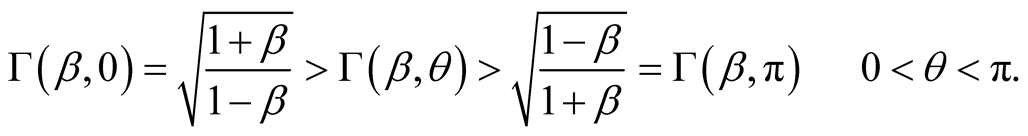 (8.4)
(8.4)
Also, and because
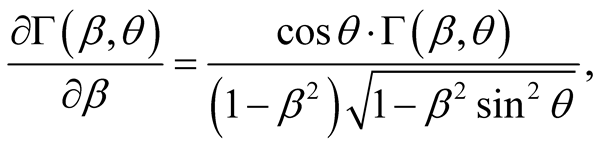 (8.5)
(8.5)
the function 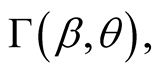 for a fixed value of
for a fixed value of 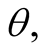 increases with
increases with 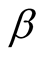 if
if 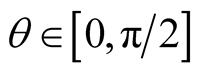 (receding source) and decreases with
(receding source) and decreases with  if
if 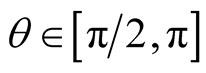 (approaching source).
(approaching source).
By its way of derivation, the STI hold 1) Between the geometric lengths R in S and r in s (the passive view), but yet the time length of a light trip is same in S and s, i.e. it is universal.
2) In the stationary frame (the active view) between the universal and geometric time lengths of a light trip  whether b (when S is stationary) or B (when s is stationary) was the source of light.
whether b (when S is stationary) or B (when s is stationary) was the source of light.
9. Viewing the Light Trip in the Universal Space—The Passive View
The STI allow for the identification of the universal space with either frame S or s, and determine the relations between the characteristics of any light trip in S when stationary and its characteristics in s when stationary. It is valid whether b or B was the true source. If b was the true source of light, then T (t) is its geometric (universal) time distance from O in S. And since the source is stationary in s, t is also its geometric time distance from o in s. If B is the true source then t (T) is its geometric (universal) time distance from o in s, and T is also its geometric time distance from O in S. In any case, the universal duration of the light’s trip, which coincides with the geometric duration in the frame in which the source is stationary, is the same in both frames. The latter fact follows from Section 2 and from the freedom of identifying the universal space with S or s. With the S and s-observers measuring the same time length of each light trip, whether its source was in S or in s, time flaws, in accordance with Section 2, equably in S and s.
As equivalent sites of one physical world, S and s should quantify, employing their intrinsic units of length, the geometric distance 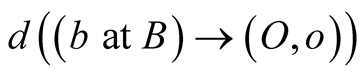 identically, i.e.,
identically, i.e., 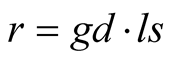 and
and 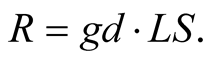 Now, by the STI (7.9)
Now, by the STI (7.9)
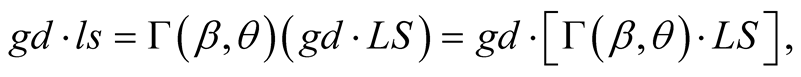 (9.1)
(9.1)
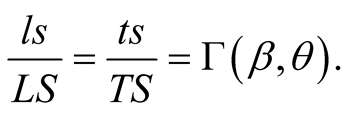 (9.2)
(9.2)
(A parallel relation to (9.1) holds for geometric time: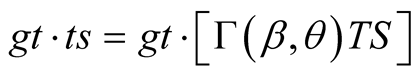 ). It is clear that
). It is clear that
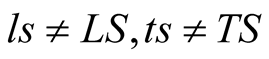 unless
unless 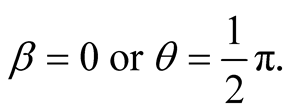
Because the time length of a trip is universal, then
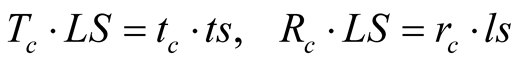 (9.3)
(9.3)
where 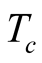 (
(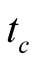 ) are what is read for the time length of the trip in S when stationary (in s when stationary) respectively. By (9.2)
) are what is read for the time length of the trip in S when stationary (in s when stationary) respectively. By (9.2)
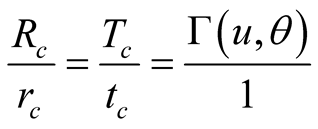 . (9.4)
. (9.4)
According to the latter relations the observed characters in S are simply the S-equivalents (means: using S intrinsic units) of the corresponding observed characters in s, and vice versa.
10. The Doppler Effect
Let s be an inertial frame that is moving relative to S at velocity , and arrange for a stationary source of light b in s to radiate monochromatic light of a characteristic wavelength
, and arrange for a stationary source of light b in s to radiate monochromatic light of a characteristic wavelength 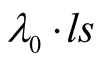 where ls is the unit of length in s. When observed from S, the wavelength of this light is equal to the S equivalent of
where ls is the unit of length in s. When observed from S, the wavelength of this light is equal to the S equivalent of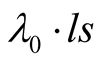 :
:
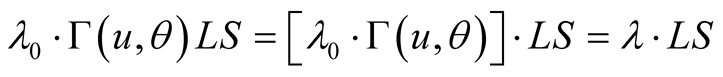 (10.1)
(10.1)
Therefore the wavelength as observed in S is
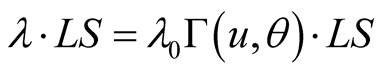 (10.2)
(10.2)
Note that the characteristic wavelength of the same monochromatic light when emitted from an S-source is 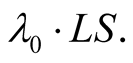 Equation (10.2) shows that
Equation (10.2) shows that
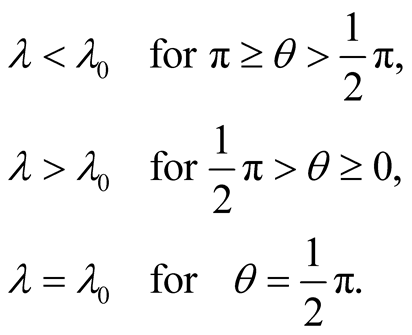 (10.3)
(10.3)
These correspond to the light’s source approaching the observer in the first case, receding from him in the second, and moving at right angle to the position vector of the body in the third.
We compare here the quantitative Doppler’s effect as determined by the UST
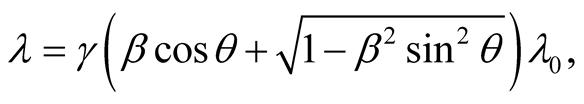 (10.4)
(10.4)
with the relativistic formula [10]
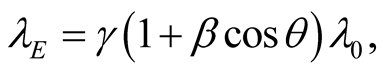 (10.5)
(10.5)
where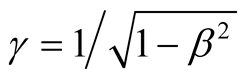 , and
, and 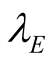 is the wavelength as predicted in special relativity. The predictions of the two theories coincides for longitudinal motion,
is the wavelength as predicted in special relativity. The predictions of the two theories coincides for longitudinal motion,
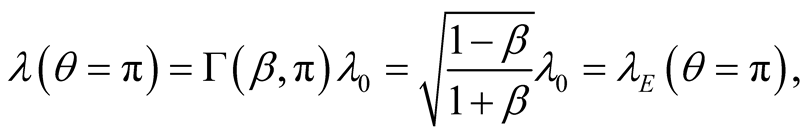 (10.6a)
(10.6a)
 (10.6b)
(10.6b)
The predictions of the two theories become qualitatively distinct for 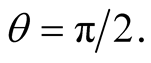 In this case the relativistic formula (10.5) predicts a red shift given by
In this case the relativistic formula (10.5) predicts a red shift given by
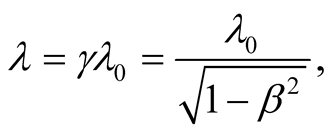 (10.7)
(10.7)
whereas the relation (11.4) reduces to
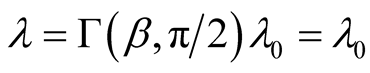 , (10.8)
, (10.8)
which contrary to the relativistic prediction, shows that there is no traverse Doppler’s effect (at right angle).
The predictions of UST are in excellent agreement with the results of the Ives-Stilwell experiment [12] -[14] . To specify the goal of the experiment, we denote the wavelengths associated with approaching and receding sources by  and
and 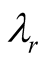 respectively. The Ives-Stilwell experiment was designed to measure the shift [10] [12] -[14]
respectively. The Ives-Stilwell experiment was designed to measure the shift [10] [12] -[14]
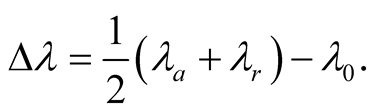 (10.9)
(10.9)
In the relativistic theory
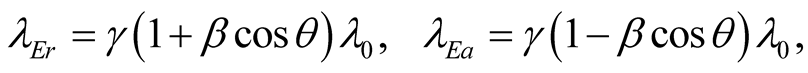 (10.10)
(10.10)
and the shift in wave length is
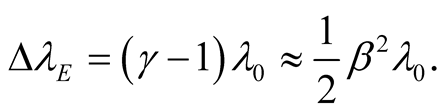 (10.11)
(10.11)
In the UST theory
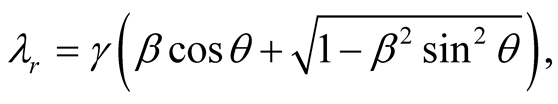 (10.12)
(10.12)
 (10.13)
(10.13)
and the wavelength shift is
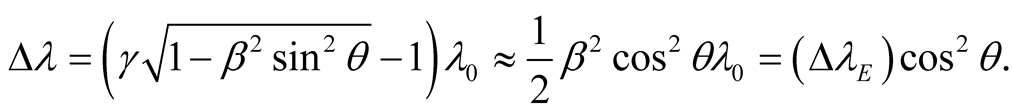 (10.14)
(10.14)
The latter relation shows that the UST predicts in general a smaller shift than the relativistic one, and the two prediction coincide for  or
or . In Ives-Stilwell’s experiment a small mirror is set at an angle
. In Ives-Stilwell’s experiment a small mirror is set at an angle 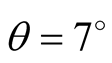 with the ions velocity to reflect the radiation emitted backwards. As (10.14) shows, the relativistic prediction should be scaled by a factor
with the ions velocity to reflect the radiation emitted backwards. As (10.14) shows, the relativistic prediction should be scaled by a factor 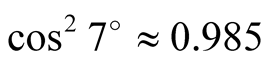 producing accordingly a smaller shift, and the predicted shifts by the UST theory can be closer to the experimental observations only when the observed shifts are less than the relativistic predictions.
producing accordingly a smaller shift, and the predicted shifts by the UST theory can be closer to the experimental observations only when the observed shifts are less than the relativistic predictions.
The following table 1 displays some of the predictions of the special theory of relativity and the UST together with the observed shift in Ives and Stilwell experiment, all measured in angstrom.
11. The Active View in Interpreting the STI
In the active view, (7.9) is considered a transformation in the universal frame, say S, between the time length of
Table 1 . The transverse Doppler’s effect as measured experimentally (first column) and predicted theoretically byrelativity and the UST (second and third columns).
the given light’s trip and its geometric length. Equivalently, the STI determines the ratio between the duration of the true light trip  and the geometric time length of the light’s trip
and the geometric time length of the light’s trip 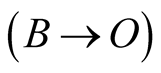 (call it the geometric trip) whether B was a true or a virtual source. If B and b were light sources, then (7.9) gives the relation between the time lengths of the corresponding light trips to O.
(call it the geometric trip) whether B was a true or a virtual source. If B and b were light sources, then (7.9) gives the relation between the time lengths of the corresponding light trips to O.
Alternatively, the transformations (7.9) hold within the universal frame s, with B is a true source while b can be a true or a virtual source. Here, T and t are the universal and geometric time lengths respectively. The expression of the universal time length in terms of the geometric length is obtained from (7.9) just by interchanging t and T and replacing 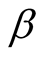 by
by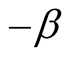 :
:
 (11.1)
(11.1)
which is (7.9) itself.
When a pulse of light that is emitted from (b at B) arrives at O the source b occupies a position 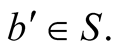 The triangle
The triangle 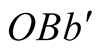 formed from the initial and final positions of the light’s source in S together with the observer
formed from the initial and final positions of the light’s source in S together with the observer 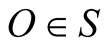 is called the body-observer triangle. We have shown that if two pulses emanate simultaneously from b when at B and from O then when the former hits O (following the path
is called the body-observer triangle. We have shown that if two pulses emanate simultaneously from b when at B and from O then when the former hits O (following the path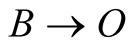 ), the latter intercepts b at
), the latter intercepts b at 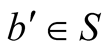 (following the path
(following the path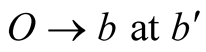 ). We shall see in the second part of this work [15] that the sides of the body-observer triangle (figure 4) are
). We shall see in the second part of this work [15] that the sides of the body-observer triangle (figure 4) are
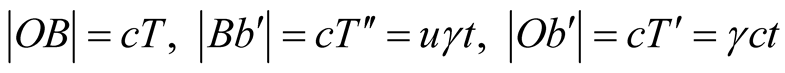 (11.2)
(11.2)
Lifetime of Meta Stable Particles
The 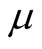 -meson particles [16] are generated at an altitude of
-meson particles [16] are generated at an altitude of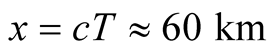 , or equivalently,
, or equivalently, 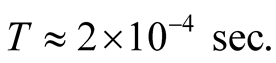 Their lifetime is
Their lifetime is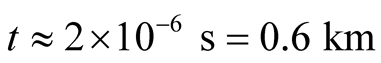 , and their velocity v is close to that of light. Equations (11.2) insure that these particles reach the earth surface provided
, and their velocity v is close to that of light. Equations (11.2) insure that these particles reach the earth surface provided 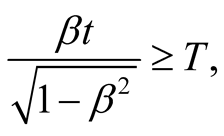 which yields
which yields 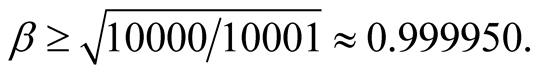
12. Conclusions
It was shown that the concept of time was consistent with motion if time and geometric length are of the same dimension, and thus essentially measurable by the same unit. Duration of time is corresponded with the time length of a certain light trip whether measured by length or time units. The resulting reduced system of units leads naturally to the well-known mass-energy equivalence formula. Adopting the intrinsic system of units is essential for a meaningful comparison between measurements in different IFs. When comparing measurements in various IFs only one frame can be chosen stationary while the other frames are moving. Based on the equivalence of the IFs as sites for one physical world, one must demand that the correspondence between geometric lengths of light trips and intervals of time (discussed in Section 2), should hold whatever is the site frame of the trip. This leads to time flowing equably in all inertial frames. The STI which allows for each frame to be

Figure 4. The body-observer triangle.
identifiable with the physical space relates the geometric lengths of the same light trip in both frames and maps intrinsic units in one frame onto intrinsic units in another. The STI was applied to explain the Doppler’s effect and the lifetime of meta-stable particles phenomenon. The quantitative predicted Doppler’s effect, which is in a striking agreement with the Ives-Stilwell experimental results, coincides with the relativistic prediction for longitudinal motion, but yet predicts complete absence of a transverse effect. Stellar aberration which is based on the deflection of the direction of a given trip in the moving frame from its direction in the stationary one will be submitted promptly.
In future works we will complete the theory and explain elaborately the drag effect, the null results of Michelson and Morley experiment, Michelson and Gale experiment, the Sagnac effect, and the translative Sagnac effect. It will also be shown that the mechanics produced by UST is identical to the relativistic mechanics.
References
- Viazminsky, C.P. and Vizminiska, P. (2014) On Universal Mechanics and Superluminal Velocities in ST. General Science Journal.
- Viazminsky, C.P. and Vizminiska, P. (2013) Digital Natural Units. General Science Journal.
- Viazminsky, C.P. and Vizminiska, P. (2012) On the Concept of Time and the Reduced System of Units. General Science Journal.
- Viazminsky, C.P. and Vizminiska, P. (2012) Inertial and Universal Velocities in the Scaling Theory. General Science Journal.
- Viazminsky, C.P. and Vizminiska, P. (2011) Observation of Motion through Light Signals.
- Viazminsky, C.P. and Vizminiska, P. (2010) The Scaling Theory—XII: Universal Timer. The Zeroth Law of Motion.
- Pfahler, E.L. (1964) Riemannian Geometry. Princeton University Press, Princeton.
- Steve, A. (1997) Relativity, an Introduction to Space-Time Physics. Taylor and Francis Ltd, London.
- Rindler, W. (2006) Essential Relativity. Springr-Verlag, Berlin.
- French, A.P. (1968) Special Relativity. Butler & Tanner Ltd., Frome and London.
- http://en.wikipedia.org/wiki/Aether_drag_hypothesis
- Faraj, A.A. (2005) The Ives-Stilwell Experiment. The General Science Journal.
- Ives, E.H. and Stilwell, G.R. (1938) An Experimental Study of the Rate of a Moving Clock. Journal of the Optical Society of America, 28, 215-226. http://dx.doi.org/10.1364/JOSA.28.000215
- Ives, H.E. and Stilwell, G.R. (1941) An Experimental Study of the Rate of a Moving Atomic Clock. II. Journal of the Optical Society of America, 31, 369-374. http://dx.doi.org/10.1364/JOSA.31.000369
- Viazminsky, C.P. and Vizminiska, P.K. (2014) On Universal Mechanics and Superluminal Velocities. Applied Mathematics (Submitted).
- http://en.wikipedia.org/wiki/Muon


