Applied Mathematics
Vol.06 No.06(2015), Article ID:56919,12 pages
10.4236/am.2015.66092
The Validity Analysis of Regression: Combining Uniform Experiment Design with Nonlinear Regression
Nan Yang1,2*, Dawei Zhang1, Yanling Tian1
1School of Mechanical Engineering, Tianjin University, Tianjin, China
2Tianjin Key Laboratory of the Design and Intelligent Control of the Advanced Mechatronical System, School of Mechanical Engineering, Tianjin University of Technology, Tianjin, China
Email: *y79nzw@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 March 2015; accepted 2 June 2015; published 5 June 2015
ABSTRACT
The data topology structure of uniform experiment design (UD) is too complex to be reasonable regressed. In this paper, the principle and method of distinguish the training data and testing data were described to make a reasonable regression when uniform experiment design combined with support vector regression (SVR). Two equivalent ways which were the smallest enclosing hypersphere perceptron (SEH) and the enclosing simplex perceptron (ES) were provided to discover the topology relationship of the process parameter datum. To give an application, a series of experiments about laser cladding layer quality were conducted by UD to get the relationship of load, velocity and wearing capacity. Results showed that only the testing datum recommended by the two perceptrons got a good forecasting by SVR. Therefore, the two perceptrons could guide experiments with process parameter data of complex topology structure. Further, the application could be extended over a much wider field of experiments.
Keywords:
Uniform Experiment Design, Support Vector Machine, The Smallest Enclosing Hyper Sphere, The Enclosing Simplex

1. Introduction
Many researches focus on experimental design combining with nonlinear regression. The experiment design method includes uniform design, central composite experimental design and Taguchi’s approach; the nonlinear regression method includes artificial neural network, support vector machine and so on. Some focus on the experimental design optimizing the nonlinear regression parameters; others focus on the nonlinear regression optimizing the experimental design to get the best process parameters under the desired results.
Yanwei Li et al. [1] used uniform design optimized support vector machine to be an experimental guide to find macrocyclic compounds which were used to detect and minimize the radiocesium pollution. Weihong Li et al. [2] proposed a multi-objective uniform design search method as a SVM model selection tool, and applied this optimized SVM classifier to face recognition. Xiaolin Yu [3] used uniform design and least support vector machines method for reliability analysis of large complex structures. Guangya Zhang [4] used support vector machine to develop the non-linear quantitative structure-property relationship model of the G/11 xylanase based on the amino acid composition, and used the uniform design to optimize the running parameters of SVM. Ni L.J. [5] improved v-support vector machines method to build classification models for discriminating adulteration milks based on near infrared spectra of different sample sets, and used uniform design table to find good value of parameters of v and sigma. Xiaolin Yu et al. [6] proposed the reliability analysis method based on uniform design method and supported vector machine to get the failure probability. A joint optimization method is proposed by Changsheng Xiang et al. [7] for phase space reconstruction and least square support vector machine parameters. The phase space reconstruction and least squares support vector machine parameters are jointly designed using uniform design. Wang Zhi-ming et al. [8] developed a small-scale search method based on uniform design using support vector regression. Chuang S.C. et al. [9] realized that one found many non-rectangular types of input domains on which traditional UD methods could not be adequately applied when conducting a typical computer experiment, and proposed a new UD method that was suitable for design area. Pan Jinshui et al. [10] investigated the possibility of optimizing mammalian cells transfection efficiency by using a method referred to as least-squares support vector machine, which required only a few experiments based on UD to maintain fairly high accuracy. Xiao Wang et al. [11] used the central composite rotatable experimental design combining with the artificial neural network (ANN) to establish the relationships among the laser power, velocity, clamp pressure, joint strength, and joint width. 30 experiments were conducted based on four factors five-level design. Yuwen Sun et al. [12] , focused on the influence of laser power, scanning speed and powder feed rate on the shape factor and the cladding bead geometry (layer width, layer height and molten depth) with regard to injecting Ti6Al4V powder on TC4 substrate. Response surface methodology was used to build the mathematical model. Dongxia Yang et al. [13] , carefully selected the laser welding parameters of laser power, welding speed and wire feed rate to produce a weld joint with the minimum weld bead width and the fusion zone area. Taguchi approach was used as a statistical design of experimental technique for optimizing the parameters. They found that the effect of welding parameters on the welding quality decreased in the order of welding speed, wire feed rate, and laser power. They also found the optimal combination of welding parameters. H. Beygi et al. [14] , fabricated Ni coated aluminum nanoparticles by electroless nickel deposition. Effect of two groups of parameters on the process plating rate were investigated: bath composition (main salt, reducing agent and complexing agent concentration) and process parameters (pH, plating time and bath temperature). Simulation of the process was performed using ANN. It was based on the ANN model to design a high efficiency electroless bath, while minimum received materials were used and maximum plating rate was obtained. Wang Zhifei et al. [15] proposed an optimization design scheme based on orthogonal testing and support vector machines to get relationships between each parameter and product quality features. Orthogonal testing design was used to estimate the appropriate initial value and variation domain of each variable to decrease the number of iterations and improve the identification accuracy and efficiency.
However, an important step has been neglected in existing research, which is the regression validity. The searching point might go out of the experimental domain, which is not obvious to know. So the searching point will find a bad forecasting value on the regression surface, particularly when the process parameters arranged by the experimental design have complex topology boundary, for example the uniform design.
In this paper, we choose a case of uniform design combining with support vector machine to proposed two perceptrons to determine the parameters topology boundary (distinguish training data and testing data). And then an experimental datum set of wear behavior of laser cladding layer is studied to show the function of the two perceptrons.
2. Principle
The process parameter vector should be inside the domain of the experiment, if not, the forecasting is not reasonable because of data absence. For example, in Figure 1(a)), 10 experiment data are regressed by SVR (horizontal axis is process parameter, and vertical axis is the target), the curve goes horizontally towards a constant value outside the experiment domain, which is exactly the constant b of the pattern function of SVR (Equation (9)). For two-dimension case, in Figure 1(b)), the SVR surface gives good forecast only above the parameter 1- parameter 2 plane where the experimental data exist, whereas SVR surface keeps constant in other place.
Should the forecasting value always be constant outside the experiment data space because we do not do the experiment? Certainly, no. So, the SVR forecasts well within the experiment data space, while it could not forecast the outside of the experiment data space.
The forecasting is false outside the experiment domain by SVR. The curve/surface goes horizontally towards a constant value (which is the constant b (Equation (9)) of the pattern function of SVR) outside the experiment domain and causes a false forecasting.
Although distinguishing the inside and outside of the experiment data space is easy in one-dimension (only one parameter in Figure 1), the task in higher dimension (two or above) is not so easy. Therefore, the method for higher dimension is elaborated below.
2.1. The Task: Distinguishing the Training Data and Testing Data
In this paper, the task is to distinguish the training data and the testing data among lots of experimental data when the experiment is conducted by UD. The key point is whether the testing data lie inside the training data domain or not, because the function of regression is generated by the training data. So, if the testing data lie outside the training data domain, the regression is not reasonable because of data insufficiency.
Two equivalent perceptrons are provided to discover this topology relationship in higher dimension of parameter space. They are the smallest enclosing hypersphere (SEH) perceptron and the enclosing simplex (ES) perceptron.
2.1.1. The SEH Perceptron
The SEH in a feature space defined by a kernel k enclosing a dataset  is computed by finding
is computed by finding  as solution of the optimization problem:
as solution of the optimization problem:
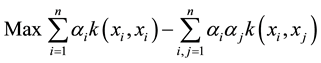 (1)
(1)

Figure 1. The diagrammatic sketch of outside and inside of the experiment data space. (a) One-dimension; (b) Two-dimen- sion.
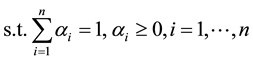 (2)
(2)
The pattern function is:
 (3)
(3)
where:
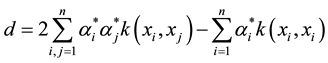 (4)
(4)
And k is a radical base kernel:
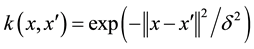 (5)
(5)
where  is Gauss parameter. So, calculate Equation (3), if
is Gauss parameter. So, calculate Equation (3), if , then x lies inside the SEH, if
, then x lies inside the SEH, if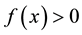 , then x lies outside the SEH, specially, x lies on the SEH edge with
, then x lies outside the SEH, specially, x lies on the SEH edge with . The SEH is not a “pure round sphere” shape; it can adapt the data “shape” automatically.
. The SEH is not a “pure round sphere” shape; it can adapt the data “shape” automatically.
2.1.2. The ES Perceptron
Another simple method could judge whether a point lies inside or outside a point set. A point inside the specimen point set should be enclosed in the simplex consisted of n closest points. In s dimension space, n equals to s + 1. For example, in 2D space, an internal point should be enclosed by the 3 closest points (for example, in Figure 2, point 18 is enclosed by point 8, 11, 13), while an external one do not (for example, point 17 is not in the triangle of the 3 closest points 2, 4, 7).
Generally, in s dimension space, there are s + 2 determinants about a point 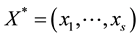 and its s + 1 closest points:
and its s + 1 closest points: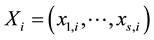 ,
,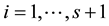 :
:
Figure 2. The 16 load-velocity 2D points based on UD, point 17 and 18 represent new process data; point 18 is enclosed by the 3 closest points (point 8, 11, 13), so it lies inside the point set, but point 17 is not enclosed by its 3 closest points (point 2, 4, 7), so it lies outside.

If



The distance L between two points 

2.1.3. Comparison of the Two Perceptron
The ES perceptron includes distance calculation, reorder, and determinant calculation, while the SEH perceptron iterates depend on 3 artificial parameters (
2.2. Regression of SVR
Considering a training dataset:
Choosing parameter 


With the optimization solution


where

SVR could get a nonlinear regression function g(x) based on a training dataset without artificial judgment of the function power ahead of time. And the training dataset is recommended by the SEH or ES perceptron.
3. Experiment
UD was proposed by Wang Yuan and Fang Kaitai [16] , which is an efficient way to reduce the experiment times. The experiment time is related to the parameter levels instead of the factors (dimensions of parameters). But the regression analysis needs complex method, not similar to orthogonal experiment whose data distribution boundary is in good order. So, before regression analysis, the data distribution region should be found firstly. Further, UD is used to arrange process parameters where exist two kinds of data: training data and testing data. Training data are used for regression by SVR, while testing data are used to test the generalization of the regression function. The SEH or ES perceptron is used to distinguish the testing data from the training data among all the process parameters.
A laser cladding layer quality forecasting experiment is conducted for a clear view of the principle. We coat the Ni-based alloy on the CrMo in order to develop the resistance to wear of the substrate material via laser cladding process. The experiment task is to get wearing capacity under the variety of the combinations of the load (the pressure to the material) and the loading velocity (the velocity of moving the material). So, in this experiment, we have two experimental factors (process parameters): load and velocity, and the experimental target is wearing capacity.
The levels number of the load and velocity could be given as any natural number you want, and it means that you should do much more experiments if the levels number is higher. When the experiment factors and levels are determined, the experiment could be arranged by UD table and its application table which could be known in Ref. [16] .
Here, the levels are given as 16, so, it means that we need only 16 experiments (orthogonal experiment needs 162 = 256 experiments). The levels of the load and velocity are respect 1 - 16 Mpa and 0.24 - 3.87 m/s. The combination of the two parameters and corresponding experimental results are listed in Table 1.
4. Results and Discussion
The wearing capacity varies with different load and velocity, so the regression aim is to obtain the function: wearing capacity = f (load, velocity). But it is troublesome that the domain is not in good order. If the testing data we choose lie outside of the domain, the testing data is invalid. Here, we use the SEH or ES perceptron to judge whether the testing data lie inside the domain or not.
Firstly, the process parameters are normalization. The corresponding nondimensional quantities are shown in Table 2, which are arranged by unitary processing blow.

Table 1. The processing parameters (load and velocity) and experimental results (wearing capacity) based on UD.
Table 2. The nondimensional processing parameters and experimental results.
where p is given process parameter, pmin and pmax are the minimum and maximum of p, and u is the unitary processing result. The 16 load-velocity 2D points are shown in Figure 2, where 17 and 18 represent new experiments which will be discussed later.
The strategies described in this paper have been implemented in Delphi package, and the artificial parameters for SEH are given as: δ2 = 0.5, iteration step length = 0.01, iterations = 100000. There are no artificial parameters for ES.
4.1. The SEH Perceptron
If the training data and testing data are chosen randomly (among the 16 points), the testing data might lie outside the training data, so the regression analysis is invalid. For example, if point 15 (an edge point)is chosen as the testing data and the remain as the training data, it is found that point 15 lies outside the training data, and this could be felt by the SEH perceptron, as shown in Figure 3. Point 15 could not get an effective forecasting value, because the curve surface collapses without any support data.
However, if an internal point is chosen as the testing data, the situation will be changed. As shown in Figure 4, point 11 is an internal point, so, it is circled in the SEH. The forecasting result is also good, the 3D point is almost on the surface which is regressed by point 1 to 16 not include 11, the error between the forecasting value and the testing value is small as shown in Table 3. Furthermore, the surface regressed by point 1 to 16 (the regression error is shown in Table 4) agrees perfectly with the surface regressed by point 1 to 16 excluding point 11 in Figure 5(a), that is to say point 11 don’t affect the regression surface. The contour of regression surface is shown in Figure 5(b), from which we can see that a low velocity with a high load or a high velocity with a low load may cause a low wear capacity.
If a point at the edge of the training data which is also in the SEH is chosen as a testing datum, the forecasting result will be just as good as shown in Figure 6 and Table 5. For example, point 7, the forecasting value agrees with the testing value very well. The testing errors are bigger than training errors because the training data are still sparse, so, this could be improved by increasing the number of experiments. Further, the measured value of wearing capacity even varies under the same experimental parameters.

Figure 3. Point 15 is chosen as testing datum and the rest are training data, so the SVR is fail to forecast point 15 via 3D regression surface. (a) Point 15 lies outside the SHE; (b) Point 15 is far away from the 3D regression surface.

Figure 4. Point 11 is chosen as a testing datum and the rest are training data, so the SVR forecasts point 11 via 3D regression surface successfully. (a) Point 11 lies inside the SHE; (b) Point 11 agrees with the regression surface.
When point i is a testing datum and others (exclude i) are training data, the forecasting value is compared with experimental value in Table 6. If point i is a vertex (labeled with “*”) of the points set, it has a large error; while if point i is an internal point, it agrees with the experiment well. Therefore, the SEH perceptron could make sure whether a process parameter vector is fitted for being a testing datum or not. It is important to point out the limitation of SEH that the domain which encloses the training data is not the minimum, and this could be solved by the ES perceptron.
Table 3. The comparison of the regressive value and experimental value, 11 is testing datum while the rest are training data.
Table 4. The comparison of the regressive value and experimental value, all points are training data.

Figure 5. The meshed surface is regressed by point 1-16, while the unmeshed one is regressed by point 1-16 except 11. The two surfaces agree with each other very well. The minimum of wearing capacity could be found from the contour map. (a) The regression surface; (b) Contour map of the regression surface.
Figure 6. Successful forecasting of point 7. Point 7 is an edge point but also inside the SEH, so, it could be well forecasted.
4.2. The ES Perceptron
If point 5 is chosen as a testing datum, the three closest points are 3, 8, 10, (Figure 2) and then calculate the determinants:
Table 5. The comparison of the regressive value and experimental value, 7 is testing datum while the rest are training data.
Table 6. The forecasting value with testing datum i, and the rest which exclude i are training data.
*Vertex of the specimen parameter points set.


If a point lies outside the domain slightly, ES will found this, while SEH won’t. So, the domain determined by ES is smaller than SEH.
5. Conclusions
The important contribution of this paper is to answer such a question: why and how to distinguish the training data and testing data when uniform experiment design combined with nonlinear regression.
In this paper, two equivalent perceptrons which are the SEH perceptron and the ES perceptron are proposed to discover the topology boundary of the process parameter vectors and to distinguish training data and testing data. The distinguishing procedure is to determine if a testing datum lies inside the training datum domain. To give an application, experiments about laser cladding layer quality forecasting are conducted to prove if it is better that SEH or ES combines with SVR. The forecasting values of the testing data recommended by the two perceptrons are compared with their experimental values which are conducted based on uniform design. Results show that only the testing data recommended by the two perceptrons get a good forecasting by SVR, and the domain determined by ES is smaller than SEH.
So, the two perceptrons could guide experiments with process parameter data of complex topology structure. Further, not restricted to the experiment in this paper, the application could be extended over a wider field of experiments.
Acknowledgements
This work was supported by China Post-doctoral Foundation No. 2012M520572, Tianjin Municipal Education Commission Grant No.20120401, and Tianjin Municipal Science and Technology Commission Key Grant No. 14JCZDJC39500.
Table 7. Testing data recommended by the ES perceptron.
*Represents the order number of new experiment.
*Corresponding author.
None.
References
- Li, Y.W., Su, L., Zhang, X.Y., Huang, X.Y. and Zhai, H.L. (2011) Prediction of Association Constants of Cesium Chelates Based on Uniform Design Optimized Support Vector Machine. Chemometrics and Intelligent Laboratory Systems, 105, 106-113. http://dx.doi.org/10.1016/j.chemolab.2010.11.005
- Li, W.H., Liu, L.J. and Gong, W.G. (2011) Multi-Objective Uniform Design as a SVM Model Selection Tool for Face Recognition. Expert Systems with Applications, 38, 6689-6695. http://dx.doi.org/10.1016/j.eswa.2010.11.066
- Yu, X.L., Zheng, H.B., Yan, Q.S. and Li, W. (2011) A Least Square Support Vector Machine Approach Based on Uniform Design Method for Structural Reliability Analysis. Advanced Materials Research, 163-167, 3348-3353. http://dx.doi.org/10.4028/www.scientific.net/AMR.163-167.3348
- Zhang, G.Y. and Ge, H.H. (2012) Prediction of Xylanase Optimal Temperature by Support Vector Regression. Electronic Journal of Biotechnology, 15. http://dx.doi.org/10.2225/vol15-issue1-fulltext-8
- Ni, L.J., Zhang, L.G., Tang, M.Y., Xue, Z.B., Zhang, X., Gu, X. and Huang, S.X. (2012) Discrimination of Adulteration Cow Milk by Improved v-Support Vector Machines and near Infrared Spectroscopy. 2012 8th International Conference on Natural Computation, Chongqing, 29-31 May 2012, 69-73. http://dx.doi.org/10.1109/ICNC.2012.6234508
- Yu, X.L. and Yan, Q.S. (2011) Reliability Analysis of Self-Anchored Suspension Bridge by Improved Response Surface Method. Applied Mechanics and Materials, 90-93, 869-873. http://dx.doi.org/10.4028/www.scientific.net/AMM.90-93.869
- Xiang, C.S., Yuan, Z.M. and Zhou, Z.Y. (2011) Parameters Joint Optimization of Chaotic Time Series Prediction Model. Information and Control, 40, 673-679.
- Wang, Z.M., Tan, X.S., Yuan, Z.M. and Wu, Z.H. (2010) Parameters Optimization of SVM Based on Self-Calling SVR. Journal of System Simulation, 22, 376-378.
- Chuang, S.C. and Hung, Y.C. (2010) Uniform Design over General Input Domains with Applications to Target Region Estimation in Computer Experiments. Computational Statistics & Data Analysis, 54, 219-232. http://dx.doi.org/10.1016/j.csda.2009.08.008
- Pan, J.-S., Hong, M.-Z., Zhou, Q.-F., Cai, J.-Y., Wang, H.-Z., Luo, L.-K., Yang, D.-Q., Dong, J., Shi, H.-X. and Ren, J.-L. (2009) Integrated Application of Uniform Design and Least-Squares Support Vector Machines to Transfection Optimization. BMC Biotechnology, 9, 52. http://dx.doi.org/10.1186/1472-6750-9-52
- Wang, X., Zhang, C., Li, P., Wang, K., Hu, Y., Zhang, P. and Liu, H.X. (2012) Modeling and Optimization of Joint Quality for Laser Transmission Joint of Thermoplastic Using an Artificial Neural Network and a Genetic Algorithm. Optics and Lasers in Engineering, 50, 1522-1532. http://dx.doi.org/10.1016/j.optlaseng.2012.06.008
- Sun, Y.W. and Hao, M.Z. (2012) Statistical Analysis and Optimization of Process Parameters in Ti6Al4V Laser Cladding Using Nd:YAG Laser. Optics and Lasers in Engineering, 50, 985-995. http://dx.doi.org/10.1016/j.optlaseng.2012.01.018
- Yang, D.X., Li, X.Y., He, D.Y., Nie, Z.R. and Huang, H. (2012) Optimization of Weld Bead Geometry in Laser Welding with Filler Wire Process Using Taguchi’s Approach. Optics & Laser Technology, 44, 2020-2025. http://dx.doi.org/10.1016/j.optlastec.2012.03.033
- Beygi, H., Vafaeenezhad, H. and Sajjadi, S.A. (2012) Modeling the Electroless Nickel Deposition on Aluminum Nanoparticles. Applied Surface Science, 258, 7744-7750. http://dx.doi.org/10.1016/j.apsusc.2012.04.132
- Wang, Z.F. and Wang, H. (2012) Inflatable Wing Design Parameter Optimization Using Orthogonal Testing and Support Vector Machines. Chinese Journal of Aeronautics, 25, 887-895. http://dx.doi.org/10.1016/S1000-9361(11)60459-7
- Wang, Y. and Fang, K.T. (1981) About Uniform Distribution and Experimental Design: Number Theory Method. Chinese Science Bulletin, 2, 65-70.
NOTES
*Corresponding author.








