Applied Mathematics
Vol.5 No.4(2014), Article ID:43575,8 pages DOI:10.4236/am.2014.54065
Improve Results for Set Identities
Yonghong Liu
School of Automation, Wuhan University of Technology, Wuhan, China
Email: hylinin@163.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 21 December 2013; revised 21 January 2014; accepted 28 January 2014
ABSTRACT
In this work, we presented a new law which was based on the well-known duality property for the set identities. We introduced the diagrams that could be applied to the proof for the set identities. Some prime examples were also provided to illustrate the proposed law.
Keywords:Set Theory; Duality Property; Identity

1. Introduction
The set identities are used in many fields, including probability, statistics, propositional logic, Boolean algebra (the binary operations ∨, ∧ and a unary operation ˉ), lattices (the binary operations ∨ and ∧), BCL/ BCL+-algebra [1] -[4] (the binary operation * ) and computer science. De Morgan’s laws are a pair of transformation rules that are both valid rules of inference, and Venn diagrams are used to analyze logical arguments and to illustrate relationships between sets.
About the set theory and Boolean algebra, “Identities come in pairs” is now often stated as the relationship between the two identities in each pair we use the concept of a dual, it is certainly nothing new, such as the famous De Morgan laws, dating back to the 19th century, and expresses the duality of the set identities, but it has long been thought that the law of the double complement does not have duality. This is an interesting problem, shedding new light on the operations of sets.
And, Venn diagrams do not prove whether equality is true or not. So, this is the problem of basic theory, and we are to dope out a solution to the problem.
In this work we present a new law, and we also put the definition of difference evolved into law (i.e. the dual of difference-set law), domination laws and the identity laws. The results show that the diagram can meet proof of sets that this research could be useful to understand the set essence. In fact, the laws come in pairs, and it is possible to prove many other identities.
2. Set Identities
Table 1 presents some set identities that arise firstly. In general, we have the following law, and we prove that first.
Law 2.1 (Liu’s law). .
.
Note that the so called “Liu’s law” for propositions, named after the Yonghong Liu.
Proof. We have
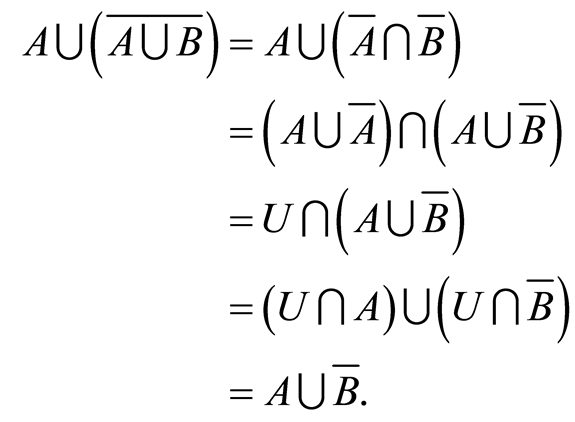 (2.1)
(2.1)
The proof is completed.
Corollary 2.1 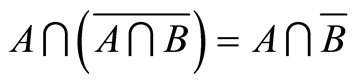 (Difference-set law) and
(Difference-set law) and 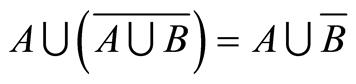 (Liu’s law) is a dual law (see Table 1).
(Liu’s law) is a dual law (see Table 1).
The Liu’s law is to fill gaps in an existing textbook [5] . The most important set identities, such as domination laws and De Morgan’s laws (first De Morgan’s law and second De Morgan’s law) are dual laws.
3. Diagrams and Definitions
As we know, Venn diagrams are often used to indicate the relationships among sets. But, it lacks the proof for set identities. New, here’s the problem that we confront, and we must change and find new solutions.
Set can be represented graphically using curve. We draw a curved surface to indicate the universal set , which is the set of the curve. We use notation
, which is the set of the curve. We use notation  to denote the curve diagram of the sets, and
to denote the curve diagram of the sets, and 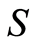 is a finite set. In curved surface, let
is a finite set. In curved surface, let  and
and  be a coordinate set of operation. Let
be a coordinate set of operation. Let  be an operation, then we have the following definitions.
be an operation, then we have the following definitions.
Definition 3.1 Let 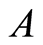 and
and 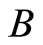 be sets. Set
be sets. Set  is a subset of set
is a subset of set , and is denoted by
, and is denoted by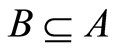 . This is illustrated in Figure 1. That is, if and only if
. This is illustrated in Figure 1. That is, if and only if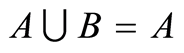 , then
, then .
.
Definition 3.2 The intersection of the sets  and
and , denoted by
, denoted by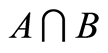 . This is illustrated in Figure 2.
. This is illustrated in Figure 2.
Definition 3.3 The union of the sets 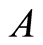 and
and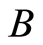 , denoted by
, denoted by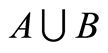 . This is illustrated in Figure 3.
. This is illustrated in Figure 3.
Definition 3.4 The Liu’s law is illustrated in Figure 4.
Table 1. Set identities.

Figure 1.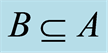 .
.

Figure 2.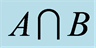 .
.
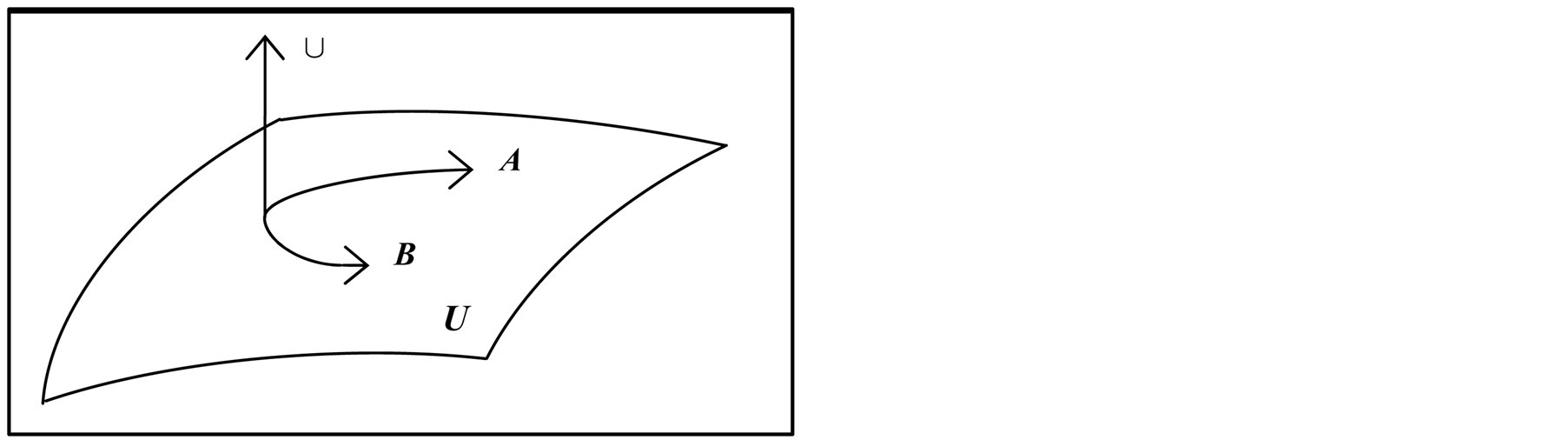
Figure 3. .
.
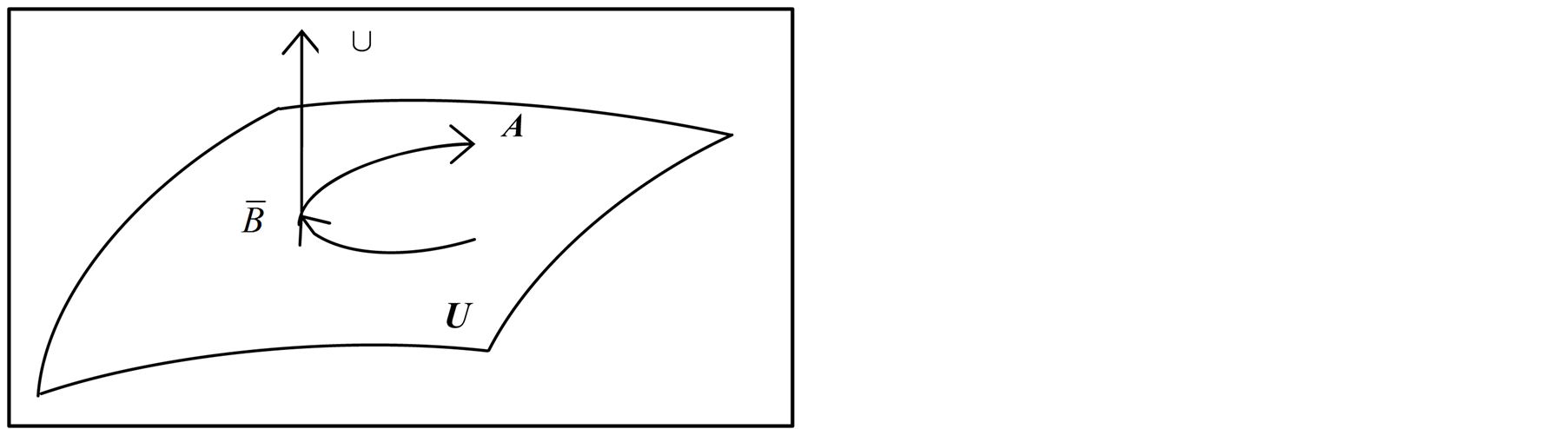
Figure 4.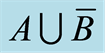 .
.
Definition 3.5 The difference of the sets 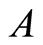 and
and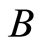 , denoted by
, denoted by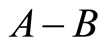 . This is illustrated in Figures 5(a) and (b).
. This is illustrated in Figures 5(a) and (b).
Definition 3.6 The complement of the set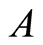 , denoted by
, denoted by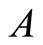 . This is illustrated in Figures 6(a) and (b).
. This is illustrated in Figures 6(a) and (b).
Definition 3.7 The domination laws are illustrated in Figure 7.
Definition 3.8 The domination laws can be decomposed into null set 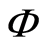 and universal set
and universal set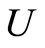 . This is illustrated in Figures 8(a) and (b).
. This is illustrated in Figures 8(a) and (b).
4. Applications
Law 4.1 (Associative law). Use diagram to prove that
 . (4.1)
. (4.1)
Proof. Let  be a machine on the set. Let
be a machine on the set. Let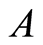 ,
, 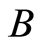 , and
, and 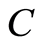 be sets with
be sets with , and let
, and let . We use the coordinate sets to show that
. We use the coordinate sets to show that
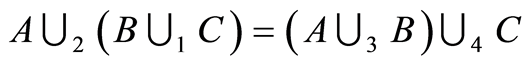 . (4.2)
. (4.2)
The associative law is proved in Figures 9(a) and (b). We have (see Figures 9(a) and (b))
Figure 9 displays the graphs of the set . Here, if and only if,
. Here, if and only if,
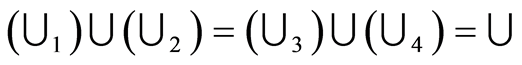 and
and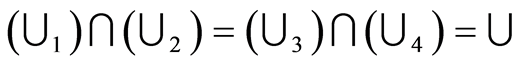 .
.
Then ,
,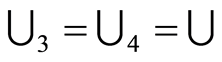 . Since the curve diagrams for
. Since the curve diagrams for 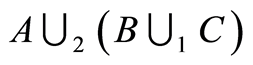 and
and  is same. That is, the two curved surfaces are set-preserving equivalent. The identity of associative law is valid.
is same. That is, the two curved surfaces are set-preserving equivalent. The identity of associative law is valid.


Figure 5. A – B. (a)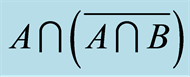 ; (b)
; (b)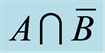 .
.


Figure 6.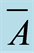 . (a) The
. (a) The  model for
model for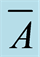 ; (b) The
; (b) The  model for
model for .
.

Figure 7. Set of the domination laws.
Law 4.2 (Distributive law). Use diagram to prove that
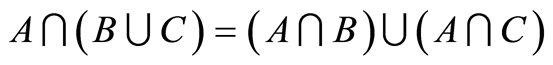 . (4.3)
. (4.3)
Proof. Let  be a machine on the set. Let
be a machine on the set. Let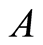 ,
, 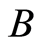 , and
, and 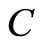 be sets with
be sets with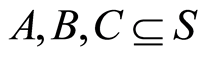 . The distributive law is proved in Figures 10(a) and (b). We have (see Figures 10(a) and (b))
. The distributive law is proved in Figures 10(a) and (b). We have (see Figures 10(a) and (b))
Where  and
and 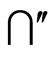 be coordinate set of operation with
be coordinate set of operation with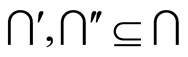 , we have
, we have
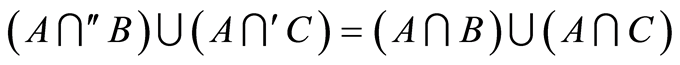 . (4.4)
. (4.4)
If and only if,
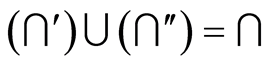 and
and then
then . Hence, by Figure 10(a), we have
. Hence, by Figure 10(a), we have

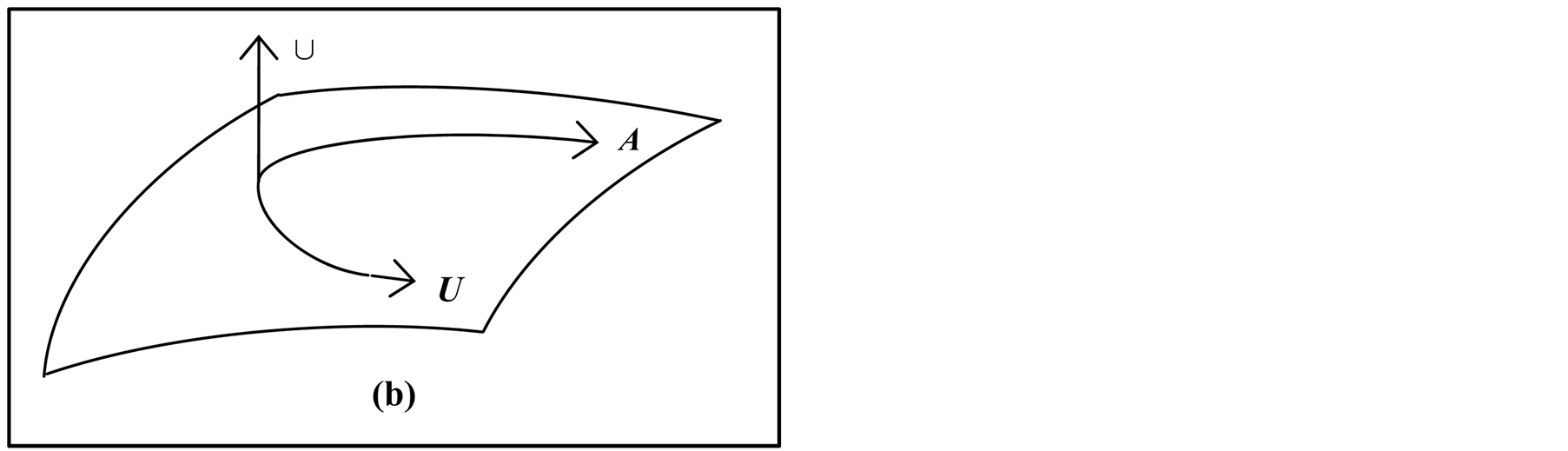
Figure 8.  and
and . (a) The ith term of
. (a) The ith term of ; (b) The ith term of
; (b) The ith term of .
.


Figure 9. Set of the associative law. (a)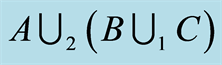 ; (b)
; (b)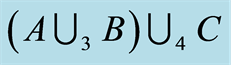 .
.
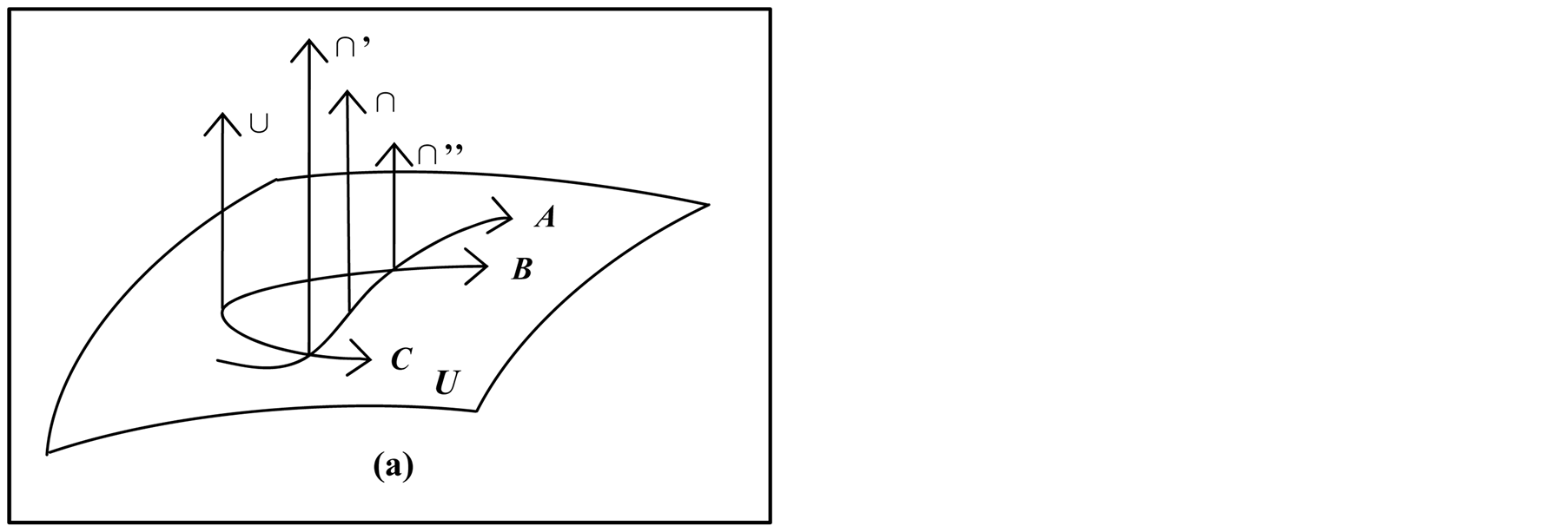

Figure 10. Set of the distributive law. (a) ; (b)
; (b)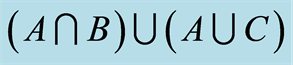 .
.
 . (4.5)
. (4.5)
This is what we needed to prove.
Example 4.1 Use set identities to prove that
 (4.6)
(4.6)
Whether the system has a unique solution
 . (4.7)
. (4.7)
Proof. Let 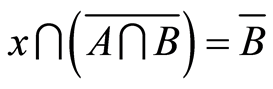 be equivalent to saying that two equations
be equivalent to saying that two equations
 (4.8)
(4.8)
thus
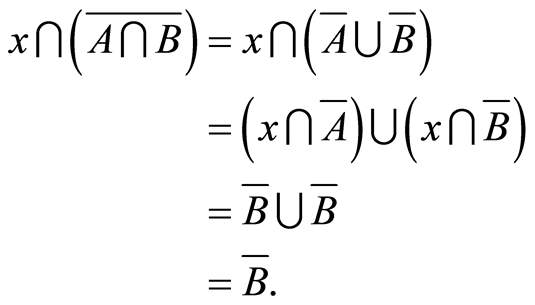 (4.9)
(4.9)
Let  we also have
we also have
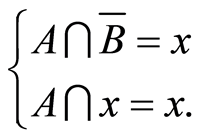 (4.10)
(4.10)
thus
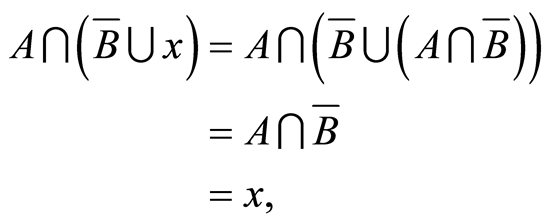 (4.11)
(4.11)
and thus
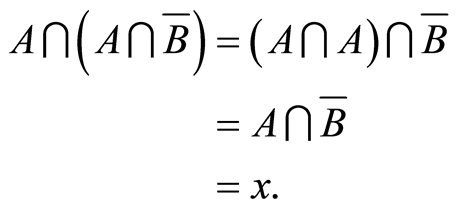 (4.12)
(4.12)
Conversely, if , then
, then
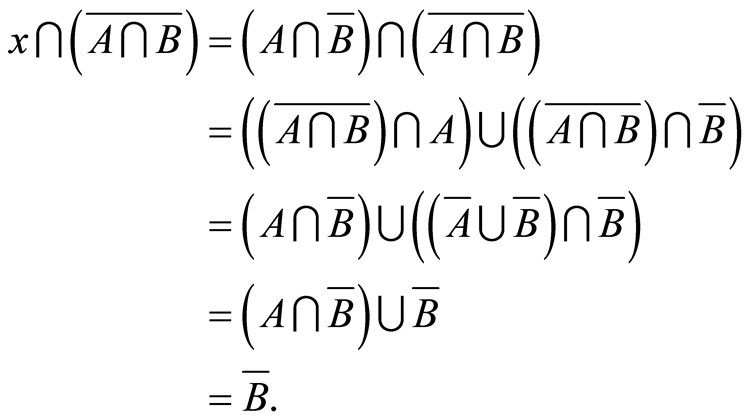 (4.13)
(4.13)
thus
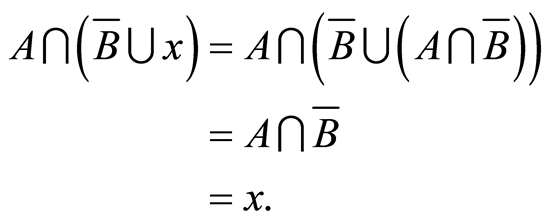 (4.14)
(4.14)
Example 4.1 is proved.
Example 4.2 Use set identities to prove that
 (4.15)
(4.15)
Whether the system has a unique solution
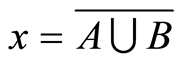 . (4.16)
. (4.16)
Proof. Let 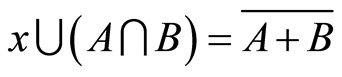 be equivalent to saying that two equations
be equivalent to saying that two equations
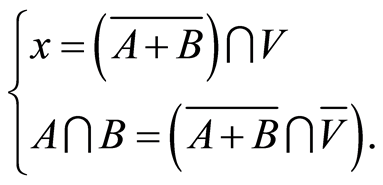 (4.17)
(4.17)
where for all 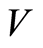 in
in  we have
we have
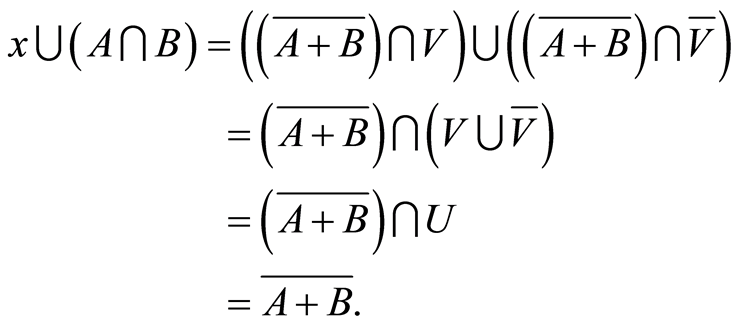 (4.18)
(4.18)
Let 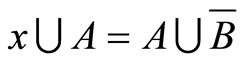 we also have
we also have
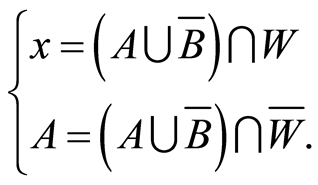 (4.19)
(4.19)
where for all 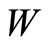 in
in 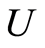 we have
we have
 (4.20)
(4.20)
Conversely, if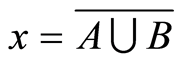 , then
, then
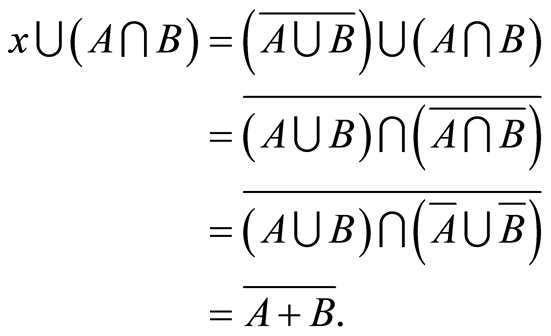 (4.21)
(4.21)
and thus
 (4.22)
(4.22)
The proof is complete.
References
- Liu, Y.H. (2011) A New Branch of the Pure Algebra: BCL-Algebras. Advances in Pure Mathematics, 1, 297-299. http://dx.doi.org/10.4236/apm.2011.15054
- Liu, Y.H. (2012) On BCL+-Algebras. Advances in Pure Mathematics, 2, 59-61. http://dx.doi.org/10.4236/apm.2012.21012
- Deena, A.K. and Rodyna, H. (2013) On BCL-Algebra. Journal of Advances in Mathematics, 3, 184-190.
- Liu, Y.H. (2013) Partial Orders in BCL+-Algebra. Journal of Advances in Mathematics, 5, 630-634.
- Rosen, K.H. (1998) Discrete Mathematics and Its Applications. 4th Edition, McGraw-Hill, New York.


