Applied Mathematics
Vol.5 No.1(2014), Article ID:41673,10 pages DOI:10.4236/am.2014.51011
Optimum Probability Distribution for Minimum Redundancy of Source Coding
Department of Mathematics, Guru Nanak Dev University, Amritsar, India
Email: omparkash777@yahoo.co.in, priyanka_kakkar85@yahoo.com
Received October 8, 2013; revised November 8, 2013; accepted November 15, 2013
ABSTRACT
In the present communication, we have obtained the optimum probability distribution with which the messages should be delivered so that the average redundancy of the source is minimized. Here, we have taken the case of various generalized mean codeword lengths. Moreover, the upper bound to these codeword lengths has been found for the case of Huffman encoding.
Keywords:Mean Codeword Length; Uniquely Decipherable Code; Kraft’s Inequality; Entropy; Optimum Probability Distribution; Escort Distribution; Source Coding
1. Introduction
Any message that brings a specification in a problem which involves a certain degree of uncertainty is called information and it was Shannon [1] who named this measure of information as entropy. In coding theory, the operational role of entropy comes from the source coding theorem which states that if 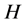 is the entropy of the source letters for a discrete memoryless source, then the sequence of source outputs cannot be represented by a binary sequence using fewer than
is the entropy of the source letters for a discrete memoryless source, then the sequence of source outputs cannot be represented by a binary sequence using fewer than  binary digits per source digit on the average, but it can be represented by a binary sequence using as close to
binary digits per source digit on the average, but it can be represented by a binary sequence using as close to  binary digits per source digit on the average as desired. To be clearer, let us consider the discrete source
binary digits per source digit on the average as desired. To be clearer, let us consider the discrete source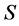 that emits symbols
that emits symbols 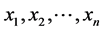 with probability distribution
with probability distribution
 where
where . The aim of source coding is to encode the source using an alphabet of size
. The aim of source coding is to encode the source using an alphabet of size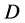 , that is, to map each symbol
, that is, to map each symbol 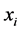 to a codeword
to a codeword 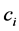 of length
of length  expressed using the
expressed using the 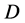 letters of the alphabet. It is known that if the set of lengths
letters of the alphabet. It is known that if the set of lengths  satisfies Kraft’s [2] inequality
satisfies Kraft’s [2] inequality
 (1.1)
(1.1)
then there exists a uniquely decodable code with these lengths, which means that any sequence  can be decoded unambiguously into a sequence of symbols
can be decoded unambiguously into a sequence of symbols . In this respect, Shannon [1] proved the first noiseless coding theorem for the uniquely decipherable code in the form of following inequality
. In this respect, Shannon [1] proved the first noiseless coding theorem for the uniquely decipherable code in the form of following inequality
 (1.2)
(1.2)
where 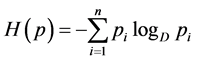 is a Shannon’s entropy and
is a Shannon’s entropy and 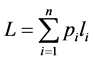 is the mean codeword length.
is the mean codeword length.
Later, Campbell [3] and Kapur [4] proved the source coding theorems for their own exponentiated mean codeword length in the form of following inequalities
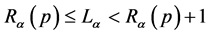 (1.3)
(1.3)
and
 (1.4)
(1.4)
respectively, where

is Campbell’s [3] mean codeword length,

is Kapur’s [4] mean codeword length and
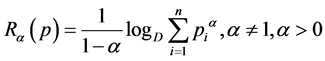
is Renyi’s [5] measure of entropy.
Recently, Parkash and Kakkar [6] introduced two mean codeword lengths given by
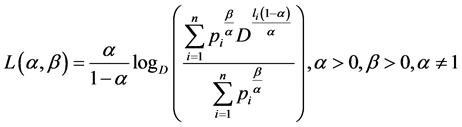 (1.5)
(1.5)
and
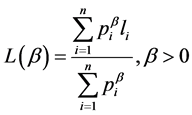 (1.6)
(1.6)
Further, the authors provided two source coding theorems which show that for all uniquely decipherable codes, the mean codeword lengths 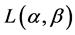 and
and  satisfy the relation:
satisfy the relation:
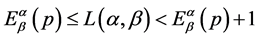 (1.7)
(1.7)
and
 (1.8)
(1.8)
respectively where

is a Kapur’s [4] two parameter additive measure of entropy and

is measure of entropy developed by Parkash and Kakkar [6].
This is to emphasize that in the entire literature of source coding theorems, one can observe that the mean codeword length is lower bounded by the entropy of the source and it can never be less than the entropy of the source but can be made closer to it. This phenomenon provides the idea of absolute redundancy which is the number of bits used to transmit a message minus the number of bits of actual information in the message, that is, the mean codeword length minus the entropy of the source. The objective of the present communication is to minimize this redundancy in order to increase the efficiency of the source encoding. For this purpose we have made use of the concept of escort distribution as follows:
If 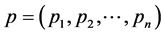 is the original distribution, then its escort distribution is given by
is the original distribution, then its escort distribution is given by 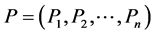
where 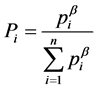 for some parameter
for some parameter . Many researchers including Harte [7], Bercher [8,9], Beck and Schloegl [10] etc. used this distribution in their respective findings.
. Many researchers including Harte [7], Bercher [8,9], Beck and Schloegl [10] etc. used this distribution in their respective findings.
The aim of the present paper is to obtain the optimum probability distribution with which the source should deliver messages in order to minimize the absolute redundancy. To obtain our goal, we have taken into consideration the above mentioned generalized mean codeword lengths. Moreover, the upper bound to these codeword lengths has been found for Huffman [4] encoding.
2. Optimum Probability Distribution to Minimize Absolute Redundancy
Let us assume that for discrete source  that emits symbols
that emits symbols 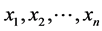 with probability distribution
with probability distribution , the codewords
, the codewords 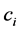 having lengths
having lengths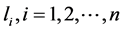 , have been obtained using some encoding procedure on noiseless channel. Further, we assume that entropy of the source is
, have been obtained using some encoding procedure on noiseless channel. Further, we assume that entropy of the source is 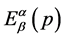 and average codeword length is
and average codeword length is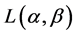 . Since from (1.7), we have
. Since from (1.7), we have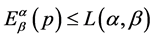 , therefore, the average redundancy of the source code is given by
, therefore, the average redundancy of the source code is given by
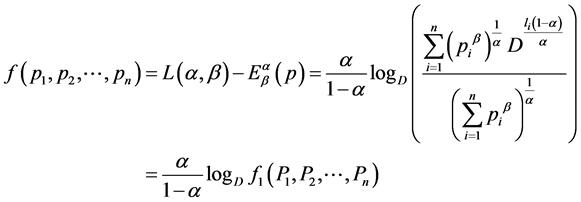 (2.1)
(2.1)
where  and
and .
.
In order to minimize the average redundancy, we resort to the following theorem:
Theorem 1: The optimum probability distribution that minimizes the absolute redundancy  of the source with entropy
of the source with entropy 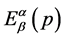 and the mean codeword length
and the mean codeword length  is the escort distribution, given by
is the escort distribution, given by
 (2.2)
(2.2)
Proof: To minimize the redundancy, we need to minimize
 (2.3)
(2.3)
subject to the constraint
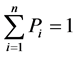 (2.4)
(2.4)
To prove this, we first of all, find the extremum of 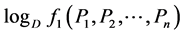 which is equivalent to extremizing
which is equivalent to extremizing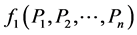 and then use the fact that
and then use the fact that 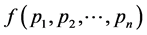 is minimum or maximum will depend upon the value of parameter
is minimum or maximum will depend upon the value of parameter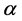 .
.
So, in order to extremize , we consider the Lagrangian given by
, we consider the Lagrangian given by

where  is Lagrange’s multiplier.
is Lagrange’s multiplier.
Now
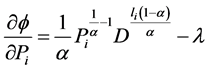 (2.5)
(2.5)
Letting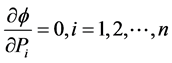 , we get
, we get
 (2.6)
(2.6)
Substituting (2.6) in (2.4), we get
 (2.7)
(2.7)
Substituting (2.7) in (2.6), we get the result (2.2).
Now,
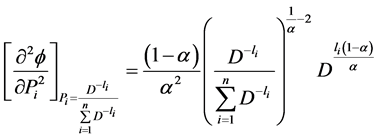 (2.8)
(2.8)
We see that  for
for 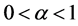 and
and 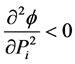 for
for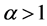 .
.
Also,
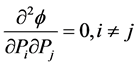
So, 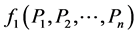 has minimum value for
has minimum value for 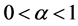 and maximum for
and maximum for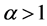 .
.
Thus,  has minimum value for
has minimum value for  and maximum for
and maximum for 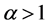 and consequently, observing the function
and consequently, observing the function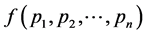 , we see that it has minimum value for
, we see that it has minimum value for ,
, .
.
Thus, the minimum value is given by
 . (2.9)
. (2.9)
Again, the necessary condition for the construction of uniquely decipherable codes is given by
 (2.10)
(2.10)
Therefore, from (2.9), we have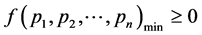 .
.
NOTE: It is to be noted that  if the source is Huffman [11] encoded since for the Huffman encoding, we have
if the source is Huffman [11] encoded since for the Huffman encoding, we have
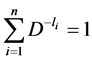 . (2.11)
. (2.11)
Therefore, for this case, (2.2) becomes
 (2.12)
(2.12)
Similarly, if we consider the codeword length  which satisfies the relation
which satisfies the relation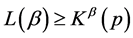 , then the absolute redundancy of the source code in this case is given by
, then the absolute redundancy of the source code in this case is given by
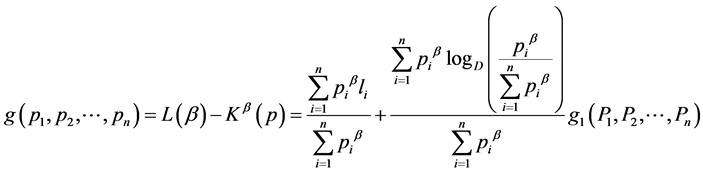
where 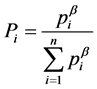 and
and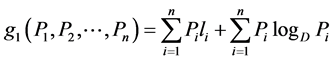 .
.
Theorem 2. The optimum probability distribution that minimizes the absolute redundancy 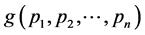 of the source with entropy
of the source with entropy  and mean codeword length
and mean codeword length 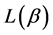 is the escort distribution, given by
is the escort distribution, given by
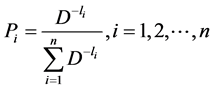 (2.13)
(2.13)
Proof: We will find the extremum of 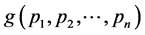 which is equivalent to extremizing
which is equivalent to extremizing  subject to constraint
subject to constraint
 (2.14)
(2.14)
Let us consider the Lagrangian given by
 (2.15)
(2.15)
where 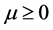 is a Lagrange’s multiplier.
is a Lagrange’s multiplier.
For an extremum, let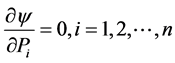 , that is,
, that is,
 (2.16)
(2.16)
Using (2.14), we get
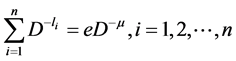 (2.17)
(2.17)
Substituting (2.17) in (2.16), we get (2.13).
Also,

and
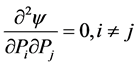
So, 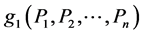 reaches its minimum value when
reaches its minimum value when  and is given by
and is given by

that is,

Note: Again in this case also, if the source is Huffman [11] encoded, then the probabilities are given by 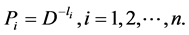
Next, we will find the upper bound on the codeword lengths  and
and  when the source is Huffman encoded.
when the source is Huffman encoded.
Theorem 3. The exponentiated codeword length 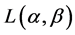 satisfies the following inequality
satisfies the following inequality
 (2.18)
(2.18)
if the source is encoded using Huffman procedure.
Proof: The exponentiated codeword length  can be written in the following form
can be written in the following form
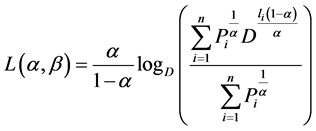 (2.19)
(2.19)
where .
.
Considering (2.12), (2.19) becomes
 (2.20)
(2.20)
where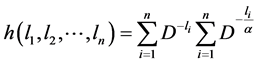 .
.
We need to find the extremum of 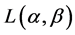 subject to constraint
subject to constraint 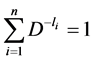 (as the source is encoded using Huffman Procedure).
(as the source is encoded using Huffman Procedure).
For this purpose, we first of all, find the extremum of 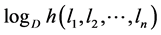 which is equivalent to extremizing
which is equivalent to extremizing 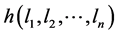 and then use the fact that
and then use the fact that 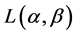 is minimum or maximum depending upon the value of parameter
is minimum or maximum depending upon the value of parameter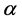 .
.
So, we consider the Lagrangian given by
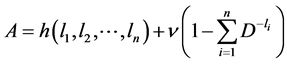 (2.21)
(2.21)
where 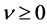 is a Lagrange’s multiplier Put
is a Lagrange’s multiplier Put , (2.21) becomes
, (2.21) becomes

Letting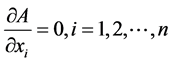 , we get
, we get
 (2.22)
(2.22)
Now, 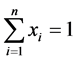 gives
gives
 (2.23)
(2.23)
Using (2.23) in (2.22), we get

that is, 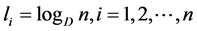
Now,
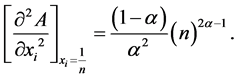
We see that  for
for  and
and  for
for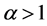 .
.
Also,

So,  has minimum value for
has minimum value for 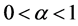 and maximum for
and maximum for .
.
Therefore,  has minimum value for
has minimum value for 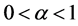 and maximum for
and maximum for 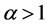 and consequently, observing the exponentiated mean codeword length
and consequently, observing the exponentiated mean codeword length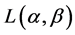 , we see that it has maximum value for
, we see that it has maximum value for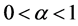 ,
,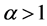 .
.
Thus, the maximum value is given by
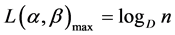 .
.
Theorem 4. The mean codeword length 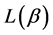 is upper bounded by
is upper bounded by  , that is,
, that is,
 (2.24)
(2.24)
if the source is encoded using Huffman procedure.
Proof: The exponentiated codeword length 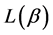 can be written in the following form
can be written in the following form
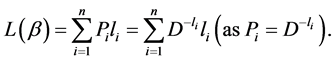 (2.25)
(2.25)
We need to find the extremum of  subject to constraint
subject to constraint 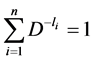 (as the source is encoded using Huffman Procedure).
(as the source is encoded using Huffman Procedure).
So, we consider the Lagrangian given by
 (2.26)
(2.26)
where 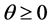 is a Lagrange’s multiplier .
is a Lagrange’s multiplier .
Letting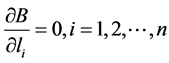 , we get
, we get
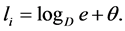 (2.27)
(2.27)
Since 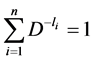 , we have
, we have
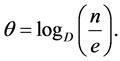 (2.28)
(2.28)
Substitute (2.28) in (2.27), we get
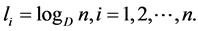
Now,
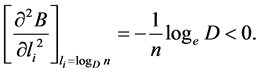
Also,

So, the mean codeword length 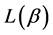 has maximum value when
has maximum value when 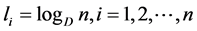 , and is given by
, and is given by
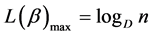 .
.
Note-I: For the case of Campbell’s codeword length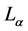 , we have from (1.3),
, we have from (1.3),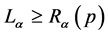 . So, the average redundancy of the source code in this case is given by
. So, the average redundancy of the source code in this case is given by

where 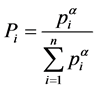 and
and 
The absolute redundancy in the case of Campbell’s [3] mean codeword length is the same as in case of exponentiated mean codeword length 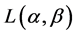 developed by Parkash and Kakkar [6] as given in (2.1). Thus, we see that similar results as proved in theorem (2.1) and theorem (2.3) hold for Campbell’s case also.
developed by Parkash and Kakkar [6] as given in (2.1). Thus, we see that similar results as proved in theorem (2.1) and theorem (2.3) hold for Campbell’s case also.
Note-II: Absolute redundancy when we use Kapur’s[4] mean codeword length is given by

where 
Theorem 5: The optimum probability distribution that minimizes the absolute redundancy of the source with entropy 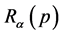 and mean codeword length
and mean codeword length  is given by
is given by
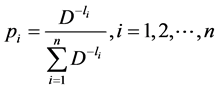 . (2.29)
. (2.29)
Proof: To minimize the redundancy, we need to minimize
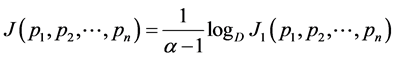 (2.30)
(2.30)
subject to the constraint
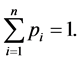 (2.31)
(2.31)
To prove this, we first of all find the extremum of  which is equivalent to extremizing
which is equivalent to extremizing 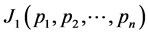 and then using the fact that
and then using the fact that 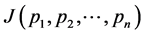 is minimum or maximum depending upon the value of parameter
is minimum or maximum depending upon the value of parameter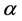 .
.
So, in order to extremize , we consider the Lagrangian given by
, we consider the Lagrangian given by
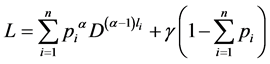
where 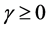 is Lagrange’s multiplier.
is Lagrange’s multiplier.
 (2.32)
(2.32)
Letting , we get
, we get
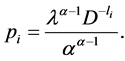 (2.33)
(2.33)
Substituting (2.33) in (2.31), we get
 (2.34)
(2.34)
Substituting (2.34) in (2.33), we get the result (2.29).
Now, 
We see that  for
for 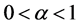 and
and  for
for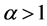 .
.
Also, 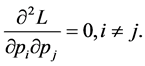
So,  has maximum value for
has maximum value for  and minimum value for
and minimum value for .
.
Therefore, 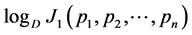 has maximum value for
has maximum value for  and minimum value for
and minimum value for  and consequently observing the function
and consequently observing the function , we see that it has minimum value for
, we see that it has minimum value for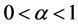 ,
,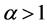 .
.
The minimum value is given by
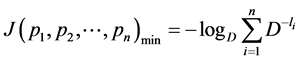 .
.
Theorem 6. The Kapur’s [8] mean codeword length  satisfies the following inequality
satisfies the following inequality
 (2.35)
(2.35)
if the source is encoded using Huffman procedure.
Proof: Proceeding as in Theorem 2.3, we can prove the Theorem 6.
Acknowledgements
The authors are thankful to Council of Scientific and Industrial Research, New Delhi, for providing the financial assistance for the preparation of the manuscript.
REFERENCES
- C. E. Shannon, “A Mathematical Theory of Communication,” Bell System Technical Journal, Vol. 27, 1948, pp. 379-423 (Part I) 623-656 (Part II).
- L. G. Kraft, “A Device for Quantizing Grouping and Coding Amplitude Modulated Pulses,” M.S. Thesis, MIT, Cambridge, 1949.
- L. L. Campbell, “A Coding Theorem and Renyi’s Entropy,” Information and Control, Vol. 8, No. 4, 1965, pp. 423-429.
- J. N. Kapur, “Entropy and Coding,” Mathematical Sciences Trust Society (MSTS), New Delhi, 1998.
- A. Renyi, “On Measures of Entropy and Information,” Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1, 1961, pp. 547-561.
- O. Parkash and P. Kakkar, “Development of Two New Mean Codeword Lengths” Information Sciences, Vol. 207, 2012, pp. 90-97.
- D. Harte, “Multifractals: Theory and Applications,” Chapman and Hall London, 2001.
- J. F. Bercher, “Source Coding with Escort Distributions and Renyi Entropy Bounds,” Physics Letters A, Vol. 373, No. 36, 2009, 3235-3238.
- J. F. Bercher, “Tsallis Distribution as a Standard Maximum Entropy Solution with ‘Tail’ Constraint,” Physics Letters A, Vol. 372, No. 35, 2008, pp. 5657-5659.
- C. Beck and F. Schloegl, “Thermodynamics of Chaotic Systems,” Cambridge University Press, Cambridge, 1993.
- D. A. Huffman, “A Method for the Construction of Minimum Redundancy Codes,” Proceedings of the Institute of Radio Engineers, Vol. 40, No. 10, 1952, pp. 1098-1101.

