Applied Mathematics
Vol.4 No.8A(2013), Article ID:35180,9 pages DOI:10.4236/am.2013.48A011
Modeling Convection Diffusion with Exponential Upwinding
Department of Mathematics, Washington State University, Pullman, USA
Email: #mano@wsu.edu
Copyright © 2013 Humberto C. Godinez, Valipuram S. Manoranjan. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 13, 2013; revised June 13, 2013; accepted June 20, 2013
Keywords: Convection Dominated Diffusion; Exponential Upwinding; Iteration Matrix; Convergence; Spectral Radius
ABSTRACT
This paper shows the usefulness of the exponential upwinding technique in convection diffusion computations. In particular, it is demonstrated that, even when convection is dominant, if exponential upwinding is employed in conjunction with either the Jacobi or the Gauss-Seidel iteration process, one can obtain computed solutions that are accurate and free of unphysical oscillations.
1. Introduction
Convection diffusion equations are commonly used to describe a wide variety of physical phenomena. For example, when one studies how temperature is being convected by a moving fluid [1] or when modeling insect dispersal in a windy region or in describing transport of contaminants in groundwater, convection diffusion models are extremely useful.
In many of these physical processes there is a massive amount of data to be analyzed and studied. Therefore, when studying these processes and the associated convection diffusion equations computationally, it is desirable to implement methods that are amenable to parallel computing. If we develop a computational method discretizing a convection diffusion model either in two or three dimensions, at the end, we are left to solve a linear system of equations. One could employ the Jacobi or the Gauss-Seidel iterative methods to solve such a linear system of equations, since they could be easily adapted to parallel computing. However, there is a problem in employing either the Jacobi or the Gauss-Seidel iterative method if the convection terms are very dominant in the convection diffusion equation. Because, in such cases, when carrying out the iterative computations, unphysical oscillations will appear leading to non convergence of the iterative process. This is due to the fact that the iteration matrices of the Jacobi and the Gauss-Seidel methods, in such cases (i.e., when convection is very dominant) would have spectral radii greater than one [2,3]. Thus, violating the condition for convergence of the iterative process.
One way to deal with such unwanted oscillations is by refining the spatial mesh widths. However, most of the time, the refinements have to be so extreme, that it may not be viable to carryout the computations. So, one is forced to modify the computational method, for example, by using an upwinding technique, or some other technique to suppress the undesirable oscillations.
There are a variety of upwinding techniques to solve convection diffusion problems [1]. In this paper, we focus on an exponential upwinding technique and use it in conjunction with a finite element method. Importantly, we study the effect of exponential upwinding on the spectral radii of the resulting Jacobi and Gauss-Seidel iteration matrices.
The motivation for applying an exponential upwinding technique is the following. Let us consider the one-dimensional convection diffusion problem:
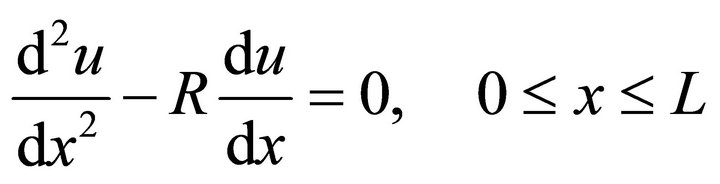 (1)
(1)
with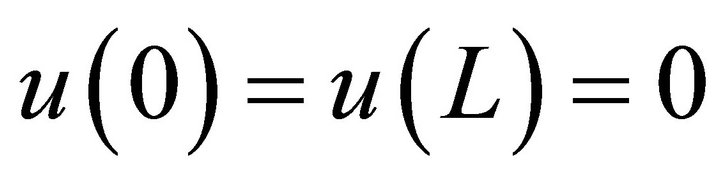 . (2)
. (2)
Introducing an integrating factor, (1) is equivalent to:
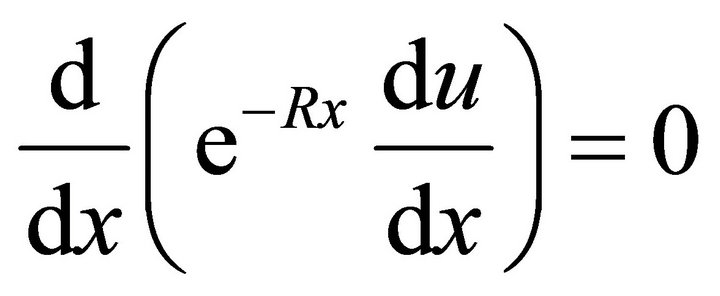 . (3)
. (3)
Spatial discretization of (3) will give
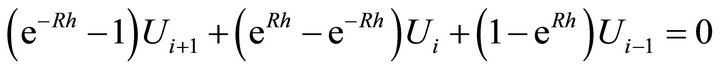 (4)
(4)
with the following boundary conditions:

where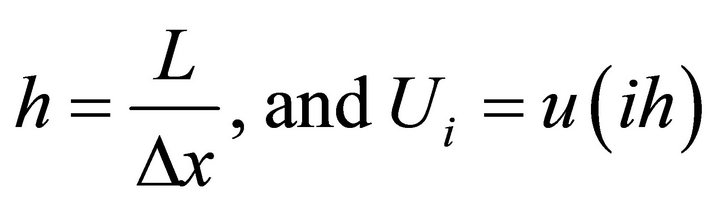 . N is the total number of mesh points.
. N is the total number of mesh points.
Equation (4) could be viewed as the exponentially upwinded difference form of Equation (1).
If we solve (1)-(2) simply by integrating twice, we have the solution:
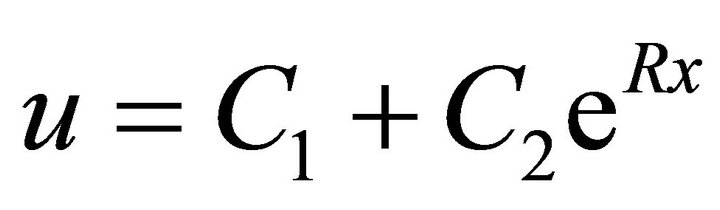
where,  and
and 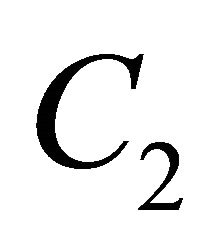 are constants that can be determined by the conditions given in (2).
are constants that can be determined by the conditions given in (2).
Now, the solution for the difference Equation (4) is:
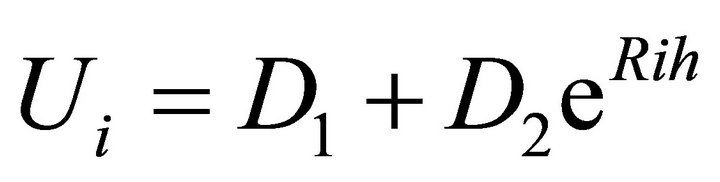
where, D1 and D2 are constants that can again be determined by the boundary conditions in (2).
So, it is clear (since ih = xi) that the solution for the differential Equation (1) and the solution for the difference Equation (4) are exactly the same. This means that solving (3) numerically, using the exponentially upwinded form (4), will give us the exact solution of (1)-(2).
Although we know that this is not the case when dealing with convection diffusion equations in higher dimensions, we wish to examine the usefulness of this type of idea (i.e., exponential upwinding) and the effect that it will have on the Jacobi and the Gauss-Seidel iterative methods, particularly, on the spectral radii of the respecttive iteration matrices.
2. Convection Diffusion—Steady State Model
Let us consider the two-dimensional steady state convection diffusion model given by
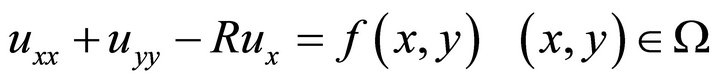 (5)
(5)
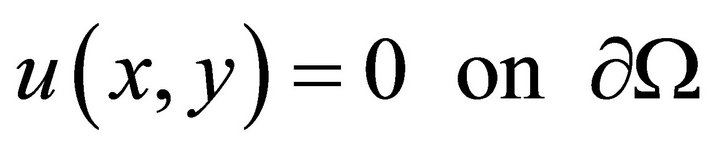 (6)
(6)
where, 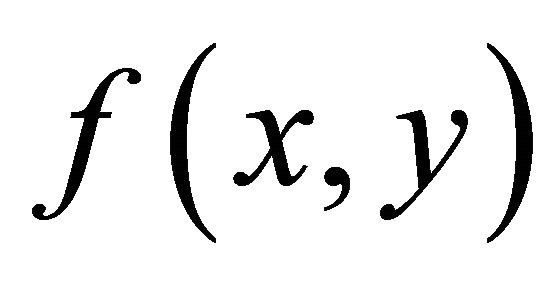 is a given function and R, a non-zero parameter.
is a given function and R, a non-zero parameter.
If we apply a finite element method, we are left with a system of linear equations
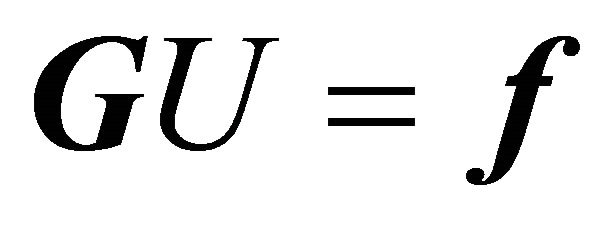 (7)
(7)
where
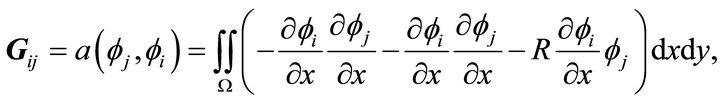
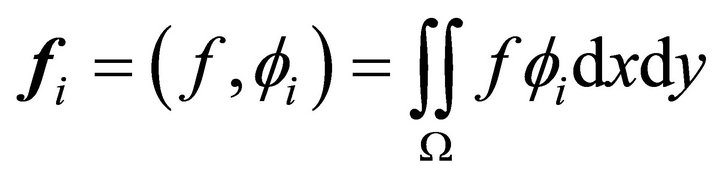 , and
, and ![]() are the basic linear piecewise functions for
are the basic linear piecewise functions for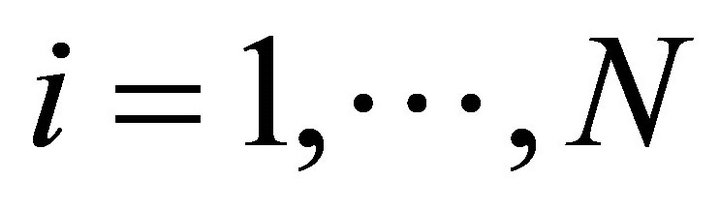 .
.
When R is relatively small, the system of linear equations given by (7) can be solved easily with either the Jacobi or the Gauss-Seidel iterative methods. However, as R increases (i.e., as convection becomes dominant), the spectral radii of both the Jacobi and the Gauss-Seidel iteration matrices will begin to grow and eventually become greater than one, giving us non-convergence (of the iterative processes) in the form of oscillations [4].
For our computational modeling, we choose 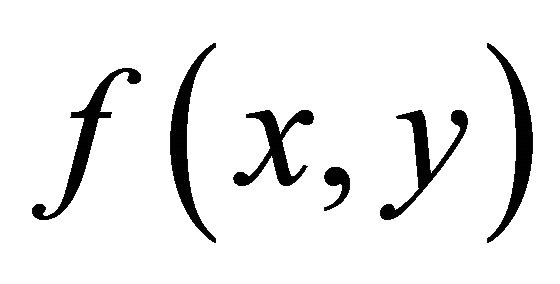 such that
such that 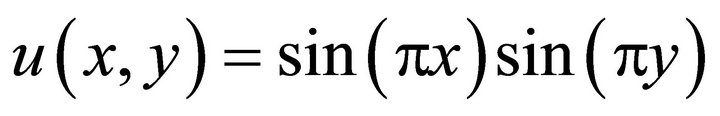 is the exact solution of (5)-(6) where
is the exact solution of (5)-(6) where 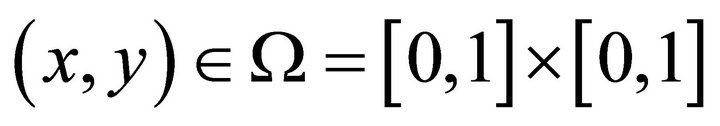 and
and
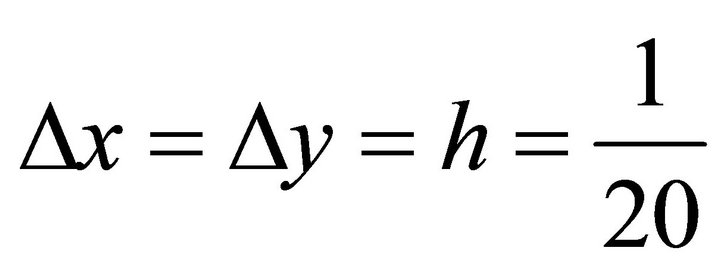 . Figure 1 shows the oscillations that are generated when the Jacobi iterative process is used with R = 85. For bigger values of R the oscillations will overshadow the solution completely giving us extremely large oscillations. For comparison, Figure 2 presents the exact solution of the problem (5)-(6).
. Figure 1 shows the oscillations that are generated when the Jacobi iterative process is used with R = 85. For bigger values of R the oscillations will overshadow the solution completely giving us extremely large oscillations. For comparison, Figure 2 presents the exact solution of the problem (5)-(6).
One way to avoid this problem is to solve (7) with an
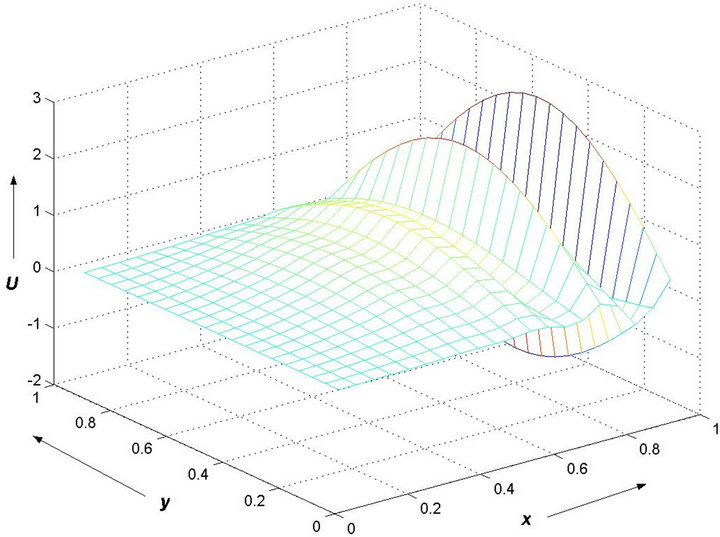
Figure 1. Numerical solution of (5)-(6) with R = 85 using 1000 iterations.
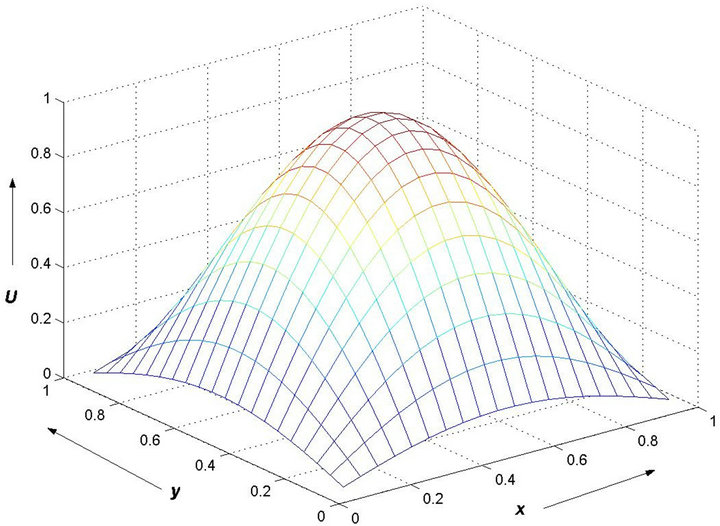
Figure 2. Exact Solution of (5)-(6) with R = 85.
eigenspectrum enveloping technique proposed in [4]. In that paper, the authors study a two step-Jacobi and GaussSeidel iterative methods by constructing an ellipse, in the complex plane, that envelopes the eigenvalues of the iteration matrices.
In this paper, we seek the same objective—the need to eliminate unphysical oscillations when solving convection dominated diffusion problems. However, we will try to accomplish this by modifying the numerical scheme for the partial differential equation, instead of modifying the iterative method directly.
Let us rewrite Equation (5) as
![]() . (8)
. (8)
We are applying the same idea, discussed in the introduction, to only one of the spatial variables, in this case x.
The weak form of (8) is
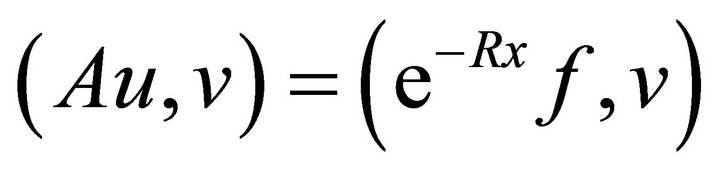
where 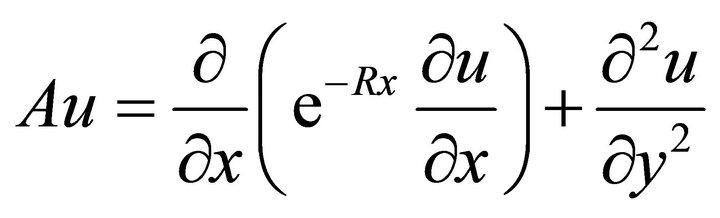 and
and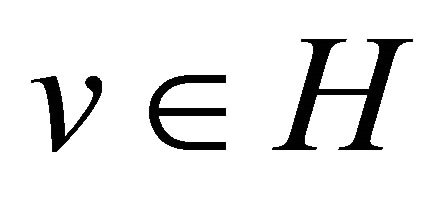 . H is the space of admissible test functions. Now, applying a Galerkin method we get
. H is the space of admissible test functions. Now, applying a Galerkin method we get
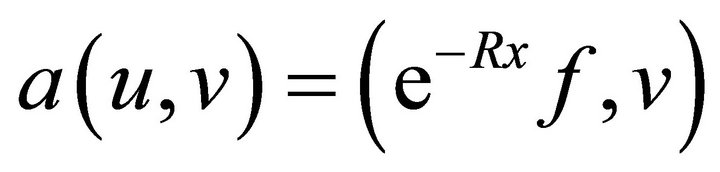 (9)
(9)
where
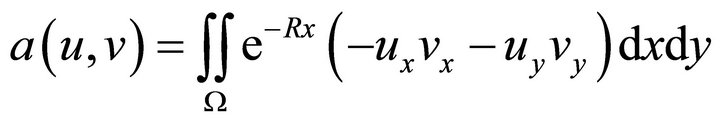 .
.
Let 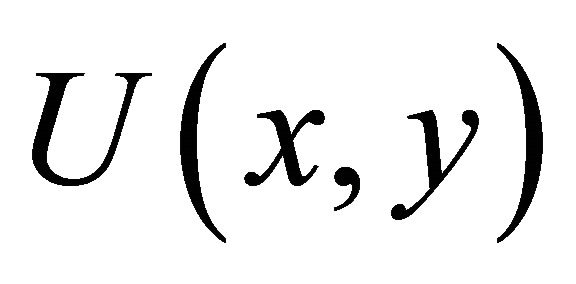 be the Galerkin approximation for u(x, y)
be the Galerkin approximation for u(x, y)
and 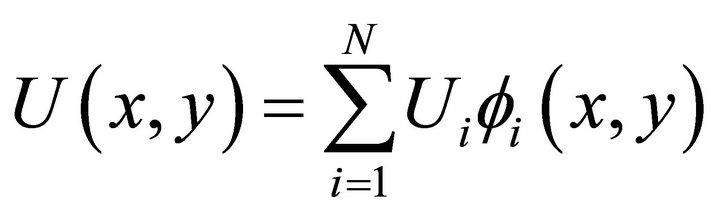 where the
where the ![]() are the basic linear piecewise functions for
are the basic linear piecewise functions for 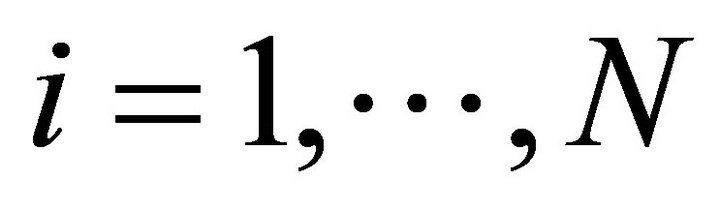 and v(x, y) = fi(x, y). Substituting
and v(x, y) = fi(x, y). Substituting 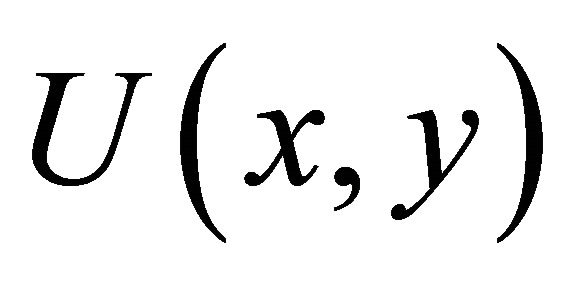 in (9) we get the linear system of equations given by
in (9) we get the linear system of equations given by
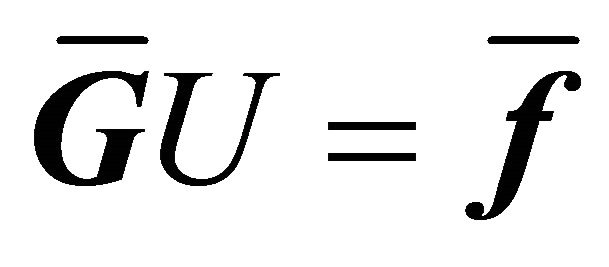
where 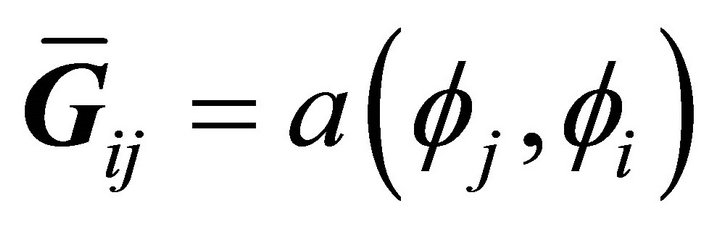 and
and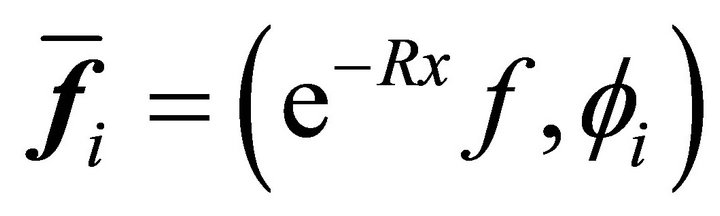 .
.
With this new system of equations, we analyze the spectral radii of the Jacobi and the Gauss-Seidel iteration matrices to determine whether the respective iterative processes will converge for large R values. Figures 3 and 4 show the eigenspectra of the respective iteration matrices when R = 100, a large value.
We see that in both cases the spectral radii of the iteration matrices are less than one. This means that the iterations will lead to convergence. Our computations show that this is indeed the case. Also, we do not get any unwanted oscillations.
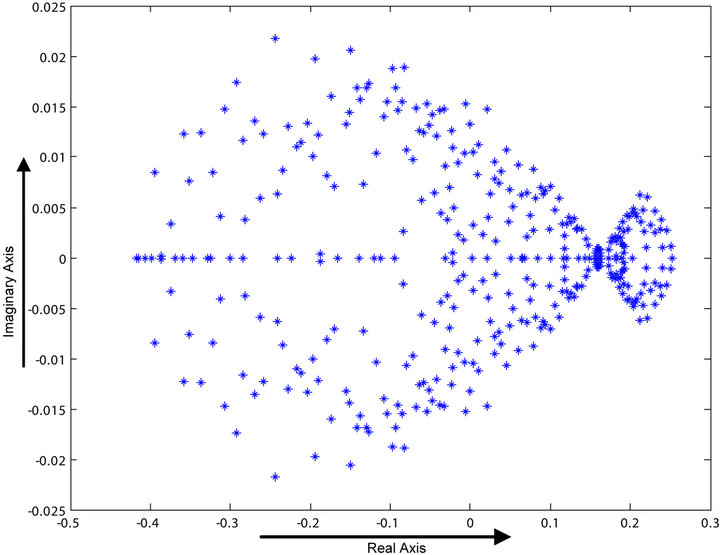
Figure 3. Eigenspectrum of the Jacobi iteration matrix with R = 100.
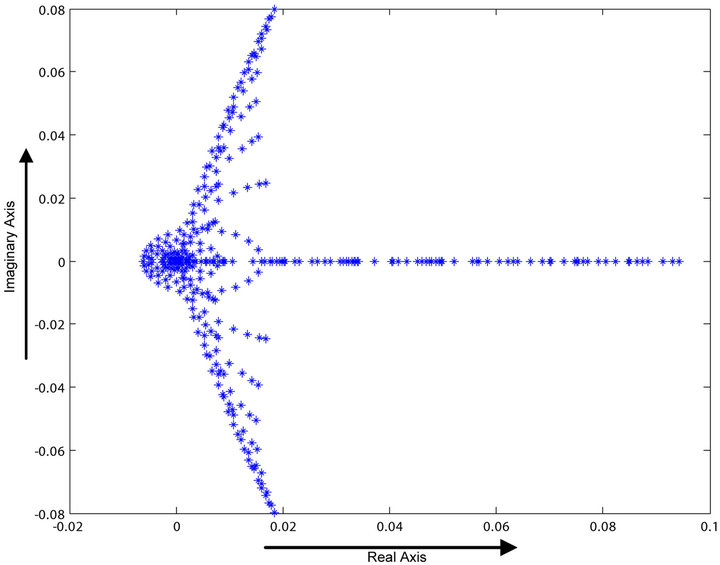
Figure 4. Eigenspectrum of the Gauss-Seidel iteration matrix with R = 100.
In Table 1 we show the percentage error and the number of iterations for convergence (to the solution) for different values of R. In all the cases, the number of iterations the Gauss-Seidel method took was less than half the number of iterations the Jacobi method took for convergence.
3. Convection Diffusion Transport Equation
In our previous model, the convection was only present in one spatial variable. In order to further investigate the effectiveness of this upwinding technique, we would like to explore a problem with convection on both spatial variables (x and y) and see what effects it has on the eigenspectra of the Jacobi and the Gauss-Seidel iterative matrices.
For this purpose we analyze the following convection diffusion transport equation
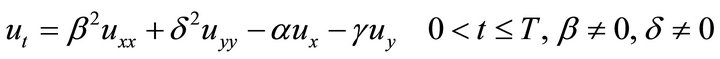 (10)
(10)
subject to the following boundary and initial conditions:
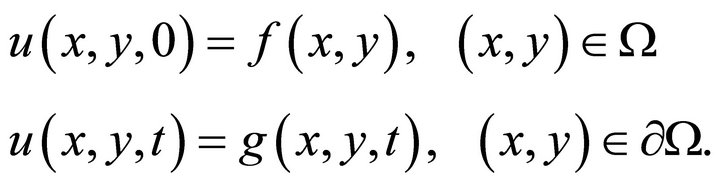 (11)
(11)
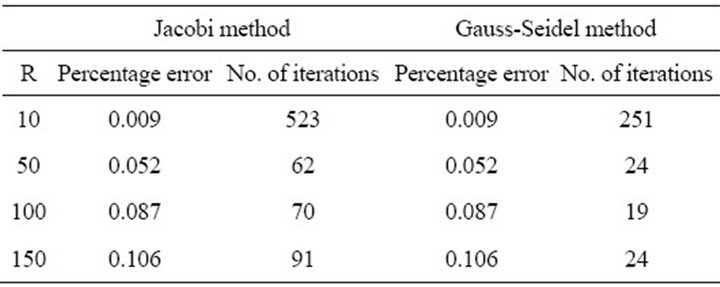
Table 1. Number of iterations and associated error for iterative methods.
Applying a Galerkin semi-discrete finite element method [5], in which we discretize only the spatial variables, we are left with the following system of ordinary differential equations:
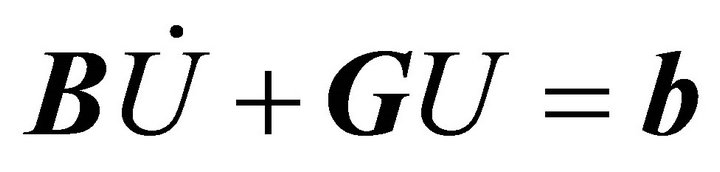 (12)
(12)
where 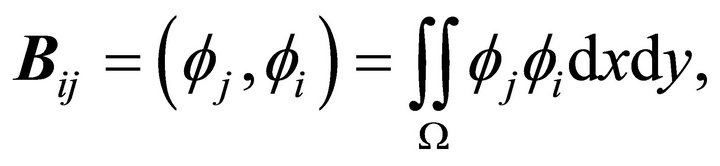
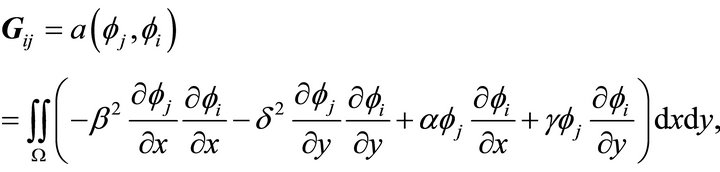
and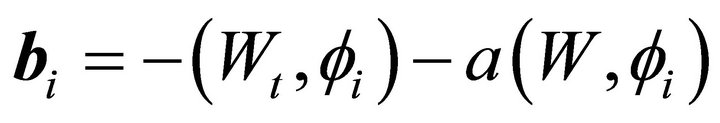 .
.
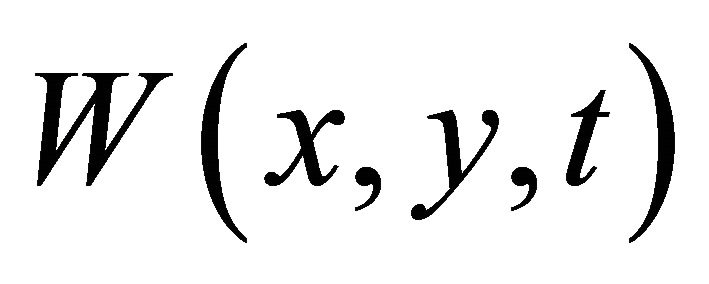
is a function that satisfies the boundary condition, and ![]() are the basic linear piecewise functions for
are the basic linear piecewise functions for .
.
In order to discretize in time, we will use the CrankNicolson method [6,7] and so, (12) becomes:
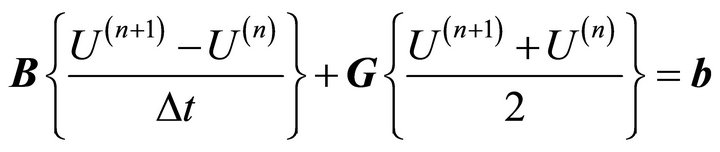
or
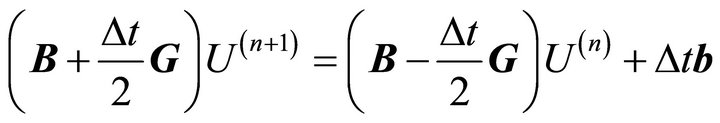 . (13)
. (13)
Therefore, at each time step, we need to solve the linear system (13). The stability of this method will depend on the amplification matrix [8]
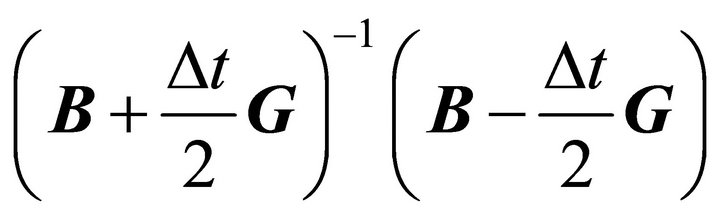 .
.
When ![]() and
and  are small compared with
are small compared with 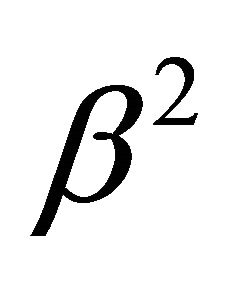 and
and 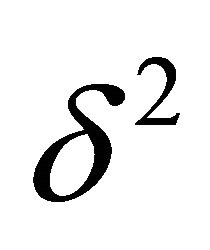 respectively, we will have convergence; however, when they are large (i.e., when convection is dominant), the numerical solution will have oscillations and it will not converge to the correct solution. In the latter case, if we try to solve the system of linear equations with the Jacobi or the Gauss-Seidel iteration method, the spectral radii of the iteration matrices will be greater than one. Figure 5 shows the numerical solution for
respectively, we will have convergence; however, when they are large (i.e., when convection is dominant), the numerical solution will have oscillations and it will not converge to the correct solution. In the latter case, if we try to solve the system of linear equations with the Jacobi or the Gauss-Seidel iteration method, the spectral radii of the iteration matrices will be greater than one. Figure 5 shows the numerical solution for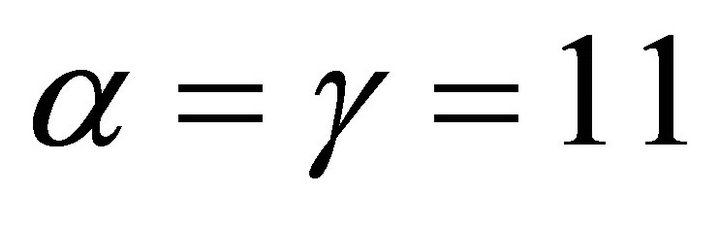 , and one can clearly see the oscillations that result from Jacobi iterations.
, and one can clearly see the oscillations that result from Jacobi iterations.
In [8] the authors address this problem by proposing an alternating direction implicit method with exponential upwinding. In that paper the idea of applying exponential upwinding to each spatial variable comes naturally, since one is solving the system one variable at a time. So, it is intuitive that the idea discussed in the introduction will lead to good results.
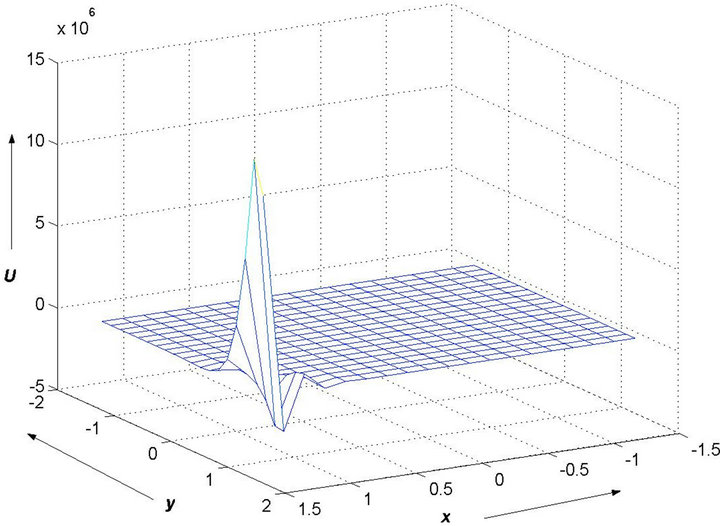
Figure 5. Numerical solution of (10)-(11) using 1000 iterations with α = 11 and γ = 11.
In this paper, to avoid the oscillations presented in the computed solution, we will rewrite Equation (10) as:
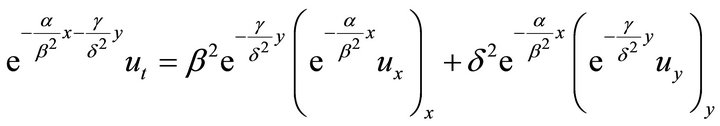 . (14)
. (14)
We apply exponential upwinding to both spatial variables. The weak form of (14) is:
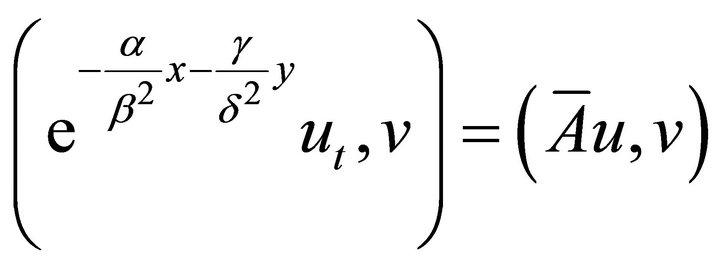 (15)
(15)
where
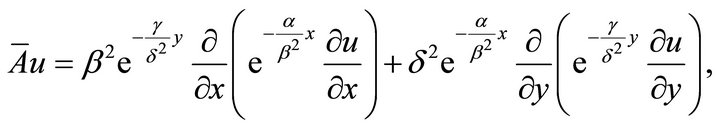
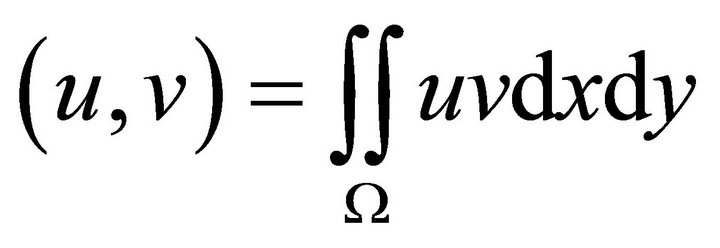 and
and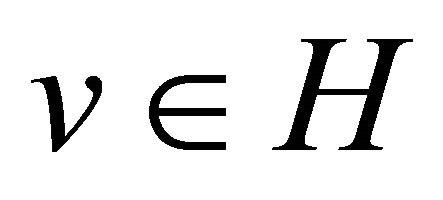 . H is the space of admissible test functions. So the Galerkin form of (15) is
. H is the space of admissible test functions. So the Galerkin form of (15) is
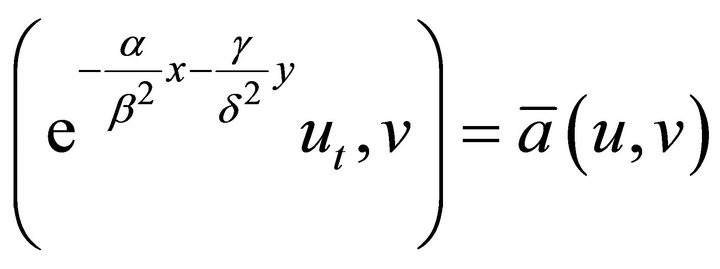 (16)
(16)
where
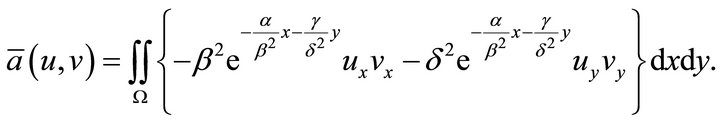
Let 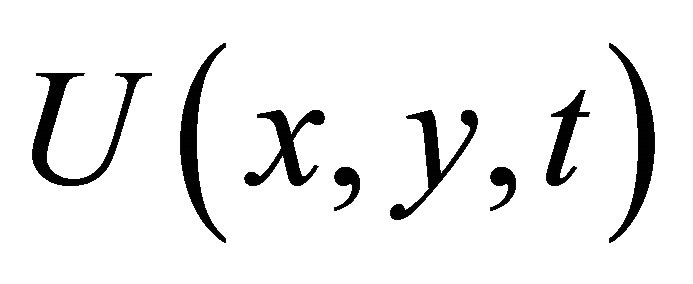 be the Galerkin approximation for u(x, y, t). Since we have an inhomogeneous Dirichlet boundary condition, we choose
be the Galerkin approximation for u(x, y, t). Since we have an inhomogeneous Dirichlet boundary condition, we choose
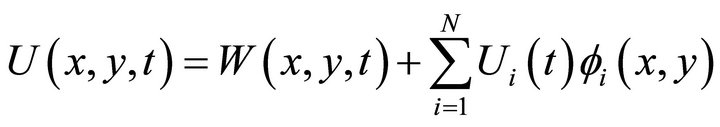 (17)
(17)
where![]() ’s are the piecewise bilinear basis functions for
’s are the piecewise bilinear basis functions for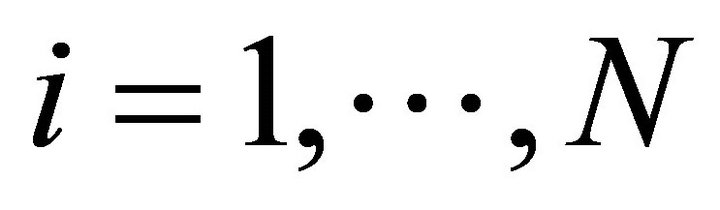 , and
, and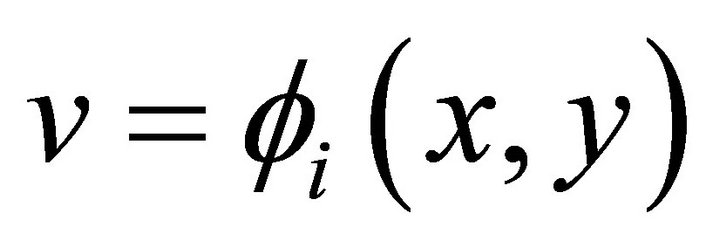 .
. 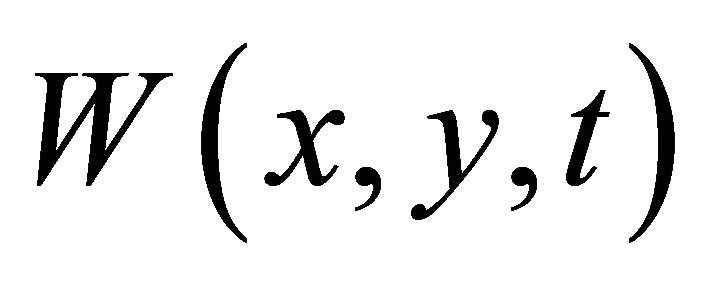 satisfies the boundary condition and we will interpolate the boundary condition to include it in our Galerkin approximation. So we have
satisfies the boundary condition and we will interpolate the boundary condition to include it in our Galerkin approximation. So we have
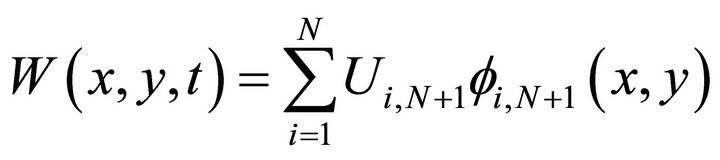
where 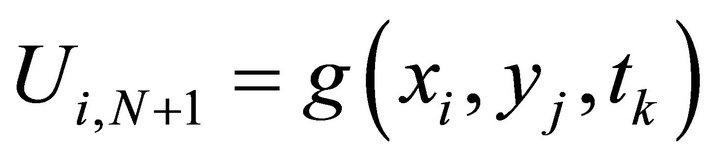 and
and 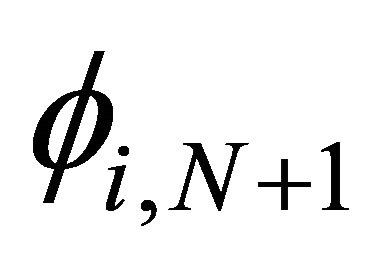 are the piecewise bilinear basic functions on the boundary. Now our Galerkin approximation takes the form
are the piecewise bilinear basic functions on the boundary. Now our Galerkin approximation takes the form
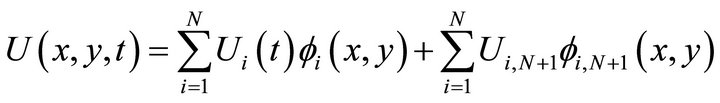 .
.
Substituting (17) into (16) we get the following system of ordinary differential equations in terms of t
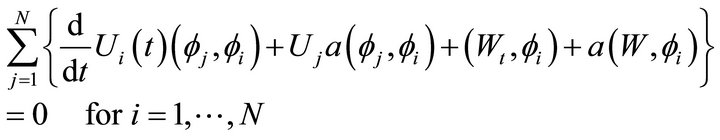
and the initial condition becomes

where 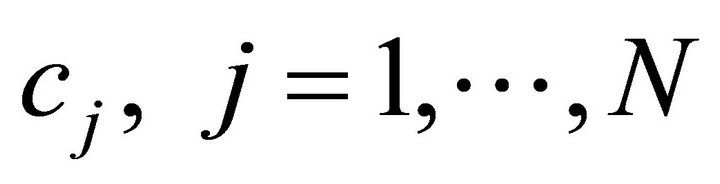 are the solutions to the system
are the solutions to the system
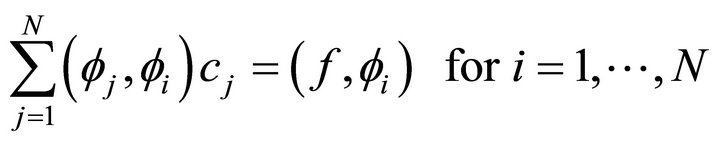 .
.
Written in matrix form we obtain
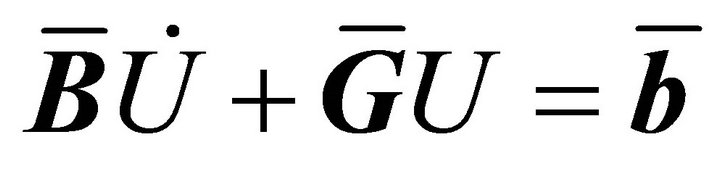
where
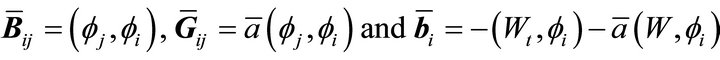 .
.
Applying the Crank-Nicolson method to discretize with respect to time, we have the new system of equations given by
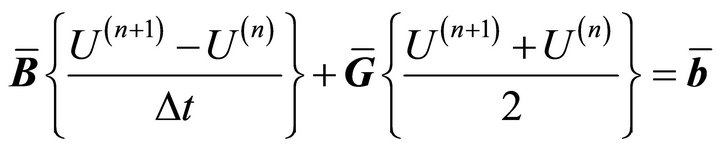
or
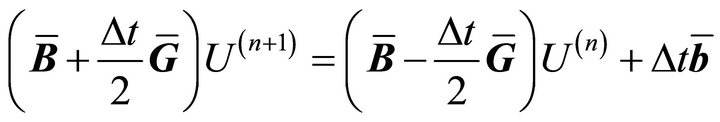 . (18)
. (18)
It can be shown that this method is unconditionally stable [8].
In order to determine whether the iterative processes could produce a converging solution for (18), we analyze the spectral radii of the Jacobi and the Gauss-Seidel iteration matrices.
For the numerical computations, we consider our equation on a specific domain, such that
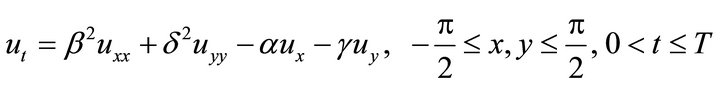 (19)
(19)
with the following boundary conditions:
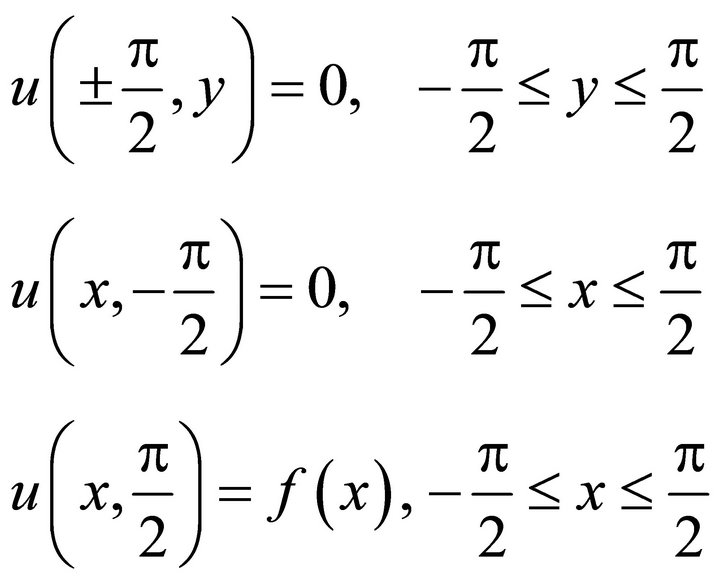
where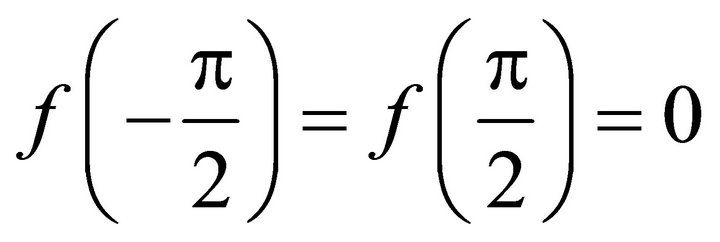 . For every computation we take
. For every computation we take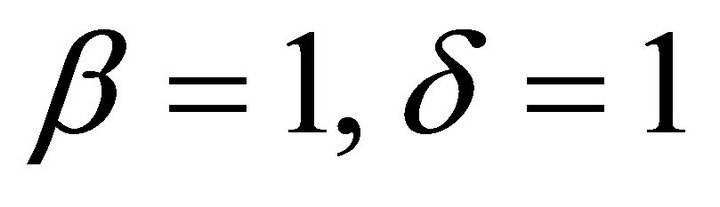 . We will take the steady state solution to be our initial condition and we will interpolate the boundary condition so that we have
. We will take the steady state solution to be our initial condition and we will interpolate the boundary condition so that we have
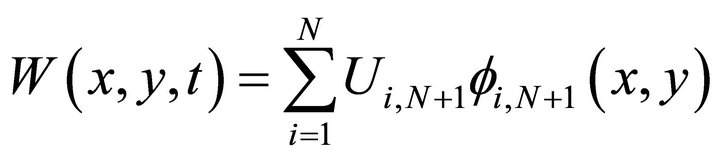
where 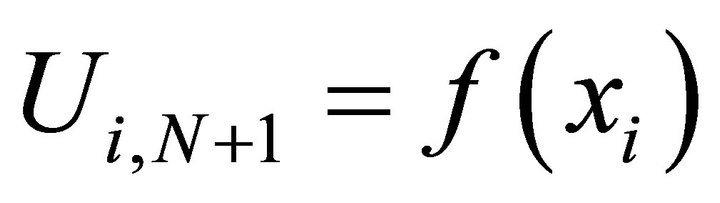 and
and 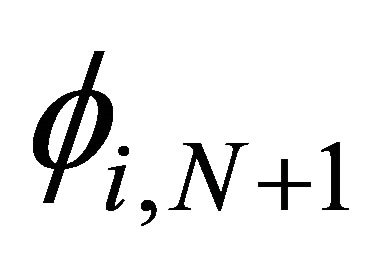 are the piecewise bilinear basic functions on the boundary
are the piecewise bilinear basic functions on the boundary  for
for . So our Galerkin approximation takes the form
. So our Galerkin approximation takes the form
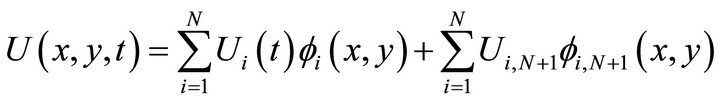 .
.
Hence, we have the linear system
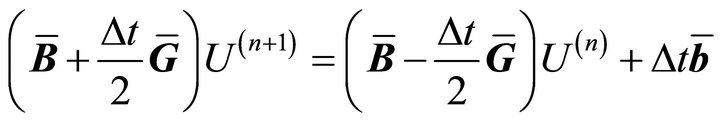
where 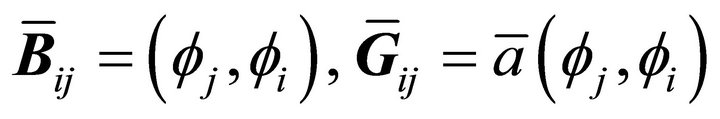 and
and
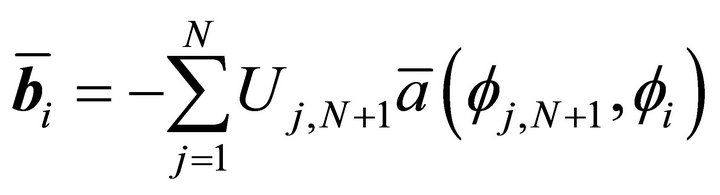 .
.
Using separation of variables [8], it is easy to show that the time dependent solution will tend to a steady state solution of the form:
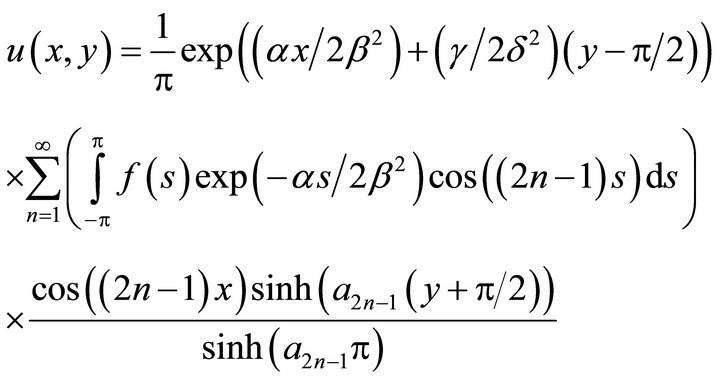 (20)
(20)
where
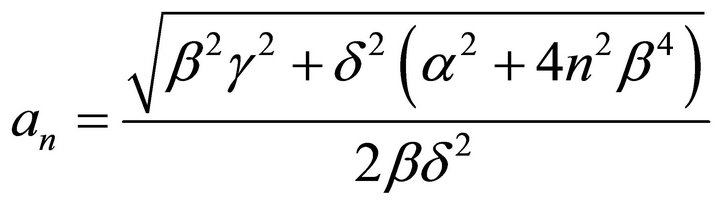 .
.
If 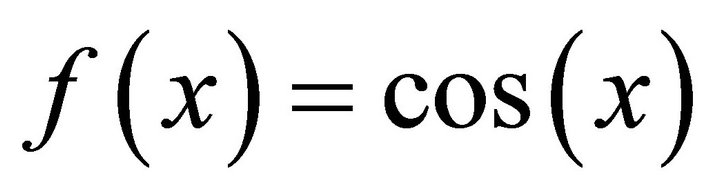 with
with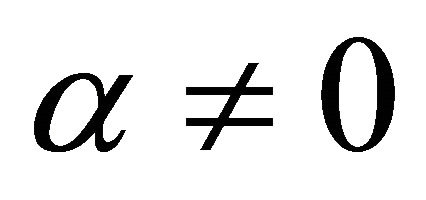 , then (20) reduces to
, then (20) reduces to
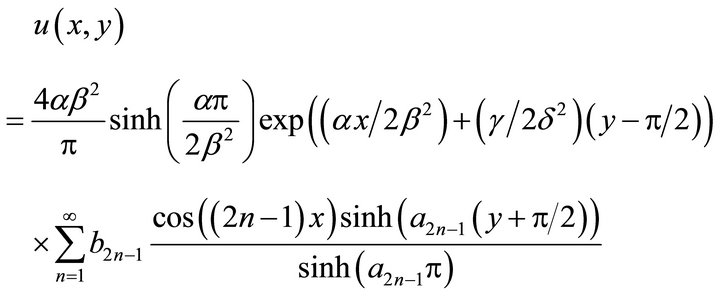 (21)
(21)
where
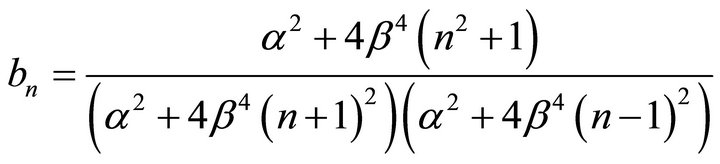 .
.
Notice that when 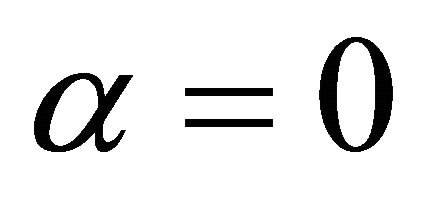 we get a steady state equation similar to (5), so we are interested in the case
we get a steady state equation similar to (5), so we are interested in the case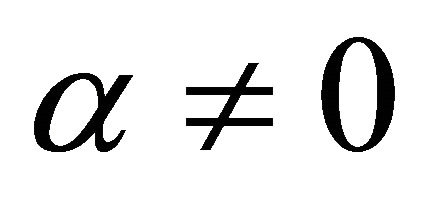 . For our numerical computations we will choose
. For our numerical computations we will choose  such that the steady state solution consists of only the first two terms of the series solution (21). Now, the steady state solution takes the form
such that the steady state solution consists of only the first two terms of the series solution (21). Now, the steady state solution takes the form
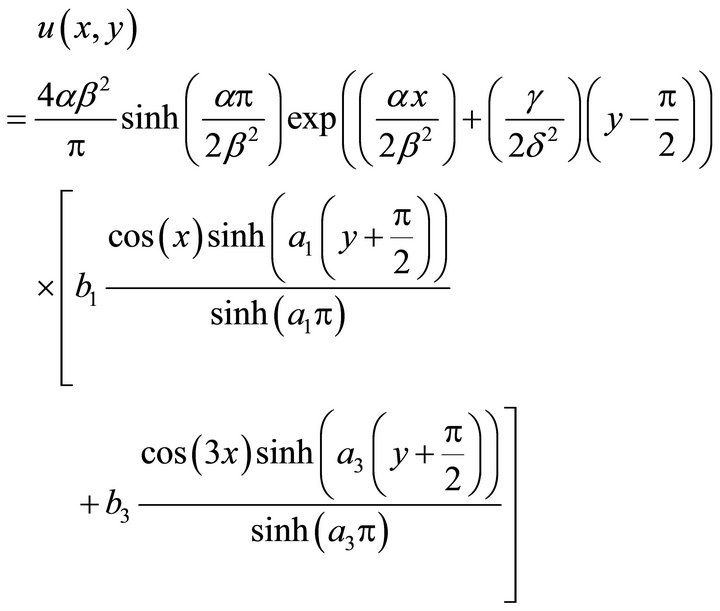
given that the boundary condition at 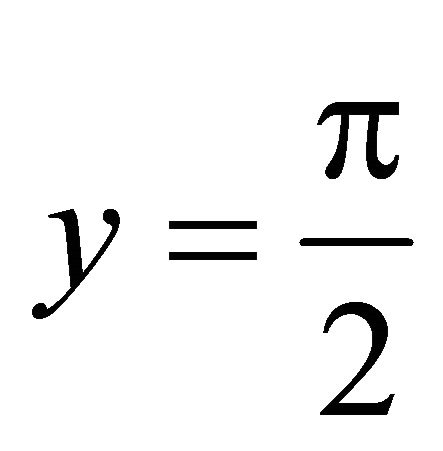 is
is
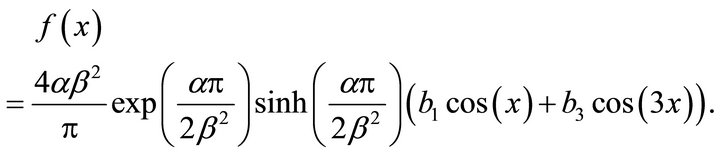
We will take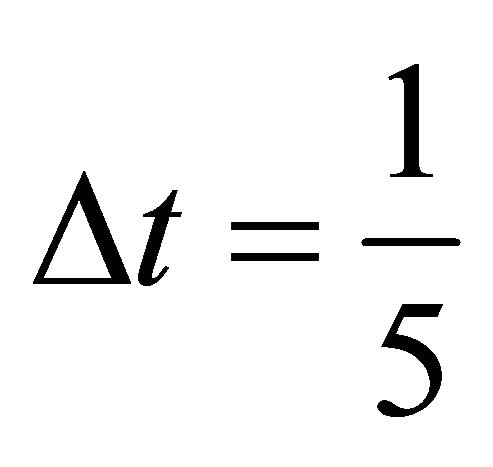 , and
, and 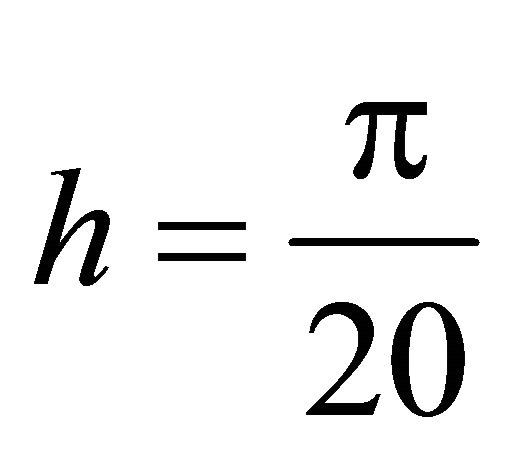 for all our computations.
for all our computations.
Figures 6 and 7 show the eigenspectra of the Jacobi and the Gauss-Seidel iteration matrices respectively when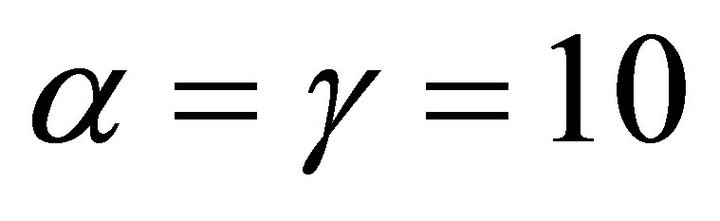 . We can clearly see that the spectral radii are less than one and so, we are sure to have convergence.
. We can clearly see that the spectral radii are less than one and so, we are sure to have convergence.
The graphs in Figure 8 show the steady state solutions when α = 10, γ = 1, and α = 1, γ = 10 respectively. Figures 9 and 10 show the errors in the computed solutions when using the Gauss-Seidel iteration method with α = 10, γ = 1, and α = 1, γ = 10 respectively. The computed solutions with the Jacobi method are exactly the same; the only difference is that the Gauss-Seidel method converges a lot faster. Also, the computed solutions do not produce any unphysical oscillations when using either the Gauss-Seidel or the Jacobi iteration process.
4. Conclusion
In this paper, we are able to demonstrate that exponential
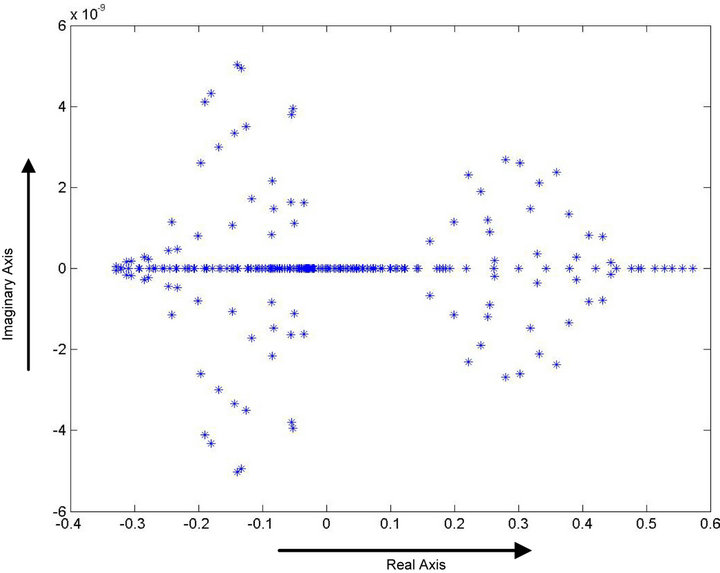
Figure 6. Eigenspectrum of the Jacobi iteration matrix for α = 10 and γ = 10.
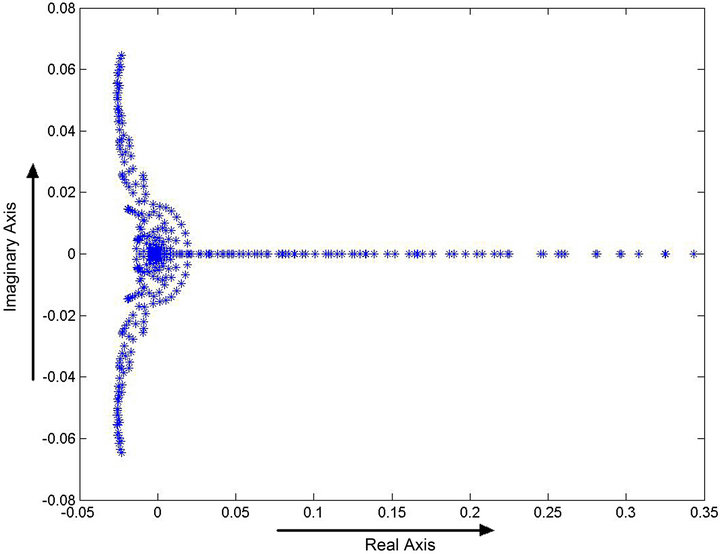
Figure 7. Eigenspectrum of the Gauss-Seidel iteration matrix for α = 10 and γ = 10.
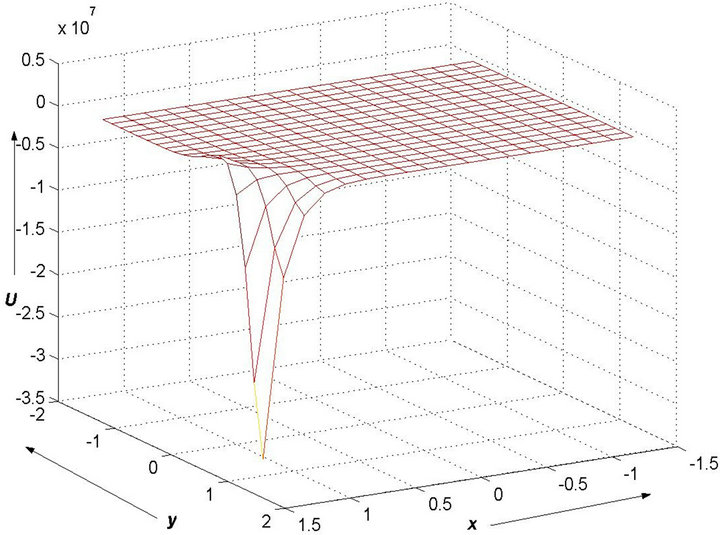 (a)
(a)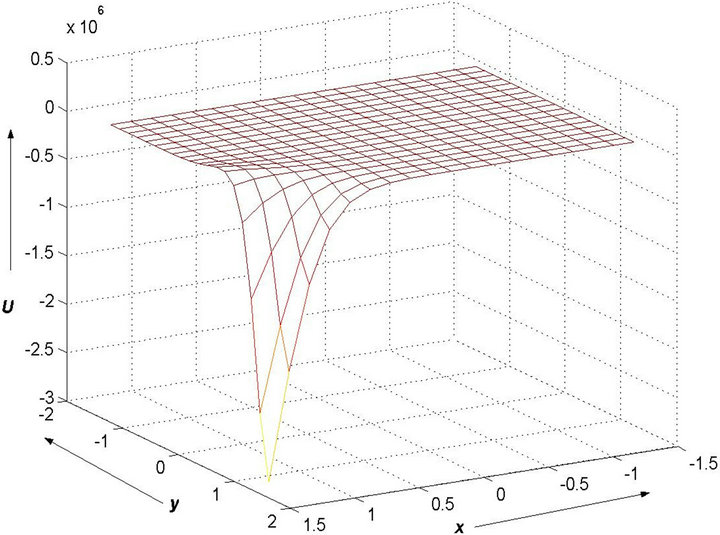 (b)
(b)
Figure 8. Analytical steady state solutions with (a) α = 10, β = 1, γ = 1, δ = 1 and (b) α = 1, β = 1, γ = 10, δ = 1.
upwinding is an extremely useful technique in convection diffusion computations. Even, if convection is dominant, employing exponential upwinding helps one to compute the solution without any difficulty. In particular, we have shown that one could easily use either the Jacobi or the Gauss-Seidel iteration process on the linear system of equations resulting from an exponentially upwinded scheme and obtain a converged solution that is free of unwanted oscillations. This is possible because, in the exponentially upwinded case, the spectral radii of the
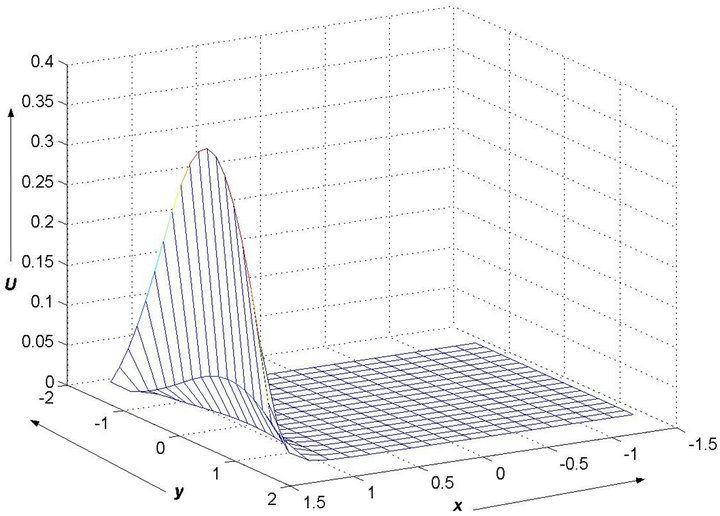
Figure 9. Error in the computed solution when using GaussSeidel method with α = 10, β = 1, γ = 1, δ = 1.
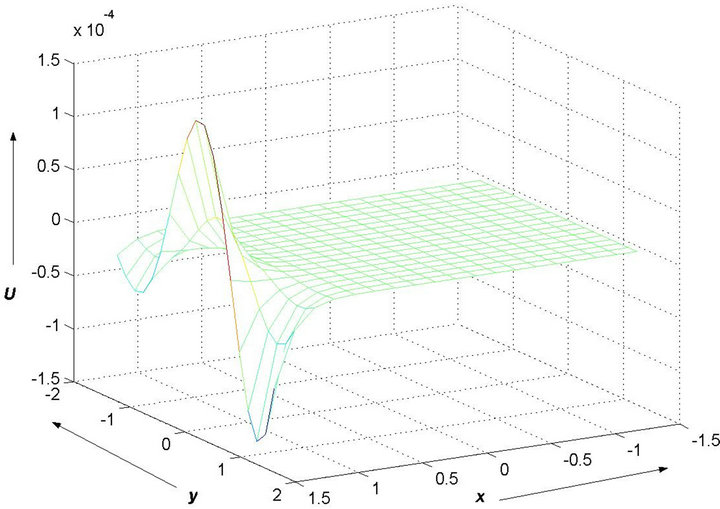
Figure 10. Error in the computed solution when using GaussSeidel method with α = 1, β = 1, γ = 10, δ = 1.
corresponding iteration matrices are always found to be less than one. Thus, satisfying the condition for convergence of the chosen iteration process.
REFERENCES
- D. F. Griffiths and A. R. Mitchell, “On Generating Upwind Finite Element Methods,” Finite Element Methods for Convection Dominated Flows, Vol. 34, 1979, pp. 91- 104.
- G. H. Golub and C. F. Van Loan, “Matrix Computations,” The Johns Hopkins University Press, Baltimore, 1990.
- R. S. Varga, “Matrix Iterative Analysis,” Prentice-Hall, Upper Saddle River, 1962.
- V. S. Manoranjan and R. Drake, “A Spectrum Enveloping Technique for Convection-Diffusion Computations,” IMA Journal of Numerical Analysis, Vol. 13, No. 3, 1993, pp. 431-443. doi:10.1093/imanum/13.3.431
- R. Wait and A. R. Mitchell, “Finite Element Analysis and Applications,” John Wiley and Sons, New York, 1985.
- A. R. Mitchell, “Computational Methods in Partial Differential Equations,” John Wiley and Sons, London, 1969.
- K. W. Morton and D. F. Mayers, “Numerical Solution of Partial Differential Equations,” Cambridge University Press, Cambridge, 2001.
- V. S. Manoranjan and M. O. Gomez, “Alternating Direction Implicit Method with Exponential Upwinding,” Computers & Mathematics with Applications, Vol. 30, No. 11, 1995, pp. 47-58. doi:10.1016/0898-1221(95)00163-S
NOTES
*Currently at Los Alamos National Laboratory, Los Alamos, NM, USA.
#Corresponding author.

