Applied Mathematics
Vol.4 No.3(2013), Article ID:28859,8 pages DOI:10.4236/am.2013.43073
On Retractions of Lobachevsky Space
1Mathematics Department, Faculty of Science, Tanta University, Tanta, Egypt
2Mathematics Department, Faculty of Science, Taibah University, Madinah, Saudi Arabia
Email: a_elahmady@hotmail.com
Received November 13, 2012; revised January 14, 2013; accepted January 21, 2013
Keywords: Lobachevsky Space; Lagrangian Equations; Retractions; Deformation Retractions; Foldings
ABSTRACT
Our aim in the present article is to introduce and study new types of retractions of Lobachevsky space. Types of the deformation retracts of Lobachevsky space are presented. The relations between the folding and the deformation retract of Lobachevsky space are deduced .Types of minimal retractions of Lobachevsky space are also presented. Also, the isometric and topological folding in each case and the relation between the deformation retracts after and before folding have been obtained. New types of homotopy maps are deduced. Theorems governing this connection are achieved.
1. Introduction
Lobachevsky space represents one of the most intriguing and emblematic discoveries in the history of geometry. Although if it were introduced for a purely geometrical purpose, they came into prominence in many branches of mathematics and physics. This association with applied science and geometry generated synergistic effect: applied science gave relevance to Lobachevsky space and Lobachevsky allowed formalizing practical problems ElAhmady [1,2].
Most folding problems are attractive from a pure mathematical standpoint, for the beauty of the problems themselves. The folding problems have close connections to important industrial applications Linkage folding has applications in robotics and hydraulic tube bending. Paper folding has application in sheet-metal bending, packaging, and air-bag folding. Following the great Soviet geometer, also, used folding to solve difficult problems related to shell structures in civil engineering and aero space design, namely buckling instability El-Ahmady [3,4]. Isometric folding between two Riemannian manifold may be characterized as maps that send piecewise geodesic segments to a piecewise geodesic segments of the same length El-Ahmady [5]. For a topological folding the maps do not preserves lengths El-Ahmady [6,7], i.e. A map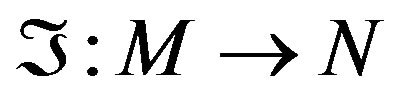 , where
, where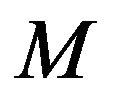 and
and 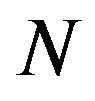 are
are  Riemannian manifolds of dimension m and n respectively is said to be an isometric folding of M into N, iff for any piecewise geodesic path
Riemannian manifolds of dimension m and n respectively is said to be an isometric folding of M into N, iff for any piecewise geodesic path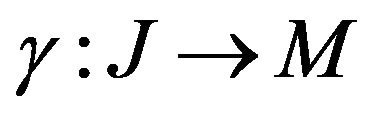 , the induced path
, the induced path 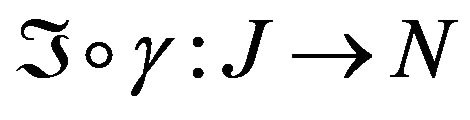 is a piecewise geodesic and of the same length as
is a piecewise geodesic and of the same length as . If
. If  does not preserve length, then
does not preserve length, then  is a topological folding El-Ahmady [8,9].
is a topological folding El-Ahmady [8,9].
A subset A of a topological space X is called a retract of X if there exists a continuous map 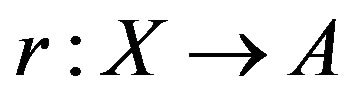 such that
such that 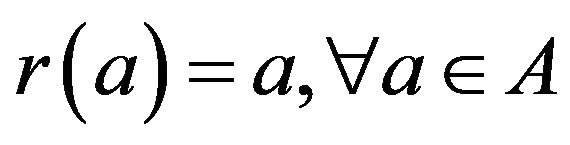 where A is closed and X is open El-Ahmady [10-20]. Also, let X be a space and A a subspace. A map
where A is closed and X is open El-Ahmady [10-20]. Also, let X be a space and A a subspace. A map 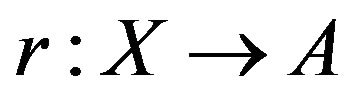 such that
such that  is called a retraction of X onto A and A is the called a retract of X Reid [21]. This can be re stated as follows. If
is called a retraction of X onto A and A is the called a retract of X Reid [21]. This can be re stated as follows. If  is the inclusion map, then
is the inclusion map, then 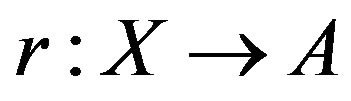 is a map such that
is a map such that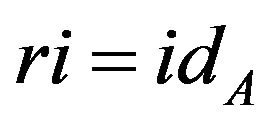 . If, in addition,
. If, in addition, 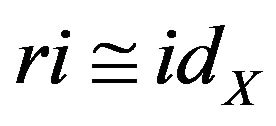 , we call
, we call  a deformation retract and A a deformation retract of X Arkowitz [22], Shick [23] and Storn [24]. The aim of this paper is to describe and study new types of retraction, deformation retract and folding the of Lobachevsky space.
a deformation retract and A a deformation retract of X Arkowitz [22], Shick [23] and Storn [24]. The aim of this paper is to describe and study new types of retraction, deformation retract and folding the of Lobachevsky space.
2. Main Results
We start with a metric of the Lobachevsky space 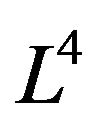 in the special spherical Riemann mode
in the special spherical Riemann mode 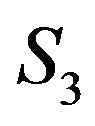 Kudryashov [25].
Kudryashov [25].
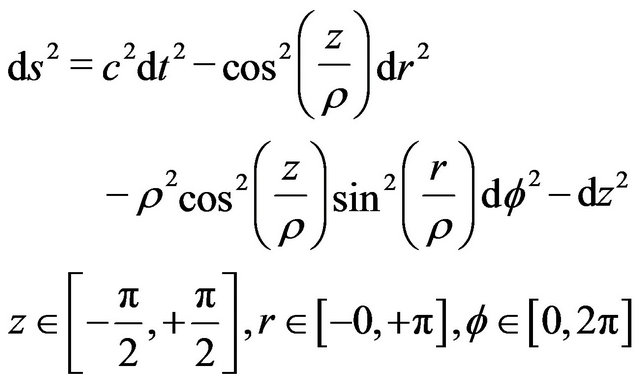 (1)
(1)
And  is a curvature radius. The spherical coordinates are given by
is a curvature radius. The spherical coordinates are given by
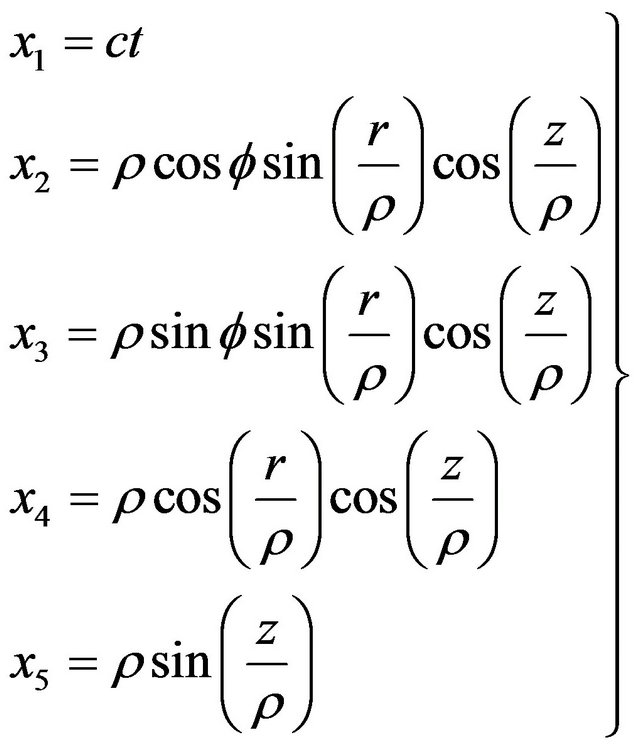 (2)
(2)
Using Lagrangian equations
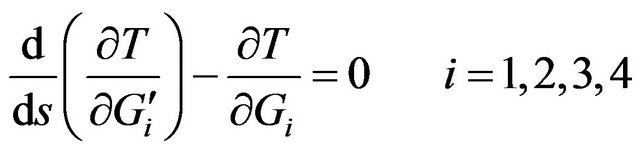
To find a geodesic which is a subset of spherical Riemann model . Since
. Since
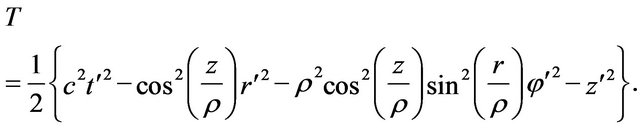
Then the Lagrangian equations are expressed as
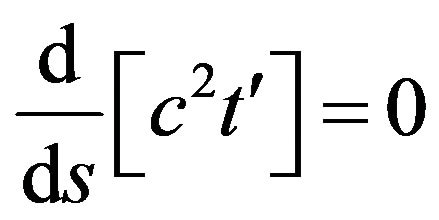 (3)
(3)
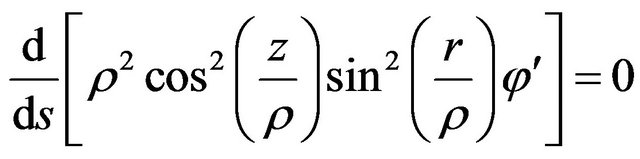 (4)
(4)
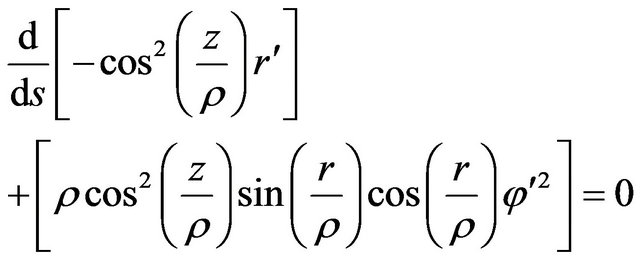 (5)
(5)
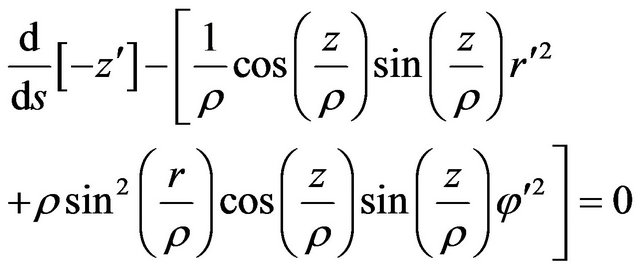 (6)
(6)
From Equation (4) we obtain 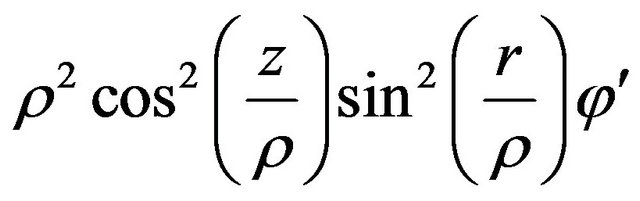
= constant say , if
, if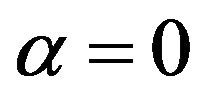 , we obtain the following cases, if
, we obtain the following cases, if 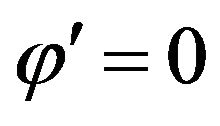 then
then ; if
; if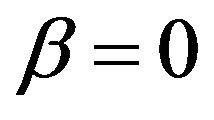 , then from (2) we obtain
, then from (2) we obtain
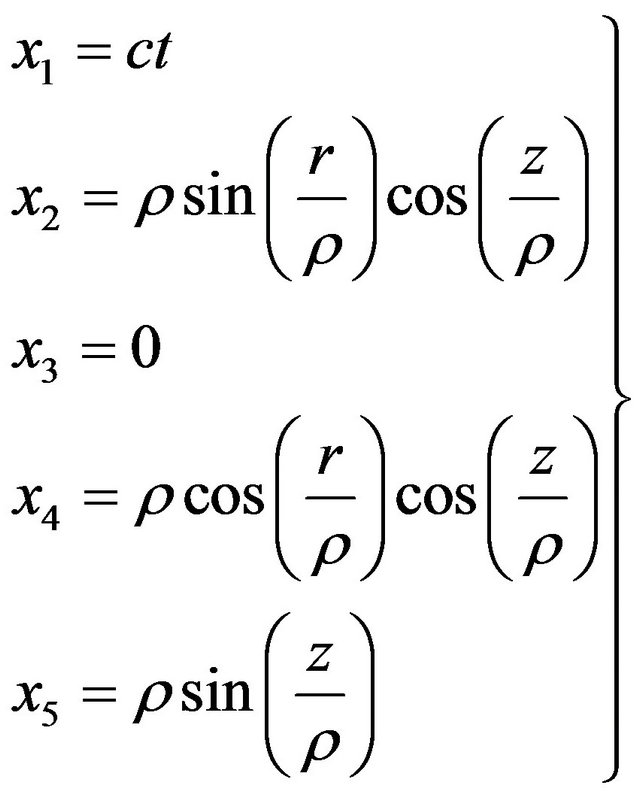 (7)
(7)
which is a Riemann sphere  in Lobachevsky space
in Lobachevsky space  with
with 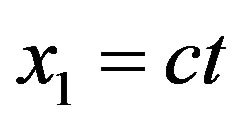 and
and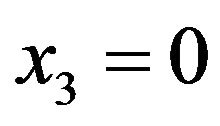 , which is a retraction and geodesic. Specially if
, which is a retraction and geodesic. Specially if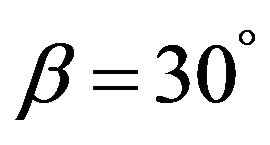 , hence we get the coordinates are defined by
, hence we get the coordinates are defined by
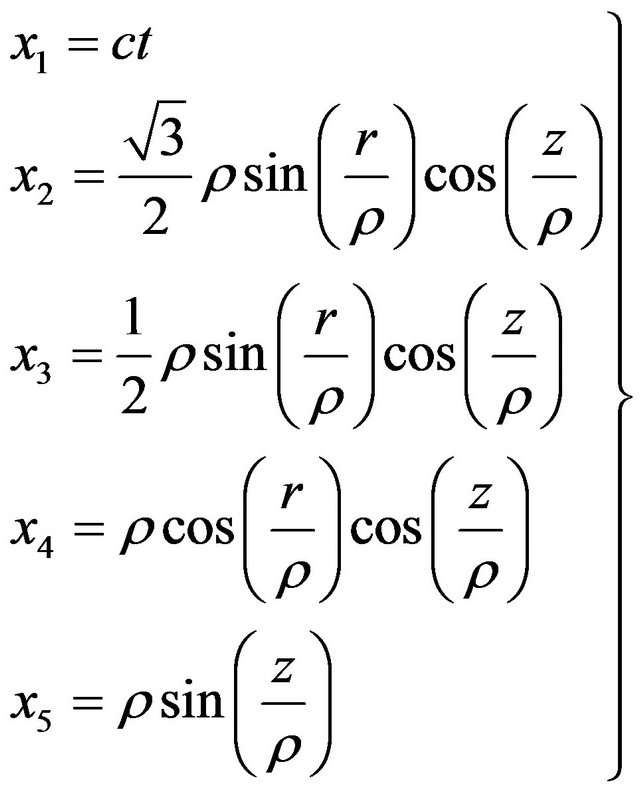 (8)
(8)
which is a hypersurface  in Lobachevsky space
in Lobachevsky space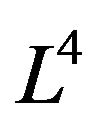 , with
, with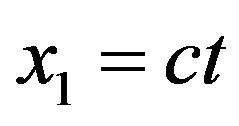 , which is a retraction and geodesic. Also if
, which is a retraction and geodesic. Also if  takes the values
takes the values ,
,  ,
,  ,
,  ,
, 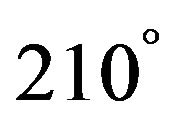 ,
,  ,
, 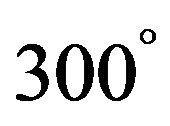 and
and 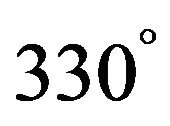 we get new types of hypersurface
we get new types of hypersurface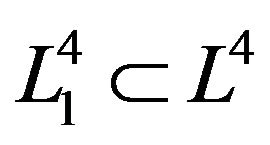 , i = 2 - 9 in Lobachevsky space L4 with x1 = ct. Specially if β = 90˚ hence we get the coordinates are defined by
, i = 2 - 9 in Lobachevsky space L4 with x1 = ct. Specially if β = 90˚ hence we get the coordinates are defined by
 (9)
(9)
Which is a Riemann sphere 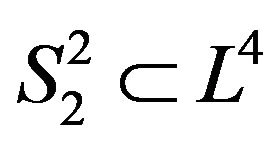 in Lobachevsky space, it is a geodesic and retraction. Also, if
in Lobachevsky space, it is a geodesic and retraction. Also, if 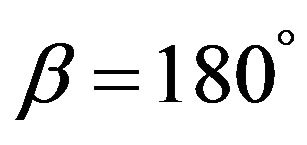 we have a Riemann sphere
we have a Riemann sphere , it is a geodesic and retraction. Where
, it is a geodesic and retraction. Where
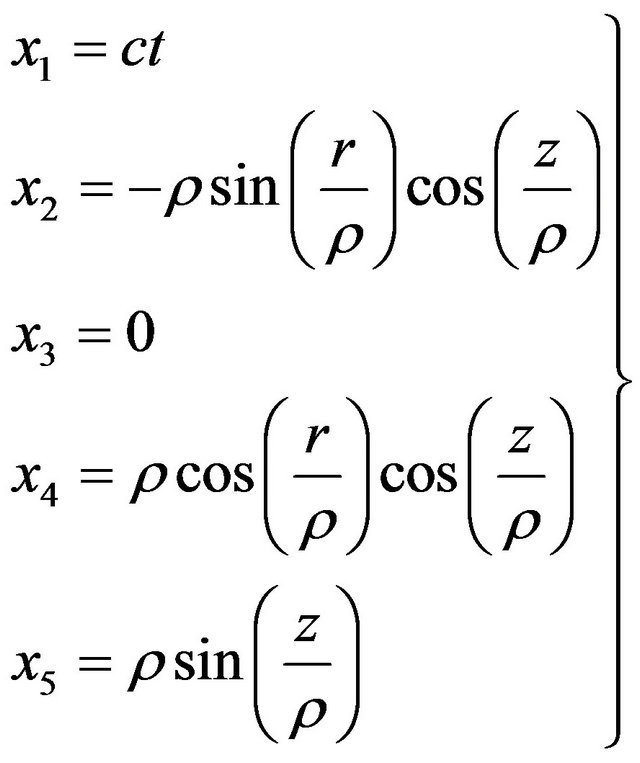 (10)
(10)
And also, if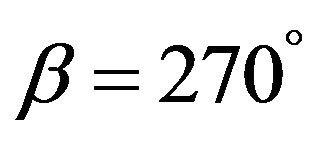 , we have a Riemann sphere
, we have a Riemann sphere 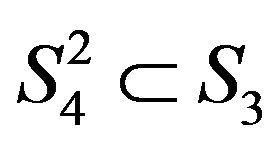 in Lobachevsky space, it is a geodesic and retraction, where
in Lobachevsky space, it is a geodesic and retraction, where
 (11)
(11)
Now, if 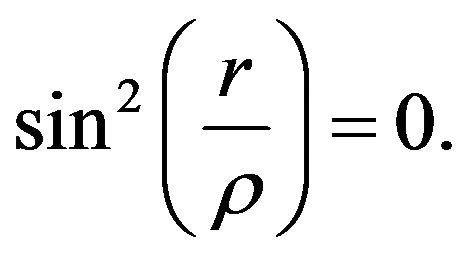 Then we get the following coordinates
Then we get the following coordinates
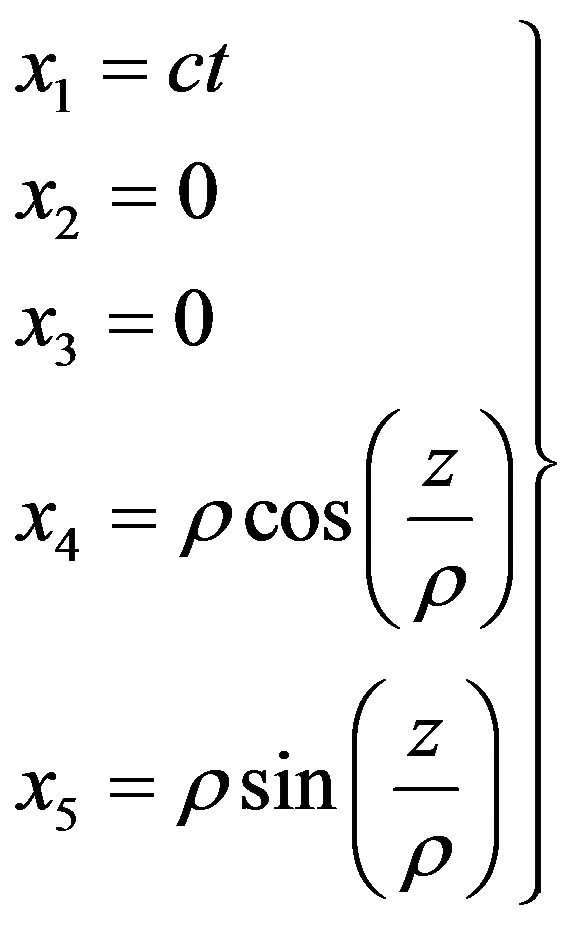 (12)
(12)
Hence, 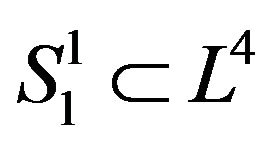 is the great circle, it is a geodesic and retraction.
is the great circle, it is a geodesic and retraction.
Also, if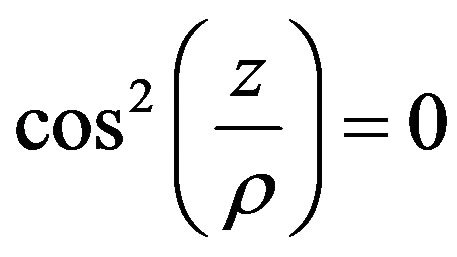 ,
, 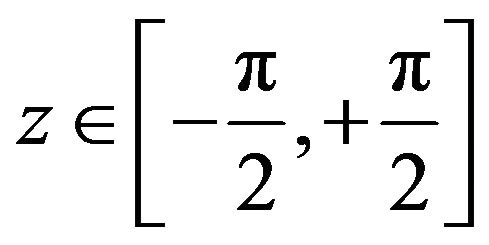 , then the Riemann point
, then the Riemann point 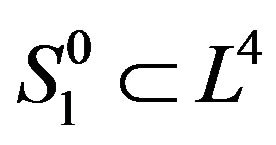 in Lobachevsky space is represented by the following coordinates
in Lobachevsky space is represented by the following coordinates
 (13)
(13)
it is a minimal retraction in Lobachevsky space .
.
Now, if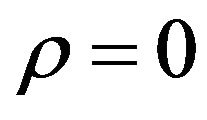 , then
, then the retraction is represented by the following coordinates
the retraction is represented by the following coordinates
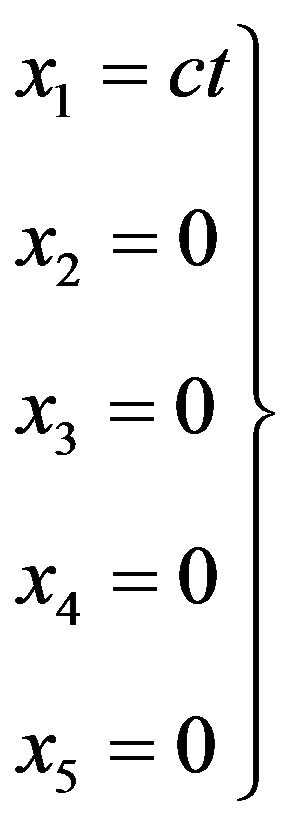 (14)
(14)
Which is a Riemann point  in Lobachevsky space.
in Lobachevsky space. . From Equation (3) we obtain
. From Equation (3) we obtain , if
, if , then we get the following coordinates
, then we get the following coordinates
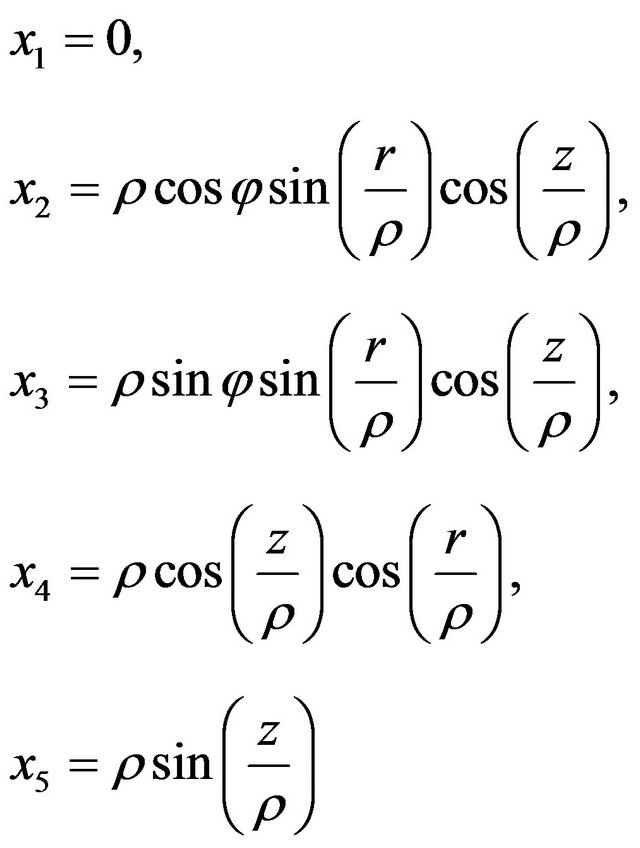 (15)
(15)
Hence, 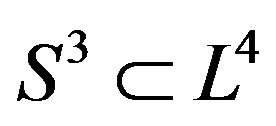 is a Riemann hyper sphere, it is a geodesic and retraction.
is a Riemann hyper sphere, it is a geodesic and retraction.
Theorem 1. The retractions of Lobachevsky space 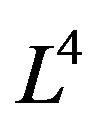 are geodesics Riemann hypersphere, great circles, Riemann point and hyper subspace.
are geodesics Riemann hypersphere, great circles, Riemann point and hyper subspace.
In this position, we present some cases of the deformation retract of Lobachevsky space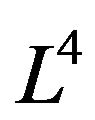 . The retraction of the open Lobachevsky space
. The retraction of the open Lobachevsky space 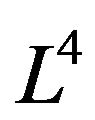 is given by
is given by
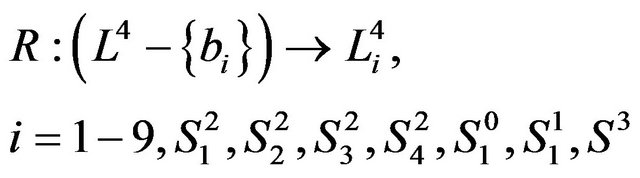
The deformation retract of Lobachevsky space is
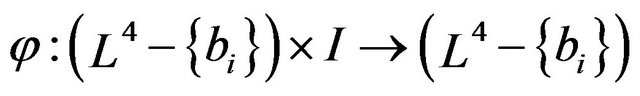
where  is the open Lobachevsky space and I is the closed interval [0,1], be present as
is the open Lobachevsky space and I is the closed interval [0,1], be present as
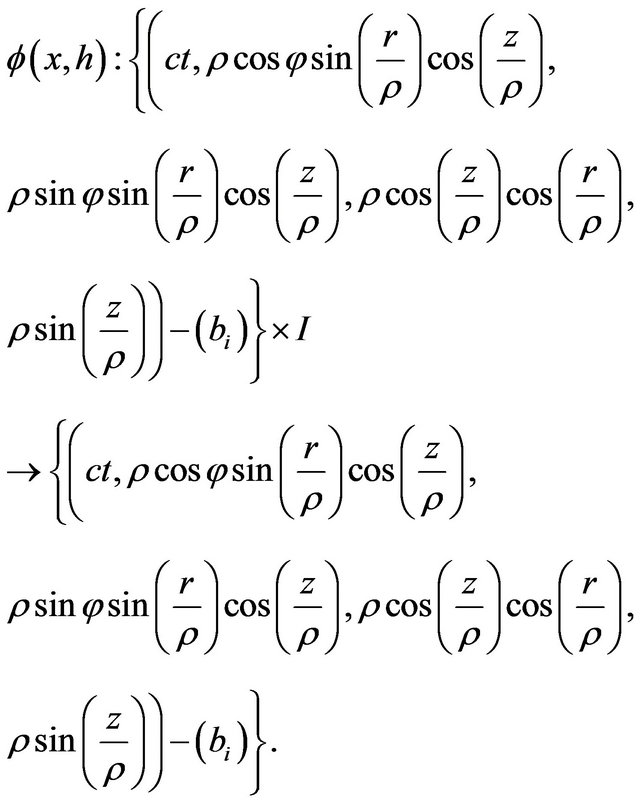
The deformation retract of the Lobachevsky space 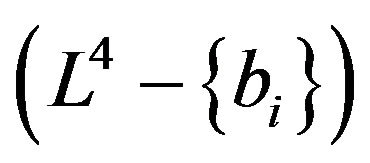 into the retraction Riemann sphere
into the retraction Riemann sphere  is
is
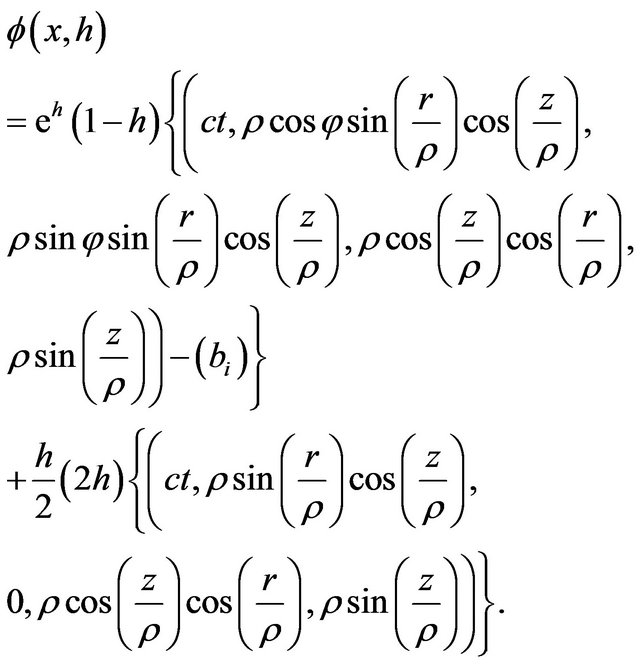
where

And

The deformation retract of the Lobachevsky space 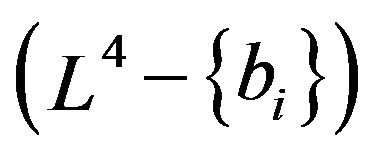 into the retraction hyper surface
into the retraction hyper surface 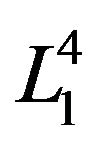 is
is
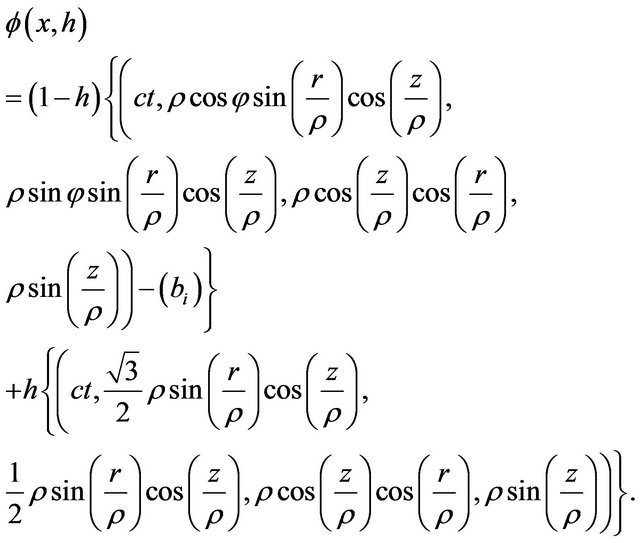
The deformation retract of the Lobachevsky space  into the retraction Riemann sphere
into the retraction Riemann sphere 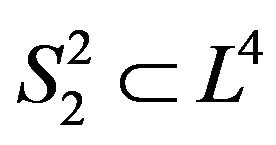 is defined as
is defined as
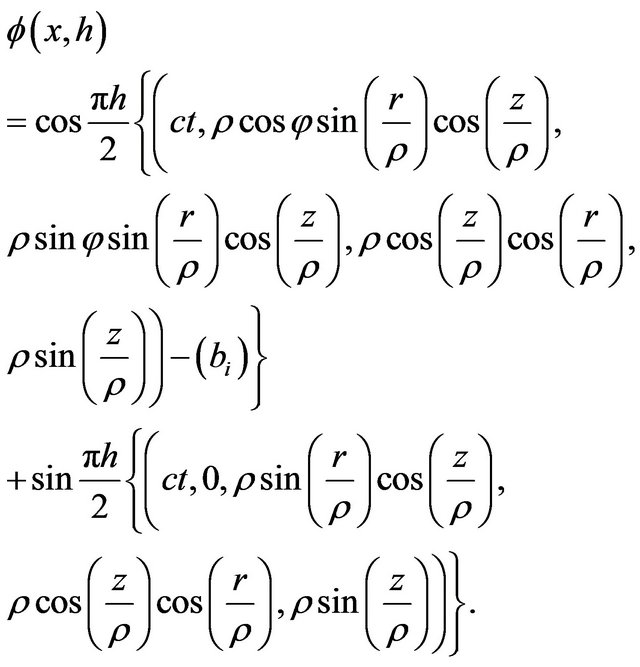
The deformation retract of the Lobachevsky space  into the retraction Riemann sphere
into the retraction Riemann sphere 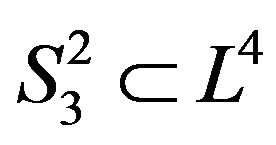 is
is
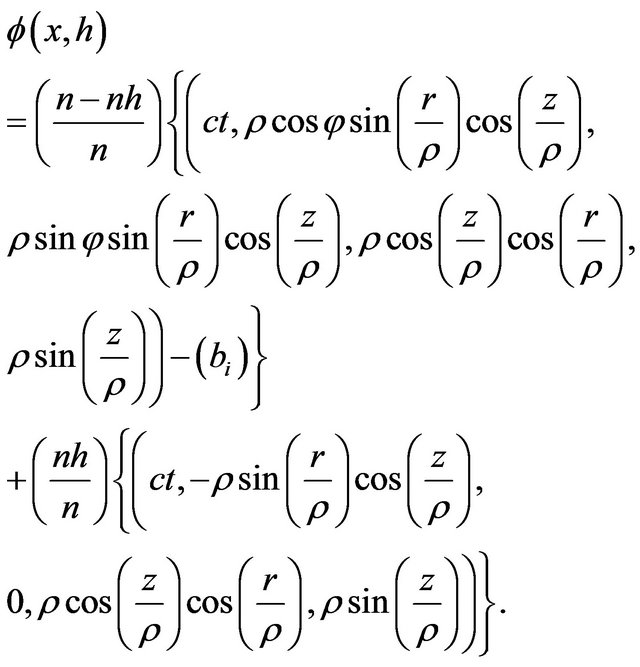
The deformation retract of the Lobachevsky space  into the retraction Riemann sphere
into the retraction Riemann sphere  is defined as
is defined as
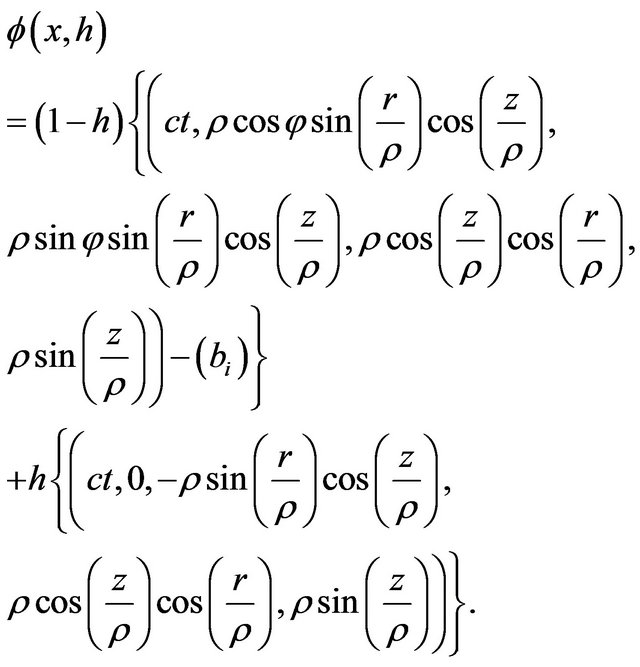
The deformation retract of the Lobachevsky space  into the great circle
into the great circle  is defined by
is defined by
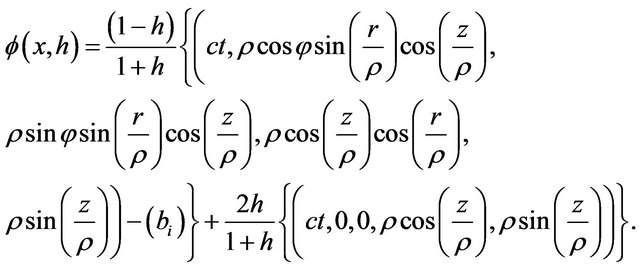
The deformation retract of the Lobachevsky space  into the retraction Riemann point
into the retraction Riemann point  is given by
is given by
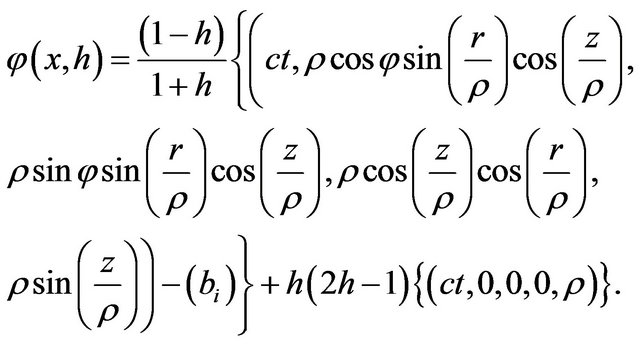
The deformation retract of the Lobachevsky space  into the retraction Riemann point
into the retraction Riemann point  is defined as
is defined as
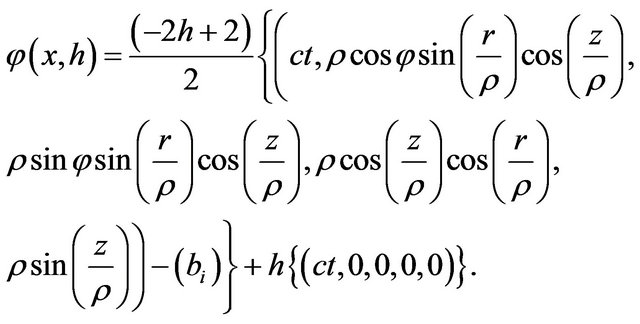
The deformation retract of the Lobachevsky space  into the geodesic Riemann hyper sphere
into the geodesic Riemann hyper sphere  is
is
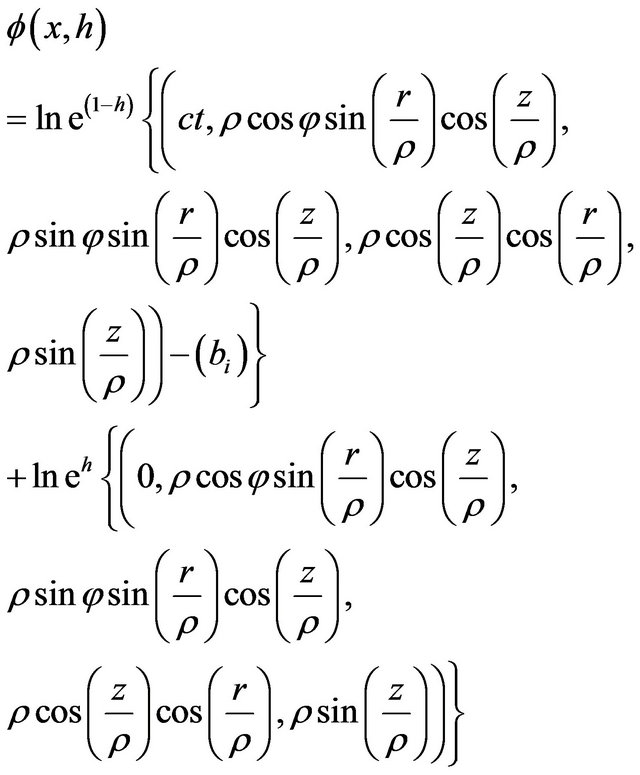
Now, we are going to discuss the folding 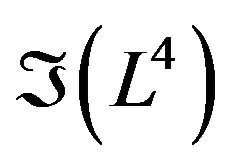 of the Lobachevsky space. Let
of the Lobachevsky space. Let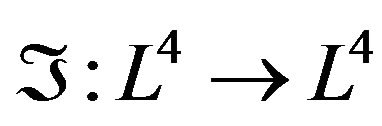 , where
, where
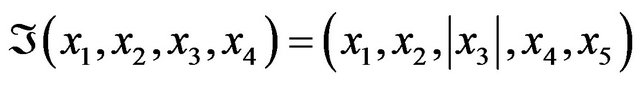 (16)
(16)
An isometric folding of the Lobachevsky space  into itself may be defined by
into itself may be defined by
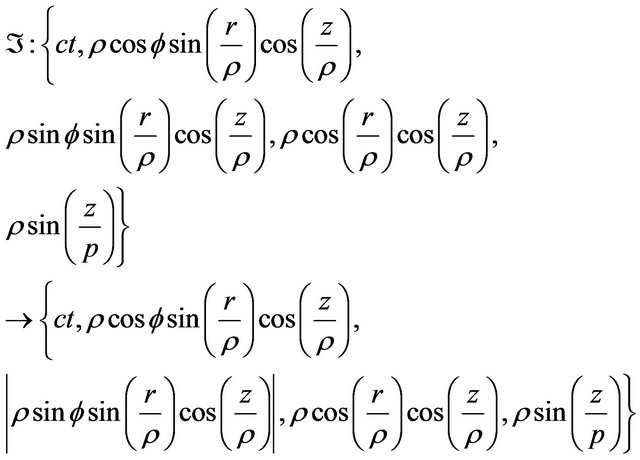
The deformation retract of the folded Lobachevsky space 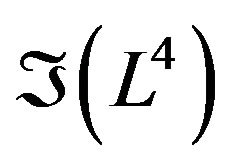 into the folded geodesic
into the folded geodesic 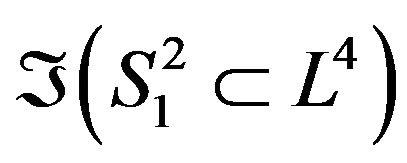 is
is
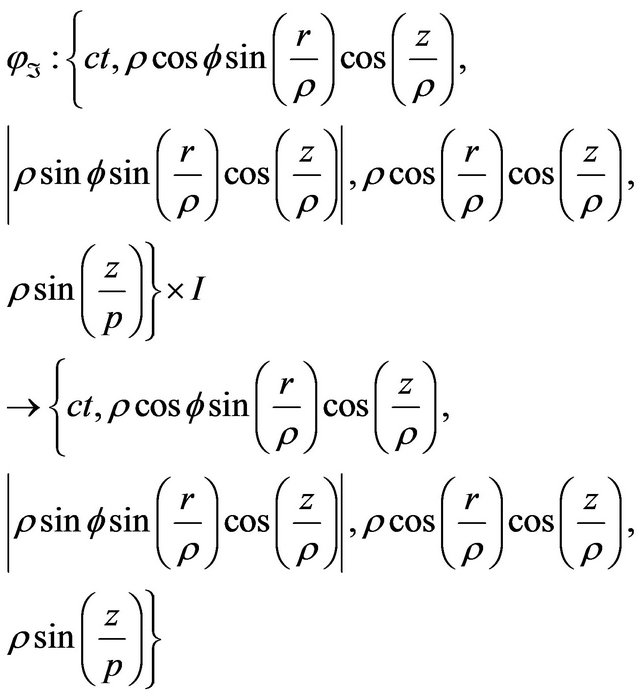
With

The deformation retract of the folded Lobachevsky space 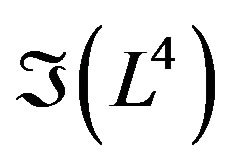 into the folded geodesic
into the folded geodesic 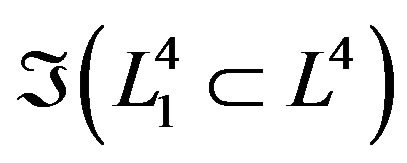 is
is
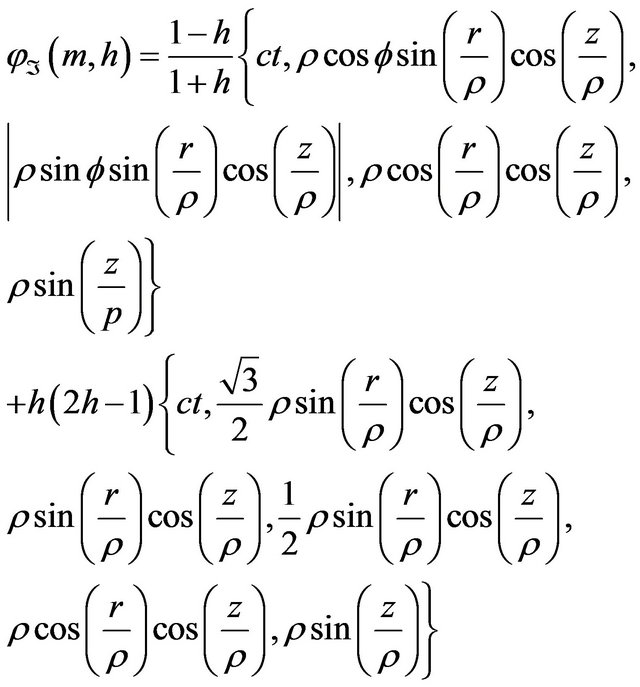
The deformation retract of the folded Lobachevsky space 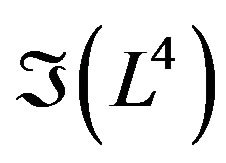 into the folded geodesic
into the folded geodesic 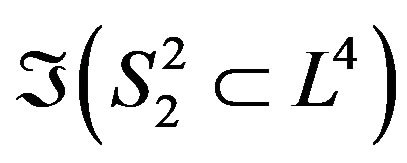 is
is

Then, the following theorem has been proved.
Theorem 2. Under the defined folding, the deformation retract of the folded Lobachevsky space i.e. 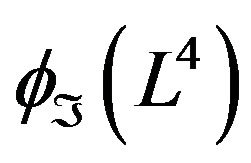 into the folded geodesic is the same as the deformation retract of the Lobachevsky space into the geodesics.
into the folded geodesic is the same as the deformation retract of the Lobachevsky space into the geodesics.
Now, if the folding is defined by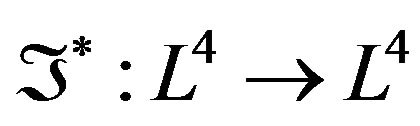 , where
, where
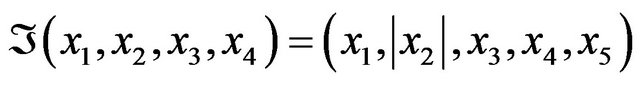 (17)
(17)
The isometric folded Lobachevsky space time 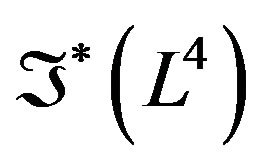 is defined as
is defined as

The deformation retract of the folded Lobachevsky space 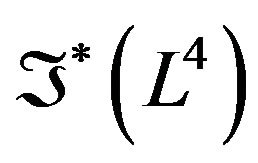 into the folded geodesic
into the folded geodesic 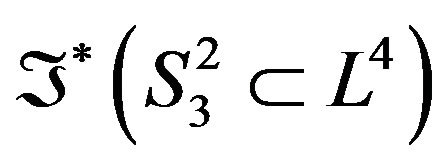 is given by
is given by
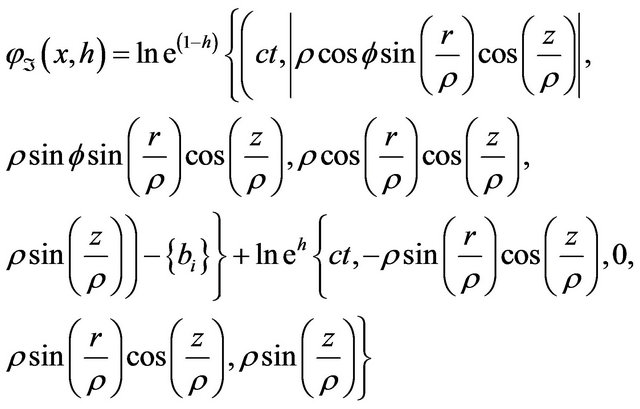
Hence, we can formulate the following theorem .
Theorem 3. Under the defined folding, the deformation retract of the folded Lobachevsky space into the folded geodesic is different from the deformation retract of the Lobachevsky space into the geodesics.
If we let 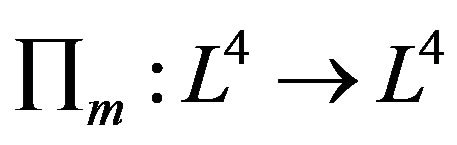 be given by
be given by
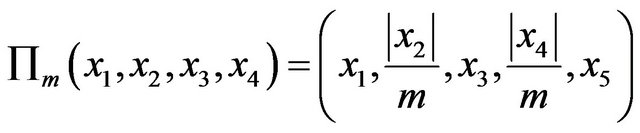 (18)
(18)
Then, the isometric chain folding of Lobachevsky space  into itself may be defined by:
into itself may be defined by:
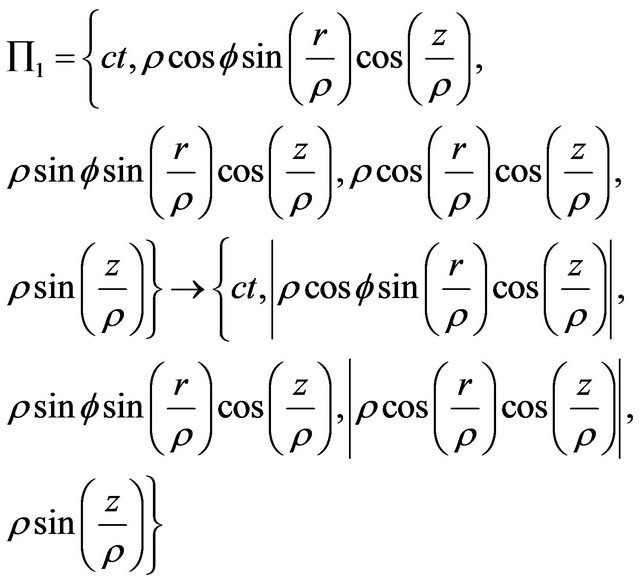
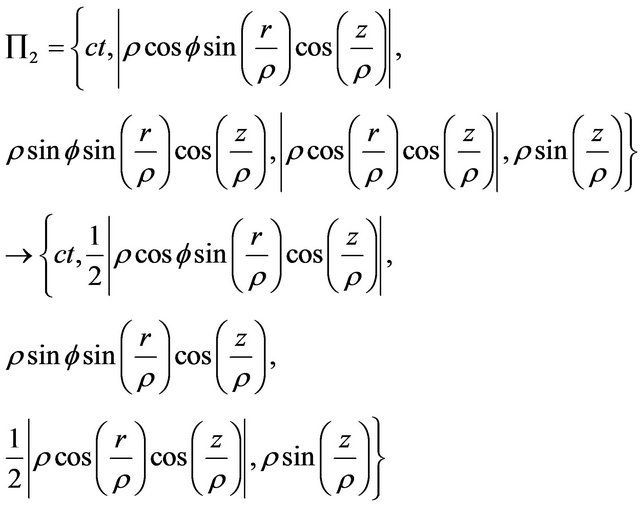
 ,
,
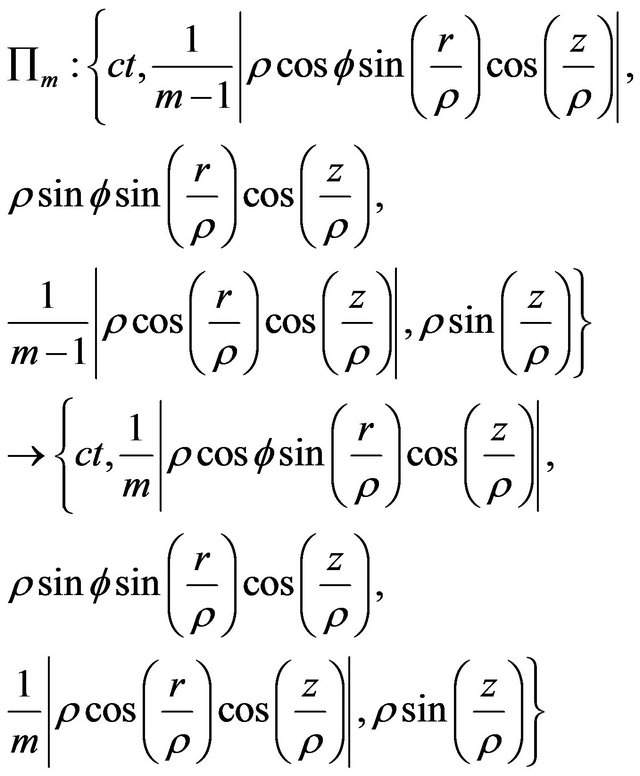
 Then we get
Then we get
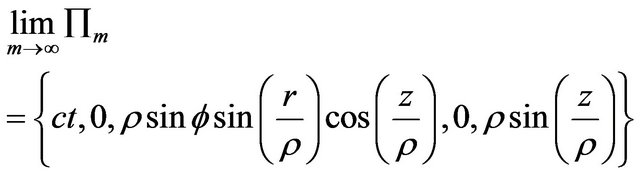
which is hypersurface 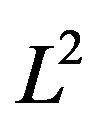 in Lobachevsky space.
in Lobachevsky space.
From the above discussion we will arrive to the following theorem.
Theorem 4. The limit folding of the Lobachevsky space 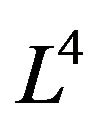 into itself, under Condition (18), is different from the retraction of the Lobachevsky space
into itself, under Condition (18), is different from the retraction of the Lobachevsky space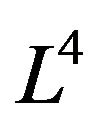 .
.
If the folding is defined by 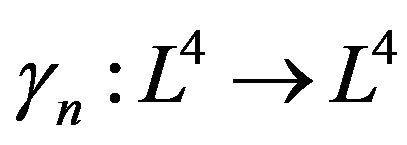 such that
such that
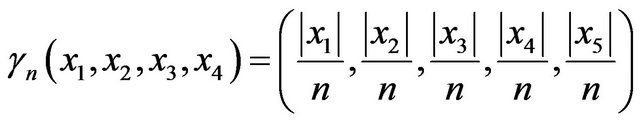 (19)
(19)
Then, the isometric chain folding of Lobachevsky space 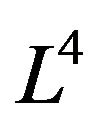
 into itself may be defined by:
into itself may be defined by:


 ,
,

Then we get 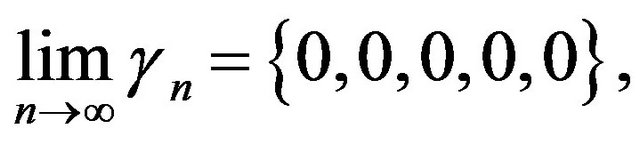 which a zero-dimensional hypersphere in Lobachevsky space
which a zero-dimensional hypersphere in Lobachevsky space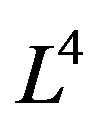 .
.
Thus the following theorem is obtained.
Theorem 5. The limit folding of the Lobachevsky space  into itself, under Condition (19), is equivalent to the zero-dimensional sphere in Lobachevsky space.
into itself, under Condition (19), is equivalent to the zero-dimensional sphere in Lobachevsky space.
Theorem 6. The end of the limits of the foldings of Lobachevsky space 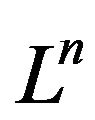 of dimension n is a 0-dimensional Lobachevsky space.
of dimension n is a 0-dimensional Lobachevsky space.
Proof: If we let
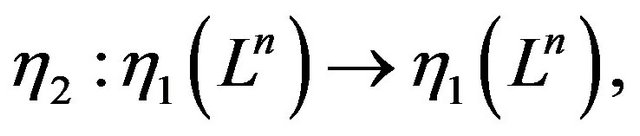
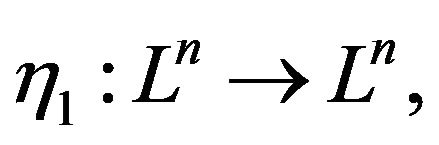
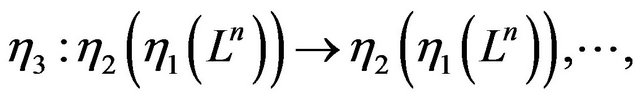

then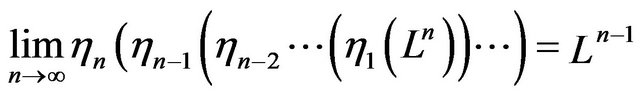 , which is the Lobachevsky space of dimensional
, which is the Lobachevsky space of dimensional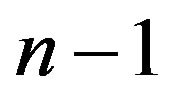 .
.
Also, if we consider
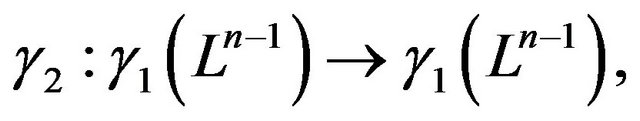
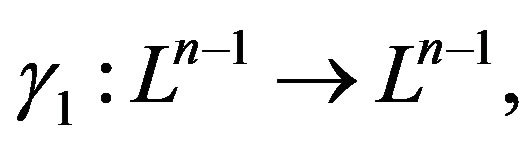
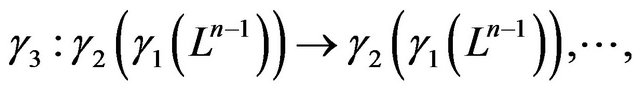
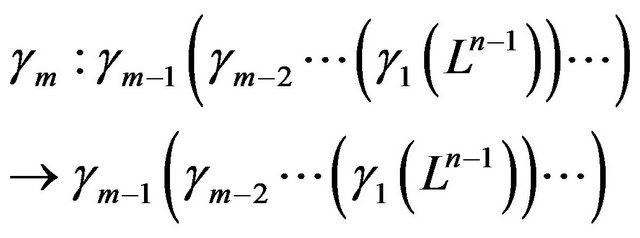
Then
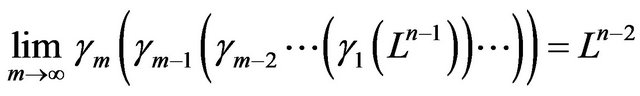 , which is the Lobachevsky space of dimensional n − 2. Consequently,
, which is the Lobachevsky space of dimensional n − 2. Consequently,
 which is a zerodimensional space.
which is a zerodimensional space.
Proposition 1. Under Condition (19) the retraction of 0-dimensional Lobachevsky space is a 0-dimensional space.
Theorem 7. Under Condition (19) the limit of foldings of Lobachevsky space 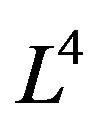 into itself coincide with minimal retraction.
into itself coincide with minimal retraction.
3. Conclusion
In this paper we achieved the approval of the important of the geodesic retractions of the Lobachevsky space. The relations between folding, retractions, deformation retract, limits of folding and limits of retractions of Lobachevsky space are discussed. Theorems which governs these relations are presented.
REFERENCES
- A. E. El-Ahmady, “Fuzzy Folding of Fuzzy Horocycle,” Circolo Matematico di Palermo Serie II, Tomo L III, 2004, pp. 443-450. doi:10.1007/BF02875737
- A. E. El-Ahmady, “Fuzzy Lobachevskian Space and Its Folding,” The Journal of Fuzzy Mathematics, Vol. 12, No. 2, 2004, pp. 609-614.
- A. E. El-Ahmady, “Folding and Fundamential Groups of Buchdahi Space,” Indian Journal of Science and Technology, Vol. 6, No. 1, 2013, pp. 3940-3945.
- A. E. El-Ahmady, “On the Fundamential Group and Folding of Klein Bottle,” International Journal of Applied Mathematics and Statistics, Vol. 37, No. 6, 2013, pp. 56-64.
- A. E. El-Ahmady, “The Geodesic Deformation Retract of Klein Bottle and Its Folding,” The International Journal of Nonlinear Science, Vol. 9, No. 3, 2011, pp. 1-8.
- A. E. El-Ahmady, “Retraction of Chaotic Black Hole,” The Journal of Fuzzy Mthematics, Vol. 19, No. 4, 2011, pp. 833-838.
- A. E. El-Ahmady, “Folding of Fuzzy Hypertori and Their Retractions,” Proceedings of the Mathematical and Physical Society of Egypt, Vol. 85, No. 1, 2007, pp. 1-10.
- A. E. El-Ahmady, “Limits of Fuzzy Retractions of Fuzzy Hyperspheres and Their Foldings,” Tamkang Journal of Mathematics, Vol. 37, No. 1, 2006, pp. 47-55.
- A. E. El-Ahmady, “The Variation of the Density Functions on Chaotic Spheres in Chaotic Space-Like Minkowski Space Time,” Chaos, Solitons and Fractals, Vol. 31, No. 5, 2007, pp. 1272-1278. doi:10.1016/j.chaos.2005.10.112
- A. E. El-Ahmady, “The Deformation Retract and Topological Folding of Buchdahi Space,” Periodica Mathematica Hungarica, Vol. 28, No. 1, 1994, pp. 19-30. doi:10.1007/BF01876366
- A. E. El-Ahmady, “Folding of Some Types of Einstein Spaces,” The International Journal of Nonlinear Science, in Press.
- A. E. El-Ahmady and K. Al-Onema, “On the Folding of Lobachevsky Space,” International Journal of Applied Mathematics and Statistics, Vol. 4, No. 10, 2013, pp. 13-23.
- A. E. El-Ahmady, “On Elastic Klein Bottle and Fundamental Groups,” Applied Mathematics, Accepted.
- A. E. El-Ahmady, “The Deformation Retract and Topological Folding of the Schwarzchild Space,” Journal of Mathematical Physics, Vol. 25, No. 3, 1991.
- A. E. El-Ahmady and N. Al-Hazmi, “Retractions of One Dimensional Manifold,” Applied Mathematics, Vol. 3, No. 10, 2012, pp. 1135-1143.
- A. E. El-Ahmady and E. Al-Hesiny, “Folding and Deformation Retract of Hyperhelix,” Journal of Mathematics and Statistics, Vol. 8, No. 2, 2012, pp. 241-247.
- A. E. El-Ahmady and E. Al-Hesiny, “The Topological Folding of the Hyperbola in Minkowski 3-Space,” The International Journal of Nonlinear Science, Vol. 11, No. 4, 2011, pp. 451-458.
- A. E. El-Ahmady and A. S., Al-Luhaybi, “A Calculation of Geodesics in Flat Robertson-Walker Space and Its Folding,” International Journal of Applied Mathematics and Statistics, Vol. 33, No. 3, 2013, pp. 83-91.
- A. E. El-Ahmady and A. Al-Rdade, “A Geometrical Characterizations of Reissner-Nordström Spacetime and Its Retractions,” International Journal of Applied Mathematics and Statistics, Vol. 33, No. 3, 2013, pp. 83-91.
- A. E. El-Ahmady and A. S. Al-Luhaybi, “Ageometrical Characterization of Spatially Curved Robertson-Walker Space and Its Retractions,” Applied Mathematics, Vol. 3, No. 10, 2012, pp. 1153-1160.
- M. Reid and B. Szendroi, “Topology and Geometry,” Cambridge University Press, Cambridge, New York, 2005.
- M. Arkowitz, “Introduction to Homotopy Theory,” Springer-Verlage, New York, 2011. doi:10.1007/978-1-4419-7329-0
- P. I. Shick, “Topology: Point-Set and Geometry,” Wiley, New York, 2007.
- J. Strom, “Modern Classical Homotopy Theory,” American Mathematical Society, 2011.
- V. V. Kudryashov, Yu. A. Kurochkin, E. M. Ovsiyuk and M. Red’kow, “Motion Caused by Magnetic Field in Lobachevsky Space,” 2010.

