Applied Mathematics
Vol.3 No.12(2012), Article ID:25460,7 pages DOI:10.4236/am.2012.312261
Propagation of Waves in a Two-Temperature Rotating Thermoelastic Solid Half-Space without Energy Dissipation
1Department of Mathematics, Post Graduate Government College, Chandigarh, India
2Department of Mathematics, Government College, Barwala, India
3Department of Mathematics, Singhania University, Rajasthan, India
Email: bsinghgc11@gmail.com, kirandulat@gmail.com
Received September 11, 2012; revised October 9, 2012; accepted October 17, 2012
Keywords: Two-Temperature; Generalized Thermoelasticity; Reflection; Reflection Coefficients; Energy Dissipation; Rotation
ABSTRACT
The present paper is concerned with the propagation of plane waves in an isotropic two-temperature generalized thermoelastic solid half-space in context of Green and Naghdi theory of type II (without energy dissipation). The governing equations in x-z plane are solved to show the existence of three coupled plane waves. The reflection of plane waves from a thermally insulated free surface is considered to obtain the relations between the reflection coefficients. A particular example of the half-space is chosen for numerical computations of the speeds and reflection coefficients of plane waves. Effects of two-temperature and rotation parameters on the speeds and the reflection coefficients of plane waves are shown graphically.
1. Introduction
Lord and Shulman [1] and Green and Lindsay [2] extended the classical dynamical coupled theory of thermoelasticity to generalized thermoelasticity theories. These theories treat heat propagation as a wave phenomenon rather than a diffusion phenomenon and predict a finite speed of heat propagation. Ignaczak and Ostoja-Starzewski [3] explained in detail, the above theories in their book on “Thermoelasticity with Finite Wave Speeds”. The theory of thermoelasticity without energy dissipation is another generalized theory, which was formulated by Green and Naghdi [4]. It includes the isothermal displacement gradients among its independent constitutive variables and differs from the previous theories in that it does not accommodate dissipation of thermal energy. The representative theories in the range of generalized thermoelasticity are reviewed by Hetnarski and Ignaczak [5]. Wave propagation in thermoelasticity has many applications in various engineering fields. Some problems on wave propagation in coupled or generalized thermoelasticity are studied by various researchers, for example, Deresiewicz [6], Sinha and Sinha [7], Sinha and Elsibai [8,9], Sharma, et al. [10], Othman and Song [11], Singh [12,13], and many more.
Gurtin and Williams [14,15] suggested the second law of thermodynamics for continuous bodies in which the entropy due to heat conduction was governed by one temperature, that of the heat supply by another temperature. Based on this suggestion, Chen and Gurtin [16] and Chen et al. [17,18] formulated a theory of thermoelasticity which depends on two distinct temperatures, the conductive temperature  and the thermodynamic temperature
and the thermodynamic temperature![]() . The two-temperature theory involves a material parameter
. The two-temperature theory involves a material parameter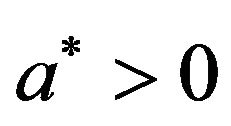 . The limit
. The limit 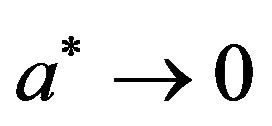 implies that
implies that 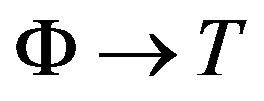 and the classical theory can be recovered from two-temperature theory. The two-temperature model has been widely used to predict the electron and phonon temperature distributions in ultrashort laser processing of metals. Warren and Chen [19] stated that these two temperatures can be equal in time-dependent problems under certain conditions, whereas
and the classical theory can be recovered from two-temperature theory. The two-temperature model has been widely used to predict the electron and phonon temperature distributions in ultrashort laser processing of metals. Warren and Chen [19] stated that these two temperatures can be equal in time-dependent problems under certain conditions, whereas  and
and ![]() are generally different in particular problems involving wave propagation. Following Boley and Tolins [20], they studied the wave propagation in the two-temperature theory of coupled thermoelasticity. They showed that the two temperatures
are generally different in particular problems involving wave propagation. Following Boley and Tolins [20], they studied the wave propagation in the two-temperature theory of coupled thermoelasticity. They showed that the two temperatures ![]() and
and , and the strain are represented in the form of a travelling wave plus a response, which occurs instantaneously throughout the body. Puri and Jordan [21] discussed the propagation of harmonic plane waves in two temperature theory. Quintanilla and Jordan [22] presented exact solutions of two initial-boundary value problems in the two temperature theory with dualphase-lag delay. Youssef [23] formulated a theory of twotemperature generalized thermoelasticity. Kumar and Mukhopadhyay [24] extended the work of Puri and Jordan [21] in the context of the linear theory of two-temperature generalized thermoelasticity formulated by Youssef [23]. Magana and Quintanilla [25] studied the uniqueness and growth of solutions in two-temperature generalized thermoelastic theories. Recently, Youssef [26] presented a theory of two-temperature thermoelasticity without energy dissipation.
, and the strain are represented in the form of a travelling wave plus a response, which occurs instantaneously throughout the body. Puri and Jordan [21] discussed the propagation of harmonic plane waves in two temperature theory. Quintanilla and Jordan [22] presented exact solutions of two initial-boundary value problems in the two temperature theory with dualphase-lag delay. Youssef [23] formulated a theory of twotemperature generalized thermoelasticity. Kumar and Mukhopadhyay [24] extended the work of Puri and Jordan [21] in the context of the linear theory of two-temperature generalized thermoelasticity formulated by Youssef [23]. Magana and Quintanilla [25] studied the uniqueness and growth of solutions in two-temperature generalized thermoelastic theories. Recently, Youssef [26] presented a theory of two-temperature thermoelasticity without energy dissipation.
In the present paper, we have applied Youssef [26] theory to study the wave propagation in an isotropic twotemperature thermoelastic solid. The governing equations are solved to obtain the cubic velocity equation. The required boundary conditions at thermally insulated stress free surface are satisfied by the appropriate solutions in an isotropic thermoelastic solid half-space and we obtain three relations between the reflection coefficients for an incident plane wave. The speeds and reflection coefficients of plane waves are also computed numerically for a particular model of the half-space to capture the effect of the two-temperature and rotation parameters.
2. Basic Equations
We consider a two-temperature thermoelastic medium, which is rotating uniformly with an angular velocity , where
, where ![]() is a unit vector representing the direction of the axis of rotation.The displacement equation of motion in the rotating frame of reference has two additional terms: Centripetal acceleration,
is a unit vector representing the direction of the axis of rotation.The displacement equation of motion in the rotating frame of reference has two additional terms: Centripetal acceleration,  due to time-varying motion only and the Corioli's acceleration,
due to time-varying motion only and the Corioli's acceleration,  where
where ![]() is the dynamic displacement vector. These terms do not appear in non-rotating media. Following Youssef [26], the governing equations for a rotating two-temperature generalized thermoelastic halfspace without energy dissipation are taken in the following form:
is the dynamic displacement vector. These terms do not appear in non-rotating media. Following Youssef [26], the governing equations for a rotating two-temperature generalized thermoelastic halfspace without energy dissipation are taken in the following form:
(i) The heat conduction equation
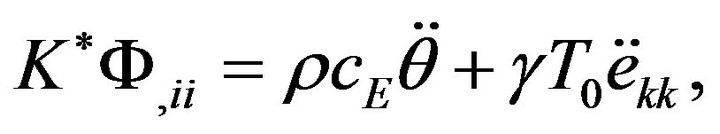 (1)
(1)
(ii) The displacement-strain relation
 (2)
(2)
(iii) The equation of motion
 (3)
(3)
(iv) The constitutive equations
 (4)
(4)
where  is a coupling parameter and
is a coupling parameter and  is the thermal expansion coefficient.
is the thermal expansion coefficient. ![]() and
and 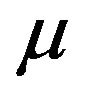 are called Lame’s elastic constants,
are called Lame’s elastic constants, 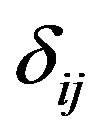 is the Kronecker delta,
is the Kronecker delta,  is material characterstic constant, T is the mechanical temperature,
is material characterstic constant, T is the mechanical temperature, 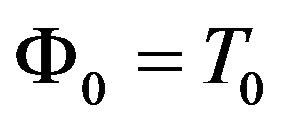 is the reference temperature,
is the reference temperature, 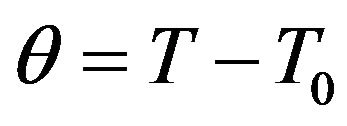 with
with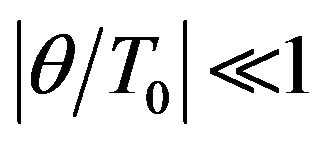 ,
, 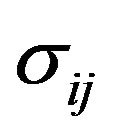 is the stress tensor,
is the stress tensor, 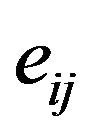 is the strain tensor,
is the strain tensor,  is the mass density,
is the mass density,  is the specific heat at constant strain,
is the specific heat at constant strain, 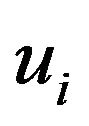 are the components of the displacement vector,
are the components of the displacement vector,  is the conductive temperature and satisfies the relation
is the conductive temperature and satisfies the relation
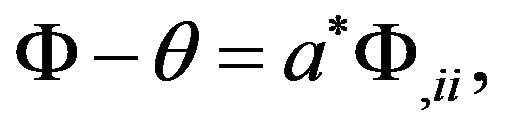 (5)
(5)
where 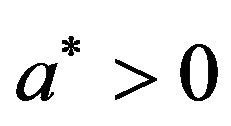 is the two-temperature parameter.
is the two-temperature parameter.
3. Analytical 2D Solution
We consider a homogeneous and isotropic thermoelastic medium of an infinite extent with Cartesian coordinates system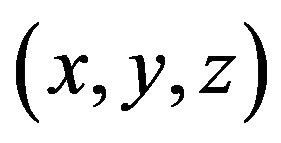 , which is previously at uniform temperature
, which is previously at uniform temperature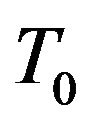 . The origin is taken on the plane surface
. The origin is taken on the plane surface 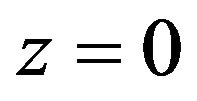 and the z-axis is taken normally into the medium
and the z-axis is taken normally into the medium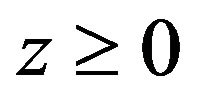 . The surface
. The surface 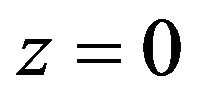 is assumed stress-free and thermally insulated. The present study is restricted to the plane strain parallel to x-z plane, with the displacement vector
is assumed stress-free and thermally insulated. The present study is restricted to the plane strain parallel to x-z plane, with the displacement vector  and rotational vector
and rotational vector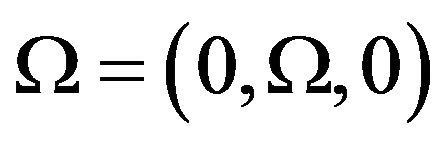 . Now, the Equation (3) has the following two components in x-z plane
. Now, the Equation (3) has the following two components in x-z plane
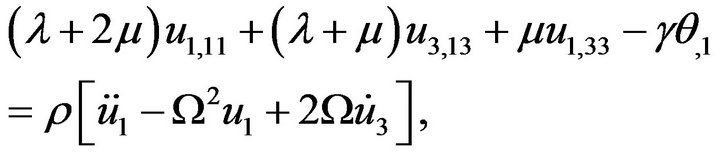 (6)
(6)
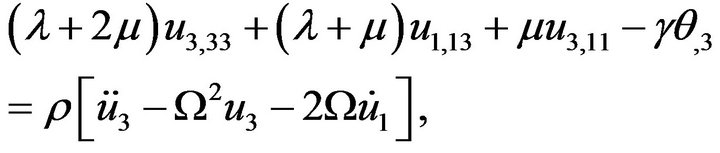 (7)
(7)
The heat conduction Equation (1) is written in x-z plane as
 (8)
(8)
and, the Equation (5) becomes,
 (9)
(9)
The displacement components 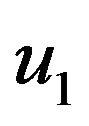 and
and 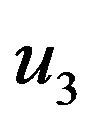 are written in terms of potentials
are written in terms of potentials  and
and 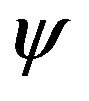 as
as
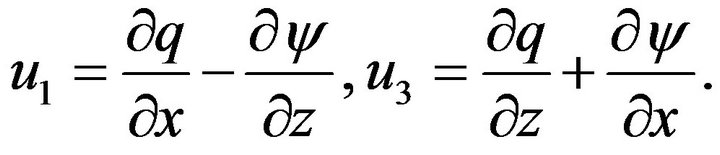 (10)
(10)
Using Equations (9)-(10) in Equations (6)-(8), we obtain
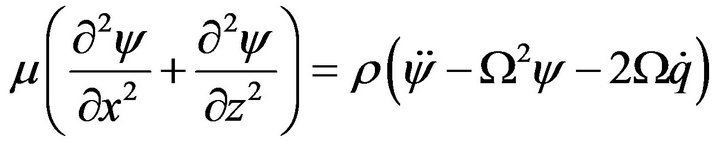 (11)
(11)
 (12)
(12)
 (13)
(13)
Solutions of Equations (11)-(13) are now sought in the form of harmonic travelling wave
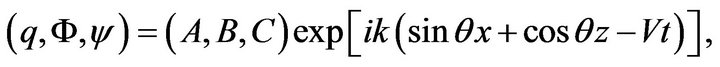 (14)
(14)
in which 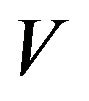 is the phase speed,
is the phase speed,  is the wave number and
is the wave number and  denotes the projection of wave normal onto x-z plane. Making use of Equation (14) into the Equations (11)-(13), we obtain a homogenous system of equations in A, B and C, which admits the non-trivial solution if
denotes the projection of wave normal onto x-z plane. Making use of Equation (14) into the Equations (11)-(13), we obtain a homogenous system of equations in A, B and C, which admits the non-trivial solution if
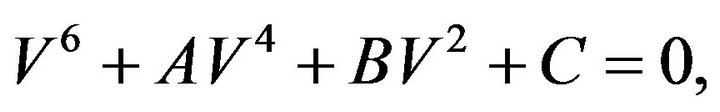 (15)
(15)
where
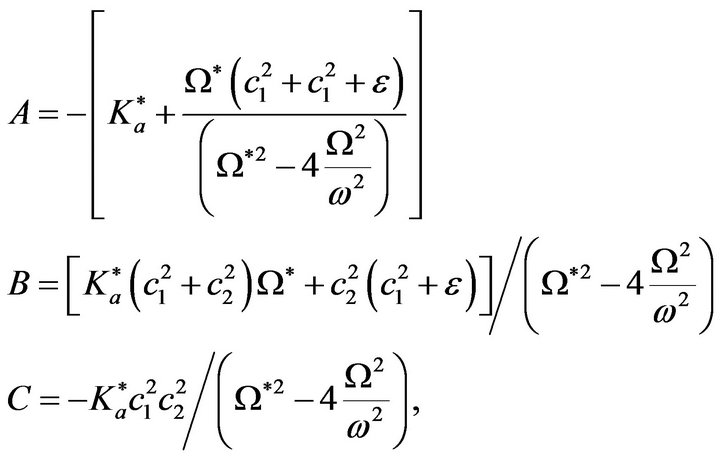
and
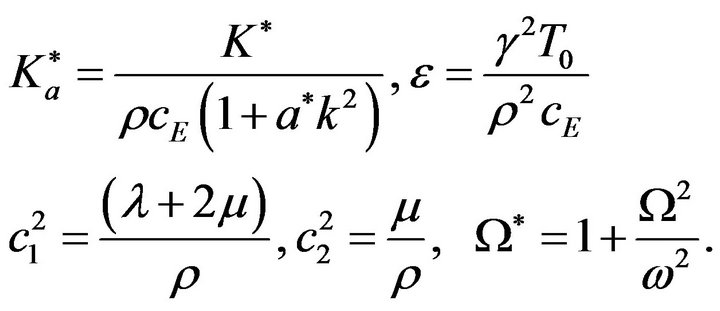
The three roots of the cubic Equation (15) are complex. Using the relation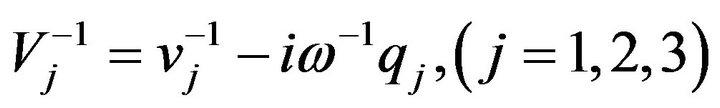 , we obtain three real values
, we obtain three real values  of the speeds of three plane waves, namely,
of the speeds of three plane waves, namely, 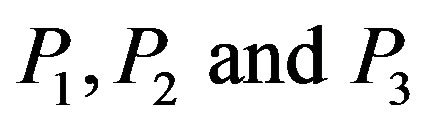 waves, respectively.
waves, respectively.
4. Limiting Cases
4.1. In Absence of Rotation Parameters
In absence of rotation parameters, we have 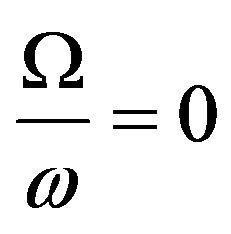 and the velocity Equation (15) reduces to
and the velocity Equation (15) reduces to
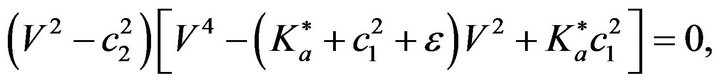 (16)
(16)
which gives the speeds of P, thermal and SV waves in an isotropic two-temperature thermoelastic medium without energy dissipation.
4.2. In Absence of Rotation and Thermal Parameters
In absence of rotation and thermal parameters, we have  and the Equation (15) reduces to
and the Equation (15) reduces to
 (17)
(17)
which gives the speeds of P and SV waves in an isotropic elastic media.
5. Boundary Conditions
We consider the incidence of  wave. The boundary conditions at the stress-free thermally insulated surface
wave. The boundary conditions at the stress-free thermally insulated surface 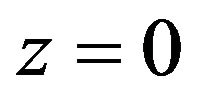 are satisfied, if the incident
are satisfied, if the incident 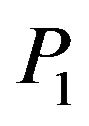 wave gives rise to a reflected
wave gives rise to a reflected 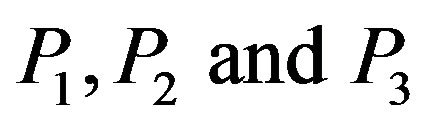 waves. The required boundary conditions at free surface
waves. The required boundary conditions at free surface 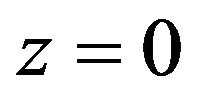 are as
are as
(i) Vanishing of the normal stress component
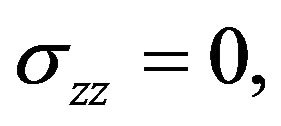 (18)
(18)
(ii) Vanishing of the tangential stress component
 (19)
(19)
(iii) Vanishing of the normal heat flux component
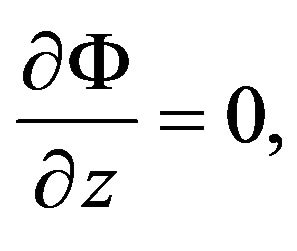 (20)
(20)
where
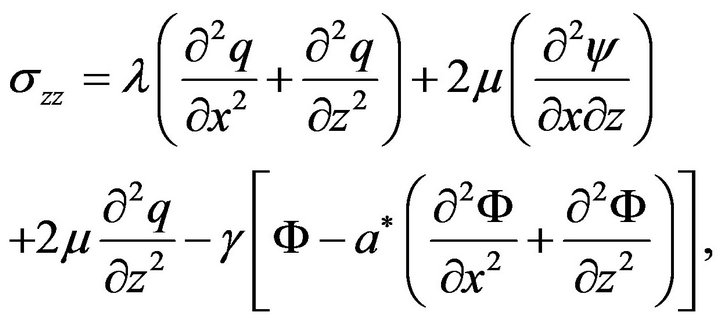 (21)
(21)
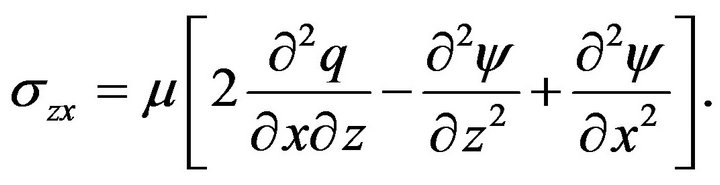 (22)
(22)
The appropriate displacement and temperature potentials 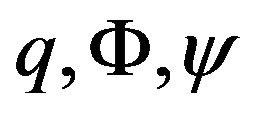 are taken in the following form
are taken in the following form
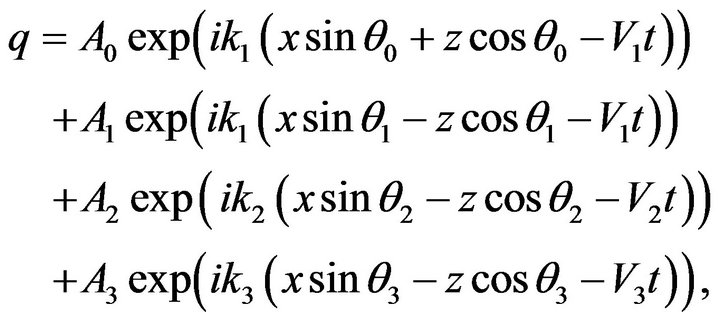 (23)
(23)
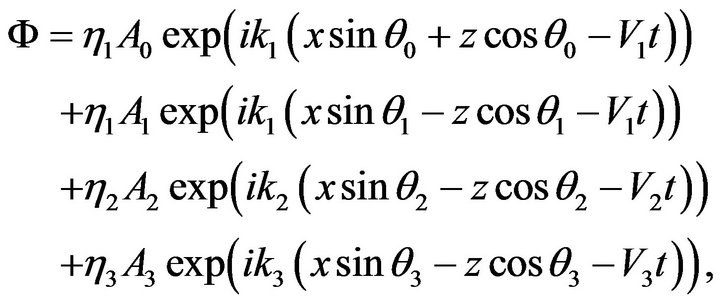 (24)
(24)
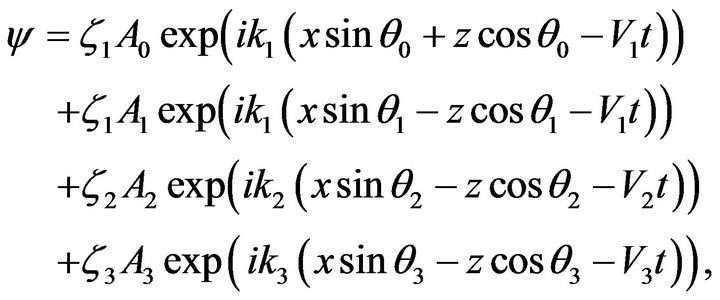 (25)
(25)
where the wave normal to the incident 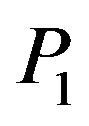 wave makes angle
wave makes angle 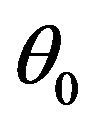 with the positive direction of z-axis and those of reflected
with the positive direction of z-axis and those of reflected  waves make angles
waves make angles 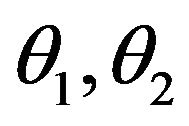 and
and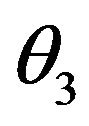 , respectively with the same direction, and
, respectively with the same direction, and

where
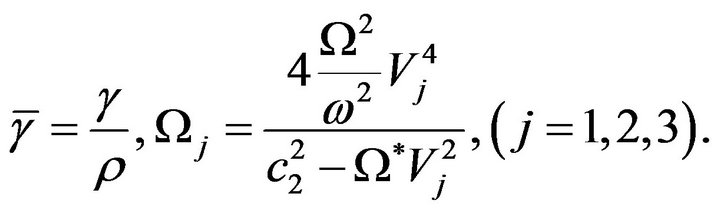
6. Reflection Coefficients
The ratios of the amplitudes of the reflected waves to the amplitude of incident 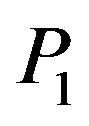 wave, namely
wave, namely 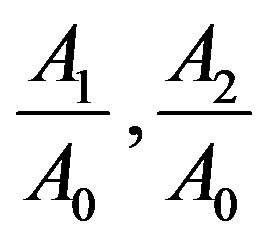 and
and 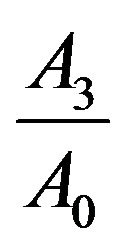 are the reflection coefficients (amplitude ratios) of reflected
are the reflection coefficients (amplitude ratios) of reflected 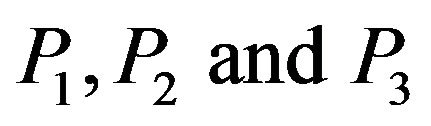 wave, respectively. The wave numbers
wave, respectively. The wave numbers 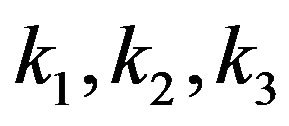 and the angles
and the angles 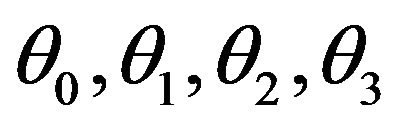 are connected by the relation
are connected by the relation
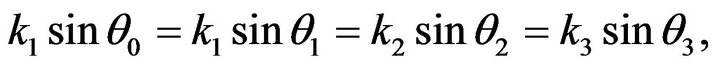 (26)
(26)
at surface z = 0. In order to satisfy the boundary conditions (18)-(20), the relation (26) is also written as
 (27)
(27)
with the help of the potentials given by Equations (23)- (25) and the Snell’s law Equations (26) and (27), the boundary conditions (18)-(20) results into a system of following three non-homogeneous equations
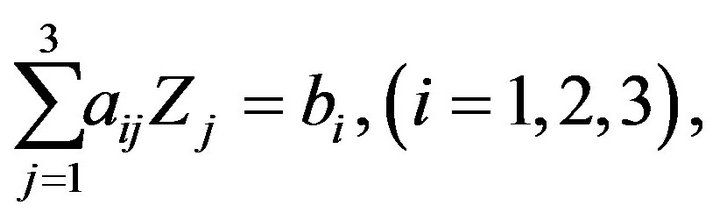 (28)
(28)
where 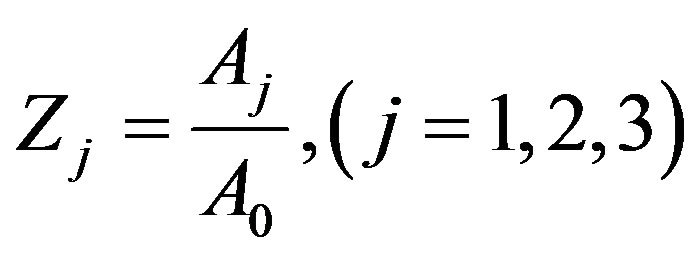 are the reflection coefficients of reflected
are the reflection coefficients of reflected  waves, and
waves, and
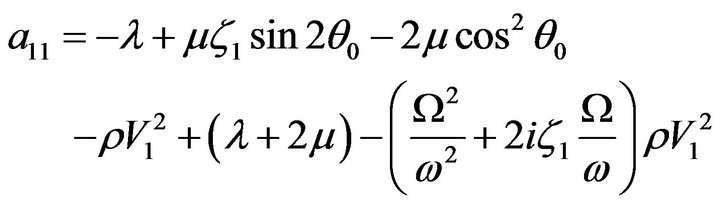
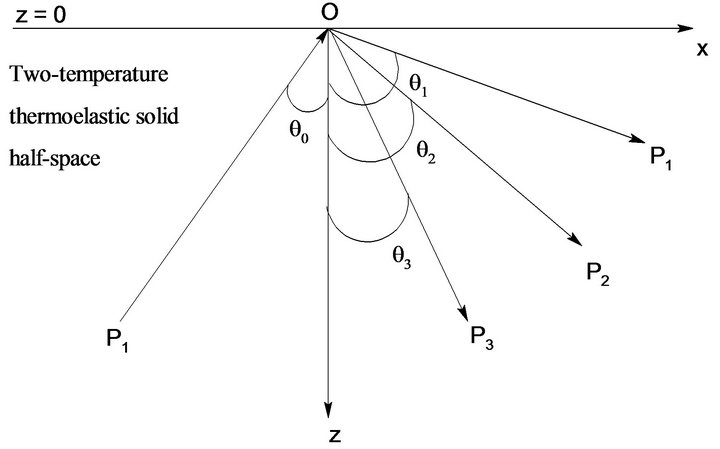
Figure 1. Geometry of the problem.
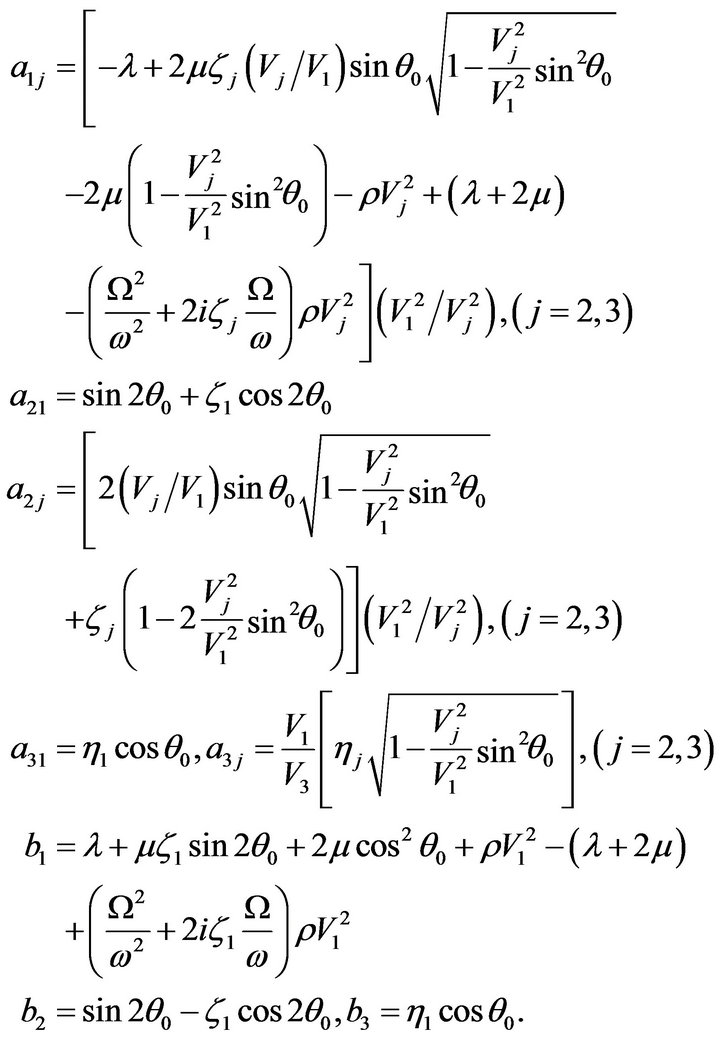
7. Numerical Results and Discussion
To study the effects of two-temperature and rotation parameters on the speeds of propagation and reflection coefficients of plane waves, we consider the following physical constants of aluminium as an isotropic thermoelastic solid half space
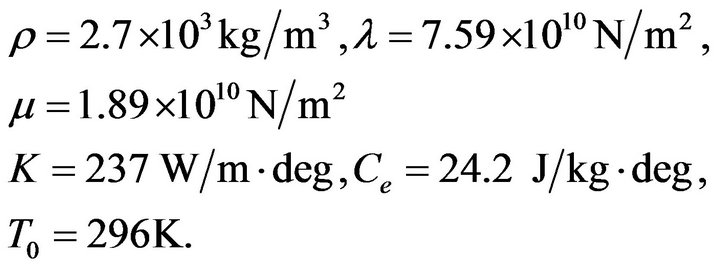
Using the relation 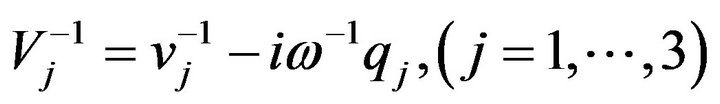 in Equation (15), the real values of the propagation speeds of
in Equation (15), the real values of the propagation speeds of 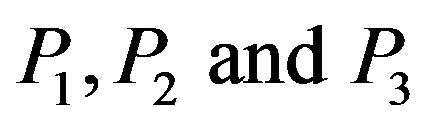 waves are computed for the range
waves are computed for the range 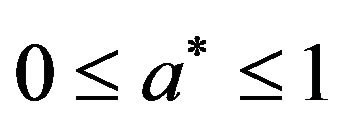 of two-temperature parameter, when
of two-temperature parameter, when 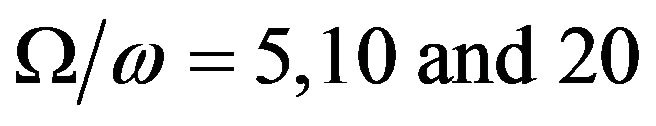 . The speeds of
. The speeds of 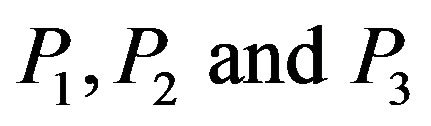 waves are shown graphically versus the two-temperature parameter
waves are shown graphically versus the two-temperature parameter 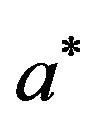 in Figure 2. The speed of
in Figure 2. The speed of 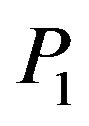 wave decreases with an increase in two-temperature parameter, whereas the speeds of
wave decreases with an increase in two-temperature parameter, whereas the speeds of 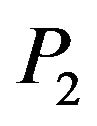 and
and  wave are affected less due to the change in two-temperature parameter. It is also observed from Figure 2 that the speed of each plane wave decreases with the increase in value of rotation parameter.
wave are affected less due to the change in two-temperature parameter. It is also observed from Figure 2 that the speed of each plane wave decreases with the increase in value of rotation parameter.
With the help of Equation (28), the reflection coefficients of reflected  waves are computed for the incidence of
waves are computed for the incidence of 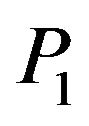 wave. For the range
wave. For the range 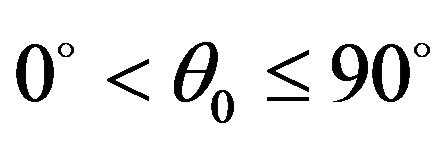 of the angle of incidence of
of the angle of incidence of  wave, the reflection coefficients of the
wave, the reflection coefficients of the 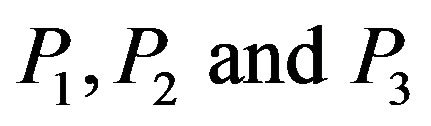 waves are shown graphically in Figure 3, when the rotation parameter
waves are shown graphically in Figure 3, when the rotation parameter 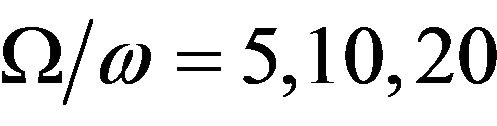 and two-temperature parameter
and two-temperature parameter . For
. For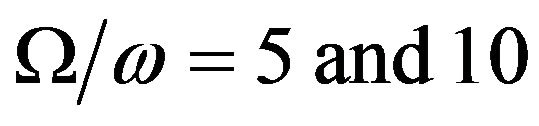 , the reflection coefficient of
, the reflection coefficient of 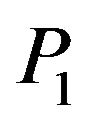 wave increases from its minimum value at
wave increases from its minimum value at 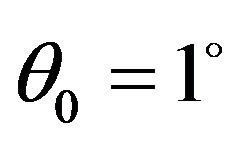 to its maximum value one at
to its maximum value one at  and for
and for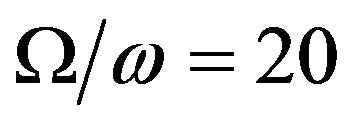 , its reflection coefficient first decreases to its minimum value zero at
, its reflection coefficient first decreases to its minimum value zero at  and then increases to its maximum value one at
and then increases to its maximum value one at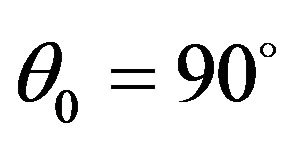 . For each value of
. For each value of , the reflection coefficient of
, the reflection coefficient of 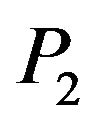 wave first increases slightly and then decreases to its minimum value zero at
wave first increases slightly and then decreases to its minimum value zero at . For all value of
. For all value of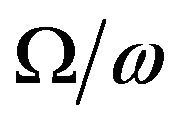 , the reflection coefficient of
, the reflection coefficient of  wave decreases from its maximum value at
wave decreases from its maximum value at 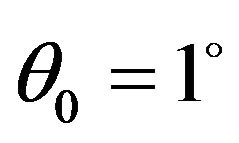 to its minimum value zero at
to its minimum value zero at . From Figure 3, it is also observed that the effect of rotation parameter
. From Figure 3, it is also observed that the effect of rotation parameter 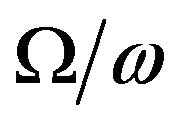 on reflection coefficients of
on reflection coefficients of 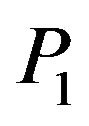 is maximum near
is maximum near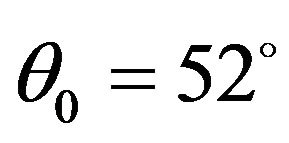 , whereas it is maximum at
, whereas it is maximum at 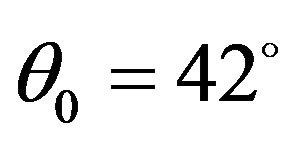 for
for  wave. There is no effect of rotation parameter on these reflected waves at grazing incidence. The reflection coefficients of
wave. There is no effect of rotation parameter on these reflected waves at grazing incidence. The reflection coefficients of 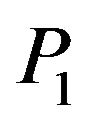 and
and 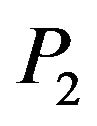 waves decrease with the increase in value of rotation parameter at each angle of incidence except the grazing incidence, whereas the reflection coefficient of
waves decrease with the increase in value of rotation parameter at each angle of incidence except the grazing incidence, whereas the reflection coefficient of 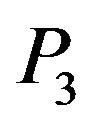 wave increases.
wave increases.
For the range  of the angle of incidence of P1 wave, the reflection coefficients of the
of the angle of incidence of P1 wave, the reflection coefficients of the  waves are shown graphically in Figure 4, when twotemperature parameter
waves are shown graphically in Figure 4, when twotemperature parameter  and rotation parameter
and rotation parameter . For all values of
. For all values of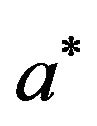 , the reflection coefficient of
, the reflection coefficient of 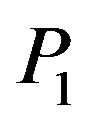 wave increases from its minimum value at
wave increases from its minimum value at 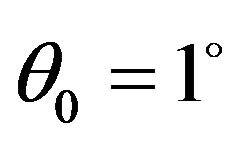 to its maximum value one at
to its maximum value one at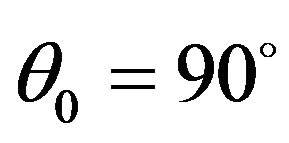 . For all values of
. For all values of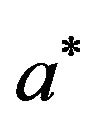 , the reflection coefficient of
, the reflection coefficient of 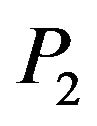 wave first increases and then decreases to its minimum value zero
wave first increases and then decreases to its minimum value zero
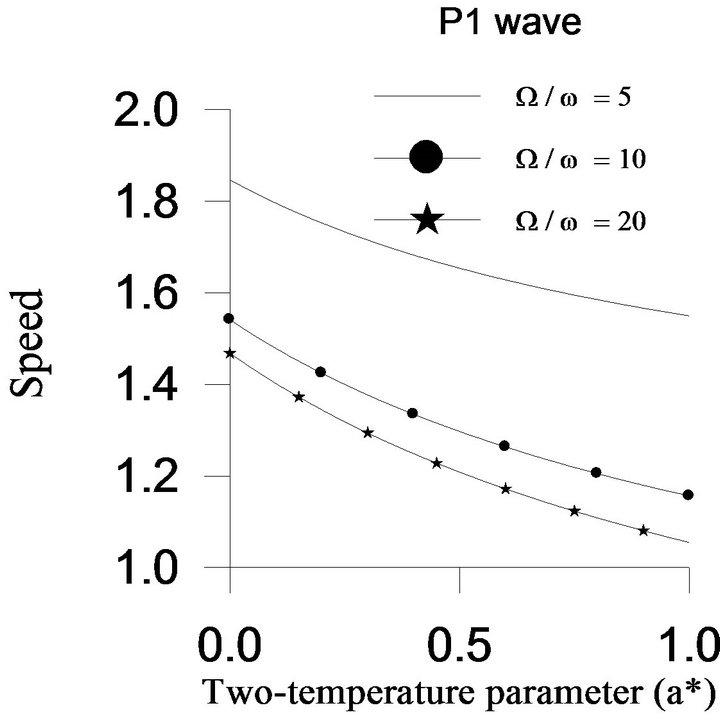
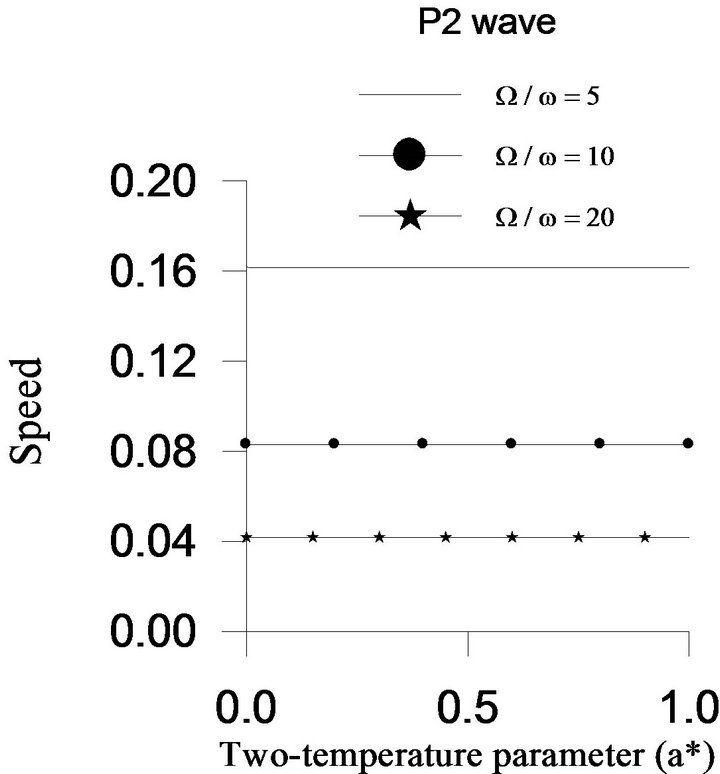
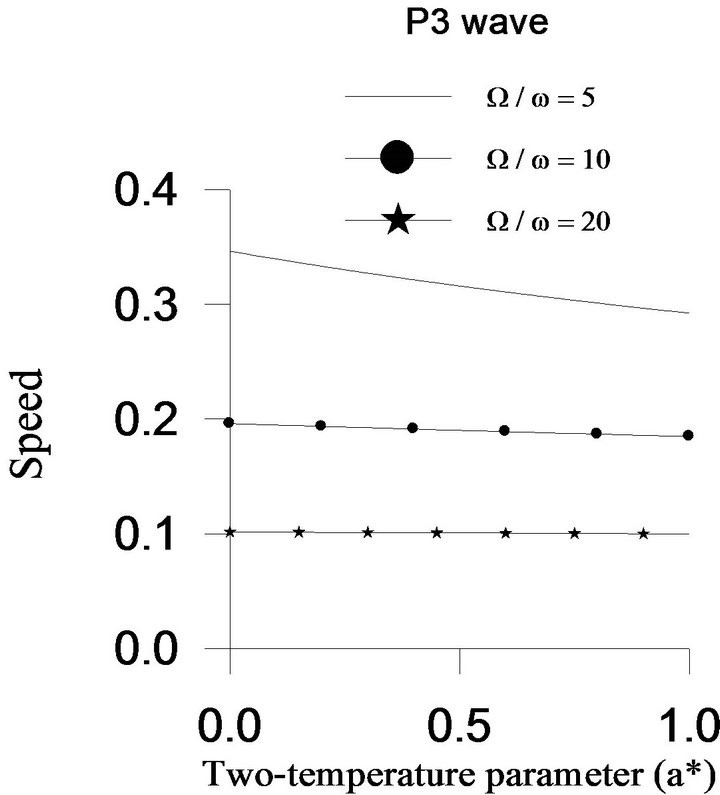
Figure 2. Variations of the speeds of plane waves versus two-temperature parameter a*.
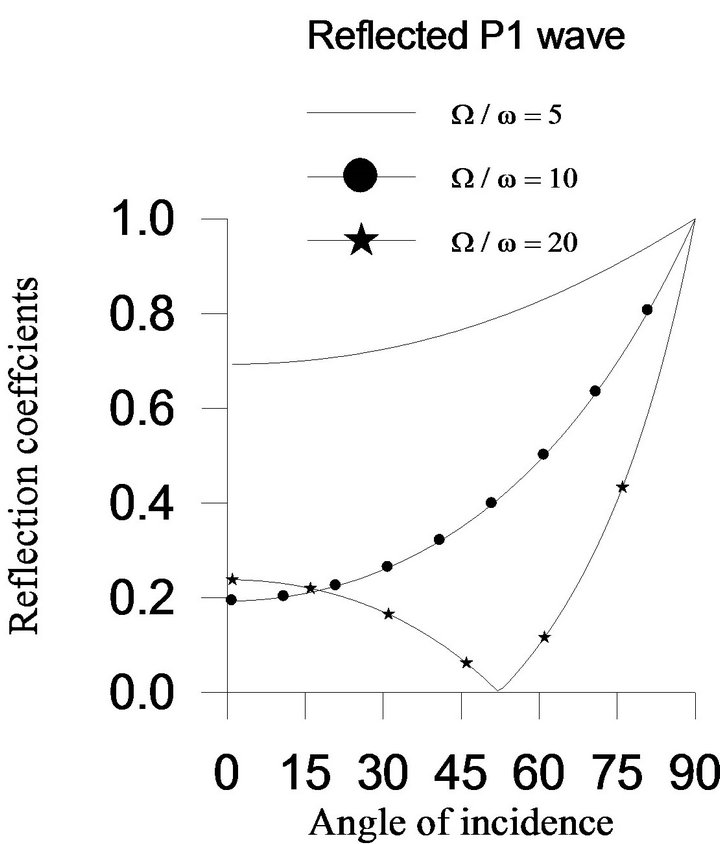
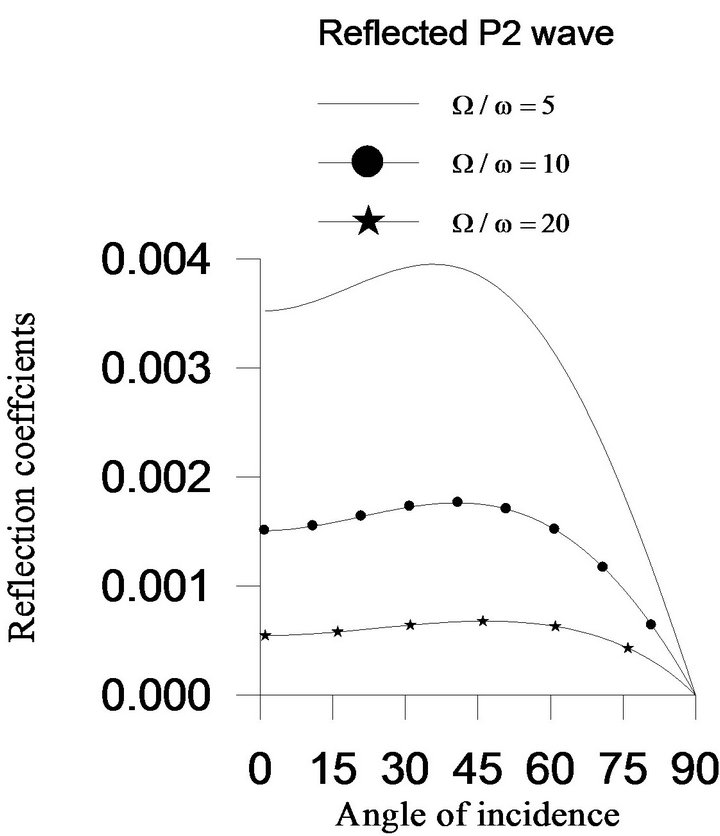
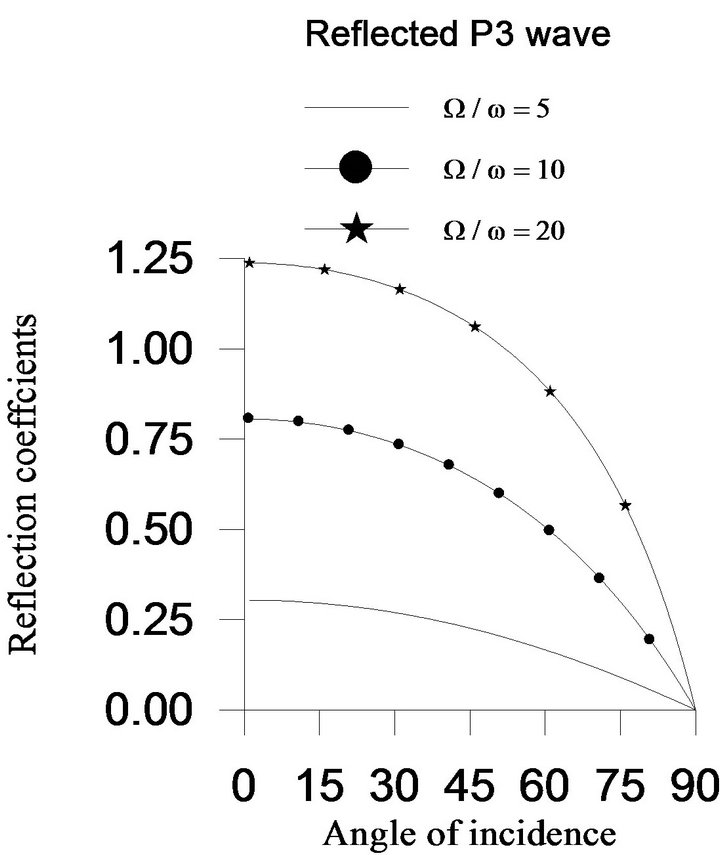
Figure 3. Variations of the reflection coefficients versus angle of incidence when two-temperature parameter a* = 0.5.
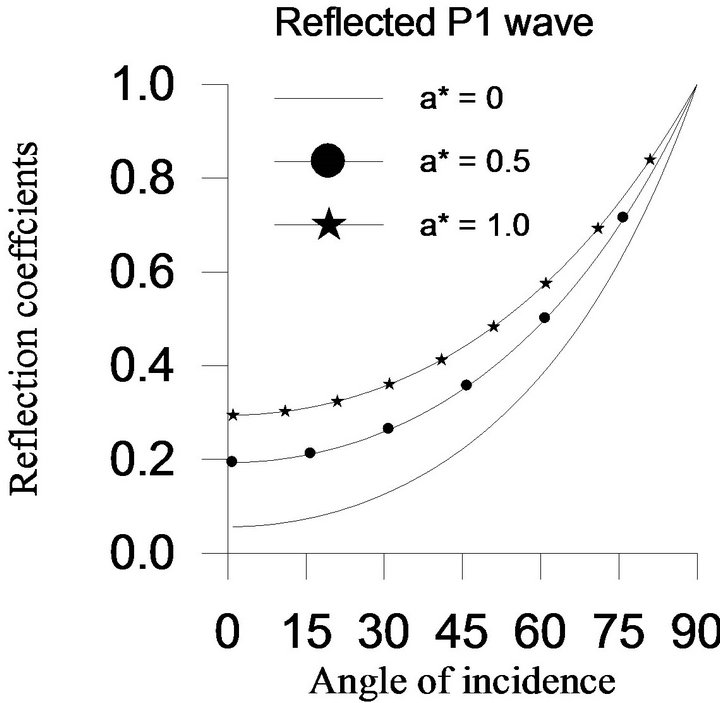
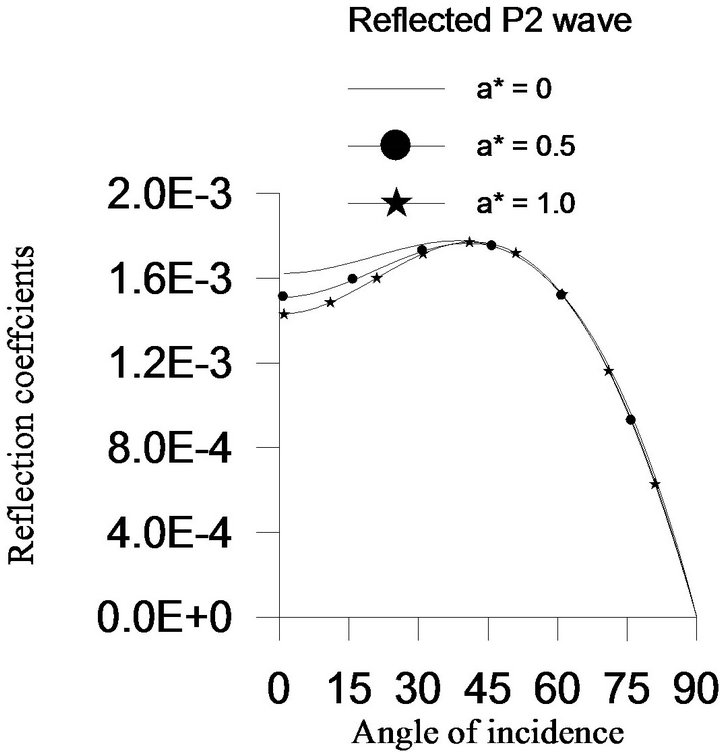
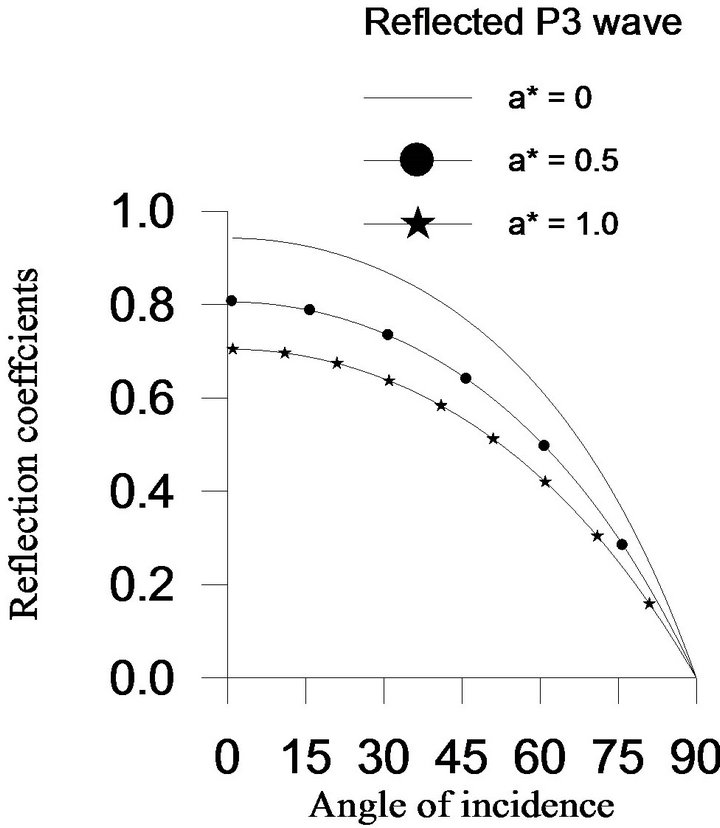
Figure 4. Variations of the reflection coefficients versus angle of incidence when rotation parameter W/w = 10.
at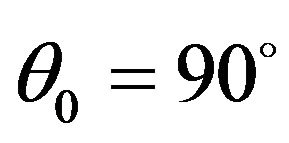 . The reflection coefficient of
. The reflection coefficient of  wave decreases from its maximum value at
wave decreases from its maximum value at 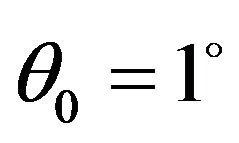 to its minimum value zero at
to its minimum value zero at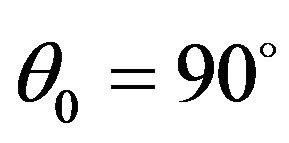 . From Figure 4, it is also observed that the effect of two-temperature parameter
. From Figure 4, it is also observed that the effect of two-temperature parameter  on all reflected waves is maximum near normal incidence. For grazing incidence, there is no effect of twotemperature parameter on all the reflected waves. The reflection coefficients of
on all reflected waves is maximum near normal incidence. For grazing incidence, there is no effect of twotemperature parameter on all the reflected waves. The reflection coefficients of  wave increases with the increase in value of two-temperature parameter at each angle of incidence except grazing incidence, whereas the reflection coefficient of
wave increases with the increase in value of two-temperature parameter at each angle of incidence except grazing incidence, whereas the reflection coefficient of 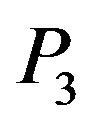 wave decreases. For the range
wave decreases. For the range  of the angle of incidence of
of the angle of incidence of 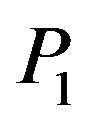 wave, the reflection coefficients of the
wave, the reflection coefficients of the 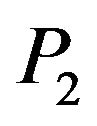 decreases with an increase in two-temperature parameter. Beyond
decreases with an increase in two-temperature parameter. Beyond , there is little effect of two-temperature parameter on the reflection coefficients of the
, there is little effect of two-temperature parameter on the reflection coefficients of the 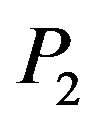 wave.
wave.
8. Conclusion
Two-dimensional solution of the governing equations of an isotropic two-temperature thermoelastic medium without energy dissipation indicates the existence of three plane waves, namely, 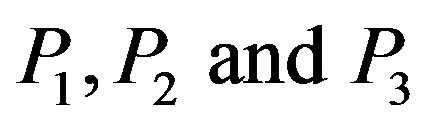 waves. The appropriate solutions in the half-space satisfy the required boundary conditions at thermally insulated free surface and the relations between reflection coefficients of reflected
waves. The appropriate solutions in the half-space satisfy the required boundary conditions at thermally insulated free surface and the relations between reflection coefficients of reflected 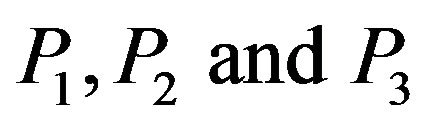 waves are obtained for the incidence of
waves are obtained for the incidence of 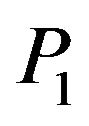 wave. The speeds and reflection coefficients of plane waves are computed for a particular material representing the model. From theory and numerical results, it is observed that the speeds and reflection coefficients of plane waves are significantly affected by the two-temperature and rotation parameters.
wave. The speeds and reflection coefficients of plane waves are computed for a particular material representing the model. From theory and numerical results, it is observed that the speeds and reflection coefficients of plane waves are significantly affected by the two-temperature and rotation parameters.
REFERENCES
- H. Lord and Y. Shulman, “A Generalised Dynamical Theory of Thermoelasticity,” Journal of the Mechanics and Physics of Solids, Vol. 15, No. 5, 1967, pp. 299-309. doi:10.1016/0022-5096(67)90024-5
- A. E. Green and K. A. Lindsay, “Thermoelasticity,” Journal of Elasticity, Vol. 2, No. 1, 1972, pp. 1-7. doi:10.1007/BF00045689
- J. Ignaczak and M. Ostoja-Starzewski, “Thermoelasticity with Finite Wave Speeds,” Oxford University Press, Oxford, 2009.
- A. E. Green and P. M. Naghdi, “Thermoelasticity without Energy Dissipation,” Journal of Elasticity, Vol. 31, No. 3, 1993, pp. 189-208. doi:10.1007/BF00044969
- R. B. Hetnarski and J. Ignaczak, “Generalized Thermoelasticity,” Journal of Thermal Stresses, Vol. 22, No. 4, 1999, pp. 451-476. doi:10.1080/014957399280832
- H. Deresiewicz, “Effect of Boundaries on Waves in a Thermo-Elastic Solid: Reflection of Plane Waves from Plane Boundary,” Journal of the Mechanics and Physics of Solids, Vol. 8, No. 3, 1960, pp. 164-172. doi:10.1016/0022-5096(60)90035-1
- A. N. Sinha, and S. B. Sinha, “Reflection of Thermoelastic Waves at a Solid Half Space with Thermal Relaxation,” Journal of Physics of the Earth, Vol. 22, No. 2, 1974, pp. 237-244. doi:10.4294/jpe1952.22.237
- S. B. Sinha and K. A. Elsibai, “Reflection of Thermoelastic Waves at a Solid Half-Space with Two Thermal Relaxation Times,” Journal of Thermal Stresses, Vol. 19, No. 8, 1996, pp. 763-777. doi:10.1080/01495739608946205
- S. B. Sinha and K. A. Elsibai, “Reflection and Refraction of Thermoelastic Waves at an Interface of two Semi-Infinite Media with Two Thermal Relaxation Times,” Journal of Thermal Stresses, Vol. 20, No. 2, 1997, pp. 129-146. doi:10.1080/01495739708956095
- J. N. Sharma, V. Kumar and D. Chand, “Reflection of Generalized Thermoelastic Waves from the Boundary of a Half-Space,” Journal of Thermal Stresses, Vol. 26, No. 10, 2003, pp. 925-942. doi:10.1080/01495730306342
- M. I. A. Othman and Y. Song, “Reflection of Plane Waves from an Elastic Solid Half-Space under Hydrostatic Initial Stress without Energy Dissipation,” International Journal of Solids and Structures, Vol. 44, No. 17, 2007, pp. 5651-5664. doi:10.1016/j.ijsolstr.2007.01.022
- B. Singh, “Effect of Hydrostatic Initial Stresses on Waves in a Thermoelastic Solid Half-Space,” Applied Mathematics and Computation, Vol. 198, No. 2, 2008, pp. 494- 505. doi:10.1016/j.amc.2007.08.072
- B. Singh, “Reflection of Plane Waves at the Free Surface of a Monoclinic Thermoelastic Solid Half-Space,” European Journal of Mechanics—A/Solids, Vol. 29, No. 5, 2010, pp. 911-916. doi:10.1016/j.euromechsol.2010.05.005
- M. E. Gurtin and W. O. Williams, “On the Clausius-Duhem Inequality,” Zeitschrift für angewandte Mathematik und Physik, Vol. 17, No. 5, 1966, pp. 626-633. doi:10.1007/BF01597243
- M. E. Gurtin and W. O. Williams, “An Axiomatic Foundation/or Continuum Thermodynamics,” Archive for Rational Mechanics and Analysis, Vol. 26, No. 2, 1967, pp. 83-117. doi:10.1007/BF00285676
- P. J. Chen and M. E. Gurtin, “On a Theory of Heat Conduction Involving Two Temperatures,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 19, No. 4, 1968, pp. 614-627. doi:10.1007/BF01594969
- P. J. Chen, M. E. Gurtin and W. O. Williams, “A Note on Non-Simple Heat Conduction,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 19, No. 6, 1968, pp. 969-970. doi:10.1007/BF01602278
- P. J. Chen, M. E. Gurtin and W. O. Williams, “On the Thermodynamics of Non-Simple Elastic Materials with Two Temperatures,” Zeitschrift für Angewandte Mathematik und Physik, Vol. 20, No. 1, 1969, pp. 107-112. doi:10.1007/BF01591120
- W. E. Warren and P. J. Chen, “Wave Propagation in the Two-Temperature Theory of Thermoelasticity,” Acta Mechanica, Vol. 16, No. 1-2, 1973, pp. 21-33. doi:10.1007/BF01177123
- B. A. Boley and I. S. Tolins, “Transient Coupled Thermoplastic Boundary Value Problems in the Half-Space,” Journal of Applied Mechanics, Vol. 29, No. 4, 1962, pp. 637-646. doi:10.1115/1.3640647
- P. Puri and P. M. Jordan, “On the Propagation of Harmonic Plane Waves under the Two-Temperature Theory,” International Journal of Engineering Science, Vol. 44, No. 17, 2006, pp. 1113-1126. doi:10.1016/j.ijengsci.2006.07.002
- R. Quintanilla and P. M. Jordan, “A Note on the Two Temperature Theory with Dual-Phase-Lag Delay: Some Exact Solutions,” Mechanics Research Communications, Vol. 36, No. 7, 2009, pp. 796-803. doi:10.1016/j.mechrescom.2009.05.002
- H. M. Youssef, “Theory of Two-Temperature Generalized Thermoelasticity,” IMA Journal of Applied Mathematics, Vol. 71, No. 3, 2006, pp. 383-390. doi:10.1093/imamat/hxh101
- R. Kumar and S. Mukhopadhyay, “Effects of Thermal Relaxation Time on Plane Wave Propagation under TwoTemperature Thermoelasticity,” International Journal of Engineering Science, Vol. 48, No. 2, 2010, pp. 128-139. doi:10.1016/j.ijengsci.2009.07.001
- A. Magana and R. Quintanilla, “Uniqueness and Growth of Solutions in Two-Temperature Generalized Thermoelastic Theories,” Mathematics and Mechanics of Solids, Vol. 14, No. 7, 2009, pp. 622-634. doi:10.1177/1081286507087653
- H. M. Youssef, “Theory of Two-Temperature Thermoelasticity without Energy Dissipation,” Journal of Thermal Stresses, Vol. 34, No. 2, 2011, pp. 138-146. doi:10.1080/01495739.2010.511941

