Applied Mathematics
Vol. 3 No. 11 (2012) , Article ID: 24510 , 8 pages DOI:10.4236/am.2012.311228
Zero-M-Cordial Labeling of Some Graphs
Department of Mathematics, Scott Christian College, Nagercoil, India
Email: freedasam1969@gmail.com, robinchel@rediffmail.com
Received August 14, 2012; revised September 28, 2012; accepted October 5, 2012
Keywords: Zero-M-Cordial Labeling; Split Graphs; Cartesian Product; H-Cordial
ABSTRACT
In this paper we prove that the complete bipartite graph km,n where m and n are even, join of two cycle graphs cn and cm where  (mod 4), split graph of cn for even “n”,
(mod 4), split graph of cn for even “n”, 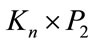 where n is even are admits a Zero-M-Cordial labeling. Further we prove that
where n is even are admits a Zero-M-Cordial labeling. Further we prove that 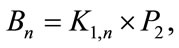
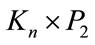 of odd n admits a Zero-M-Cordial labeling.
of odd n admits a Zero-M-Cordial labeling.
1. Introduction
We begin with finite, connected and undirected graph G = (V(G), E(G). If the vertices of the graph are assigned values subject to certain conditions then it is known as graph labeling. Any graph labeling will have the following three common characteristics. A set of numbers from which Vertex labels are chosen; 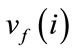 = number of vertices of G having label i under f
= number of vertices of G having label i under f
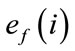 = number of edges of G having label i under f*.
= number of edges of G having label i under f*.
The concept of cordial labeling was introduced by I. Cahit, who called a graph G is Cordial if there is a vertex labeling  such that the induced labeling
such that the induced labeling
 , defined by
, defined by
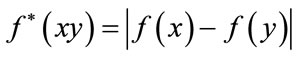 , for all edges
, for all edges 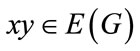 and with the following inequalities holding and
and with the following inequalities holding and
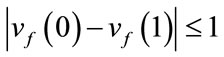 and
and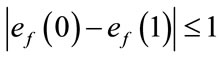 .
.
In [1] introduced the concept of H-Cordial labeling. Cahit calls a graph H-Cordial if it is possible to label the edges with the numbers from the set 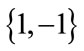 in such a way that, for some k, at each vertex v the sum of the labels on the edges incident with v is either k or –k and the inequalities
in such a way that, for some k, at each vertex v the sum of the labels on the edges incident with v is either k or –k and the inequalities 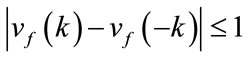 and
and
 are also satisfied where v(i)and e(j) are respectively, the number of vertices labeled with i and the number of edges labeled with j. He calls a graph Hn-Cordial if it is possible to label the edges with the numbers from the set
are also satisfied where v(i)and e(j) are respectively, the number of vertices labeled with i and the number of edges labeled with j. He calls a graph Hn-Cordial if it is possible to label the edges with the numbers from the set  in such a way that, at each vertex v the sum of the labels on the edges incident with v is in the set
in such a way that, at each vertex v the sum of the labels on the edges incident with v is in the set 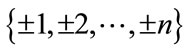 and the inequalities
and the inequalities 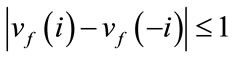 and
and 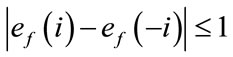 are also satisfied for each i with
are also satisfied for each i with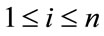 . The concept of Zero-M-Cordial labeling is defined in [2]. A labeling f of a graph G is called Zero-M-Cordial, if for each vertex v, f(v) = 0. A graph G is called to be Zero-M-Cordial, if it admits a Zero-M-Cordial labeling. The usefulness of the above definition appears when one tries to find an HCordial labeling for a given graph G. If H is a ZeroM-Cordial subgraph of G then H-Cordiality of G\E(H) simply implies H-Cordiality G.
. The concept of Zero-M-Cordial labeling is defined in [2]. A labeling f of a graph G is called Zero-M-Cordial, if for each vertex v, f(v) = 0. A graph G is called to be Zero-M-Cordial, if it admits a Zero-M-Cordial labeling. The usefulness of the above definition appears when one tries to find an HCordial labeling for a given graph G. If H is a ZeroM-Cordial subgraph of G then H-Cordiality of G\E(H) simply implies H-Cordiality G.
In [1] proved that kn,n is H-Cordial if and only if n > 2 and “n” is even; and km,n, m ≠ n is H-Cordial if and only if n ≡ 0 (mod4), m is even and m > 2, n > 2.
In [2] proved that kn is H-Cordial if and only if n ≡ 0 or 3 (mod4) and n ≠ 3. Wn is H-Cordial if and only if n is odd. kn is not H2-Cordial if n ≡ 1 (mod4). Also [2] prove that every wheel has an H2-Cordial labeling.
In [3] several variations of graph labeling such as graceful, bigraceful, harmonious, cordial, equitable, humming etc. have been introduced by several authors. For definitions and terminologies in graph theory we refer to [4].
In this paper we investigate Zero-M-Cordial labeling on some Cartesian product of graphs, join of two graphs, and bipartite graph.
1.1. Definition: The join G = G1 + G2 of graph G1 and G2 with disjoint point sets V1 and V2 and edge sets E1 and E2 denoted by G = G1 + G2 is the graph union 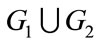 together with all the edges joining v1, v2. If G1 is (p1,q1) graph and G2 is (p2,q2) graph then
together with all the edges joining v1, v2. If G1 is (p1,q1) graph and G2 is (p2,q2) graph then 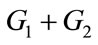 is a
is a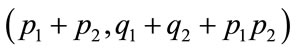 .
.
1.2. Definition: Let G1 = (V1, E1) and G2 = (V2, E2) be two graphs. The Cartesian product of G1 and G2 which is denoted by G1 G2 is the graph with vertex set v = v1 × v2 consisting of vertices
G2 is the graph with vertex set v = v1 × v2 consisting of vertices 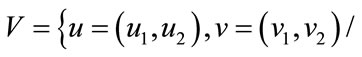 u and v are adjacent in
u and v are adjacent in  whenever u1 = v1 and u2 adjacent to v2 or u1 adjacent to v1 and
whenever u1 = v1 and u2 adjacent to v2 or u1 adjacent to v1 and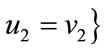 .
.
1.3. Definition: For a graph G the split graph is obtained by adding to each vertex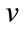 , a new vertex
, a new vertex 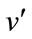 such that
such that 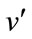 is adjacent to every vertex that is adjacent to
is adjacent to every vertex that is adjacent to 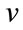 in G. The resultant graph is denoted by spl (G).
in G. The resultant graph is denoted by spl (G).
2. Main Results
Theorem 2.1: Every cycle Cn of even order admits a Zero-M-Cordial labeling Proof: Let 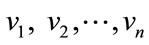 be the vertices of cycle Cn
be the vertices of cycle Cn
Define f: 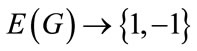 two cases are to be considered.
two cases are to be considered.
Case (i) n 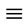 2 (mod 4)
2 (mod 4)
For 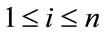
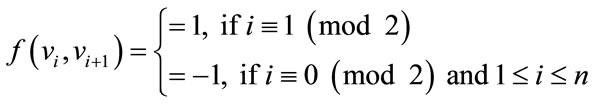
In view of the above labeling pattern we give the proof as follows:
When n 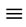 2 (mod 4)
2 (mod 4)
The total number of edges labeled with 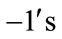 are given by
are given by 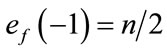 and the total number of edges labeled with
and the total number of edges labeled with 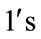 are given by
are given by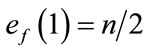 . Therefore the total difference between the edges labeled with
. Therefore the total difference between the edges labeled with 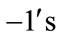 and
and  are given by
are given by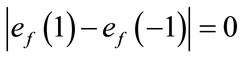 . The induced vertex labels are equal to zero. Thus for each vertex v,
. The induced vertex labels are equal to zero. Thus for each vertex v, 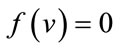 and
and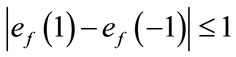 .
.
Case (ii) n  0 (mod 4)
0 (mod 4)
The total number of edges labeled with 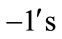 are given by
are given by 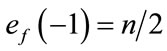 and the total number of edges labeled with
and the total number of edges labeled with  are given by
are given by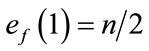 . Therefore the total difference between the edges labeled with
. Therefore the total difference between the edges labeled with 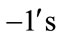 and
and  are given by
are given by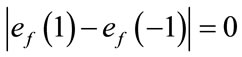 . The induced vertex labels are equal to zero. Thus for each vertex v,
. The induced vertex labels are equal to zero. Thus for each vertex v, 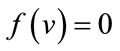 and
and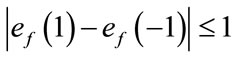 .
.
Hence the cycle graph cn, even n admits a zero-Mcordial labeling.
The vertex and the edge conditions are given in Table 1. The illustration is given in Figures 1 and 2.
In Figure 1 illustrates the Zero-M-Cordial labeling for the cycle graph C6. Among the six edges three edges receive the label +1 and the other three edges receive the label –1. In Figure 2 illustrates the Zero-M-Cordial labeling for the cycle graph C8. Among the eight edges four edges receive the label +1 and the other four edges receive the label –1.
Theorem 2.2: The complete bipartite graph km,n admits a Zero-M-Cordial labeling for all m, n such that m + n 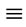 0, 2 (mod 4).
0, 2 (mod 4).
Proof: Let 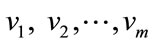 and
and 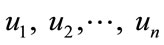 are the vertex set of the bipartite graph km,n. The number of vertices and the edges of km,n is m + n and mn respectively.
are the vertex set of the bipartite graph km,n. The number of vertices and the edges of km,n is m + n and mn respectively.
Define f: 

Table 1. The vertex and the edge conditions of cycle graph Cn.
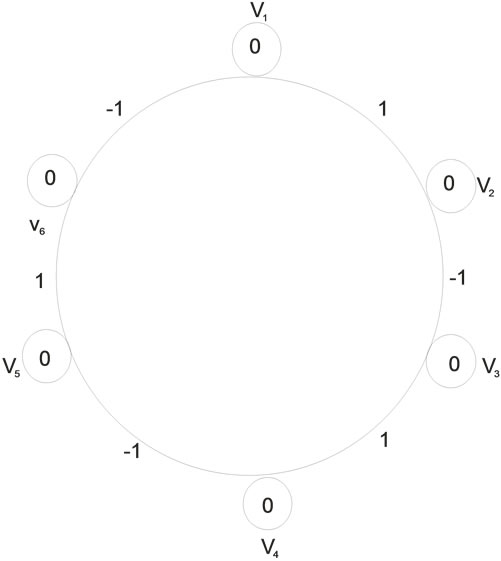
Figure 1. Zero-M-Cordial labeling on C6.
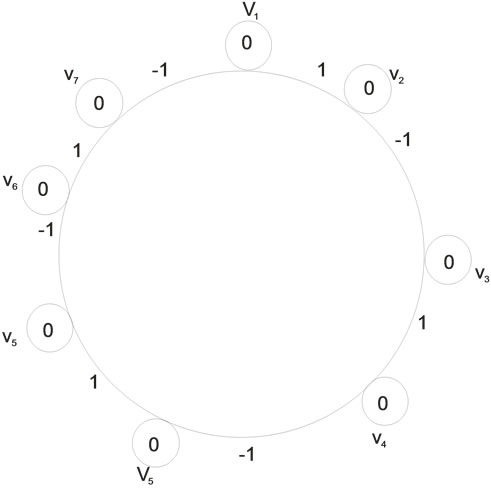
Figure 2. Zero-M-Cordial labeling on C8.
The edge matrix of km,n is given in Table 2.
In view of the above edge matrix we give the proof as follows.
Case (i) when m + n  0 (mod 4), m = n.
0 (mod 4), m = n.
Consider the bipartite graph k4,4.
Using Table 2 the edge label matrix of k4,4 is given by

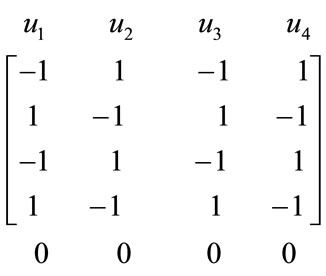

Table 2. Edge matrix of km,n.
With respect to the above labeling the total number of edges labeled with  and
and 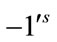 are given by
are given by 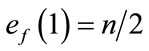 and
and . Therefore the total difference between the edges labeled with
. Therefore the total difference between the edges labeled with 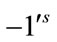 and
and 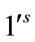 are given by
are given by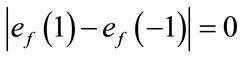 . The induced vertex labels are equal to zero. Thus for each vertex v,
. The induced vertex labels are equal to zero. Thus for each vertex v, 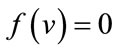 and
and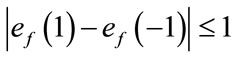 .
.
Hence the bipartite graph K4,4 admits a Zero-M-Cordial labeling. The vertex and the edge conditions are given in Table 3. The illustration is given in Figure 3.
Figure 3 illustrates the Zero-M-Cordial labeling on K4,4. Among the Sixteen edges eight edges receive the label +1 and the other eight edges receive the label –1.
Case (ii) When m + n 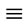 2 (mod 4),
2 (mod 4),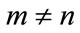 .
.
Consider the bipartite graph K2,4.
Using Table 2 the edge label matrix is given by



With respect to the above labeling the total number of edges labeled with 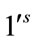 and
and 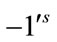 are given by
are given by 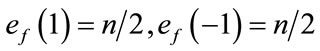 . Therefore the total difference between the edges labeled with
. Therefore the total difference between the edges labeled with  and
and  are given by
are given by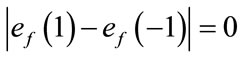 . The induced vertex labels are equal to zero. Thus for each vertex v,
. The induced vertex labels are equal to zero. Thus for each vertex v, 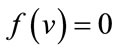 and
and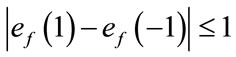 .
.
Hence the bipartite graph k2,4 admits a zero-M-cordial labeling.
Figure 4 illustrates the Zero-M-Cordial labeling on k2,4. Among eight edges four edges receive the label +1 and other four edges receive the label –1.
Case (iii) When m + n 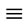 0 (mod 4) and
0 (mod 4) and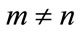 .
.
Consider the bipartite graph k2,6.
Using Table 2 the edge label matrix is given by

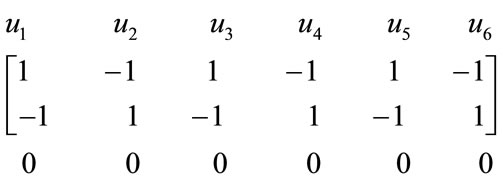
With respect to the above labeling the total number of edges labeled with  and
and 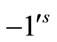 are given by
are given by

Table 3. The vertex and the edge conditions of the bipartite graph Km,n.
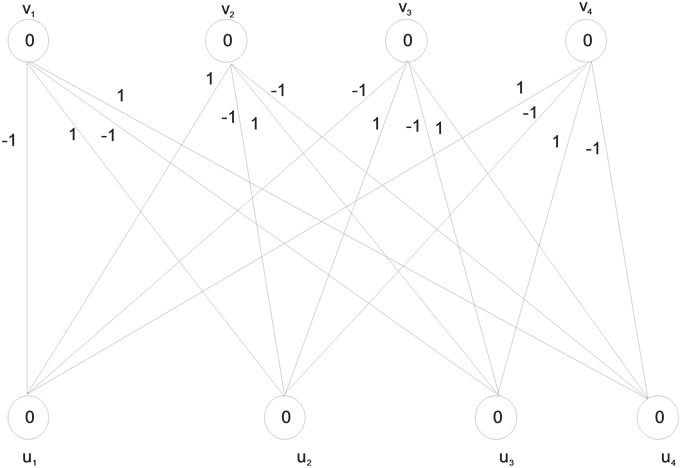
Figure 3. Zero-M-Cordial labeling on k4,4.
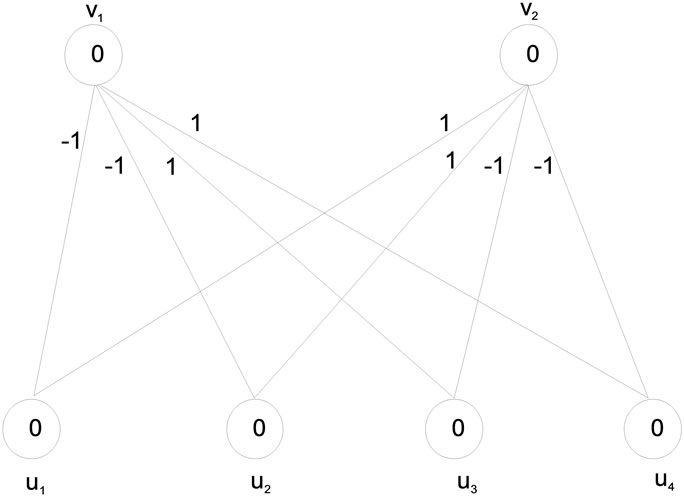
Figure 4. Zero-M-Cordial labeling on k2,4.
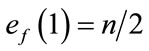 and
and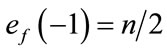 . Therefore the total difference between the edges labeled with
. Therefore the total difference between the edges labeled with 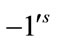 and
and 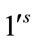 are given by
are given by . The induced vertex labels are equal to zero. Thus for each vertex v,
. The induced vertex labels are equal to zero. Thus for each vertex v, 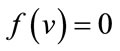 and
and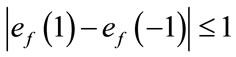 .
.
Hence the bipartite graph k2,6 admits a Zero-M-Cordial labeling. The vertex and the edge conditions are given in Table 3.
Figure 5 illustrates the Zero-M-Cordial labeling on k2,6. Among the Twelve edges six edges receive the label +1 and the other six edges receive the label –1.
Theorem 2.3: The join of two cycle graphs Cn and Cm
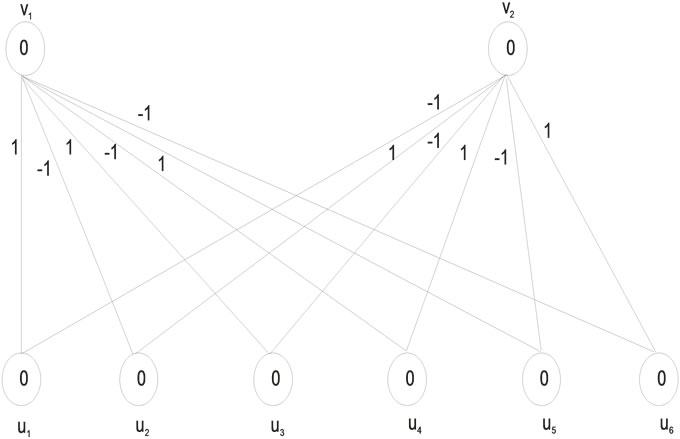
Figure 5. Zero-M-Cordial labeling on k2,6.
admits a Zero-M-Cordial labeling if n + m 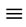 0 (mod 4).
0 (mod 4).
Proof: Let 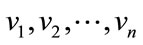 and
and 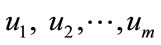 are the vertex set of the cycles Cn and Cm. The edge set E1 and E2 is the graph union of Cn and Cm together with all the edges joining the vertex set
are the vertex set of the cycles Cn and Cm. The edge set E1 and E2 is the graph union of Cn and Cm together with all the edges joining the vertex set 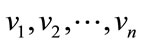 and
and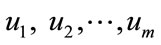 .
.
We note that  and
and .
.
Define f: 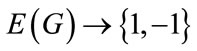
The edge matrix of cn + cm is given in Table 4.
In view of the above labeling pattern we give the proof as follows:
When n + m  0 (mod 4)
0 (mod 4)
Consider the join of two cycle graphs C4 + C4. Using Table 4 the edge label matrix of C4 & C4 is given by


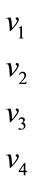
With respect to the above labeling the total number of edges labeled with 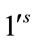 and
and 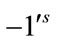 are given by
are given by 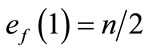 and
and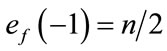 . Therefore the total difference between the edges labeled with
. Therefore the total difference between the edges labeled with  and
and 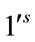 are given by
are given by . The induced vertex labels are equal to zero. Thus for each vertex v,
. The induced vertex labels are equal to zero. Thus for each vertex v,  and
and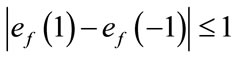 .
.
Hence the join of two cycle graphs C4 and C4 admits a Zero-M-Cordial labeling. The vertex and the edge conditions are given in Table 5.
In Figure 6 illustrates the zero-M-Cordial labeling on c4 + c4. Among the twenty four edges twelve edges receive the label +1 and the other twelve edges label –1.
Theorem 2.4: The split graph of Cn, for even n, admits

Table 4. Edge matrix of Cn + Cm.

Table 5. The vertex and the edge conditions of two cycle graphs Cn and Cm.
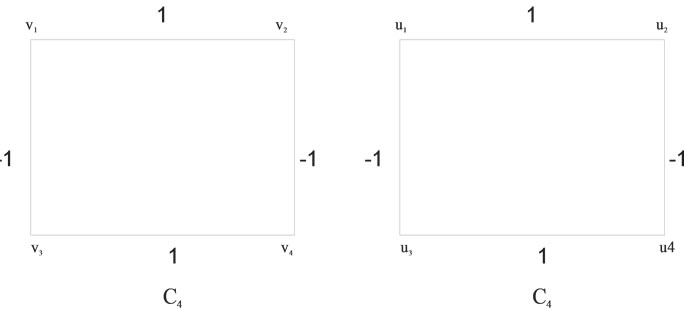

Figure 6. Zero-M-Cordial Labeling on C4 + C4.
a zero-M-cordial labeling.
Proof:
Let 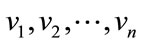 be the vertices of cycle Cn and
be the vertices of cycle Cn and 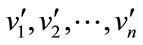 be the newly added vertices when n is even.
be the newly added vertices when n is even.
Let G be the split graph of cycle Cn with
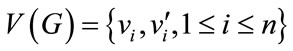 ,
,
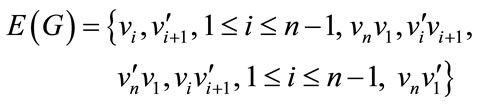
we note that  and
and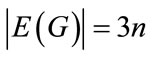 .
.
Define  two cases are to be considered.
two cases are to be considered.
Case (i) when n  0 (mod 4)
0 (mod 4)
For 
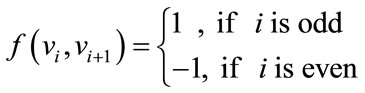
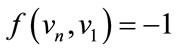
For 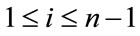
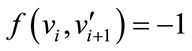
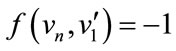
For 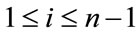

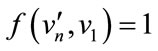
Case (ii) when n  2 (mod 4)
2 (mod 4)
For 
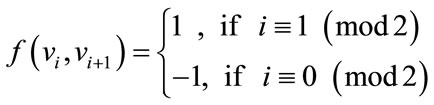
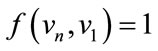
For 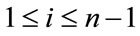
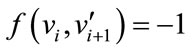
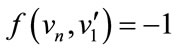
For 
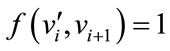
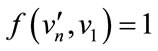
With respect to the above labeling pattern we give the proof as follows.
The total number of edges labeled with  and
and  are given by
are given by 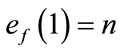 and
and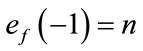 . Therefore the total difference between the edges labeled with
. Therefore the total difference between the edges labeled with 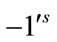 and
and 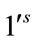 are given by
are given by 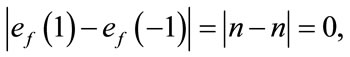 differ by zero. The induced vertex labels are equal to zero. Thus for each vertex v,
differ by zero. The induced vertex labels are equal to zero. Thus for each vertex v, 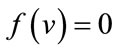 and
and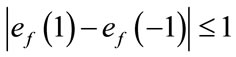 .
.
Hence the split graph of Cn for even n admits a ZeroM-Cordial labeling. The vertex and the edge conditions are given in Table 6.
In Figure 7 illustrates the Zero-M-Cordial labeling on split c8. Among the twenty four edges twelve edges receive the label +1 and the other twelve edges receive the label –1.
Theorem 2.5:  admits a Zero-M-Cordial labeling for even n.
admits a Zero-M-Cordial labeling for even n.
Proof: Let G be the graph 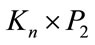 where n is even and
where n is even and 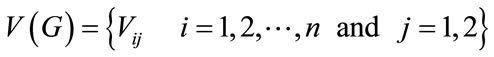 be the vertices of the graph G.
be the vertices of the graph G.
We note that 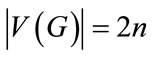 and
and  as
as
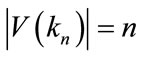 and
and 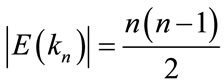
Define 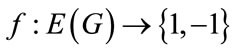 as follows For
as follows For 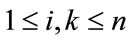
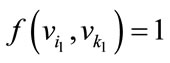
For 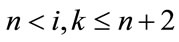

For 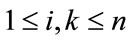
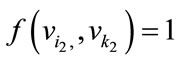
For 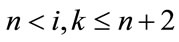
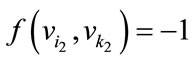
For 
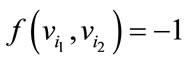
With respect to the above labeling pattern we give the proof as follows.
The total number of edges labeled with 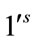 and
and 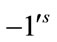 are given by
are given by 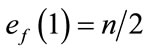 and
and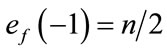 . Therefore the total difference between the edges labeled with
. Therefore the total difference between the edges labeled with 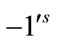 and
and 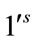 are given by
are given by 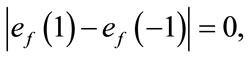 differ by 0. The induced vertex labels are equal to zero. Thus for each vertex v,
differ by 0. The induced vertex labels are equal to zero. Thus for each vertex v, 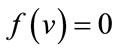 and
and .
.
Hence 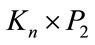 admits a Zero-M-Cordial labeling for even n. The vertex and the edge conditions are given in Table 7.
admits a Zero-M-Cordial labeling for even n. The vertex and the edge conditions are given in Table 7.
Figure 8 illustrates the Zero-M-Cordial labeling on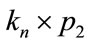 . Among the sixteen edges eight edges label +1 and the other eight edges label –1.
. Among the sixteen edges eight edges label +1 and the other eight edges label –1.
Theorem 2.6:  admits a Zero-M-Cordial labeling for odd n.
admits a Zero-M-Cordial labeling for odd n.
Proof: Let G be the graph 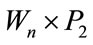 where n is odd and
where n is odd and 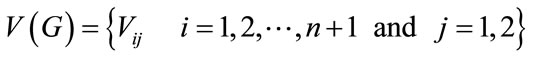 be the vertices of graph G.
be the vertices of graph G.
We note that 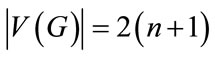 and
and 
as 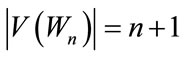 and
and 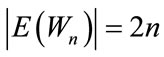

Table 6. The vertex and the edge conditions of split of Cn.

Table 7. Vertex and the edge condition of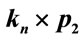 .
.

Figure 7. Zero-M-Cordial labeling on split C8.
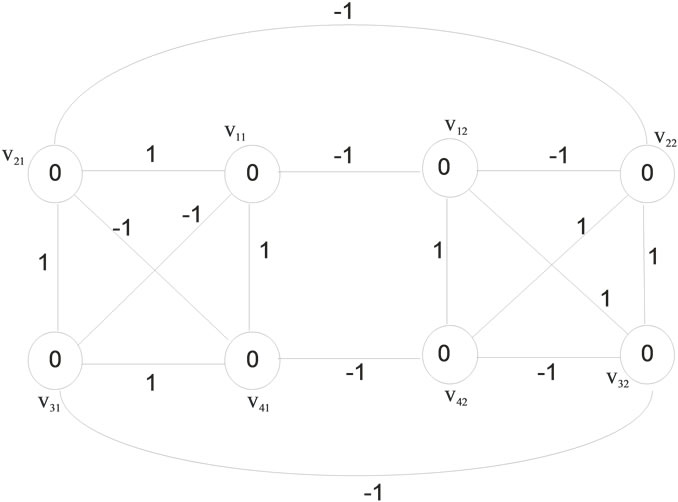
Figure 8. Zero-M-Cordial labeling on .
.
Define 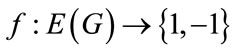 as follows For
as follows For 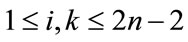

For 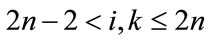
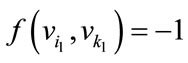
For 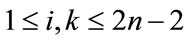
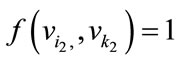
For 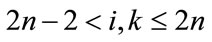
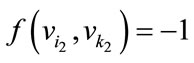
For 
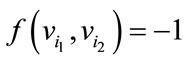
The total number of edges labeled with  and
and 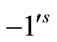 are given by
are given by 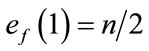 and
and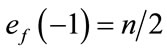 . Therefore the total difference between the edges labeled with
. Therefore the total difference between the edges labeled with 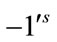 and
and 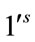 are given by
are given by  differ by 0. The induced vertex labels are equal to zero. Thus for each vertex v,
differ by 0. The induced vertex labels are equal to zero. Thus for each vertex v, 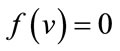 and
and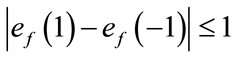 .
.
Hence  admits a Zero-M-Cordial labeling for odd n. The vertex and the edge conditions are given in Table 8.
admits a Zero-M-Cordial labeling for odd n. The vertex and the edge conditions are given in Table 8.
Figure 9 illustrates the Zero-M-Cordial labeling on . Among the sixteen edges eight edges receive the label +1 and the other eight edges label –1.
. Among the sixteen edges eight edges receive the label +1 and the other eight edges label –1.
Theorem 2.7:  (also known as book graph) admits a Zero-M-Cordial labeling for odd n.
(also known as book graph) admits a Zero-M-Cordial labeling for odd n.
Proof: Let G be the graph 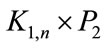 where n is odd and
where n is odd and 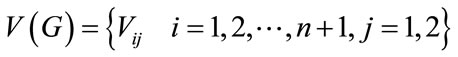 be the vertices of G.
be the vertices of G.
We note that 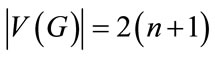 and
and .
.
Define 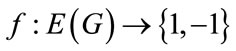 as follows For
as follows For 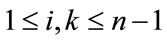
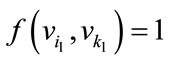
For 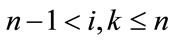
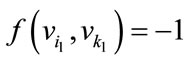
For 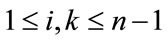
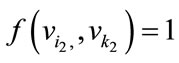
For 
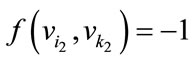
For 
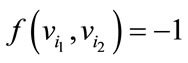
For 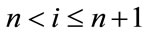
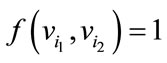
The total number of edges labeled with  and
and 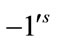 are given by
are given by 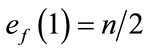 and
and . Therefore the total difference between the edges labeled with
. Therefore the total difference between the edges labeled with 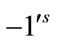
and 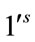 are given by
are given by 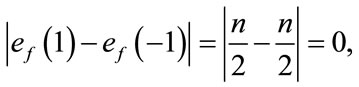
differ by 0. The induced vertex labels are equal to zero. Thus for each vertex v,  and
and

Table 8. Vertex and the edge condition of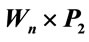 .
.

Table 9. Vertex and the edge condition of .
.
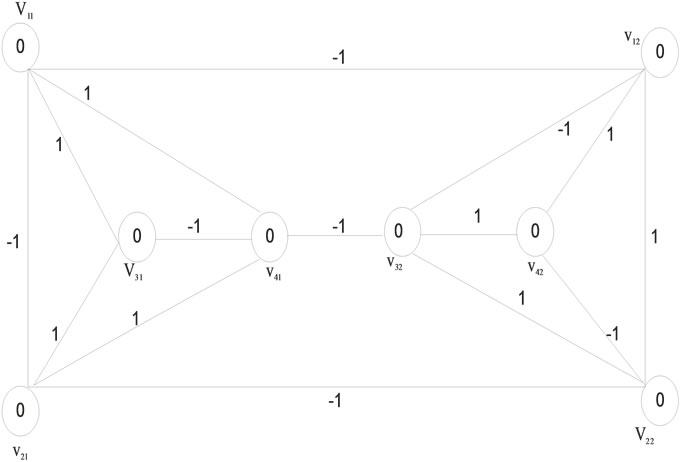
Figure 9. Zero-M-Cordial labeling on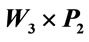 .
.
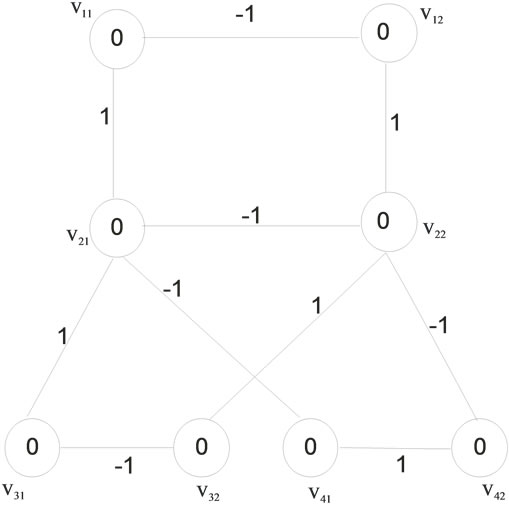
Figure 10. Zero-M-Cordial labeling on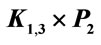 .
.
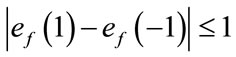 .
.
Hence 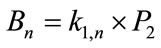 (also known as book graph) admits a Zero-M-Cordial labeling for odd n. The vertex and the edge conditions are given in Table 9.
(also known as book graph) admits a Zero-M-Cordial labeling for odd n. The vertex and the edge conditions are given in Table 9.
Figure 10 illustrates Zero-M-Cordial labeling on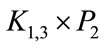 . Among the ten edges five edges receive the label +1 and the other five edges receive the label –1.
. Among the ten edges five edges receive the label +1 and the other five edges receive the label –1.
3. Concluding Remark
Here we investigate Zero-M-Cordial labeling for Cartesian product of some graphs, join of two cycle graphs, split graphs and bipartite graphs. Similar results can be derived for other graph families and in the context of different graph labeling problem is an open area of research.
REFERENCES
- I. Cahit, “H-Cordial Graphs,” Bulletin of the Institute of Combinatorics and Its Applications, Vol. 18, 1996, pp. 87-101.
- M. Ghebleh and R. Khoeilar, “A Note on ‘H-Cordial graphs’,” Bulletin of the Institute of Combinatorics and Its Applications, Vol. 31, 2001, pp. 60-68.
- J. A. Gallian, “A Dynamic Survey of Graph Labeling,” The Electronics Journal of Combinatories, Vol. 18, 2011.
- F. Harary, “Graph Theory,” Addison Wesley, Reading, 1972.

