ABSTRACT

In this paper we show that we can have the same conclusion for the limit of the solution 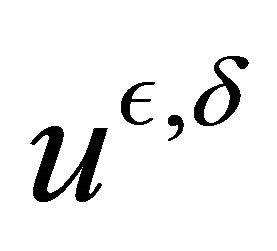if we suppose the case of hypoellipticity.

1. Introduction

Let us consider the parabolic PDE:

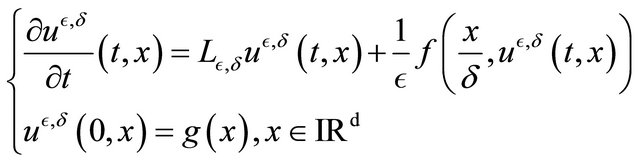(1)

We study in this paper the behavior of 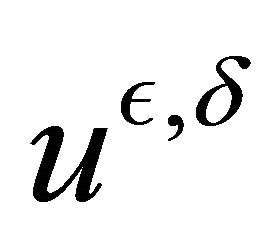when

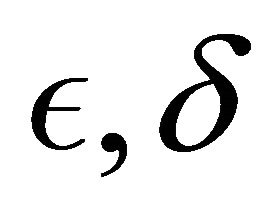tend to zero, and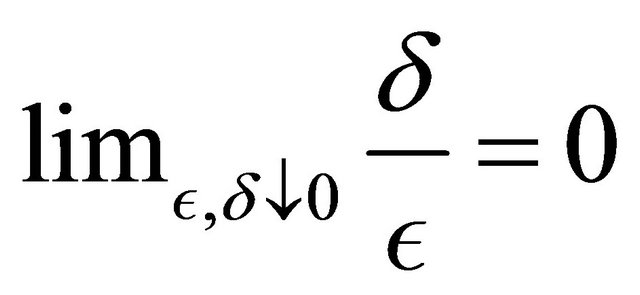. We suppose that the matrix of the second order coefficients of 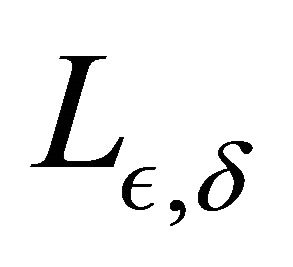is degenerate, in fact we formulate here a hypoellipticity condition of Hörmander type (see e.g. David Nualart [1]). Diédhiou and Manga in [2] studied the limit of 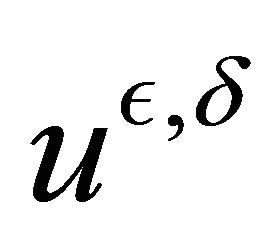with a nondegenerate condition of the matrix. In Freidlin & Sowers[3], three cases are considered, with the assumption that the matrix is non, but we formulate here a hypoellipticity condition of. Since the parameter (homogeneization parameter) decreases quickly than (large deviations principle parameter) to zero we must homogenize first and apply the large deviations principle.

We use essentially probabilistic tools to solve our problem.

Let 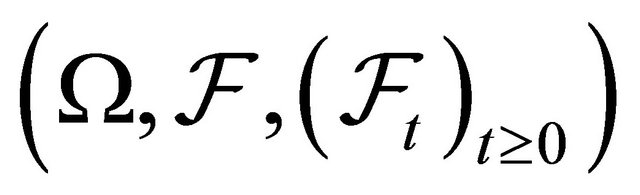a probability filtered space. We consider the 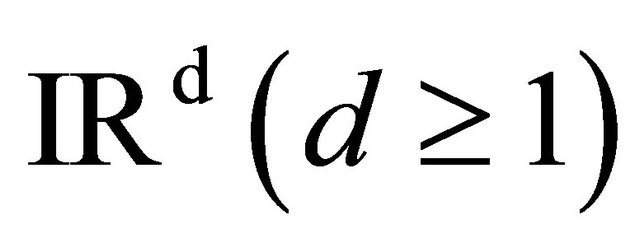valued process 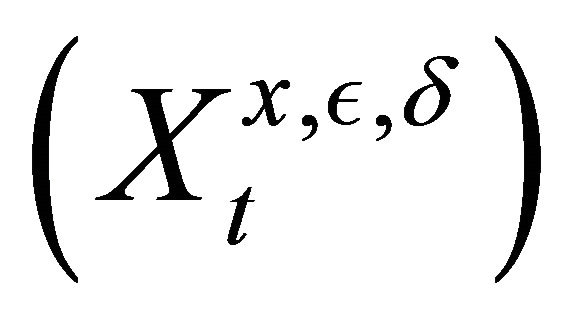solution of the SDE:

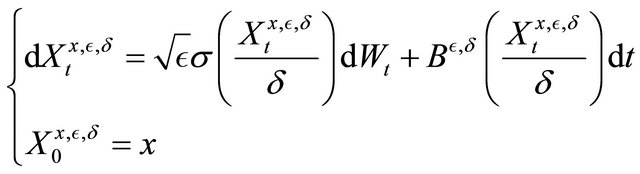(2)

where 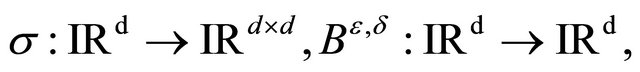and

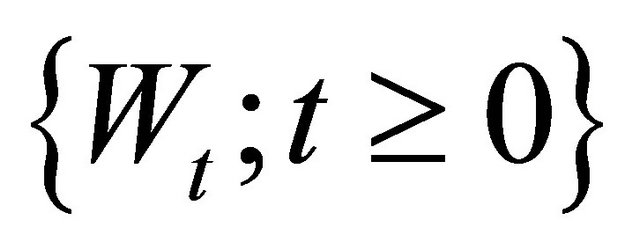is a d-dimensional standard Brownian motion.

We assume that and 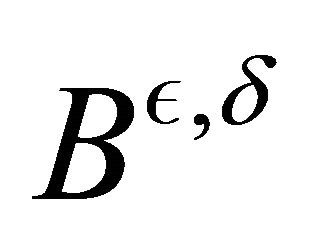are smooth mappings from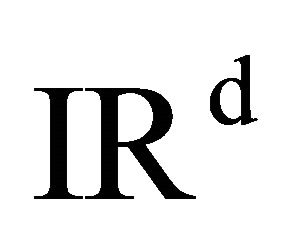, and periodic with period one in each direction.

The mapping 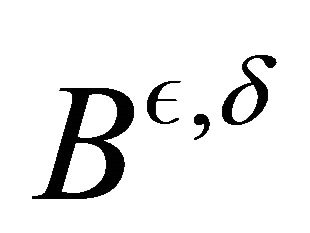is assumed to be of the form :

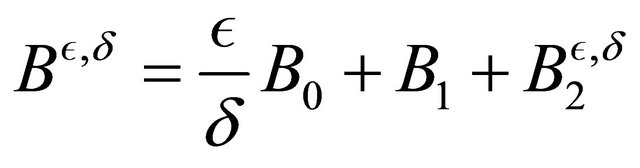
where 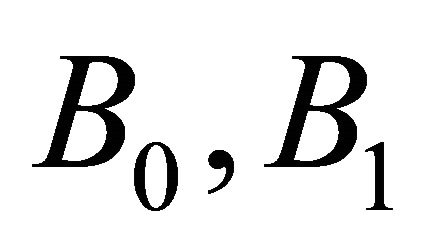and 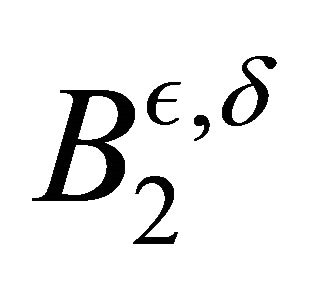are in 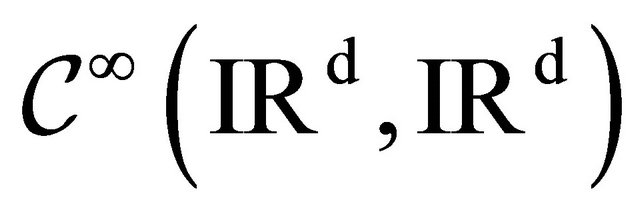for every 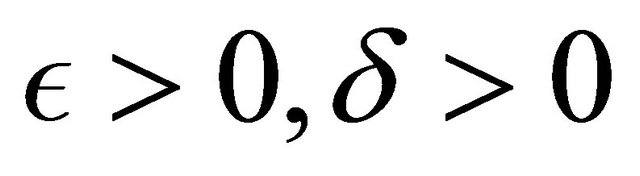and

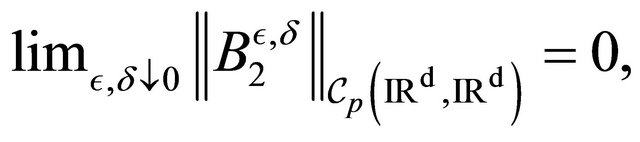
where 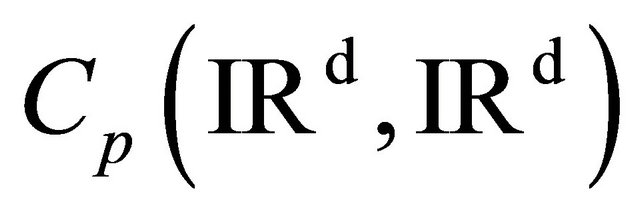be the collection of periodic continuous mappings from 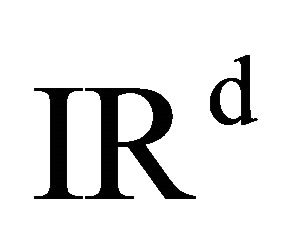into.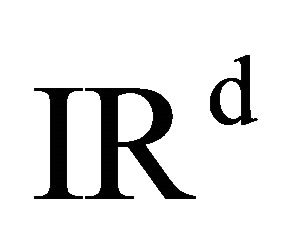

The infinitesimal generator 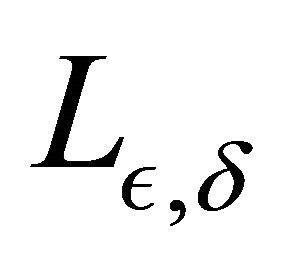is gigen by

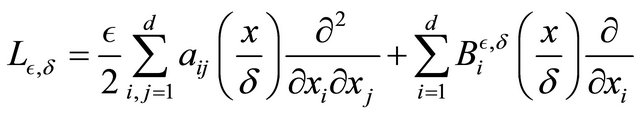
and where 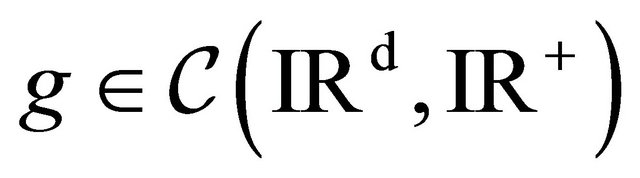is a bounded function and we set

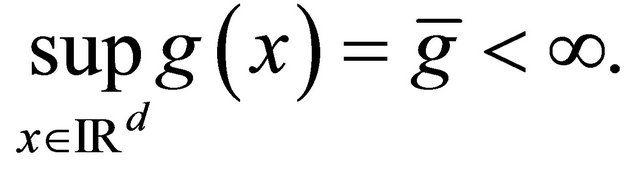
Let set

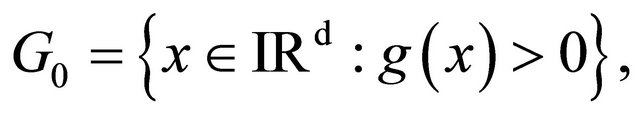
since is continuous we have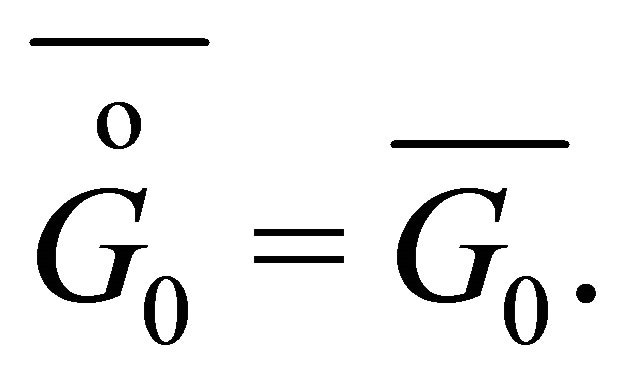

We assume that 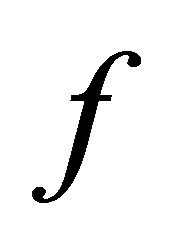is periodic in each direction, with respect to the first argument, and it verifies:

•

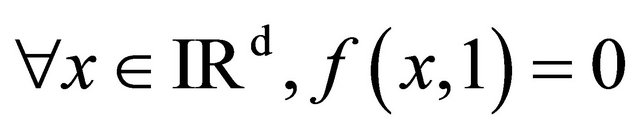
• There exists 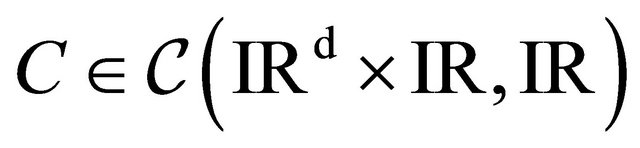bounded such that

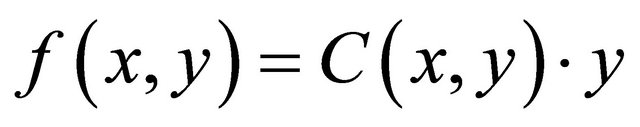
with

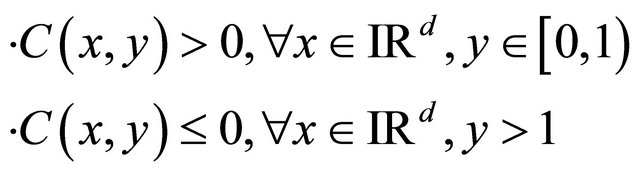
and we assume that

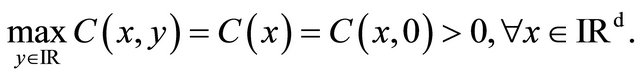
Let us consider the progressive measurable process 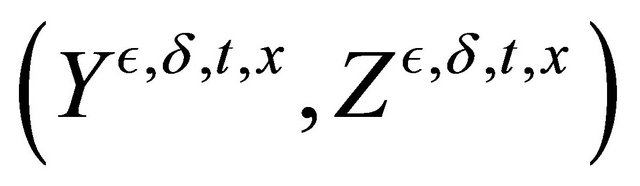solution of the BSDE:

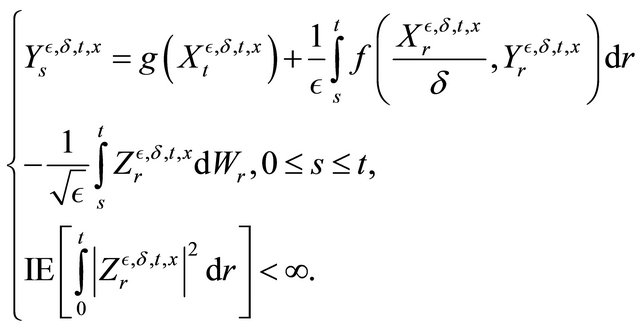
By Pardoux and Peng [4], we have for all

,

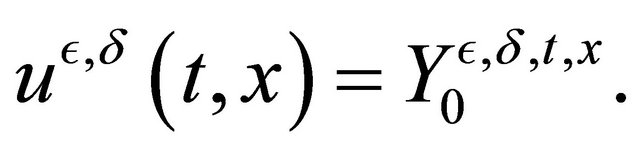
The matrix 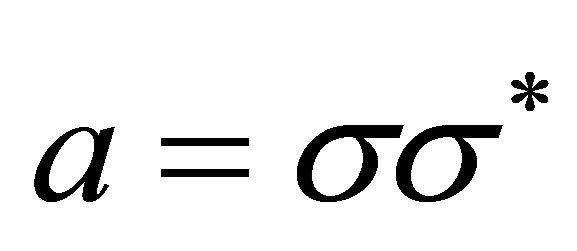(where is the symbol of transposition) is degenerate. Let us consider the Definition 1.1 The Lie bracket between the vector fields 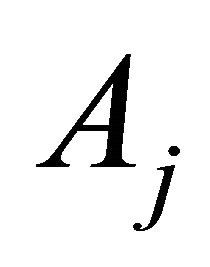and 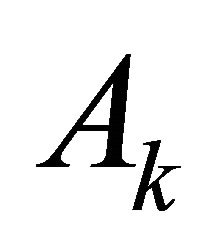is defined by

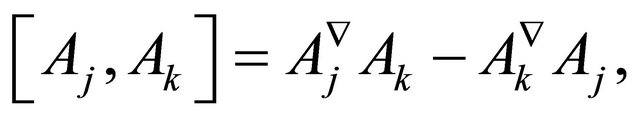
where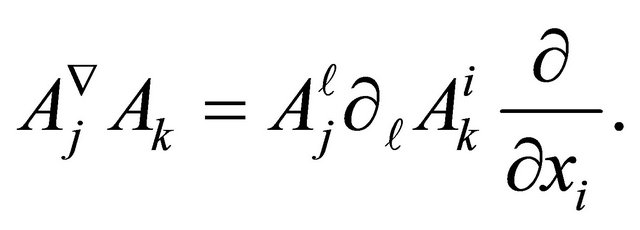

We assume that the matrix of the column vectors verifies the strong Hörmander condition, defined by the Definition 1.2 Let 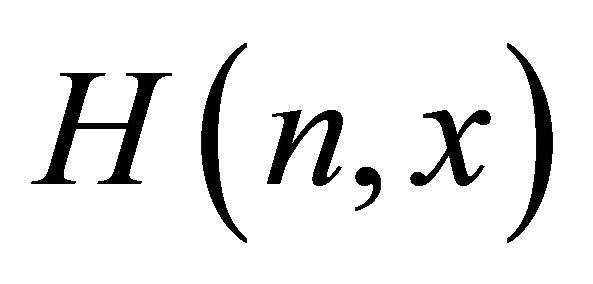be the set of Lie brackets of 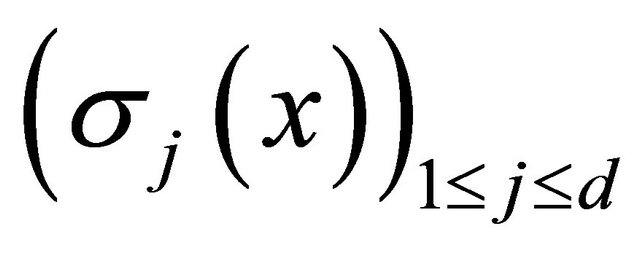of order lower than at the point

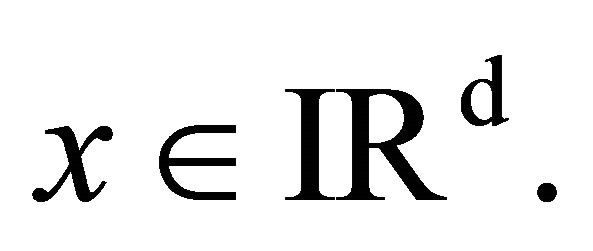
We say that the matrix satisfies the strong Hörmander condition (called SHC) if for all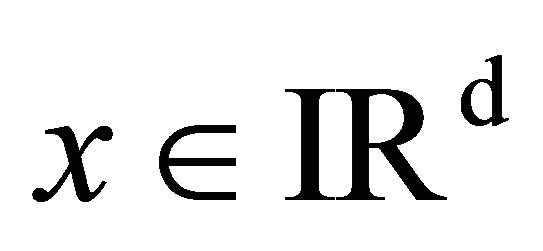, there exists 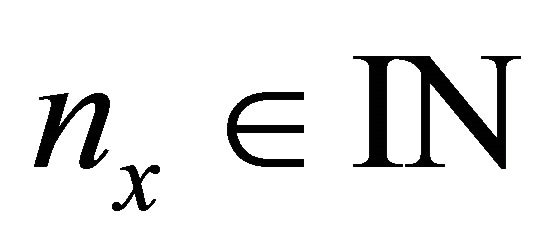such that 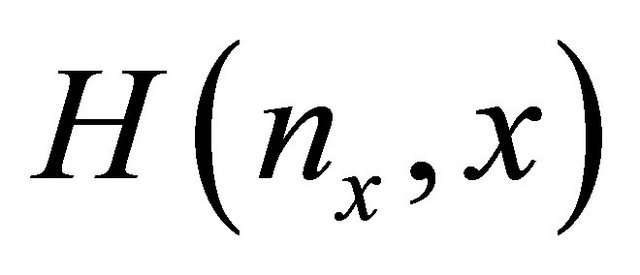generates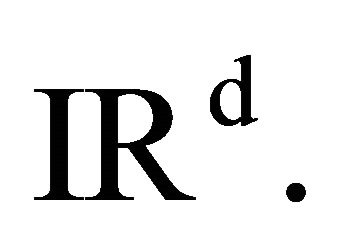

We organize this paper as follows. Section 2 contains the results of large deviations principle. In Section 3 we study the behavior of the solution of the PDE (1).

2. Large Deviations Principle

Since, 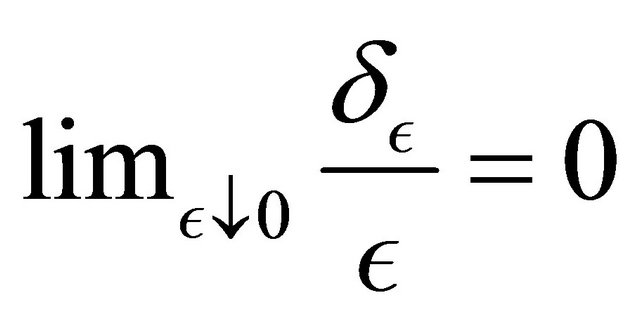(when we set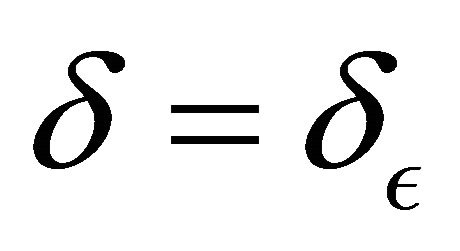) we have a problem of homogenization because the matrix

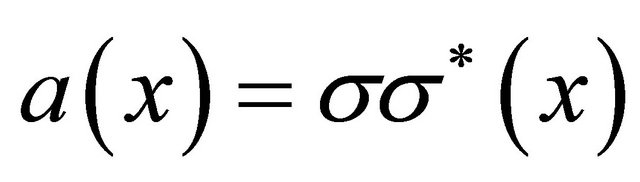is not elliptic.

Since tends to zero faster than, the homogenization dominates, and the large deviations principle will be applied to the problem with constant coefficients.

For the homogeneization in the hypoellipticy case, we use the results of Diédhiou and Pardoux [5] and Pardoux [4,6,7].

Setting: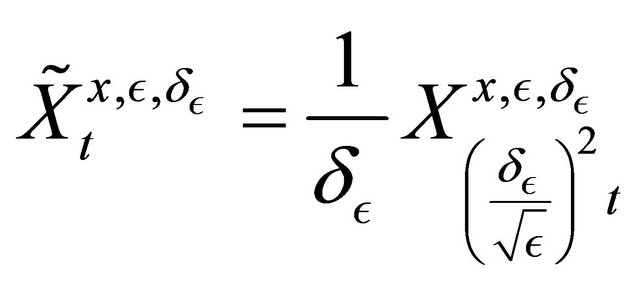, we have

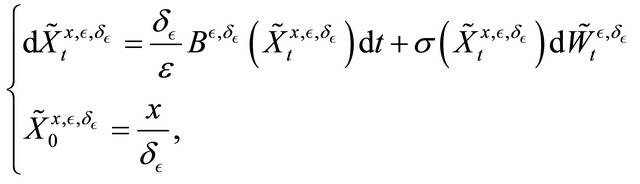
where 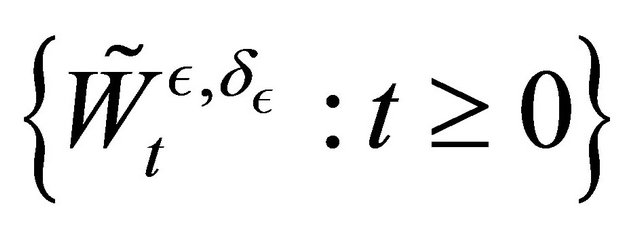is a standard Brownian motion.

The 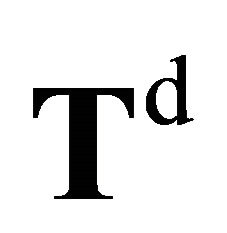-valued process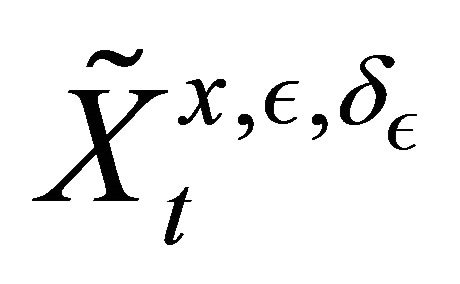, is a Feller process, then has a unique invariant measure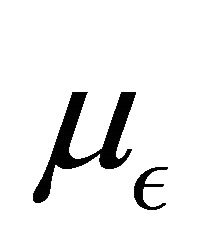, and we have 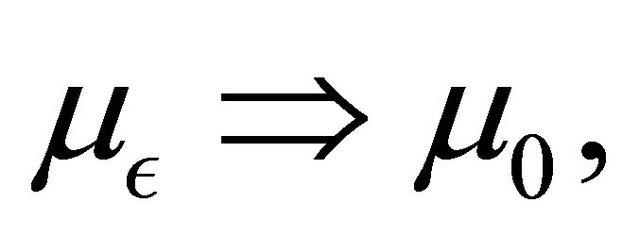when see [5].

We assume that

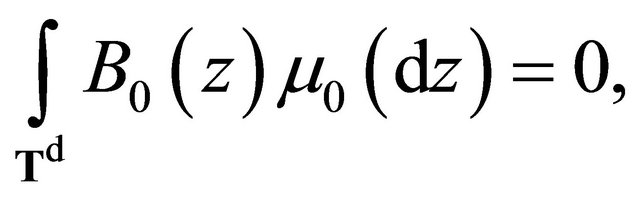(3)

and the homogenized coefficients see [3] are

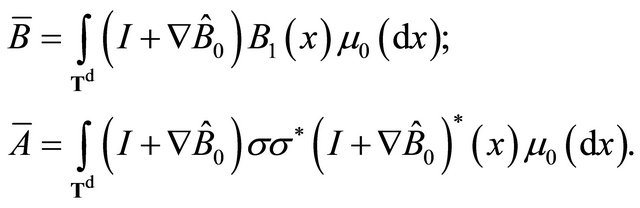
Let us define, for each and

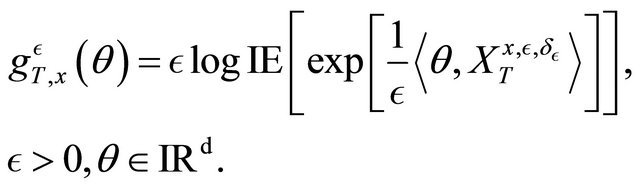
We have

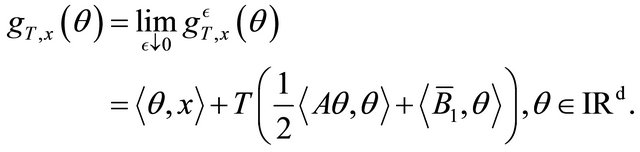
The details of the calculation of this limit are the same as in Freidlin and Sowers [3].

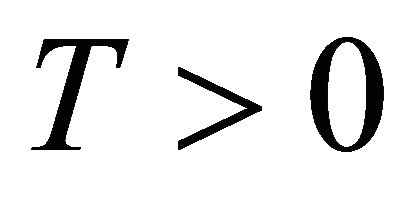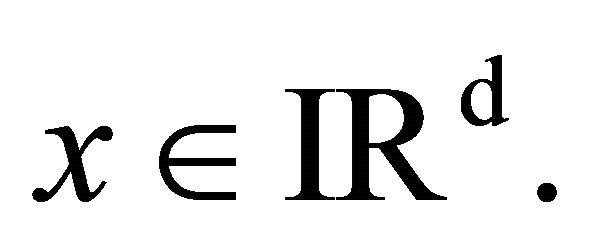In order to establish a large deviations principle, we will consider the Theorem 2.1 ([8]) Fix and Assume that 1) For each 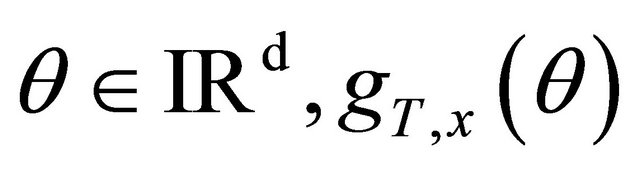is well-defined in.

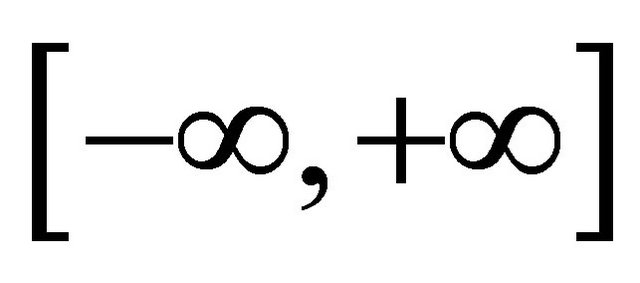2) The origin is in the interior of the set

.

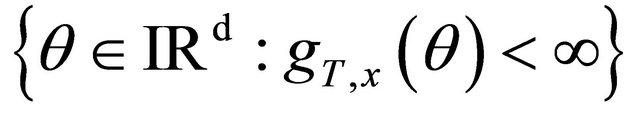3) The set 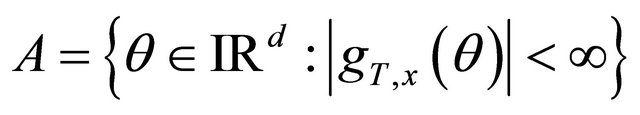has a nonempty interior 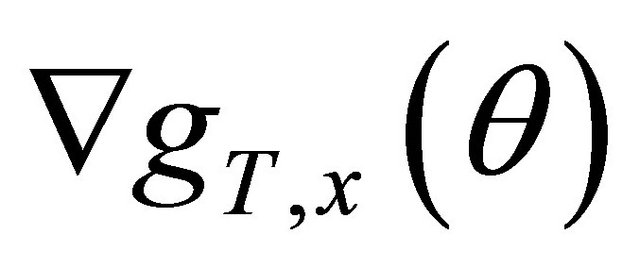is well-defined for all

and

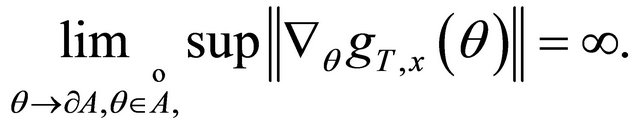
Then the random variables 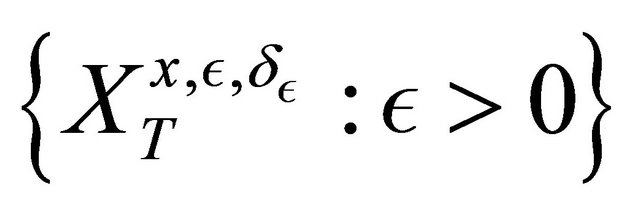satisfy a large deviations principle with rate function 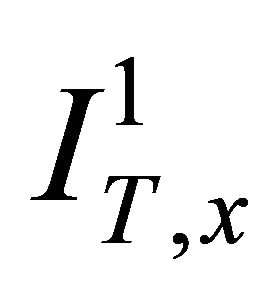defined by

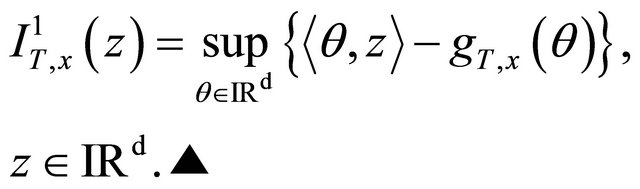
The limit 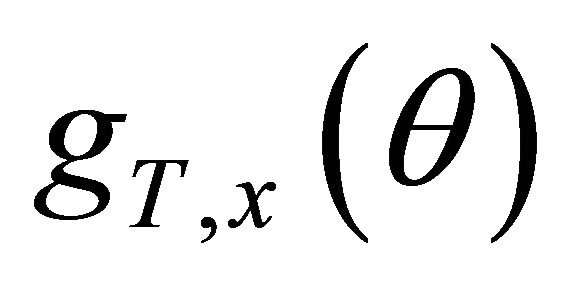satisfies the conditions 1) and 2). For the condition 3) we may assume more that the matrix is strictly positive-definite. In fact it is not a strong assumption, for Example 2.2 If we choose 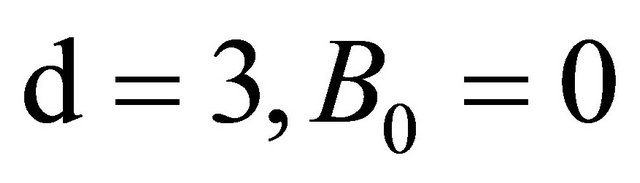and

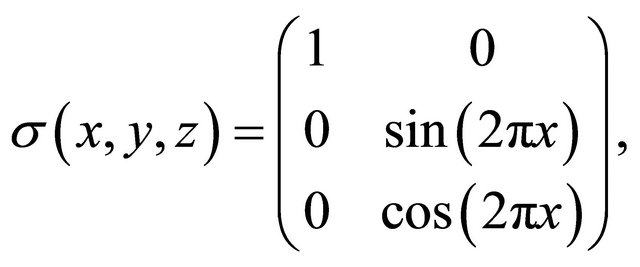
this matrix satisfies the Hörmander condition, and

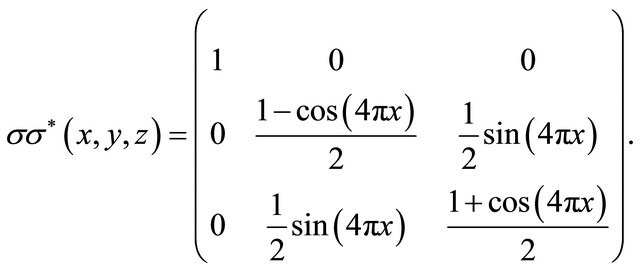
The invariant measure 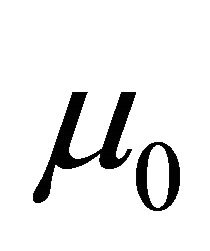has the density

.

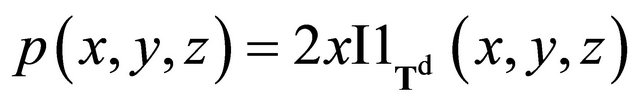Then we have

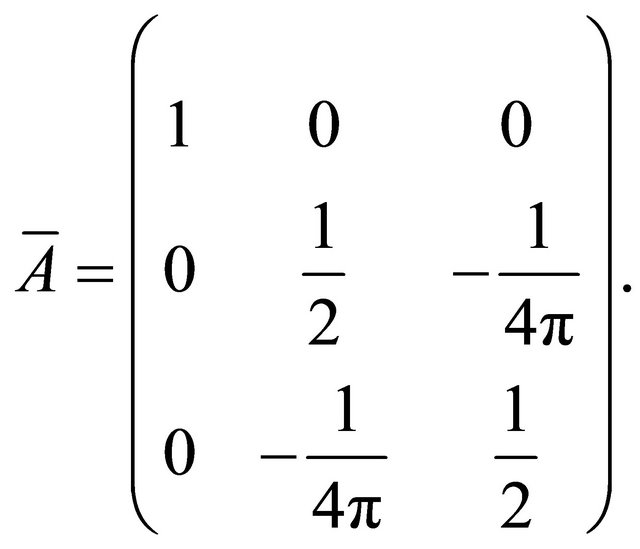
Let us consider

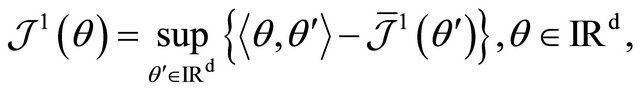
by the assumption on, we get

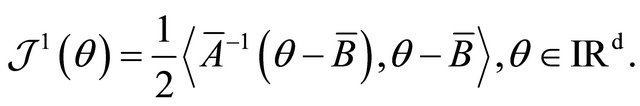
Thus the form of and the assumption on imply that 3) is true.

We have the Theorem 2.3 (Freidlin and Sowers [3]) Fix and assume that the assumption (3) is true. For every and 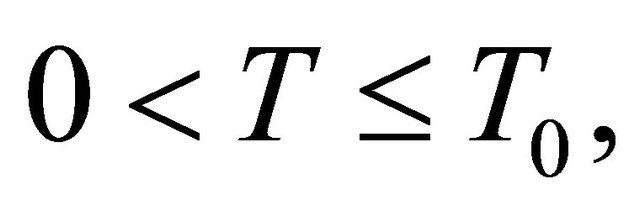the family 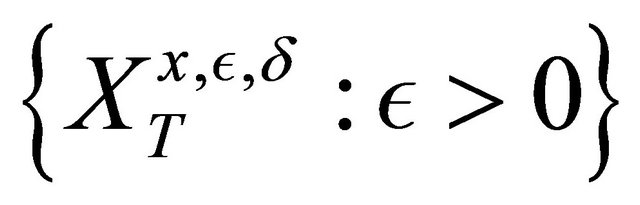of 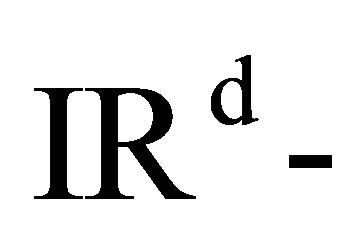valued random variables satisfies a large deviations principle (LDP) with rate function

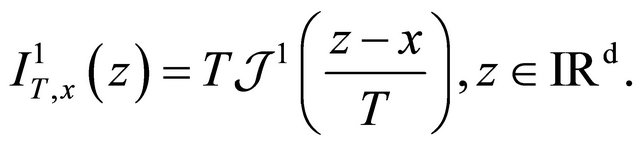
Furthermore, this LDP is uniform for all 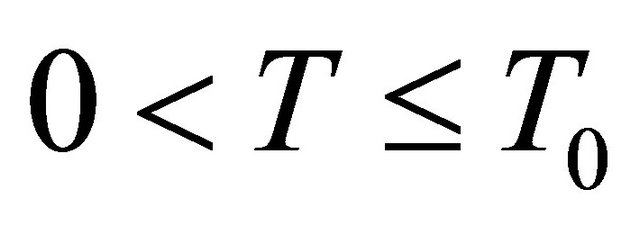and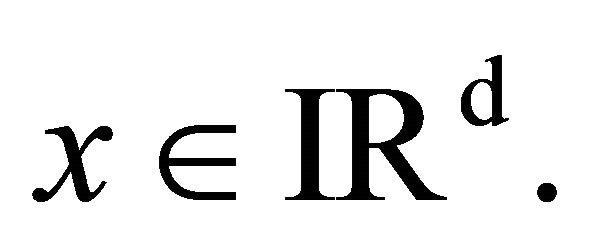

Proof: See Freidlin and Sowers [3].

Let us consider some definitions:

Since the function 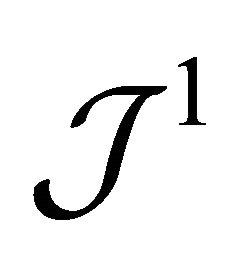is convex we can show that

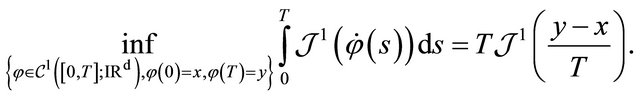
So we have the Theorem 2.4 For all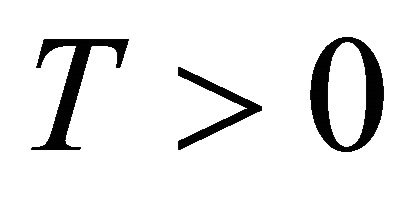, we assume that the assumption (3) holds. The family

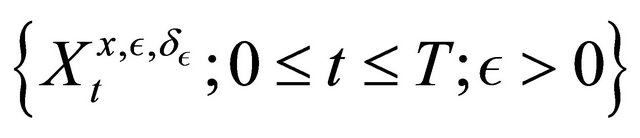of 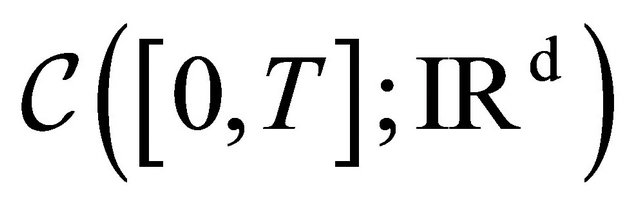-valued random variables satisfies a Large Deviations Principle (LDP) with rate function 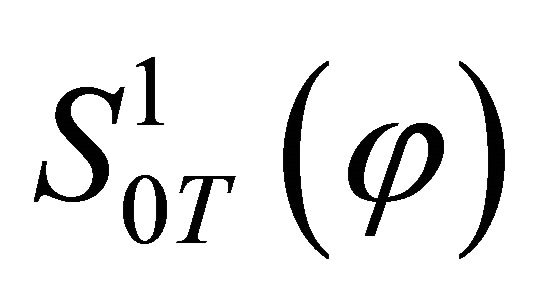for all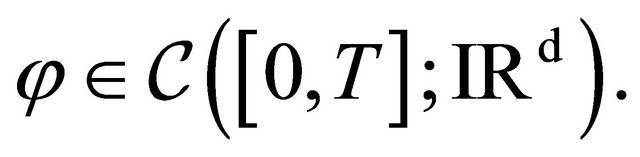

Proof: See Freidlin and Sowers [3].

3. Asymptotic Behavior of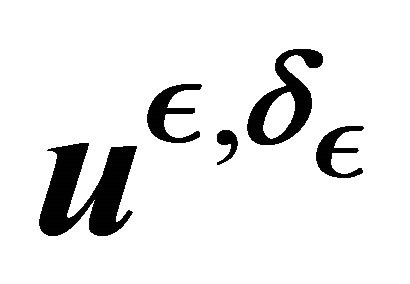

We want to apply the technics used by [6], so we consider now the BSDE:

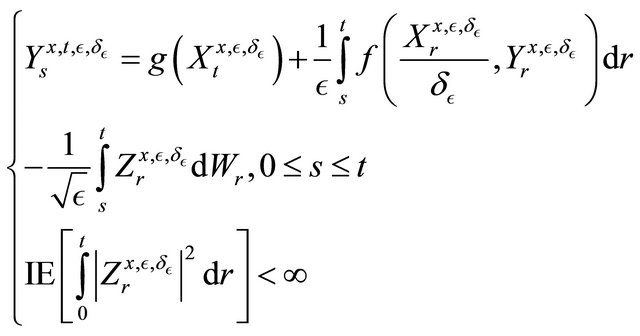
We know that for all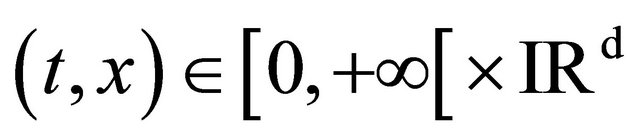, the solution 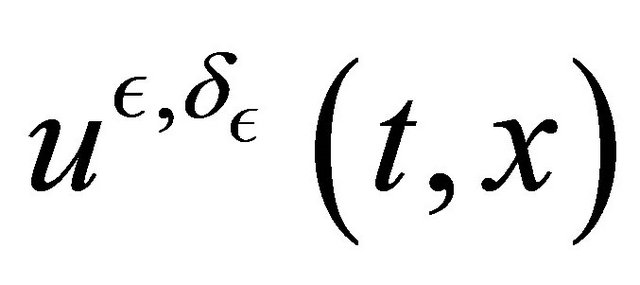of the PDE is of the form:

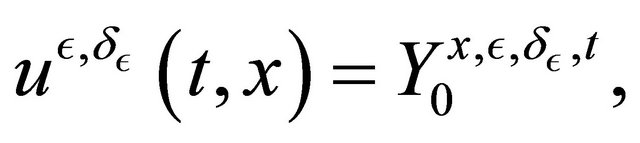
and by the Feynman-Kac formula, we have

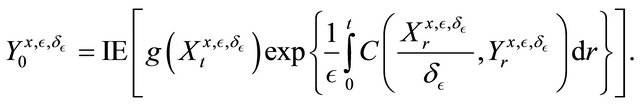
Our aim is to study the behavior of the 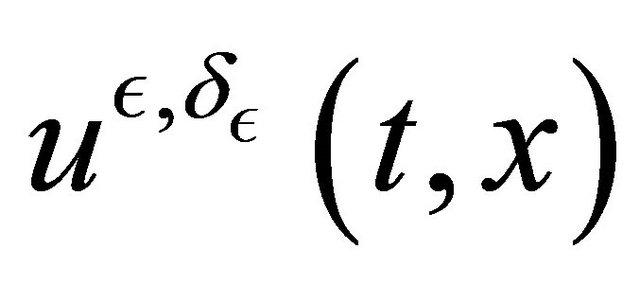when tends to zero.

• Remark 3.1

• If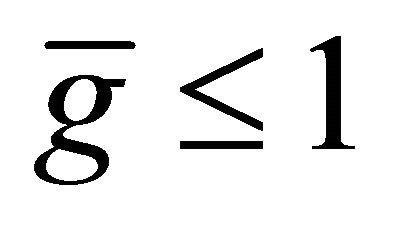, then•

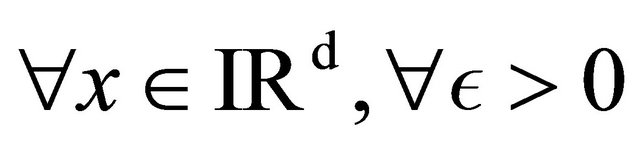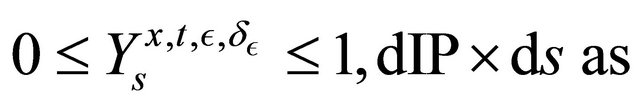
• In the other cases, if

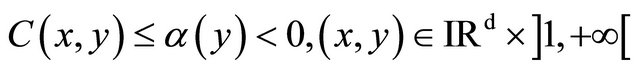
where is Lipschitz continuous, then

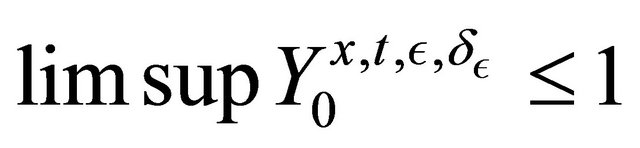
uniformly in any compact set of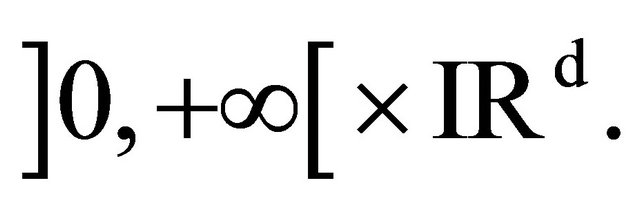

We give the Definition 3.2 A functional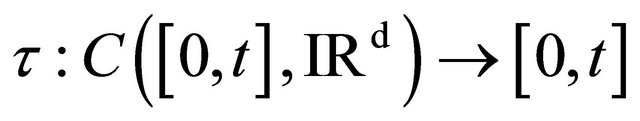

is a stopping time if for all 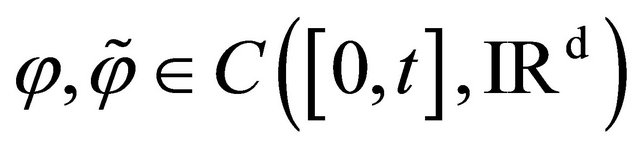and all

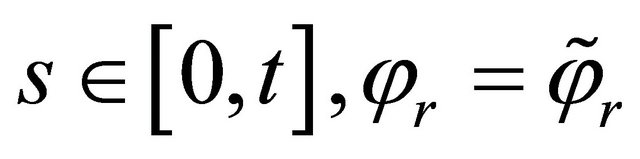for all 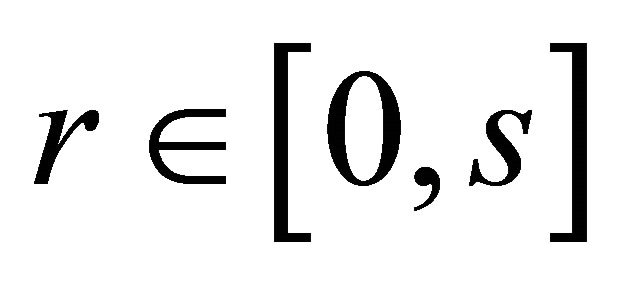and 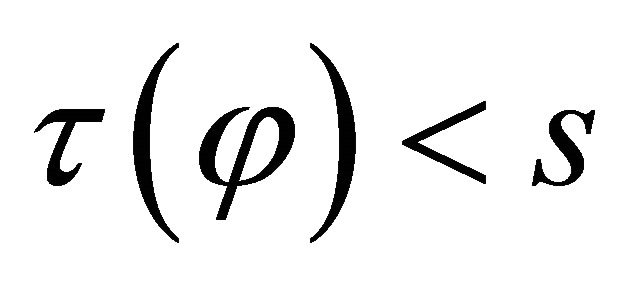imply

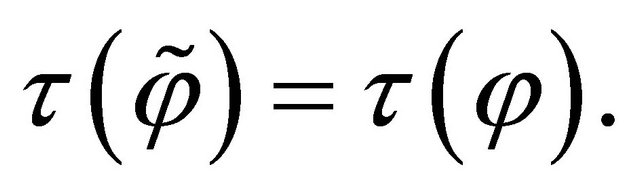
Let us set 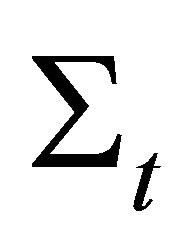the set of stopping times and the set of elements of 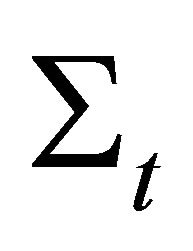such that there exists such that for all

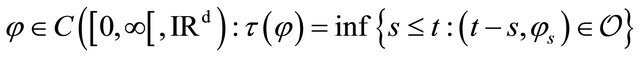
with the convention 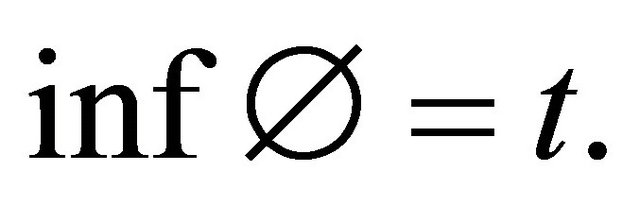is hence a well defined element of 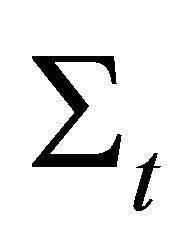and is the open set associated.

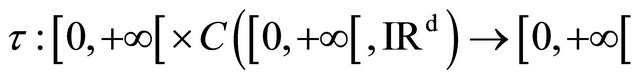
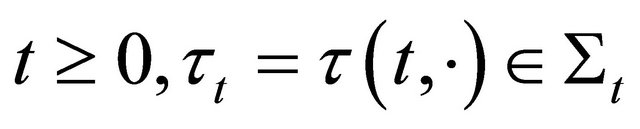is an element of (resp.) if and only if, for all (resp.) where

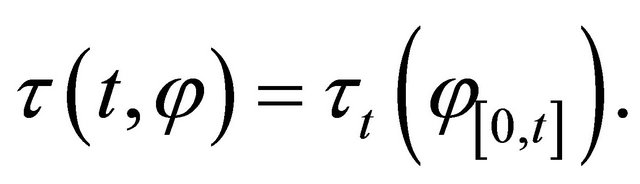
Let us consider the function 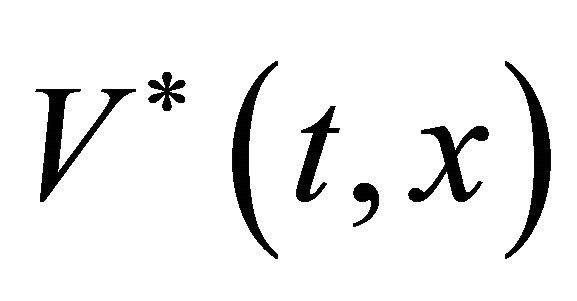defined in 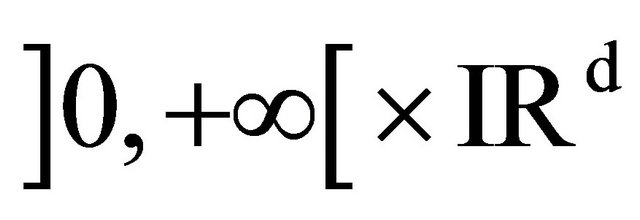by,

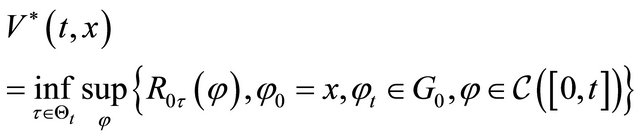
where

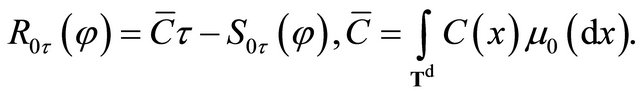
Let 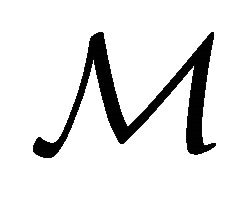and be a partition of,

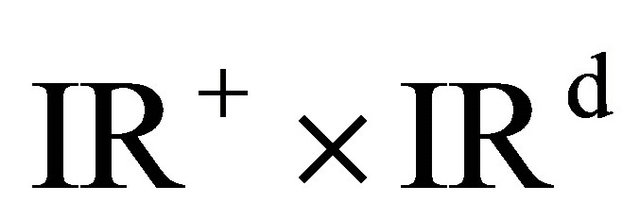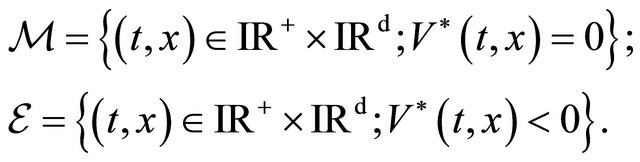
We have

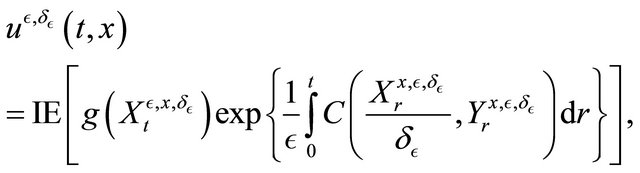
then we deduce that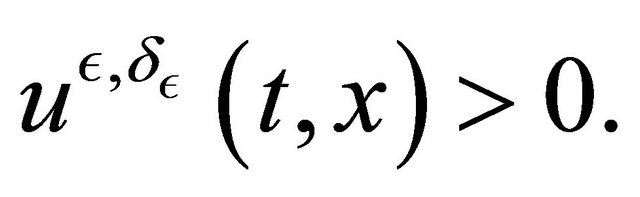

We have the Theorem 3.3 For 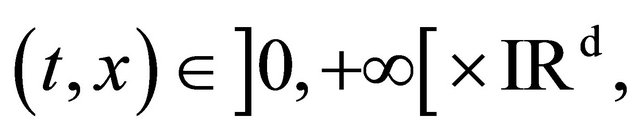we have 1)

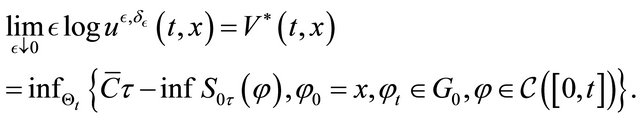
2)

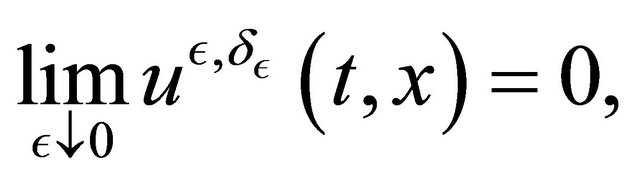
uniformly in any compact set 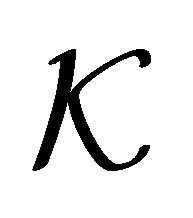of.

3)

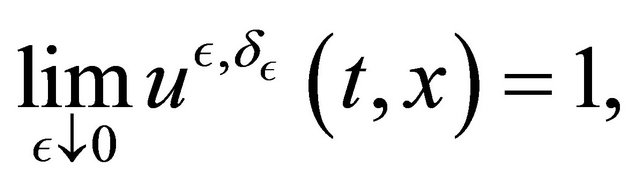
in all compact set 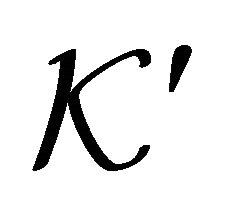of.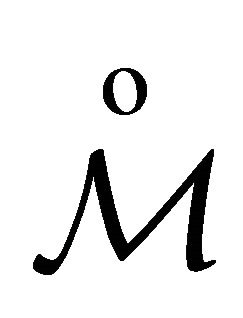

Proof: For first item, the proof is the same as in [2].

For the second point we can see that there exists 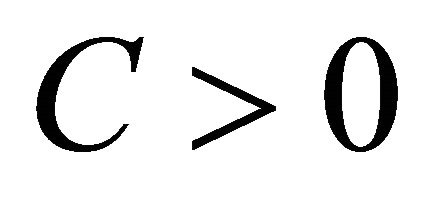such that

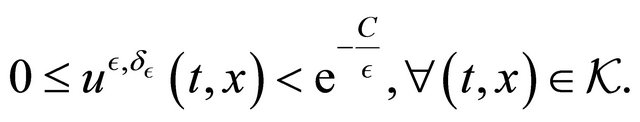
The third item is an immediate consequence of 1).

REFERENCES

NOTES

^*This work was supported, in part, by grants from FIRST (Fonds d’Impulsion pour la Recherche Scientique et Technique).