Applied Mathematics
Vol.3 No.4(2012), Article ID:18887,4 pages DOI:10.4236/am.2012.34056
The Study about Autumobile Insurance Based on Linear Empirical Bayesian Estimation
1Department of Mathematics, Southwest University of Science and Technology, Mianyang, China
2Department of Mathematics, Jining University, Jining, China
3Finance Institute, Zhongnan University of Economics and Law, Wuhan, China
Email: yaozongjing@163.com
Received February 10, 2012; revised March 7, 2012; accepted March 14, 2012
Keywords: Automobile Insurance; Linear Empirical Bayesian Estimation; Claim Size
ABSTRACT
Automobile insurance is one of the most popular research areas, and there are a lot of different methods for it. We uses linear empirical Bayesian estimation for the study of automobile insurance, giving the estimator of the policy’s future claim size. Thus, a new point of view is given on the pricing of automobile insurance.
1. Introduction
Automobile insurance is one of the most important insurance in property insurance. Recently, automobile insurance premium income grows steadily in our country. Since 2000, automobile insurance premium income accounted for the proportion of insurance premium income and has been maintained at above 60%. Cao Jing, Li Ping, Gao Yuan (2006) [1] studied the incentive contract in auto Insurance market based on the optimal the strategy game between the insurer and the insured, giving the linear relationship between the optimal indemnity and insurance premium when the insurance company have the biggest benefits. Xu Yun-Bao (2007) [2] established a dynamic theoretical model on the probabilistic moral hazard and the incomplete information between the insurer examination and verification influenced by insured person, studied the optimum games of strategy. Furthermore, insurance fixed price formula such that the insurer’s expectation profit was given.
In the current, actuary pricing risk premium in auto insurance usually use the claim number mean and optimal estimation to calculate the claim amount. We commonly use the following methods to study the optimal estimation model of the claim size. For example: Poisson-inverse Gauss distribution, Mixed Pareto distribution Model, Mixed two-parameters Exponential distribution Model, Three parameters of Mixed Gamma distribution Model, Two dimensional Risk Model, Two negative binomial model, compound PNB distribution model, and so on. For the claim amount, there are only a few optimal estimation models, and now the relatively mature model is Pareto model [3]. However, when the Pareto model is not suitable for the amount of the claim, we can only setting the price according to the number of the history claim pricing times the insured did, and the result may be that the claim amount is different but the amount of insurance premium is the same, which is obviously unfair. Yu Jiamin, Hao Xudong (2008) [4,5] elicited an optimal estimator of the policy’s future claim size by constructing the structure function of claim size lognormal distribution parameter. An empirical rating actuarial model with allowance for claim frequency and claim severity was presented. Thus, the price on automobile insurance is more equitable and reasonable. Furthermore, a typical rating actuarial model fit for Chinese automobile insurance reality was put forward, preliminary to the promotion of rates allowance for claim severity. However, there still have parameter 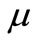 in the optimal estimation of the future policy claim expectation when having the history claim information
in the optimal estimation of the future policy claim expectation when having the history claim information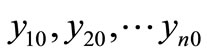 , we have to estimate the parameter
, we have to estimate the parameter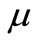 , and it’s inconvenience for practical application.
, and it’s inconvenience for practical application.
Based on linear empirical Bayesian method (L.E.B method) [6], we study the estimation of the future claim amount, and the parameter estimation is obtained, the calculation is that the minimum mean square error 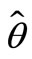 is equal to the weighted average value between the true value
is equal to the weighted average value between the true value 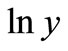 and the experience value
and the experience value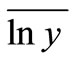 , and the weight is respectively
, and the weight is respectively  and
and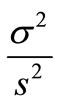 . By statistical theory, we indicate that this estimate is the optimal estimation method, at the same time it avoids the estimation of parameter
. By statistical theory, we indicate that this estimate is the optimal estimation method, at the same time it avoids the estimation of parameter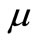 , and the result is not only concise but also convenient for practical application.
, and the result is not only concise but also convenient for practical application.
2. Linear Empirical Bayesian Method (L.E.B. Method)
First we introduce two Lemmas [6]:
Lemma 1: [6]  are two vectors. Suppose
are two vectors. Suppose 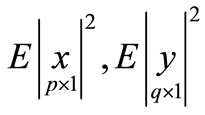 are existed, then the following equation
are existed, then the following equation
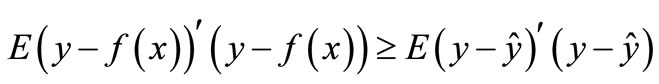 (1)
(1)
is right for all functions , where
, where  is a vector, Representing the functions of
is a vector, Representing the functions of  with the number
with the number , and the second-order moments of
, and the second-order moments of  are existed with
are existed with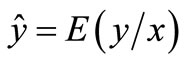 .
.
The Explaining of equation (1) is that: conditional expectation 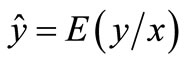 is the closest function to
is the closest function to 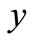 in all functions of
in all functions of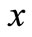 , and the Close degree can be measured with the mean square error
, and the Close degree can be measured with the mean square error 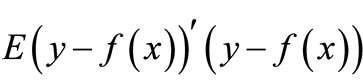 between
between 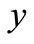 and
and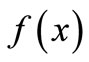 . However, it’s difficult to calculate the conditional expectation, so if the linear functions are taken into account, the problem will be solved. This is the following conclusion:
. However, it’s difficult to calculate the conditional expectation, so if the linear functions are taken into account, the problem will be solved. This is the following conclusion:
Lemma 2: [6] 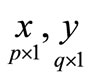 are two vectors. Suppose
are two vectors. Suppose 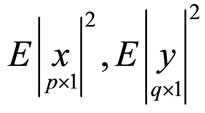 are existed, A is a constant matrix, b is a Constant vector, then
are existed, A is a constant matrix, b is a Constant vector, then
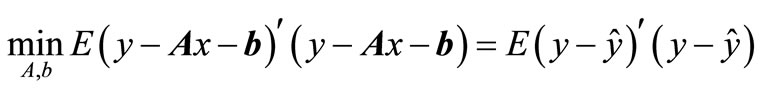 (2)
(2)
in which
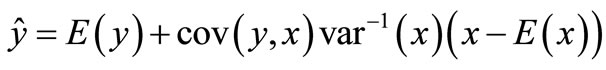 (3)
(3)
The results show that 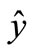 is the closest function to y in all linear functions of x. with Lemma 2, if we replace y with the parameter vector
is the closest function to y in all linear functions of x. with Lemma 2, if we replace y with the parameter vector 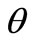 of statistical problems, and regard x as a sample, then the estimation of parameter
of statistical problems, and regard x as a sample, then the estimation of parameter 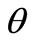 will be
will be
 (4)
(4)
And it will be the minimum mean square error estimation. From Equation (4), if we can find the values of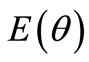 ,
, 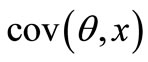 ,
, 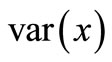 and
and 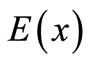 in the right equation, the estimation of parameter vector
in the right equation, the estimation of parameter vector 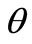 can be calculated. If we suppose variable X-normal distribution
can be calculated. If we suppose variable X-normal distribution 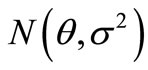 for which the variance
for which the variance  is known, with the above results, we can give the estimation expression of parameter
is known, with the above results, we can give the estimation expression of parameter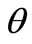 . With
. With  is known in statistical problems, and
is known in statistical problems, and  is a conditional probability density with parameter
is a conditional probability density with parameter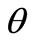 , so
, so 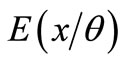 and
and 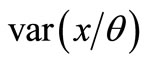 can be evaluated.
can be evaluated.
Theorem 1: If the conditional probability density of normal distribution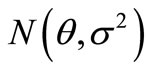 is
is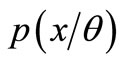 , then
, then 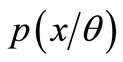 have the following two properties:
have the following two properties:
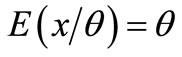 (5)
(5)
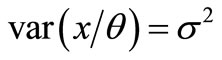 (6)
(6)
And the estimation of parameter vector 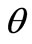 will be
will be
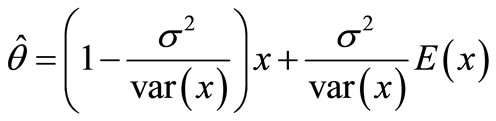 (7)
(7)
Proof: With the conditions in the theorem, we can get
 (8)
(8)
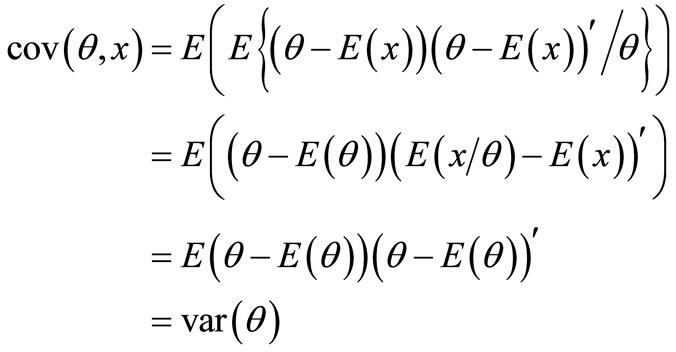 (9)
(9)
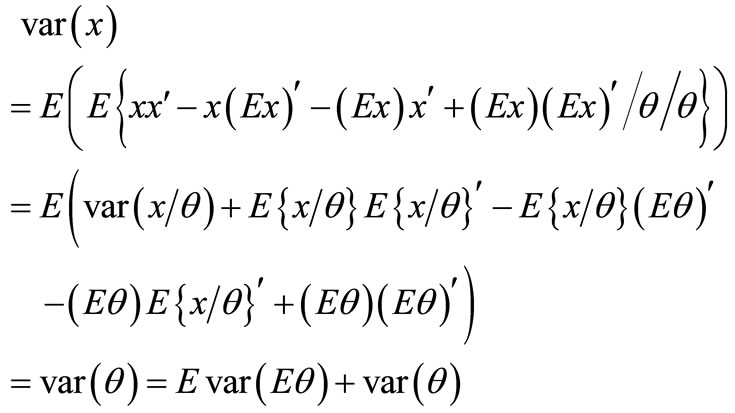
So the variance
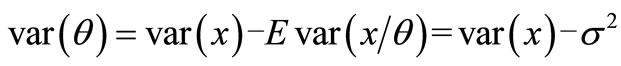 (10)
(10)
Now we simultaneously substitute Equation (10) and Equation (8), Equation (9) on Equation (4), and we gain parameter estimation:
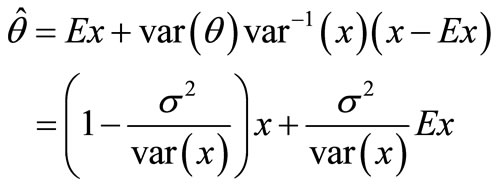
From Equation (7), as long as we have the history data 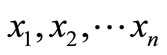 of the sample, we can figure out that the sample mean is
of the sample, we can figure out that the sample mean is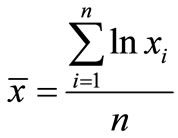 , and the sample variance is
, and the sample variance is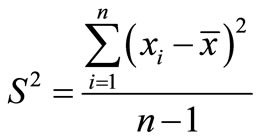 .
.
With classical statistics methods, we can estimate 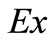 with
with , while we can estimate
, while we can estimate 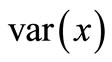 with
with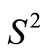 , then
, then
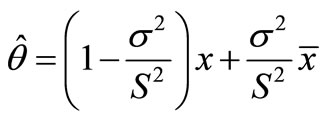 .
.
3. The Optimal Estimation of Insurance Slip’s Future Claim Amount
Assuming that the amount claim  is subject to lognormal distribution with the parameters
is subject to lognormal distribution with the parameters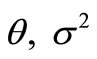 , with the variance
, with the variance 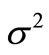 is known, and its probability density function is
is known, and its probability density function is
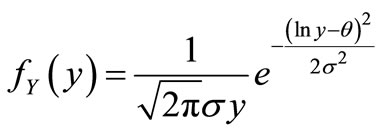 (11)
(11)
for which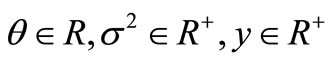 . With Equation (11), the expectations of the future claimed amount for a single insurance slip in insurance companies will be
. With Equation (11), the expectations of the future claimed amount for a single insurance slip in insurance companies will be
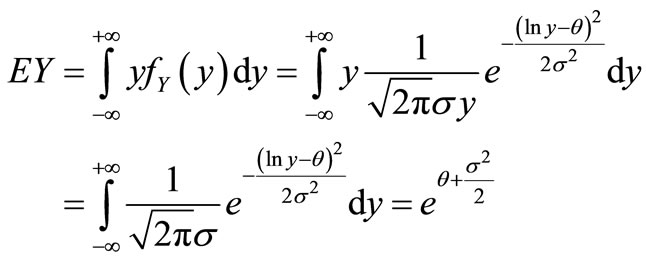 (12)
(12)
Thus if we get the optimal estimation of the parameter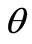 , we can calculate the expectation of Y.
, we can calculate the expectation of Y.
Suppose the Claim history of a single insurance slip in the insurance company is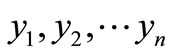 , and assume the current new observation is a vector y. Now we Calculate the estimation of parameter
, and assume the current new observation is a vector y. Now we Calculate the estimation of parameter  by using the L.E.B method in the classic statistics. Because when a single insured claim occurs, the claim amount of money Y is subject to log-normal distribution with the parameters
by using the L.E.B method in the classic statistics. Because when a single insured claim occurs, the claim amount of money Y is subject to log-normal distribution with the parameters , that is
, that is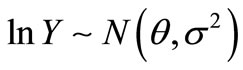 . So we can get that
. So we can get that
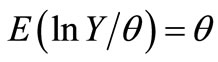 ,
,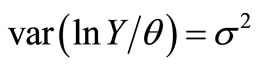 .
.
When variance 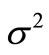 is known, we get the estimation of the parameter
is known, we get the estimation of the parameter 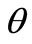 with
with
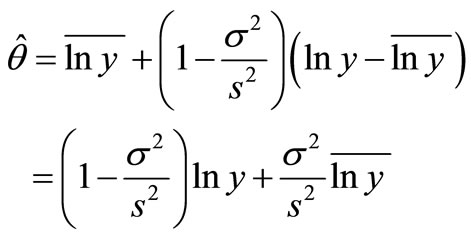 (13)
(13)
For which

so when we use L.E.B. method to calculate the estimation 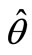 of the parameter
of the parameter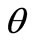 ,
, 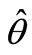 is equal to the weighted average value between the true value
is equal to the weighted average value between the true value 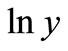 and the experience value
and the experience value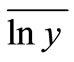 , and the weight is respectively
, and the weight is respectively
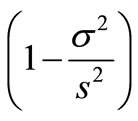 and
and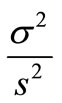 . So when the Claim history of a single insurance slip is
. So when the Claim history of a single insurance slip is , and assume the current new observation is a vector
, and assume the current new observation is a vector , from Equation (12) we can get that the expected estimation of the future claimed amount for a single insurance slip is
, from Equation (12) we can get that the expected estimation of the future claimed amount for a single insurance slip is
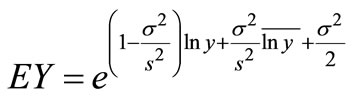 (14)
(14)
4. Model Application-Automobile Insurance Premium Prediction
Now suppose that automobile insurance claim number X obey mixed three parameter gamma distribution, and the historic claim frequency information for insurance slip is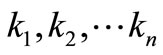 , we can calculate the optimal claim frequency estimation for
, we can calculate the optimal claim frequency estimation for  (seeing Reference [7]).
(seeing Reference [7]).
While it is assumed that the claim amount 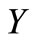 is subject to lognormal distribution with parameter
is subject to lognormal distribution with parameter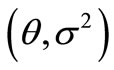 , and when the history Claim of a single insurance slip is
, and when the history Claim of a single insurance slip is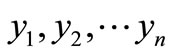 , and assume the current new observation is a vector y, we can get that the expected estimation of the future claimed amount is
, and assume the current new observation is a vector y, we can get that the expected estimation of the future claimed amount is 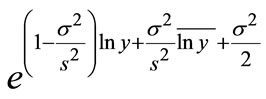 based on L.E.B. method, so we can calculate the Optimal estimation of future premiums with
based on L.E.B. method, so we can calculate the Optimal estimation of future premiums with
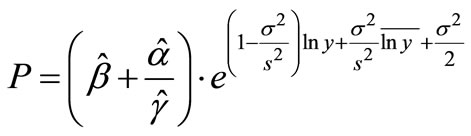 .
.
5. The End
In recent years, with the rapid increase of motor vehicles, automobile insurance premium income accounted for the proportion of insurance income has been gradually improved, thus insurance premium price becomes particularly important. This paper mainly studies the policy’s future claim amount estimation value, and on this basis, predicting the premium price through the establishment of model. Through the use of linear empirical Bayesian method (L.E.B method), given the parameter estimation of  in the lognormal distribution with its parameter
in the lognormal distribution with its parameter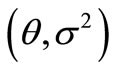 . the result is that the minimum mean square error estimation
. the result is that the minimum mean square error estimation 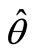 is the weighted average value of the observed value
is the weighted average value of the observed value 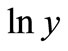 and the experience value
and the experience value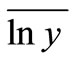 with its weights
with its weights 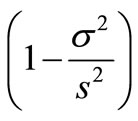 and
and . At the same timeaccording to (12), we calculate the policy’s future claim amount expected value estimation is
. At the same timeaccording to (12), we calculate the policy’s future claim amount expected value estimation is
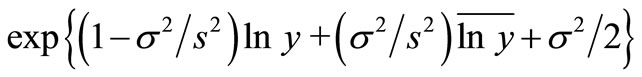
Finally, in the hypothesis that claim number X obey three parameters with mixed gamma distribution, gets the optimal premium predictive value for insurance premium, provides certain theory basis in the pricing problem.
6. Acknowledgements
This work was supported by the Sichuan Provincial Office of education projects for Humanities and Social Sciences LY09-10.
REFERENCES
- J. Cao, P. Li and Y. Gao, “The Strategy Game Based on the Optimal Incentive Contract in Auto Insurance Market,” Statistics and Decision, Vol. 20, 2006, pp. 52-53.
- Y.-B. Xu, Y.-X. Tian and D. Zhu, “The Property Insurance Pricing Research under Moral Hazard of the Insured Affecting Losing Probability,” The Second International Workshop on Intelligent Finance, Chengdu, 6-8 July 2007.
- S.-W. Meng and W. Yuan, “Bonusmalus Systems in Automobile Insurance,” Chinese Journal of Applied Probability and Statistics, Vol. 15, No. 1, 1999, pp. 48-52.
- X.-D. Hao and J.-M. Yu, “An Empirical Rating Actuarial Model with Claim Size Following Lognormal Distribution in Automobile Insurance,” Journal of Harbin University of Commerce (Natural Sciences Edition), Vol. 24, No. 3, 2008, pp. 382-384.
- J.-M. Yu and X.-D. Hao, “An Empirical Rating Actuarial Model with Claim Size Following Lognormal Distribution in Automobile Insurance,” Journal of Shanghai Jiaotong University (Science), Vol. 42, No. 11, 2008, pp. 1836- 1838.
- X.-T. Zhang and H.-F. Chen, “Bayesian Statistical Inference,” Science and Technology Press, 1991.
- P. Hu and Z.-H. Yuan, “Claimant Number of Times Essence Studies When Risk Is Not Same Quality,” Statistics and Decision, Vol. 11, 2007, pp. 21-22.

