ABSTRACT

Let G be a simple graph with vertex set 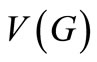and edge set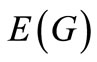. An edge coloring C of G is called an edge cover coloring, if each color appears at least once at each vertex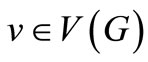. The maximum positive integer k such that G has a k edge cover coloring is called the edge cover chromatic number of G and is denoted by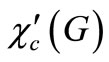. It is known that for any graph G,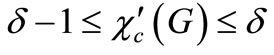. If, then G is called a graph of CI class, otherwise G is called a graph of CII class. It is easy to prove that the problem of deciding whether a given graph is of CI class or CII class is NP-complete. In this paper, we consider the classification on double graph of some graphs and a polynomial time algorithm can be obtained for actually finding such a classification by our proof.

1. Introduction

The edge coloring problem finds a partition of all the edges in a graph into a collection of subsets of edges such that, for each subset in the partition, no edges share a common vertex. Here the objective is to minimize the number of subsets in a partition. This problem has interesting real life applications in the optimization and the network design, such as the file transfers in computer networks [1]. For the file transfer problem in computer networks, each computer x has a limited number f(x) of communication ports. For each pair of computers there are a number of files which are transferred between the pair of computers. In such a situation the problem is how to schedule the file transfers so as to minimize the total time for the overall transfer process. The file transfer problem in which each file has the same length can be formulated as an edge coloring [1]. The problem can be generalized to require the subsets to have other properties. In this work, we are interested in the partition of edges into the subsets such that each covers all the vertices. The objective, instead, is to maximize the number of such subsets.

Our terminology and notation will be standard. The reader is referred to [2] for the undefined terms. Graphs in this paper are simple, unless otherwise stated, i.e., they have no loops or multiple edges. We use V(G) and E(G) to denote, respectively, the vertex set and edge set of a graph G. A k-edge coloring of a graph G is an assignment of k colors 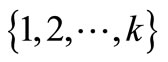to the edges of G. The coloring is proper if no two adjacent edges have the same color. Unless otherwise stated, the edge coloring of graphs in this paper are not necessarily proper. An edge cover of G is a subset S of E(G) that saturates each vertex of G, i.e., each vertex of G is an end vertex of an edge in S. An edge cover coloring of G is an edge coloring such that the edges assigned the same color formed an edge cover of G. Clearly, the edge cover coloring may not be proper. The edge cover chromatic number 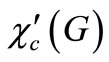of G is the maximum size of a partition of E(G) into edge covers of G. G is said to be k-edge cover colorable if there is an edge cover coloring of G with k colors. An important theorem of Gupta [3] states that

From the above result, we can see that the edge cover chromatic number of any graph must be equal to 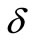or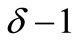, This immediately gives us a simple way of classifying graphs into two types according to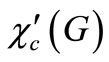. More precisely, we say that G is of CI class if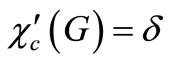, and that G is of CII class if. Wang and Liu discuss the classification problem of nearly bipartite graphs and gave some sufficient conditions for a nearly bipartite graph G to be of CI-class [4]. Xu and Liu considered the edge cover chromatic number of multigraphs [5]. Hilton generalized the edge cover coloring and obtained many interesting results, the following theorem can be found in [6].

Theorem 1.1. If G is a bipartite multigraph, then G has a k-edge coloring such that the number of distinct colors represented at v is min 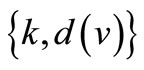for each.

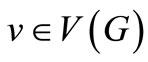By Theorem 1.1, for any bipartite graph G with minimum degree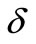, it must have a -edge cover coloring. So, we can see that all bipartite graphs are of CI class. In this paper, we discuss the classification problem on double graph of some graphs, and a good algorithm for edge cover coloring on double graph of k-regular graph can be obtained by the proof of theorem.

2. The Classification of Double Graph

Let 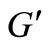be a copy of simple graph G. Let u_i be the vertex of G, and v_i be the vertex of correspond with u_i. A new graph, denoted by D(G) is called the double graph of G if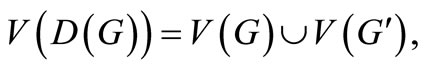

It is easy to see that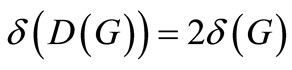, and we have the following result.

Theorem 2.1. Let G be a graph of CI class, then D(G) is also a graph of CI class.

Proof. It’s enough to give a 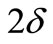-edge cover coloring of D(G) with the color set.

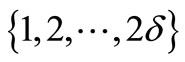Since G is of CI class, G has a 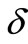-edge cover coloring, and we can also give a same 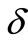-edge cover coloring of 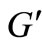with the color set. Next, we color the edges between the vertices of G and.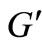

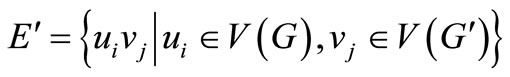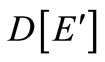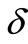Let, the induced subgraph of D(G) by, denoted by. It must be a bipartite graph. By Theorem 1.1, has a -edge cover coloring with color set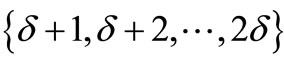. Clearly, we give an edge coloring of D(G) such that each color of 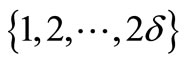appears at least once at each vertex 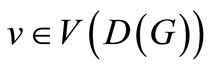. That is, D(G) has a 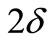-edge cover coloring. This proves the Theorem.

By Theorem 2.1, for each CI class graph G, D(G) is also of CI class. Now we consider that if G is of CII class, what about D(G)? This question seems very difficult to answer in the current, but we can study some special CII class graphs. We have known that some regular graphs are of CI class and some regular graphs are of CII class [7]. It is well known that the Petersen graph P is of CII class, but its double graph D(P) is of CI class. For all k-regular graph, we have the following result.

Theorem 2.2. Let G be a k-regular graph, then the double graph D(G) is of CI class.

In order to prove Theorem 2.2, we need the following useful lemma.

Lemma 2.3. Let H be a 2k-regular graph, then H contains k edge-disjoint spanning 2-factors, and.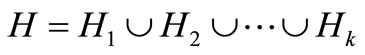

Proof. Let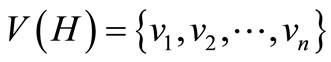, Since H is a 2kregular graph, it must be an Euler graph. Let T be an Euler tour of H. Now, we conform a bipartite graph by T. Let,.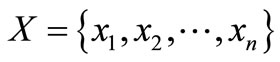

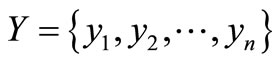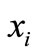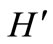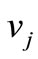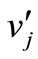The vertex and are adjacent in if and only if and are adjacent sequentially in T. Clearly, 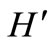must be a k-regular bipartite graph. By theorem 1.1, 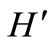has k edge-disjoint perfect matches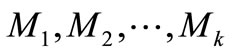. We notice that each perfect match 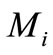in 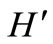is exact a spanning 2-factor of H. Then H contains k edge-disjoint spanning 2-factors, and we have. The lemma is true.

The Proof of Theorem 2.2. Since G is a k-regular graph, the double graph D(G) is a 2k-regular graph. By Lemma 2.3, D(G) contains k edge-disjoint spanning 2-factors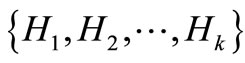, and . We notice that the order of D(G) is even, then each of 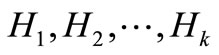is an even cycle. By Theorem 1.1, for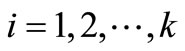, has 2-edge cover coloring with color set. So, we give a 2k-edge cover coloring of D(G) with color set.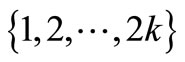

This proves the Theorem.

3. Remarks and Discussion

It is easy to see that a polynomial time algorithm for edge cover coloring of the double graph of any regular graph can be obtained by our proof. But in general, the problem of determining the edge cover chromatic number of any graphs is NP-hard because deciding whether a 3-connected 3-regular graph G is proper 3-edge colorable is NP-complete [8], which is the special case of our general problem. On the other hand, for each CII class graph G it is not known whether determining the classification of its double graph D(G) is NP-hard. But we have the following conjecture.

Conjecture 3.1. Let G be a graph of CII class, then D(G) must be a graph of CI class.

It is seems very difficult to prove the above conjecture, but one can prove that the conjecture is true for some special CII class graphs.

REFERENCES

NOTES

^*This work was supported by NSFC (10901097) and the Nature Science Foundation of Shandong Province (Y2008A20).