Applied Mathematics
Vol. 3 No. 6 (2012) , Article ID: 20277 , 7 pages DOI:10.4236/am.2012.36086
Kelvin-Helmholtz Instability in a Fluid Layer Bounded Above by a Porous Layer and Below by a Rigid Surface in Presence of Magnetic Field
1Department of Mathematics, Government First Grade College, Yellapur, India
2Department of Mathematics, Manipal Institute of Technology, Manipal, India
3Department of Mathematics, Maharani’s Science College for Women, Bangalore, India
Email: {*ckrishna2002, nnkatagi, awati_vb}@yahoo.com
Received November 25, 2011; revised February 22, 2012; accepted March 1, 2012
Keywords: KHI; Magnetic Field; BJ-Slip Condition; Porous Layer; Dispersion Relation
ABSTRACT
We study the stability of an interface between two fluids of different densities flowing parallel to each other in the presence of a transverse magnetic field. A simple theory based on fully developed flow approximations is used to derive the dispersion relation for the growth rate of KHI. We replace the effect of boundary layer with Beavers and Joseph slip condition. The dispersion relation is derived using suitable boundary and surface conditions and results are discussed graphically. The magnetic field is found to be stabilizing and the influence of the various parameters of the problem on the interface stability is thoroughly analyzed. These are favorable to control the surface instabilities in many practical applications discussed in this paper.
1. Introduction
The Kelvin-Helmholtz instability (KHI) occurs when two fluids are in relative motion on either side of a common boundary. The KHI is important in understanding a variety of space and astrophysical, geophysical phenomena involving plasma flow. The linear study of the KHI was investigated by Chandrasekhar [1]. He discussed the effect of surface tension, variable density, rotation and applied magnetic field on the behavior of the stability. The study of electrohydrodynamic (EHD) K-H instability of free charges, separating two semi-infinite dielectric streaming fluids and influenced by an electric field, has been discussed by Lyon [2]. Also, he added the effect of compressibility and applied electric field, but he neglected the surface tension. The nonlinear development of the KHI has been studied by Drazin [3] for the case of where the amplitude of an unstable wave is uniform in space and growing in time. Weissman [4] extended the Drazin [3] work, and treated the case where the amplitude of an unstable wave is dependent on both time and space. Hsieh and Chen [5] first formulated the KHI problem in terms of a variational principle. By choosing a single Fourier mode with time-dependent amplitudes, they derived the evolution equations of the amplitudes. They analyzed and discussed the limiting states and their stability of the evolution equation. Also, they studied a sinusoidal wave state and derived a nonlinear dispersion relation. Elhefnawy [6] studied the nonlinear KHI problem under the influence of an oblique electric field by employing the method of multiple scales. He found that the nonlinear effects may be stabilized or destabilized depending on both density and dielectric constant. The dynamic instability of an excited horizontal interface supporting surface charges and admitting mass and heat transfer has been investigated by Moatimid [7]. Also, he [8] studied the dynamic instability of an excited cylindrical interface supporting surface charges and admitting mass and heat transfer. He investigated the linear stability of two dielectric inviscid fluids separated by a cylindrical interface. The interface allows mass and heat transfer. The system is stressed by radial periodic electric field that allows the presence of surface charges at the interface. The presence of surface charges made the radial electric field play a dual role in the criterion, which shows some analogy to the nonlinear theory of stability.
Many technological processes involve the parallel flow of fluids of different viscosity and density through porous media. Such parallel flows exist in packed bed reactor in the chemical industry, in petroleum production engineering, in boiling in porous media (countercurrent flow of liquid and vapour), and in many other processes. The instability of the plane interface between two uniform superposed and streaming fluids through porous medium has been investigated by Sharma and his collaborators [9-11] for different cases of interest. A linear theory of the KHI for parallel flow in porous media was introduced by Bau [12] for the Darcian and non-Darcian flows. In both cases, Bau found that the velocities should exceed some critical value for the instability to manifest itself. The instability of plane interface between two uniform superposed fluids through a porous medium was investigated by Kumar [13], and the KHI for flow in porous media was studied by El-Sayed [14]. They used linear stability analysis to obtain a characteristic equation for the growth of the disturbance.
Electrohydrodynamics, on the other hand, is the field of the mechanics of continua, which studies the motion of media interacting with the electric field. This subject is treated in vast literature [15]. The least stueid is the class of electrohydrodynami problems where the electric field or electric charges arise as a result of a contact between media of different nature. The relations between electrohydrodynamics parameters at the interfaces of different meida are of critical importance for solution of these problems. Problems of linear and nonlinear electrohydrodynamic stability of the plane interface between two uniform superposed fluids have been treated extensively by Melcher [16], Mohammed and Elsehehawey [17], Mohamed et al. [18] and El-Sayed [19], among others. Later, El-Sayed [20] has studied the EHD KHI in viscous porous medium permeated with suspended particles. In this paper he deals with the effect of suspended particles and a horizontal electric field on the stability of suspended streaming dielectric fluids in porous medium. The problem finds its usefulness in chemical engineering and several geophysical situations, since in many geophysical fluid dynamical problems encountered, the fluid is dielectric and the uniform electric field of the earth pervades the system. The stability conditions are discussed in detail in the absence and presence of surface tension.
The nonlinear Kelvin-Helmholtz instability of a horizontal interface between a magnetic inviscid incompressible liquid and an inviscid laminar subsonic magnetic gas is investigated in the presence of a normal magnetic field by Zakaria [21]. El-Sayed [22] investigated the RTI problem of rotating stratified conducting fluid layer through porous medium in the presence of an inhomogenous magnetic field. This problem corresponds physically (in astrophysics) to the RTI of an equatorial section of a planetary magnetosphere or of stellar atmosphere when rotation and magnetic field are perpendicular to gravity. The KHI of two superposed viscous fluids in a uniform vertical magnetic field is discussed in the presence of effects of surface tension and permeability of porous medium by Bhatia and Sharma [23]. Following Babchin et al., [24] and Rudraiah et al., [25], a simple theory based on Stokes and lubrication approximations is used in this study by replacing the effect of the boundary layer with a Beavers and Joseph [26] slip condition, with the primary objective of using porous layer to suppress the growth rate of KHI. In the above studies the fluid has been considered to be Newtonian. El-Dib and Matoog [27] have studied the Electrorheological Kelvin-Helmholtz instability of a fluid sheet. This work deals with the gravitational stability of an electrified Maxwellian fluid sheet shearing under the influence of a vertical periodic electric field. The field produces surface charges on the interfaces of the fluid sheet. Due to the rather complicated nature of the problem a mathematical simplification is considered where the weak effects of viscoelastic fluids are taken into account. Asthana and Agrawal [28] applied the viscous potential theory to analyze Kelvin-Helmholtz instability with heat and mass transfer and observed that heat and mass transfer has destabilizing effect on relative velocity when lower fluid viscosity is low while it has stabilizing effect when lower fluid viscosity is high. Khalil Elcoot [29] has studied the new analytical approximation forms for non-linear instability of electric porous media. In this work, we have examined the effects of stability of the normal electric field on the porous media, in view of the non-linear theory. The main purpose is to discuss a modulation instability of a finite wavetrain solution by using the method of multiple scales perturbation, and comparing the results with the linear instability theory. Non-linear electrohydrodynamic Kelvin-Helmholtz instability (EKHI) was developed in the parallel flow of two statically stable fluids through porous media for Darcian and non-Darcian flows. The interface separating two semi-infinite dielectric fluids were influenced by a normal electric field in the absence of surface charges. Recently, Chavaraddi et al., [30] have studied the electrohydrodynamic KelvinHelmholtz instability in a fluid layer bounded above by a porous layer and below by a rigid surface. The objective of this paper is to study the effect of Kelvin-Helmholtz discontinuity between two viscous conducting fluids in a transverse magnetic field through a porous medium in the presence of the effects of surface tension using B-J condition at the interface.
The paper is organized as follows. The basic equations are established in Section 2 together with Maxwell’s Equations. The basic equations are simplified and nondimensionalized using the Stokes and lubrication approximations in this section. The resulting dispersion relation is derived using suitable boundary and surface conditions in Section 3. The cutoff and maximum wave numbers and the corresponding maximum growth rate are also obtained in Section 3. The results are discussed and some important conclusions are drawn in final section of this paper.
2. Mathematical Formulation
The physical configuration is shown in Figure 1. We consider a thin target shell in the form of a thin film of unperturbed thickness h (Region 1) filled with an incompressible, viscous, poorly electrically conducting light fluid of density  bounded below by a rigid surface at y = 0 and above by an incompressible, viscous poorly conducting heavy fluid of density
bounded below by a rigid surface at y = 0 and above by an incompressible, viscous poorly conducting heavy fluid of density 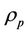 saturating a dense porous layer of large extent compared to the shell thickness h. The co-ordinates x and y spans the horizontal and vertical directions. The interfacial y = h is denoted by
saturating a dense porous layer of large extent compared to the shell thickness h. The co-ordinates x and y spans the horizontal and vertical directions. The interfacial y = h is denoted by . When the interface is flat then
. When the interface is flat then  when y = h. The fluid velocity vector
when y = h. The fluid velocity vector 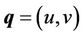 and the fluid is assumed to be Newtonian, viscous electrically conducting and incompressible. The viscosity of fluid (porous medium) is given by
and the fluid is assumed to be Newtonian, viscous electrically conducting and incompressible. The viscosity of fluid (porous medium) is given by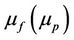 ,
,  the porous parameter,
the porous parameter,  the permeability of the porous medium and
the permeability of the porous medium and  is the slip parameter at the interface. The stress gradient
is the slip parameter at the interface. The stress gradient  is related to the gravitational acceleration through the relation
is related to the gravitational acceleration through the relation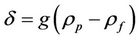 . The perturbed interface
. The perturbed interface  is along the y direction.
is along the y direction.
The basic equations for clear fluid layer (Region-1) and those for porous layer (Region-2) are as given below:
Region-1.
 (2.1)
(2.1)
 (2.2)
(2.2)
Maxwell’s Equations:
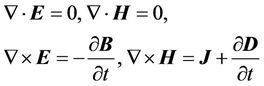 (2.3)
(2.3)
and the auxiliary equations
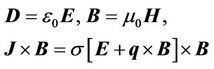 (2.4)
(2.4)
Region-2.
 (2.5)
(2.5)
where 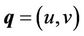 the fluid velocity, E the electric field, H the magnetic field, J the current density, D the dielectric field, B the magnetic induction,
the fluid velocity, E the electric field, H the magnetic field, J the current density, D the dielectric field, B the magnetic induction,  the electrical conductivity, k the permeability of the porous medium, p the pressure,
the electrical conductivity, k the permeability of the porous medium, p the pressure, 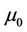 magnetic permeability,
magnetic permeability,  the uniform Darcy velocity,
the uniform Darcy velocity,  the fluid viscosity and
the fluid viscosity and 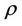 the fluid density.
the fluid density.
The basic equations are simplified using the following
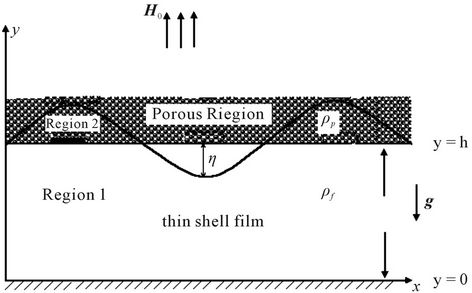
Figure 1. Physical configuration.
Stokes and lubrication and electrohydrodynamic approximations (See Rudraiah et al. [25]):
1) The electrical conductivity of the liquid, s, is negligibly small, i.e., .
.
2) The film thickness h is much smaller than the thickness H of the dense fluid above the film. That is
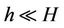
3) The surface elevation h is assumed to be small compared to film thickness h. That is
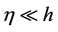
4) The Strauhal number S, a measure of the local acceleration to inertial acceleration in Equation (2.2), is negligibly small.
That is
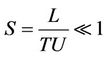
where  is the characteristic velocity,
is the characteristic velocity, 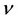 the kinematic viscosity,
the kinematic viscosity,  the characteristic length and
the characteristic length and  the characteristic time.
the characteristic time.
Under these approximations Equations (2.1) and (2.2) for fluid in the film, after making dimensionless using
 (2.6)
(2.6)
become (after neglecting the asterisks for simplicity)
Region-1.
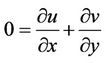 (2.7)
(2.7)
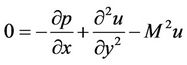 (2.8)
(2.8)
 (2.9)
(2.9)
where  is the Hartmann number which is the ratio of Darcy resistance to the viscous force.
is the Hartmann number which is the ratio of Darcy resistance to the viscous force.
Region-2.
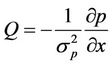 (2.10)
(2.10)
where  is the porous parameter.
is the porous parameter.
3. Dispersion Relation
To find the dispersion relation, first we have to find the velocity distribution from Equation (2.8) using the following boundary and surface conditions:
 (3.1)
(3.1)
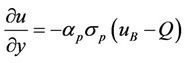 at y = 1(3.2)
at y = 1(3.2)
where
 (3.3)
(3.3)
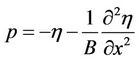 at y = 1.(3.4)
at y = 1.(3.4)
Here 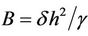 is the Bond number and
is the Bond number and 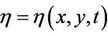 is the elevation of the interface.
is the elevation of the interface.
The solution of (2.8) subject to the above conditions is
 (3.5)
(3.5)
where
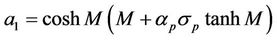
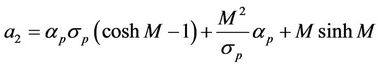
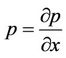 .
.
After integrating Equation (2.7) with respect to y between y = 0 and 1 and using Equation (3.5), we get
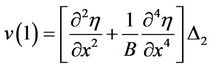 (3.6)
(3.6)
where
 .
.
Then Equation (3.3), using Equations (3.6) and (3.4), becomes
 (3.7)
(3.7)
To investigate the growth rate, n, of the periodic perturbation of the interface, we look for the solution of Equation (3.7) in the form
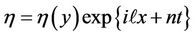 (3.8)
(3.8)
where 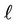 is the wave number and
is the wave number and 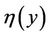 is the amplitude of perturbation of the interface.
is the amplitude of perturbation of the interface.
Substituting Equation (3.8) into (3.7), we obtain the dispersion relation in the form
 (3.9)
(3.9)
Also, Equation (3.9) can be expressed as
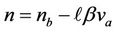 (3.10)
(3.10)
where
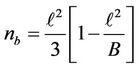 ,
,  ,
,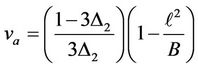 .
.
Setting n = 0 in Equation (3.9), we obtain the cut-off wavenumber,  in the form
in the form
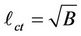 (3.11)
(3.11)
because 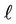 and
and  are non-zero.
are non-zero.
The maximum wavenumber,  obtained from Equation (3.9) by setting
obtained from Equation (3.9) by setting  is
is
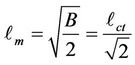 (3.12)
(3.12)
because  and
and  are different from zero.
are different from zero.
The corresponding maximum growth rate, nm, is
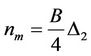 (3.13)
(3.13)
Similarly, using , we obtain
, we obtain
 (3.14)
(3.14)
and hence
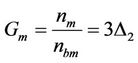 (3.15)
(3.15)
The growth rate given by Equation (3.9) is computed numerically for different values of parameters and the results are presented graphically in Figures 2-4.
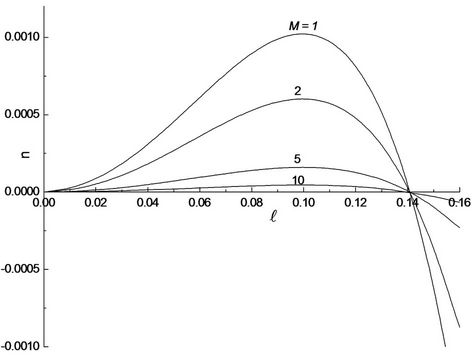
Figure 2. Growth rate, n versus the wavenumber, 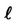 for different values of Hartmann number, M when ap = 0.1, B = 0.02 and sp = 4.
for different values of Hartmann number, M when ap = 0.1, B = 0.02 and sp = 4.
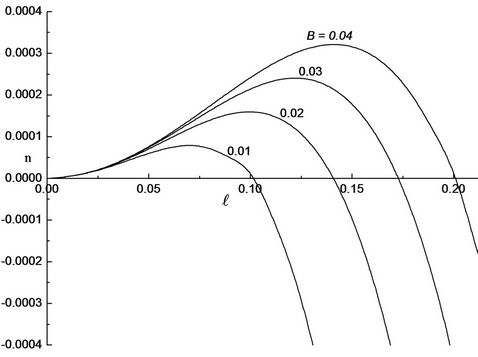
Figure 3. Growth rate, n versus the wavenumber, 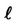 for different values of Bond number, B when ap = 0.1, M = 5 and sp = 4.
for different values of Bond number, B when ap = 0.1, M = 5 and sp = 4.

Figure 4. Growth rate, n versus the wavenumber,  for different values of Porous parameter, sp when ap = 0.1, B = 0.02 and M = 5.
for different values of Porous parameter, sp when ap = 0.1, B = 0.02 and M = 5.
4. Results and Discussion
In this study we have shown the surface instability of KH type in a fluid layer bounded above by a porous layer and below by a rigid surface is affected by the effect of magnetic field. Numerical calculations were performed to determine the growth rate at different wavenumbers for various fluid properties like Hartmann number M, Bond number B and porous parameter sp. We have plotted the dimensionless growth rate of the perturbation against the dimensionless wavenumber for some of the cases only.
When we fix all the input parameters except the ratio of the Hartmann number M, we find that the higher the Hartmann ratio the more stable the interface is. In Figure 2, we have plotted the the growth rate against the wave number in the case where ap = 0.1, B = 0.02 and sp = 4 for different values of the Hartmann number M. Increasing the Hartmann ratio results in slightly increasing the critical wavenumber and decreasing the maximum growth rate. It thus has a stabilizing effect for the selected values of input parameters due to the increased in Hartmann ratio (Lorentz force to viscous force).
In addition, we have investigated the effect of the surface tension of the fluid on the instability of the interface. In our sample calculations, we have taken ap = 0.1, M = 5 and sp = 4 and varied the Bond number B. For this input parameters, the critical wavenumber and maximum growth rate decreased as the ratio of the Bond number B decreased from 0.4 to 0.1 as observed in Figure 3. The Bond number is reciprocal of surface tension and thus showing that an increase in surface tension decreases the growth rate and hence make the interface more stable.
However, in order to understand the effect of the porous properties on the instability, we now fix values of other parameters ap = 0.1, B = 0.02 and M = 5 and vary the ratios of the porous parameters. Figure 4 displays the results of our calculations, showing that increasing the ratio of porous parameters sp from 4 to 100 (and thus increasing the Darcy resistance compared to the viscous force) increases the critical wavelength and decreases the maximum growth rate, thus having a stabilizing effect by this parameter. We conclude that an increase in sp also stabilizes the EKHI due to the resistance offered by the solid particles of the porous layer to the fluid.
5. Conclusion
We have studied the linear stability of a two-fluid flow in a channel where the fluids are assumed to be Newtonian with different fluid properties (Hartmann number, Surface tension and porous parameter) and subjected to magnetic field normal to their interface. For this purpose, we have derived and then linearized the equations of motion where the interaction between the hydrodynamic and electric problems occurs through the stress balance at the fluid interface. The growth rate of the perturbation was then computed by using the normal mode method and its variation studied as a function of the dimensionless parameter Hartmann M, as well as Bond number B and porous parameter sp. While two layer flows in channels of small dimensions are rather stable, the instability of the fluid-porous interface is highly desirable in certain cases, particularly for chemical industry, in petroleum production engineering applications where the mixing of reagents are crucial steps in the process. However, in systems of larger scale, the instability of the fluid-porous interface in a channel is often an undesired physical phenomemon. In such situations, controlling the flow requires the stabilization of the interface. In searching for a method capable of either stabilizing a potentially unstable interface or destabilizing a potentially stable one, we have investigated the role of the magnetic field on the two-layer channel flow problem, demonstrated that either destabilization or stabilization can be obtained and presented growth rates in situations where the magnetic field is stabilizing or destabilizing over a broad range of wavenumbers for increasing in Hartmann number M. But in the case of variation in Bond number is to increase in surface tension decreases the growth rate and hence make the interface more stable. Also we conclude that the increase in the porous parameter is to decrease the growth rate showing thereby the stabilizing effect on the interface.
6. Acknowledgements
The authors (KBC), (NNK) and (VBA) wish to thank the Management and Director/Principal of their respective colleges for encouragement and support.
REFERENCES
- S. Chandrasekhar, “Hydrodynamic and Hydromagnetic Stability,” Dover Publications, New York, 1961.
- J. F. Lyon, “The Electrodynamic Kelvin-Helmholtz Instability,” M.Sc Thesis, MIT, Cambridge, 1962.
- P. G. Drazin, “Kelvin-Helmholtz Instability of Finite Amplitude,” Journal of Fluid Mechanics, Vol. 42, 1970, pp. 321-335. doi:10.1017/S0022112070001295
- M. A. Weissman, “Nonlinear Wave Packets in the Kelvin-Helmholtz Instability,” Philosophical Transactions of the Royal Society A, Vol. 290, No. 1377, 1979, pp. 639- 681.
- D. Y. Hsieh and F. Chen, “A Nonlinear Study of the Kelvin-Helmholtz Instability,” Physics of Fluids, Vol. 28, 1985, p. 1253. doi:10.1063/1.865008
- A. R. F. Elhefnawy, “Nonlinear Electrohydrodynamic Kelvin-Helmholtz Instability under the Influence of an Oblique Electric Field,” Physica A, Vol. 182, 1992, pp. 419-435. doi:10.1016/0378-4371(92)90352-Q
- G. M. Moatimid, “Dynamic Instability of an Excited Horizontal Interface Supporting a Surface Charge and Admitting Mass and Heat Transfer,” International Journal of Engineering, Vol. 32, No. 3, 1994, pp. 535-543. doi:10.1016/0020-7225(94)90140-6
- G. M. Moatimid, “Dynamic Instability of an Excited Cylindrical Interface Supporting Surface Charges and Admitting Mass and Heat Transfer,” Journal of Physics D: Applied Physics, Vol. 27, No. 7, 1994, pp. 1390-1398. doi:10.1088/0022-3727/27/7/009
- R. C. Sharma and T. J. T. Spanos, “The Instability of Streaming Fluids in a Porous Medium,” Canadian Journal of Physics, Vol. 60, No. 10, 1982, pp. 1391-1395. doi:10.1139/p82-187
- R. C. Sharma and V. Kumari, “Hydromagnetic Instability of Streaming Fluids in Porous Medium,” Czechoslovak Journal of Physics, Vol. 41, No. 5, 1991, pp. 459-465. doi:10.1007/BF01597949
- R. C. Sharma and N. D. Sharma, “The Instability of Streaming Fluids with Fine Dust in Porous Medium,” Czechoslovak Journal of Physics, Vol. 42, 1992, pp. 907-918. doi:10.1007/BF01605167
- H. H. Bau, “Kelvin-Helmholtz Instability Parallel Flow in Porous Media; A Linear Theory,” Physics of Fluids, Vol. 25, No. 10, 1982, pp. 1719-1722. doi:10.1063/1.863642
- P. Kumar, “Rayeligh-Taylor of Viscous-Viscoelastic Fluids in Presence of Suspended Particles through Porous Medium,” Zeitschrift für Naturforschung, Vol. 51A, 1996, p. 17.
- M. F. El-Sayed, “Electrohydrodynamic Instability of Two Superposed Viscous Streaming Fluids through Porous Medium,” Canadian Journal of Physics, Vol. 75, No. 7, 1997, pp. 499-508.
- V. V. Gogosov and G. A. Shaposhnikova, “Electrohydrodynamics of Surface Phenomena,” International Journal of Applied Electromagnetics in Materials, Vol. 1, No. 1, 1990, pp. 45-48.
- J. R. Melcher, “Field Coupled Surface Waves,” MIT Press, Cambridge, 1963.
- J. R. Melcher, “Continuum Electromechanics,” MIT Press, Cambridge, 1981. doi:10.1016/0169-5983(89)90016-6
- A. A. Mohamed and E. F. Elshehawey, “Nonlinear Electrohydrodynamic Rayleigh-Taylor Instability,” Fluid Dynamic Research, Vol. 5, 1989, pp. 117-133. doi:10.1016/0377-0427(94)00048-6
- A. A. Mohamed, E. F. Elshehawey and M. F. El-Sayed, “Electrohydrodynamic Kelvin-Helmholtz Instability for a Velocity Stratified Fluid,” Journal of Computational and Applied Mathematics, Vol. 60, No. 3, 1995, pp. 331-346. doi:10.1139/p97-008
- M. F. El-Sayed, “EHD KHI in Viscous Porous Medium Permeated with Suspended Particles,” Czechoslovak Journal of Physics, Vol. 49, No. 4, 1999, p. 473. doi:10.1023/A:1022864808337
- K. Zakaria, “Nonlinear Kelvin-Helmholtz Instability of a Subsonic Gas-Liquid Interface in the Presence of a Normal Magnetic Field,” Physica A, Vol. 273, No. 3, 1999, pp. 248-271. doi:10.1016/S0378-4371(99)00201-0
- M. F. El-Sayed, “Effect of Variable Magnetic Field on the Stability of a Stratified Rotating Fluid Layer in Porous Medium,” Czechoslovak Journal of Physics, Vol. 50, 2002, p. 607. doi:10.1023/A:1022854217365
- P. K. Bhatia and A. Sharma, “KHI of Two Viscous Superposed Conducting Fluids,” Proceedings of the National Academy of Sciences, Vol. 73(A) , No. 4, 2003, p. 497.
- A. J. Babchin, A. L. Frenkel, B. G. Levich and G. I. Shivashinsky, “Nonlinear Saturation of Rayleigh-Taylor Instability in Thin Films,” Physics of Fluids, Vol. 26, 1983, pp. 3159-3161. doi:10.1063/1.864083
- N. Rudraiah, R. D. Mathad and H. Betigeri, “The RTI of Viscous Fluid Layer with Viscosity Stratification,” Current Science, Vol. 72, No. 6, 1997, p. 391.
- G. S. Beavers and D. D. Joseph, “Boundary Conditions at a Naturally Permeable Wall,” Journal of Fluid Mechanics, Vol. 30, No. 1, 1967, pp. 197-207. doi:10.1017/S0022112067001375
- Y. O. El-Dib and R. T. Matoog, “Electrorheological Kelvin-Helmholtz Instability of a Fluid Sheet,” Journal of Colloid and Interface Science, Vol. 289, No. 1, 2005, pp. 223-241. doi:10.1016/j.jcis.2005.03.054
- R. Asthana and G. S. Agrawal, “Viscous Potential Flow Analysis of Kelvin-Helmholtz Instability with Mass Transfer and Vaporization,” Physica A, Vol. 382, 2007, pp. 389-404. doi:10.1016/j.physa.2007.04.037
- A. E. Khalil Elcoot, “New Analytical Approximation Forms Fornon-Linear Instability of Electric Porous Media,” International Journal of Non-Linear Mechanics, Vol. 45, No. 1, 2010, pp. 1-11. doi:10.1016/j.ijnonlinmec.2009.08.011
- K. B. Chavaraddi, N. N. Katagi and N. P. Pai, “Electrohydrodynamic Kelvin-Helmholtz Instability in a Fluid Layer Bounded Above by a Porous Layer and Below by a Rigid Surface,” International Journal of Engineering and Technoscience, Vol. 2, No. 4, 2011, pp. 281-288.
NOTES
*Corresponding author.

