Applied Mathematics
Vol. 3 No. 1 (2012) , Article ID: 16764 , 9 pages DOI:10.4236/am.2012.31011
Non-Linear Analysis of Vibrations of Non-Linear System Subjected to Multi-Excitation Forces via a Non-Linear Absorber
1Department of Medical Archives, Faculty of Applied Medical Science, Taif University, Taif, Kingdom of Saudi Arabia
2Department of Mathematics and Statistics, Faculty of Science, Taif University, Taif, Kingdom of Saudi Arabia
Email: Taha_elghareeb@yahoo.com
Received October 26, 2011; revised December 7, 2011; accepted December 16, 2011
Keywords: Perturbation method; control; stability; resonance; jump phenomenon
ABSTRACT
The dynamic response of mechanical and civil structures subjected to high-amplitude vibration is often dangerous and undesirable. Sometimes controlled vibration is desirable as in the machinery used in the formation of rigid hard material as Ceramics and diamond. This process is done via the passive control methods. The main purpose of this paper is to how reduction of vibration of nonlinear system subjected to multi-excitation forces via a nonlinear absorber. The nonlinear differential equations describing the model, which describe ultrasonic cutting machine are solved by using perturbation method. The effects of different parameter on the response of the system are studied. The stability of the numerical solution is investigated by using frequency response equations and phase-plane method. The simulation results are achieved using Matlab and Maple programs. A comparison is made with the available published work.
1. Introduction
Vibrations are the cause of discomfort, disturbance, damage, and sometimes destruction of machines and structures. It must be reduced or controlled or eliminated. One of the most common methods of vibration control is the dynamic absorber. It has the advantages of low cost and simple operation at one modal frequency. In the domain of many mechanical vibration systems the coupled non-linear vibration of such systems can be reduced to non-linear second order differential equations which are solved analytically and numerically. Queini and Nayfeh [1] proposed a non-linear active control law to suppress the vibrations of the first mode of a cantilever beam when subjected to a principal parametric excitation. The method of multiple scales is applied throughout. The analysis revealed that cubic velocity feedback reduced the amplitude of the response. Asfar [2] took material non-linearity into consideration in the analysis of the performance of an elastomeric damper with a spring hardening cubic effects near primary resonance condition applying multiple time scale method. Eissa [3] reported that when using a dynamic absorber, its damping coefficient should be kept minimal for better system performance. Eissa [4] has shown that for controlling the vibration of a system subjected to harmonic excitations, the fundamental or the first harmonic absorber is the most effective one. Eissa and El-Ganaini [5,6] studied the control of both vibration and dynamics chaos of mechanical system having quadratic and cubic non-linearities, subjected to harmonic excitation using multi-absorbers. Kamel and Amer [7] studied the behavior of one-degreeof-freedom system with different quadratic damping and cubic stiffness non-linearities simulating the axial vibration of a cantilever beam under multi-parametric excitation forces. Song et al. [8] investigated the vibration response of the spring mass damper system with a parametrically excited pendulum hinged to the mass using the harmonic balance method. The stability analysis showed that the area of unstable motion of the system obtained from the third order approximation.
Soom [9] and Jordanov [10] studied the optimal parameter design of linear and non-linear dynamic vibration absorbers for damped primary systems. They examined optimization criteria other than the traditional one and obtained small improvements in steady state response by using non-linear springs. However, the presence of the non-linearities introduces dangerous instability, which in some cases may result in amplification rather than reduction of the vibration amplitudes [11,12]. Natsiavas [13] applied the method of averaging to investigate the steady state oscillations and stability of nonlinear dynamic vibration absorbers. He pointed out that proper selection of the system parameters would result insubstantial improvements of non-linear absorbers and avoid dangerous effects that are likely to occur due to the presence of the non-linearities. Zhu et al. [14] studied the non-linear dynamics of a two-degree-of freedom vibrating system having both non-linear damping and nonlinear spring using the averaging method. Results showed that the vibration amplitude can be reduced by properly selecting the values of non-linear damper, non-linear spring stiffness and the range of exciting frequency.
Nayfeh [15] compared application of the method of multiple scales with reconstitution and the generalized method of averaging for determining higher-order approximations of three single-degree-of-freedom systems and a two-degree-of-freedom system. Amer [16] investigated the coupling of two non-linear oscillators of the system and absorber representing ultrasonic cutting process. A threshold value of linear damping has been obtained, where the system vibration can be reduced dramatically. Eissa and Sayed [17-19] and Sayed [20], studied the effects of different active controllers on simple and spring pendulum at the primary resonance via negative velocity feedback or its square or cubic. Hamed et al. [21-23] studied USM model subject to multi-external or both multi-external and multi-parametric and both multi-external and tuned excitation forces. The model consists of multi-degree-of-freedom system consisting of the tool holder and absorbers (tools) simulating ultrasonic machining process. The advantages of using multi-tools are to machine different materials and different shapes at the same time. Sayed and Hamed [24] studied the response of a two-degree-of-freedom system with quadratic coupling under parametric and harmonic excitations. The method of multiple scale perturbation technique is applied to solve the non-linear differential equations and obtain approximate solutions up to and including the second-order approximations. Sayed and Kamel [25,26] investigated the effects of different controllers on the vibrating system and the saturation control of a linear absorber to reduce vibrations due to rotor blade flapping motion. Amer and Sayed [27], studied the response of one-degree-of freedom, non-linear system under multi-parametric and external excitation forces simulating the vibration of the cantilever beam.
2. Mathematical Analysis
Using a non-linear absorber connected to the main system, a model of a two degree-of-freedom oscillator under consideration can be written in the forms:
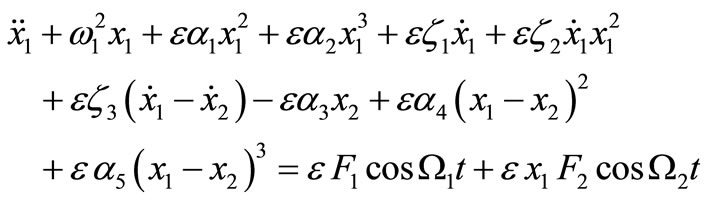 (1)
(1)
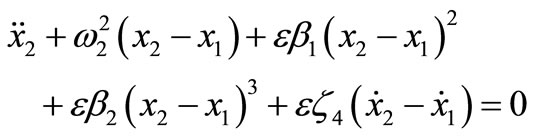 (2)
(2)
where x1, x2 are the displacement of the main system and absorber, w1, w2 are the natural frequencies, Wj (j = 1, 2) forcing frequencies, e small perturbation parameter, fj the forcing amplitudes, ai, bj non-linear parameters (i = 1, ···, 5), zs damping coefficient (s = 1, ···, 4). A first-order uniform solution of equations (1) and (2) is sought using the method of multiple scales [28] in the form:
 (3)
(3)
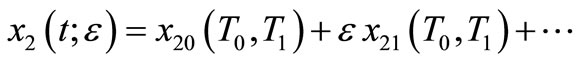 (4)
(4)
where T0 = t is the fast time scale, which is associated with changes occurring at the frequencies wj and Wj and T1 = et is the slow time scale, which is associated with modulations in the amplitudes and phases resulting from the non-linearities and parametric resonance. In term of T0 and T1 the time derivatives became
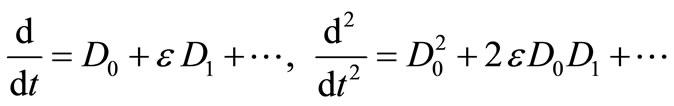 (5)
(5)
where Dn differential operators; Dn = ¶/¶Tn (n = 0,1). Substituting equations (3) and (4) into equations (1) and (2) and equating the coefficients of same power of e in both sides, we obtain:
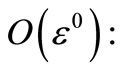
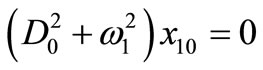 (6)
(6)
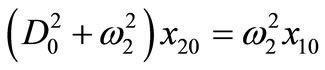 (7)
(7)
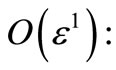
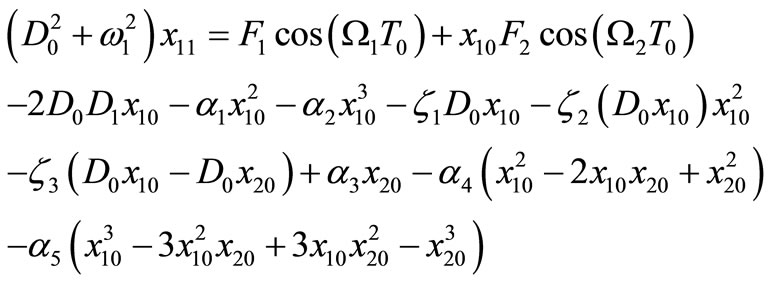 (8)
(8)
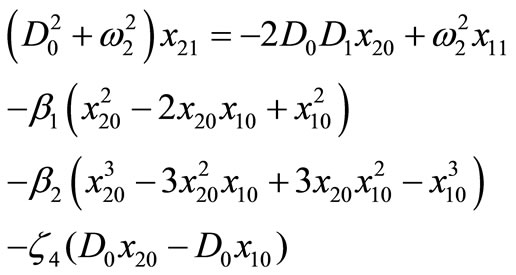 (9)
(9)
The general solution of equations (6) and (7) can be expressed in the form
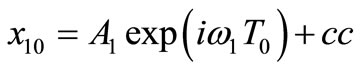 (10)
(10)
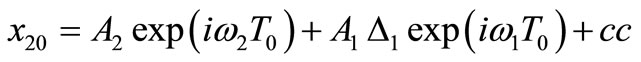 (11)
(11)
where 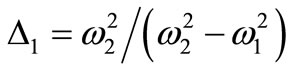 and A1, A2 are unknown functions in T1, which can be determined from eliminating the secular terms at the next approximation, and cc stands for the conjugate of the preceding terms. The particular solutions of equations (8) and (9) after eliminateing the secular terms are given by:
and A1, A2 are unknown functions in T1, which can be determined from eliminating the secular terms at the next approximation, and cc stands for the conjugate of the preceding terms. The particular solutions of equations (8) and (9) after eliminateing the secular terms are given by:
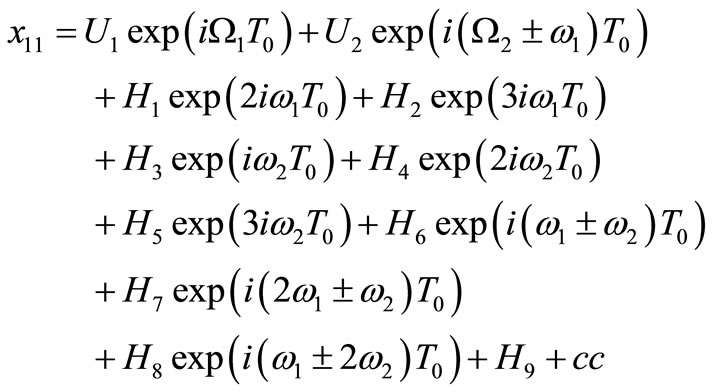 (12)
(12)
 (13)
(13)
where Ui, i = 1 to 4, Hi, i = 1 to 18, are complex functions in T1. The general solution of x1 and x2 up to the second-order approximation is given by
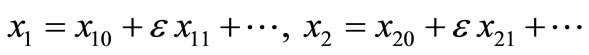
From the above derived solutions, the reported resonance cases are
1) Primary resonance: W1 @ w1, W1 @ w2
2) Sub-harmonic resonance: W2 @ 2w1
3) Internal resonance: w1 @ nw2, w2 @ nw1, n = 1, 2, 3
4) Combined resonance: W2 @ ± w1 ± w2
5) Simultaneous resonance: Any combination of the above resonance cases is considered as simultaneous resonance.
3. Stability of the System
The stability of the system is investigated at one of the worst resonance cases (confirmed numerically), which is the simultaneous primary, sub-harmonic and internal resonance where W1 @ w1, W2 @ 2w1 and w2 @ w1 Using the detuning parameters s1, s2 and s3 such that:
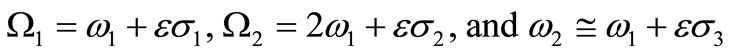 (14)
(14)
Substituting equation (14) into equations (8) and (9) and eliminating the secular terms leads to the solvability conditions as
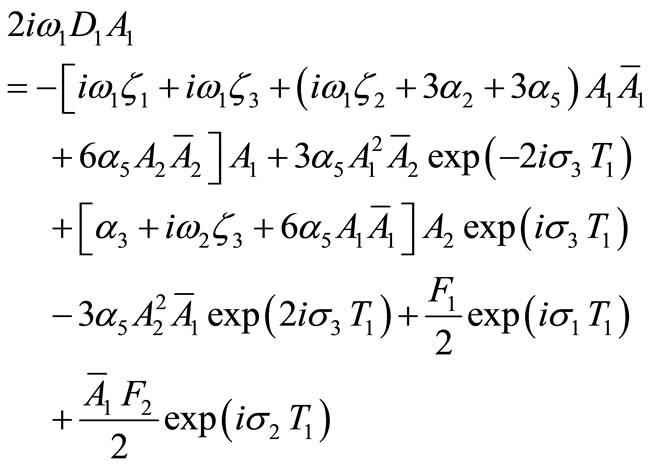 (15)
(15)
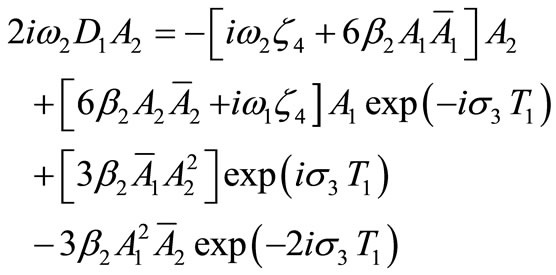 (16)
(16)
To analyze the solutions of Equations (15) and (16), we express A1 and A2 in the polar form
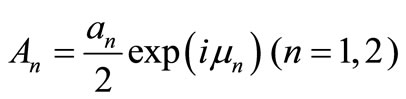 (17)
(17)
where an and mn are real of T1. Substituting Equation (17) into Equations (15) and (16) and separating real and imaginary part yields,
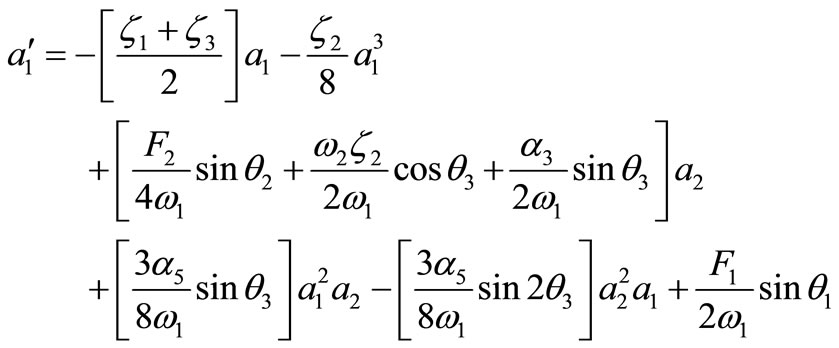 (18)
(18)
 (19)
(19)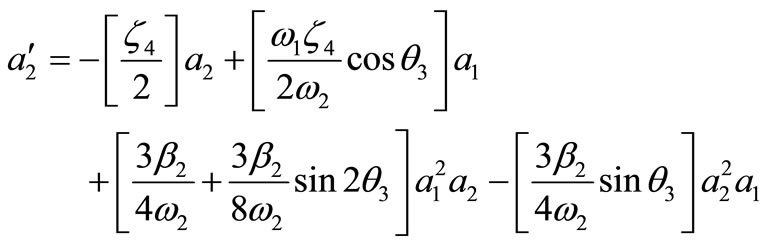 (20)
(20)
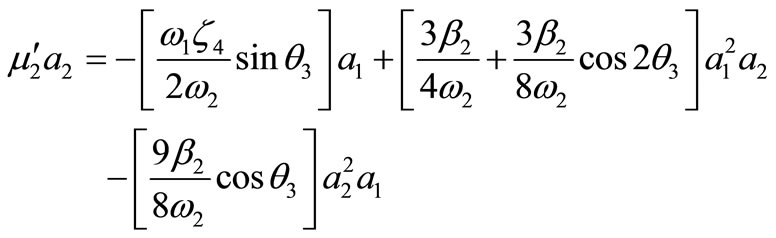 (21)
(21)
where
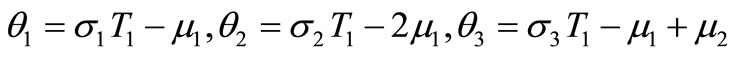 (22)
(22)
For the steady state solution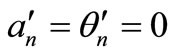 . Then from equation (22) yields
. Then from equation (22) yields
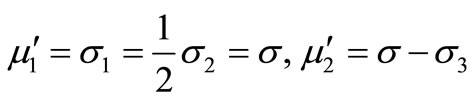 (23)
(23)
Then it follows from equations (18)-(21) that the steady state solutions are given by
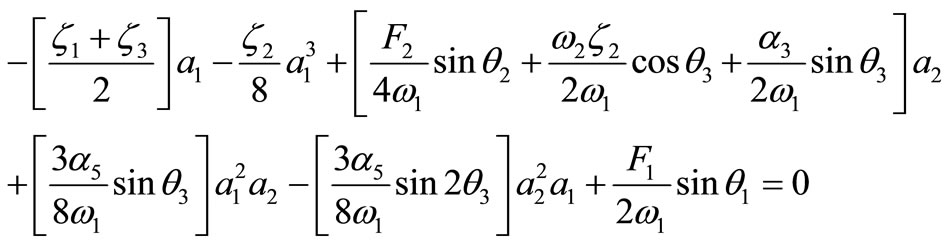 (24)
(24)
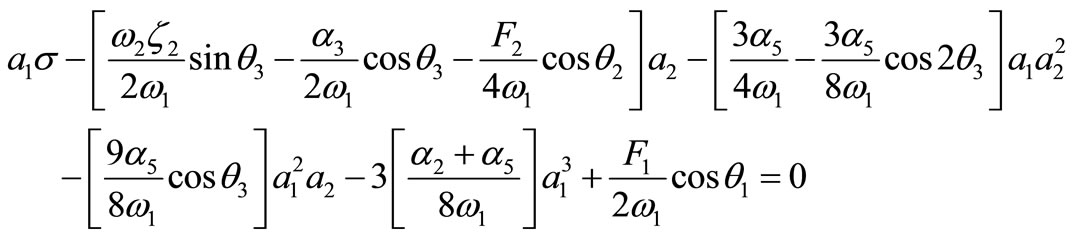 (25)
(25)
 (26)
(26)
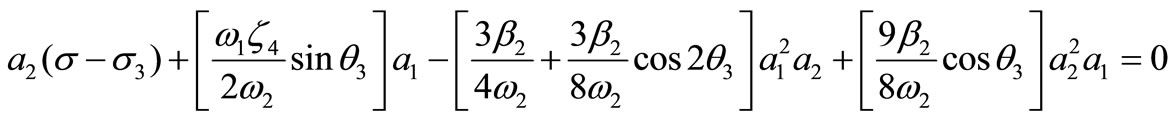 (27)
(27)
Solving the resulting algebraic equations yields two possibilities for the fixed points for each case.
Case (1): The controller is deactivated (a1 ≠ 0, a2 = 0), the frequency response equation can be obtained in the form (after eliminating all parameters corresponding to the controller).
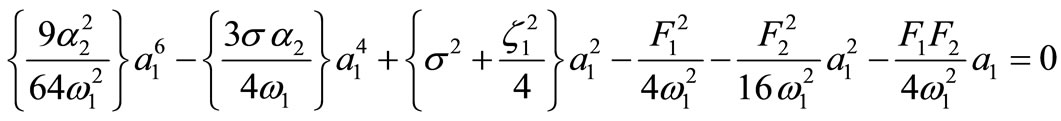 (28)
(28)
Case (2): The controller is activated (a1 ≠ 0, a2 ≠ 0), the resulting two equations are obtained
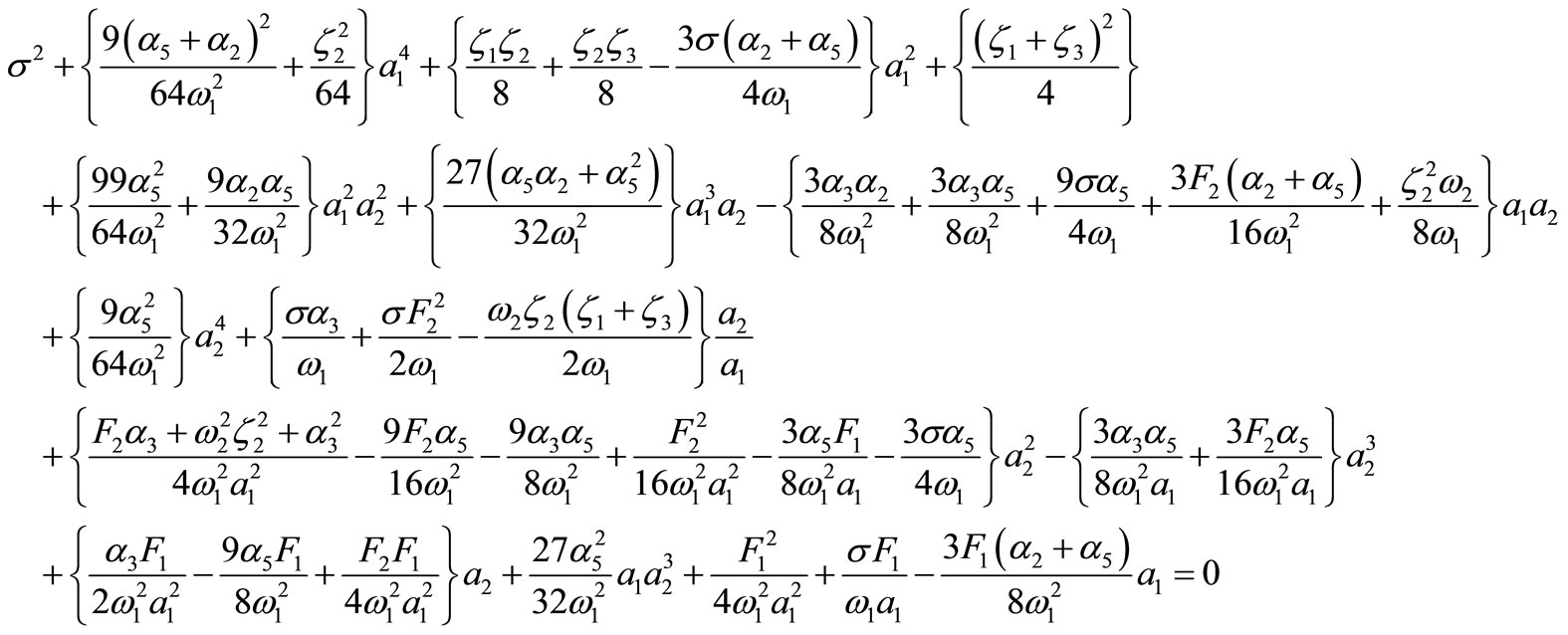 (29)
(29)
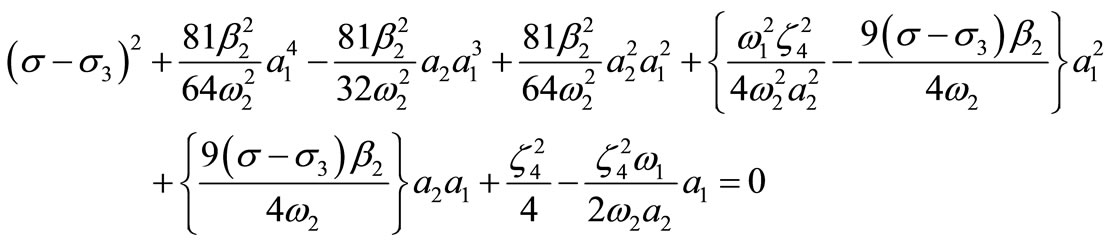 (30)
(30)
4. Results and Discussion
The differential equation (1) governing the oscillating main system is solved numerically (applied Runge-Kutta 4th order method) after eliminating all parameters corresponding to the controller.
Table 1 summaries the worst resonance cases with and without absorber.
Figure 1 shows the steady state amplitude and phase plane of the main system at the primary resonance where W1 @ w1. In this figure, we observe that the steady state amplitude is about four of the maximum excitation force amplitude F1. The system is stable with multi-limit cycle and the response of the system is tuned with some chaos.
Figure 2 shows the steady state amplitude and phase plane of the main system at the sub-harmonic resonance case where W2 @ 2w1. We note that the steady state amplitude is about 3 of the maximum excitation force amplitude F1. Also the chaotic wave motion will increase.
The steady state amplitude and phase plane of the main system at simultaneous primary and principle parametric resonance respectively where W1 @ w1, W2 @ 2w1 is shown in Figure 3. In this figure, the steady state amplitude is about 5 of the maximum excitation force amplitude F1 respectively. The system is stable with fine

Table 1. Summary of worst resonance cases.
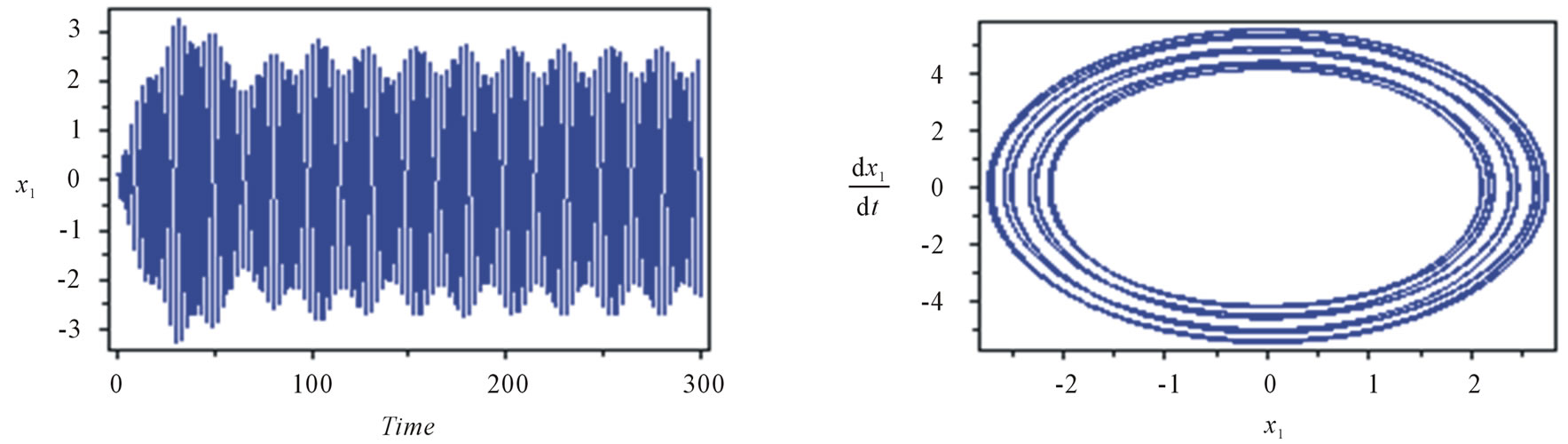
Figure 1. System behavior without absorber at W1 @ w1 and W2 is a way from w1. ξ1 = 0.05, α1 = 0.03, α2 = 0.04, F2 = 0.3.
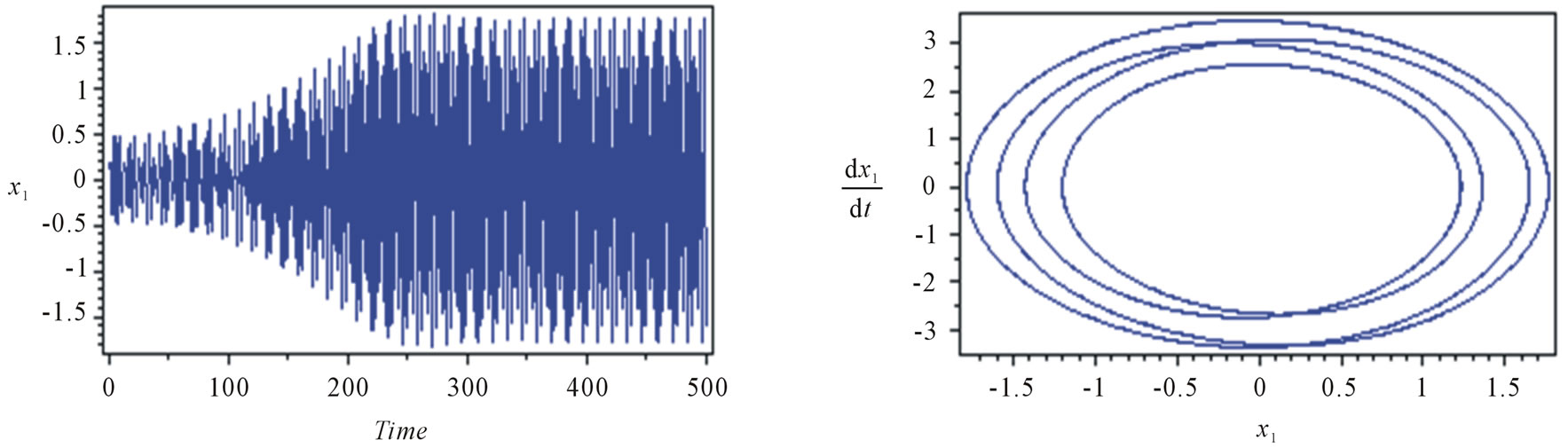
Figure 2. System behavior without absorber at W2 @ 2w1 and W1 is a way from w1.
limit cycle, denoting that the system is free from dynamic chaos.
4.1. Effect of the Controller
Figure 4 shows that the steady state amplitude of the system with absorber at the simultaneous resonance W1 @ w1, W2 @ 2w1 and w2 @ w1. It can be seen for the main system that the steady state amplitude is 0.33%, but the steady state amplitude of the controller is about 42% of excitation amplitude F1. This means that the effectiveness of the absorber Ea (Ea = the steady state amplitude of the main system without absorber/the steady state amplitude of main system with absorber) is about 1500. Also, the oscillations of the system and absorber have multi-limit cycle and limit cycle respectively.
4.2. Frequency Response Curves
The frequency response equations (29) and (30), practical case are nonlinear algebraic equations, which are solved numerically. The numerical results are shown in figures 5-14. These figures, show the steady state response-frequency curve for the stability second case (practical case), where a1, a2 ≠ 0 in the case of simultaneous primary, sub-harmonic resonance in the presence of one-to-one internal resonance. Figure 5 shows that the effect of the detuning parameter s1 on the steady state amplitude of the main system. In this figure, we observe that, the amplitude a1 has one continuous curve. From this figure, we observe that the steady state amplitude of the main system have multi-valued solutions.
For increasing excitation forces F1, F2 and for increas-
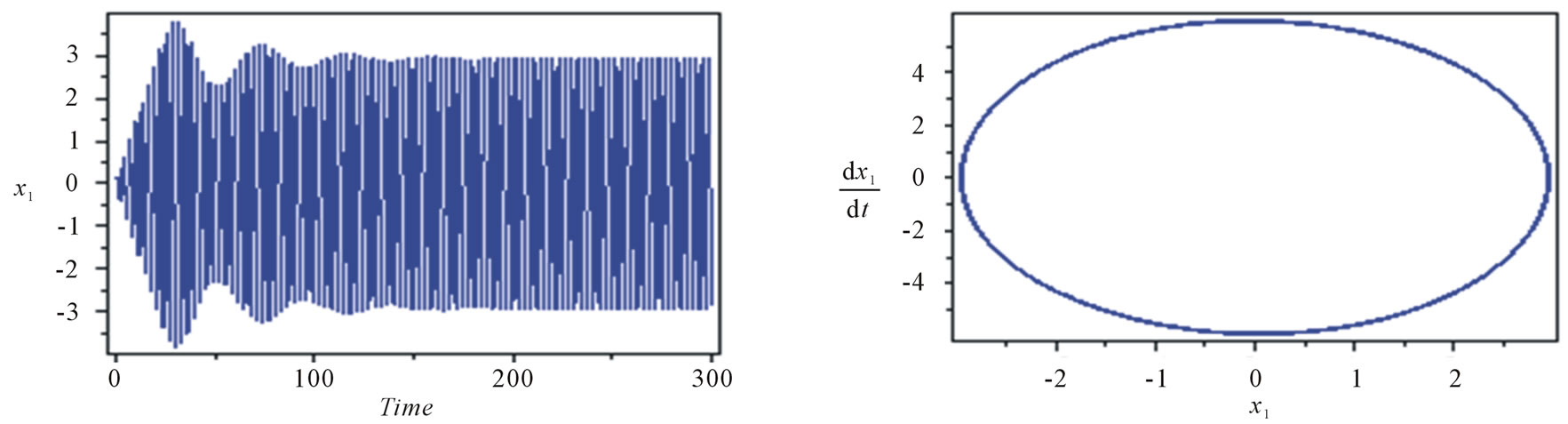
Figure 3. System behavior without absorber at W1 @ w1 and W2 @ 2w1.
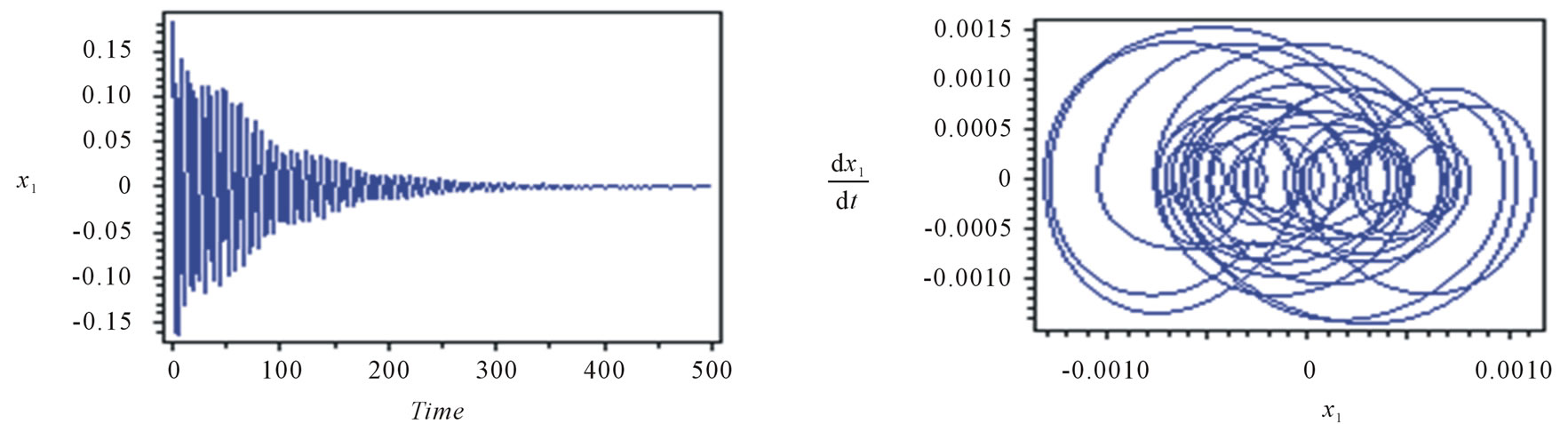
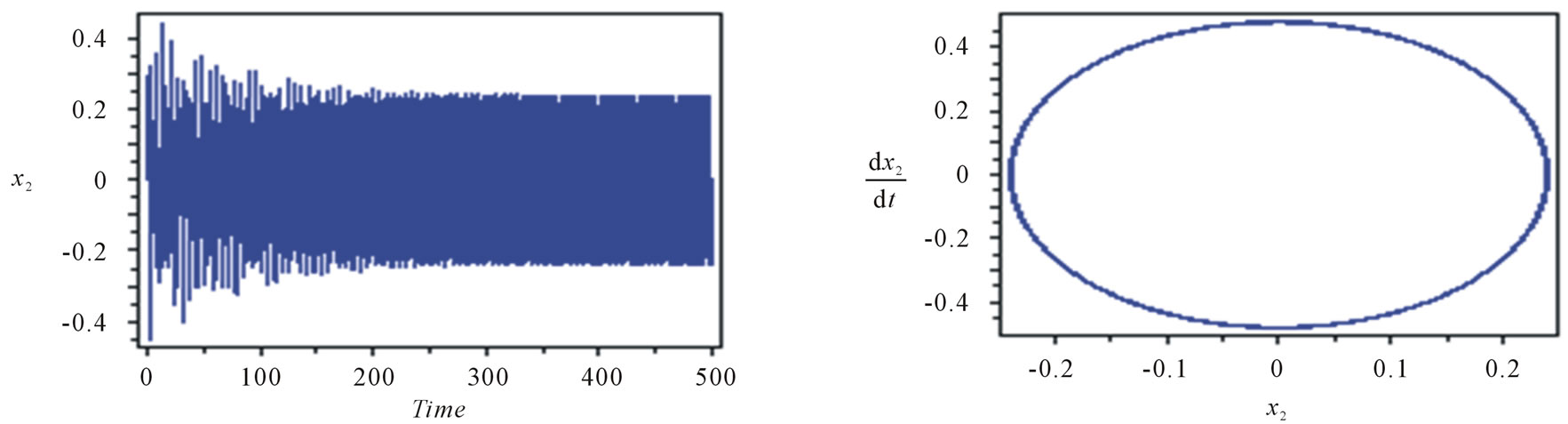
Figure 4. Response of the system and absorber at W1 @ w1, W2 @ 2w1 and w2 @ w1.
ing natural frequencies, we note that the steady state magnitude of the main system is increased as shown in Figures 6-8. Figures 9 and 10 show that as non-linear spring stiffness a3 or a5 are increased positively the continuous curve is moved downwards and has decreased magnitudes. It can be concluded that increasing the nonlinear spring stiffness a3 or a5 can reduce the amplitude of the system and obtain the effect of reduction of the vibration amplitude. Also for negative value of non-linear spring stiffness a3 or a5 the response amplitude is bent to the left and the stability region is decreased.
Figure 11, shows that the effects of detuning parameter s3 on the amplitude of the absorber. From this figure, we observe that the steady state amplitude of the absorber has single-valued solution. From Figures 12-14 we note that for decreasing natural frequencies or decreasing non-linear parameter b2 or decreasing linear damping coefficient z4 the curves diverge down and the steady state amplitude is decreasing.
5. Conclusions
The system consists of the main system and the absorber representing the vibration of many applications in machine tools, ultrasonic cutting process, subjected to ex-
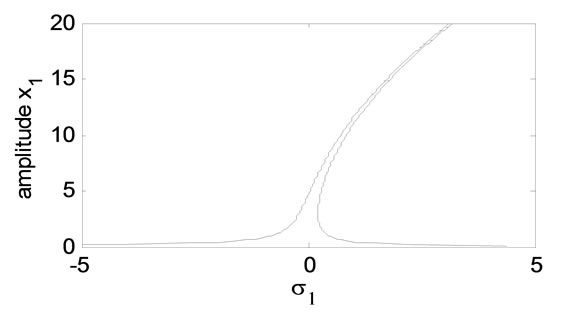
Figure 5. Effects of the detuning parameter s1.
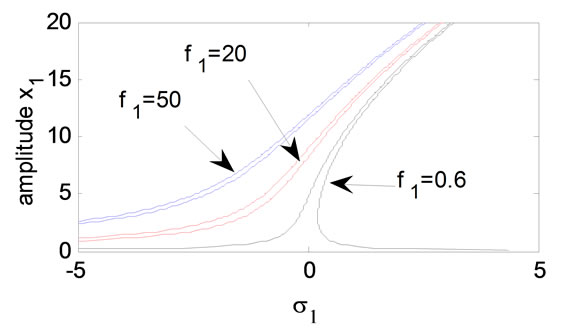
Figure 6. Effects of the excitation amplitude F1.

Figure 7. Effects of the excitation amplitude F2.

Figure 8. Effects of the natural frequencies.
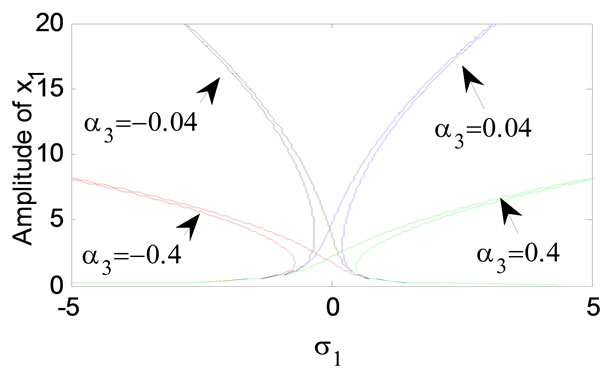
Figure 9. Effects of the non-linear parameter a3.
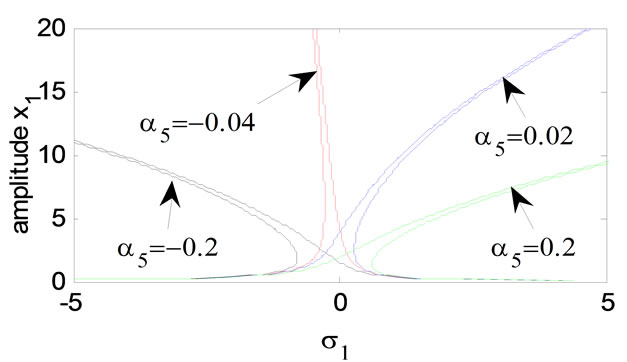
Figure 10. Effects of the non-linear parameter a5.

Figure 11. Effects of the detuning parameter s3.
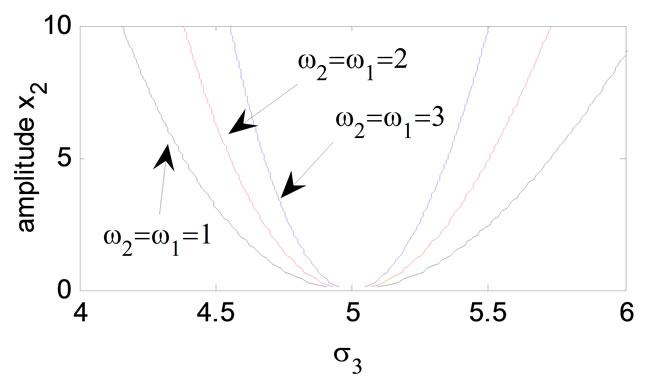
Figure 12. Effects of the natural frequencies.
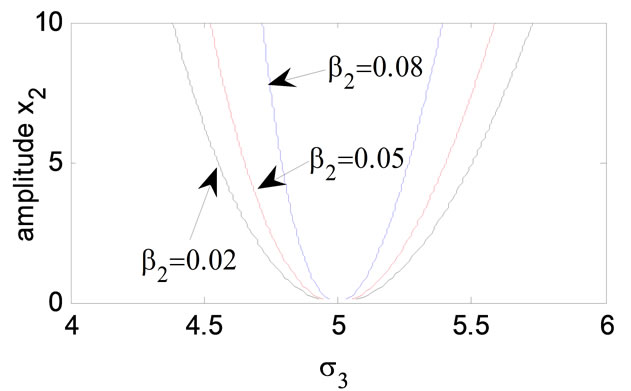
Figure 13. Effects of the non-linear parameter b2.

Figure 14. Effects of the damping coefficient z4.
ternal and parametric excitation forces is considered and solved using the method of multiple scale perturbation. A simple and powerful effective method is demonstrated to reduce (control passively) both vibration and dynamic chaos in the non-linear system using non-linear absorber. One of the most common methods of vibration control is the dynamic absorber. Multiple scales perturbation technique is applied to determine approximate solutions of the coupled non-linear differential equations. Steady state solutions and their stability are studied for selected values of different parameters. Frequency response equations are deduced to investigate system stability. It can be seen from the results that the optimal working conditions of the system is simultaneous primary, sub-harmonic and internal resonance W1 @ w1, W2 @ 2w1, w2 @ w1. From the above study the following may be concluded.
1) The optimum working conditions for the system are when, W1 @ w1, W2 @ 2w1, w2 @ w1 since the steady state amplitude of the main system is reduced to 0.33% of its maximum value. This means that the effectiveness of the absorber Ea = 1500.
2) The steady state amplitude is a monotonic increasing function to the excitation amplitudes F1, F2 and natural frequency w1.
3) The zones of multi-valued region are increased for large values of F1.
4) For increasing positive value of non-linear spring stiffness a5 the continuous curve is shifted downwards produce hard spring.
5) For negative values of a3, the curve is bent to the left produce soft spring; the region of unstable is increased.
6) The region of multi-valued is disappeared from the steady state amplitude of the absorber for increasing value of damping coefficient z4, and the continuous curve has a single-valued curve which is shifted downwards.
7) Increasing the non-linear spring stiffness a5 can reduce the amplitude of the main mass and obtain the effect of reduction of the vibration amplitude, which is a good agreement with Reference [14].
8) Numerical simulations show the system exhibits periodic motions and chaotic motions, which is a good agreement with Reference [14].
REFERENCES
- S. S. Oueini and A. H. Nayfeh, “Single-mode control of a cantilever beam under principal parametric excitation,” Journal of Sound and Vibration, Vol. 224, No. 1, 1999, pp. 33-47. doi:10.1006/jsvi.1998.2028
- K. R. Asfar, “Effect of non-linearities in elastomeric material dampers on torsional vibration control,” International Journal of Non-Linear Mechanics, Vol. 27, No. 6, 1992, pp. 947-954. doi:10.1016/0020-7462(92)90047-B
- M. Eissa, “Vibration control of non-linear mechanical systems via neutralizers,” Electronic Engineering Bulletin, No. 18, 1999.
- M. Eissa, “Vibration and chaos control in I.C engines subject to harmonic torque via non-linear absorbers,” Proceedings of ISMV Conference, Islamabad, 2000.
- M. Eissa and W. El-Ganaini, “Part I, Multi-absorbers for vibration control of non-linear structures to harmonic excitations,” Proceedings of ISMV Conference, Islamabad, 2000.
- M. Eissa and W. El-Ganaini, “Part II, Multi-absorbers for vibration control of non-linear structures to harmonic excitations,” Proceedings of ISMV Conference, Islamabad, 2000.
- M. M. Kamel and Y. A. Amer, “Response of parametrically excited one-degree-of-freedom system with nonlinear damping and stiffness,” Physica Scripta, Vol. 66, No. 6, 2002, pp. 410-416. doi:10.1238/Physica.Regular.066a00410
- Y. Song, H. Sato, Y. Iwata and T. Komatsuzaki, “The response of a dynamic vibration absorber system with a parametrically excited pendulum,” Journal of Sound and Vibration, Vol. 259, No. 4, 2003, pp. 747-759. doi:10.1006/jsvi.2002.5112
- A. Soom and M. Lee, “Optimal design of linear and nonlinear vibration absorbers for damped system,” Journal of Vibration, Acoustic Stress, and Reliability in Design, Vol. 105, No. 4, 1983, pp. 112-119. doi:10.1115/1.3269054
- I. N. Jordanov and B. I. Cheshankov, “Optimal design of linear and non-linear dynamic vibration absorbers,” Journal of Sound and Vibration, Vol. 123, No. 1, 1988, pp. 157-170. doi:10.1016/S0022-460X(88)80085-3
- H. J. Rice, “Combinational instability of the non-linear vibration absorber,” Journal of Sound and Vibration, Vol. 108, No. 4, 1986, pp. 526-532. doi:10.1016/S0022-460X(86)80046-3
- J. Shaw, S. W. Shaw and A. G. Haddow, “On the response of the non-linear vibration absorber,” International Journal of Non-Linear Mechanics, Vol. 24, No. 4, 1989, pp. 281-293. doi:10.1016/0020-7462(89)90046-2
- S. Natsiavas, “Steady state oscillations and stability of non-linear dynamic vibration absorbers,” Journal of Sound and Vibration, Vol. 156, No. 2, 1992, pp. 227-245. doi:10.1016/0022-460X(92)90695-T
- S. J. Zhu, Y. F. Zheng and Y. M. Fu, “Analysis of nonlinear dynamics of a two-degree-of-freedom vibration system with non-linear damping and non-linear spring,” Journal of Sound and Vibration, Vol. 271, No. 1-2, 2004, pp. 15-24. doi:10.1016/S0022-460X(03)00249-9
- A. H. Nayfeh, “Resolving Controversies in the Application of the Method of Multiple Scales and the Generalized Method of Averaging,” Nonlinear Dynamics, Vol. 40, No. 1, 2005, pp. 61-102. doi:10.1007/s11071-005-3937-y
- Y. A. Amer, “Vibration control of ultrasonic cutting via dynamic absorber,” Chaos, Solutions and Fractals, Vol. 33, No. 5, 2007, pp. 1703-1710. doi:10.1016/j.chaos.2006.03.038
- M. Eissa and M. Sayed, “A comparison between passive and active control of non-linear simple pendulum Part-I,” Mathematical and Computational Applications, Vol. 11, No. 2, 2006, pp. 137-149.
- M. Eissa and M. Sayed, “A comparison between passive and active control of non-linear simple pendulum Part-II,” Mathematical and Computational Applications Vol. 11, No. 2, 2006, pp. 151-162.
- M. Eissa and M. Sayed, “Vibration reduction of a three DOF non-linear spring pendulum,” Communication in Nonlinear Science and Numerical Simulation, Vol. 13, No. 2, 2008, pp. 465-488. doi:10.1016/j.cnsns.2006.04.001
- M. Sayed, “Improving the mathematical solutions of nonlinear differential equations using different control methods,” Ph.D. Thesis, Menofia University, Shebin ElKoom, 2006.
- Y. S. Hamed, W. El-Ganaini and M. M. Kamel, “Vibration suppression in ultrasonic machining described by non-linear differential equations,” Journal of Mechanical Science and Technology, Vol. 23, No. 8, 2009, pp. 2038-2050. doi:10.1007/s12206-009-1208-9
- Y. S. Hamed, W. El-Ganaini and M. M. Kamel, “Vibration suppression in multitool ultrasonic machining to multi-external and parametric excitations,” Acta Mechanica Sinica, Vol. 25, No. 3, 2009, pp. 403-415. doi:10.1007/s10409-009-0229-7
- Y. S. Hamed, W. El-Ganaini and M. M. Kamel, “Vibration reduction in ultrasonic machine to external and tuned excitation forces,” Applied Mathematical Modelling, Vol. 33, No. 6, 2009, pp. 2853-2863. doi:10.1016/j.apm.2008.08.020
- M. Sayed and Y. S. Hamed, “Stability and response of a nonlinear coupled pitch-roll ship model under parametric and harmonic excitations,” Nonlinear Dynamics, Vol. 64, No. 3, 2011, pp. 207-220. doi:10.1007/s11071-010-9841-0
- M. Sayed and M. Kamel, “Stability study and control of helicopter blade flapping vibrations,” Applied Mathematical Modelling, Vol. 35, No. 6, 2011, pp. 2820-2837. doi:10.1016/j.apm.2010.12.002
- M. Sayed and M. Kamel, “1:2 and 1:3 internal resonance active absorber for non-linear vibrating system,” Applied Mathematical Modelling, Vol. 36, No. 1, 2012, pp. 310-332. doi:10.1016/j.apm.2011.05.057
- Y. A. Amer and M. Sayed, “Stability at Principal Resonance of Multi-Parametrically and Externally Excited Mechanical System,” Advances in Theoretical and Applied Mechanics, Vol. 4, No. 1, 2011, pp. 1-14.
- A. H. Nayfeh, “Introduction to Perturbation Techniques,” John Wiley & Sons, New York, 1981.

