Modern Economy
Vol.07 No.03(2016), Article ID:64946,7 pages
10.4236/me.2016.73035
Evaluating Investments Using Higher Moments
Demissew Diro Ejara
Department of Finance, University of New Haven, West Haven, CT, USA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 February 2016; accepted 20 March 2016; published 24 March 2016
ABSTRACT
This paper compares performance of long-short equity hedge funds with the market index by using mean-variance criteria and criteria including higher moments. Based on the mean-variance criteria, the majority of the long-short equity hedge funds outperform the market index. When higher moments are used to evaluate the performance, a greater proportion of the hedge funds underperform the market index. This implies the importance of including higher moments in portfolio optimization.
Keywords:
Higher Moments, Investment, Hedge Funds, Financial Econometrics, Portfolio Performance Evaluation, Taylor Series Expansion, CRRA

1. Introduction
Investment performance evaluation compares achieved returns with model derived expected returns. The models are almost exclusively based on expected return and risk, measured by standard deviation. Models such as the Sharpe Ratio, Jensen’s alpha, Treynor’s Ratio, Capital Asset Pricing Model (CAPM), and multi-factors models all use the first two moments to establish optimized benchmark for performance evaluation. There are two basic underlying assumptions of these models: normality of return distributions and efficient capital market. However, these assumptions are questioned by both academics and investment professionals. Academic studies are abundant with cases of violations of efficient market hypothesis. They show significant and persistent differences in performance of portfolios based on size, momentum and style. They also show that returns are negatively skewed and fat tailed than normally distributed.
Investment managers, especially the multi-billion hedge fund industry, try to exploit these observed inconsistencies with efficient markets and the non-normality of return distributions. They follow long-short strategy where they long securities perceived to perform better and short those expected to perform poorly. Examples include the 130/30 portfolio. Some try to create risk-free, zero investment portfolios with positive returns.
This raises a question about a proper model to evaluate investment performance. Some studies derived optimization models that included higher moments to account for the non-normality in return distributions. These studies are limited to just the derivation of mathematical models. The present study tries to fill the void by providing empirical analysis of performance evaluation using higher moments.
The arguments for inclusion of higher moments are investors’ preference for alternatives with high positive skewness and low kurtosis, and the fact that returns are not normally distributed, which necessitates inclusion of higher moments. The long-short hedge funds provide an ideal opportunity to test performance evaluation by using higher moments. This study uses a model with higher moments to compare the performances of long-short equity hedge funds. Specifically, I test if the long-short portfolios enhance utility of a risk-averse investor better than the general market index. I use a general Constant Relative Risk Aversion (CRRA) utility function and test if these portfolios provide superior utility than a general market index.
The results show that while the majority of the hedge funds outperform the market index based solely on the mean-variance optimization techniques such as the Sharpe ratio and Jensen’s Alpha, the majority underperform the market index when skewness and kurtosis are included in the performance evaluation. This result has an important implication. Both theoretical portfolio optimization models and investment managers should take into account higher moments.
The rest of the paper is organized as follows. Section 2 summarizes the extant literature on the topic. Section 3 presents the model. Section 4 presents the data and empirical results and Section 5 concludes.
2. Review of Literature
Markowitz [1] developed a model of portfolio optimization based on expected return and variance. Based on the mean-variance analysis, the Capital Asset Pricing Model (CAPM) was developed as an equilibrium model. Further risk-adjusted performance criteria such as Sharpe ratio, Treynor’s ratio and Jensen’s Alpha are developed based on these assumptions and widely used to evaluate investment performance. The assumption of market efficiency precludes persistent extra return above the risk-adjusted return. Other multifactor asset pricing models such as Fama and French [2] and Chen, Ross and Roll [3] seek to include more risk factors to explain returns under the same assumption of normality.
Both the assumptions of normality and market efficiency are challenged by several studies with empirical evidence. Stock returns are negatively skewed and have fatter tails than the normal distribution. Daniel and Titman [4] provide empirical evidence that portfolios based on size, style, and momentum persistently show return variations that cannot be explained by differences in risk.
Other studies derive portfolio optimization models by including higher moments (See for example, Harvey, Liechty, Liechty and Muller [5] , Cvitanic, Polimenis and Zapatero [6] , Mhiri and Prigent [7] and Xiong and Idzorek [8] ). These studies derive optimization models by including skewness and kurtosis to the mean and variance and illustrate by numerical examples. The inclusion of higher moments is expected to improve portfolio optimization by taking into account the curvature of the returns distribution.
This paper directly evaluates the performance of long-short hedge funds established with the aim of exploiting the market inefficiencies. These portfolios aim at achieving either high Sharpe ratio or positive alpha. Both of these measures depend on mean-variance analysis. I test how these portfolios perform relative to a general market index if higher moments are included in their performance evaluation. I use CRRA utility function and Taylor series expansion to derive the evaluation model following Mhiri and Prigent [7] .
3. Model
The mean-variance based investment analysis models use the Sharpe ratio, Jensen’s Alpha and Treynor’s ratio to evaluate portfolios. I use these variables to compare the performances of the long-short equity portfolios with the market portfolio. Since the hedge funds are specifically designed to exploit market inefficiencies with respect to size, momentum, styles, and other factors and generate either high Sharpe and Treynor ratios or positive Jensen’s Alpha, they are expected to outperform the general market index based on these measures.
To include skewness and kurtosis in the performance evaluation, I use infinitely differentiable CRRA utility function following Gerber and Pafumi [9] and Mhiri and Prigent [7] .
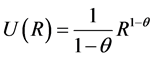 (1)
(1)
where U(R) is utility as a function of total return, R is return or (1 + rate of return), and θ is a coefficient of risk aversion with positive values different from 1.
Taylor series expansion of U(R) around mean of R gives us
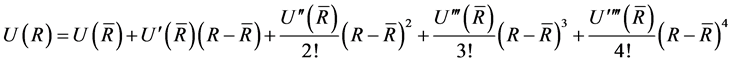 (2)
(2)
Taking expectation of the above, we have
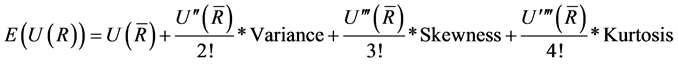 (3)
(3)
Substituting from (1), we have,
 (4)
(4)
where σ is standard deviation, S is skewness and K is kurtosis. And α, γ and δ are constants as follows:
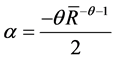
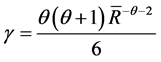
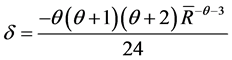
These equations are consistent with the notion that rational utility maximizing investors prefer higher returns, lower variance, positive skewness and lower kurtosis. Expected utilities will be estimated for the hedge funds and the market portfolio by using the above model.
4. Analyses and Results
List of US Long-Short Equity hedge funds and their monthly returns data are obtained from Morningstar EnCorr. A final sample of 400 is used in the analyses after imposing a minimum of 30 months returns. The period covered ranges from 1974 to 2012. Due to variations in the lives of the hedge funds, the number of return observations varies across funds. The number of observations range from a minimum of 30 to a maximum of 468 months. Monthly returns over corresponding period are also obtained for the S&P500 index and 30-day Treasury bill. Table 1 presents summary statistics of the hedge funds and the market portfolio.
The average of mean returns for the 400 funds is 0.826%. Average monthly returns varied from a minimum of −1.086% to a maximum of 4.518%. The corresponding mean return on the S&P 500 index is 0.937%, which is statistically significantly greater than the average of the hedge funds return at 1% level. The median distribution also reflects the same. The hedge funds on average have lower returns than the average market. In fact only 149 (37.3%) of the hedge funds have mean returns greater the average for the market index. The geometric means and median distributions even magnify the return underperformance of the hedge funds.
The standard deviation of the hedge funds varied from a low of 0.021% to a high of 16.379% with median standard deviation of 4.184%. The average standard deviation of the hedge funds is 4.684% compared to the market portfolio’s 4.533%. The difference is not statistically significant, but 224 (56%) of the funds have standard deviations lower than that of the market index. The hedge funds do better when it comes to the systematic risk. The average (median) beta of the hedge funds is 0.483 (0.428) compared to the market portfolio’s 1 and the difference is significant at 1% level. Further 357 (89.3%) of the funds have beta lower than 1, only 10.8% have beta greater than that of the market. These results are consistent with what can be expected from hedge funds
Table 1. Descriptive statistics of return distributions. This table presents descriptive statistics of the 400 long/short equity hedge funds and those of S&P500 Index and US T-bill rate. The statistics are based on monthly returns. The means, medians and other figures are cross-sectional values. So mean of 0.826% monthly return is actually average value of the cross- sectional mean returns.
***Figure is significantly different from that of S&P 500 index at 1% level.
since many of them aim at reducing or eliminating risk and generating return in excess of the risk-free rate.
The majority of the hedge funds (56.8%) as well as the S&P500 index are negatively skewed, but 67% of the funds have skewness coefficient greater than that of the market index. Skewness ranges from a low of −3.496 to a high of 6.081. The mean (median) skewness coefficient is −0.024 (−0.123). The table also reports the fourth moment as excess kurtosis. The S&P 500 index has excess kurtosis of 1.911 while the average excess kurtosis for the hedge funds is 3.492 (median is 2.082). About 53% of the hedge funds have higher kurtosis than the market index. A great majority, 93.3%, are leptokurtic, peaked distribution than normal. Only 6.8% are platokurtic. The skewness and kurtosis reported in the table indicate that the majority of the hedge funds are negatively skewed and have more fat tail. Although they appear to be more desirable on the average than the market portfolio in terms of skewness, they exhibit greater fat tails than the market portfolio. When it comes to higher moments, a portfolio with fat tails and positive skewness is preferred.
Table 2 presents statistical distributions of the mean-variance based performance evaluation criteria. The Sharpe ratio, Jensen’s Alpha and Treynor’s ratio are reported. The hedge funds perform better on the average than the market index based on these measures. The average Sharpe ratio for the funds is 0.223 compared to the market’s 0.112 and the difference is significant at 5% level. 65.3% of the funds in the sample have Sharpe ratios greater than that of the market portfolio. The results of alpha and Treynor’s ratio are similar. Alpha, comparatively favors the hedge funds strongly than the Sharpe ratio does. Average alpha of the funds is 0.473 and 83.8% of the funds have positive alpha. Treynor’s ratio is 0.507 for the S&P 500 index and averages 12.18 for the hedge funds. The difference is significant at 5% level, and 58.3% of the hedge funds have higher Treynor’s ratio than the market index. These results are consistent with Daniel and Titman [4] . Daniel and Titman [4] show that as mutual funds increase the proportion of their investment in long-short portfolios, their Sharpe ratios and alphas increase monotonously. These results are also consistent with the usually declared objective of hedge funds. They long stocks with expected positive performance and short stocks with expected negative performance thereby reducing beta and generating positive alpha. The long-short equity funds in this sample performed consistent with that notion, because the majority of them have low beta and positive alpha. The last column of Table 2
Table 2. Distributions of mean-variance based performance measures. Panel A reports the distributions of mean-variance based performance measures for the long-short equity hedge funds. Mean values are reported for the S&P 500 index and the 30 day Treasury bill. VaR @ 5% indicates Value at Risk with 5% tail probability. So there is a 5% probability of losing 6.542% in the S&P 500 index and 6.903% on average in the hedge funds in one month. Panel B reports the correlations among the mean-variance measures and with skewness and kurtosis. Panel C reports rank correlations when the hedge funds are ranked by the mean-variance measures. The number of hedge funds in the sample is 400.
** and *** indicate that the figure is significantly different from the corresponding S&P 500 mean at 5% and 1% levels respectively.
reports Value at Risk (VaR) at 5% probability. There is a 5% probability of losing 6.542% per month from investment in the market portfolio. The average VaR for the hedge funds is 6.903%. So an investment of $1,000,000 will lose in a month $65,420 in the market index and $69,030 in an average hedge fund with 5% probability. The median figure shows that the hedge funds are better than the market index. 44% of the funds have lower expected VaR than the market index.
Panel B of Table 2 reports correlations among the mean-variance measures and with skewness and kurtosis. Correlations between pairs of these measures are very low. The correlation between skewness and kurtosis is 48.34%. The correlation between skewness and alpha is 31.39% implying that investing in positively skewed alternatives will more likely generate positive alpha. The other correlation figures are small. Even the mean-va- riance measures of alpha and Sharpe ratio are correlated only 8.73%. Panel C reports higher values for rank correlations among the mean-variance measures. The rank correlation between Sharpe ratio and alpha is 76.71% and between alpha and Treynor’s ratio is 67.74%.
Utility Based Analysis
Table 3 presents estimated utility levels based on Equation 4 for different levels of risk aversion coefficient. Utility seems to be U-shaped in the degree of risk aversion in the range estimated. At all levels of the degree of
Table 3. Distribution of utility for different levels of risk aversion. The table presents utilities for the S&P 500 index and 30-day T-bill and utility cross-sectional distribution for the long-short equity hedge funds. Utilities are computed as a function of expected return, variance, skewness and kurtosis. Utilities are computed at different levels of the degree of risk aversion coefficient (θ).
***indicates the figure is significantly different from the S&P 500 index figure at 1% level.
risk aversion, the T-bill dominates both the market index and the average of the hedge funds. Unlike the mean-variance based measures, the average utility of the hedge funds is lower than that of the market index. At a degree of risk aversion coefficient, θ of 0.1, 60.5% of the hedge funds have lower utility than the market index. As θ increases, a greater proportion of hedge funds show better utility than the market index. At θ of 0.9, 50.9% of the hedge funds have higher utility than the market although the average utility of the hedge funds as a whole is less than that of the market index1. As θ increases, the cross-sectional dispersion of the hedge funds’ utility also increases as evidenced by cross sectional standard deviations of 1.48 at θ = 0.1 and standard deviation of 19.377 at θ = 0.9.
Table 4 reports the correlations between utilities, and higher moments and mean-variance based measures (Panel A). Skewness is positively correlated with utility. Positively skewed return distributions tend to increase utility. Kurtosis is negatively correlated with utility at lower levels of θ, but positively correlated at higher levels of θ. The three mean-variance measures are all positively correlated with utility. But the correlation coefficients are small in magnitude except for alpha’s. The correlation of alpha with utility is 54.11% at θ of 0.1 and monotonically decreases to 29.95% for θ of 0.9. Such pattern of correlation structure is true for Sharpe ratio and Treynor’s ratio. As the degree of risk aversion increases, the mean-variance measures get less correlated with utility.
Panel B of Table 4 presents rank correlations of the hedge funds based on utilities at different levels of θ and the mean-variance measures. The results reflect the same information as in Panel A but the correlation magnitudes are larger. Rank correlations are higher at lower levels of θ and decrease as θ increases. Unlike in Panel A, Sharpe ratio rank correlations are stronger than the other two mean-variance measures.
These results indicate that the higher moments have significant information content that should be considered in investment selection as well as performance evaluation. The results are consistent with the notion that positive skewness and low kurtosis are desirable features of investments.
5. Conclusions
This paper questions the return and risk only based approaches to investment analysis on the grounds that stock returns are not normally distributed and also that the market efficiency hypothesis has been violated as empirically shown by previous studies based on size, momentum and style portfolios. Previous studies that call for the inclusion of higher moments in portfolio optimization are appraised. But these previous studies are limited to derivation of optimization models by including the higher moments.
Table 4. Correlation between utility and mean-variance measures. (A) Correlations between utility computed at different levels of θ and the mean-variance measures of investment performance. Utility is computed as a function of expected return, variance, skewness and kurtosis. (B) Rank correlations based on utility at different levels of θ and mean-variance measures.
Direct test of investment performance by including higher moments (skewness and kurtosis) is proposed with the use of CRRA utility function. Empirical results are presented by using long-short equity hedge funds. These funds long stocks with expected high returns and short those with expected low returns. Some try to create zero (or low) beta portfolios and generate positive alpha. Therefore, they present a conducive opportunity to test the relevance of higher moments in investment analysis.
The empirical analyses show that the long-short equity hedge funds outperform the general market index based on the mean-variance measures of Sharpe ratio, alpha and Treynor’s ratio. But when the evaluation includes the higher moments of skewness and kurtosis with utility function, the general market index dominates the hedge funds. This indicates the importance of these higher moments in investment analysis. Theoretical models as well as investment managers should include skewness and kurtosis in their models of portfolio optimization and evaluation.
This study clearly shows the importance of including higher moments in performance evaluation. But it is limited in that only one form of utility function is assumed. Also, hedge funds are used as sample of analysis. Further research is necessary to refine ways of including the higher moments on other general portfolios and alternative utility functions to test for robustness of results.
Cite this paper
Demissew DiroEjara, (2016) Evaluating Investments Using Higher Moments. Modern Economy,07,320-326. doi: 10.4236/me.2016.73035
References
- 1. Markowitz, H. (1952) Portfolio Selection. Journal of Finance, 7, 77-91.
http://dx.doi.org/10.1111/j.1540-6261.1952.tb01525.x - 2. Fama, E. and French, K. (1993) Common Risk Factors in the Returns on Stocks and Bonds. Journal of Financial Economics, 33, 3-56.
http://dx.doi.org/10.1016/0304-405X(93)90023-5 - 3. Chen, N., Roll, R. and Ross, S. (1986) Economic Forces and the Stock Market. Journal of Business, 59, 386-403.
- 4. Daniel, K. and Titman, S. (1999) Market Efficiency in an Irrational World. Financial Analysts Journal, 55, 28-40.
http://dx.doi.org/10.2469/faj.v55.n6.2312 - 5. Harvey, C., Liechty, J., Liechty, M. and Muller, P. (2010) Portfolio Selection with Higher Moments. Quantitative Finance, 10, 469-485.
http://dx.doi.org/10.1080/14697681003756877 - 6. Cvitanic, J., Polimenis, V. and Zapatero, F. (2008) Optimal Portfolio Allocation with Higher Moments. Annals of Finance, 4, 1-28.
http://dx.doi.org/10.1007/s10436-007-0071-5 - 7. Mhiri, M. and Prigent, J. (2010) International Portfolio Optimization with Higher Moments. International Journal of Economics and Finance, 2, 157-169.
http://dx.doi.org/10.5539/ijef.v2n5p157 - 8. Xiong, J. and Idzorek, T. (2011) The Impact of Skewness and Fat Tail on the Asset Allocation Decision. Financial Analysts Journal, 67, 23-35.
http://dx.doi.org/10.2469/faj.v67.n2.5 - 9. Gerber, H.U. and Pafumi, G. (1998) Utility Functions: From Risk Theory to Finance. North American Actuarial Journal, 2, 74-100.
http://dx.doi.org/10.1080/10920277.1998.10595728
NOTES
1Three hedge funds for which the utility calculation resulted in extremely low figures are excluded. If they are included, the market index dominance will be more magnified.



