Modern Economy
Vol.3 No.2(2012), Article ID:18149,8 pages DOI:10.4236/me.2012.32029
Regional Economic Integration and the Formation of Global Trading Blocs: A Historical Analysis of the 1980s
1Department of Economics and Legal Studies, Oklahoma State University, Stillwater, USA
2Department of Finance, Oklahoma State University, Stillwater, USA
3Department of Economics, Korea University, Seoul, Korea
Email: orley.amos@okstate.edu
Received January 17, 2012; revised February 22, 2012; accepted February 29, 2012
Keywords: Trade Bloc; International Trade; Economic Integration; Regional Analysis
ABSTRACT
This paper undertakes an historical analysis of regional trading bloc formation in the 1980s. This time period was characterized by the formation of major global trading blocs, especially the European Union and the North American Free Trade Agreement (NAFTA), at the same time existing national structures broke apart, most notably the Soviet Union. A gravity model based analysis of trade flow data indicates that two forces operated simultaneously during the study period, one leading to the formation of trading blocs (as captured by a dummy variable for “same regions”) and the other leading to the dissolution of trading blocs (based on the interaction of GNP and the dummy variable for “same regions”).
1. Introduction
At the end of the last century, especially during the 1980s, the global economy experienced two seemingly contradictory trends—the formation of supranational trading blocs (e.g. European Union and North American Free Trade Agreement) and the dissolution of existing national structures (e.g. the break up of the Soviet Union). This paper undertakes an historical analysis of the forces underlying these simultaneous trends of integration and division through the analysis of the flow of international trade using the gravity model, a technique of analysis that explains trade flows by the sizes of the countries involved and the distances between them, concentrating on this late 1980s time period.
2. Background
The 1980s marked a key transitional period for the global economy and provides an excellent time frame for this analysis. The European Union was undertaking important steps toward consolidation and economic integration. Moreover the groundwork for the formal creation of the North American Free Trade Agreement (NAFTA) was being laid. Economic integration was also, albeit less formally, underway in Asia. Various nations in Oceania, South America, and Africa undertook economic integration and trade liberalization treaties, as well.
Simultaneous to economic integration during this period was the dissolution of existing structures. Most pronounced was the break up of the former Soviet Union. Other nations, including Yugoslavia and Czechoslovakia, also began breaking up. The primary focus of this study is on the forces underlying economic integration and the formation of regional trading blocs, while simultaneously investigating the forces that might generate dissolution.
The impetus for the formation of an integrated European Union during the last century was undoubtedly the expansion of trade throughout the global economy and the resulting competition from the United States and Japan. The United States responded to this competition in its own way through the North American Free Trade Agreement with Mexico and Canada. While economic integration in Asia was less formalized and remains so, Japan has extensive economic ties throughout the western half of the Pacific rim.
The consequence of this economic integration was the emergence of three major regional trading blocs in North America, Asia, and Europe and several smaller, regional trading blocs primarily dispersed throughout Latin America and Africa.
3. Economic Integration and Trading Blocs
According to Balassa [1] economic integration arrangements take a variety of forms: 1) preferential tariff agreements between countries; 2) free trade areas that eliminate tariffs among the participating nations, but maintain their own tariff schedule against non-participating nations; 3) customs unions that eliminate tariffs among the member nations, and establish a common tariff schedule against non-member nations; 4) common markets that eliminate non-tariff restrictions on factor movements (e.g. labor) as well as the elimination of tariffs; 5) economic unions where national economic policies are integrated; and 6) total economic integration that assumes a unification of all economic policies such as fiscal, monetary and employment policy, and also assumes a setup of supranational institutions that govern all member countries. These six forms of economic integration can be thought of as a hierarchical series of steps that progress from the level of cooperative independent nations to the level that creates a political entity just short of a formal nation.
Regional trading blocs are associations that develop among nations located in a particular region of the globe. As noted by Schott, proximity is one of several basic characteristics of trading blocs. For simplicity, a trading bloc can be defined as an association of countries that reduce intra-regional impediments to the free flow of commodities. “Trading blocs seek to 1) generate welfare gains through income and efficiency effects and trade creation; 2) augment negotiating leverage with third countries; and 3) sometimes promote regional political cooperation.” [2].
A criterion of a trading bloc is that there exists a discriminatory application of economic policy among members of the grouping. Another criterion is often the existence of a discriminatory policy against nonmember countries. Trading blocs are known to concentrate on discriminatory border restrictions, mainly tariffs. Correspondingly, trading blocs affect the quantity and prices of internationally exchanged commodities or factors of production.
Regional trading blocs can exhibit any of the levels of economic integration. The European Community moved from the common market described in level (4) to the economic union described in level (5) during 1992. The Japan/Asian trading bloc remained around levels (1) and (2) and NAFTA placed North America near the (2) and (3) levels of economic integration.
4. Theoretical Framework of Gravity Model
Spatial interaction models are used to facilitate the explanation and forecast of social and economic interaction over geographical space. In Niedercorn and Bechdolt, H. C. Carey defined the “gravity law” of spatial interaction by stating that “the degree of attraction varies directly with the mass, or concentration of persons or things, and inversely with distance” [3]. This is adapted from Newton’s law of universal gravitation which states that the force of attraction between object i and object j, 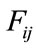 , is proportional to their respective masses, mi and mj, and inversely related to the square of the distance between masses,
, is proportional to their respective masses, mi and mj, and inversely related to the square of the distance between masses,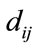 . The gravity law, as one of the spatial models used in behavioral science, also describes “social phenomena in space, such as population migration, flow of goods, money, and information, traffic movement and tourist travel” [3].
. The gravity law, as one of the spatial models used in behavioral science, also describes “social phenomena in space, such as population migration, flow of goods, money, and information, traffic movement and tourist travel” [3].
Mathematically, the gravity law is expressed as follows:
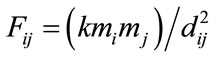 (1)
(1)
where k is a constant.
This formula is often slightly modified when applied to socioeconomic interactions. The exponent of the distance variable is not necessarily fixed at two and is often estimated for the specific interaction being studied.
Gravity models can be classified according to “1) the type of data used, 2) the type of interaction being studied, and 3) the point of view from which the interaction is being studied” [3]. In empirical studies, the specific gravity model is determined by the estimation technique and the interactions. This study uses a bidirectional trade flow model in which exports from country i to country j and exports from country j to country i are combined to constitute a trade flow between i and j.
5. Data and Variables
5.1. Regions
The classical method of conceptualizing regions in regional economics is based on three criteria: 1) homogeneous regions; 2) nodal (or polarized) regions; and 3) planning (or programming) regions. With the homogeneous criterion, regions are delineated based on one or more common traits, such as production, natural resources, culture, or language [4]. With the nodality criterion, regions are delineated based on a high degree of interdependence and interaction with a central point of attraction (usually a city or urban area). With the planning criterion, regions are delineated based on political jurisdiction and policy oversight. Delineating an international region for this study relies largely on the first two criteria, homogeneity and nodality.
The seven multi-national regions used as the basis for this study are: North America (United States, Canada, Mexico); Far East Asia (Japan, Korea, China, Taiwan, Hong Kong); Europe (Germany, France, United Kingdom, Italy, Spain, Netherlands, Belgium, Luxembourg, Switzerland, Sweden, Austria, Norway, Denmark, Finland, Ireland, Portugal, Greece); Southeastern Asia (Singapore, Malaysia, Thailand, Asia Indonesia, Philippines); Oceanian (Australia and New Zealand); South America (Brazil, Venezuela, Argentina, Chile, Colombia, Peru, Ecuador, Uruguay, Bolivia, Paraguay); and Southeastern Africa (South Africa, Kenya, Tanzania, Uganda, Africa, Mozambique).
These seven regions are geographically separated from one another. Therefore, each group has its own economic, political, and geographical characteristics that are often distinctive from the others.
The 46 countries included in this study include both developed countries (DC), newly industrialized countries (NIC), less developed countries (LDC). The developed countries included all of the G-7 (Group of Seven) countries and 22 OECD (Organisation for Economic Co-operation and Development) countries, excluding Iceland and Turkey.
5.2. Trade Flows
The proxy for international economic interactions—the gravitational force of interaction—is trade flows between countries. The specific trade flow variable used in this study is the sum of exports and imports between two countries. In trade theory, conventional trade flow models deal with exports and imports separately. The method of dealing with exports and imports here is to combine the unidirectional interactions, in order to obtain a bidirectional gravity model.
From the standpoint of trade theory, the sum of exports and imports is equal to the volume of trade. Aside from the theoretical basis backed by trade theory and the gravity model, the bidirectional model has a number of advantages: 1) it indicates the overall interaction between any two countries not captured by exports and imports separately; 2) it reduces a considerable amount of missing data, which is inevitable in unidirectional models, without any deterioration of the theoretical essentials;1 3) it also reduces the computational work by applying a single equation of trade flows, unlike unidirectional models which have two equations; and 4) it has a smoothing function for the trade flow data, which by averaging exports and imports reduces fluctuations in less-developed countries that have lower trade volumes.
Data from the “Direction of Trade Statistics” Yearbook published by the International Monetary Fund (IMF) for the year of 1988 are used for this research. The 46 nations, each trading with 45 other nations, potentially have a total of 2070 (=46 × 45) trade flow observations between all pairs of two countries. This number is reduced to 1035 by pairwise, export-import aggregation of trade flows. For countries in which 1988 data are unavailable, either three-year average values for 1987-1989 or, in rare cases, five-year averages from 1985-1989 are utilized. The minimum trade value reported in the Statistical Yearbook is 100,000 US dollars. This means that any trade flows less than 50,000 US dollars are rounded off and dropped out of the data source, making the data “not available (NA)”. However, compensation for this data deficiency is possible, in part, by using the threeyear average.
Zero trade flows usually occur for two reasons. First, in smaller countries trade statistics may be too small to be recorded and reported to the relevant international institution. Second, countries impose trade embargoes on one another for political reasons. For example, no trade flows exist between China and Taiwan, China and South Korea, and China and South Africa.
In total only 38 of 1035 potential trade flow observations are not available either because of missing data or trade embargoes. Table 1 presents the nations and their trading partners with zero trade flows. Thus 997 international trade flows are used as the observations for the dependent variable in this study.
The trade flow data are collected and organized from largest to smallest trade flow. The largest country is utilized to collect 45 pairs of bidirectional trade flows, then the second largest country is used to collect 44 pairs, and so on until all pair wise collections are made. This approach is used because larger countries usually have more accurate, and reliable data.
5.3. GNP
According to the gravity model, socioeconomic interactions (or the “gravitational force” of attraction) between two regions is directly proportional to the “mass” of both regions. Income, population, and output are often used to indicate the mass of a region. In this study GNP is used to proxy “mass”.
GNP is thus hypothesized to determine the size of trade flows. The GNP of a larger economy is hypothesized to influence trade flows more than the GNP of a smaller economy. To test this hypothesis, the GNP data
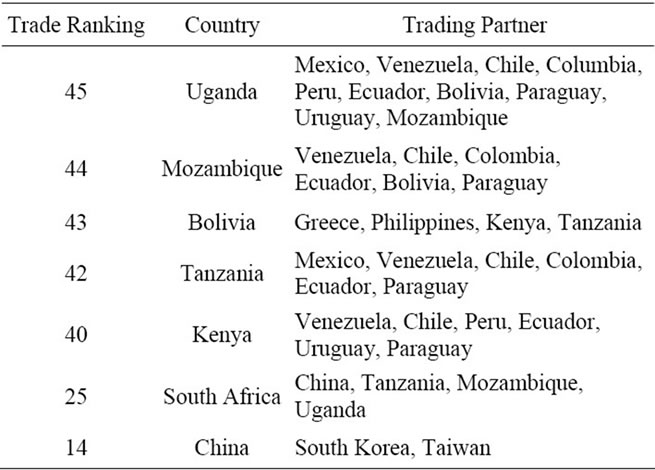
Table 1. Countries with zero trade volume.
from the larger economy in each pair of countries is consistently specified to be an origin GNP variable. If larger GNP observations are employed as the origin GNP, its magnitude is believed to be greater than the magnitude of the destination GNP variable.
GDP observations are alternatively used in five countries (Hong Kong, Bolivia, Mexico, Finland, and Argentina) where GNP statistics are not available for 1988. According to Linnemann’s study covering 80 countries in the early 1960s, 27 out of 52 countries having both GNP and GDP statistics showed differences of less than one percent. Moreover, another 12 cases showed differences of less than two percent [5].
The GNP (GDP) observations in this study come from the IMF International Financial Statistics (IFS) Yearbook for 1990. Observations are converted into millions of United States dollars. The GNP data are computed by the use of Line “af” that appears in the Yearbook for the Market Rate/Par or Central Rate.
5.4. Land Area
Land area, expressed in square kilometer (km), is included for two reasons. First, it is assumed to represent a proxy for the size of the market area of a country. This assumption implies that a larger land area means a larger domestic market area. A country with a larger domestic market area tends to be more self-sufficient, hence having a lower foreign trade ratio out of GNP.
Second, land area is assumed to capture the role of natural resources. A country possessing certain natural resources not available in other countries may have an important impact on its foreign sector. A country specializing in an industry in which it has abundant resources is likely to increase production. The increased production is channeled into either reducing imports or expanding exports. This assumes that the possession of a variety of natural resources leads to more self-sufficiency. These two assumptions lead to the expectation that land area is a significant variable explaining the negative international trade flows. It is interesting to employ land area in the empirical analysis, because land area has not been used in the gravity model. Land areas are obtained for this study from Rand McNally “The New International Atlas” [6].
5.5. Geographic Distance
Classical trade theory customarily excludes spatial dimensions. Trade theorists tend to overlook the advantages of geographical proximity in judging the desirability of customs unions [1]. Likewise, some public sector leaders do the same in judging the desirability of trading blocs [7,8].
Despite the importance of transportation costs in international trade, reliable data are not readily available. For this reason, distance has been commonly used in the related research as a proxy for transportation cost. Therefore it is hypothesized that distance is inversely related to trade flows.
On the practical level in this study, distance is measured as a combination of sea and land. For sea distances, the measurement of the shortest navigation distances between two countries’ major seaports is obtained from the publication Defense Mapping Agency [9]. The distance between two countries is then obtained by the summation of the sea distance and the overland distance from the major port to the economic center of gravity of each nation. If a country has more than one major seaport, those seaports are used as well. For example, Pacific and Atlantic ports are both used for Mexico, Columbia, Canada and the United States. Atlantic and Mediterranean ports are both used for Spain and France. Though the overland transportation cost is considerably higher than that of sea transportation, the overland distance is added to the sea distance.
An element of subjectivity in the selection of the locations inevitably leads to possible inaccuracies in the measurement of the overland distances. This study borrows Linnemann’s calculation of overland distances where possible [5]. For bordering countries, at least one of which has no seaport, the road distances between the economic centers are obtained from 1) a road atlas in the case of Europe and 2) from approximations in the case of South America and Africa. This is applied to the inland countries of Switzerland, Austria, Bolivia, Paraguay and Uganda.
In addition, for countries that have mainly overland interactions, especially in Europe, the road distances between two economic centers are estimated.
5.6. Preferential Trade Factors
A number of preferential groups can be delineated among the 46 selected countries to show that the preferences clearly exist in international trade flows. The selection of these preferential factors in this study relies on the concept of location. The spatial approach to preference relations excludes unnecessary non-spatial factors in order to pursue an analysis of spatial interactions in terms of geographical proximity. The preference relations are estimated in the form of qualitative or interactive dummy variables.
1) A dummy variable for bordering countries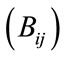 .
.
Adjacency is expected to positively influence trade volume between countries. Neighboring countries are likely to have more intense trade activities than countries that are separated by sea or another nation. Common language or cultural heritage between adjacent nations tends to provide a rationale for this trade-enhancing effect. The intensity of trading activities is also plausible partly due to the trade flows between domestic regions along the common border.
2) A dummy variable for countries of the same region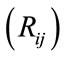 . Countries in the same international region are expected to have enhanced trade volume with other countries in the region. In terms of transportation costs, the results of the regional preference are expected to shed more light on the role of a region on the regional concentration of trade flows. Higher transportation costs are involved in intra-regional trade between countries without contiguous borders than in trade across contiguous borders. Regions defined by factors in addition to geographical proximity are expected to play a key role in explaining the formation of regional trading blocs.
. Countries in the same international region are expected to have enhanced trade volume with other countries in the region. In terms of transportation costs, the results of the regional preference are expected to shed more light on the role of a region on the regional concentration of trade flows. Higher transportation costs are involved in intra-regional trade between countries without contiguous borders than in trade across contiguous borders. Regions defined by factors in addition to geographical proximity are expected to play a key role in explaining the formation of regional trading blocs.
3) A dummy variable for the membership of both countries in the OECD or NIC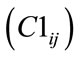 . Developed countries (DCs) are indicated by their Organisation for Economic Co-operation and Development (OECD) membership and Newly Industrialized Country (NIC) status. This dummy variable captures the influence on trade flows between two developed countries. Four NICs and 22 of 24 OECD member countries are included in this study.
. Developed countries (DCs) are indicated by their Organisation for Economic Co-operation and Development (OECD) membership and Newly Industrialized Country (NIC) status. This dummy variable captures the influence on trade flows between two developed countries. Four NICs and 22 of 24 OECD member countries are included in this study.
4) A dummy variable for the membership of either country in the OECD or NIC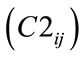 . This variable captures the trade pattern between a developed country (DC) and a less-developed country (LDC).
. This variable captures the trade pattern between a developed country (DC) and a less-developed country (LDC).
5) An interaction term representing the interaction between the regional dummy variable 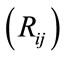 and the origin (larger) country’s economy
and the origin (larger) country’s economy . It is hypothesized to measure the effect of the larger economy’s GNP on the trade flows within a region in which the country belongs. If its coefficient, termed the differential slope coefficient, is statistically significant,
. It is hypothesized to measure the effect of the larger economy’s GNP on the trade flows within a region in which the country belongs. If its coefficient, termed the differential slope coefficient, is statistically significant,  affects the coefficient of the
affects the coefficient of the 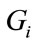 variable. As to the direction of the coefficient sign, it is assumed that the interaction variable for the same region reduces the effect of
variable. As to the direction of the coefficient sign, it is assumed that the interaction variable for the same region reduces the effect of  on the intra-regional trade flows. The dummy variable here tests the hypothesis that as
on the intra-regional trade flows. The dummy variable here tests the hypothesis that as 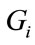 becomes larger, country i’s power to augment intra-regional trade becomes smaller.
becomes larger, country i’s power to augment intra-regional trade becomes smaller.
6) An interaction term representing the interaction between the regional dummy variable 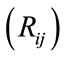 and the destination (smaller) country’s economy
and the destination (smaller) country’s economy . This variable is analogous to the previous variable but for the smaller destination country.
. This variable is analogous to the previous variable but for the smaller destination country.
6. The Empirical Model
The cross-sectional regression model is estimated using 1988 data for the variables. The log-linear model is:
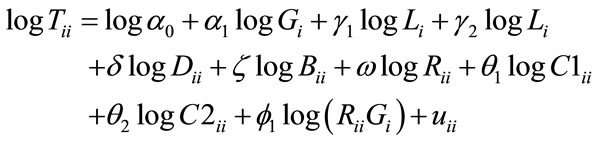 (2)
(2)
where: Tij = trade flow between countries i and j; α0 = constant; Gi = gross national product of larger origin country i; Gj = gross national product of smaller destination country j; Li = land area of larger origin country i; Lj = land area of smaller destination country j; Dij = distance between countries i and j; Bij = adjacency dummy variable equal to (e ≈ 2.718) if trading partners are neighboring countries and equal to 1 if not; Rij = same region dummy variable equal to e if trading partners are neighboring countries and equal to 1 if not; C1ij = DC region dummy variable equal to e if both trading partners are either OECD members or an NIC and equal to 1 if not; C2ij = DC/LDC region dummy variable equal to e if one trading partner is either OECD members or an NIC and equal to 1 if not; RijGi = interaction variable between the same region dummy and gross national product of larger origin country i; RijGj = interaction variable between the same region dummy and gross national product of smaller destination country j; uij = error term; and  coefficients of the explanatory variables.
coefficients of the explanatory variables.
The trade flow (Tij) and GNP (Gi and Gj) are measured in millions of US dollars. The land area (Li and Lj) is measured in square kilometers, geographic distance (Dij) is in nautical miles and dummy variables take e (≈2.718)2 if the qualitative class is applied. If not, they take the value of 1.
7. Empirical Results
7.1. The Cross-Sectional Gravity Model
The OLS coefficient estimates of the trade flow model are obtained by using the gravity Equation (3) and are summarized in Table 2, along with t-statistics and sig-
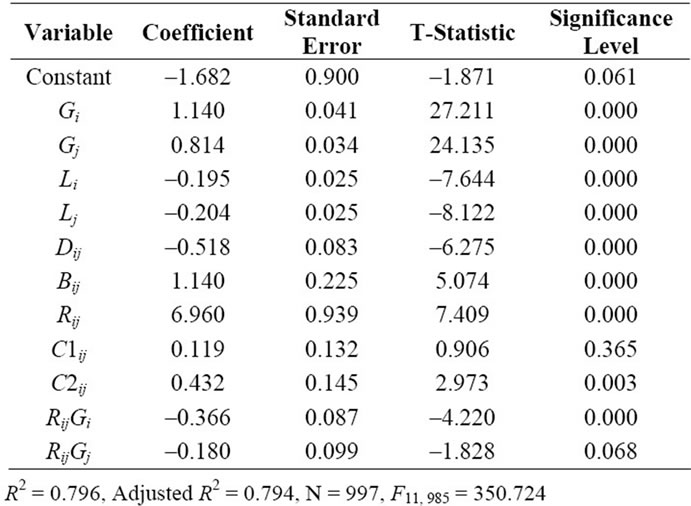
Table 2. Ordinary Least Squares (OLS) cross-sectional estimates of international trade flows.
nificance levels. The GNP parameters [1.140 (α1) and 0.814 (α1)] fall within the range of previous estimations in other studies. The reliability of the elasticities of trade flows with respect to GNP has a critical affect on trade flows. The elasticities on GNP are empirically tested to center around 1.3
The estimated coefficients and their signs for land areas of origin country i (Li) and destination country j (Lj) are –0.195 (γ1) and –0.204 (γ2) with t-ratios significant at the one percent level, consistent with expectations. Though most studies estimate the gravity equation using population as a factor affecting bilateral trade flow, the land area variable, which is unique in this study, is significant at the 1 percent level. The result for the land area is different than Linnemann [5] who concluded that the inclusion of a land area in the analysis of a country’s potential foreign supply will contribute little or nothing to a systematic explanation of trade flows.
The coefficient for the distance variable (Dij), δ = –0.517 has the expected negative sign, indicating an inverse relation with trade. It is statistically significant at the 1 percent level. The value of δ (Dij) falls well within the range of previous estimates. These results strongly imply that trading blocs are most likely to form among nations that are in close proximity.
The coefficient estimates on the adjacency dummy variable (Bij) and the same region dummy variable (Rij), ζ = 1.140 and ω = 6.960, respectively, have the expected signs, and relatively large t-values. Though both dummy variables are significant at the 1 percent level, the value of the coefficient of same region dummy (Rij) 6.690 is much larger than the adjacent dummy (Bij) 1.140. This is consistent with Linnemann who found that the adjacency effect is of minor importance [10].
The dummy variables (C1ij, C2ij) for OECD membership and/or NIC status have expected signs, but are substantially smaller than the adjacency or same region dummy variables. However, only θ2, the coefficient for either country’s membership variable (C2ij), is significant at the 1 percent level. Notably, the coefficient value of C1ij is much less than the variable C2ij. This clearly supports the hypothesis that OECD or NIC status of only one of the two trading partners, that is, trade between developed countries (DCs) and less developed countries (LDCs), is more important than trade only between developed countries.
The coefficients measuring the effects of RijGi and RijGj on the trade augmenting power of a geographical cluster (same region), 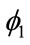 (–0.366) and
(–0.366) and 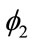 (–0.180), have the expected signs, and are significant at the 1 and almost 5 percent level respectively. These results indicate that the GNP “mass” of both trading partners is modified by membership in the same trading bloc. In particular GNP is less important as a factor influencing trade flows for two nations within the same regional bloc than for two nations in different trading blocs.
(–0.180), have the expected signs, and are significant at the 1 and almost 5 percent level respectively. These results indicate that the GNP “mass” of both trading partners is modified by membership in the same trading bloc. In particular GNP is less important as a factor influencing trade flows for two nations within the same regional bloc than for two nations in different trading blocs.
7.2. Regional Trading Bloc Formation
Results obtained from this analysis highlight the underlying regional trading bloc formation process that existed in the last part of the 20th Century. The first indication of this process lies with the same region dummy variable Rij (6.960). Clearly nations in the same regional trading bloc are more likely to engage in trade than nations in two different trading blocs. This interaction of trade flows creates a powerful force and incentive to form trading blocs. The desire to reinforce trade flows and reduce barriers to trade is a strong motivation to form trading blocs.
Trading bloc formation, however, is qualified by the results for the two GNP coefficients [Gi(α1 = 1.140) and Gj(α2 = 0.814)]. The two magnitudes have a sizable difference. The discernable difference between the coefficient of the origin country’s GNP (Gi), α1 = 1.140, and the coefficient of the destination country’s GNP (Gj), α2 = 0.814, makes intuitive sense.
Recall that the observations are arranged in a descending order of GNP size. For example, because United State has the largest economy and GNP, it is thus used as the origin GNP for all relevant trade flows with other countries. Japan has the second largest economy and thus it is used as the origin GNP in all trade flows except when paired with the larger economy of the United States. The interpretation is thus that Gi is always for the larger of any two trading partners and Gj always captures the effect of the smaller of the two nations. Results indicate that the larger economy’s GNP has a stronger effect on the trade flows than the smaller economy’s GNP. Therefore, the hypothesis that Gi influences the overall trade flows more than Gj is empirically supported. This result suggests that larger economies naturally exerted an attractive force over smaller trading partners, thus creating an incentive to form trading blocs, if enabled by close proximity.
The incentive to form trading blocs is qualified by the results of the variables capturing the interaction of GNP and the same region dummy variable (Rij). The fact that RijG for both origin and destination trading partners have negative signs is important. These interaction terms change the GNP slope of the original regression. The interaction coefficient for origin GNP-same region dummy, 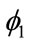 (–0.366), generates a new elasticity value (α1 +
(–0.366), generates a new elasticity value (α1 +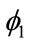 )for origin GNP of 0.774 = [1.140 + (–0.366)]. Moreover, the interaction coefficient for the destination GNPsame region dummy,
)for origin GNP of 0.774 = [1.140 + (–0.366)]. Moreover, the interaction coefficient for the destination GNPsame region dummy, 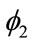 (–0.180), generates a new elasticity value (α2 +
(–0.180), generates a new elasticity value (α2 +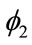 ) for origin GNP of 0.634 = [0.814 + (–0.180)]. This indicates that the role of GNP, the “mass” of the trading partners, is less important for nations in the same trading bloc than for nations in two different trading blocs. The gravitational force of attraction within trading blocs (0.774 and 0.634) is less than the force of attraction outside trading blocs (1.140 and 0.814). In other words, countries within a trading bloc look beyond their regions (or natural trading blocs) in search of trade with other countries.
) for origin GNP of 0.634 = [0.814 + (–0.180)]. This indicates that the role of GNP, the “mass” of the trading partners, is less important for nations in the same trading bloc than for nations in two different trading blocs. The gravitational force of attraction within trading blocs (0.774 and 0.634) is less than the force of attraction outside trading blocs (1.140 and 0.814). In other words, countries within a trading bloc look beyond their regions (or natural trading blocs) in search of trade with other countries.
The critical implication is that even as forces act to create trading blocs (indicated by the same region dummy variable (Rij)), other forces work to break up trading blocs as countries look beyond their nearby global neighborhood for trade. The negative differential slope coefficients indicate the eventual breakdown of trading blocs even as they are being formed. Interestingly, this long-run prediction is in conformity with views of the leaders of the principal economies, especially G-7 countries, that “free trade is a powerful, important goal, and that lapsing back into a protectionist era would have tremendous dangers for us” [11].
World trade indicates that each country has a variety of sizes of market areas for different commodities, and an increase in a certain country’s GNP causes an increase in world trade through an expansion of the country’s market area beyond the international region as well as over the national boundary. The rise in world trade is divided into intra-regional trade and world trade outside the region. The RijGi coefficient, 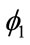 (–0.366), indicates that as GNP gets larger, the dummy variables for the same region lose the power to augment intra-regional trade. Therefore, the existence of an incentive to pursue world free trade is confirmed empirically. A similar position from the standpoint of current history is offered by Garten, who states, “The superblocs need to stimulate a new way of thinking about the purposes of foreign policy beyond the givens of promoting peace, prosperity and human rights. In the world of superblocs, the objective should be to promote outward-looking blocs in a framework of cooperative allied relations.” [12].
(–0.366), indicates that as GNP gets larger, the dummy variables for the same region lose the power to augment intra-regional trade. Therefore, the existence of an incentive to pursue world free trade is confirmed empirically. A similar position from the standpoint of current history is offered by Garten, who states, “The superblocs need to stimulate a new way of thinking about the purposes of foreign policy beyond the givens of promoting peace, prosperity and human rights. In the world of superblocs, the objective should be to promote outward-looking blocs in a framework of cooperative allied relations.” [12].
There are several possible reasons for the validity of the above proposition. First, as intra-regional trade approaches a saturation point, an increase in GNP will affect outer-regional trade as an outlet for the increased output created by an improved scale economy. Second, as production costs fall, an economic market area is expanded, thus causing outer-regional trade to increase. Third, as GNP increases, more goods are thought of as necessary goods by consumers, thus leading to an increase in world trade through an increase in consumption. Fourth, an increase in production efficiency obtained through trade creation along with a rise in production results in the specialization of production on the basis of comparative advantage. This causes the goods concerned to flow beyond the perimeter of an international region.
The destination GNP interaction variable, RijGj, also fits expectations with respect to sign and size. Even the smaller size of the coefficient 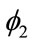 (–0.180) is plausible compared with the coefficient of RijGi,
(–0.180) is plausible compared with the coefficient of RijGi, 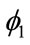 (–0.366). The size difference indicates that smaller countries do not have the same power to augment world trade as larger countries.
(–0.366). The size difference indicates that smaller countries do not have the same power to augment world trade as larger countries.
8. Summary and Conclusions
International commodity flows are most affected by the four major factors in the study; GNP, land area, same region and geographic distance. The gravity model used in the study gives particular attention to the treatment of the distance variable and two dummy variables which are conceptually similar to distance variable, but qualitative in nature. The two dummy variables represent the effect of adjacency and the effect of countries located in the same geographical region respectively.
As a proxy for transportation cost, the distance variable clearly shows a trade-reducing effect. The other two qualitative variables, however, possess a significantly trade-enhancing effect.
A multinational region, the delineation of which heavily relies on geographical aspects, is a key factor in explaining the ongoing formation of trading blocs in an international region. The close proximity of two countries in a region is likely to lead to a much greater possibility of trade between the two countries, ceteris paribus. GNP is known to be a crucial factor determining international trade. It is also a major variable in the gravity equation. The GNP variable combined with a dummy variable for the same geographical location of nations is shown to be a key factor affecting the direction of an international trade flow and trading bloc formation. This is true, after adjusting for distance and other variables that explain trade patterns. Thus the attribute of same region as a qualitative variable helps to provide an overall explanation for regional economic integration. The economic rationale behind the same region effect is that within the same region a shorter distance reflects a lower transport cost, an easier flow of information on external markets within the international region, and cultural or social similarities. The factor of the same international region, or relatively closer geographical locations outside the region, implies that trade flow distortions arising mainly from political conflicts such as ideological confrontation and disagreements of governments will be adjusted in the way that economic forces dominate. This prediction is based on the important contribution of geographical proximity to the attainment of post-war regional economic integration.
In concluding this study, two major findings concerning the issue of a trading bloc are stressed. First, spatial factors contribute to trade, even after taking GNP and other factors into account. This is why trading blocs have been forming on the basis of geographic proximity. As the empirical results show, the formation of trading blocs is one type of spatial interaction over national borders. Geographical proximity, which is the basic factor in spatial interactions, is important to evaluate the issue of trading bloc formation. This factor plays a larger role in the process of forming trading blocs than has been previously recognized. The degree of the role of propinquity varies considerably from region to region. Other factors affect the process of integration within a region, however, the role of geographical proximity is widely believed to be important in the long run in spite of modern technological innovations in transportation and communications.
Second, this study discovers that the same region interaction variable reduces the impact of geographical proximity on trade flows as GNP increases. This variable is seen to indicate that there still exists a strong force towards global free trade. However, because the effect of this variable is lower than the same region dummy variable, representing relative geographical proximity, the trend of forming trading blocs will continue for the time being. The counteracting effect of the same region and GNP interaction variables, RijGi and RijGj, indicates that larger economies have a smaller effect on trade within the same region than on trade outside of that region. This leaves a possibility that worldwide free trade will be induced in the long run. This is likely to cause the breakup of trading blocs, even as they are currently being formed. This prediction is consistent with the advocates of regionalism in the context that trading blocs are a way of promoting world free trade through easier negotiations between the blocs in the long run.
REFERENCES
- B. Balassa, “The Theory of Economic Integration,” Richard D. Irwin, Inc., Homewood, 1961.
- J. J. Schott, Ed., “Free Trade and US Trade Policy,” Institute for International Economics, Washington, 1989, p. 32.
- J. H. Niedercorn and B. V. Bechdolt Jr., “An Economic Derivation of the ‘Gravity Law’ of Spatial Interaction,” Journal of Regional Science, Vol. 9, No. 2, 1969, p. 273. doi:10.1111/j.1467-9787.1969.tb01340.x
- B. M. Russett, “International Regions and the International System: A Study in Political Ecology,” Rand McNally & Company, Chicago, 1967, p. 2.
- H. Linnemann, “An Econometric Study of International Trade Flow,” North-Holland Publishing Company, Amsterdam, 1966.
- R. McNally, “The New International Atlas,” McNally and Company, Chicago, 1983.
- J. J. Schott, “Trading Blocs and the World Trading System,” World Economy, Vol. 14, No. 1, 1991, pp. 2-3.
- L. C. Thurow, “GATT Is Dead,” Journal of Accountancy, Vol. 170, No. 3, 1990, pp. 36-39.
- DefenseMapping Agency, Hydrographic/Topographic Center, “Distances Between Ports,” US Government, Washington DC, 1985.
- V. J. Geraci and W. Prewo, “Bilateral Trade Flows and Transport Costs,” Review of Economics and Statistics, Vol. 59, No. 1, 1977, pp. 67-74. doi:10.2307/1924905
- J. Rappleye, C. Willard and F. Maurice, “Interview, Strong: Adaptations of the Blocs,” Financier, Vol. 13, No. 4, 1989.
- J. E. Garten, “Trading Blocs and the Evolving World Economy,” Current History, Vol. 88, No. 534, 1989, pp. 15-16 and 54-56.
NOTES
1The trade flow data expressed as trade volume reduces the missing data problem more than exports or imports data do, because one country’s trade volume is the sum of its exports and imports.
2The other frequently used value in log-linear models is 2, and the natural logarithm of the number is 0.69315. The natural logarithmic value of e is 1, so slightly different from the above value, 0.69315. However, the other number represents a different attribute (or class) and is the same in both models, making the logarithmic value zero.
3The 99.1 percent confidence interval for the t test statistic is:
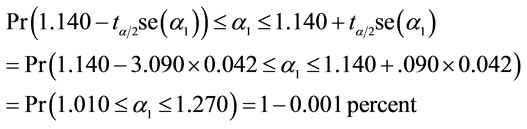
Thus if we let H0:  (estimated 1) = 1 and H1:
(estimated 1) = 1 and H1: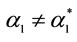 , the confidence interval becomes Pr(0.870 ≤ 1 ≤ 1.130). Since the t test statistic is
, the confidence interval becomes Pr(0.870 ≤ 1 ≤ 1.130). Since the t test statistic is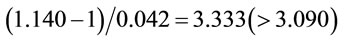 , it lies in the critical region and the conclusion remains the same; H0 is rejected, that is, 1 is significantly different from 1. If we let H0:
, it lies in the critical region and the conclusion remains the same; H0 is rejected, that is, 1 is significantly different from 1. If we let H0:  (estimated 2) = 1 and H1: 2*, the confidence interval becomes Pr(0.895 ≤ 2 ≤ 1.105). Since the t test statistic is
(estimated 2) = 1 and H1: 2*, the confidence interval becomes Pr(0.895 ≤ 2 ≤ 1.105). Since the t test statistic is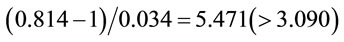 , it lies in the critical region and H0 is rejected. This means that 2 is significantly different from 1. As to the F test, H0:
, it lies in the critical region and H0 is rejected. This means that 2 is significantly different from 1. As to the F test, H0: 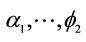 (all true parameters) = 0. Since the computed F ratio, 350.72 is greater than the critical F value for 11 and 985 degrees of freedom at the 1 percent, 2.25, the null hypothesis that the explanatory variables have no influence on the trade flows is rejected.
(all true parameters) = 0. Since the computed F ratio, 350.72 is greater than the critical F value for 11 and 985 degrees of freedom at the 1 percent, 2.25, the null hypothesis that the explanatory variables have no influence on the trade flows is rejected.

