Modern Economy
Vol. 3 No. 3 (2012) , Article ID: 19172 , 9 pages DOI:10.4236/me.2012.33045
Role of Knowledge in Supporting Growth across Indian States: A Co-Integration and Causality Approach
International Management Institute B-10, Qutab Institutional Area, New Delhi, India
Email :arindambanik@imi.edu, rabiarabs1@gmail.com
Received October 1, 2011; revised November 10, 2011; accepted December 9, 2011
Keywords: Co-Integration; Indian States; Education Expenditure; Growth
ABSTRACT
This paper uses cointegration and vector error-correction models to analyse the causal relationship between education and development across select Indian states using annual data from 1980-81 to 2008-09. Expenditure on education per capita is used as the proxy for education, while State domestic product per capita is the proxy for development. The empirical results provide some evidence of bi-directional causality in Indian States such as Kerala, Karnataka, Andhra Pradesh, Maharashtra and Tamil Nadu. There is also evidence of causation running from per capita expenditure on education to per capita State domestic product in either the short or long run in states such as Bihar, Arunachal Pradesh, Uttar Pradesh, West Bengal, Punjab, Orissa, Madhya Pradesh, Gujarat, Rajasthan, Haryana and Punjab. Thus, there is some indication that the observed positive correlation across states between expenditure on education and growth reflects primarily the influence of government effective intervention in the education sector.
1. Introduction
The fundamental importance of investing in education because of its impact on growth and development has long been argued by Denison [1] and others. In recent years, it has been observed that the main channel through which investment in education can influence growth and, hence, development, in developing countries consists of activities that lead to catching up with foreign technological progress [2]. Interestingly empirical studies of these issues have been mixed. Benhabeb and Spiegel [3] for example, finds that long-term growth series confirm that improving the level of education has contributed significantly to the growth observed over the last three to four decades in East Asian Economies such as Japan, Taiwan, South Korea, and Singapore.
In the East Asian context, for example, it is the egalitarian education policies which have played a pivotal role in their economic growth [4]. It is further argued that the increased equality has led to enhanced political and social stability, thereby creating a better investment environment [5]. The cognitive skills, in addition to increasing the literacy rate, may be considered as a precondition for economic development. Lucas [6] and Stiglitz [7] illustrate that this precondition may explain the seeming failure of capital to flow to the capital-poor countries in spite of the higher marginal return to capital. The lack of complementary factors such as non-availability of skilled labour further added to the problem of capital flow to the capital-poor countries. Pritchett [8] examined two aspects of quality of education and skills. In some countries, schooling has been enormously effective in transmitting knowledge and skills, while in others it has been essentially worthless and has created no skills.
On the other hand, the study of Berthelemy et al. [2] has not reconfirmed such argument in the context of Senegal. A major implication of the mixed results concerns the educational policy set out in both countries. In the case of East Asian economies, a sequential policy that assigns priority first to primary education, then to secondary education, and then to higher education was implemented.
In the context of the Caribbean, educational policy set out with considerable emphasis on secondary school, and higher education, did not bear fruit given the rise in the number of graduates who cannot find employment, and an economic environment that is not conducive to the efficient use of available skilled labor [9].
There has been a dearth of empirical literature in the Indian context analyzing the diverse pictures that relate the transformation from manufacturing to knowledge economy across Indian states. This is important in the Indian context due to the fact that the country has benefited due to positive contribution made by a select group of states and their education system.
In this paper, we aim to examine how governments’ investment in education affects growth and, therefore, development, in the select Indian States such as Kerala, Karnataka, Andhra Pradesh, Maharashtra, Tamil Nadu. Bihar, Arunachal Pradesh, Uttar Pradesh, West Bengal, Punjab, Orissa, Madhya Pradesh, Gujarat, Rajasthan, Haryana and Punjab.
Section 2 reviews pertinent literature that highlights the possible interactions between education and development. Section 3 presents the methodology and discuses the data used in the paper, while Section 4 focuses on the empirical results. Conclusions and policy implications are presented in the final section.
2. Possible Interactions between Education and Development
The literature offers several arguments predictive of an interactive effect between education and development. These arguments can be organised with reference to the level of development reached by a given economy. The first argument pertains to the efficiency of the educational system. Some authors imply that the efficiency of the educational system may depend on the number of human capital that is available in a given economy. Hence, the demand for education rises with the level attained. The second argument focuses on the financial constraints facing poor economies. It is argued that the poorer the states, the smaller the amount of expenditure on education, interestingly, the second argument points to the fact that a low level of human capital and growth are thus mutually reinforcing a situation where an economy gets stuck in a poverty trap or driven towards sustained growth [10].
It is useful to consider a single year i.e. 2003-2004 in order to explore the impact of education expenditure on select state characteristics. This way we are not in a position to interpret the time dimension of the transition. This transition we have documented in econometric part of the paper. Incidentally, our effort may be useful in exploring interesting insights that are so far not available in the existing literature in the Indian context.
Figures 1 and 2 shows the current structure of the select state economies with the help of broad primary and secondary sectors’ contribution to state domestic product in 2003-2004. Three clear pictures are discernible. One, the contribution of the tertiary sector to the respective state domestic product (SDP) appears to be dominating for the southern states. Two, as regards the northern states, the role of the primary sector is distinct. Gujarat on the other hand has taken a commanding position with the help of its secondary sector (Figure 3). This postulates the possibility of convergence and divergence across states.
Figures 4-6 reveal the beneficial effects of investment in human capital and institutions across states. Quite significantly, the new economy services contributed to NSDP in southern states and hence raising their per capita income. Interestingly West Bengal and Maharashtra have recently encroached in these areas. Basic literacy on the other hand has little role to play in raising the per capita income (Figure 7). This implies possibility of further investment in human capital. The cities are now hungrier for skilled populations. The poor in backward states are less likely at school despite the government regulation of education till age 16. Figure 8 depicts such facets.

Figure 1. Structure of the economy (tertiary contribution-wise).
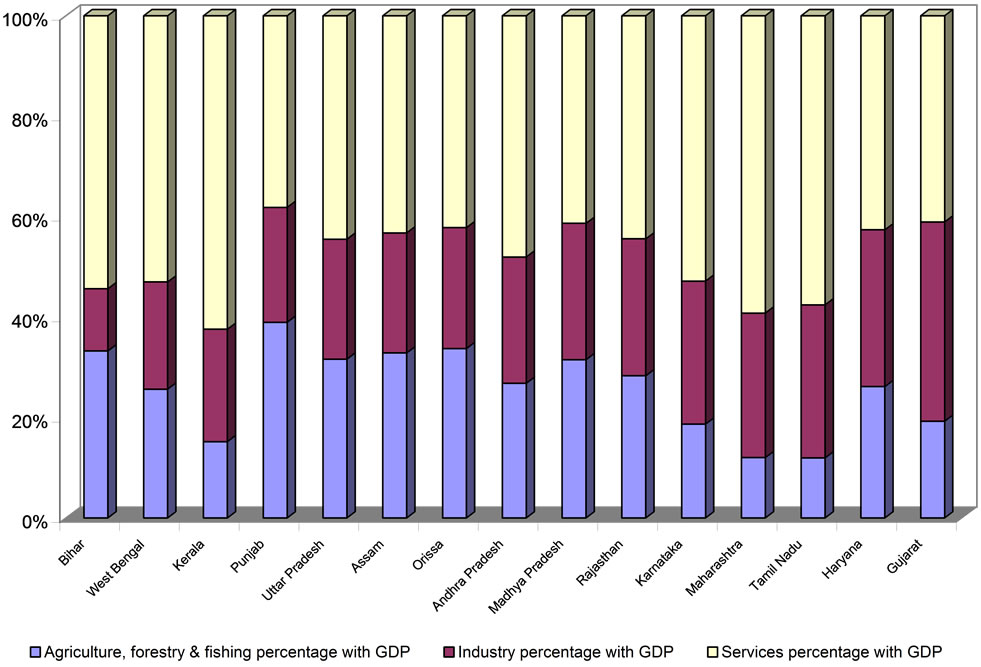
Figure 2. Structure of the economy (secondary contribution-wise).
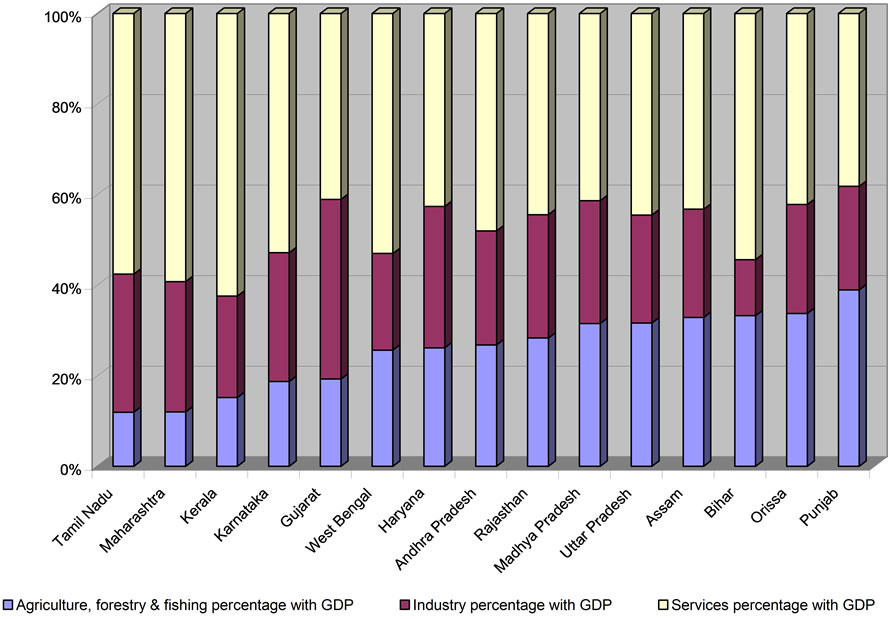
Figure 3. Structure of the economy (primary contribution-wise).

Figure 4. New services vs all services (size of bubble represents per capita GDP).
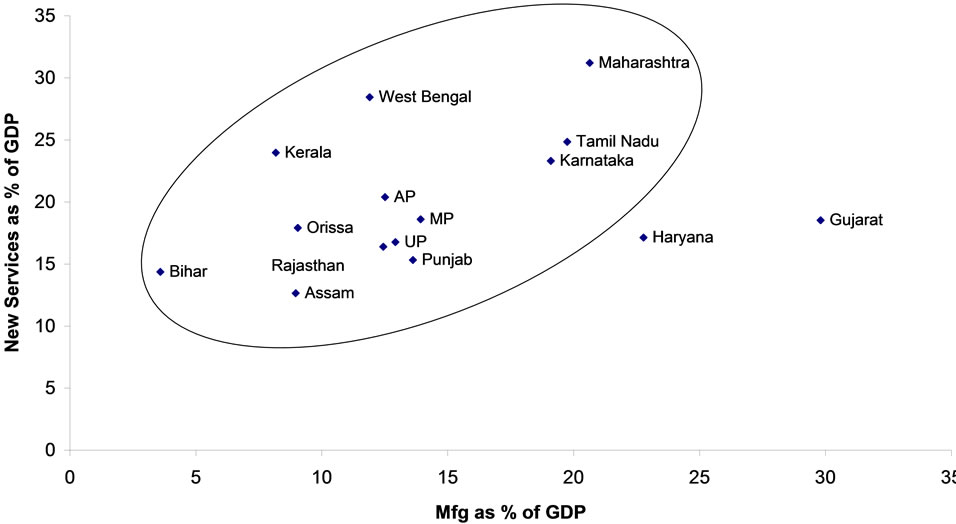
Figure 5. Mfg and new services.
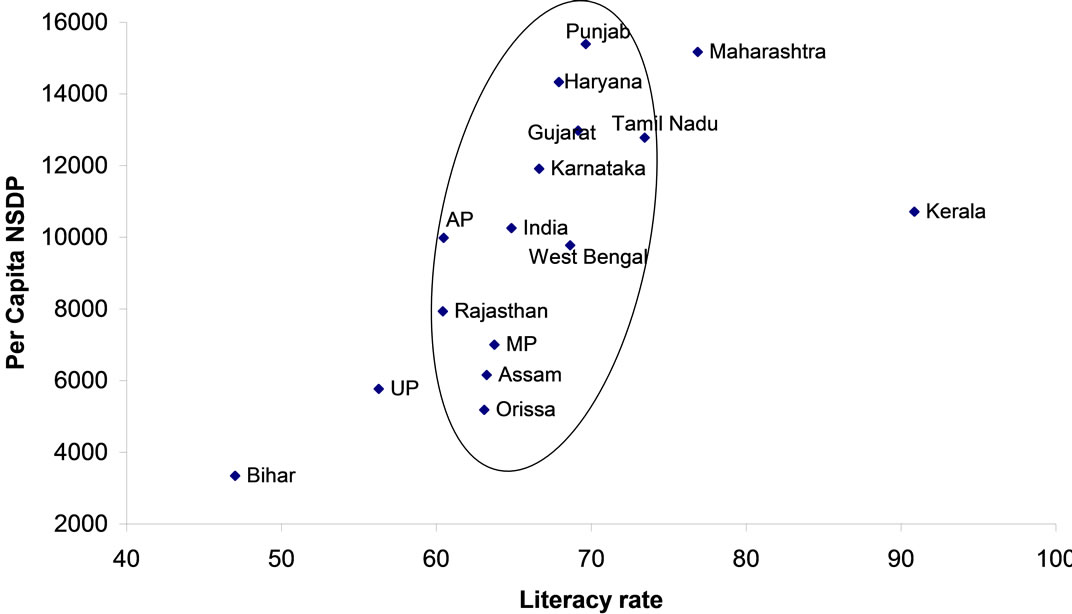
Figure 6. Per capita NSDP vs literacy rate.
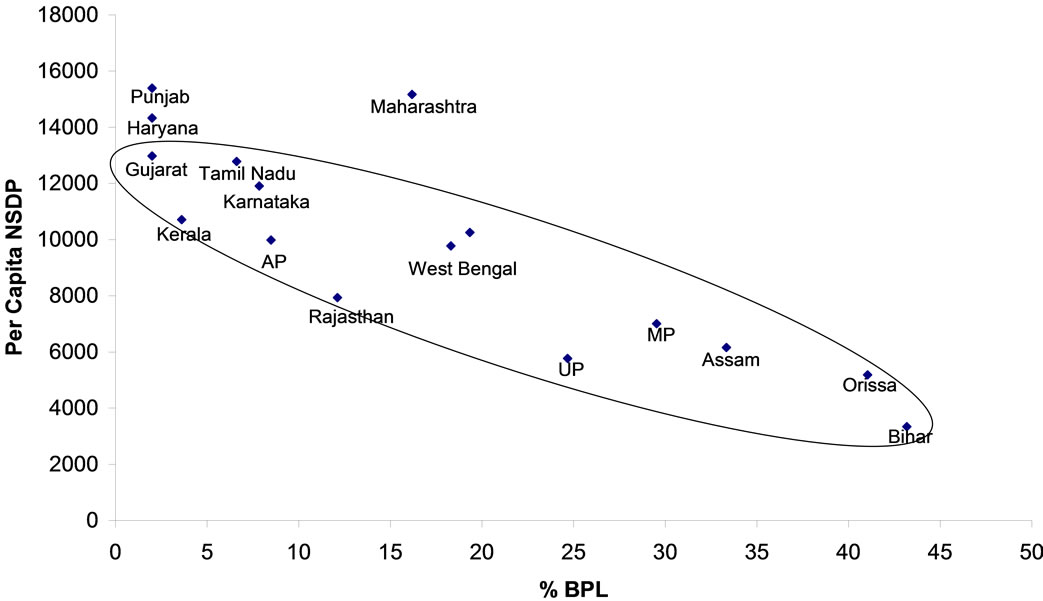
Figure 7. Per capita NSDP vs %BPL.
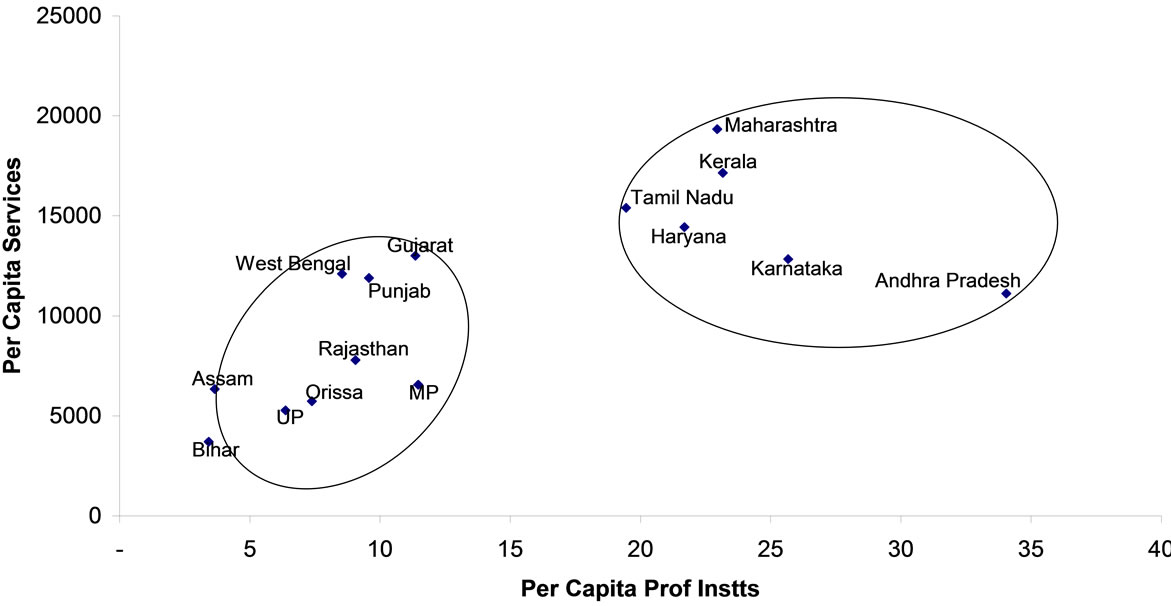
Figure 8. Services and educational institutions (per capita).
Interestingly, the rise of “knowledge industries” is a new aspect of India’s future development. This is the Indian edition of “leapfrog” where human capital in the high technology sector has acted as a powerful engine of growth. We find that the states (such as Gujarat, Maharashtra) which are relatively well-developed due to manufacturing, have human capital in the low technology sector, less intervention by the state sector and their geographical closeness to prosperous cities.
3. Econometric Methodology and Data
3.1. Econometric Methodology
Following Granger [11], the Granger-causality test has been developed to ascertain whether or not the inclusion of past values of a variable X do or do not help in the prediction of present values of another variable Y. If variable Y is better predicted by including past values of X than by not including them, then, X is said to Granger-cause Y. Similarly, if the past values of Y can be used to predict X more accurately than simply using the past values of X, then, Y is said to Granger-cause x. If the analysis reveals that X Granger-causes Y, and Y also Granger-causes X, there is bi-directional causality. In order to avoid spurious causality both of the variables under consideration need to be stationary. The existence of a long run equilibrium relationship between X and Y is referred to in the literature as co integration. According to Granger [12], standard tests for causality are valid only if X and Y are co-integrated. Therefore, a necessary precondition to causality testing is to check the co integrating properties of the variables under consideration.
Granger [13], Engle and Granger [14], and Engle and Yoo [15] have investigated the causal relationship between two variables when a common trend exits between them. Granger [11] and Engle and Granger[12] define a non-stationary time series Xt to be integrated of order d, that is, I (d), if Xt becomes stationary after being differenced d times. If d = 0, Xt is stationary in levels and no differencing is necessary. However, if d = 1, first differencing is required to convert Xt to a stationary time series. If two series Xt and Yt are both I (d), Engle and Granger op cit have shown that a linear combination, Zt= Yt – aXt, will also, in general, be I (d). To be co-integrated, both Xt and Yt must have the same order of integration (Engle and Granger op cit, and Granger op cit).
A two-step approach to testing for causality or cointegration between education (EDE) and development (GROWTH) is followed. The first step requires a determination of the time series properties of each variable based on unit root tests. This is accomplished by performing the augmented Dickey-Fuller (ADF) test [16]. The ADF test based on the regression equation with the inclusion of a constant and a trend of the form,
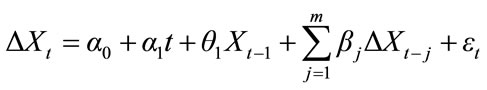
where DXt = Xt – Xt-1 and Xt is the variable under consideration; m is the number of lags in the dependent variable, which is chosen so as to .induce a white noise error term; and et is the stochastic error term. The stationarity of the variable is tested using the null hypothesis of |q1| = 1 against the alternative hypothesis of |q1| < 1. The critical values of ADF statistic as reported in Engle and Yoo op cit and McKinnon [17] can be used to test this hypothesis. Failure to reject the null hypothesis implies that the time series is non-stationary at a given significance level and therefore it requires taking first or higher differencing of the level data to establish stationarity. [11] prefers the ADF test due to the stability of its critical values as well as its power to different sampling experiments. The optimum lag length (m) in the ADF regression is selected using the minimum final prediction error (FPE) criterion developed by Akaike.
Having tested the stationarity of each time series, the second step is to search for co-integration between the two variables. This is accomplished by using the EngleGranger two step co-integration procedure. The EngleGranger two-stage procedure involves first testing both variables for unit roots and estimating two co-integration regressions (direct an reverse) between GROWTHt and EDEt using OLS. The second step involves testing the stationarity of the error processes of the two co integration regressions generated m the first step. According to Engle and Granger op cit, if GROWTHt and EDEt are co integrated, there must exist an error-correction representation that may take the following form:



where 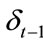 and
and  are the error-correction terms. The inclusion of error-correction terms in Equations (2) and (3) introduces an additional channel through which Granger causality could be detected. According to Granger op cit, the error-correction models produce better short run forecasts and provide the short run dynamics necessary to obtain long run equilibrium. However, in the absence of co integration, a vector auto-regression (VAR) in firstdifferences form can be constructed. In this case, the error-correction terms will be eliminated from Equations (2) and (3). If the series are co-integrated, then the errorcorrection models given in Equations (2) and (3) are valid and the coefficients g and h are expected to capture the adjustments of DGROWTHt and DEDEt towards long run equilibrium, while DGROWTHt-j and DEDEt-j are expected to capture the short run dynamics of the model.
are the error-correction terms. The inclusion of error-correction terms in Equations (2) and (3) introduces an additional channel through which Granger causality could be detected. According to Granger op cit, the error-correction models produce better short run forecasts and provide the short run dynamics necessary to obtain long run equilibrium. However, in the absence of co integration, a vector auto-regression (VAR) in firstdifferences form can be constructed. In this case, the error-correction terms will be eliminated from Equations (2) and (3). If the series are co-integrated, then the errorcorrection models given in Equations (2) and (3) are valid and the coefficients g and h are expected to capture the adjustments of DGROWTHt and DEDEt towards long run equilibrium, while DGROWTHt-j and DEDEt-j are expected to capture the short run dynamics of the model.
3.2. Data
We have used data provided by the Indiastat.com. This source is considered as the authentic source for Indian statistics collected from the various sources for information and statistics on India. Since this paper addresses the education development nexus across select states of India, the empirical methodology focuses on testing the causal relationship between expenditure on education per head (the proxy for education) and State Domestic Product per capita (the proxy for development) in all three over the period 1980/81-2008/09.
4. Empirical Results
Table 1 presents the results of unit root tests obtained using the augmented Dickey-Fuller test. The evidence does overwhelmingly support the presence of unit roots (in terms of levels) in all the series for all countries. This is confirmed by the fact that the null hypothesis that the series (in levels) are non-stationary is rejected in every instance, under different assumptions. Clearly, for all cases, both series appear to be I(1) since the null hypothesis of a unit root in the first difference is rejected in favor of the alternative hypothesis that the series, in first difference, are stationary.
Given these results, the next step involves applying Engle-Granger two-step co-integration procedure to determine whether GROWTH and EDE are co-integrated for select states. The optimum lag lengths are determined using the Akaike final prediction error (FPE) criterion. The results of the ADF test applied to the residuals of the co integration equations are presented in Table 2. Together with the results, the values of the slope coefficients and Co integration Regression Durbin Watson (CROW) statistics are also presented1.
Based on the ADF test, the results presented in Table 2 suggest evidence of co-integration between GROWTH and EDE in all States. This finding is confirmed by the CRDW statistic. These results necessitate a long run relationship between education and development in all of the countries.
Furthermore, since the two variables are co-integrated in three select states, a Vector Error Correction Model (VECM) is estimated to determine the nature of causality between GROWTH and EDE.
The VECM is represented by Equations (2) and (3). The error-correction terms dt-j and ρt-j represent the long run impact of one variable on the other, while the changes of the lagged independent variable describe the short run causal impact.
The empirical results of the estimated VECM are presented in Table 3. This indicates a mixed set of outcomes. In both the short and long run, the evidence suggests that education expenditure is driving growth and development in Kerala and Karnataka. However, development causes expenditure on education in Rajasthan. These results provide some evidence of bi-directional causality in the select states.
5. Conclusion and Policy Implications
This paper applied co-integration and vector error-correction models to analyse the causal relationship between
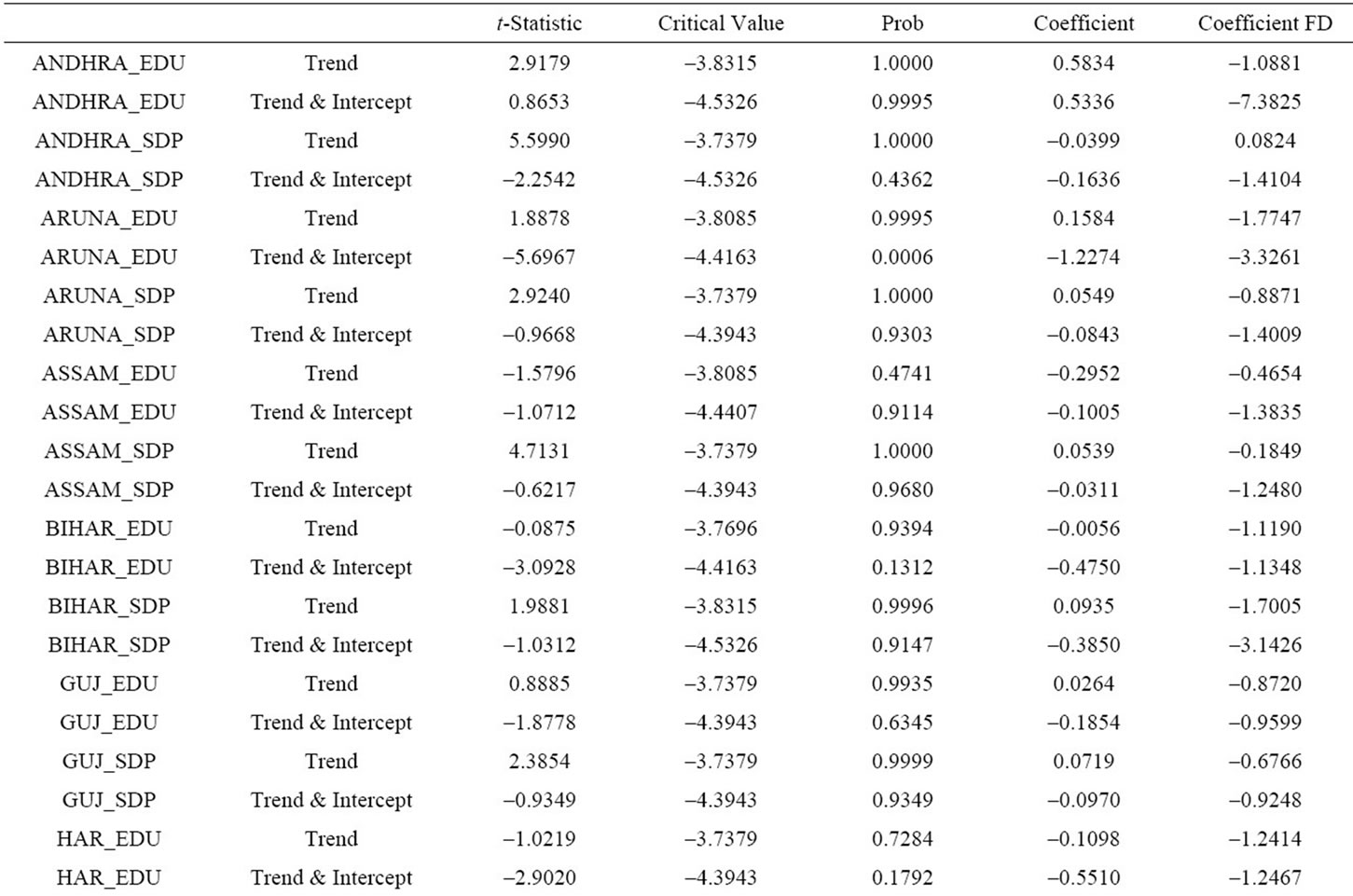
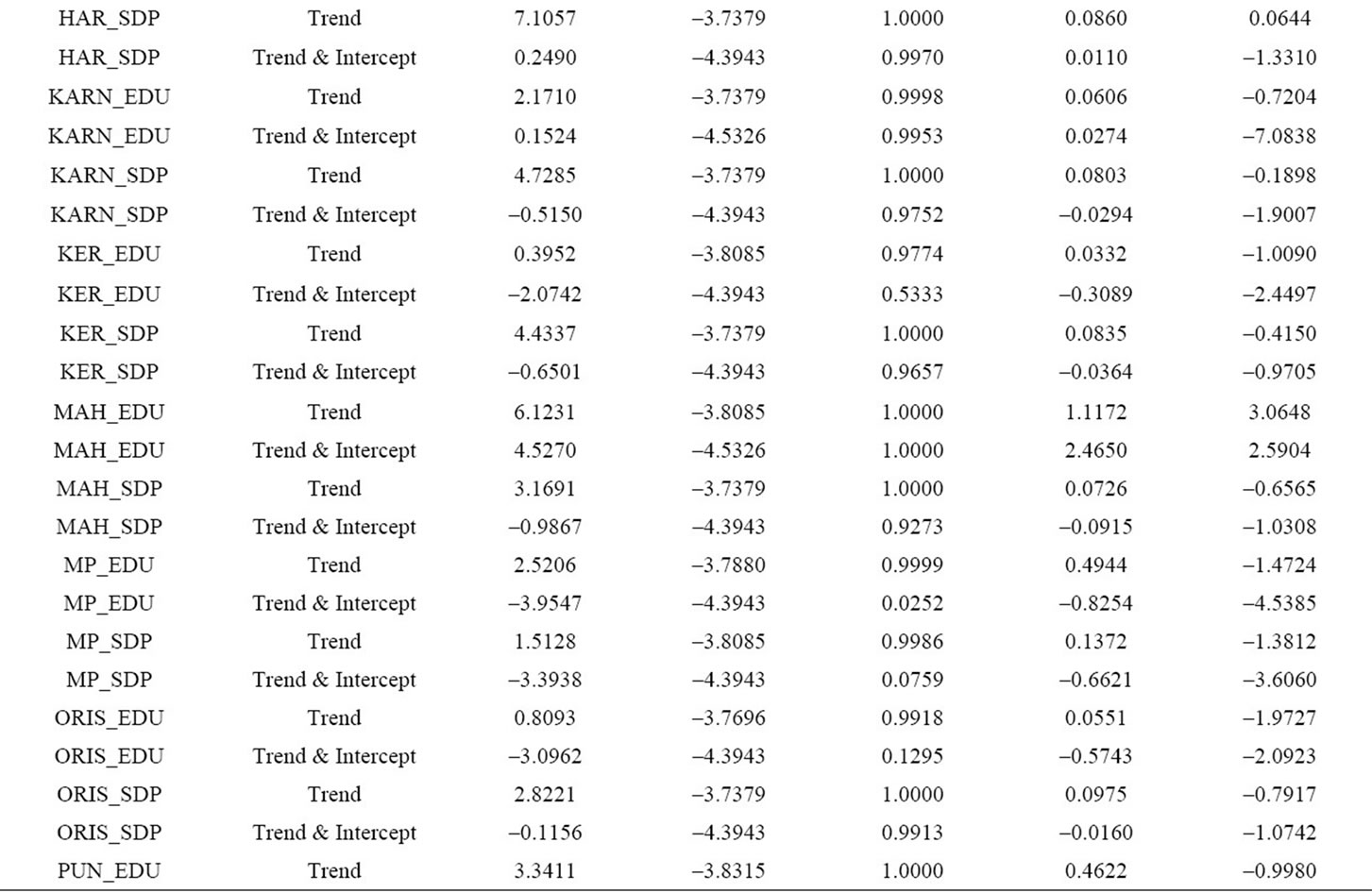
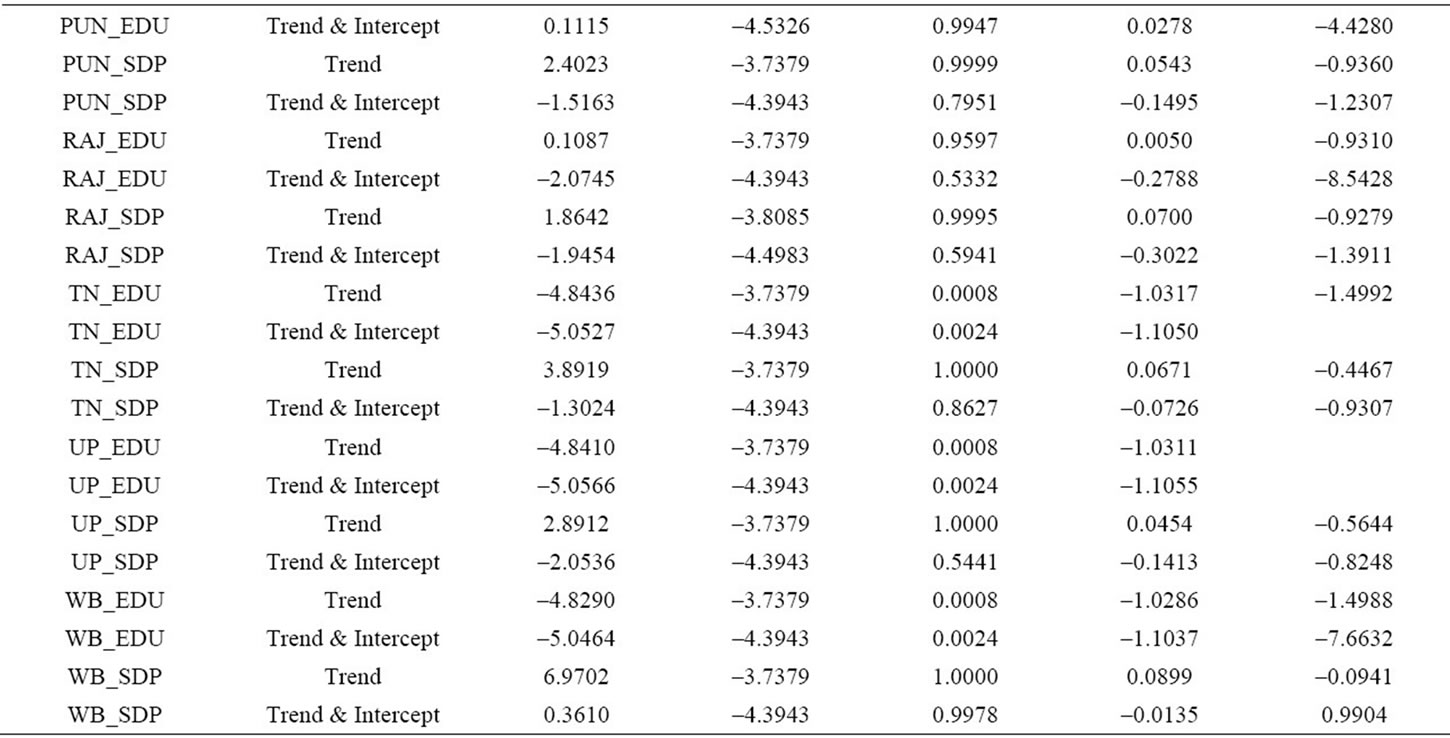
Table 1. Augmentad dicky-fuller unit root test.

Table 2. Results of Engle-Granger cointegration test.

Table 3. Results of vector error correction model (VECM).
education expenditurte and development/growth in select Indian States using data from 1980/81 to 2008/9. Expenditure on education per capita was used as the proxy for education, while state domestic product per capita was the proxy for development. The empirical results show that in both the short and long run, the evidence suggests that per capita education expenditure is driving growth and thus development in two states However, growth and development causes per capita education expenditures in Rajasthan in the short run.. These results provide some evidence of bi-directional causality in the short run. This finding is rather interesting because it contradicts most of the theoretical expectations.
Nonetheless, the empirical results have four policy implications. First, the empirical results seem to be suggesting that states with higher per capita education expenditures are now reaping the benefit revealed in their growth. This finding seems interesting for the other states of India. Second, improving the level of education appears to have failed to stimulate development in some states, a finding that is possibly reflecting the belief that the educational systems in the some states have not been adequately developed and tailored towards the implementation of curriculums along the lines of technical and scientific subjects needed for industrial growth and development [18]. Third, to a large extent, these states either failed to provide conducive environments for boosting production, or promoted atmospheres for production that fell far behind those in other states that are considered an ideal destination of foreign investment. Fourth, the current level of unemployment rates in other states suggest that improvements in the quality and level of education has not been focused on allowing labour to take advantage of the opportunities offered by technological progress.
REFERENCES
- E. Denison, “Why Growth Rates Differ?” The Brookings Institution, Washington, DC, 1967.
- J.-C. Berthelemy and A. Varoudakis, “Policies for Economic Take-Off,” Policy, Brief, Paris, 1996.
- J. Benhabib and M. M. Spiegel, “The Role of Human Capital in Economic development: Evidence from Aggregate Cross-Country Data,” Journal of Monetary Economics, Vol. 34, No. 2, 1994, pp. 143-173. doi:10.1016/0304-3932(94)90047-7
- N. Birdsall, G. Carol and R. H. Sabot, “Beyond Tradeoffs: Market Reforms and Equitable Growth in Latin America,” Inter-American Development Bank and Brookings Institution Press, Washington DC, 1998.
- J. E. Stiglitz, “Development Thinking at the MillenniumKey Note Address. Annual World Conference on Development Economics,” World Bank, Washington DC, 2000.
- R. E. Lucas, “On the Mechanics of Economic Development,” Journal of Monetary Economics, Vol. 22, No. 1, 1988, pp. 3-42. doi:10.1016/0304-3932(88)90168-7
- J. E. Stiglitz, “Economic Organization, Information and Development,” In: C. Hollis and T. N. Srinivasan, Eds., Handbook of Development Economics, Elsevier Science Publishers, New York, 1988, pp. 93-160. doi:10.1016/S1573-4471(88)01008-3
- L. Pritchett, “Where Has All the Education Gone?” The World Bank Economic Review, Vol. 15, No. 3, 2001, pp. 367-391. doi:10.1093/wber/15.3.367
- B. Francis and S. Iyare, “Education and Development in the Caribbean: A Co-Integration and Causality Approach,” Economics Bulletin, Vol. 15, No. 2, 2005, pp. 1-13.
- J.-C. Berthelemy, A. Seck and A. Vourc’h, “Growth in Senegal: A Lost opportunity?” Long-Term Growth Series, Development Centre, OECD, Paris, 1996.
- C. W. J. Granger, “Investigating Causal Relations by Econometric and Cross-Spectral Method,” Econometrica, Vol. 37, No. 3, 1969, pp. 424-438. doi:10.2307/1912791
- C. W. J. Granger, “Some Recent Developments in a Concept of Causality,” Journal of Econometrics, Vol. 39, No. 1-2, 1988, pp. 199-211. doi:10.1016/0304-4076(88)90045-0
- C. W. J. Granger, “Development in the Study of Cointegrated Economic Variables,” Oxford Bulletin of Economics and Statistics, Vol. 48, 1986, pp. 213-228.
- R. F. Engle and C. W. J. Granger, “Cointegration and ErrorCorrection: Representation, Estimation and Testing,” Econometrica, Vol. 55, No. 2, 1987, pp. 251-276. doi:10.2307/1913236
- R. F. Engle and B. S. Yoo, “Forecasting and Testing in Cointegrated Systems,” Journal of Econometrics, Vol. 35, No. 1, 1987, pp. 143-159. doi:10.1016/0304-4076(87)90085-6
- D. Dickey and W. A. Fuller, “Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root,” Econometrica, Vol. 49, No. 4, 1981, pp. 1057-1072. doi:10.2307/1912517
- J. G. MacKinnon, “Critical Values for Cointegration Tests,” In: R. F. Engle and C. W. J. Granger, Eds., Long-Run Economic Relationships: Readings in Cointegration, Oxford University Press, Oxford, 1991, pp. 267-276.
- A. Banik and S. O. Iyare, “Globalization, Model for Competitiveness and Human Skill Development in the Caribbean,” Proceedings of the 20th Annual Conference: Global Awareness Society International, Vol. 12, 2003, pp. 179-191.
NOTES
1We have restricted our analysis based on three states such as Rajasthan, Kerala and Karnataka.

