Journal of Biophysical Chemistry
Vol. 3 No. 2 (2012) , Article ID: 19450 , 5 pages DOI:10.4236/jbpc.2012.32022
A novel genetic approach for optimized biological sequence alignment
![]()
1Department of Computational Biology, Saha Institute of Nuclear Physics, Kolkata, India
2Department of Bioinformatics, DOEACC Society, Kolkata, India; *Corresponding Author: bchowdhury2410@gmail.com
Received 23 October 2011; revised 20 February 2012; accepted 30 March 2012
Keywords: Sequence Alignment; DNA; Protein; Genetic Algorithm; Computational Biology
ABSTRACT
Biological sequence alignment is one of the most important problems in computational biology. The objective of the alignment process is to maximize the alignment score between two given sequences of varying or equal length. The alignment score of two sequences is calculated based on matches, mismatches and gaps in the alignment. We have proposed a new genetic approach for finding optimized match between two DNA or protein sequences. The process is compared with two well known relevant sequence alignment techniques.
1. INTRODUCTION
In the field of Bioinformatics, sequence alignment is a crucial technique for obtaining matching pattern between a known and an unknown sequence. The pattern matching is basically a way of arranging DNA, RNA or protein sequences to detect and quantify the similarities between two sequences. Two or multiple aligned sequences of nucleotide or amino acid residues represent the functional, structural or evolutionary relationship among the sequences and share a common ancestor. By the process of evolution, living things diverge from common ancestors through changes in their DNA [1]. DNA functions as a medium to transmit information from one generation to another [2]. During the process of evolution, sequence gradually accumulate mutations and diverge over time, but some residues perform functional and structural role tend to be preserved by natural selection [3].
The sequence alignment is basically divided into two categories, namely, the global and the local alignment. In global alignment, the alignment is done over the entire length of two almost similar sequences. In local alignment, it finds locally highest similar regions of two sequences.
It is preferred for divergent sequences for searching common conserved pattern. If two sequences share of at least 30% or more identity, they are safely considered as homologous sequences i.e., they came from the common evolutionary origin.
Various pairwise sequence alignment methods are used to find the best local or global alignments of two sequences. Dynamic programming is a method that determines optimal alignment by matching two sequences by constructing 2D matrix [3]. The best scoring alignment is commonly found by the Dynamic Programming (DP) algorithms, such as Smith-Waterman algorithm [4] for local alignment and Needleman-Wunsch algorithm [5] for global alignment. Dynamic programming solves pairwise sequence alignment optimally but it suffers from heavy burden of high dimensional problems. Particularly, when two or more optimal paths are available and that need to trace backward, the complexity of the back tracing grows exponentially [6].
Many researchers have used Genetic Algorithm (GA) in sequence alignment problem for having optimal alignment by maximizing the similarities between the residues that compose them. Taneda has developed pairwise RNA sequence alignment technique based on multi-objective genetic algorithm [7]. A robust alignment approach GARD (Genetic Algorithm Recombination Detection) has been developed for screening multiple sequence alignments for evidence of phylogenetically relatedness [8]. Another two methods called RAGA (RNA sequence alignment by GA) and PRAGA (parallel RAGA) also use genetic approach for optimized alignments. They are applied for the alignment between two homologous RNA sequences and the secondary structure of one RNA is known. PRAGA is allowed to optimize an objective function that describes the quality of a RNA pairwise alignment, taking into account both primary and secondary structure. In PRAGA several genetic algorithms run in parallel and exchange individual solutions [9].
In this article we have proposed a genetic algorithm based sequence alignment technique which is efficiently used for finding the similarity between two DNA or protein sequences without introducing gap. The technique is named as Sequence Alignment with Genetic Algorithm (SAGA). The novelty of the alignment process is the efficiency in terms of computation time and simple to use. The process can also be extended for multi-sequence alignment. Since in the natural evolutionary processes insertion and deletion are relatively rare in comparison of substitutions [3], we have not introduced gap to avoid complication. We have compared our method with relevant pairwise sequence matching techniques.
The rest of the paper is organized as follows. Section 2 provides general description of the conventional genetic algorithm. The proposed method SAGA is discussed with examples in Section 3. Experimental results are provided in Section 4. Section 5 concludes the article with discussion.
2. GENETIC ALGORITHM FOR OPTIMIZATION
We have used GA as an optimization tool to find optimized sequence alignment. The process of sequence alignment is discussed in the following section. We now describe the genetic method algorithmically.
Step 1. Generate randomly the initial population of N individuals and let generation g = 1. Initialize pc as the one point crossover probability and pm as the mutation probability.
Step 2. Evaluate the fitness score for each individual xi, 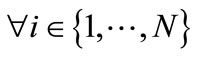 of the population based on the objective function, f (xi).
of the population based on the objective function, f (xi).
Step 3. Select a pair of individuals xα and xβ at random, depending on their fitness values (using roulette wheel method) from the population of N individuals.
Step 4. Conduct crossover between the chosen individuals xα and xβ with pc and mutate each of their bits with probability pm. Each pair of parents (xα, xβ) thus creates a pair of new individuals called offsprings (x′α, x′β) to generate a pool of individuals,  ,
,  as a population of next generation.
as a population of next generation.
Step 5. Terminate the process if the stopping criterion (g > Gmax) is satisfied. Otherwise, g = g + 1 and go to Step 2.
3. SEQUENCE ALIGNMENT WITH GENETIC ALGORITHM (SAGA)
In sequence analysis the search for similarity is the primary requirement in Bioinformatics and has been studied for many years [10]. When given a sequence (DNA/RNA/ protein), called query sequence, one usually performs a similarity search within databases that consists of all available genomes and known proteins. Eventually the search yields many sequences with varying degree of similarities. It is then up to the user to identify those that may well turn out to be homologous. However, there is a possibility to incorporate false positive. Our objective is to reduce it as much as possible.
In pairwise sequence alignment, the alignment is performed with the GA to specifically address the issue of optimized matching. In case of optimization problems, GAs provide the advantages to perform global search in a space. After several generations or iterations, GA has the ability to converge to the best solution which is either a global or a near-global solution. If the parameters are chosen properly, GAs are capable of finding the best solution. In our pairwise sequence alignment problem, we consider one sequence as a database sequence denoted by D and other one as a query sequence denoted by Q. D remains unchanged but Q is dependent on the chromosome pattern in the population of the GA. We generate a population of probable solutions of the input query sequence by a binary string of {0, 1} of length equal to the given query sequence. Each binary string is called a chromosome and the 1’s in the chromosome represent the presence of the residues in the corresponding positions of Q. Similarly, the 0’s indicate the absence of the residues in Q.
In the proposed method (SAGA) we have used all three operators of the conventional GA. In each iteration/generation the SAGA generally advances towards a better solution by creating a better population. The crossover is performed between two randomly selected fittest chromosomes. The fitness score is evaluated using the following fitness function F.
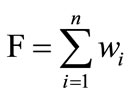 (1)
(1)
where
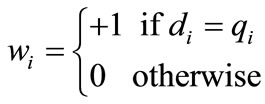
Here, n is the total number of residues to be aligned, wi is the score of the i-th position of D and Q. For straight alignment wi = +1 if di = qi but for shift alignment wi = +1 if di = qj where i ≠ j. di represents the residue in the i-th position of D and qi is the residue in the i-th place of Q.
The fitness score determines the similarity or identity level between two sequences D and Q. We will now describe how the fitness score is calculated for pairwise alignment between two sequences D and Q. It is evaluated in two ways. The scoring procedure for straight alignment is different from the alignment with left or right shift.
Let us consider the following two nucleotide sequences of D and Q.
D = A T G C T T A G T C
Q = A C G C A T A G A C
According to Eq.1 in case of straight alignment the fitness score in an intermediate generation of GA is 4 if we consider the following binary string in a population as a probable solution of query sequence Qp.
Qp = 0 1 1 0 1 0 1 1 0 1
The equivalent Qp by replacing 1 with the corresponding residue of Q is as follows (’_’ denotes the presence of 0 in Qp).
Qp = _C G _A _A G _C
The straight alignment technique is illustrated as below.
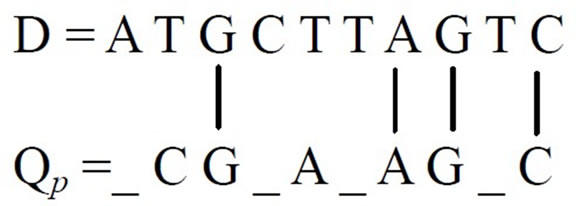
Let us now consider another two equal length sequences D and Q to demonstrate the sequence alignment by shifting.
D = A T G C T T A G T C
Q = A C T T A G T A A C
We can get 2 as the best straight alignment score. However, if we align the above two sequences by shifting Q right, the best score will be 6 because of the following match.

For the sake of demonstration of left shift alignment we consider the following query sequence.
Q = A T G C T T A G T A
Then the fitness score will be 7 for the match given below.
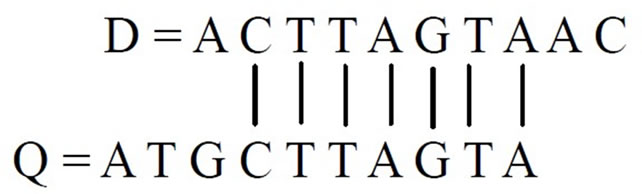
For evaluation of fitness score we perform all three alignment (straight, shift right and left) techniques. However, the selection of position to start alignment depends on the randomly chosen number. Since minimum 30% matching between two sequences is expected, we have generated random numbers between 1% and 70% of the length of any sequence. If a sequence length is 100, we shall identify a position between 1st and 70th residues of D or Q depending on the alignment type. The length of D is considered for straight and right shift alignments. However, the length of D is considered for left shift alignment if it is smaller or equal to Q, else the length of Q is chosen. The three types of alignment techniques are continued based on the average length of D and Q. In our problem it is 30% of the average length i.e., if the average length is 200, the alignment techniques will be continued for 60 times. We have achieved good results in the experiment with the figure 30%. Now the best matching score is extracted from 60 results given by three alignment techniques.
In protein sequences alignment, certain amino acids with similar physicochemical properties are observed to be substituted more easily with each other in homologous sequences thus they are assigned a positive score [3]. We have used BLOSUM62 scoring matrix into our fitness score and optimize the alignment by considering the number of similar and identical residues in a chromosome.
4. EXPERIMENTAL RESULTS
4.1. Setup Parameters
In the experiment we have chosen the following parameters. The population size N is 40, the crossover probability pc = [0.6-0.8], the mutation probability pm = [0.0006-0.0009]. The maximum number of generations Gmax = 1000 to find the optimal sequence alignment score.
4.2. Results of Sequence Alignment
We have implemented the proposed method SAGA using C programming language on a machine with the windows XP operating system and the configuration of Intel Dual Core processor with 1.60 GHz CPU speed, 1GB RAM. The performance of SAGA is compared with the performance of Basic Local Alignment Search Tool (BLAST) (http://blast.ncbi.nlm.nih.gov/Blast.cgi) and Dynamic Programming (DP) (http://www.ebi.ac.uk/Tools/emboss/align/).
BLAST is a sequence similarity search program that can be used as a web interface. BLAST is a heuristic method that finds short matches between two sequences and attempts to start alignment from these. Here, the sequence is split into smaller sequences and the presence of these subsequences in the database sequence is determined. The disadvantage of the BLAST is that it encounters the false positive and also does not guarantee to find optimal alignment [3].
DP solves the pairwise sequence alignment problem optimally but suffers from the burden of high dimensional problems. However, DP cannot be extended to multiple sequence alignment without prohibitive costs [6]. Searching a large database using DP is very slow and impractical in a limited computational source [3].
We have tabulated the results of the proposed pairwise sequence matching in Tables 1 and 2. It is noticed that the performance of SAGA is better or equivalent but never worse than any of the other methods. We have extended our experiment for matching a query with multiple sequences in a database. The DNA database consists of 50 sequences of RNA polymerase gene of Mycobacterium tuberculosis strains and protein database consists of 25 sequences of 60S Ribosomal subunit protein component. Tables 3 and 4 demonstrate the matching result. In such cases we have calculated the percentage of identity or similarity (for protein) I(S) as follows [3].
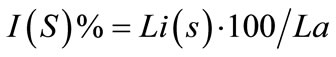 (2)
(2)
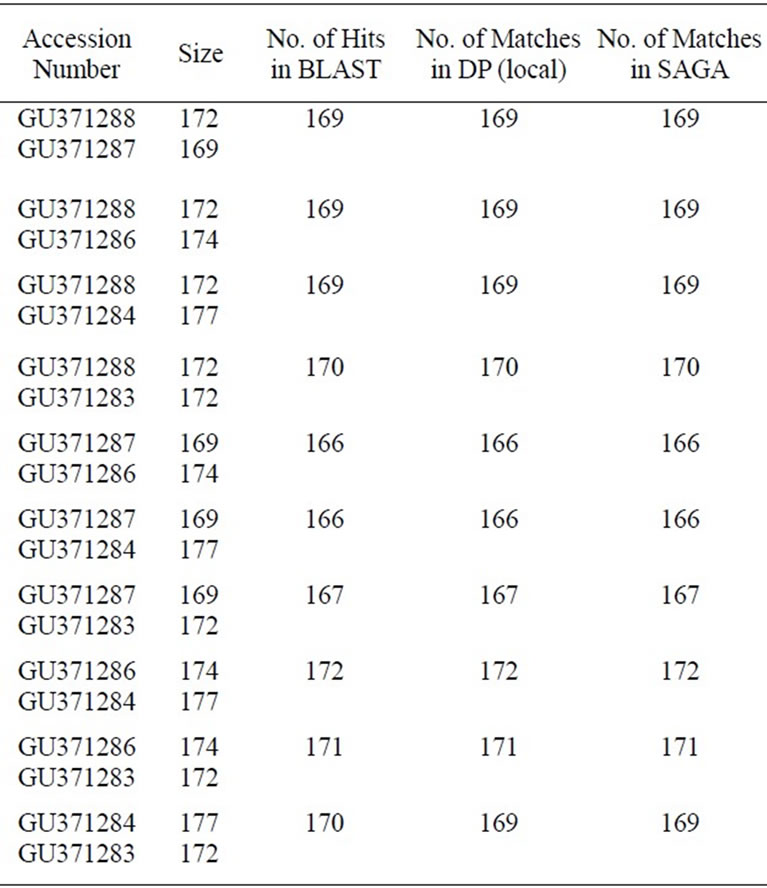
Table 1. Comparative alignment results of two nucleotide sequences for the SAGA, BLAST and Dynamic Programming (DP). Source of the given sequences is NCBI (http://www.ncbi.nlm.nih.gov).
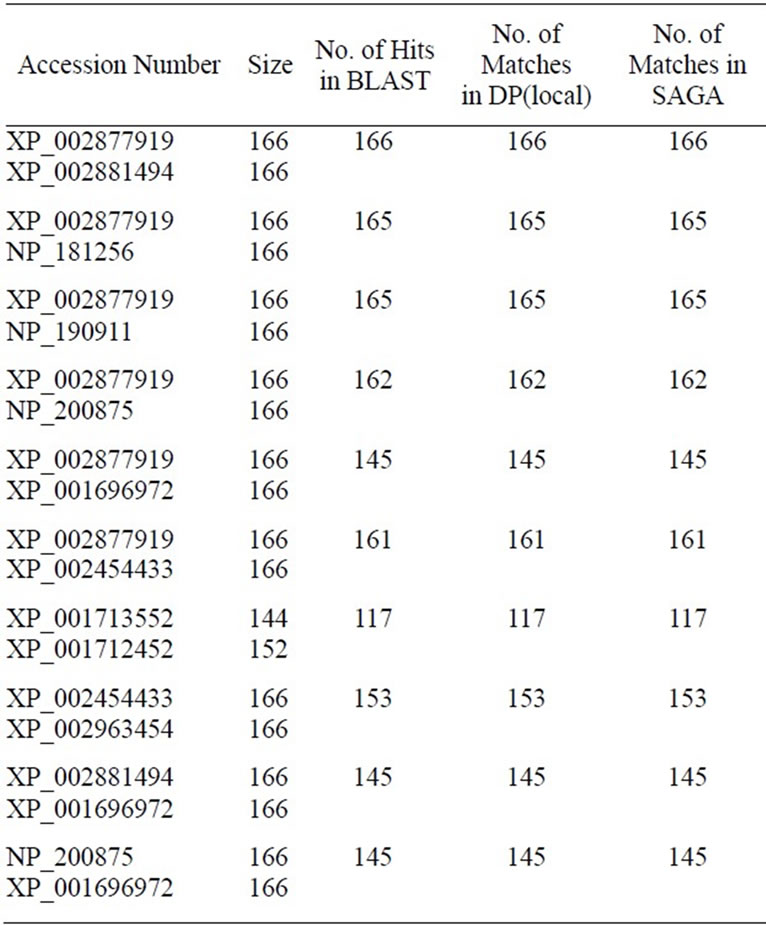
Table 2. Comparative alignment results of two amino acid sequences of 60S Ribosomal protein for the SAGA, BLAST and Dynamic Programming (DP). Source of the given sequences is NCBI (http://www.ncbi.nlm.nih.gov/proteinclusters).
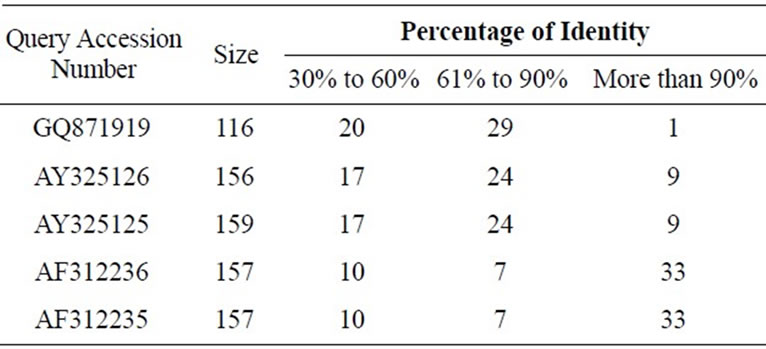
Table 3. Sequence alignment between the given query sequences and the constructed database of 50 DNA sequences.
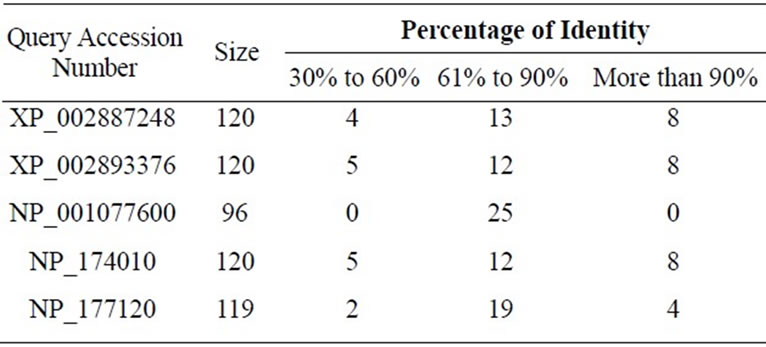
Table 4. Sequence alignment between the given query sequences and the constructed database of 25 protein sequences.
where Li(s) is the number of aligned residues and La is the length of the shorter of the two sequences.
5. CONCLUSION AND DISCUSSION
The method SAGA is simple and efficient for finding the similarities between two or multiple sequences. The users also do not require to set too many input parameters. Here we have shown the alignment score of one query sequence with a database consisting of 50 different nucleotide sequences and also with a database containing 25 different protein sequences. The Genetic approach can also be extended for sequence alignment of multiple query sequences. Moreover, the SAGA consists of simple data structure, does not require back-tracing, any complex operators or any matrix formation.
REFERENCES
- Carroll, S.B., Grenier, J.K. and Weatherbee, S.D. (2001) From DNA to diversity: Molecular genetics and the evolutionary of animal designs. Blackwell Science, Malden
- Graur, D. and Li, W.H., (2000) Fundamental of Molecular Evolution. 2nd Edition, Sinauer Associates, Sunderland.
- Xiong, J. (2006) Essential Bioinformatics. Cambridge University Press, Cambridge.
- Smith, T.F. and Waterman, M.S. (1981) Identification of common molecular subsequences. Journal of Molecular Biology, 147, 195-197. doi:10.1016/0022-2836(81)90087-5
- Needleman, S.B. and Wunsch, C.D. (1970) A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology, 48, 443-453. doi:10.1016/0022-2836(70)90057-4
- Othman, M.B., Cherif, A.H. and Azim, G.A. (2008) Genetic algorithms and scalar product for pairwise sequence alignment. International Journal of Computers, 2, pp. 134-147.
- Taneda, A., (2010) Multi-objective pairwise RNA sequence alignment. Oxford Journals, Bioinformatics, 26, 2383-2390. doi:10.1093/bioinformatics/btq439
- Pond, S.L.K., Posada, D., Gravenor, M.B., Woelk, C.H. and Frost, S.D.W., (2006) GARD: A genetic algorithm for recombination detection. Oxford Journals, Bioinformatics, 22, 3096-3098. doi:10.1093/bioinformatics/btl474
- Notredame, C., O’Brien E.A. and Higgins, D.G. (1997) RAGA: RNA sequence alignment by genetic algorithm. Nucleic Acids Research, 25, 4570-4580. doi:10.1093/nar/25.22.4570
- Batzoglou, S. (2005) The many faces of sequence alignment. Briefings in Bioinformatics, 6, 6-22. doi:10.1093/bib/6.1.6

