Psychology
Vol.07 No.03(2016), Article ID:64958,6 pages
10.4236/psych.2016.73039
How Do Orders Impact Structural Equation Model? Empirical Evidence from Patient Satisfaction
Zhihan Liu
School of Public Administration, Central South University, Changsha, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 January 2016; accepted 21 March 2016; published 24 March 2016
ABSTRACT
There haven’t been enough empirical evidences of orders’ impact on structural equation model and satisfaction index results. This study is conducted to figure out the problem by making a com- parison between the first-order and high-order structural equation models building with the same sample from healthcare. As expected, results showed that the path coefficients and goodness-of-fit indices of high-order structural equation model were basically the same with its counterpart, suggesting the structural equation model’s orders would not affect the index and play the role of simplifying the model. Besides, compared with the conventional first-order structural equation model in patient satisfaction, the high-order model tended to be an improvement, for providing the probability of analyzing intermediate latent variables and forming the theoretical basis of multi-level structural equation modeling study.
Keywords:
Structural Equation Model, Order, Patient Satisfaction, Index, Evaluation

1. Introduction
Patient satisfaction is the primary objective of the healthcare provider innately. It gives us useful data about the structure, process and outcome of healthcare, and satisfied and dissatisfied patients have various behavioral intentions such as different level of compliancy (Kazemi et al., 2013) . There are common defects in the traditional multi-factor analysis methods in patient satisfaction evaluation resulted in the limitation of these methods, for instance, the lack of consideration for measuring error of psychological variables and the relatively simple setting of relationship among them, and so on. The traditional multivariate techniques, including multiple regression, path analysis, and factor analysis, could not take into account the interaction effects among the posited variables (both dependent and independent) (Cheng, 2001) . The Structural Equation Modeling (SEM) method put forward by Jöreskog (1970) showed great improvement over other multivariate techniques as it can not only calculate the satisfaction, but also help to build the satisfaction index model (Bollen, 1989) .
However, it was noteworthy that although the second-order (or high-order) construct was prevalent for current SEM analyses of patient satisfaction (Amin & Zahora Nasharuddin, 2013; Andaleeb & Kara, 2014; Kazemi et al., 2013; Qin, 2014) , most previous patient satisfaction models based on Chinese samples were still limited to the first-order ones (Lei & Jolibert, 2012) and they rarely mentioned the impact of models’ orders on the result. As Ping Jr. said, little is known about interactions involving second-order latent variables (LVs) (i.e., LVs that have other LVs as “indicators”) in structural equation models (Ping Jr., 2015) . In fact, a lot of latent variables were indirectly related to observable variables through intermediary variables in patient satisfaction, which needed to be evaluated by establishing high-order structural equation model. But there haven’t been enough reports about the application of high-order models in patient satisfaction in China. Moreover, empirical evidence of the effects of structural equation model’s orders on patient satisfaction index results was even less (Liu, 2015) . To figure out the problem, this study was designed to make an empirical analysis by building first-order and high-order structural equation models respectively and making a comparison between them.
2. Method
2.1. Theory of SEM
SEM is a type of Confirmatory Factor Analysis (CFA) technology. Its essence is a cause-and-effect model, containing two sub-models: Measurement Model and Structural Model. The measurement model is the external model identifying and evaluating relationships between observable variables and latent variables by the CFA approach, with the form of following matrix of regression equations:
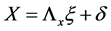 (1)
(1)
 . (2)
. (2)
Among them, X is observable value of the exogenous latent variable ξ, with the measurement error δ and the factor loading matrix Λx; Y is observable value of the endogenous latent variable η, with the measurement error ε and the factor loading matrix Λy.
The structural model is always referred to as the internal model that reflects the causal relationship between latent variables. It could be expressed as the following matrix of regression equation:
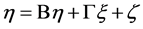 (3)
(3)
ζ is residual error of the endogenous latent variable η. The regression coefficient matrix B represents the association between endogenous latent variables. The regression coefficient matrix Γ reflects the impact of the exogenous latent variable ξ on η.
2.2. Participants & Procedures
This study selected a regional representative and influential (with the position as a regional medical center) hospital in each part of five regions (north, south, east, west and central) in China1 and carried out intercept surveys at odd intervals from 2011 to 2012. A total of 501 effective questionnaires (the effective rate was 98.2%) was finally received, complied with the sample size requirements suggested by Breckler (1990) . The socio-demo- graphic characteristics of all samples were as shown in Table 1.
2.3. Proposed Structure of Model
The Patient Satisfaction Index (PSI) model that established by this study involved 6 latent variables: “hospital
Table 1. Descriptive statistic results of the sample (n = 501).
identity” (Q1), “quality expectation” (Q2), “quality perception” (Q3), “value perception” (Q4), “patient satisfaction” (Q5) and “patient loyalty” (Q6). Q1 was related to 3 observable variables: “word of mouth” (Q11), “specialized characteristics” (Q12) and “therapeutic advantage” (Q13); Q2 was related to “technology” (Q21), “management” (Q22) and “general expectations” (Q23); Q4 was evaluated by “reasonable charge” (Q41); Q5 consisted of “comparison with other hospitals” (Q51) and “general satisfaction” (Q52); Q6 was related to 2 observable variables: “wish to visit again” (Q61) and “wish to recommend to kith and kin” (Q62). Q3 was explained by 13 observable variables: “waiting room order” (Q311), “symbols of facilities” (Q312), “logistics cleaning” (Q313), “registration service” (Q321), “leading examining and consulting” (Q322), “charging service” (Q323), “pharmacy” (Q324), “waiting time” (Q331), “healthcare workers’ attitude” (Q332), “guiding medication” (Q333), “auxiliary examination” (Q334), “outpatient treatment” (Q335) and “symptoms improvement” (Q336).
3. Result
3.1. First-Order PSI Structural Equation Model
3.1.1. Standardized Path Coefficients
By using AMOS19.0, SEM analysis was conducted to get the standardized path coefficients of the first-order PSI model created by this study, which was shown in Figure 1.
3.1.2. Test for MODEL Fit
The common indices of model fit test were listed in Table 2. The CMIN/DF (χ2 /df) was lower than the suggested cutoff value of 3 (Wu, 2011) , implied the acceptableness of the model. The RMSEA (root-mean-square error of approximation) is 0.047, less than the suggested value of 0.05 (Steiger, 1989) ; what’s more, the values of GFI (goodness-of-fit index), AGFI (adjusted goodness-of-fit index), NFI (normed fit index), IFI (incremental fit index), TLI (Tucker-Lewis index, or “non-normed fit index (NNFI)”) and CFI (comparative fit index) were all greater than the cutoff of 0.9 (Bollen & Long, 1993; Hu & Bentler, 1999) , suggesting the excellence of model fit. All of the regression coefficients of the model were significant in the test (p < 0.01).
3.2. High-Order PSI Structural Equation Model
3.2.1. Standardized Path Coefficients
In the first-order PSI model, the 13 observed variables used to explain the latent variables “quality perception” (Q3) were referred to three different factors of assessing hospital services in actual work, i.e., “medical care environment”, “ancillary services” and “medical services”. Obviously, the first-order structural equation model could not reflect the differences among the three categories, thus I built the high-order structural equation model by introducing these three factors as intermediate variables: “medical environment” (Q31), “ancillary services” (Q32) and “medical service” (Q33). The standardized path coefficients of thus formed high-order PSI model was as shown in Figure 2. All of the regression coefficients of the model were significant (p < 0.01).
3.2.2. Test for Model Fit
A list of goodness-of-fit indices for the high-order model―just exactly the same as it was shown in Table 2― was obtained through model fitting. It showed that the high-order model was reasonable and acceptable and also illustrated that the model fit degree has not been changed along with the change of orders.
Figure 1. Standardized path coefficients of the first-order PSI model.
Figure 2. Standardized path coefficients of the high-order PSI model.
Table 2. The main goodness-of-fit indices for the first-order PSI model.
4. Discussion
4.1. Comparisons for Path Coefficients and Regression Coefficients between Models of Different Orders
It could be found from the figures above that the path coefficients of high-order model were almost consistent with the first-order model’s except for several individuals differed slightly which were resulted from the computer truncation errors instead of the model itself. Besides, all the regression coefficients of observable variables of the high-order model were exactly the same with the first-order model except those correlated with the latent variable “quality perception” (Q3). The difference was led by the different hierarchical structures in this part of the two models.
4.2. Structural Model Analyses on Models of Different Orders
The “patient satisfaction” (Q5) was influenced by “hospital identity” (Q1), “quality expectation” (Q2), “quality perception” (Q3) and “value perception” (Q4). It was the most influential of the “quality perception”, followed by the “value perception” and “hospital identity”, which validated the viewpoint of Y. Huo that quality significantly decides the customer satisfaction (Huo, 2004) .
Both the high-order model and the first-order model had the same paths reflecting the positive influence of Q2 on Q3 and Q4. This result conformed with the ACSI model and validated the previous view of Fornell that customer expectation would have direct effects on quality perception and value perception (Fornell, 1996) .
In addition, the result that negative path coefficients from Q2 to Q5 were detected in both models supported the “expectation-inconsistent” theory proposed by Oliver (1980) .
Among the three intermediate variables that affected “quality perception”, the “ancillary services” (Q32) and the “medical services” (Q33)―which were more concerned by patients―possessed greater impacts than the relatively insignificant “medical environment” (Q3). As the data analysis results were in complete accord with the actual situation, the high-order model containing nested levels of intermediate variable analyses was more powerful in clearly reflecting the impacts of different services areas on patients’ quality perception.
4.3. Measurement Model Analyses on Models of Different Orders
As can be seen from Figure 1 and Figure 2, the standardized regression coefficients between observable variables and latent variables of both models were in 0.5 to 0.95 range, and all the standardized path coefficients between latent variables did not reach the cutoff of 1, conformed to the principles of parameter estimate test proposed by Bagozzi & Yi (1988) .
5. Conclusion
This study performed confirmative factors analysis of patient satisfaction index with SEM method and validated that the measuring items and the supposed cause-and-effect relationship between observable variables and latent variables were properly set.
Meanwhile, basing on comparative analysis between the first-order and high-order structural equation models, the study arrived at the conclusions that the structural equation model’s orders don’t affect the measurement results of patient satisfaction index. Except for differences in the regression coefficients of the observed variables related to the intermediate variables, the other regression coefficients and path coefficients do not change.
Furthermore, the high-order models are generally senior than the current prevalent first-order models, for not only being able to reflect how observable variables explain the relative latent variables, but also to compare and evaluate the multiple intermediate variables.
Acknowledgements and Funding
This study was supported by the Project of Innovation Platform for Hunan Colleges and Universities (grant No. 15K135), the Project of Social Science Fund of Hunan Province (grant No. 15JD61) and Postdoctoral Science Foundation of Central South University (No. 153656) awarding to the author. The author declares no conflicts of interest.
Cite this paper
ZhihanLiu, (2016) How Do Orders Impact Structural Equation Model? Empirical Evidence from Patient Satisfaction. Psychology,07,368-373. doi: 10.4236/psych.2016.73039
References
- 1. Amin, M., & Zahora Nasharuddin, S. (2013). Hospital Service Quality and Its Effects on Patient Satisfaction and Behavioural Intention. Clinical Governance: An International Journal, 18, 238-254. http://dx.doi.org/10.1108/CGIJ-05-2012-0016
- 2. Andaleeb, S. S., & Kara, A. (2014). The Structure and Measures of Service Quality Perceptions for Multiple-Encounter Services: A Study of Hospitals in Bangladesh. International Journal of Healthcare Management, 7, 92-102. http://dx.doi.org/10.1179/2047971913Y.0000000054
- 3. Bagozzi, R. P., & Yi, Y. (1988). On the Evaluation of Structural Equation Models. Academic of Marketing Science, 16, 76-94. http://dx.doi.org/10.1007/BF02723327
- 4. Bollen, K. A. (1989). Structural Equations with Latent Variables (p. 4). New York: John Wiley & Sons.
- 5. Bollen, K. A., & Long, J. S. (1993). Testing Structural Equation Modeling. Newbury Park, CA: Sage.
- 6. Breckler, S. J. (1990). Applications of Covariance Structure Modeling in Psychology: Cause for Concern? Psychological Bulletin, 107, 260-273. http://dx.doi.org/10.1037/0033-2909.107.2.260
- 7. Cheng, E. W. L. (2001). SEM Being More Effective than Multiple Regression in Parsimonious Model Testing for Management Development Research. Journal of Management Development, 20, 650-667. http://dx.doi.org/10.1108/02621710110400564
- 8. Fornell, C., Johnson, M. D., Anderson, E. W., & Bryant, B. E. (1996). The American Customer Satisfaction Index: Nature, Purpose and Findings. Journal of Marketing, 60, 7-18. http://dx.doi.org/10.2307/1251898
- 9. Hu, L., & Bentler, P. M. (1999) Cutoff Criteria for Fit Indexes in Covariance Structure Analysis: Conventional Criteria versus New Alternatives. Structural Equation Modeling: A Multidisciplinary Journal, 6, 1-55. http://dx.doi.org/10.1080/10705519909540118
- 10. Huo, Y. (2004). CSI Model Building and the GME Comprehensive Estimation Research of Its Parameters. Doctoral Dissertation, Nanjing: Nanjing University of Science and Engineering. (In Chinese)
- 11. J?reskog, K. G. (1970). A General Method for Analysis of Covariance Structures. Biometrika, 57, 239-251. http://dx.doi.org/10.1093/biomet/57.2.239�
- 12. Kazemi, N., Ehsani, P., Abdi, F., & Bighami, M. K. (2013). Measuring Hospital Service Quality and Its Influence on Patient Satisfaction: An Empirical Study Using Structural Equation Modeling. Management Science Letters, 3, 2125-2136. http://dx.doi.org/10.5267/j.msl.2013.06.005
- 13. Lei, P., & Jolibert, A. (2012). A Three-Model Comparison of the Relationship between Quality, Satisfaction and Loyalty: An Empirical Study of the Chinese Healthcare System. BMC Health Services Research, 12, 436-447. http://dx.doi.org/10.1186/1472-6963-12-436
- 14. Liu, Z. (2015). Literature Review of Domestic and International Research on Patient Satisfaction. Chinese Journal of Health Policy, 8, 60-66. (In Chinese)
- 15. Oliver, R. L. (1980). A Cognitive Model of the Antecedents and Consequences of Satisfaction Decisions. Journal of Marketing Research, 17, 460-469. http://dx.doi.org/10.2307/3150499
- 16. Ping Jr., R. A. (2015). A Note on Estimating Second-Order Interactions and Quadratics in Latent Variables (p. 304). New York: Springer. http://dx.doi.org/10.1007/978-3-319-11845-1_105
- 17. Qin, H., Prybutok, V. R., Peak, D. A., & Boakye, K. G. (2014). UCPERF: An Urgent Care Patient Satisfaction Instrument. The Quality Management Journal, 21, 11.
- 18. Steiger, J. H. (1989). EzPATH: A Supplementary Module for SYSTAT and SYSGRAPH [Computer Program]. SYSTAT.
- 19. Wu, M. (2011). Questionnaire Statistical Analysis and Practice—SPSS Operation and Application. Chongqing: Chongqing University Press. (In Chinese)
NOTES
1All the five hospitals are Tertiary Grade-A large general public hospitals. They are respectively: Huashan Hospital of Fudan University Medical College (east China), China-Japan Friendship Hospital of National Health and Family Planning Commission (north China), Tongji Hospital of Huazhong University of Science and Technology (central China), and West China Hospital of Sichuan University (west China), Xiangya Hospital of Central South University (south China).





