Journal of Environmental Protection
Vol.07 No.02(2016), Article ID:63833,9 pages
10.4236/jep.2016.72023
Comparative Study between Lead Oxide and Lead Nitrate Polymer as Gamma-Radiation Shielding Materials
A. M. Madbouly, E. R. Atta
Egyptian Nuclear and Radiological Regulatory Authority, Cairo, Egypt

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 December 2015; accepted 23 February 2016; published 26 February 2016
ABSTRACT
In this work, the Styrene-butadiene rubber (SBR)/lead oxide and the Styrene-butadiene rubber (SBR)/lead nitrate composites were prepared as gamma-radiation shielding materials. The investigated materials were prepared with three different weight percentage of lead oxide and lead nitrate (30, 50 and 70 wt%). The mass attenuation coefficients (μm) for all composite samples were measured experimentally at 511 and 661.6 keV photon energies. The measurements were made by performing transmission experiments with a 3'' × 3'' NaI (Tl) scintillation detector, which had an energy resolution of 7% at 0.662 MeV for the gamma-rays from the decay of 137Cs. The effective atomic numbers (Zeff) and the effective electron densities (Neff) were determined experimentally. Also they were determined theoretically using the obtained μm values for the studied composites samples by WinXCom program. The obtained results show that the experimental values of the composites are found to be in a good agreement with the theoretical values. It is recognized that the mass attenuation coefficient (μm), effective atomic numbers (Zeff) and the effective electron densities (Neff) are increased in the composite samples which contain lead oxides than which contain lead nitrates. Finally, the Styrene-butadiene rubber (SBR)/lead oxide is better than Styrene- butadiene rubber (SBR)/lead nitrate polymer as gamma radiation shielding.
Keywords:
Leads Oxide, Lead Nitrate, Mass Attenuation Coefficient, Electron Density, Effective Atomic Number, XCOM Program, Gamma Ray, Shielding

1. Introduction
With the extensive use of gamma-active isotopes in medicine, industry and agriculture, the study of absorption of gamma rays in the composite materials has become an interesting and exciting field of research. The photon mass attenuation coefficient, effective atomic number and electron density are the basic quantities required in determining the penetration of gamma photons in matter and energy deposition in shielding, biological and other dosimetric materials. The main purpose of a gamma ray shield is to protect the operating personnel from injury which may be caused by receiving a dangerous dose of radiation [1] .
Berger and Hubbell developed the theoretical tables and computer program (XCOM) for calculating attenuation coefficients for elements, compounds and mixtures for photon energies from 1 keV to 100 GeV [2] .
Recently, this well-known and much used program was transformed to the Windows platform by Gerward et al. 2004 [3] and the Windows version is being called WinXCom.
As effective atomic numbers and electron densities are useful in many technological applications, several investigators have made extensive studies of effective atomic numbers in variety of composite materials like alloys, polymers, compounds, mixtures, thermo luminescent diametric compounds, semiconductors and superconductors [4] -[16] .
For a compound or mixture, the atomic number of a material exhibits a strong and fundamental relationship with the nature of radiation interactions within that medium. There are numerous mathematical descriptions of different interaction processes that are dependent on the atomic number, Z. When dealing with composite media (i.e. a bulk material composed of more than one element), one therefore encounters the difficulty of defining Z. An effective atomic number in this context is equivalent to the atomic number but is used for compounds and mixtures of different materials. This is of most interest in terms of radiation interaction with composite materials. Several investigators have contributed to find the effective atomic numbers in different composite [17] - [20] .
2. Theory Background
The measured intensity I of the transmitted X-ray or γ -ray through a layer of material of thickness x is related to the incident intensity I0 according to the inverse exponential power law that is usually referred to as Beer-Lam- bert law [1] .
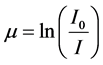 (1)
(1)
where: μ represents the linear attenuation coefficient, I0 and I are incident and transmitted intensities, respectively.
The mass attenuation coefficient is written as [21]
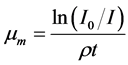 (2)
(2)
where:  is the density of material (g/cm3), t is the thickness of absorber.
is the density of material (g/cm3), t is the thickness of absorber.
Theoretical values of the mass attenuation coefficients of mixture or compound have been calculated by WinXCom, base on mixture rule [22]
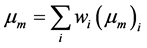 (3)
(3)
where:  is mass attenuation coefficient for individual element in mixture, and
is mass attenuation coefficient for individual element in mixture, and 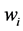 is the weight fraction of element in mixture,
is the weight fraction of element in mixture,
The cross section is a fundamental parameter to describe the photons interaction with matter; it is defined as the probability of a photon interaction for a given reaction. The total cross section of a photon interaction is defined as the sum of the partial cross sections for each type of reaction (photoelectric absorption, coherent scattering, scattering incoherent and pair production) [23]
 (4)
(4)
where: σ? is the total atomic cross section of a photon, (σph) is the photoelectric cross-section, (σcoh) is the coherent scattering cross-section, (σincoh) is the incoherent scattering cross section, Kn is the pair production in nuclear field cross section and Ke is the pair production in electron field cross-section.
The value of mass attenuation coefficients can be used to determine the total atomic cross-section (σ?) by the following relation [22]
 (5)
(5)
where NA is Avogadro’s number, Ai is atomic weight of constituent element of mixture.
Also the total electronic cross-section (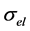 ) for the element is expressed by the following formula [21]
) for the element is expressed by the following formula [21]
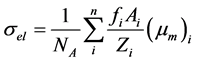 (6)
(6)
where: fi is the number of atoms of element i relative to the total number of atoms of all elements in mixture, Zi is the atomic number of the ith element in mixture.
Total atomic cross-section and total electronic cross-section are related to effective atomic number (Zeff) of the mixture through the formula [22]
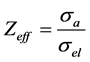 (7)
(7)
The effective electron number or electron density (Nel) (number of electrons per unit mass) can be given by the formula [23] :
 (8)
(8)
3. Experimental Procedure
Sample Preparation
The composition materials which are control, lead oxide and lead nitrate samples were prepared with three different percentage of lead oxide and lead nitrate (30, 50 and 70 wt%), where shown in Table 1. They were prepared by mixing Styrene-Butadiene Rubber powder-1502 (SBR) with metal oxides. SBR was commercial product and purchased from Egyptian Petroleum Company. Lead oxide (PbO), lead nitrate Pb(NO3)2, ZnO at constant ratio 5 pphr at all compound and Stearic acid were obtained from the British Drug Houses (BDH Laboratory Chem. Ltd.), Poole, England. The linear attenuation coefficients of the investigated samples were measured for gamma rays of energies 511 and 661.6 keV photon energies which have been obtained from 22Na point source and 137Cs point source. The experiments has been performed using gamma ray spectrometer which consists of 3'' × 3'' NaI (Tl) Scintillation detector, amplifier and 16 k multi-channel analyzer at Egyptian Nuclear and Radiological Regulatory Authority. For each sample, the gamma ray spectrum was recorded as a function of the thickness of the material. And the area under the photo peak of the spectrum is used to evaluate the intensity (I) of the transmitted beam by using the initial intensity (Io) which is the area under the photo peak obtained without any sample between detector and source.
Table 1. Different concentration ratios of the materials content for each samples.
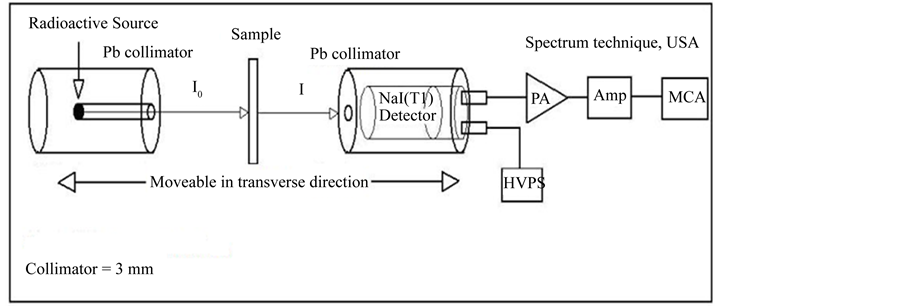
The diagram of experimental setup for mass attenuation coefficient determination is shown in Figure 1. The source and absorber system were mounted on a composite of adjustable stands. This setup can move in the transverse direction for proper beam alignment. The 137Cs and 22Na radioactive sources have activity of 5 mCi. The incident and transmitted gamma-rays intensities were measured for a fixed preset time in each experiment by recording the corresponding counts, using the 3'' × 3'' NaI (Tl) detector having an energy resolution of 7% at 662 keV (oxford model), with CANBERRA photomultiplier tube base model. The spectra were recorded using a CANBERRA PC-based multi-channel analyzer. In this experiment, the validity of the mass attenuation measurement was confirmed by measuring a lead slab.
4. Results and Discussion
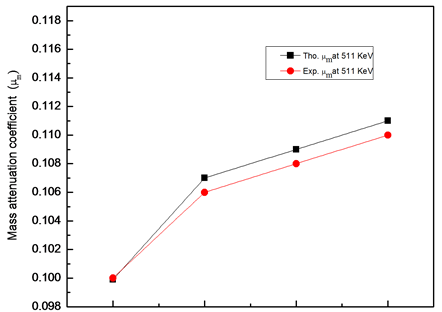
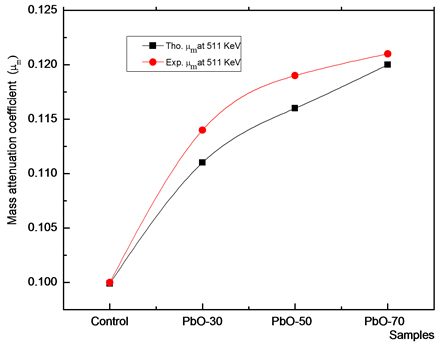
The experimental mass attenuation coefficients have been determined at the photon energies 511 keV and 662 KeV. Both experimental values and calculated values using computer code of XCOM of μ/ρ are displayed in Figure 2. It is clear that the mass attenuation coefficients decrease with the increase in photon energies. This may be attributed to the interaction mechanism of photons with the matter and it is differ for different photon energies [24] . Also it is observed that the mass attenuation coefficients of the investigated samples for all concentration of PbO are higher than that of Pb(NO3)2.
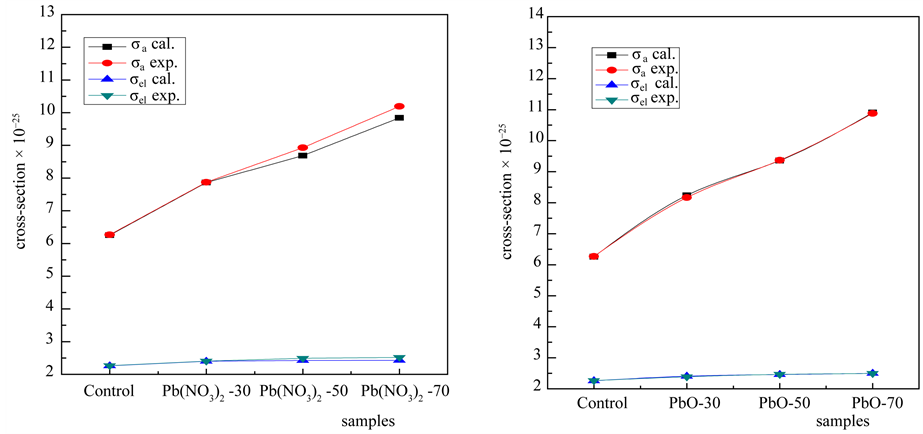
The total cross sections σ? and electronic cross sections sel have been calculated with respect to the experimental and calculated mass attenuation coefficients at energy 511 KeV and 662 KeV; the results given in the Figure 3 and Figure 4. The experimental values of total cross sections σ? and electronic cross sections sel are matched with the theoretical values. The small difference between the experimental and theoretical values might be from experimental setup, counting and efficiency errors in comparison to the calculated results of present work. The values of total cross sections sa and electronic cross sections sel for composite material contains lead oxide are more than composite material contains lead nitrate because the composite material contains lead oxide had a great contribution in various interaction with gamma-ray than composite material contains lead nitrate due to the weight fraction of Pb element is more in lead oxide than lead nitrate at the same weight. i.e the number of lead atoms in composite material contains lead oxide is more than in composite material contains lead nitrate. So electrons of lead in the last shell are fewer bands to the nucleus; this point increases the interaction probabilities for these atoms. The values of total cross sections σ? and electronic cross sections sel for all composite material at 511 KeV are higher than the values at 662 KeV may be due to the probability of absorption reduces with increasing incident photon energies.
The calculation of effective atomic number Zeff and electron density (Nel) becomes possible after finding the cross-section of the investigated samples Table 2. It is recognize that the effective atomic numbers is constant at different energies for all studied composite materials. This may be due to the dominance of photoelectric effect and Compton effect in their respective energy regions [1] [23] . Zeff value for a composite material is a very useful parameter for some applications such as physical, technological and engineering. Zeff represented with a number provides many characteristics of a material. Zeff value can provide estimation of the chemical composition of the material and it can be also utilized in the computation of absorbed dose in radiation therapy etc.
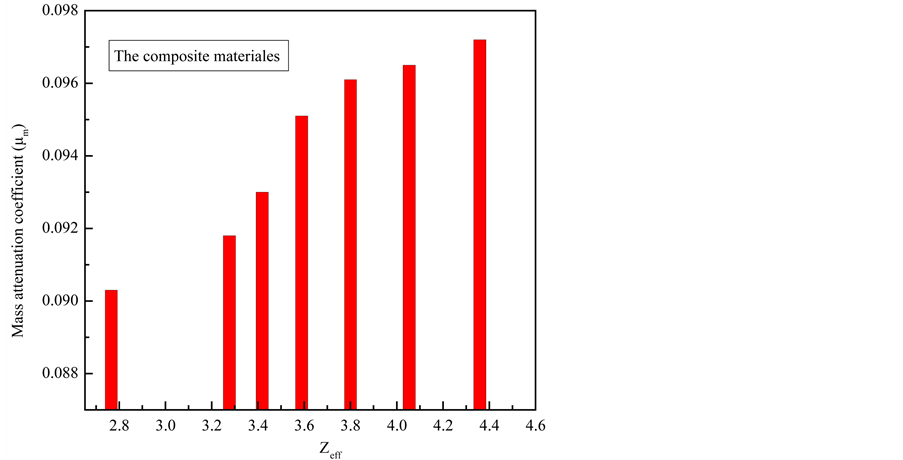
Figure 5 gives a plot of Zeff versus µ/ρ for the incident photon energy. As clearly seen that µ/ρ increases li-
Figure 1. Experimental setup for mass attenuation coefficient determination.
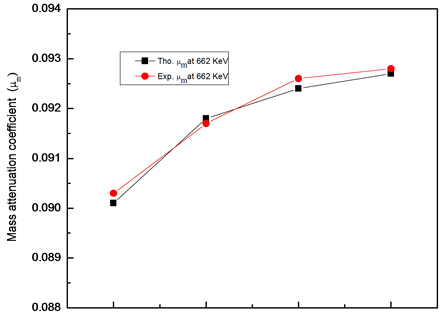
Figure 2. The theoretical and experimental value of mass attenuation coefficient (mm) for all samples at selected energies.
Figure 3. The calculated and experimental total atomic cross-section sa and the total electronic cross-section sel for samples at energy 511 KeV.
nearly with increasing Zeff. Figure 6 gives a plot of Zeff versus σa for the incident photon energy and shows that σa increases linearly with increasing Zeff. This work was carried out for low photon energies. Photons in the keV
Figure 4. The calculated and experimental total atomic cross-section sa and the total electronic cross-section sel for samples at energy 662 KeV.
Figure 5. The relation between effective atomic numbers Zeff with mass attenuation coefficient (μm) for all composite materials.
Table 2. The calculation of effective atomic number Zeff and electron density (Nel) for the investigated samples.

Figure 6. The relation between total atomic cross section (σa × 10−25) and effective atomic number (Zeff) for the investigated composite materials at 511 and 622 KeV.
range are important in radiation biology as well as in medical diagnostics and therapy [25] . In the composite materials, the interaction (such as absorption and scattering) of γ-rays is related to Zeff value of composite materials and the energy of incident photons. At low photon energies, the photoelectric interaction is the main photon interaction process and it depends on atomic number.
As shown in Table 2, there are slight differences in the Nel values for all composite materials as well as the Nel values of all composite materials contain the different concentration of PbO and Pb(NO3)2 are constant at the selected energies. The Nel values of all composite materials contain the different concentration of PbO are higher values than the Nel values of all composite materials contain the different concentration of Pb(NO3)2. The higher values of the electron density indicate an increased probability of a photon-electron energy transfer and an energy deposition into the material.
It has been found that the effective atomic numbers were increased with PbO content. The mass attenuation coefficient and effective atomic number increase with concentration of PbO. From the increasing of these parameters, we obtained the photon interaction probability is increase with higher PbO content and lead to the transmission of gamma rays were decrease with increasing the amount of lead oxide.
5. Conclusions
1) PbO composite samples are able to absorb and scatter gamma ray better than Pb(NO3)2 composite samples.
2) The obtained experimental results of the investigated shielding parameters are in a good agreement with the theoretical results which calculated by WinXCom.
3) Although both mass attenuation coefficient and effective atomic number depends upon the photon energies, the electron density does not significantly depend upon photon energy.
4) All studied shielding parameters are increase with PbO content. Moreover, these results show that the PbO is more better used in radiation shielding materials than Pb(NO3)2.
Cite this paper
A. M.Madbouly,E. R.Atta, (2016) Comparative Study between Lead Oxide and Lead Nitrate Polymer as Gamma-Radiation Shielding Materials. Journal of Environmental Protection,07,268-276. doi: 10.4236/jep.2016.72023
References
- 1. Singh, K., Singh, H., Sharma, V., Nathuram, R., Khanna, A., Kumar, R., Bhatti, S.S. and Sahota, H.S. (2002) Gamma-Ray Attenuation Coefficients in Bismuth Borate Glasses. Nuclear Instruments and Methods in Physics Research Section B, 194, 1-6.
- 2. Berger, M.J. and Hubbell, J.H. (1987/1999) XCOM: Photon Cross Sections Database, Web Version 1.2. National Institute of Standards and Technology, Gaithersburg. (Originally Published as NBSIR 87-3597 “XCOM: Photon Cross Sections on a Personal Computer”).
http://physics.nist.gov/xcom - 3. Gerward, L., Guilbert, N., Jensen, K.B. and Levring, H. (2004) WinXCom—A Program for Calculating X-Ray Attenuation Coefficients. Radiation Physics and Chemistry, 71, 653-654.
http://dx.doi.org/10.1016/j.radphyschem.2004.04.040 - 4. Murthy, R.C. (1965) Effective Atomic Numbers of Heterogeneous Materials. Nature (London), 207, 398-399.
http://dx.doi.org/10.1038/207398a0 - 5. Parthasaradhi, K. (1968) Studies of the Effective Atomic Numbers in Alloys for Gamma Ray Interactions in the Energy Region 100 - 662 keV. Indian Journal of Pure and Applied Physics, 6, 609.
- 6. Lingam, S.C., Babu, K.S. and Reddy, D.V.K. (1984) Total Gamma Ray Cross Sections and Effective Atomic Numbers in Compounds in the Energy Region 32 - 662 keV. Indian Journal of Physics, 53A, 285.
- 7. El-Kateb, A., Rizk, R.A.M. and Abdul-Kader, A.M. (2000) Determination of Atomic Cross-Sections and Effective Atomic Numbers for Some Alloys. Annals of Nuclear Energy, 27, 1333.
- 8. Govinda Nayak, N., Vijaya, M.G. and Siddappa, K. (2001) Effective Atomic Numbers of Some Polymers and Other Materials for Photoelectric Process at 59.54 keV. Radiation Physics and Chemistry, 61, 559.
http://dx.doi.org/10.1016/S0969-806X(01)00332-2 - 9. Gowda, S., Krishnaveni, S., Yashoda, T., Umesh, T.K. and Gowda, R. (2004) Photon Mass Attenuation Coefficients, Effective Atomic Numbers and Electron Densities of Some Thermoluminescent Dosimetric Compounds. Pramana— Journal of Physics, 63, 529-541.
http://dx.doi.org/10.1007/BF02704481 - 10. Içelli, O. and Erzeneoglu, S. (2004) Effective Atomic Numbers of Some Vanadium and Nickel Compounds for Total Photon Interactions Using Transmission Experiments. Journal of Quantitative Spectroscopy and Radiative Transfer, 85, 115-124.
http://dx.doi.org/10.1016/S0022-4073(03)00197-3 - 11. Içelli, O., Erzeneoglu, S., Karahan, I.H. and Çankaya, G. (2005) Effective Atomic Numbers for CoCuNi Alloys Using Transmission Experiments. Journal of Quantitative Spectroscopy and Radiative Transfer, 91, 485-491.
http://dx.doi.org/10.1016/j.jqsrt.2004.07.006 - 12. Cevik, U., Baltas, H., Celik, S., Karaca, I. and Kopya, A.I. (2005) Measurement of Mass Attenuation Coefficients for YBaCuO Superconductor at Different Energies. Superconductor Science and Technology, 18, 101-106.
http://dx.doi.org/10.1088/0953-2048/18/1/016 - 13. Çevik, U., Baltas, H., Çelik, A. and Bacaksiz, E. (2006) Determination of Attenuation Coefficients, Thicknesses and Effective Atomic Numbers for CuInSe2 Semiconductor. Nuclear Instruments and Methods in Physics Research Section B, 247, 173-179.
http://dx.doi.org/10.1016/j.nimb.2006.01.064 - 14. Hiremath, S.S. and Chikkur, G.C. (1993) Computation of Effective Atomic Number of Some Hydrocarbons Containing H, C and O Atoms in the Energy Range 54 - 1333 keV. Indian Journal of Pure and Applied Physics, 31, 855.
- 15. Manjunathaguru, V. and Umesh, T.K. (2006) Effective Atomic Numbers and Electron Densities of Some Biologically Important Compounds Containing H, C, N and O in the Energy Range 145 - 1330 keV. Journal of Physics B: Atomic, Molecular and Optical Physics, 393969.
- 16. Pawar, P.P. and Bichile, G.K. (2012) Effective Atomic Numbers and Electron Densities of Vitamins Containing H, C, N and O. Journal of Chemical and Pharmaceutical Research, 4, 59-66.
- 17. Singh, K.J., Singh, N., Kaundal, R.S. and Singh, K. (2008) Gamma-Rays Shielding and Structural Properties of PbO-SiO2 Glasses. Nuclear Instruments and Methods in Physics Research Section B, 266, 944-948.
http://dx.doi.org/10.1016/j.nimb.2008.02.004 - 18. Baltas, H., Celik, S., Cevik, U. and Yanmaz, E. (2007) Measurement of Mass Attenuation Coefficients and Effective Atomic Numbers for MgB2 Superconductor Using X-Ray Energies. Radiation Measurements, 42, 55-60.
http://dx.doi.org/10.1016/j.radmeas.2006.08.005 - 19. Akkurt, I., Kilincarslan, S. and Basyigit, C. (2004) The Photon Attenuation Coefficients of Barite, Marble, and Limra. Annals of Nuclear Energy, 31, 577-582.
http://dx.doi.org/10.1016/j.anucene.2003.07.002 - 20. Singh, K., Singh, H., Sharma, G., Gerward, L., Khanna, A., Kumar, R., Nathuram, R. and Sahota, H.S. (2005) Gamma-Rays Shielding Properties of CaO-SrO-B2O3 Glasses. Radiation Physics and Chemistry, 72, 225-228.
http://dx.doi.org/10.1016/j.radphyschem.2003.11.010 - 21. Kaewkhao, J., Laopaiboon, J. and Chewpraditkul, W. (2008) Determination of Effective Atomic Numbers and Effective Electron Densities of Cu/Zn Alloy. Journal of Quantitative Spectroscopy & Radiative Transfer, 109, 1260-1265.
http://dx.doi.org/10.1016/j.jqsrt.2007.10.007 - 22. Singh, K., Kaur, R., Vadana and Kumar, V. (1996) Study of Effective Atomic Numbers and Mass Attenuation Coefficients in Some Compounds. Radiation Physics and Chemistry, 47, 535-541.
http://dx.doi.org/10.1016/0969-806X(95)00057-5 - 23. Kaur, G., Singh, K., Lark, B.S. and Sahota, H.S. (2000) Photon Interaction Studies in Solutions of Some Alkali Metal Chlorides—I. Radiation Physics and Chemistry, 58, 315-323.
http://dx.doi.org/10.1016/S0969-806X(99)00524-1 - 24. Turgut, U., Simsek, O. and Buyukkasp, E. (2007) Measurement of Mass Attenuation Coefficients in Some Cr, Co and Fe Compounds around the Absorption Edge and the Validity of Mixture Rule. Pramana—Journal of Physics, 69, 199-207.
http://dx.doi.org/10.1007/s12043-007-0121-6 - 25. Hubbell, J.H. (1999) Review of Photon Interaction Cross Section Data in the Medical and Biological Context. Physics in Medicine and Biology, 44, R1-R22.
http://dx.doi.org/10.1088/0031-9155/44/1/001