Journal of Environmental Protection
Vol.05 No.17(2014), Article ID:52440,14 pages
10.4236/jep.2014.517157
Kinetic and Equilibrium Isotherms Studies of Adsorption of Pb(II) from Water onto Natural Adsorbent
Taha M. Elmorsi1,2*, Zeinhom H. Mohamed1, Walied Shopak1, Ahmed M. Ismaiel1
1Chemistry Department, Faculty of Science, Jazan University, Jazan, KSA
2Chemistry Department, Faculty of Science, Al-Azhar University, Cairo, Egypt
Email: *taha_elmorsi@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 October 2014; revised 5 November 2014; accepted 1 December 2014
ABSTRACT
In this research dobera leaves (DL), an agricultural waste, available in large quantity in south region of Saudi Arabia, were used as low-cost adsorbent for removal of metal ions such as Pb(II). Batch operation was used to study the equilibrium behavior of DL. The effects of initial concentration of Pb(II), solution pH, contact time and adsorbent dose were evaluated. To study the kinetics of adsorption of Pb(II) onto DL, pseudo-first-order, pseudo-second-order and intra-particle diffusion were used. Adsorption process undergoes pseudo-second-order kinetic as proved by the high value of R2. Furthermore, to design the equilibrium data of adsorption of process, four adsorption isotherm models such as Langmuir, Freundlich Temkin and Dubinin-Radushkevich (D-R) were used. It is found that Langmuir equation has the highest value of R2 (0.999) compared with other models. In presences of a mixture of Pb(II)/Ni(II), DL were found to be selective for Pb(II) ions with a high adsorptive capacity of 83 mg/g and show favorable adsorption with RL < 1. In addition, preliminary results indicate that DL are very effective adsorbent for the removal of Pb(II) ions (>90%) from drinking water with less competition of other ions present in water.
Keywords:
Dobera Leaves, Pb(II), Adsorption Kinetics, Adsorption Isotherms

1. Introduction
Environmental pollutants can be treated by chemical, biological and/or physical processes [1] - [6] . Adsorption process is one of the physical treatment methods. In this technique, adsorbate molecules accumulated onto the surface of adsorbent. It is known that water polluted with low concentration or even trace levels of heavy metals can cause serious health problems to human body [5] . Recently, one of the critical reviews on current treatment methods of removal of heavy metals [7] reported that adsorption was an effective method and was neither costly nor required various tools. In adsorption process the most effective adsorbent was reported to be activated carbon (AC) which used for the removal many pollutants, including heavy metals [2] . However, production of activated carbon by carbonizing and activating the organic substances from the proper materials is highly cost, and thus requires the search for alternatives and low-cost adsorbents [8] . A low coast adsorbent should be inexpensive materials and does not require many processing. Furthermore, it can be found in the environment naturally in a plentiful or produced as a by-product or a waste from an industry or agriculture [9] . Several low-cost adsorbents using leaf powder of different trees such as bael tree [10] , cypress, cinchona and pine [11] , neem [2] , rubber [12] , Cinnamomum camphora [13] , castor [14] , Solanum melongena [15] , and others were used for removing Pb(II) ions from aqueous solution. To make further use of leaf powder of trees, the present study is an attempt to use Dobera glabra Forssk leaves (DL), as nonconventional low-cost adsorbent for removal of some heavy metal ions such as Pb(II), and Ni(II) ions from aqueous solution. Dobera tree (an ever-green tree), is a member of the Salvadoraceae family and presents in plentiful in many countries such as Saudi Arabia. It is characterized by alternate thick skinny leaves [16] [17] . In the current study, kinetics of Pb(II) adsorption onto DL studied through a pseudo-first-order [18] - [20] , a pseudo-second-order [21] [22] and an intraparticle diffusion [18] [23] . Adsorption isotherm (adsorption equilibrium) is usually described the equilibrium state between the amount of adsorbed metal ion onto the adsorbent surface  and the concentration of metal ions in solution
and the concentration of metal ions in solution  at a fixed both temperature and pH. The common equations used to describe adsorption isotherm are Langmuir [24] [25] and Freundlich [25] [26] in addition to Temkin [27] - [29] and Dubinin-Radushkevich (D-R) equation [30] [31] . The parameters of those equations can describe both the surface properties and the affinity of the adsorbent such as DL to the adsorbate such as metal ions. Also, adsorption maximum capacity, adsorption intensity and the heat of adsorption can be determined. In this study, the linear forms of the above mentioned equations were used to describe the equilibrium data hence their applicability was evaluated by determining the correlation coefficients (R2) [31] .
at a fixed both temperature and pH. The common equations used to describe adsorption isotherm are Langmuir [24] [25] and Freundlich [25] [26] in addition to Temkin [27] - [29] and Dubinin-Radushkevich (D-R) equation [30] [31] . The parameters of those equations can describe both the surface properties and the affinity of the adsorbent such as DL to the adsorbate such as metal ions. Also, adsorption maximum capacity, adsorption intensity and the heat of adsorption can be determined. In this study, the linear forms of the above mentioned equations were used to describe the equilibrium data hence their applicability was evaluated by determining the correlation coefficients (R2) [31] .
2. Experimental
2.1. Chemicals
Analytical-grad chemicals were used in this work without further purification. To avoid any interference of other ions, all solutions were prepared using HPLC water. To evaluate the significant of the adsorbent, stock solutions (1000 mg/L) of Pb(II) was prepared from their nitrate salts (purchased from Sigma) and further diluted to perform adsorption experiments. To study the selectivity of the adsorbent, preliminary adsorption experiments performed by mixing nitrate solutions of both Pb(II) and Ni(II) in presence of dobera leaves. Dilute solutions of 1 M HNO3 (HPLC grad) and 1 M NaOH (BDH) were used to adjust pH of metal ion solutions using a pH meter.
2.2. Adsorbent
Dobera leaves (DL) was used as a natural adsorbent. DL were collected from fields around El-Ardh area (Bathan) in Jazan, Saudi Arabia. To remove dust and any other impurities present on the leaves, adsorbent was air dried and washed several times with distilled water. Powder of DL was formed by drying the leaves then ground well and sieved.
2.3. Adsorption Experiments
Pb(II) solution was used in this study as an environmental pollutants to evaluate the significant of the adsorbent. Stock solutions (1000 mg/L) of Pb(II) was prepared from their nitrate salts using HPLC water and further diluted to perform adsorption experiments. Preliminary adsorption selectivity experiment performed by mixing both Pb(II) and Ni(II) solutions. Calibration curves were prepared by serial dilutions (1.0 to 10.0 mg/L). In batch experiments, known amounts of DL were added into several 50 mL conical flasks, each containing 25.0 mL solution of Pb(II) and/or Ni(II) with an initial concentration ranging from 5.0 to 50 mg/L. Then the flasks were shaked at 120 rpm using an electric shaker at room temperature. Samples were withdrawn at interval times and a laboratory table centrifuge was used to separate DL powder from samples. Adsorption isotherms were determined by introducing 0.025 g (1.0 g/L) DL powder to respective 25.0 mL solution of different Pb(II) concentrations (5 - 50 mg/L) at room temperature.
2.4. Effect of Adsorbent (DL Powder) Mass
To investigate the effect of DL powder mass, different mass of DL 0.25 to 2 g/L (0.00625 - 0.05 g/0.025L) were introduced to a number of conical flasks containing a specific volume of a fixed [Pb(II)]0 at the same pH and room temperature. Concentrations of Pb(II) were measured at equilibrium.
2.5. Analytical Methods
Inductively coupled plasma optical emission spectrometry (ICP-OES) was used to determine the concentrations of both Pb(II) and Ni(II). These concentration measurements lead to obtain a calibration curves which used to calculate metal ion concentrations during adsorption experiments at any time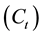 .
.
The amount of metal ion sorbed onto DL powder at any time, 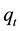 , was calculated from:
, was calculated from:
 (1)
(1)
At equilibrium,  and
and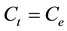 ; therefore the amount of sorbed metal ion,
; therefore the amount of sorbed metal ion, 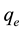 , was calculated from
, was calculated from
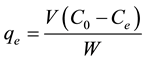 (2)
(2)
where 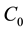 ,
,  and
and 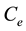 are the initial concentration, concentration at any time and equilibrium concentrations of metal ion solution (mg/L), respectively, V is the volume of the solution (L), and W is the mass of DL powder (g) [28] . Metal ion removal percentage can be calculated as follows:
are the initial concentration, concentration at any time and equilibrium concentrations of metal ion solution (mg/L), respectively, V is the volume of the solution (L), and W is the mass of DL powder (g) [28] . Metal ion removal percentage can be calculated as follows:
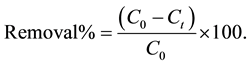 (3)
(3)
3. Results and Discussion
3.1. Effects of Contact Time
A dobera leaves (DL) dosage of 0.025 g (1.0 g/L) was added to 0.025 L of 30 mg/L of Pb(II) solution. Experiments were conducted at a temperature of 298 K for 120 min to test the effect of contact time on the adsorption process. The results (Figure 1) indicated that the adsorption of Pb(II) onto DL was very rapid in the first 15 min hence the adsorbed amount (qt) reached 24.93 mg/L, which represented about 83%, comparing to 29.76 mg/g
Figure 1. Effect of contact time on the adsorption of Pb(II) onto dobera leaves (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).
(99.2%) at 180 min. Then the adsorption of Pb(II) ions increased gradually during the following 45 min until reached equilibrium at about 150 min. The results showed that the uptake of Pb(II) ions by DL depends on contact time. This may be due to the time required for the Pb(II) to encounter the boundary layer effect, then diffuse to the surface of DL and finally diffuse to the porous structure of the adsorbent [32] . To ensure complete equilibrium of the data, adsorption samples were collected at 180 min.
3.2. Effect of Solution pH on Pb(II) Removal
It was found that initial pH has a great effect on the rate of adsorption by affecting speciation and the degree of ionization of adsorbate in addition to the surface charge of adsorbent [33] [34] .
Thus experiments were conducted at 30 mg/L [Pb]0, 1.0 g/L DL dose, and 180 min contact time at a temperature of 298 K, to study the effect of solution pH on the equilibrium adsorption capacity (qe) of Pb(II) onto DL as shown in Figure 2. It is indicated that % removal of Pb(II) reached a maximum in a slight acidic medium and decreased in slight basic medium. The % removal of Pb(II) increased from 92% at pH 3 to maximum, 95%, at pH 5. While decreased from 87% at pH 6 to reach 78.44% by increasing the pH values to 8. Therefore, further adsorption experiments were performed at pH 5 as an optimum pH value. It was reported that the predominant species of Pb(II) are Pb2+ ions at pH between 5 and 6 [33] . However, in presence of high concentration of H+ ions at pH 3, hydronium ions H3O+ ions would compete with Pb2+ ions for the binding sites, leading to lower the % removal of Pb2+ ions. While decreasing the concentration of H3O+ ions at pH 5 leads to decrease the positive charge on the surface of DL which lower the electrostatic repulsion between the surface of DL and Pb(II) hence increased % removal to 95%. A similar trend was previously reported by the adsorption of Pb(II) onto tobacco stem [24] and some metal cations onto different adsorbents [35] . Also, adsorption of Pb2+, Cd2+ and Ni2+ reached maximum biosorption at pH 5.5 using chemically modified orange peel [26] . On the other hand, increasing the pH to 8 would increase the concentration of OH− ions leading to the formation of the predominant species of Pb(OH)2. Due to the low solubility of Pb(OH)2 at 298 K, the concentration of Pb2+ ions would decrease at pH 8 mainly due to precipitation, thus adsorption process has no meaning at pH 8 for Pb2+ ions [36] . These results can be further proven by the results in our previous study for the adsorption of methylene blue dye, a cationic dye (MB dye+), onto miswak leaves, [28] . The adsorption rate found to decrease in high acidic medium at pH 2.8 due the effective compete between MB dye+ and H+ ions for binding sites.
3.3. Effect of Adsorbed Amount
At constant [Pb(II)]0 (30 mg/L), different amounts of DL (0.25 to 2.0 g/L) were added to metal ion solutions (0.025 L) to study the effect of DL amount on Pb(II) adsorption. Results in Figure 3 shows that the adsorption capacity in the first stage increased rapidly with the increase in the adsorbent dose then increased slowly until reached equilibrium with the further increase in the adsorbent dose. It can be seen that at 1.0 g/L of the adsorbent dose, the % removal of Pb(II) reached the most at 94.8%. Then an increase in the dose of DL from 1.0 to 2.0 g/L resulted only in about 3% more to reach 97.1%. Thus 1.0 g/L of DL was chosen as the optimum dose and used in the further experiments. The increase in % removal of Pb(II) with the increase in the amount of DL
Figure 2. Effect of solution pH on the adsorption of Pb(II) and Ni(II) ions onto dobera (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, V = 0.025 L, DL dosage = 1.0 g/L).
Figure 3. Effect of adsorbent dose on the adsorption of Pb(II) onto dobera (T = 298 K, time =180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 - 2.5 g/L).
up to 1.0 g can be assigned to the increase in both the surface area and the adsorption sites to Pb(II). However, the adsorption rate did not enhanced effectively by increasing the amount of the adsorbent from 1.0 to 2.0 g/L, may be due to increase the overlapping and/or aggregation of adsorbent sites at high dose [37] . Effect of dose of Rosa bourbonia waste phyto-biomass which was used for the adsorption of Pb(II) and Cu(II) from aqueous media indicated similar trend. Hence the dose of 2 g/L was the optimum when the dose of adsorbent was varying from 2.0 to 5.0 g/L [37] .
3.4. Adsorption Kinetics
Fitting the experimental data into different kinetic models enables to study the adsorption rate, model the process and predict information about adsorbent/adsorbate interaction (physisorption or chemisorption) [14] . In this study, three different models were used such as the pseudo-first-order [18] - [20] , the pseudo-second-order [21] [22] and intraparticle diffusion [18] [23] .
3.4.1. Pseudo-First-Order Equation
Pseudo-first-order equation was given by Langergren and Svenska (1898) to determine the rate constant of adsorption process as:

where 







3.4.2. Pseudo-Second-Order Rate Equation
Equation of pseudo-second-order based on equilibrium adsorption can be expressed as:

or

where 




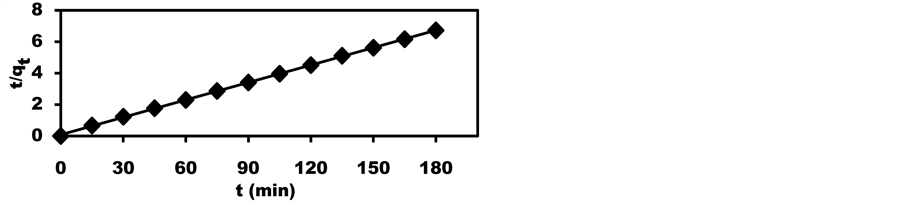
Figure 4. Pseudo-first-order kinetics for the adsorption of Pb(II) onto dobera (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).
Table 1. Adsorption kinetic parameters for the adsorption of Pb(II) onto dobera (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).
in Figure 5 show linear plots with very high values of R2 (Table 1) in addition to the good agreement between experimental and calculated values of 
3.4.3. Intra-Particle Diffusion Study
In order to investigate the mechanism of Pb(II) adsorption onto DL, intra-particle diffusion based mechanism was studied. It is proposed that the uptake of the adsorbate (Pb(II)) by the adsorbent (DL) varies almost proportionately with the square root of the contact time (t1/2) according to the following equation [13] .

where, 





time range. Also, the plot indicated that the external surface adsorption (stage 1) is absent and it is finished before 15 min. Then after 15 min, the intra-particle diffusion control (stage 2) started and kept on to 60 min. Finally, the equilibrium step (stage 3) appeared after 60 min. It can be seen that the adsorption of Pb ion onto DL involved more than one process, and the intra-particle transport is not the rate-limiting step.
3.5. Isotherms for the Sorption of Pb(II) onto Dobera Leaves
Adsorption isotherms are different models used to evaluate the affinity of studied adsorbent (DL) for the removal of Pb(II) from aqueous solution. In the current study, four isotherm models namely Langmuir, Frendulich, Temkin and D-K were used.
Figure 5. Pseudo-second-order kinetics for the adsorption of Pb(II) onto dobera (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).

Figure 6. Intra-particle diffusion plot for the adsorption of Pb(II) onto dobera (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).
3.5.1. Langmuir Isotherm
The Langmuir isotherm model assumes that a monolayer of adsorbed material (in liquid, such as Pb(II)) is adsorbed over a uniform adsorbent surface such as DL. The Langmuir-II equation is derived by some mathematical manipulation as:

where 




Figure 7 shows the linear fit of Langmuir-II for the adsorption of Pb(II) onto DL at 25˚C is. The value of 





Figure 7. Langmuir isotherm for the adsorption of Pb(II) onto dobera leaves (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).
Table 2. Langmuir, Freundlich, Temkin and D-R constants for the adsorption of Pb(II) onto dobera leaves (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).
Table 3. Comparison of the maximum monolayer adsorption of Pb(II) onto various adsorbents.
3.5.2. Separation Factor
Langmuir isotherm can be characterized by a dimensionless constant called separation factor

where 









3.5.3. Surface Coverage (θ)
Another factor can help for understanding the behavior of the adsorption of Pb(II) onto DL is the Langmuir type equation which related the surface coverage (θ) of the adsorbent (DL) to the initial concentration of Pb(II) 
Figure 8. Plot of separation factor versus initial Pb(II) concentration for the adsorption of Pb(II) onto dobera leaves (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).


where 


3.5.4. Freundlich Isotherm
The Freundlich exponential equation presumes that the adsorption process takes place on a heterogeneous surface. Both nonlinear and linear forms of Freundlich are given as:


where 

indicates both the relative distribution of energy and the heterogeneity of the adsorbent sites.
Figure 10 representing the linear plot of 



(0.981) of Freundlich is slightly lower than the value of 


3.5.5. Temkin Isotherms
The adsorption potential of adsorbent to adsorbate can be tested by applying Temkin isotherm model (Equation
Figure 9. Surface coverage (θ) for the adsorption of Pb(II) onto dobera leaves at different concentrations (T = 298 K, time = 180 min, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).
Figure 10. Freundlich isotherm for the adsorption of Pb(II) onto dobera leaves (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).
(9)). This equation supposes that increasing the coverage layer of adsorbate onto the surface of adsorbent makes the heat of adsorption (DHads) of all molecules in that layer decreased linearly by increase the coverage. The linear form of Temkin is:

where, R is common gas constant (0.008314 kJ/mol・K), T is the absolute temperature (K), 









3.5.6. Dubinin-Radushkevich (D-R) Isotherm Model
To Calculation the Sorption Energy, D-R model was used. This isotherm dose not assume constant adsorption potential or homogeneous surface for the adsorbent [1] . Thus the D-R linear form (Equation (10)) can be applied on both homogenous and heterogeneous surfaces [13] .

where, 


Figure 11. Temkin isotherm for the adsorption of Pb(II) onto dobera leaves (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).
saturation capacity based on D-R isotherm and 


where R





Mean energy of adsorption (Ea):
Applying D-R isotherm model for the adsorption data of Pb(II) onto DL allows to calculate the mean energy of adsorption 


The numerical value of 




3.6. Standard Gibbs Free Energy Change (DG˚)
Standard free energy 


where, 





3.7. Preliminary Selectivity Study of Pb(II)
Preliminary experiments were conducted to investigate the selectivity of Pb(II) from the mixture of solution with same charge. Only one mixture was tested such as Pb(II)/Ni(II). The following equations [38] were used to calculate the distribution coefficient 


where 



The results indicated that the value of 

3.8. Removal of Pb(II) from Drinking Water
Experiments were conducted to test removal of Pb(II) onto DL from drinking water. Different samples of drinking water from Jazan area, KSA, were collected from different sources such as Sadeem, Mahlia, Arghad, Areedah, Aswar, Alwasm and Abu-Ziab. All samples were undergoes the optimum conditions of adsorption batch experiments as discussed previously. The results in Figure 13 show that the % removal of Pb(II) ions were more than 91%, indicated that dobera leaves (DL) is very effective adsorbent for removal of Pb(II) ions from drinking water.
4. Conclusion
The present study showed that dobera leaves (DL) could be used as an effective adsorbent for the removal of lead ions from water. Lead adsorption was found to be pH-dependent and maximum removal was observed at pH 5.0. It was found that the equilibrium data was fitted very well with Langmuir-II equation with maximum capacity as 83 mg/g. Also, the equilibrium data can be modeled by Freundlich isotherm model. The adsorption
Figure 12. The Dubinin-Radushkevich (D-R) the adsorption of Pb(II) onto dobera leaves (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).
Figure 13. Adsorption of Pb(II) from drinking water (T = 298 K, time = 180 min, [Pb(II)]0 = 30 mg/L, pHi = 5, V = 0.025 L, DL dosage = 1.0 g/L).
of Pb(II) was favored by dobera leaves with value of RL less than unity. Furthermore, the adsorption process is spontaneous and follows pseudo-second-order kinetic. In addition the adsorption mechanism involved more than one step. DL have a very good selectivity for Pb(II) in presence of Ni(II) with large 
Acknowledgements
The Authors sincerely appreciate financial support from Deanship of Scientific Research, Jazan University, Jazan, KSA, for (project number 004/1431). Also, Authors appreciated valuable discussion from Prof. Dr. Hassan Shehata, Al-Azhar University, Cairo, Egypt.
References
- Rondón, W., Freire, D., de Benzo, Z., Sifontes, A.B., González, Y., Valero, M. and Brito, J.L. (2013) Application of 3A Zeolite Prepared from Venezuelan Kaolin for Removal of Pb(II) from Wastewater and Its Determination by Flame Atomic Absorption Spectrometry. American Journal of Analytical Chemistry, 4, 584-593. http://dx.doi.org/10.4236/ajac.2013.410069
- Shavandi, M.A., Haddadian, Z., Ismail, M.H., Abdullah, S.N. and Abidin, Z.Z. (2012) Continuous Metal and Oil Removal from Palm Oil Mill Effluent Using Natural Zeolite-Packed Column. Journal of the Taiwan Institute of Chemical Engineers, 43, 934-941. http://dx.doi.org/10.1016/j.jtice.2012.07.001
- Elmorsi, T.M., Riyad, Y.M., Mohamed, Z.H. and Abd El Bary, H.M. (2010) Decolorization of Mordant Red 73 Azo Dye in Water Using H2O2/UV and Photo-Fenton Treatment. Journal of Hazardous Materials, 174, 352-358. http://dx.doi.org/10.1016/j.jhazmat.2009.09.057
- Motsi, T., Rowson, N.A. and Simmons, M.J.H. (2009) Adsorption of Heavy Metals from Acid Mine Drainage by Natural Zeolite. International Journal of Mineral Processing, 92, 42-48. http://dx.doi.org/10.1016/j.minpro.2009.02.005
- Bhattacharyya, K.G. and Sharma, A. (2004) Adsorption of Pb(II) from Aqueous Solution by Azadirachta indica (Neem) Leaf Powder. Journal of Hazardous Materials, B113, 97-109. http://dx.doi.org/10.1016/j.jhazmat.2004.05.034
- Moyo, M. and Chikazaza, L. (2013) Bioremediation of Lead(II) from Polluted Wastewaters Employing Sulphuric Acid Treated Maize Tassel Biomass. American Journal of Analytical Chemistry, 4, 689-695. http://dx.doi.org/10.4236/ajac.2013.412083
- Barakat, M.A. (2011) New Trends in Removing Heavy Metals from Industrial Wastewater. Arabian Journal of Chemistry, 4, 361-377. http://dx.doi.org/10.1016/j.arabjc.2010.07.019
- Fu, F. and Qi, W. (2011) Removal of Heavy Metal Ions from Wastewaters: A Review. Journal of Environmental Management, 92, 407-418. http://dx.doi.org/10.1016/j.jenvman.2010.11.011
- Pollard, S.J.T., Fowler, G.D., Sollars, C.J. and Perry, R. (1992) Low-Cost Adsorbents for Waste and Waste-Water Treatment, a Review. Science of the Total Environment, 116, 31-52. http://dx.doi.org/10.1016/0048-9697(92)90363-W
- Chakravarty, S., Mohanty, A., Sudha, T.N., Upadhyay, A.K., Konar, J., Sircar, J.K., Madhukar, A. and Gupta, K.K. (2010) Removal of Pb(II) Ions from Aqueous Solution by Adsorption Using Bael Leaves (Aegle marmelos). Journal of Hazardous Materials, 173, 502-509. http://dx.doi.org/10.1016/j.jhazmat.2009.08.113
- Al-Subu, M.M. (2002) The Interaction Effects of Cypress (Cupressus semperirens), Cinchona (Eucalyptus longifolia) and Pine (Pinus halepensis) Leaves on Their Efficiencies for Lead Removal from Aqueous Solutions. Advances in Environmental Research, 6, 569-576.
- Kamal, M.H., Azira, W.M., Kasmawati, M., Haslizaidi, Z. and Saime, W.N. (2010) Sequestration of Toxic Pb(II) Ions by Chemically Treated Rubber (Hevea brasiliensis) Leaf Powder. Journal of Environmental Sciences, 22, 248-256. http://dx.doi.org/10.1016/S1001-0742(09)60101-7
- Chen, H., Zhao, J., Dai, G., Wu, J. and Yan, H. (2010) Adsorption Characteristics of Pb(II) from Aqueous Solution onto a Natural Biosorbent, Fallen Cinnamomum camphora Leaves. Desalination, 262, 174-182. http://dx.doi.org/10.1016/j.desal.2010.06.006
- Amanda, E.M., Milene, S.P., Alexandre, O.J., Marco, A.U.M., Rafael, I.V.S., Margarida, J.S. and Gustavo, R.C. (2013) The Reactive Surface of Castor Leaf (Ricinus communis L.) Powder as a Green Adsorbent for the Removal of Heavy Metals from Natural River Water. Applied Surface Science, 276, 24-30. http://dx.doi.org/10.1016/j.apsusc.2013.02.096
- Yuvaraja, G., Krishnaiah, N., Subbaiah, M.V. and Krishnaiah, A. (2014) Biosorption of Pb(II) from Aqueous Solution by Solanum melongena Leaf Powder as a Low-Cost Biosorbent Prepared from Agricultural Waste. Colloids and Surfaces B, 114, 75-81. http://dx.doi.org/10.1016/j.colsurfb.2013.09.039
- Aref, I.M., El Atta, H.A. and Al Ghtani, A.A. (2009) Ecological Study on Dobera glabra Forssk. At Jazan Region in Saudi Arabia. Journal of Horticulture and Forestry, 1, 198-204. http://www.academicjournals.org/jhf
- Bekele-Tesemma, A. (1993) Useful Trees and Shrubs for Ethiopia: Identification, Propagation, and Management for Agricultural and Pastoral Communities. In: Bekele-Tesemma, A., Birnie, A. and Tengnas, B., Eds., Technical Handbook, Regional Soil Conservation Unit, Nairobi, 194-195.
- Hashem, A. and El-Khiraigy, K. (2013) Bioadsorption of Pb(II) onto Anethum graveolens from Contaminated Wastewater: Equilibrium and Kinetic Studies. Journal of Environmental Protection, 4, 108-119. http://dx.doi.org/10.4236/jep.2013.41012
- Miah, M.Y., Volchek, K., Kuang, W. and Tezel, F.H. (2010) Kinetic and Equilibrium Studies of Cesium Adsorption on Ceiling Tiles from Aqueous Solutions. Journal of Hazardous Materials, 183, 712-717. http://dx.doi.org/10.1016/j.jhazmat.2010.07.084
- Qiu, H., Lv, L., Pan, B.-C., Zhang, Q.-J., Zhang, W.-M. and Zhang, Q.-X. (2009) Critical Review in Adsorption Kinetic Models. Journal of Zhejiang University Science A, 10, 716-724. http://dx.doi.org/10.1631/jzus.A0820524
- Ho, Y.S. and McKay, G. (1999) Pseudo-Second Order Model for Sorption Processes. Process Biochemistry, 34, 735- 742. http://dx.doi.org/10.1016/S0032-9592(98)00112-5
- Hameed, B.H., Din, A.T.M. and Ahmad, A.L. (2009) A Novel Agricultural Waste Adsorbent for the Removal of Cationic Dye from Aqueous Solutions. Journal of Hazardous Materials, 162, 305-311. http://dx.doi.org/10.1016/j.jhazmat.2008.05.036
- Priyantha, N. and Bandaranayaka, A. (2011) Investigation of Kinetics of Cr(VI)-Fired Brick Clay Interaction. Journal of Hazardous Materials, 188, 193-197. http://dx.doi.org/10.1016/j.jhazmat.2011.01.090
- Li, W., Zhang, L., Peng, J., Li, N., Zhang, S. and Guo, S. (2008) Tobacco Stems as a Low Cost Adsorbent for the Removal of Pb(II) from Wastewater: Equilibrium and Kinetic Studies. Industrial Crops and Products, 28, 294-302.
- Boamah, P.O., Zhang, Q., Hua, M., Huang, Y., Liu, Y., Wang, W. and Liu, Y. (2014) Lead Removal onto Cross- Linked Low Molecular Weight Chitosan Pyruvic Acid Derivatives. Carbohydrate Polymers, 110, 518-527. http://dx.doi.org/10.1016/j.carbpol.2014.03.034
- Feng, N.C., Guo, X.Y., Liang, S., Zhu, Y.S. and Liu, J.P. (2011) Biosorption of Heavy Metals from Aqueous Solutions by Chemically Modified Orange Peel. Journal of Hazardous Materials, 185, 49-54. http://dx.doi.org/10.1016/j.jhazmat.2010.08.114
- Singha, B., Naiya, T.K., Bhattacharya, A.K. and Das, S.K. (2011) Cr(VI) Ions Removal from Aqueous Solutions Using Natural Adsorbents―FTIR Studies. Journal of Environmental Protection, 2, 729-735.
- Elmorsi, T.M. (2011) Equilibrium Isotherms and Kinetic Studies of Removal of Methylene Blue Dye by Adsorption onto Miswak Leaves as a Natural Adsorbent. Journal of Environmental Protection, 2, 817-827. http://dx.doi.org/10.4236/jep.2011.26093
- Pahlavanzadeh, H., Keshtkar, A.R., Safdari, J. and Abadi, Z. (2010) Biosorption of Nickel(II) from Aqueous Solution by Brown Algae: Equilibrium, Dynamic and Thermodynamic Studies. Journal of Hazardous Materials, 175, 304-310. http://dx.doi.org/10.1016/j.jhazmat.2009.10.004
- Wang, Y., Lu, Y.F., Chen, R.Z., Ma, L., Jiang, Y. and Wang, H. (2014) Lead Ions Sorption from Waste Solution Using Aluminum Hydroxide Modified Diatomite. Journal of Environmental Protection, 5, 509-516. http://dx.doi.org/10.4236/jep.2014.56054
- Pokhrel, D. and Viraraghavan, T. (2008) Arsenic Removal from an Aqueous Solution by Modified A. niger Biomass: Batch Kinetic and Isotherm Studies. Journal of Hazardous Materials, 150, 818-825. http://dx.doi.org/10.1016/j.jhazmat.2007.05.041
- Senthilkumaar, S., Varadarajan, P.R., Porkodi, K. and Subbhuraam, C.V. (2005) Adsorption of Methylene Blue onto Jute Fiber Carbon: Kinetics and Equilibrium Studies. Journal of Colloid and Interface Science, 284, 78-82. http://dx.doi.org/10.1016/j.jcis.2004.09.027
- Heidari, H.Y., Mehraban, Z. and Heikkinen, H. (2013) Selective Adsorption of Pb(II), Cd(II), and Ni(II) Ions from Aqueous Solution Using Chitosan-MAA Nanoparticles. International Journal of Biological Macromolecules, 61, 251- 263. http://dx.doi.org/10.1016/j.ijbiomac.2013.06.032
- Giraldo1, L. and Moreno-Piraján, J.C. (2008) Pb2+ Adsorption from Aqueous Solutions on Activated Carbons Obtained from Lignocellulosic Residues. Brazilian Journal of Chemical Engineering, 25, 143-151.
- Srivastava, V.C., Mall, I.D. and Mishra, I.M. (2006) Characterization of Mesoporous Rice Husk Ash (RHA) and Adsorption Kinetics of Metal Ions from Aqueous Solution onto RHA. Journal of Hazardous Materials, 134, 257-267. http://dx.doi.org/10.1016/j.jhazmat.2005.11.052
- Paulino, A.T., Guilherme, M.R., Reis, A.V., Tambourgi, E.B., Nozaki, J. and Muniz, E.C. (2007) Capacity of Adsorption of Pb2+ and Ni2+ from Aqueous Solutions by Chitosan Produced from Silkworm Chrysalides in Different Degrees of Deacetylation. Journal of Hazardous Materials, 147, 139-147. http://dx.doi.org/10.1016/j.jhazmat.2006.12.059
- Manzoor, Q., Nadeem, R., Iqbal, M., Saeed, R. and Ansari, T.M. (2013) Organic Acids Pretreatment Effect on Rosa bourbonia Phyto-Biomass for Removal of Pb(II) and Cu(II) from Aqueous Media. Bioresource Technology, 132, 446- 452. http://dx.doi.org/10.1016/j.biortech.2013.01.156
- Liu, Y., Liu, Z., Gao, J., Dai, J., Han, J., Wang, Y., Xie, J. and Yan, Y. (2011) Selective Adsorption Behavior of Pb(II) by Mesoporous Silica SBA-15-Supported Pb(II)-Imprinted Polymer Based on Surface Molecularly Imprinting Technique. Journal of Hazardous Materials, 186, 197-205. http://dx.doi.org/10.1016/j.jhazmat.2010.10.105
NOTES
*Corresponding author.