Advances in Pure Mathematics
Vol.3 No.3(2013), Article ID:31464,6 pages DOI:10.4236/apm.2013.33054
Torsion Pairs in Triangulated Categories
College of Applied Sciences, Beijing University of Technology, Beijing, China
Email: fanchunyan@emails.bjut.edu.cn
Copyright © 2013 Chunyan Fan, Hailou Yao. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 28, 2013; March 30, 2013; accepted April 26, 2013
Keywords: d-Ext-Projectivity (d-Ext-Injectivity); Torsion Pairs;  -Mutation; Triangulated Category
-Mutation; Triangulated Category
ABSTRACT
We study the properties of torsion pairs in triangulated category ![]() by introducing the notions of d-Ext-projectivity and d-Ext-injectivity. In terms of
by introducing the notions of d-Ext-projectivity and d-Ext-injectivity. In terms of  -mutation of torsion pairs, we investigate the properties of torsion pairs in triangulated category
-mutation of torsion pairs, we investigate the properties of torsion pairs in triangulated category  under some conditions on subcategories
under some conditions on subcategories ![]() and
and  in
in![]() .
.
1. Introduction
The notion of torsion theory (torsion pairs) in abelian categories was introduced by Dickson in 1966. Torsion theory plays an important role in the investigation of an abelian category. An abelian category is naturally embedded in a triangulated category like the bounded derived category. The analogous definition of torsion pairs in triangulated category is closely related to the notion of a t-structure. Beilinson, Bernstein and Deligne [1] introduce the definition of a t-structure in a triangulated category![]() .The t-structure is a pair
.The t-structure is a pair 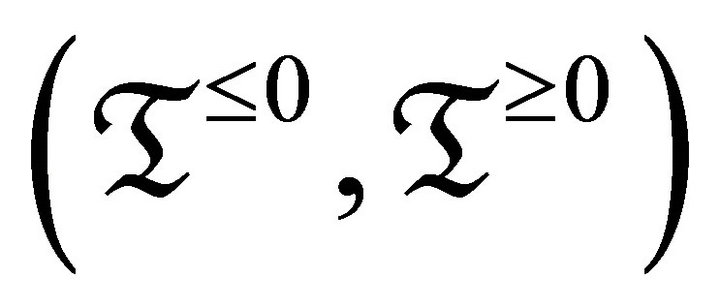 of full subcategories such that setting
of full subcategories such that setting 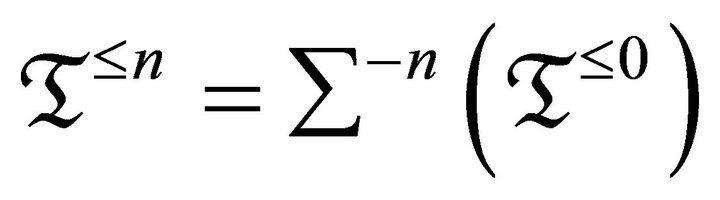 and
and
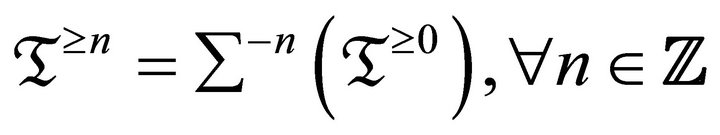 , satisfying:
, satisfying:
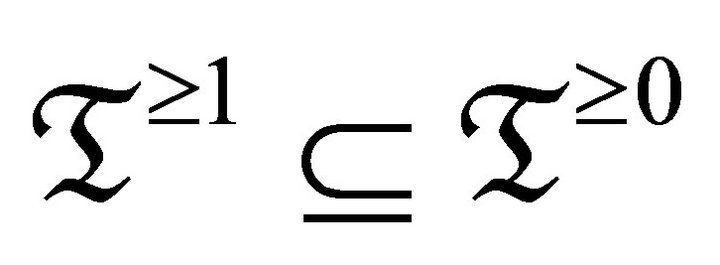
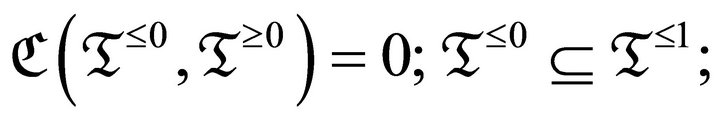 ; any object
; any object
 is included in a triangle
is included in a triangle
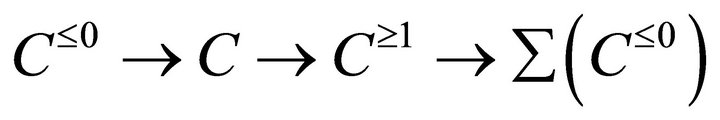 where
where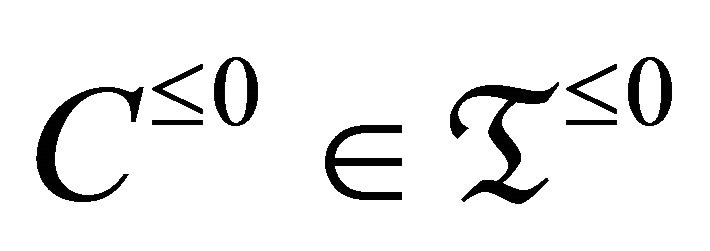 , and
, and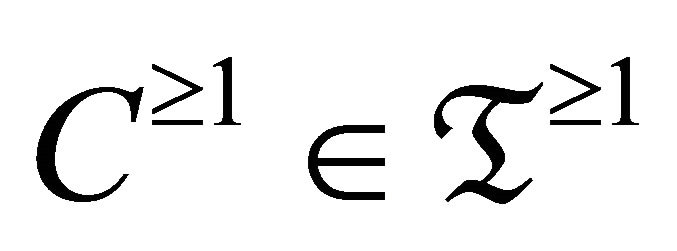 . In [2], Beligiannis and Reiten studied the torsion theory on pretriangulated, triangulated and stable categories. They discussed the connection between torsion theories in abelian and derived categories and indicated the relationship with tilting theory, they point out that the torsion pairs in triangulated category and t-structures essentially coincide. In 1987, Gorodentsev and Rudakov [3] made use of mutation when they classified the exceptional vector bundles on
. In [2], Beligiannis and Reiten studied the torsion theory on pretriangulated, triangulated and stable categories. They discussed the connection between torsion theories in abelian and derived categories and indicated the relationship with tilting theory, they point out that the torsion pairs in triangulated category and t-structures essentially coincide. In 1987, Gorodentsev and Rudakov [3] made use of mutation when they classified the exceptional vector bundles on  where
where  is a projective space. Mutation can be regarded as a categorical realization of Coxeter or braid groups. In [4] and [5], Fomin and Zelevinsky introduced cluster algebras, these algebras give an algebraic and combinational framework for the positivity and canonical basis of quantum groups, which enjoy important combinational properties given in terms of the mutation for skew symmetric matrices. Cluster categories were introduced in [6], in which the mutation of cluster tilting objects was introduced. Recently, Geiss, Leclerc and Schroer [7] applied mutation to study rigid modules over preprojective algebras and the coordinate rings of maximal unipotent subgroups of semisimple Lie groups. Later Iyama and Yoshino [8] introduced the mutation of n-cluster tilting subcategories based on approximation theory. Recently, Zhou and Zhu [9] studied the notion of
is a projective space. Mutation can be regarded as a categorical realization of Coxeter or braid groups. In [4] and [5], Fomin and Zelevinsky introduced cluster algebras, these algebras give an algebraic and combinational framework for the positivity and canonical basis of quantum groups, which enjoy important combinational properties given in terms of the mutation for skew symmetric matrices. Cluster categories were introduced in [6], in which the mutation of cluster tilting objects was introduced. Recently, Geiss, Leclerc and Schroer [7] applied mutation to study rigid modules over preprojective algebras and the coordinate rings of maximal unipotent subgroups of semisimple Lie groups. Later Iyama and Yoshino [8] introduced the mutation of n-cluster tilting subcategories based on approximation theory. Recently, Zhou and Zhu [9] studied the notion of  -mutation of torsion pairs in triangulated categories, and they proved that the
-mutation of torsion pairs in triangulated categories, and they proved that the  -mutation of torsion pairs in triangulated categories is a torsion pair.They also studied its geometric meaning when the triangulated categories are the cluster categories of type
-mutation of torsion pairs in triangulated categories is a torsion pair.They also studied its geometric meaning when the triangulated categories are the cluster categories of type 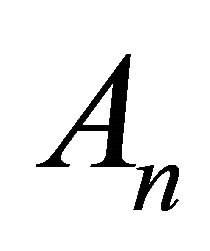 or
or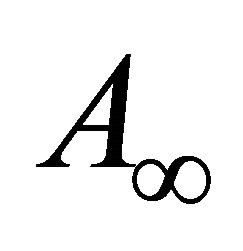 .
.
In this paper, we study the torsion pairs in triangulated categories and their properties in terms of  -mutation pair. In a fixed triangulated category
-mutation pair. In a fixed triangulated category![]() , we give the definition of torsion pairs in
, we give the definition of torsion pairs in ![]() and study their properties with the notion of subcategory
and study their properties with the notion of subcategory 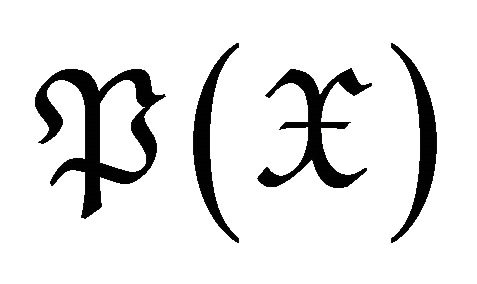 (resp.
(resp.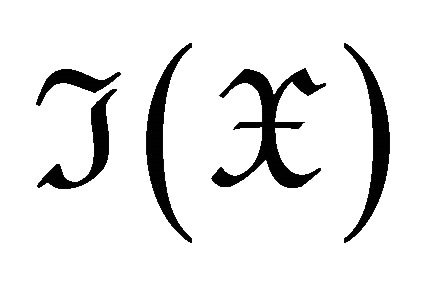 ) whose objects are d-Ext-projective (resp. d-Extinjective). Under reasonable conditions on subcategories
) whose objects are d-Ext-projective (resp. d-Extinjective). Under reasonable conditions on subcategories  and
and ![]() of
of![]() , we study the properties of torsion pairs in triangulated category
, we study the properties of torsion pairs in triangulated category  in terms of
in terms of  - mutation pair.
- mutation pair.
2. Preliminaries
Through this paper, let ![]() be a triangulated category. We introduce some basic notions which will be used. Let
be a triangulated category. We introduce some basic notions which will be used. Let  and
and  be subcategories of
be subcategories of![]() . We put
. We put
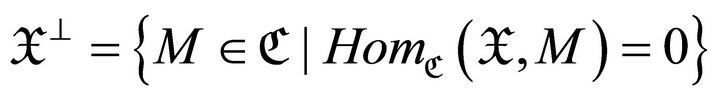
and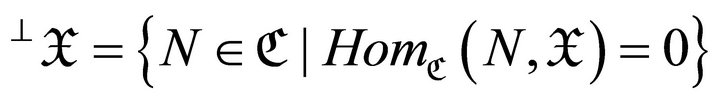 .
.
We denote by  the collection of objects in
the collection of objects in  consisting of all such
consisting of all such 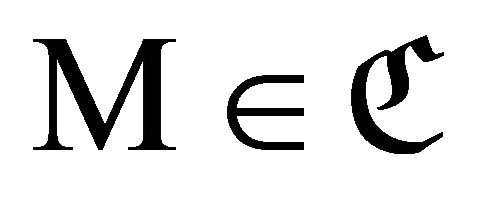 with the triangle
with the triangle

where  By the octahedralaxiom, we have
By the octahedralaxiom, we have .
.
Definition 2.1 We call a pair 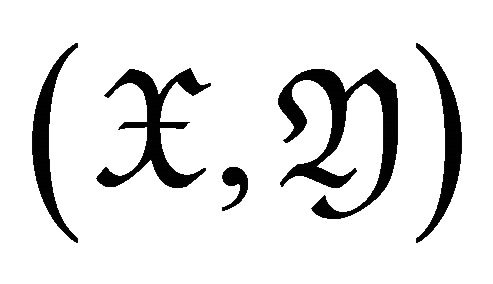 of subcategories of
of subcategories of ![]() a torsion pair if
a torsion pair if 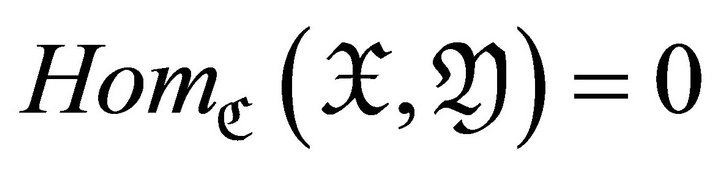 and
and
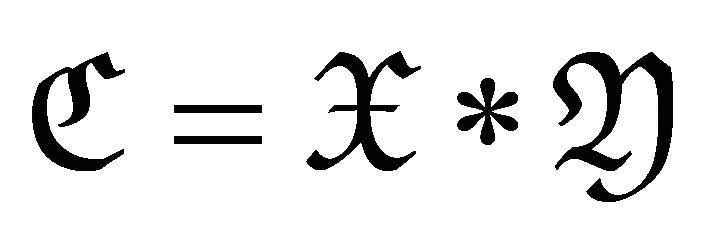 .
.
In this case, we can see that 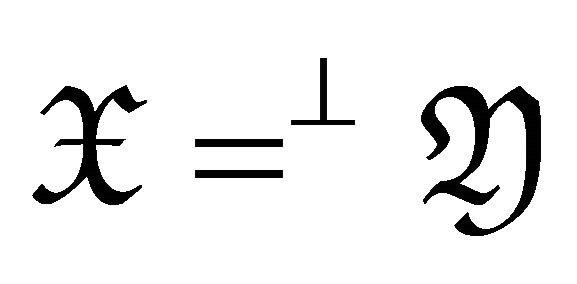 and
and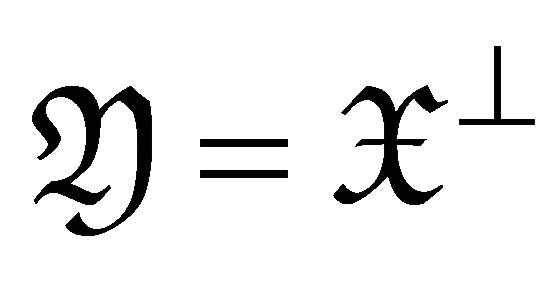 .
.
Let 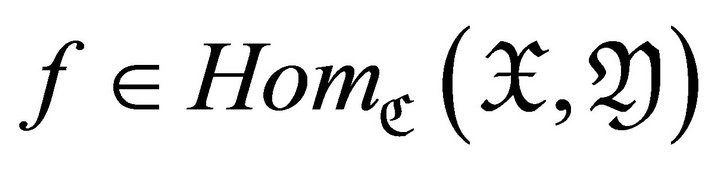 be a morphism, we call
be a morphism, we call 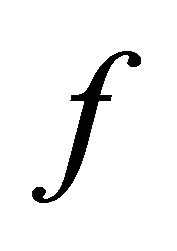 a right
a right 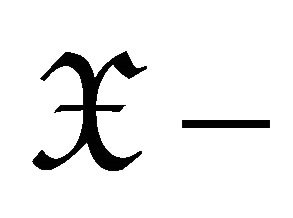 approximation of
approximation of 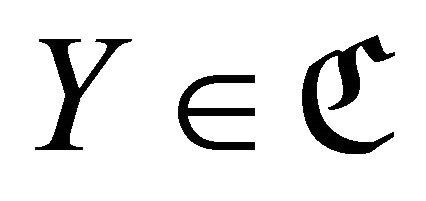 [10] if
[10] if 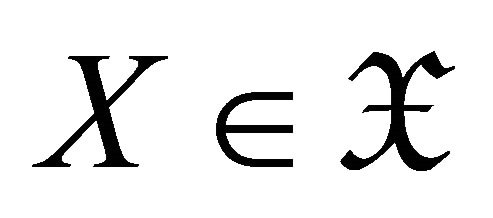 and
and
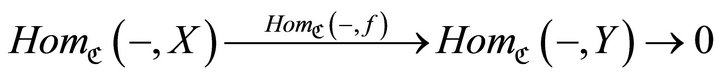
is exact as functors on . We call
. We call  a contravariantly finite subcategory of
a contravariantly finite subcategory of ![]() if any
if any 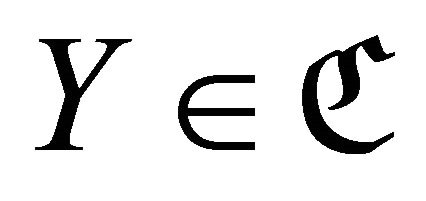 has a right
has a right  - approximation. Dually, for a morphism
- approximation. Dually, for a morphism 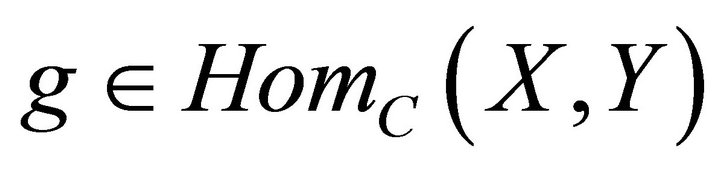 , we call
, we call ![]() a left
a left  -approximation of
-approximation of  if
if  and
and
 is exact. We call
is exact. We call ![]() a covariantly finite subcategory of
a covariantly finite subcategory of![]() if any
if any 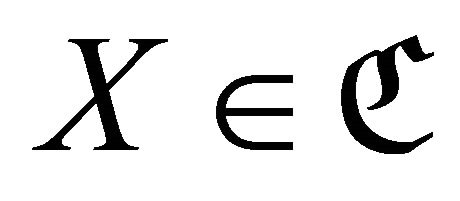 has a left
has a left  -approximation.
-approximation.
Let  be a subcategory of
be a subcategory of![]() , we call
, we call 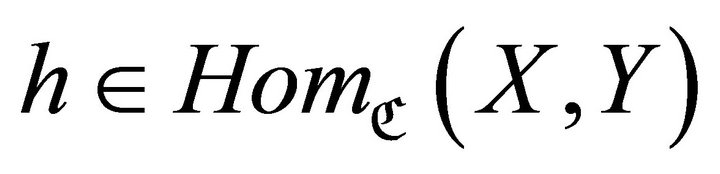
 -monic (resp.
-monic (resp.  -epic) if
-epic) if
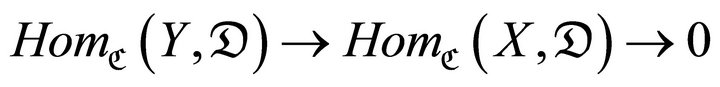 (resp.
(resp.
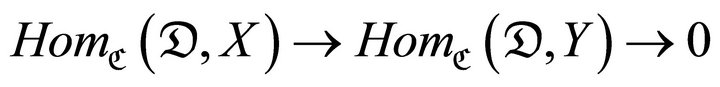 ) is exact.
) is exact.
3. Torsion Pairs in Triangulated Categories
In this section, we introduce ![]() -cluster tilting torsion pairs, rigid torsion pairs and maximal rigid torsion pairs in a triangulated category
-cluster tilting torsion pairs, rigid torsion pairs and maximal rigid torsion pairs in a triangulated category![]() , and study the properties of these torsion pairs.
, and study the properties of these torsion pairs.
Definition 3.1 Let  be an extension-closed subcategory of
be an extension-closed subcategory of![]() . An object
. An object 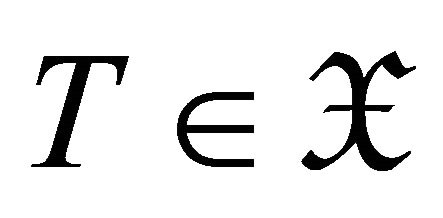 is called a d-Extprojective object of
is called a d-Extprojective object of  if
if  for all
for all 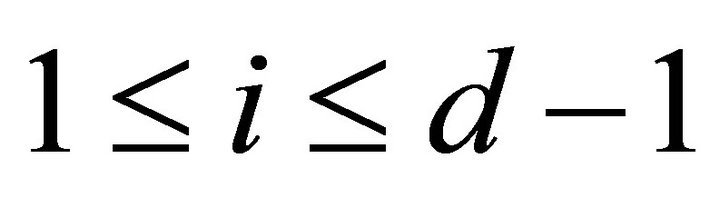 . The d-Ext-injective objects of
. The d-Ext-injective objects of are defined dually. An object
are defined dually. An object 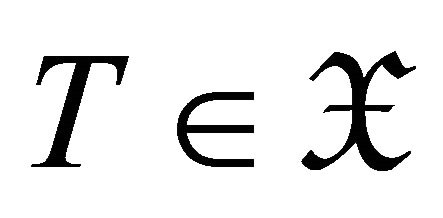 is called a d-Ext-injective object of
is called a d-Ext-injective object of  if
if 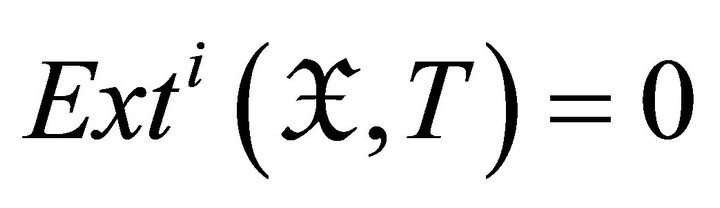 for all
for all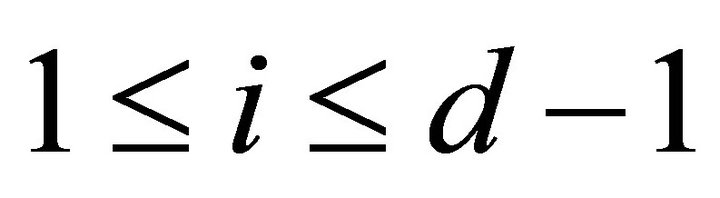 . The subcategory of
. The subcategory of  consisting of d-Ext-projective (or d-Ext-injective) objects in
consisting of d-Ext-projective (or d-Ext-injective) objects in is denoted by
is denoted by 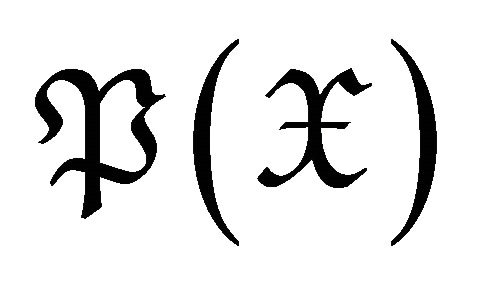 (
(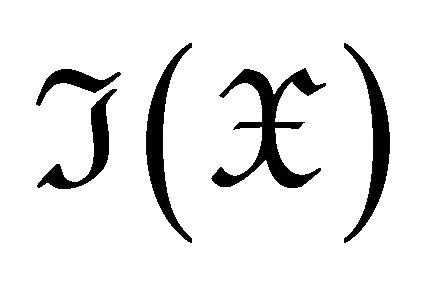 respectively).
respectively).
Definition 3.2 Let  and
and  be subcategories of the triangulated category
be subcategories of the triangulated category![]() .
.
1) The pair  is called a
is called a ![]() -cluster tilting torsion pair if
-cluster tilting torsion pair if  is a torsion pair and satisfies the property:
is a torsion pair and satisfies the property:  is functorially finite in
is functorially finite in ![]() and
and 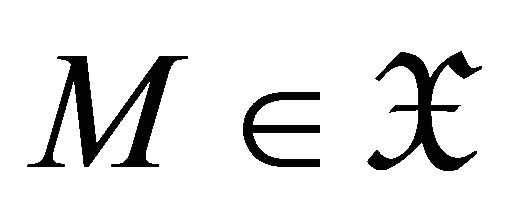 if and only if
if and only if 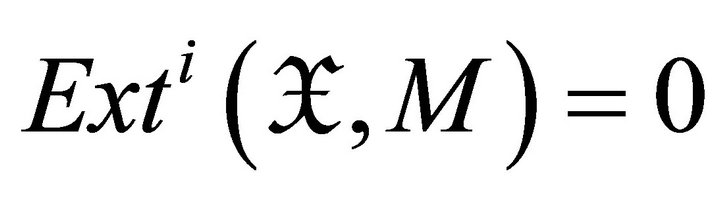 for all
for all 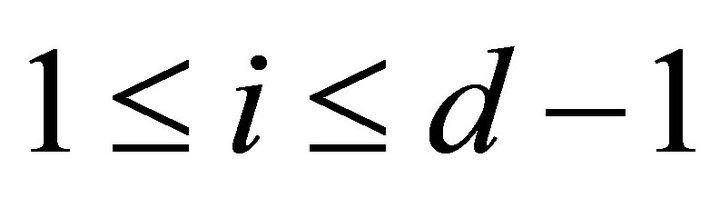 [11].
[11].
2) The pair  is called a rigid torsion pair if
is called a rigid torsion pair if 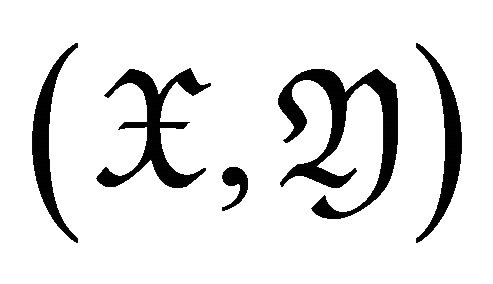 is a torsion pair and
is a torsion pair and 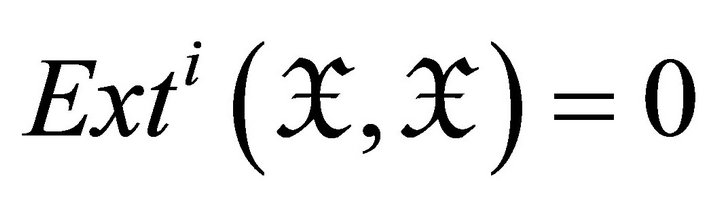 for all
for all 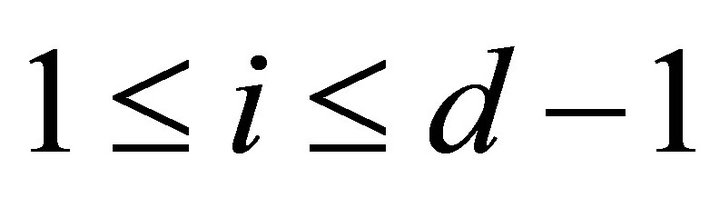 [12].
[12].
3) The pair  is called a maximal rigid torsion pair provided that
is called a maximal rigid torsion pair provided that 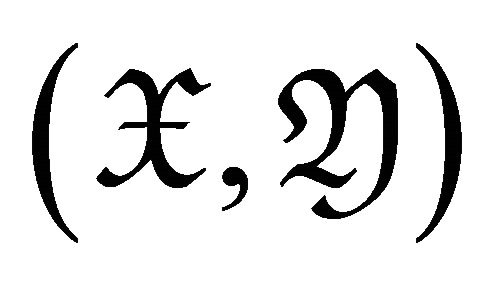 is a torsion pair,
is a torsion pair,  is a rigid subcategory and satisfies the property:
is a rigid subcategory and satisfies the property:
if 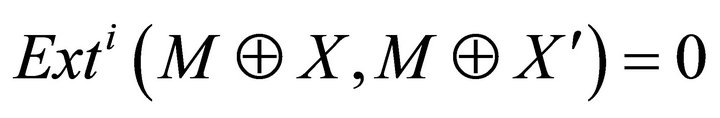 for any
for any 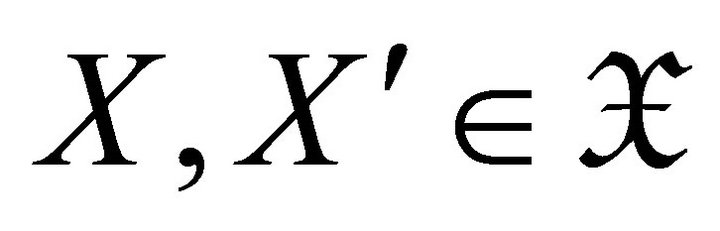 and all
and all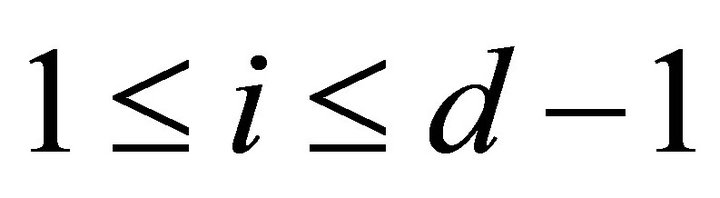 , then
, then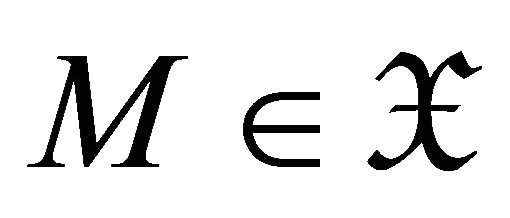 . In this case, the subcategory
. In this case, the subcategory  is called a maximal rigid subcategory [13].
is called a maximal rigid subcategory [13].
Corollary 3.3 A pair 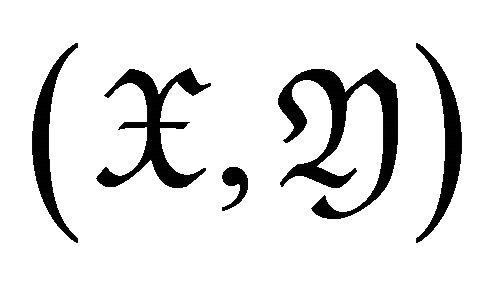 is a maximal rigid torsion pair if and only if
is a maximal rigid torsion pair if and only if  for all
for all 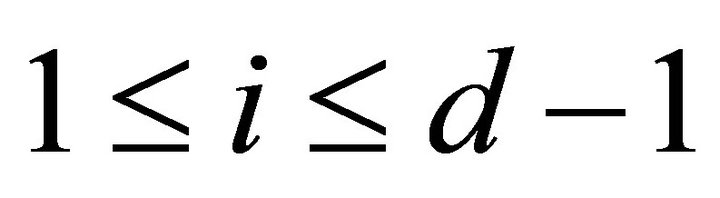 and for any rigid object
and for any rigid object 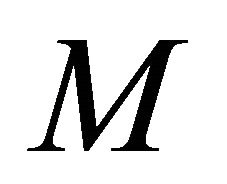 in
in![]() , we have
, we have
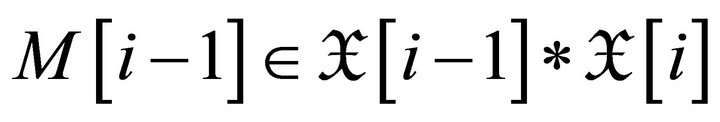 for all
for all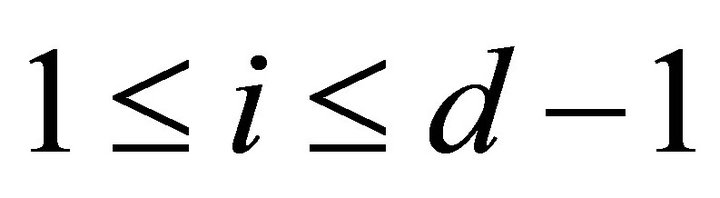 .
.
Proof: Now supposing 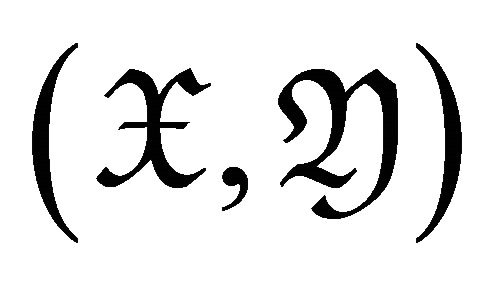 is a maximal rigid torsion pair, by the definition we have
is a maximal rigid torsion pair, by the definition we have
 and
and
 for all
for all . It implies
. It implies 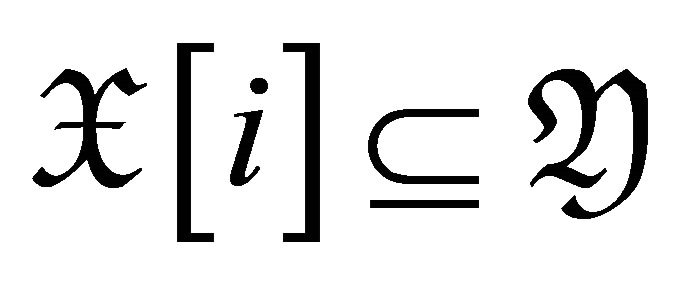 for all
for all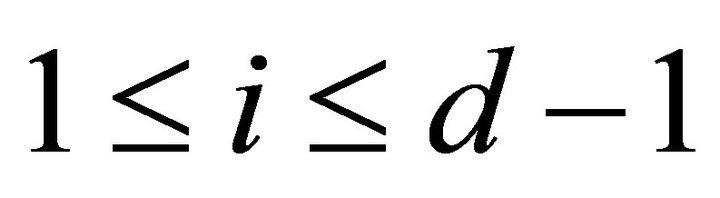 . For any rigid object
. For any rigid object  in
in![]() , take a triangle
, take a triangle
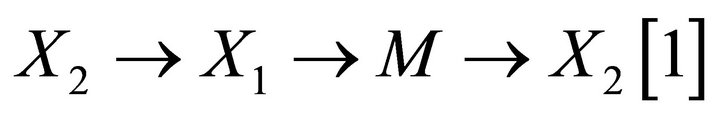
where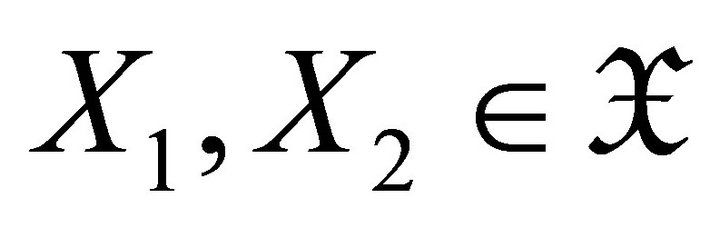 . Then we have the triangle
. Then we have the triangle
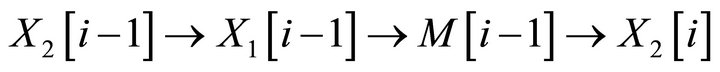
It follows that 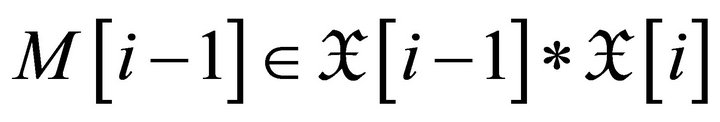 for all
for all 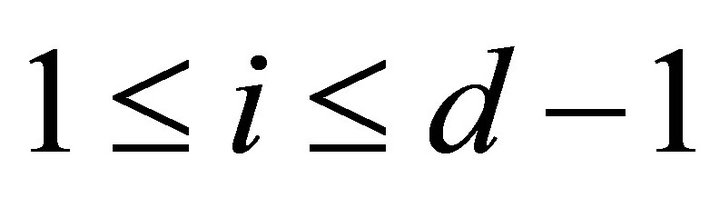 .
.
Conversely, suppose  is a torsion pair with
is a torsion pair with 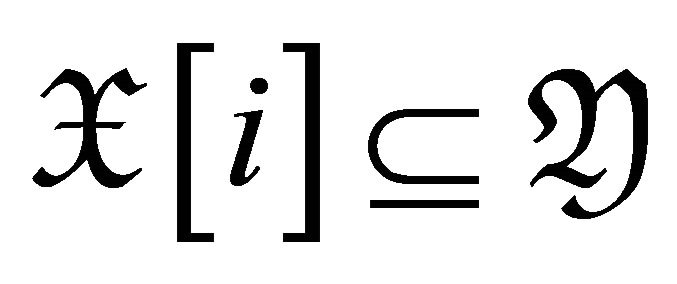 for all
for all 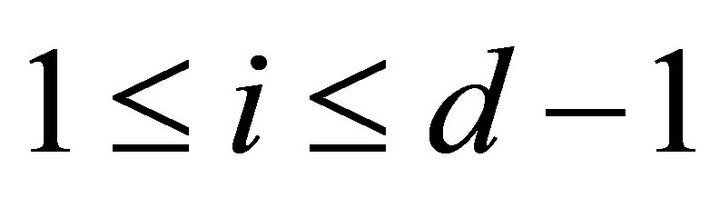 and
and
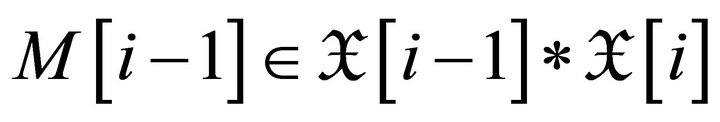 for any rigid object
for any rigid object  while
while
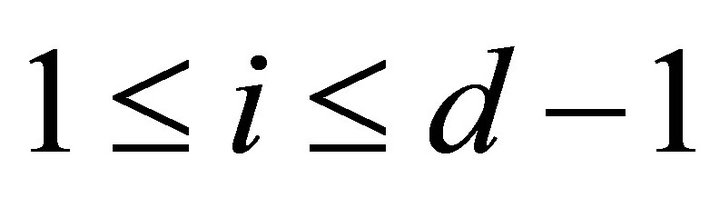 , then
, then  is rigid. If there exists an object
is rigid. If there exists an object  in
in ![]() such that
such that 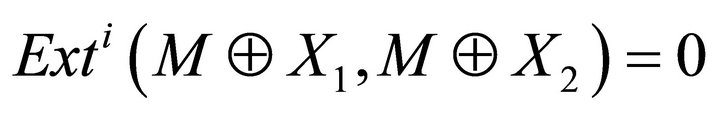 for any
for any 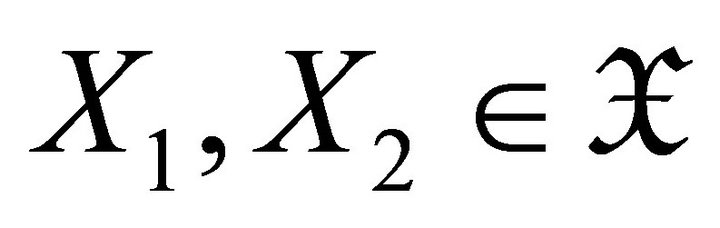 and all
and all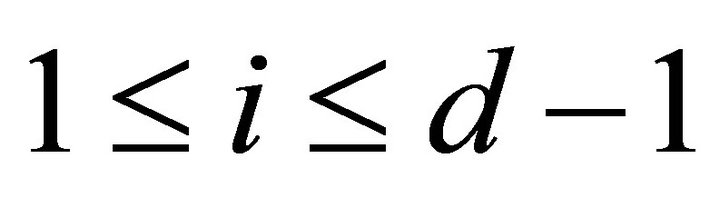 . Then
. Then 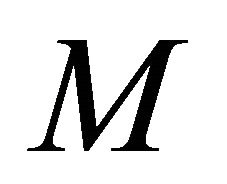 is rigid. It follows that there is a triangle
is rigid. It follows that there is a triangle
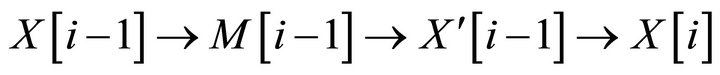
for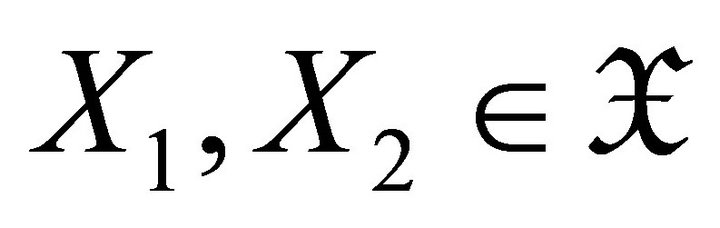 .
.
Then the above triangle splits. This implies that
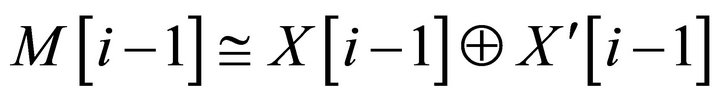
for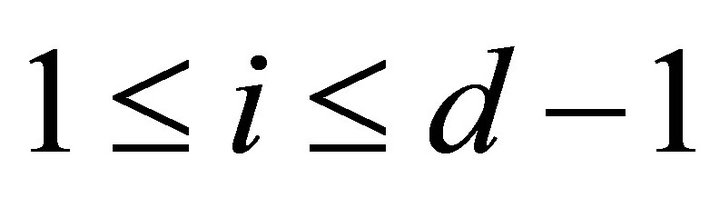 , i.e.,
, i.e., .
.  is maximal rigid.
is maximal rigid.
Corollary 3.4 A pair 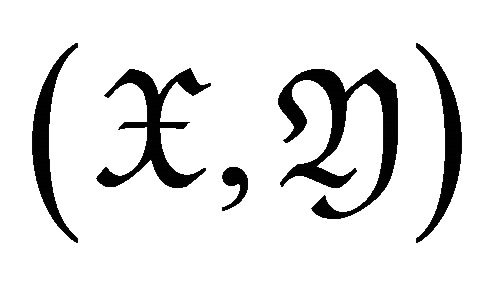 is a
is a ![]() -cluster tilting torsion pair if and only if
-cluster tilting torsion pair if and only if  is functorially finite and
is functorially finite and  for all
for all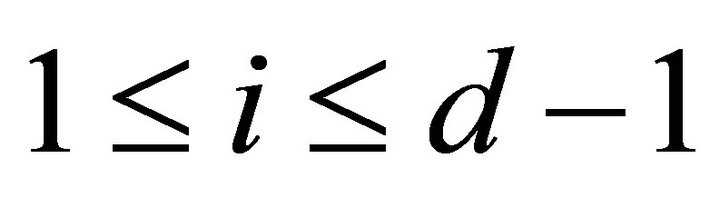 .
.
Proof: By the definition, if we have
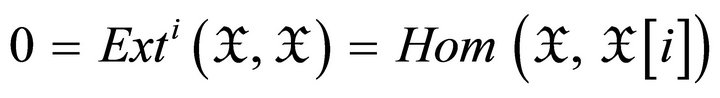 for all
for all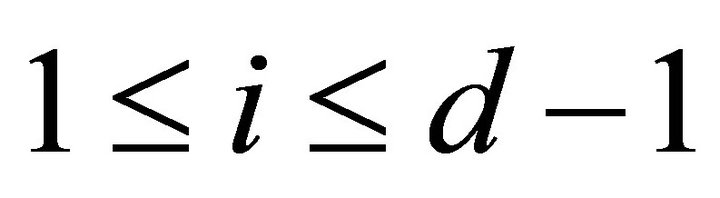 then we obtain
then we obtain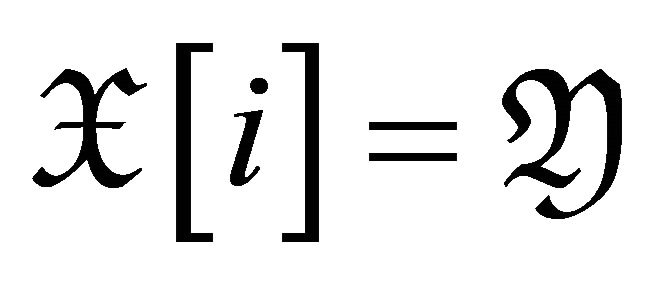 . On the other hand,
. On the other hand,
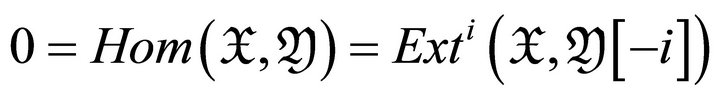 for all
for all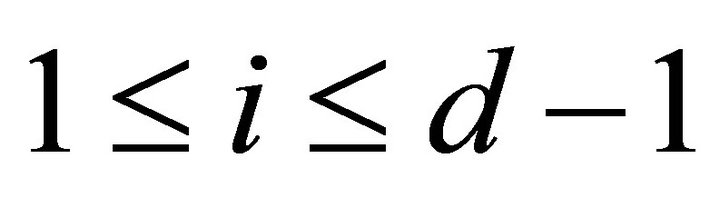 , it implys
, it implys , i.e,
, i.e, . So
. So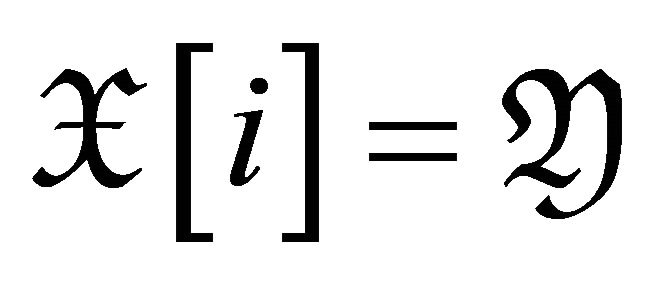 .
.
Conversely, we only need to prove that  if and only if
if and only if 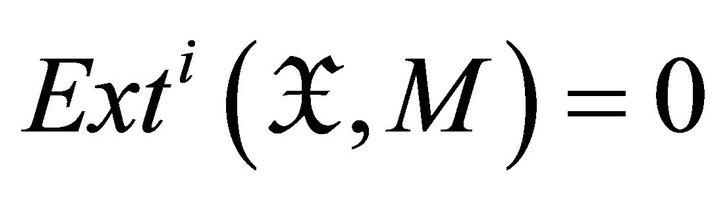 for all
for all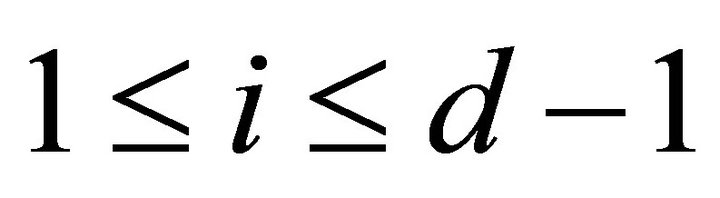 . Supposing
. Supposing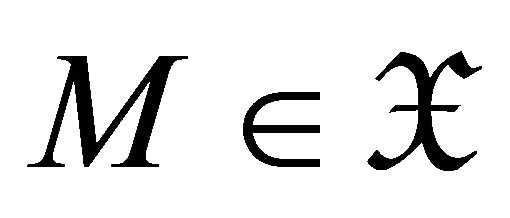 , we have
, we have
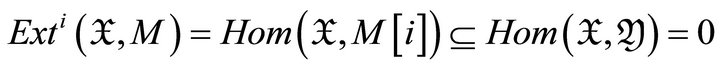 for
for
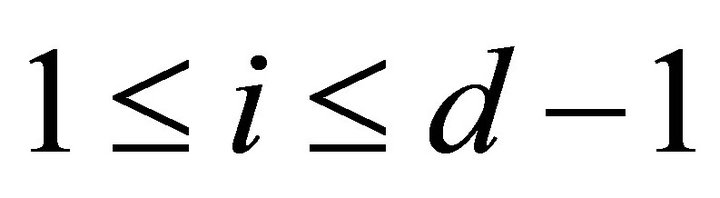 . Now, if
. Now, if 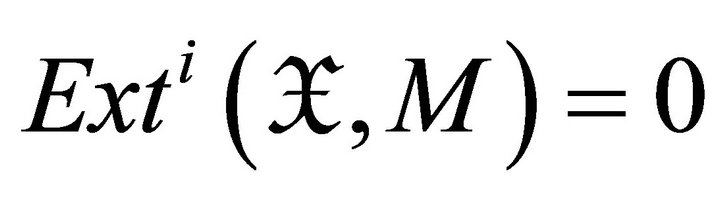 for
for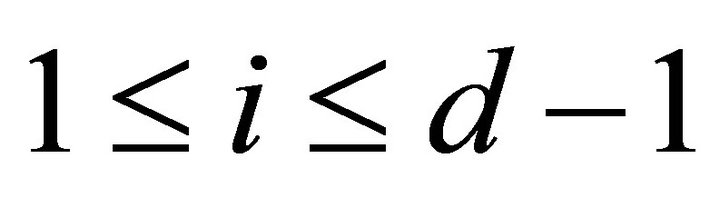 we have that
we have that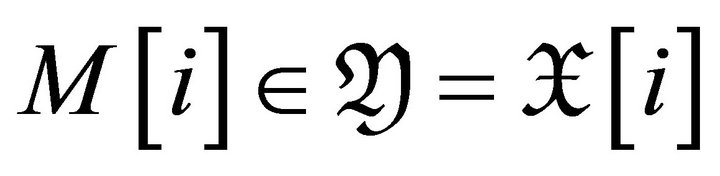 , since
, since
 . This implies
. This implies .
.
Proposition 3.5 Let 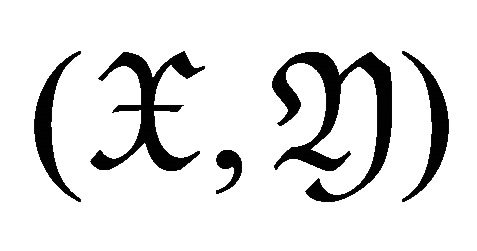 be a rigid torsion pairthen
be a rigid torsion pairthen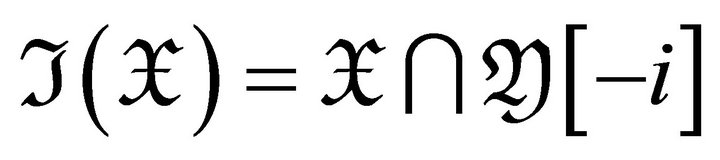 ,
, 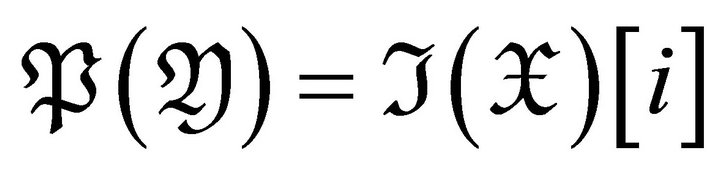 for all
for all
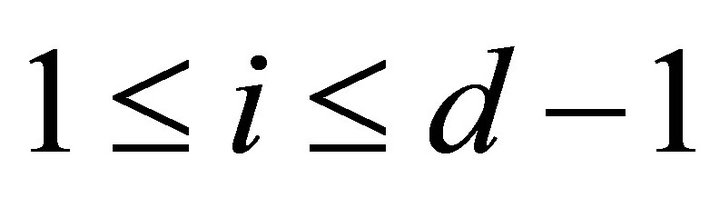 . Moreover,
. Moreover, 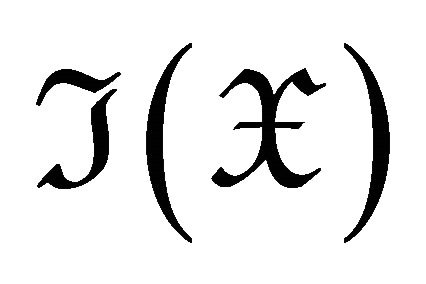 is covariantly finite in
is covariantly finite in  and
and  is contravariantly finite in
is contravariantly finite in .
.
Proof: Let , we have that
, we have that
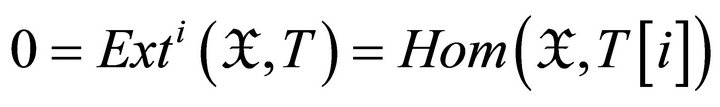 for
for  if and only if
if and only if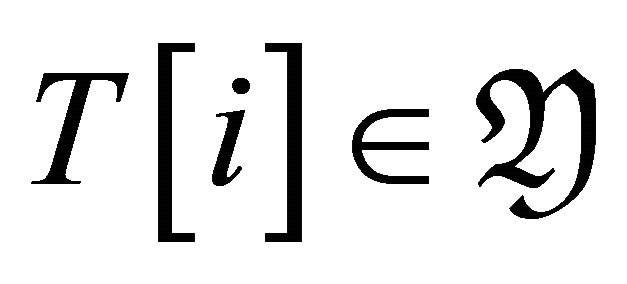 . Then
. Then 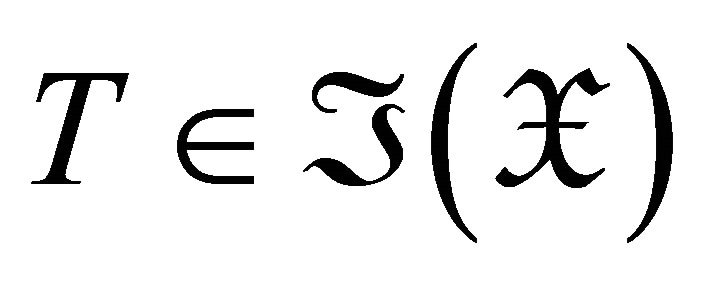 if and only if
if and only if
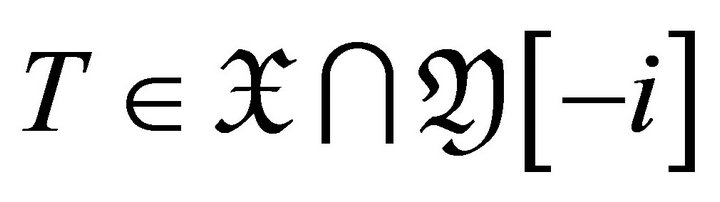 . For
. For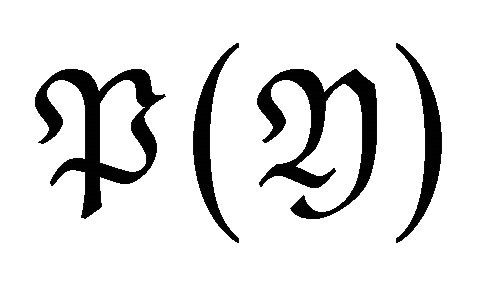 , let
, let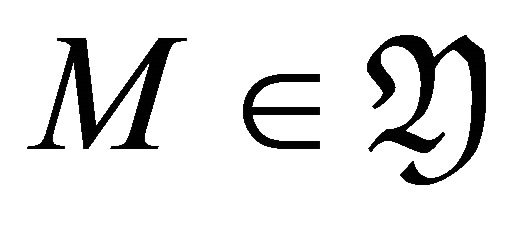 ,
,
 if and only if
if and only if
 . Since
. Since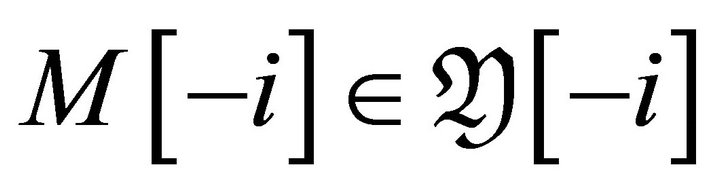 , we have that
, we have that
 if and only if
if and only if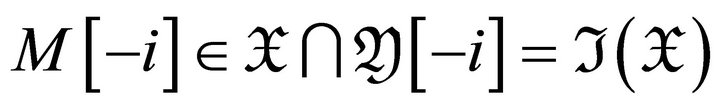 , i.e., if and only if
, i.e., if and only if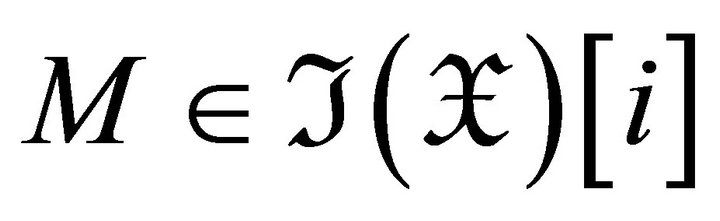 .
.
Now we prove that 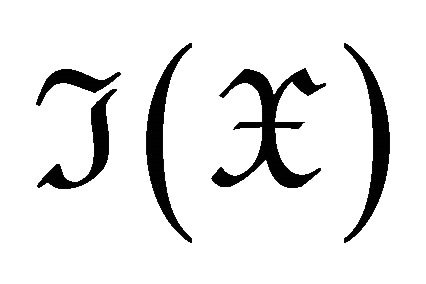 is covariantly finite in
is covariantly finite in .
.
Since 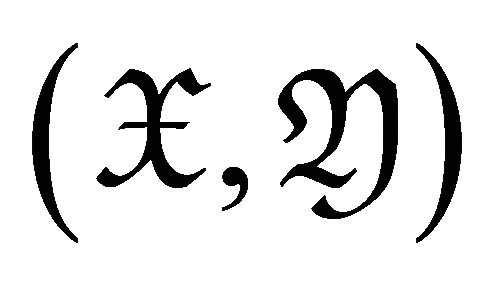 is a torsion pair, we have that
is a torsion pair, we have that
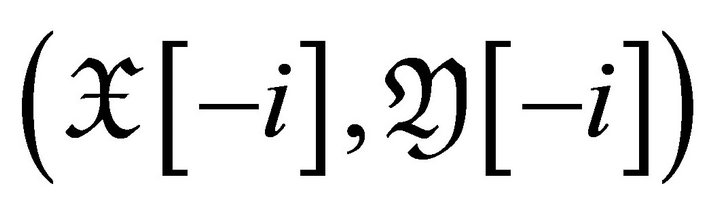 is a torsion pair for
is a torsion pair for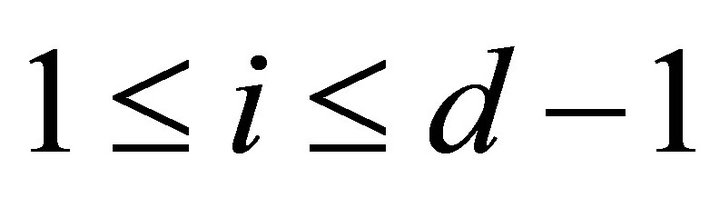 . For any object
. For any object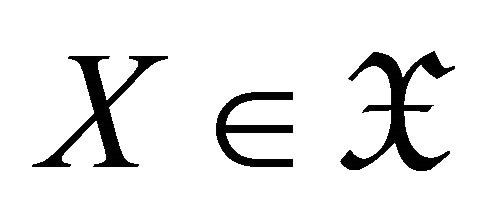 , take a triangle
, take a triangle

where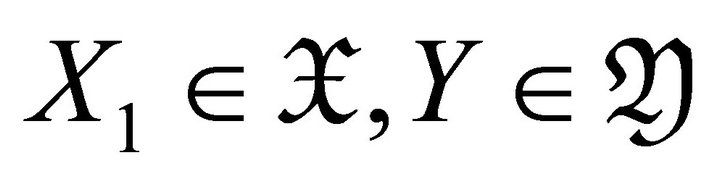 . Then we have a triangle
. Then we have a triangle
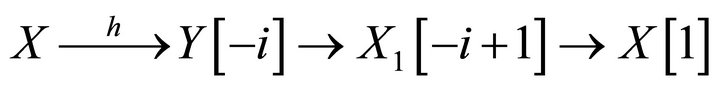 .
.
When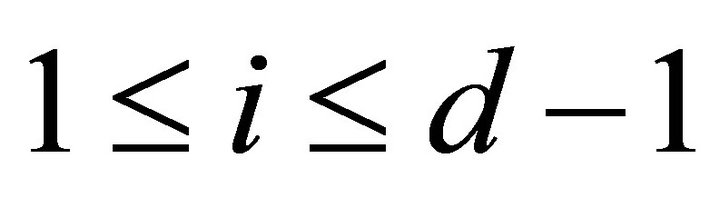 , then
, then
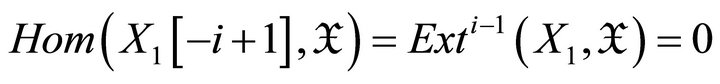 . Applying functor
. Applying functor  to the triangle above, we obtain
to the triangle above, we obtain
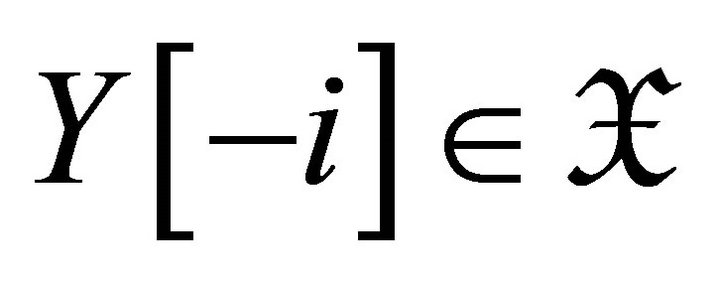 . Since
. Since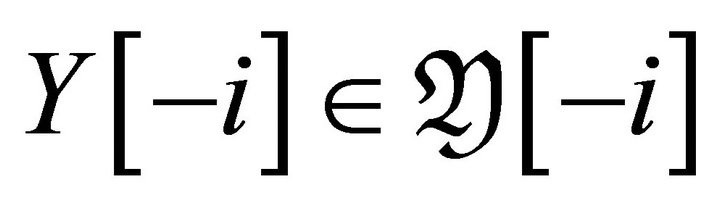 , we have
, we have
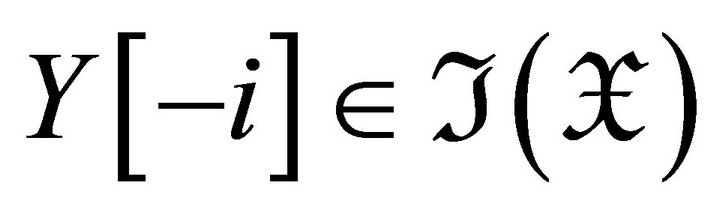 . Then
. Then  is a left
is a left 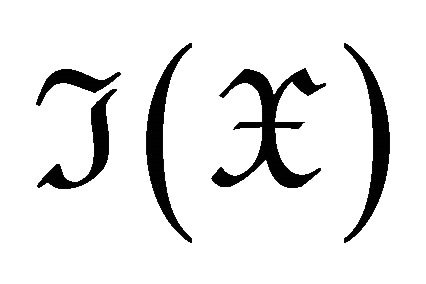 -approximation of
-approximation of . Thus
. Thus 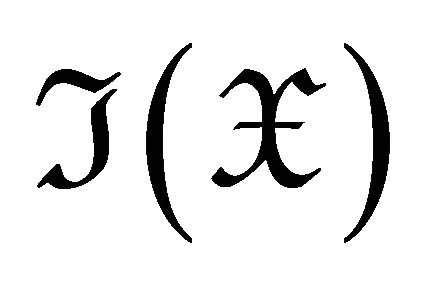 is covariantly finite in
is covariantly finite in .
.
When![]() , we have that
, we have that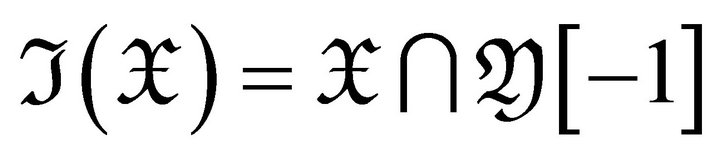 . For any
. For any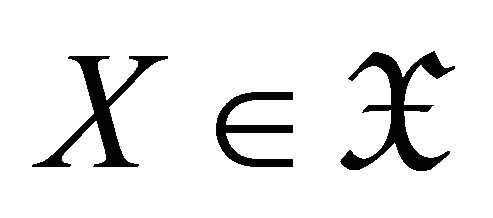 , take a triangle
, take a triangle
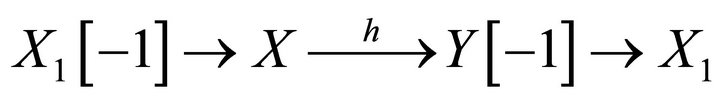
where 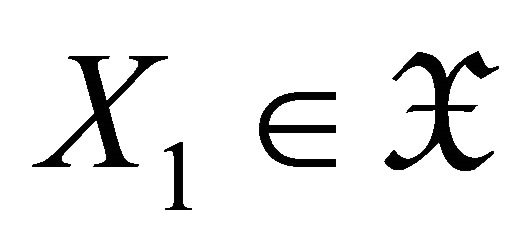 and
and . Then we have the triangle
. Then we have the triangle
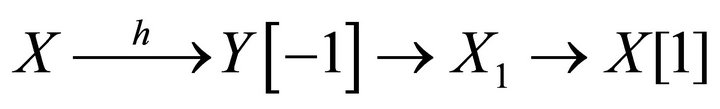
Since  is extension-closed, we obtain that
is extension-closed, we obtain that
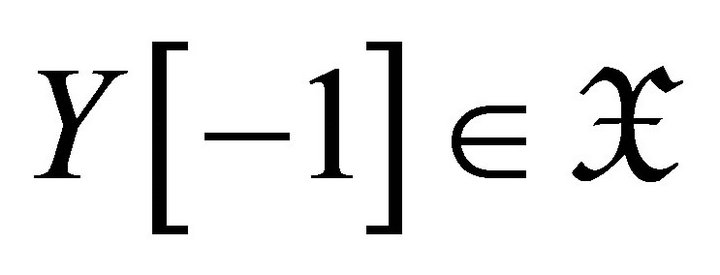 , and hence
, and hence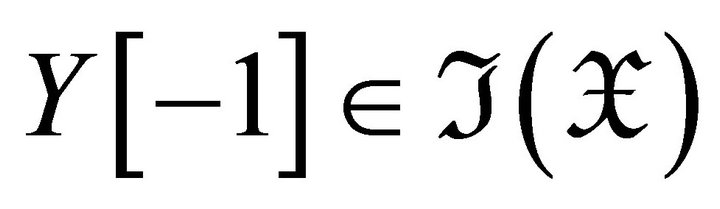 . It is easy to see that
. It is easy to see that 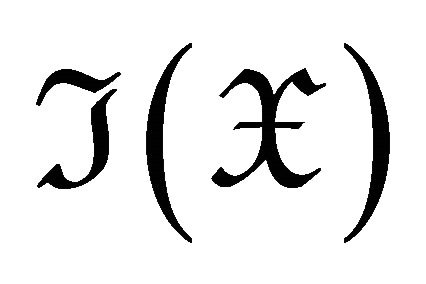 is covariantly finite in
is covariantly finite in .
.
Finally, we prove 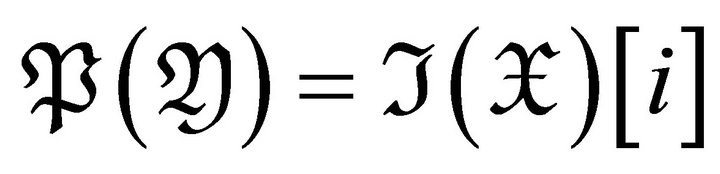 is contravariantly finite in
is contravariantly finite in . In case
. In case![]() , we have
, we have
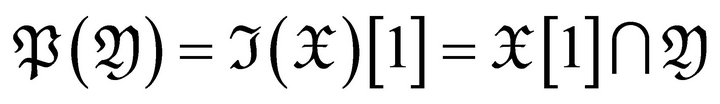 .
.
Since 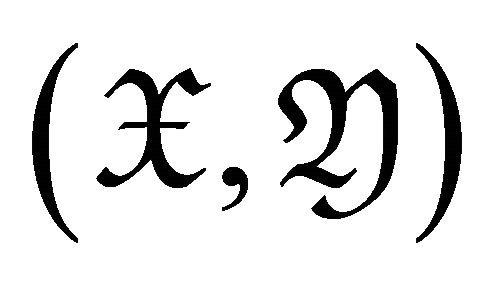 is a torsion pair, for any
is a torsion pair, for any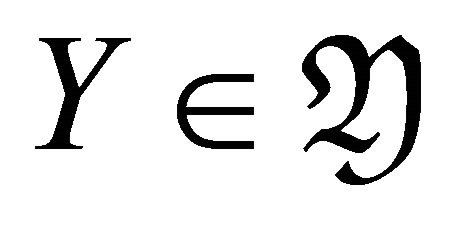 , there exists a triangle
, there exists a triangle
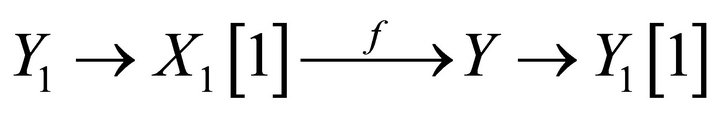
where 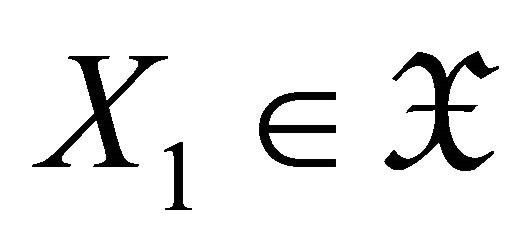 and
and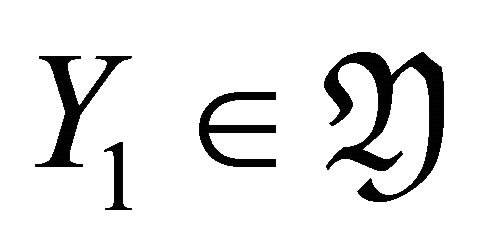 . Since
. Since 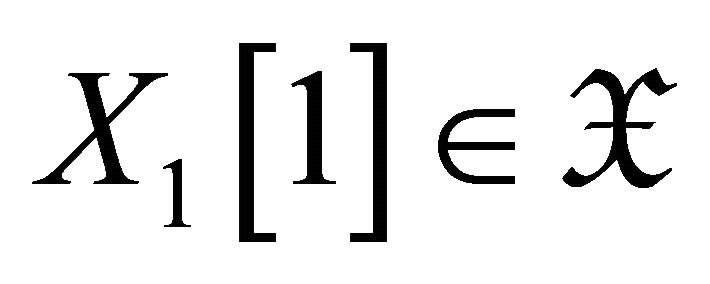 and
and ![]() is closed under extensions, we have
is closed under extensions, we have , and hence
, and hence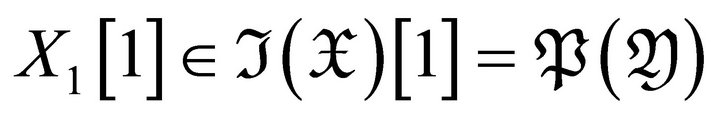 . It follows that
. It follows that  is a right
is a right  approximation of
approximation of , and then
, and then 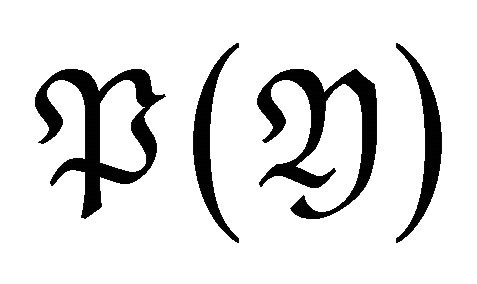 is contravariantly finite in
is contravariantly finite in .
.
In case , we have
, we have
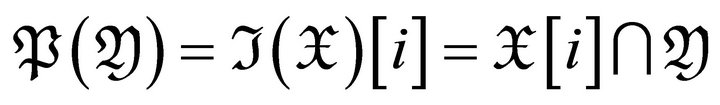 for and
for and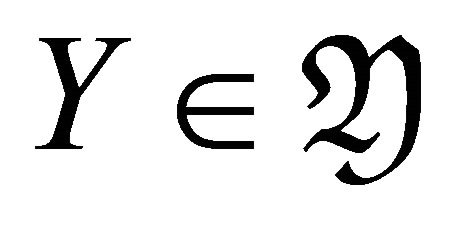 . Take a triangle
. Take a triangle
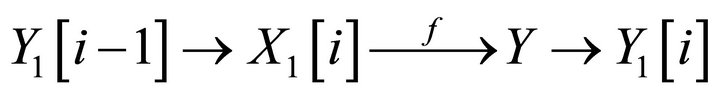
where 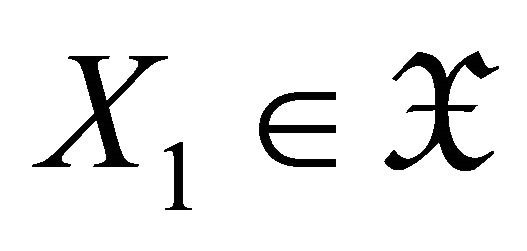 and
and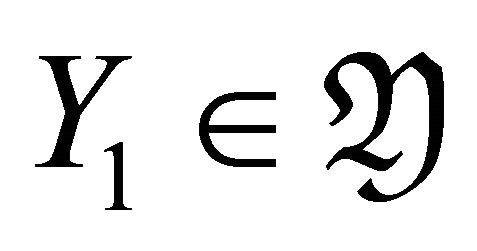 . Since
. Since 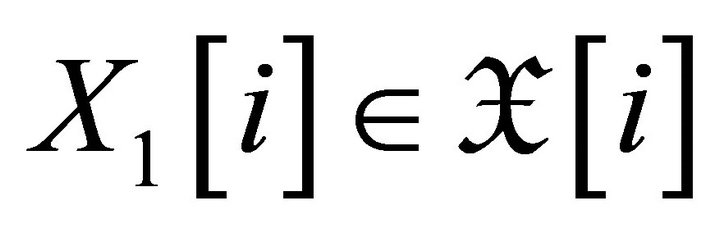 and
and
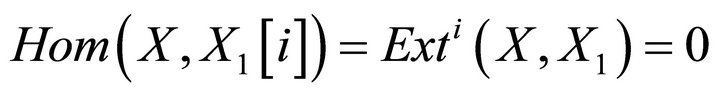 for any
for any  and
and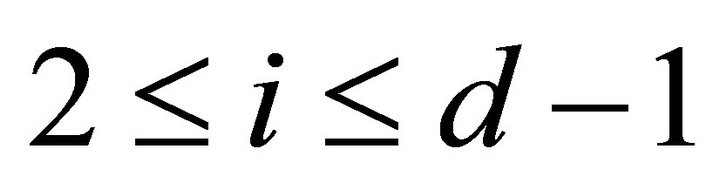 , we have that
, we have that . Hence
. Hence
 , i.e.,
, i.e.,  is a right
is a right 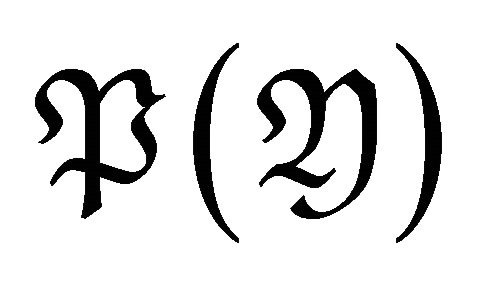 -approximation of
-approximation of . It means that
. It means that 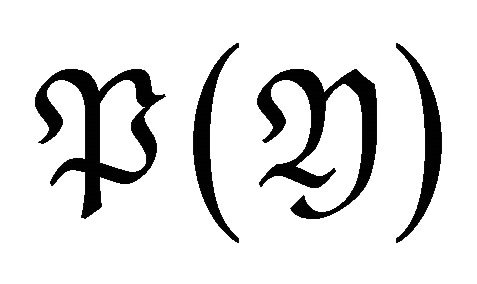 is contravariantly finite in
is contravariantly finite in .
.
Corollary 3.6 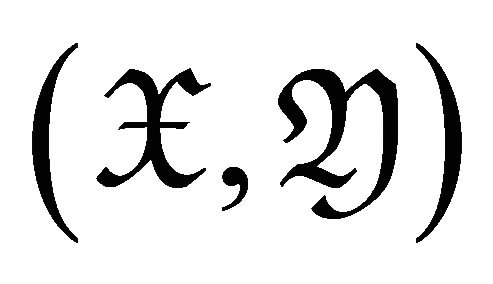 is a rigid torsion pair if and only if
is a rigid torsion pair if and only if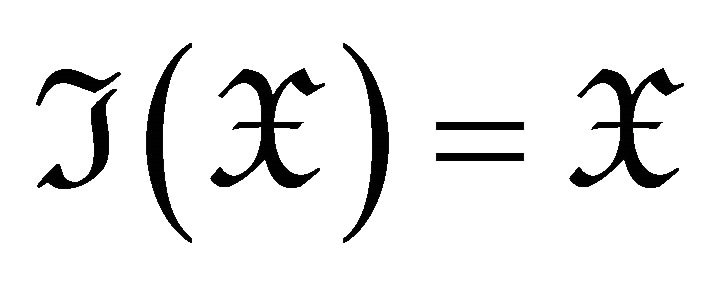 .
.
Proof: By proposition 3.5, we have that
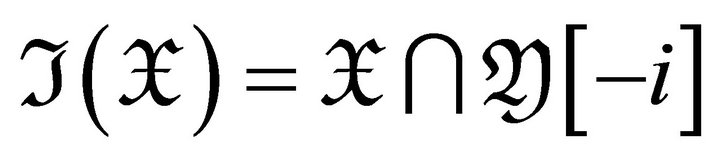 . Since
. Since
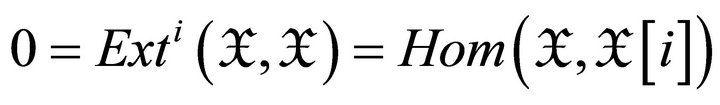 for all
for all  if and only if
if and only if 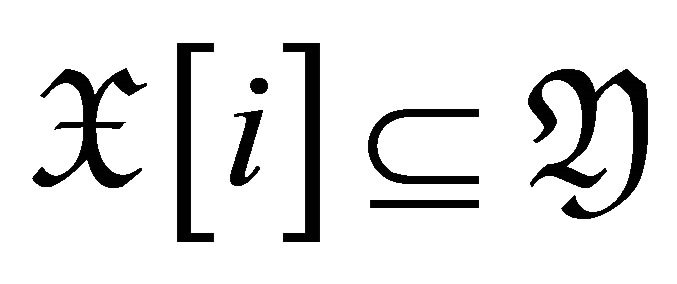 for
for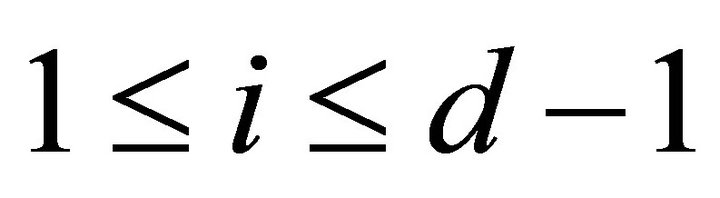 , hence in this case,
, hence in this case,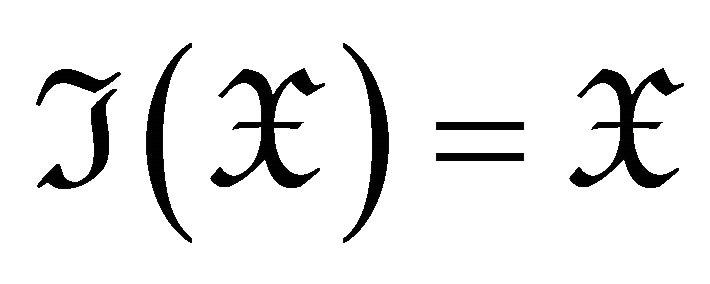 .
.
Corollary 3.7 Let  be a maximal rigid subcategory of
be a maximal rigid subcategory of![]() , then 1) Every object
, then 1) Every object 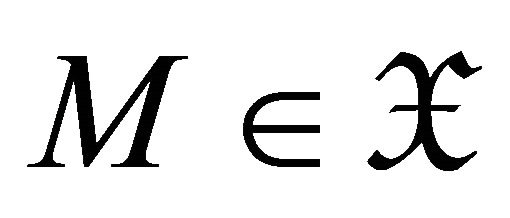 is d-Ext-projective (or d-Extinjective) in
is d-Ext-projective (or d-Extinjective) in .
.
2) An object  is d-Ext-projective in
is d-Ext-projective in  if and only if
if and only if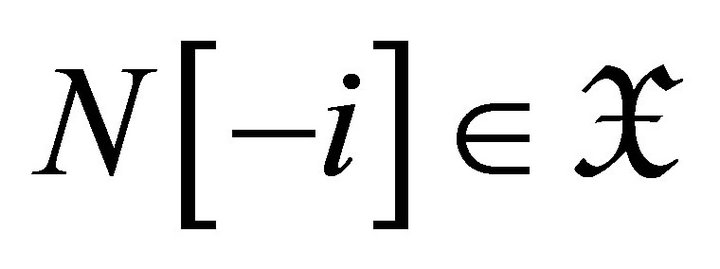 .
.
Proof: 1) By Corollary 3.6, 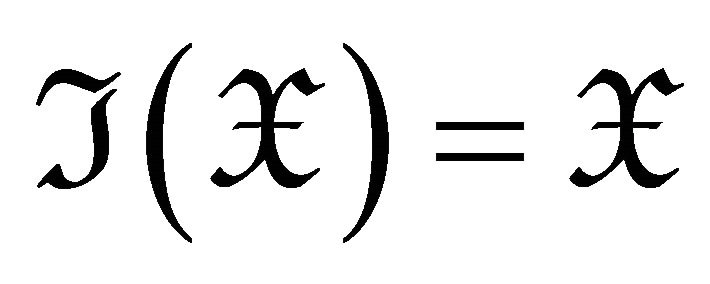 , (a) holds.
, (a) holds.
2) For any object 
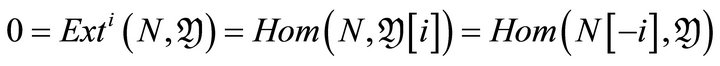
if and only if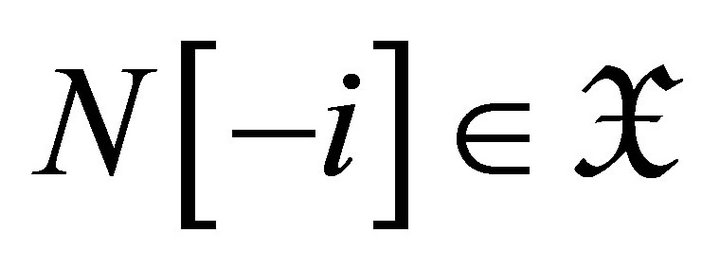 .
.
4. Torsion Pairs in 
Let ![]() be a triangulated category and
be a triangulated category and  a subcategory of
a subcategory of ![]() satisfying
satisfying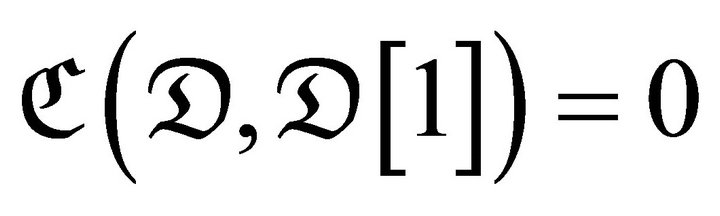 . For a subcategory
. For a subcategory  of
of![]() , put
, put . Then
. Then 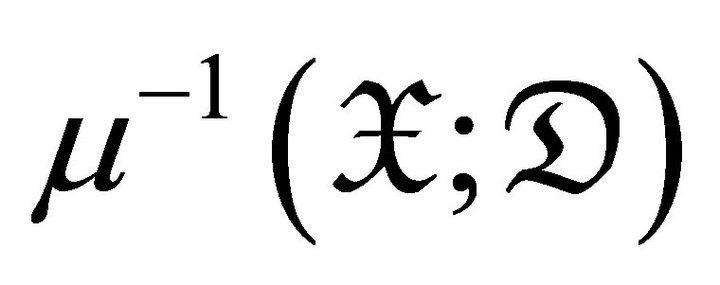 consists of all
consists of all  such that there exists a triangle
such that there exists a triangle

with 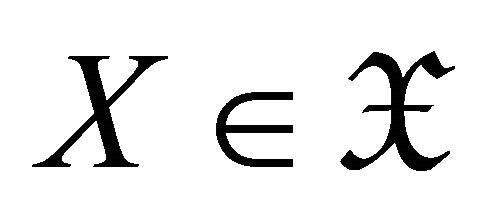 and a left
and a left  -approximation
-approximation![]() .
.
Dually, for a subcategory  of
of![]() , put
, put
![]() .
.
Then 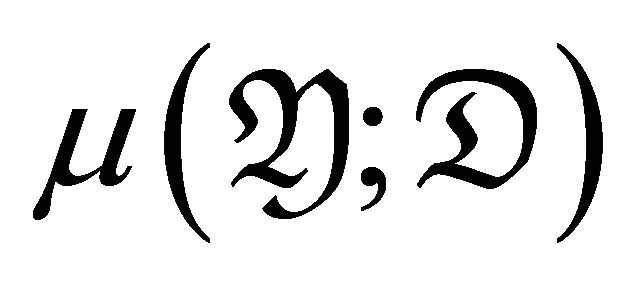 consists of all
consists of all 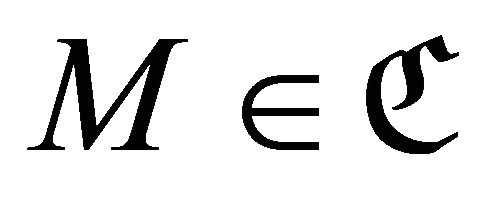 such that there exists a triangle
such that there exists a triangle  with
with 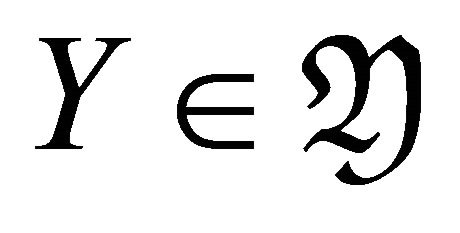 and a right
and a right  -approximation
-approximation .
.
We call a pair 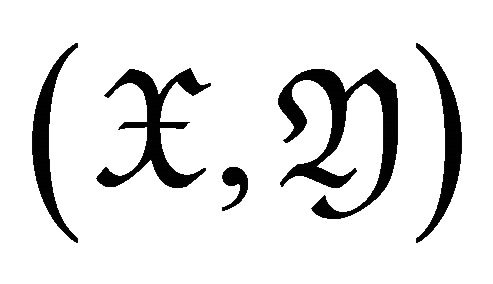 of subcategories of
of subcategories of ![]() a
a  - mutation pair [5] if
- mutation pair [5] if 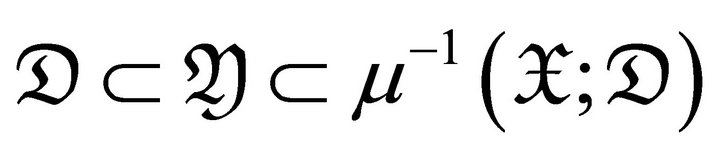 and
and 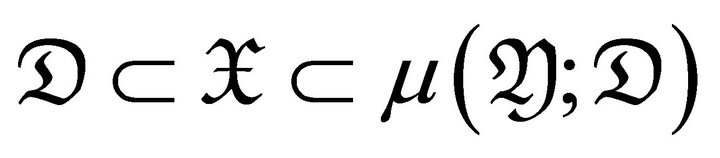 .
.
Let 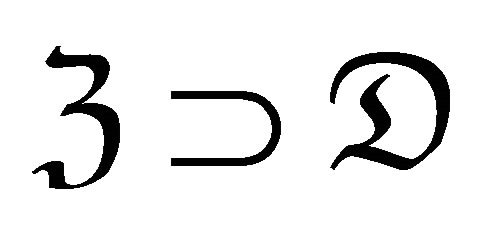 be a subcategory of
be a subcategory of![]() , we assume:
, we assume:
1) ![]() is extension closed;
is extension closed;
2) 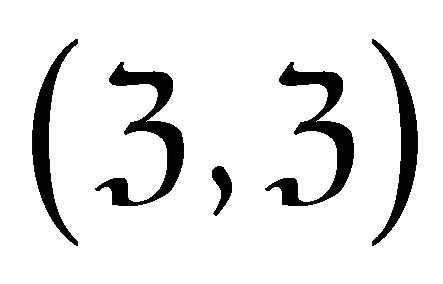 forms a
forms a  -mutation pair.
-mutation pair.
In the rest of this section, we assume that ![]() has a serre functor
has a serre functor![]() . We put
. We put 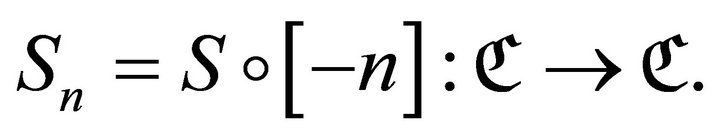 We call a subcategory
We call a subcategory  of
of ![]() an
an 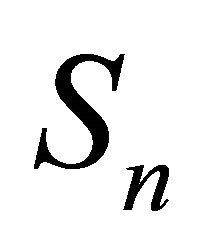 -subcategory of
-subcategory of ![]() if it satisfies
if it satisfies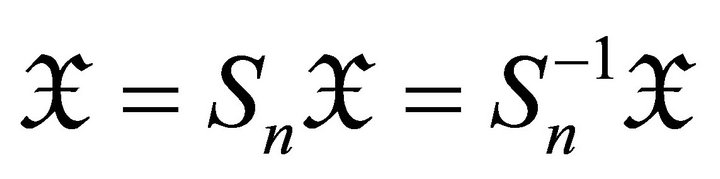 .
.
For an integer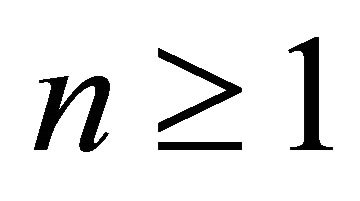 , we call a subcategory
, we call a subcategory  of
of ![]()
 if
if 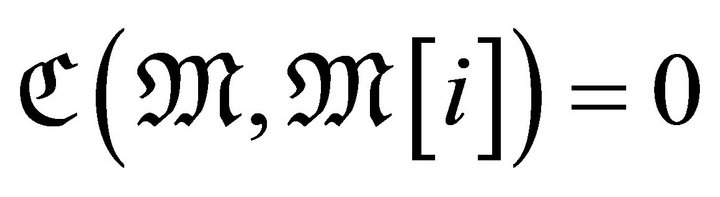 for
for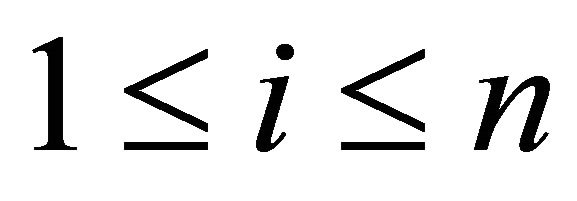 .
.
Now we assume that  is a functorially finite
is a functorially finite  subcategory of
subcategory of ![]() and
and
![]() .
.
It was proved in [8] that 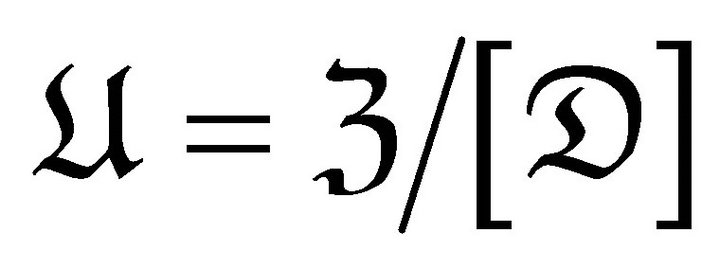 forms a triangulated category. The shift in
forms a triangulated category. The shift in 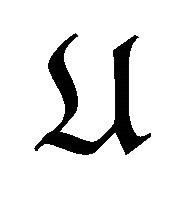 is defined as follows: for any object
is defined as follows: for any object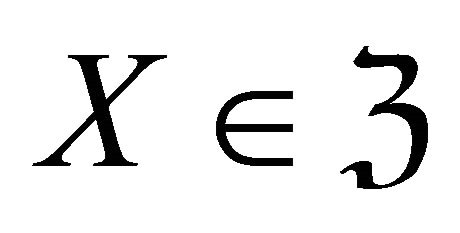 , consider the left
, consider the left  -approximation
-approximation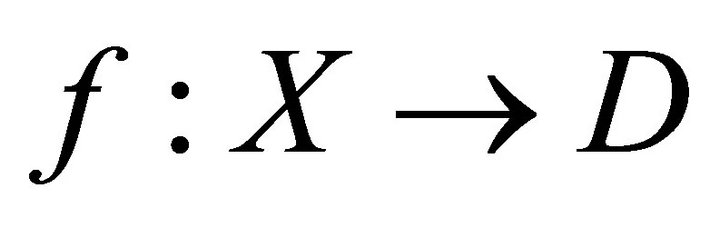 , and extend it to a triangle
, and extend it to a triangle
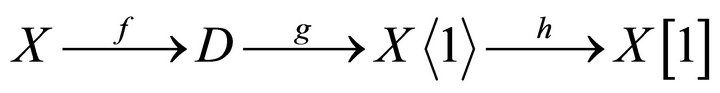
where  and
and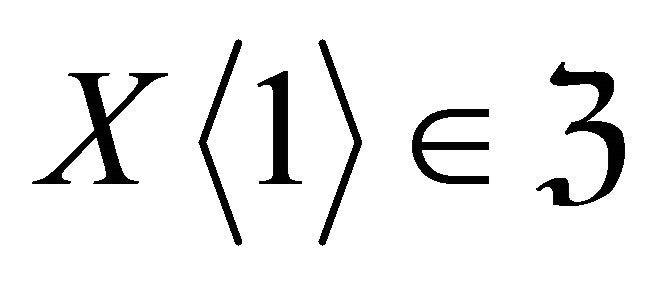 . The
. The 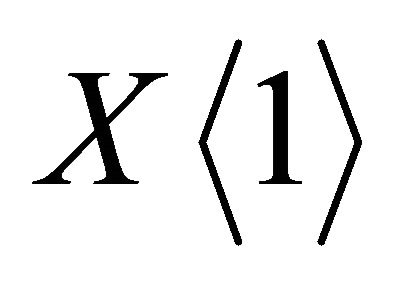 is defined as the shift of
is defined as the shift of  in
in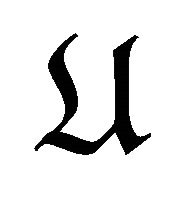 .
.
Then triangles in 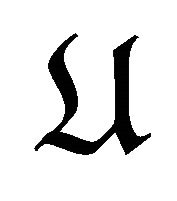 are defined as the complex
are defined as the complex
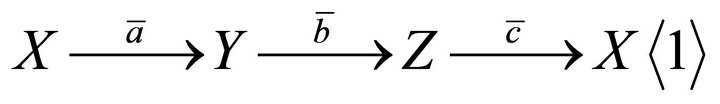
in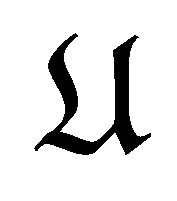 , where
, where  and
and 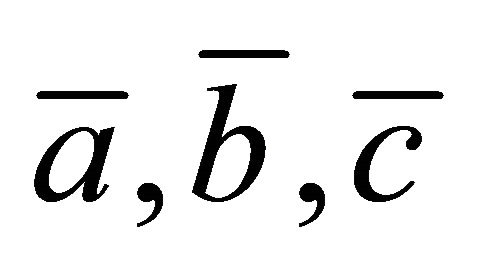 are the images of maps
are the images of maps  under the quotient functor
under the quotient functor  respectively.
respectively.
In the following,  denotes the subcategory of
denotes the subcategory of 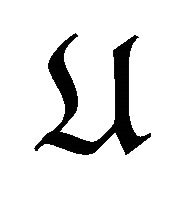 consisting of objects
consisting of objects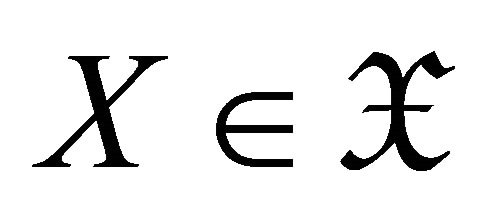 , for the subcategory
, for the subcategory 
satisfying![]() .
.
Lemma 4.1 [8] For any 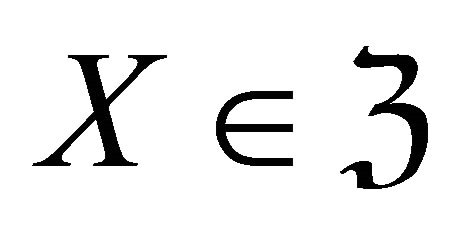 and
and![]() , there exists a triangle
, there exists a triangle
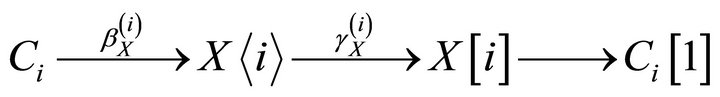
in ![]() with
with  and with
and with 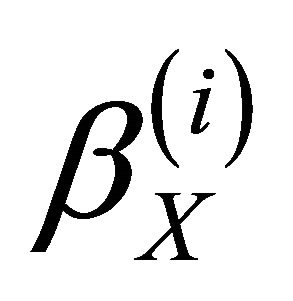 being
being  -epic.
-epic.
Lemma 4.2 If 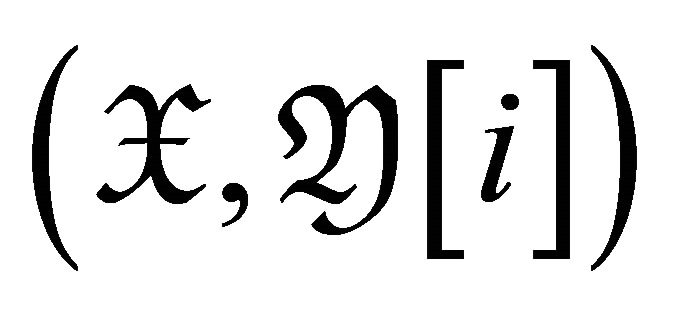 is a torsion pair for
is a torsion pair for
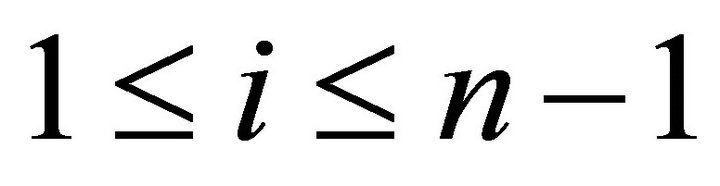 and
and![]() then
then![]() .
.
Proof: Noting that  for
for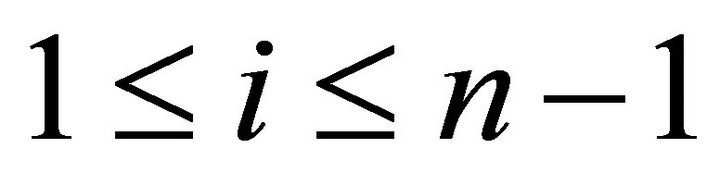 . Since
. Since![]() we have
we have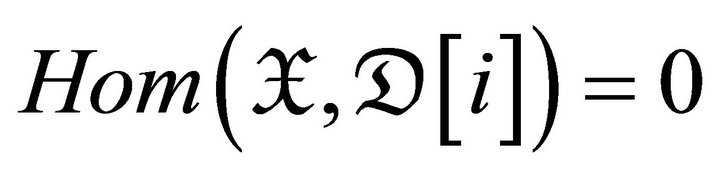 , and then
, and then
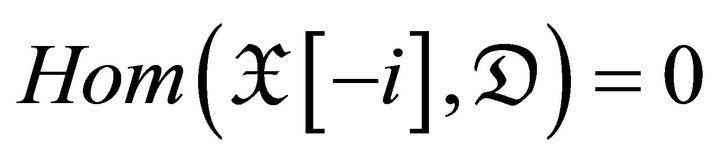 or
or . Therefore
. Therefore
![]() . Since
. Since we have that
we have that
![]() . Thus we have
. Thus we have
![]() .
.
Lemma 4.3 Let X and ![]() be two objects in
be two objects in![]() . Then
. Then 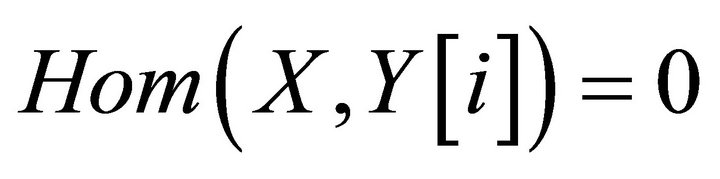 for
for 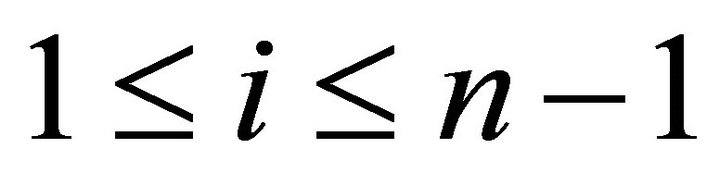 if and only if
if and only if
 for
for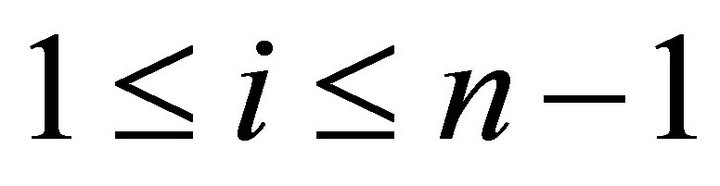 .
.
Proof: By Lemma 4.1, we have an exact sequence

where 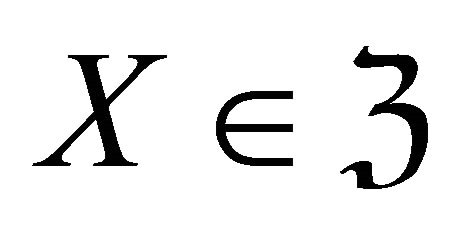 and
and 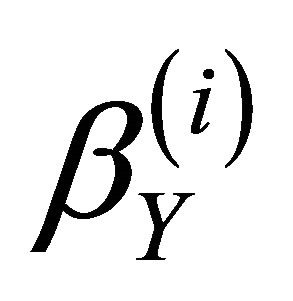 is a right
is a right  -approximation. Since
-approximation. Since
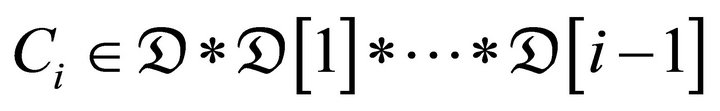 and
and
 , we have
, we have
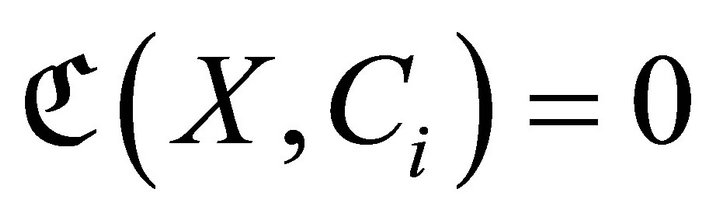 and
and 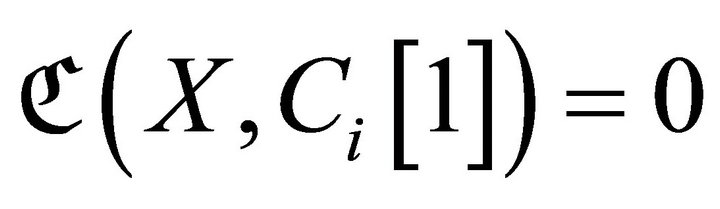 for
for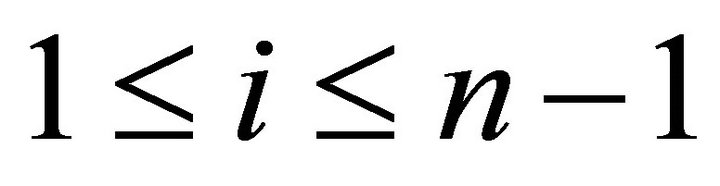 . Then
. Then 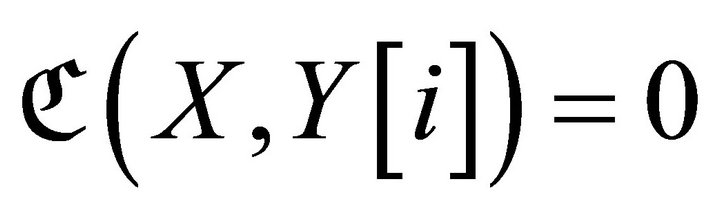 if and only if
if and only if 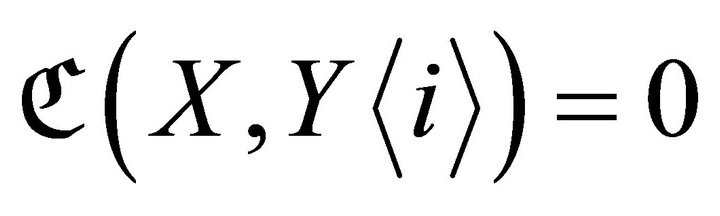 for
for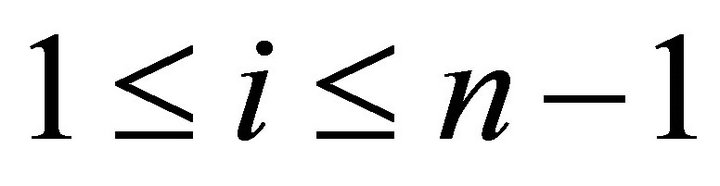 .
.
Theorem 4.4 Let  be a subcategory of
be a subcategory of ![]() satisfying
satisfying![]() . Then
. Then  is a torsion pair with
is a torsion pair with 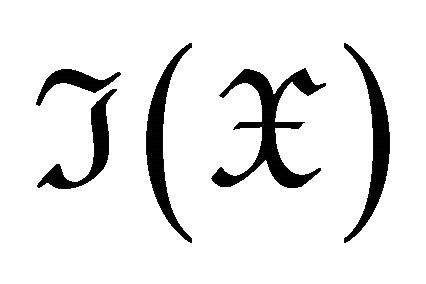 in
in ![]() for
for 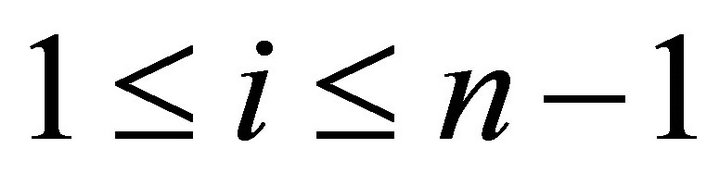 if and only if
if and only if 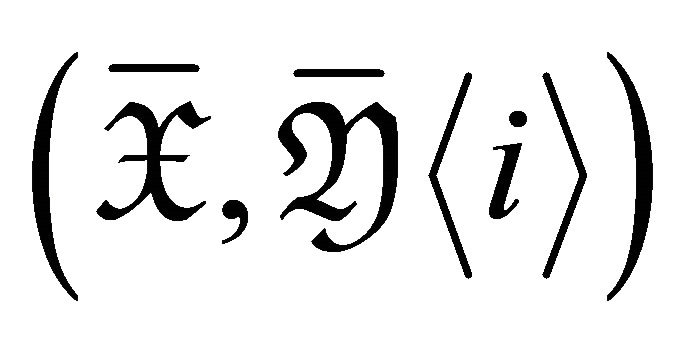 is a torsion pair with
is a torsion pair with 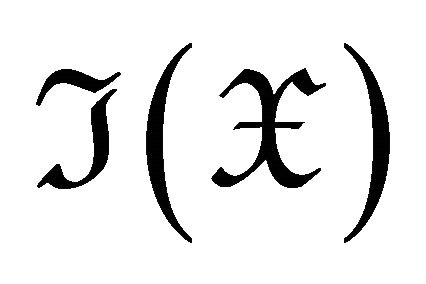 in
in  for
for
 .
.
Proof: Noting that  is a triangulated category with shift functor
is a triangulated category with shift functor , we suppose that
, we suppose that 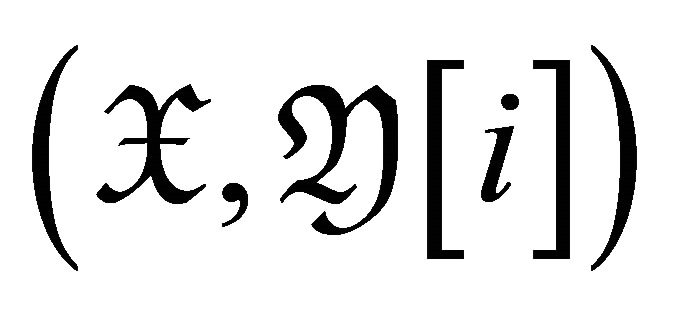 is a torsion pair
is a torsion pair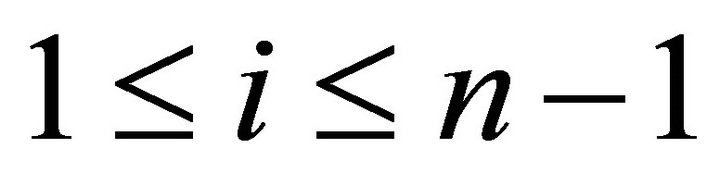 . It follows from Lemma 4.2 that
. It follows from Lemma 4.2 that
![]() . By Lemma 4.3, we have
. By Lemma 4.3, we have
 for
for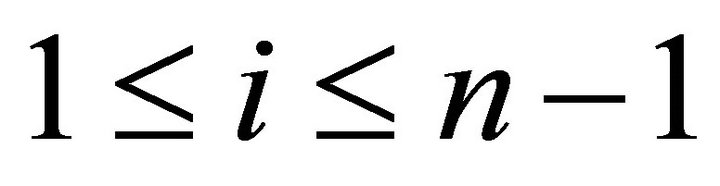 . For any
. For any , there is a triangle
, there is a triangle

where 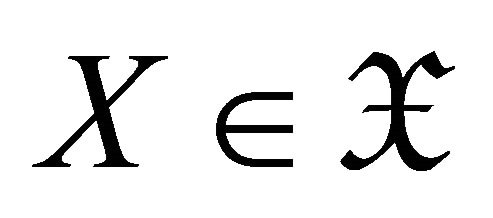 and
and 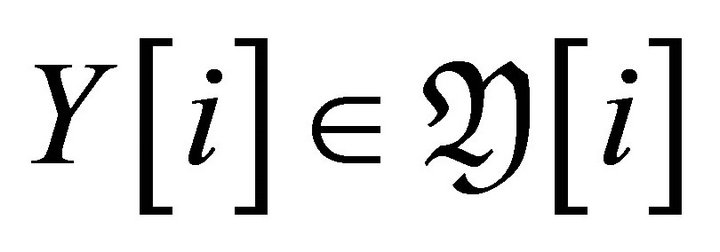 as
as 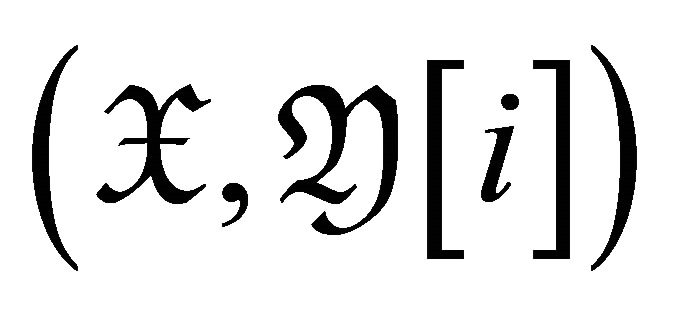 is a torsion pair in
is a torsion pair in![]() . Since all of
. Since all of  are in
are in![]() , there is a triangle
, there is a triangle
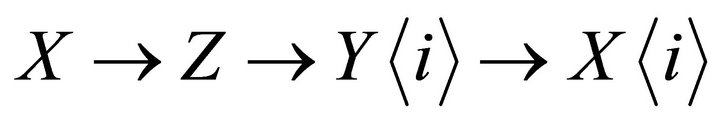
in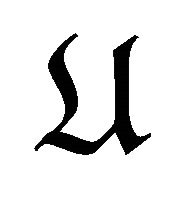 . Therefore,
. Therefore, . Hence
. Hence 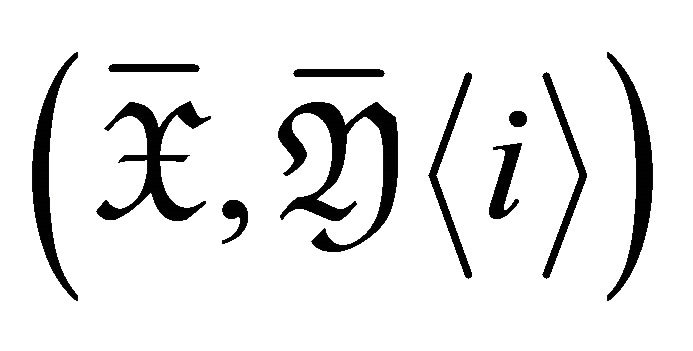 is a torsion pair in
is a torsion pair in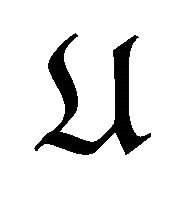 .
.
Conversely, we suppose 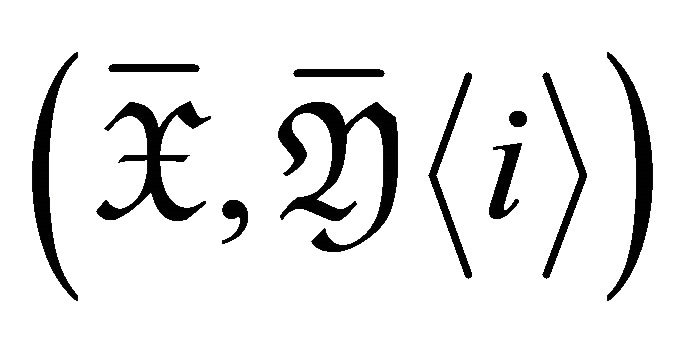 is a torsion pair for
is a torsion pair for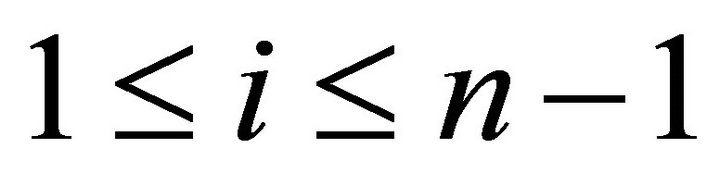 . By Lemma 4.3, we have
. By Lemma 4.3, we have
 for
for . For any
. For any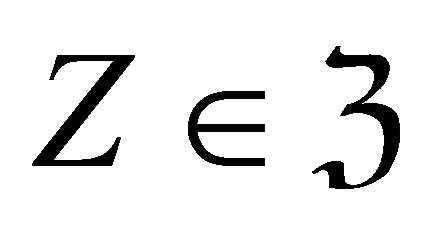 there is a triangle in
there is a triangle in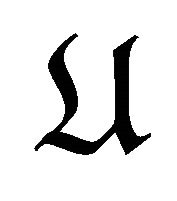 :
:
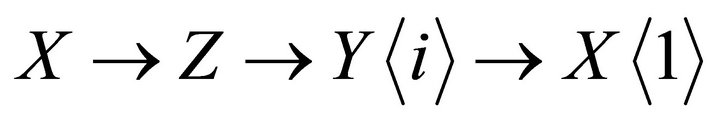
where  and
and  for
for 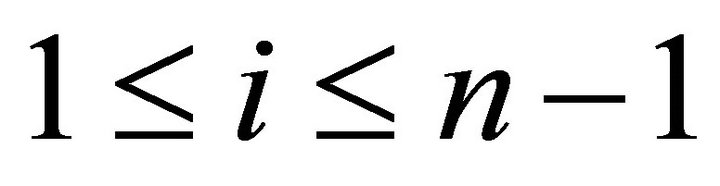 by Lemma 4.3. Then there is a triangle
by Lemma 4.3. Then there is a triangle

in ![]() such that
such that 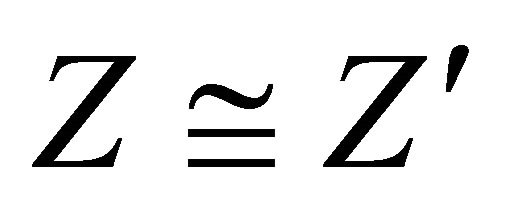 in
in . Hence
. Hence 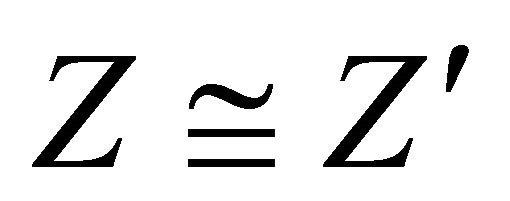 in
in ![]() up to direct summands of
up to direct summands of . Thus
. Thus ![]() is a subcategory of
is a subcategory of . Since there is a triangle in
. Since there is a triangle in ![]() for any
for any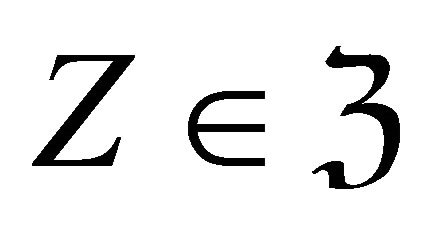 :
:
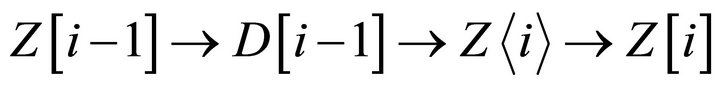
where 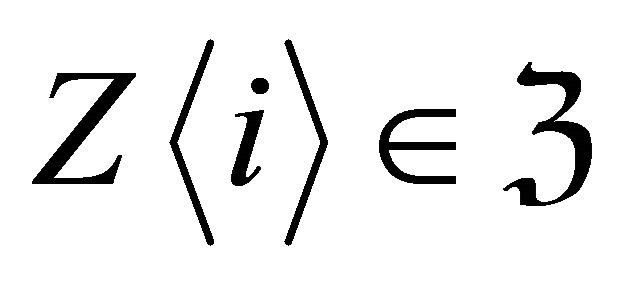 and
and![]() , we have
, we have
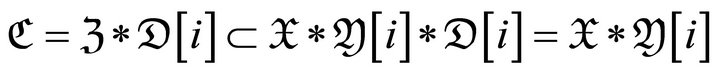 .
.
Therefore 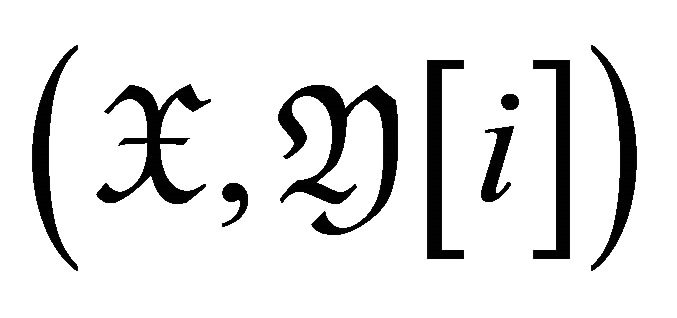 is a torsion pair in
is a torsion pair in ![]() for
for  .
.
Finally, we have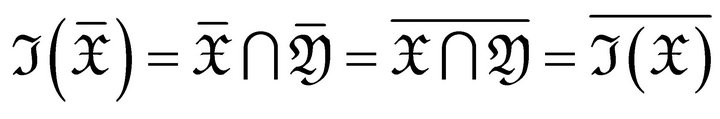 .
.
Corollary 4.5 Let  be a subcategory of
be a subcategory of ![]() satisfying
satisfying![]() , then we have the following:
, then we have the following:
1) 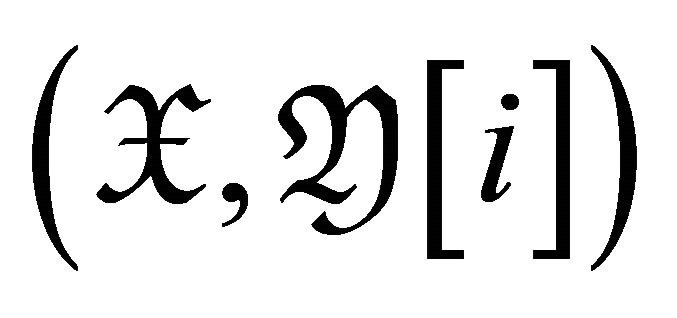 is a rigid torsion pair in
is a rigid torsion pair in ![]() for
for 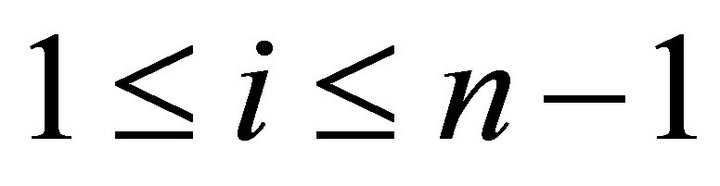 if and only if
if and only if  is a rigid torsion pair in
is a rigid torsion pair in  for
for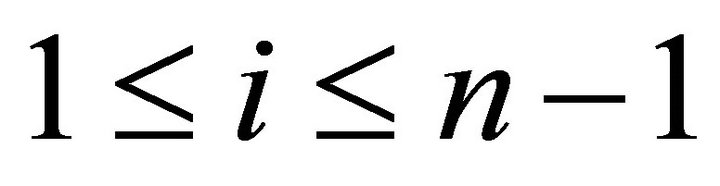 .
.
2) 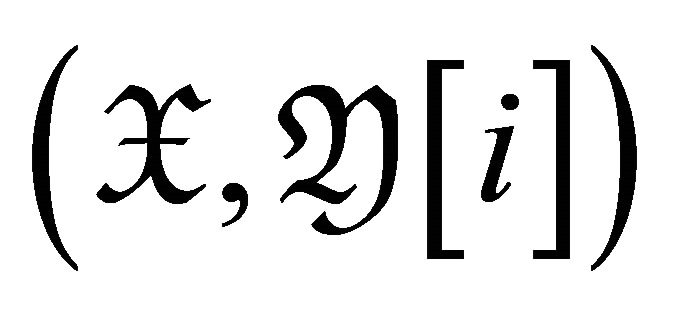 is a
is a ![]() -cluster tilting torsion pair in
-cluster tilting torsion pair in ![]()
for 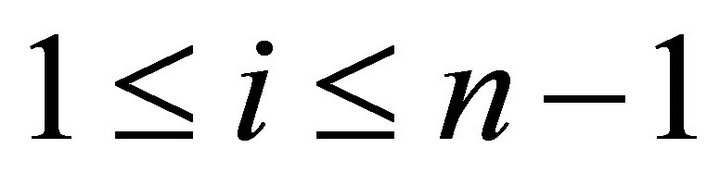 if and only if
if and only if 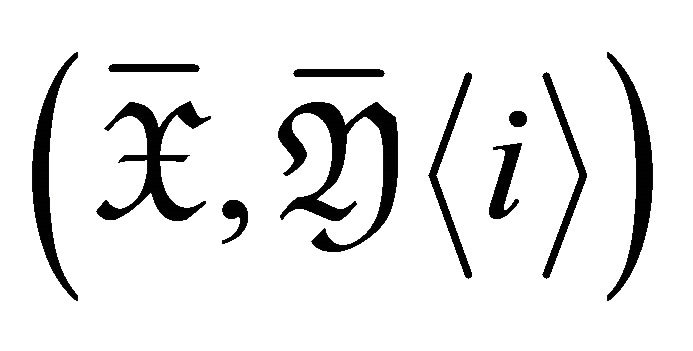 is a n-cluster tilting torsion pair in
is a n-cluster tilting torsion pair in  for
for .
.
3) 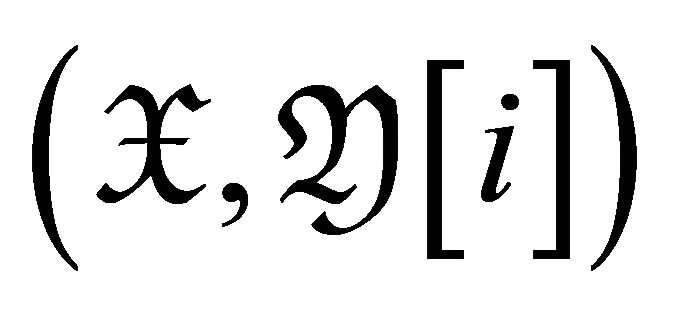 is a maximal rigid torsion pair in
is a maximal rigid torsion pair in ![]()
for  if and only if
if and only if 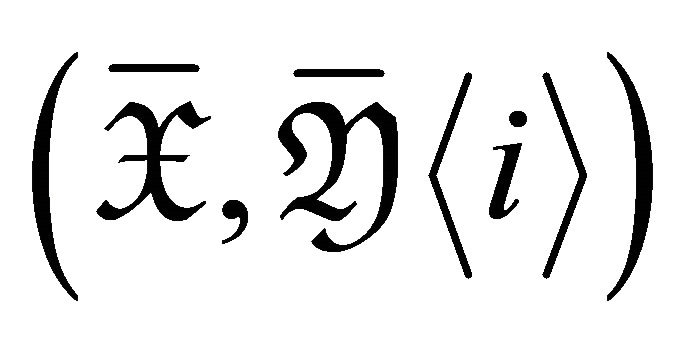 is a maximal rigid torsion pair
is a maximal rigid torsion pair 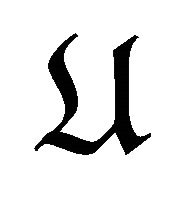 for
for .
.
Proof: 1) By Corollary 3.6, we only need to prove
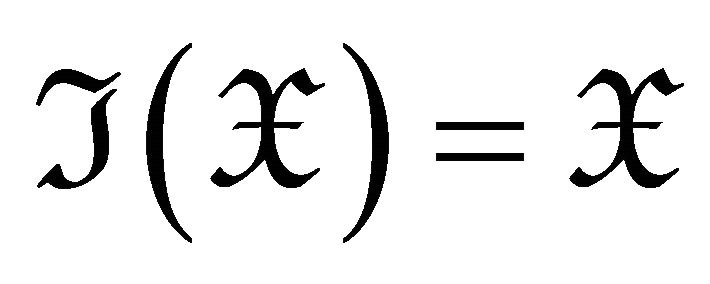 if and only if
if and only if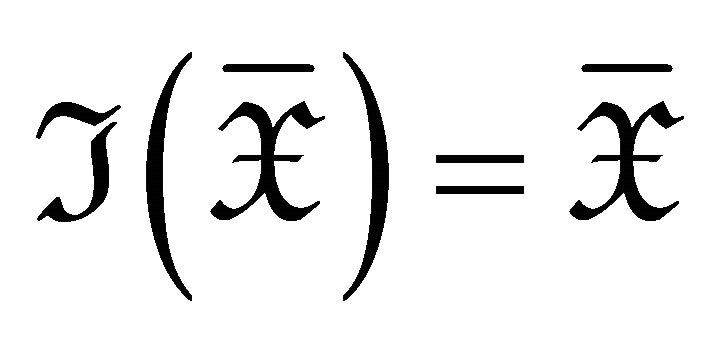 . By Theorem 4.4 we have
. By Theorem 4.4 we have .
.
2) It follows from Theorem 4.9 in [8] that we have a one-one correspondence between ![]() -cluster tilting subcategories of
-cluster tilting subcategories of ![]() containing
containing  and
and ![]() -cluster tilting subcategories of
-cluster tilting subcategories of .
.
3) It is obvious that 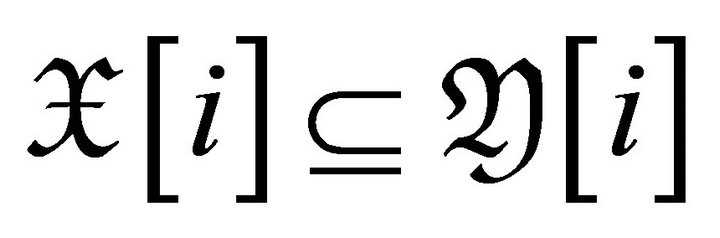 if and only if
if and only if
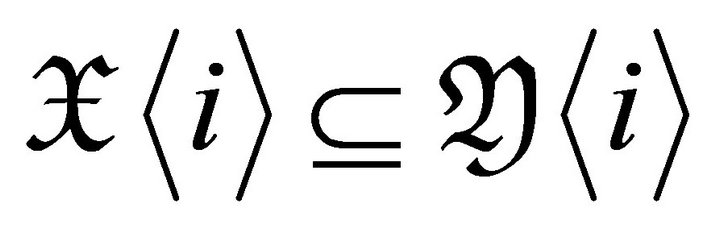 for
for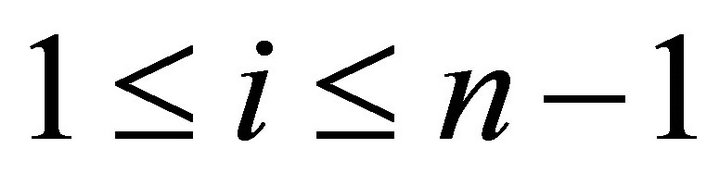 . Assume that,
. Assume that,
 while
while ![]() for any rigid object
for any rigid object 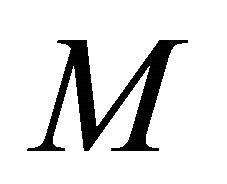 in
in![]() . For any rigid object
. For any rigid object ![]() in
in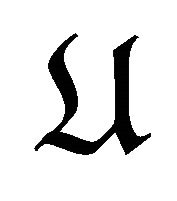 , we have that
, we have that ![]() is also rigid in
is also rigid in![]() . Then there is a triangle
. Then there is a triangle
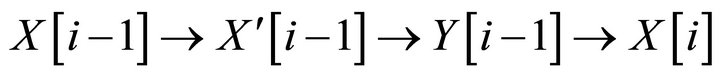
in ![]() , where
, where 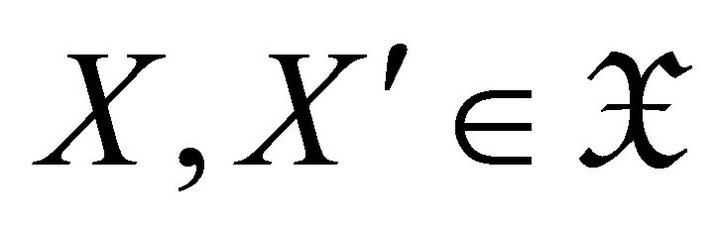 and
and![]() . Thus there is a triangle
. Thus there is a triangle

in 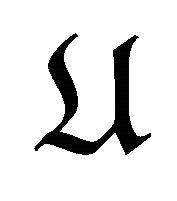 with
with![]() . Therefore,
. Therefore,
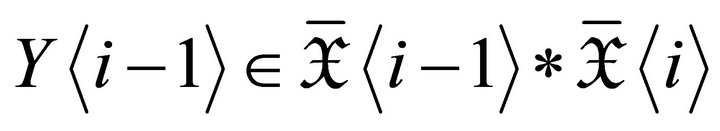 .
.
It follows from Corollary 3.3 that 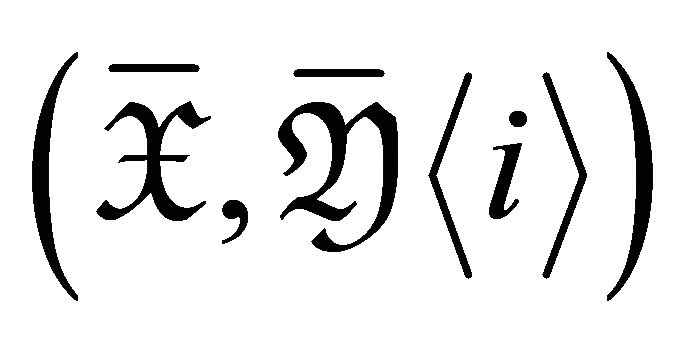 is a maximal rigid torsion pair in
is a maximal rigid torsion pair in  for
for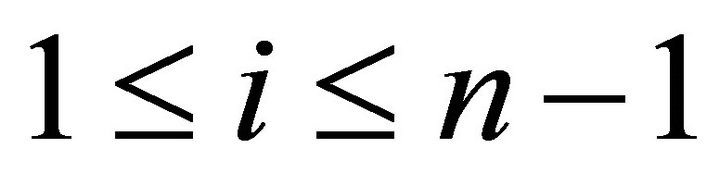 .
.
Conversely, 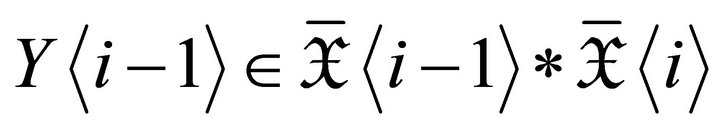 while
while ![]() for any rigid object
for any rigid object ![]() in
in . For any rigid object
. For any rigid object  in
in![]() , there is a triangle
, there is a triangle
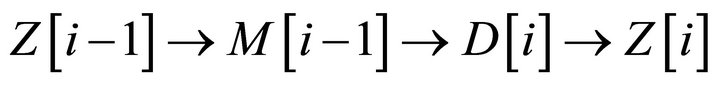

in![]() , where
, where 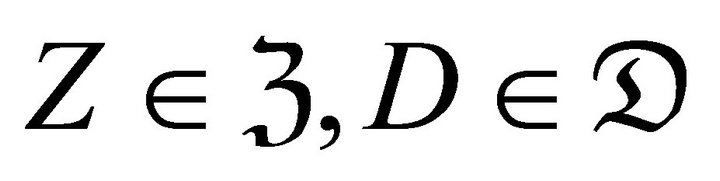 and
and![]() . Applying
. Applying
 to this triangle we obtain that
to this triangle we obtain that 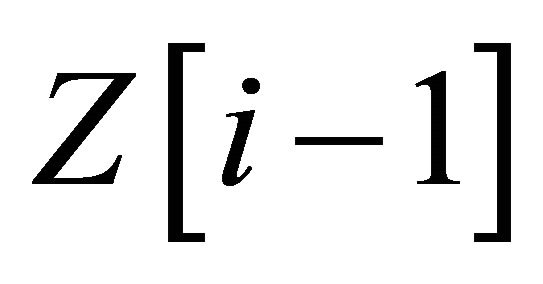 is a rigid object for
is a rigid object for![]() . Then
. Then 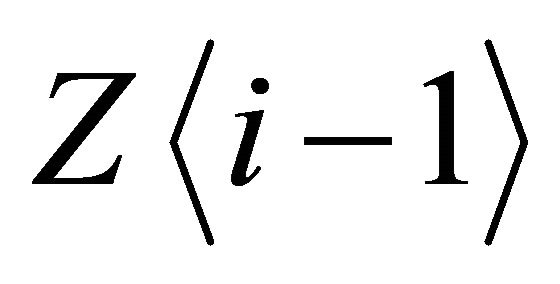 is a rigid object in
is a rigid object in 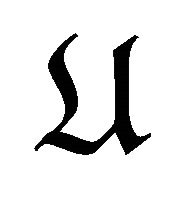 for
for![]() . And thus there is a triangle
. And thus there is a triangle
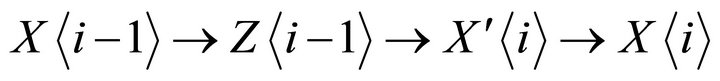
in , where
, where . Then there is a triangle
. Then there is a triangle

in ![]() such that
such that 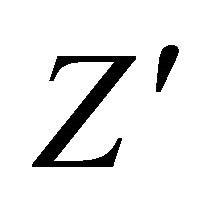 is isomorphic to
is isomorphic to  up to direct summands in
up to direct summands in . Since
. Since 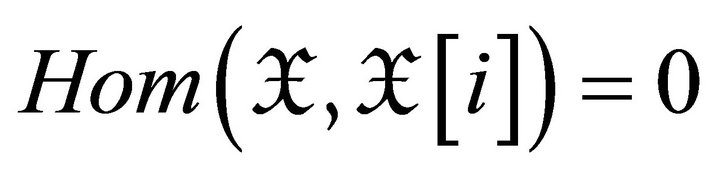 for
for
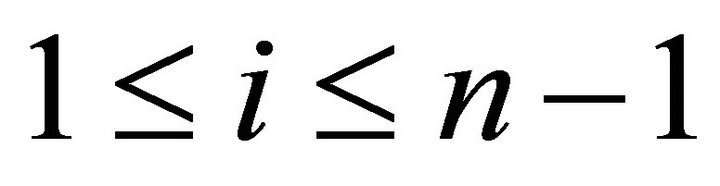 , it is easy to see that
, it is easy to see that 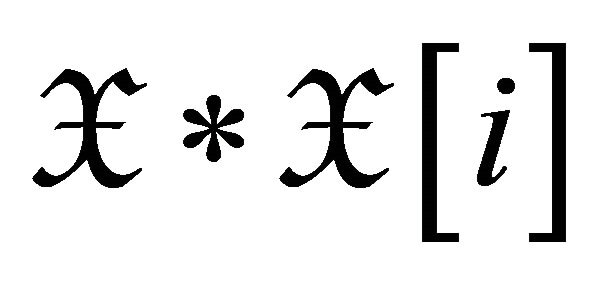 is closed under extensions for
is closed under extensions for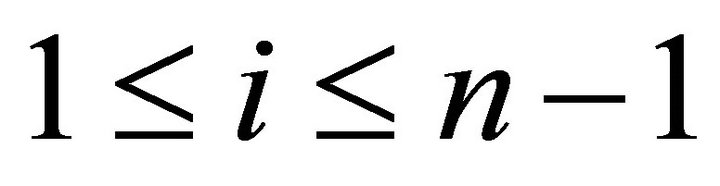 .
.
Therefore 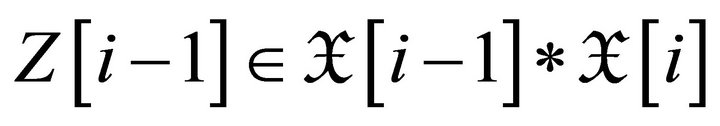 and then
and then
 because
because
 by
by . So we have that
. So we have that
 is a maximal rigid torsion pair in
is a maximal rigid torsion pair in ![]() for
for
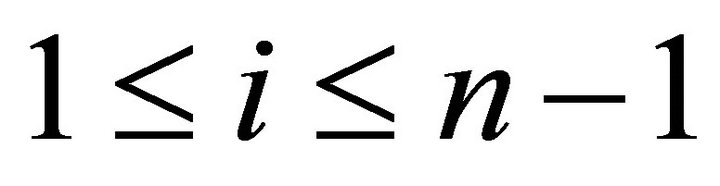 .
.
5. Acknowledgement
Supported by the National Natural Science Foundation of China (Grant No. 10971172, 11271119) and the Natural Science Foundation of Beijing (Grant No. 1122002).
REFERENCES
- A. Beilinson, J. Bernstein and P. Deligne, “Faisceaux Pervers,” Asterisque 100, 1982.
- A. Beligiannis and I. Reiten, “Homological and Homotopical Aspects of Torsion Theories,” 2007. http://www.math.uoi.gr/~abeligia/torsion.pdf
- A. L. Gorodentsev and A. N. Rudakov, “Exceptional Vector Bundles on Projective Spaces,” Duke Mathematical Journal, Vol. 54, No. 1, 1987, pp. 115-130. doi:10.1215/S0012-7094-87-05409-3
- S. Fomin and A. Zelevinsky, “Cluster Algebras I. Foundations,” Journal of American Mathematical Society, Vol. 15, No.2, 2002, pp. 497-529. doi:10.1090/S0894-0347-01-00385-X
- S. Fomin and A. Zelevinsky, “Cluster Algebras II. Finite Type Classification,” Inventiones Mathematicae, Vol. 154, No. 1, 2003, pp. 63-121. doi:10.1007/s00222-003-0302-y
- A. Buan, R. Marsh, M. Reineke, I. Reiten and G. Todorov, “Tilting Theory and Cluster Combinations,” Advances in Mathematics, Vol. 204, No. 2, 2006, pp. 572-618. doi:10.1016/j.aim.2005.06.003
- C. Geiss, B. Leclerc and J. Schroer, “Rigid Modules over Preprojective Algebras,” Inventiones Mathematicae, Vol. 165, No. 3, 2006, pp. 589-632. doi:10.1007/s00222-006-0507-y
- M. Kontsevich, “Triangulated Categories and Geometry,” The École Normale Supérieure, Paris, 1998.
- O. Iyama and Y. Yoshino, “Mutations in Triangulated Categories and Rigid Cohen-Macaulay Modules,” Inventiones mathematicae, Vol. 172, No. 1, 2008, pp. 117-168. doi:10.1007/s00222-007-0096-4
- Y. Zhou and B. Zhu, “Mutation of Torsion Pairs in Triangulated Categories and Its Geometric Realization,” arXiv.org, Los Alamos, 2011.
- M. Auslander and S. O. Smalø, “Almost Split Sequences in Subcategories,” Journal of Algebra, Vol. 69, No. 2, 1981, pp. 426-454. doi:10.1016/0021-8693(81)90214-3
- B. Keller and I. Reiten, “Cluster-Tilted Algebras Are Gorenstein and Stably Calabi-Yau,” Advances in Mathematics, Vol. 211, No. 1, 2007, pp. 123-151. doi:10.1016/j.aim.2006.07.013
- Y. Zhou and B. Zhu, “Cluster Combinatorics of d-Cluster Categories,” Journal of Algebra, Vol. 321, No. 10, 2009, pp. 2898-2915. doi:10.1016/j.jalgebra.2009.01.032

