Advances in Pure Mathematics
Vol.3 No.1(2013), Article ID:27360,16 pages DOI:10.4236/apm.2013.31011
Strong Convergence of a General Iterative Algorithm for Mixed Equilibrium, Variational Inequality and Common Fixed Points Problems*
1Department of Mathematics, School of Science, University of Phayao, Phayao, Thailand
2Centre of Excellence in Mathematics, CHE, Si Ayutthaya Rd., Bangkok, 10400, Thailand
Email: tanakit.th@up.ac.th
Received September 14, 2012; revised November 1, 2012; accepted November 20, 2012
Keywords: Nonexpansive Mapping; Mixed Equilibrium Problem; Variational Inequality; Common Fixed Points; Strong Convergence
ABSTRACT
The aim of this paper, is to introduce and study a general iterative algorithm concerning the new mappings which the sequences generated by our proposed scheme converge strongly to a common element of the set of solutions of a mixed equilibrium problem, the set of common fixed points of a finite family of nonexpansive mappings and the set of solutions of the variational inequality for a relaxed cocoercive mapping in a real Hilbert space. In addition, we obtain some applications by using this result. The results obtained in this paper generalize and refine some known results in the current literature.
1. Introduction
Let be a real Hilbert space, whose inner product and norm are denoted by
be a real Hilbert space, whose inner product and norm are denoted by  and
and 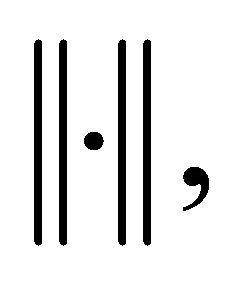 respectively. Let
respectively. Let 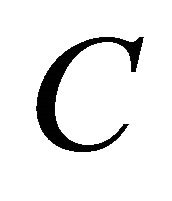 be a nonempty closed convex subset of H. A mapping
be a nonempty closed convex subset of H. A mapping 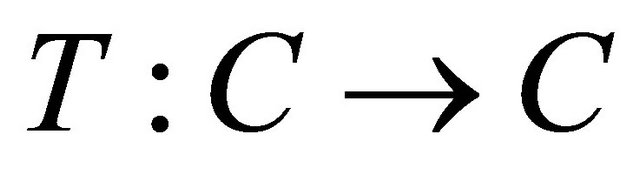 is called nonexpansive if
is called nonexpansive if 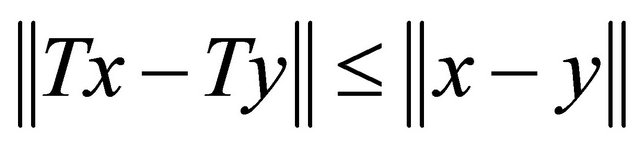 for all
for all 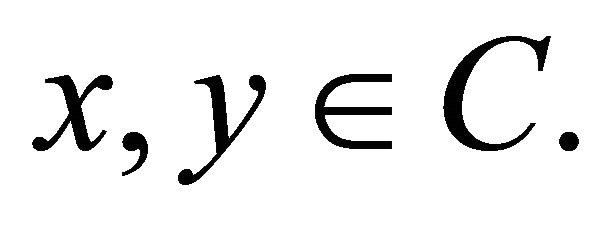 We denote by
We denote by 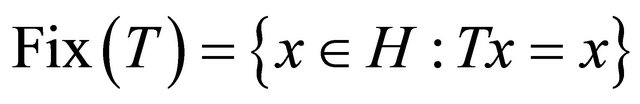 the set of fixed points of T. A linear bounded operator A is strongly positive if there is a constant
the set of fixed points of T. A linear bounded operator A is strongly positive if there is a constant 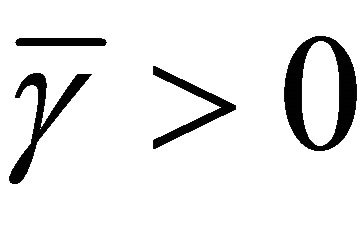 with the property
with the property 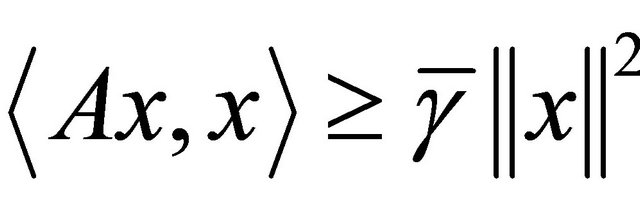 for all
for all 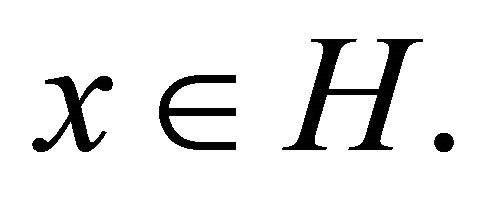 A mapping
A mapping 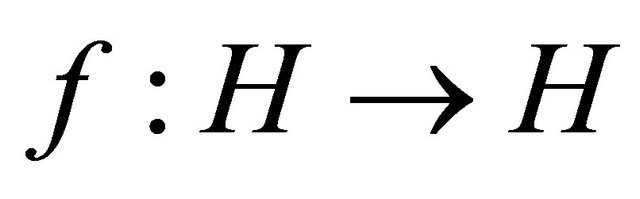 is said to be a contraction if there exists a coefficient
is said to be a contraction if there exists a coefficient 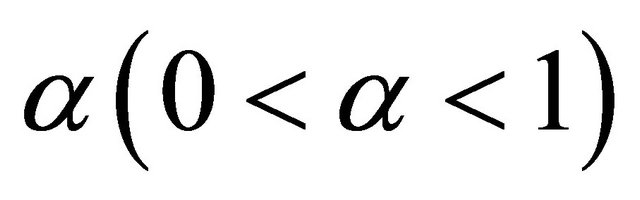 such that
such that 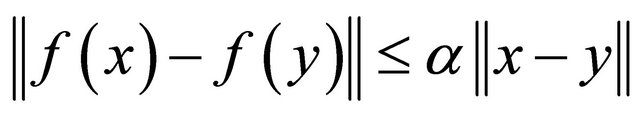 for all
for all 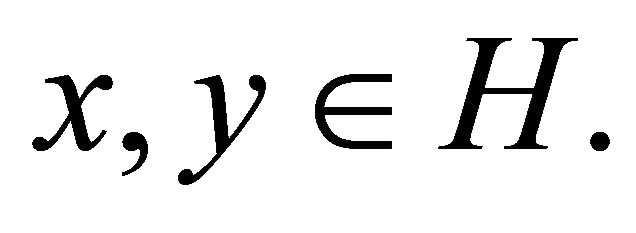 Let PC be the nearest point projection of
Let PC be the nearest point projection of  onto the convex subset
onto the convex subset 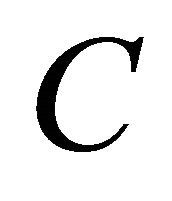 (i.e., for
(i.e., for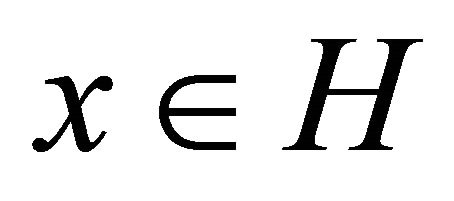 , PC is the only point in C such that
, PC is the only point in C such that 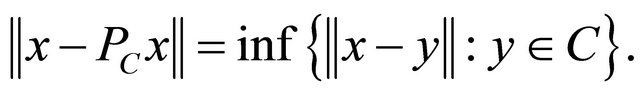 It is known that projection operator PC is nonexpansive. It is also known that PC satisfies
It is known that projection operator PC is nonexpansive. It is also known that PC satisfies 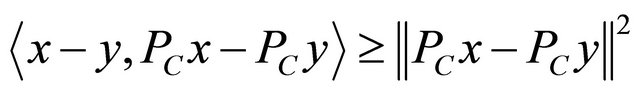 for
for 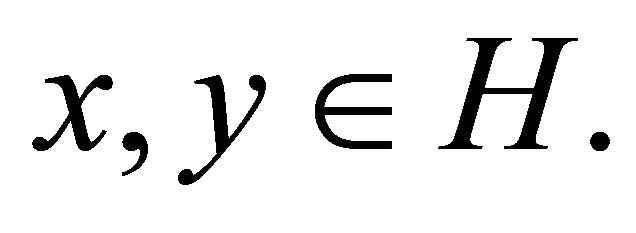 The following characterizes the projection PC Given
The following characterizes the projection PC Given 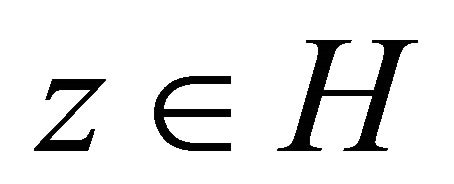 and
and 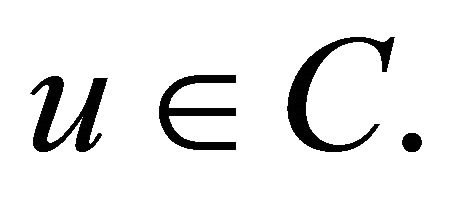 Then
Then 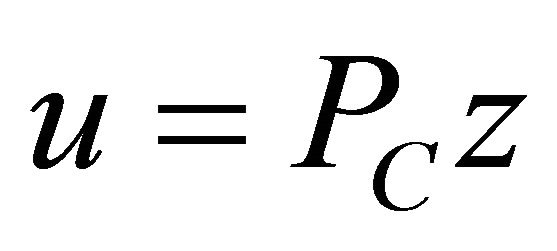 if and only if there holds the relations:
if and only if there holds the relations:
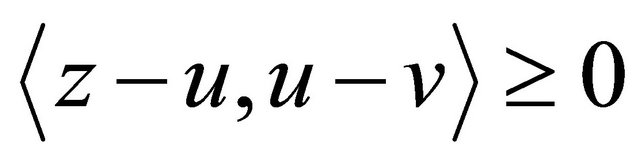 (1.1)
(1.1)
for all 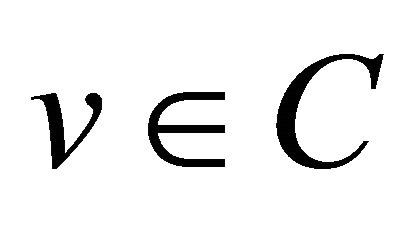 (see [1]). Moreover,
(see [1]). Moreover, 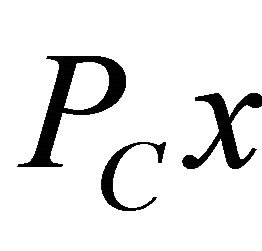 is characterized by the properties:
is characterized by the properties: 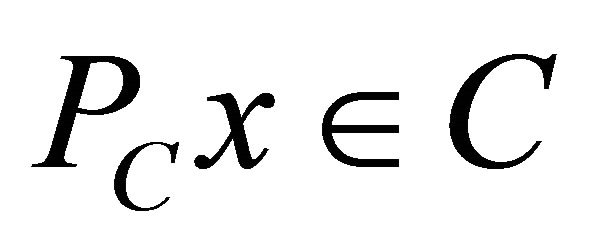 and
and 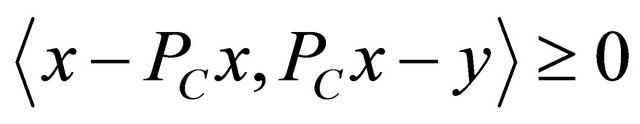 for all
for all 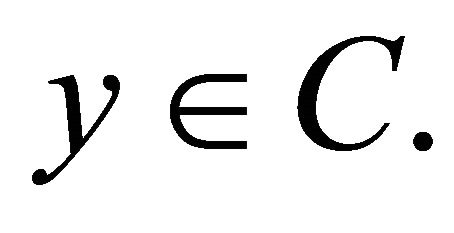 Let
Let 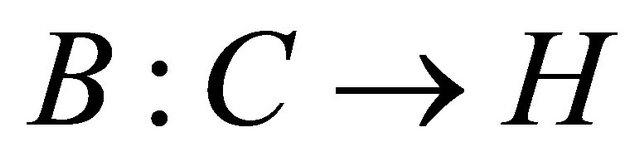 be a nonlinear map. The classical variational inequality problem, denoted by
be a nonlinear map. The classical variational inequality problem, denoted by 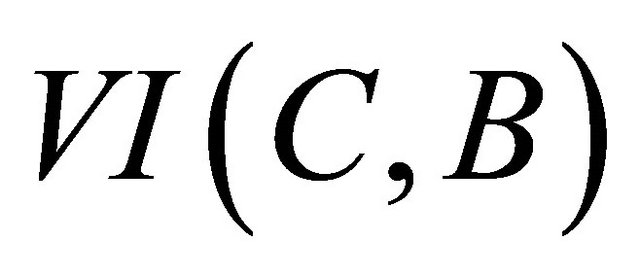 is to find
is to find 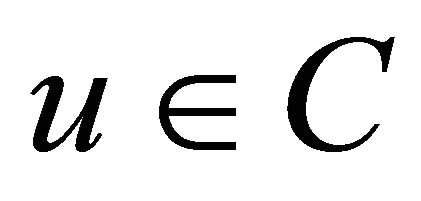 such that
such that
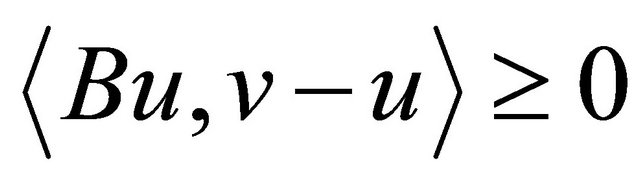 (1.2)
(1.2)
for all 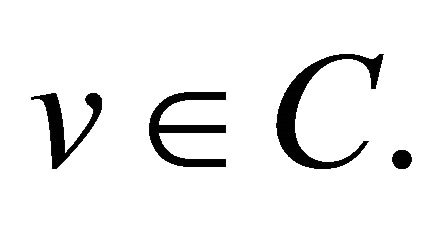 One can see that the variational inequality problem (1.2) is equivalent to the following fixed point problem: the element
One can see that the variational inequality problem (1.2) is equivalent to the following fixed point problem: the element 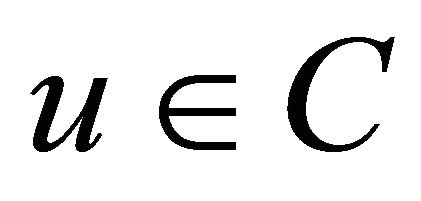 is a solution of the variational inequality (1.2) if and only if
is a solution of the variational inequality (1.2) if and only if 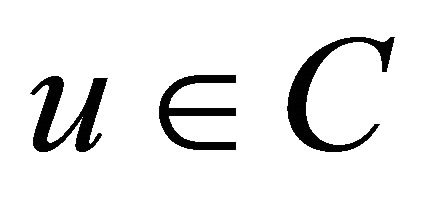 satisfies the relation
satisfies the relation 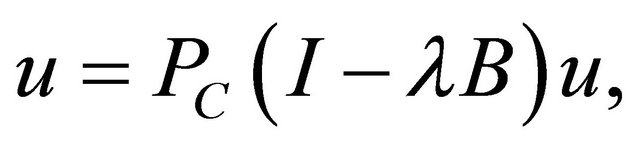 where
where 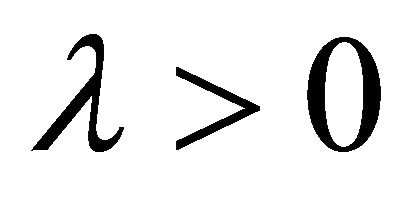 is a constant. This alternative equivalent formulation has played a significant role in the studies of the variational inequalities and related optimization problems.
is a constant. This alternative equivalent formulation has played a significant role in the studies of the variational inequalities and related optimization problems.
Iterative methods for nonexpansive mappings have recently been applied to solve convex minimization problems; see, for example, [2-6] and the references therein. A typical problem is that of minimizing a quadratic function over the set of the fixed points of a nonexpansive mapping on a real Hilbert space :
:
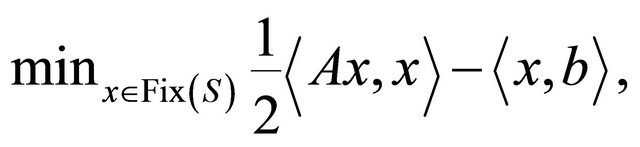 (1.3)
(1.3)
where A is a linear bounded operator and b is a given point in H. In [5] (see also [6]), it is proved that the sequence 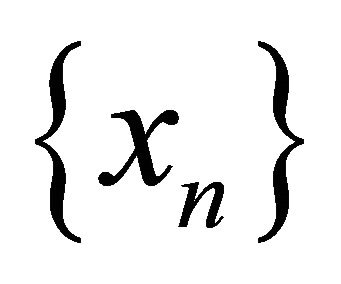 defined by the iterative method below, with the initial guess
defined by the iterative method below, with the initial guess 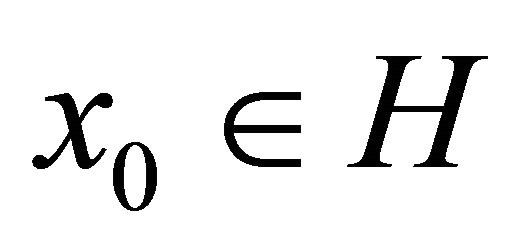 chosen arbitrarily,
chosen arbitrarily,
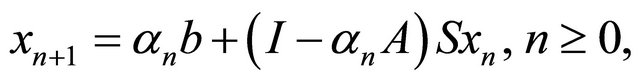
converges strongly to the unique solution of the minimization problem (1.3) provided the sequence 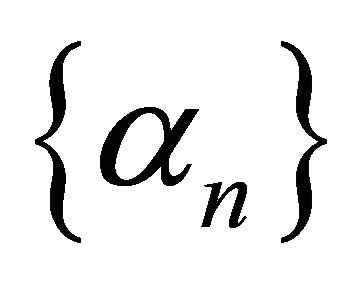 satisfies certain conditions. In 2006, Marino and Xu (see [3]) considered the following viscosity iterative method which was first introduced by Moudafi (see [7]):
satisfies certain conditions. In 2006, Marino and Xu (see [3]) considered the following viscosity iterative method which was first introduced by Moudafi (see [7]):
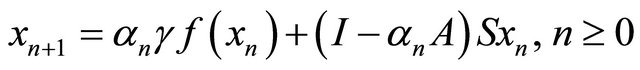 (1.4)
(1.4)
They proved that the sequence 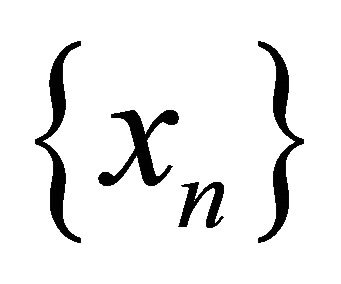 generated by iterative scheme (1.4) converges strongly to the unique solution of the variational inequality
generated by iterative scheme (1.4) converges strongly to the unique solution of the variational inequality 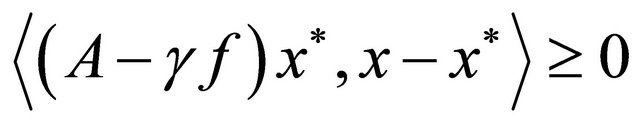 ,
, 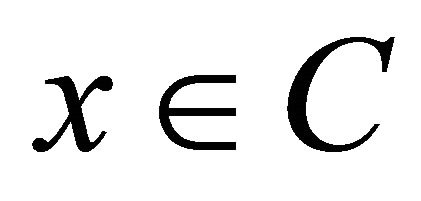 which is the optimality condition for the minimization problem
which is the optimality condition for the minimization problem
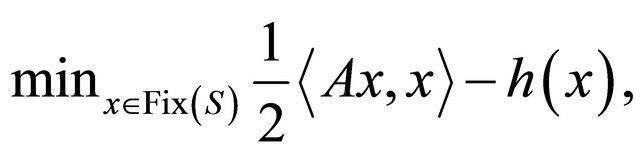
where h is a potential function for 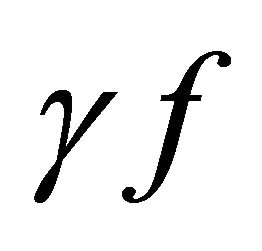 (i.e.,
(i.e., 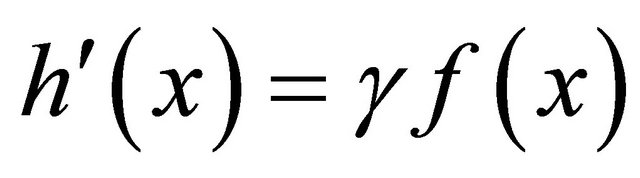 for
for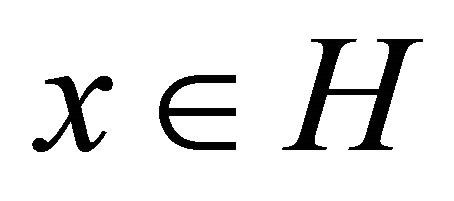 ).
).
For finding a common element of the set of fixed points of a nonexpansive mapping and the set of solutions of the variational inequality for  -cocoercive mapping, Takahashi and Toyoda (see [11]) introduced the following iterative process:
-cocoercive mapping, Takahashi and Toyoda (see [11]) introduced the following iterative process: 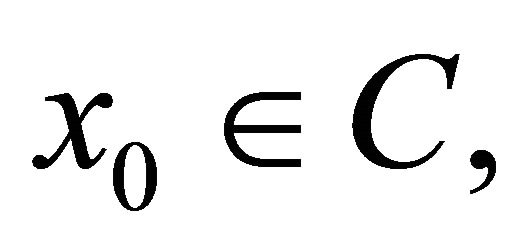
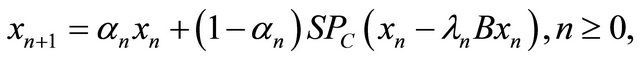 (1.5)
(1.5)
where B is  -cocoercive,
-cocoercive, 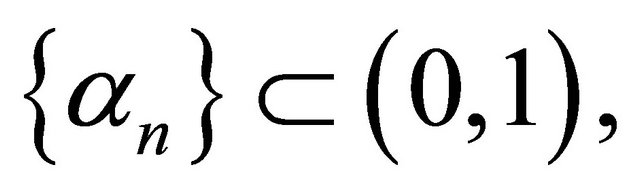 and
and 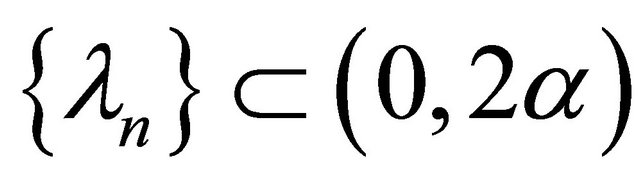 . They showed that, if
. They showed that, if 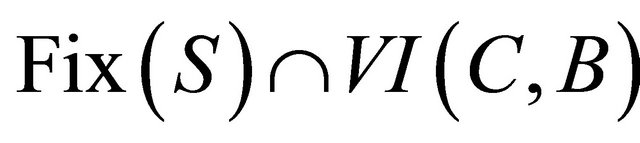 is nonempty, then the sequence
is nonempty, then the sequence 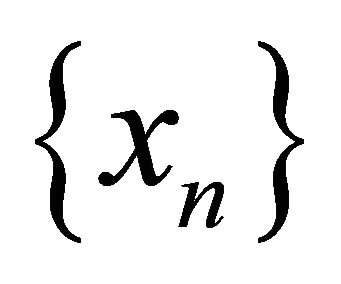 generated by (1.5) converges weakly to some
generated by (1.5) converges weakly to some 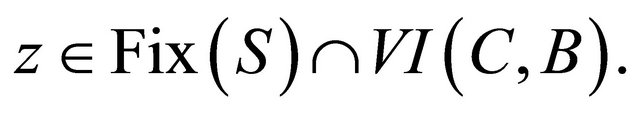 In 2005, Iiduka and Takahashi (see [12]) introduced the following iterative process:
In 2005, Iiduka and Takahashi (see [12]) introduced the following iterative process:
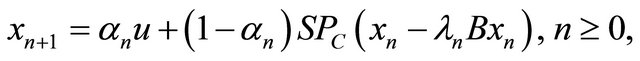 (1.6)
(1.6)
where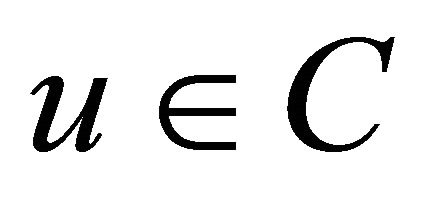 ,
, 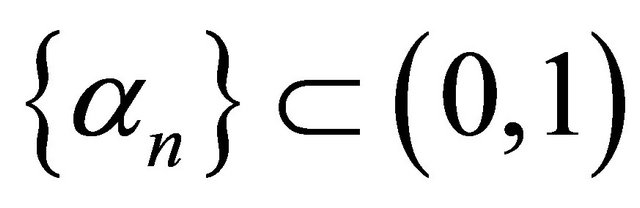 and
and 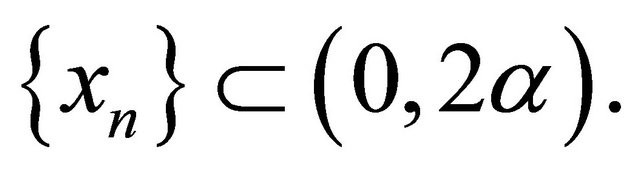 They proved that under certain appropriate conditions imposed on
They proved that under certain appropriate conditions imposed on 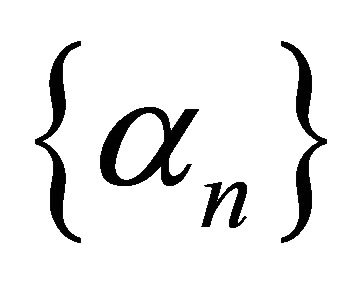 and
and 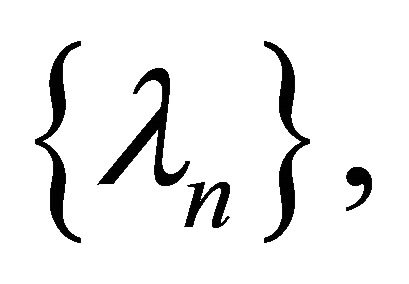 the sequence
the sequence 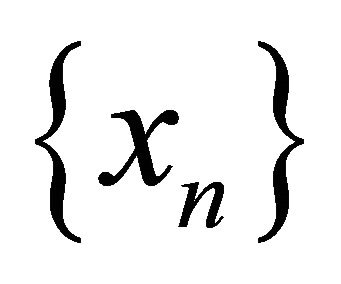 generated by (1.6) converges strongly to
generated by (1.6) converges strongly to 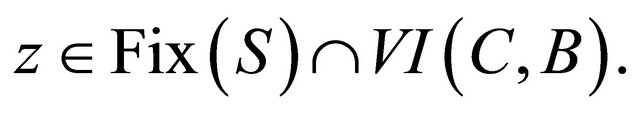 In 2009, Qin, Kang and Shang, [13] introduced the following iterative algorithm given by
In 2009, Qin, Kang and Shang, [13] introduced the following iterative algorithm given by 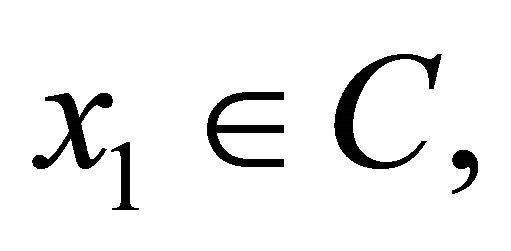
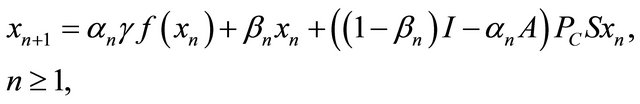 (1.7)
(1.7)
where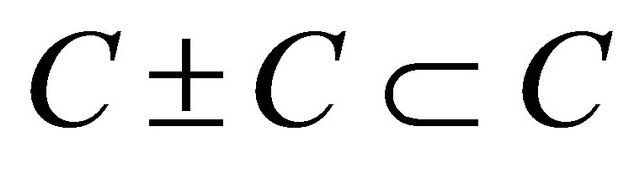 ,
, 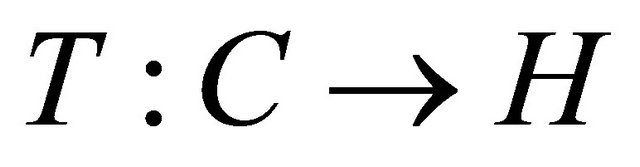 a k-strict pseudo-contraction for some
a k-strict pseudo-contraction for some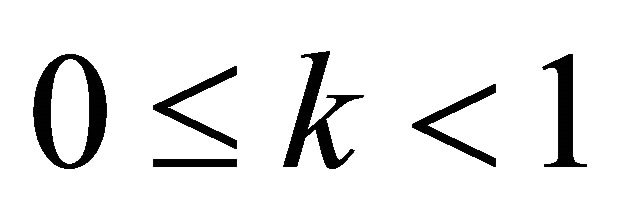 ,
, 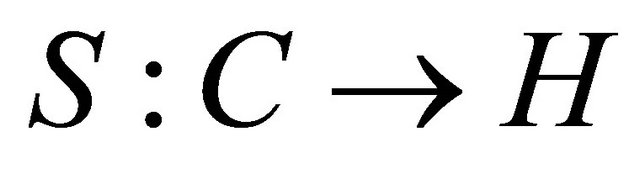 defined by
defined by 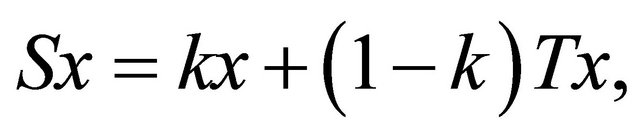 A is a strongly positive linear bounded self-adjoint operator and f is a contraction. They proved that the sequence
A is a strongly positive linear bounded self-adjoint operator and f is a contraction. They proved that the sequence 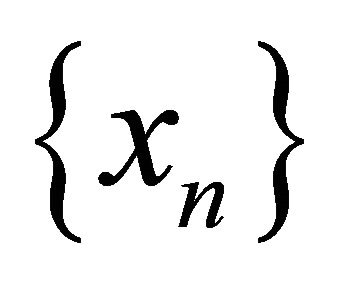 generated by the iterative algorithm (1.7) converges strongly to a fixed point of T, which solves a variational inequality related to the linear operator A.
generated by the iterative algorithm (1.7) converges strongly to a fixed point of T, which solves a variational inequality related to the linear operator A.
Let 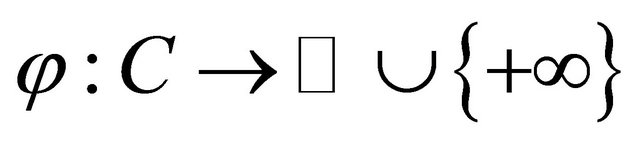 be a proper extended realvalued function and F be a bifunction from
be a proper extended realvalued function and F be a bifunction from 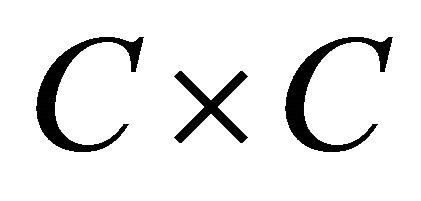 to
to  where
where  is the set of real numbers. Ceng and Yao [14] considered the following mixed equilibrium problem: Find
is the set of real numbers. Ceng and Yao [14] considered the following mixed equilibrium problem: Find 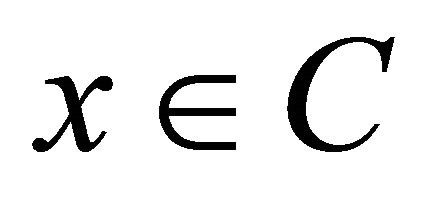 such that
such that
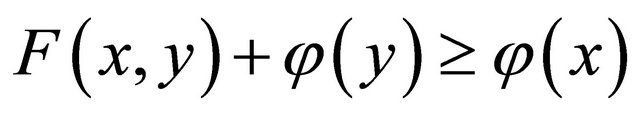 (1.8)
(1.8)
for all 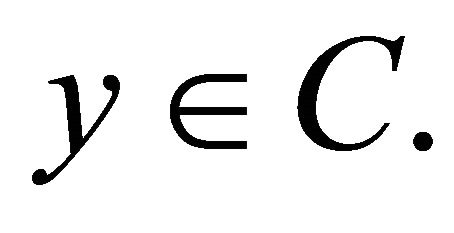 The set of solutions of (1.8) is denoted by
The set of solutions of (1.8) is denoted by 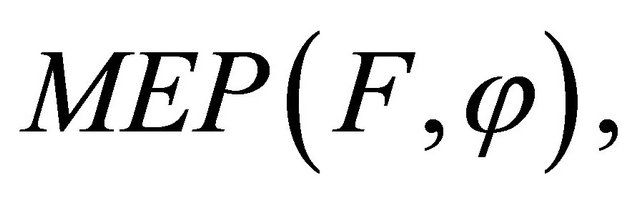 i.e.,
i.e.,
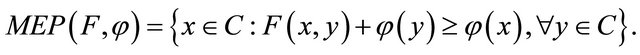
It is easy to see that x is a solution of problem (1.8) implies that 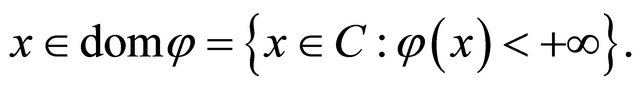 Moreover, Ceng and Yao [14] introduced an iterative scheme for finding a common element of the set of solutions of problem (1.8) and the set of common fixed points of a family of finitely nonexpansive mappings in a Hilbert space and obtained a strong convergence theorem. If
Moreover, Ceng and Yao [14] introduced an iterative scheme for finding a common element of the set of solutions of problem (1.8) and the set of common fixed points of a family of finitely nonexpansive mappings in a Hilbert space and obtained a strong convergence theorem. If 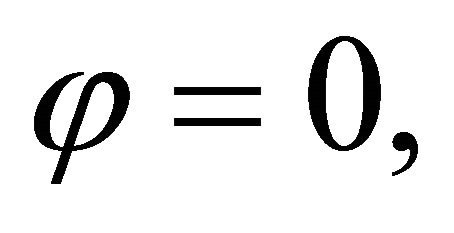 then the mixed equilibrium problem (1.8) becomes the following equilibrium problem:
then the mixed equilibrium problem (1.8) becomes the following equilibrium problem:
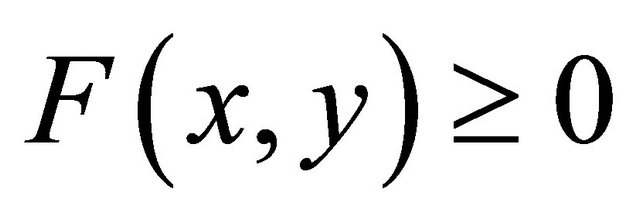 (1.9)
(1.9)
for all 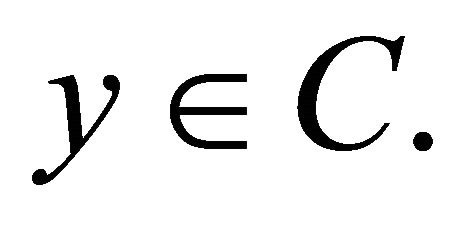 The set of solutions of (1.9) is denoted by
The set of solutions of (1.9) is denoted by 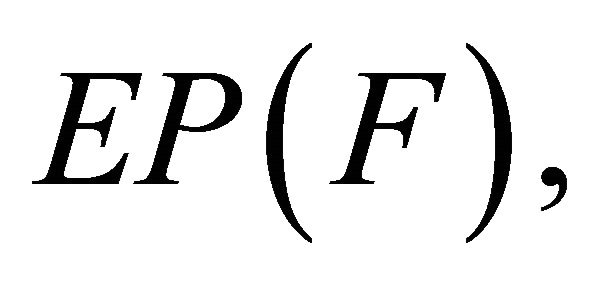 i.e.,
i.e.,
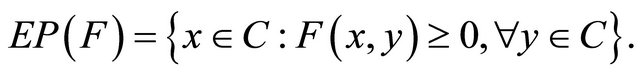
Given a mapping 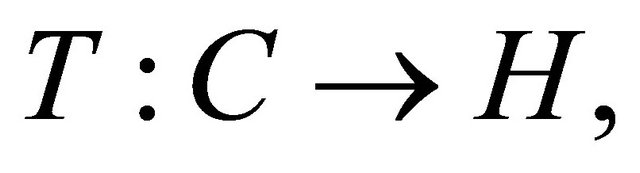 let
let  and
and 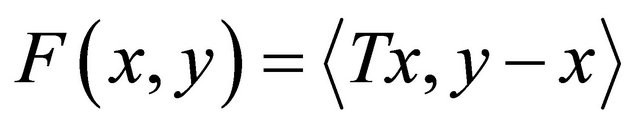 for all
for all 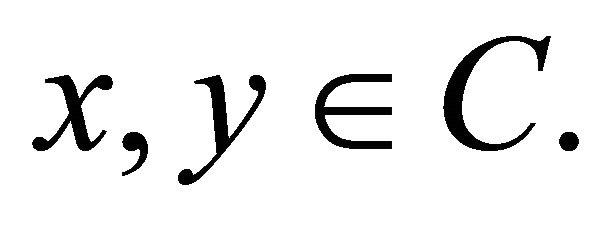 Then,
Then,  if and only if
if and only if 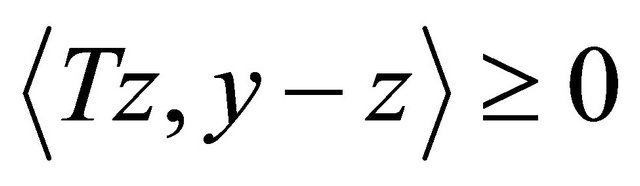 for all
for all 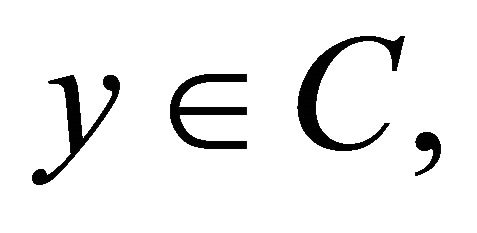 i.e., z is a solution of the variational inequality. Equilibrium problems have been studied extensively; see, for instance, [15,16]. The mixed equilibrium problem (1.8) is very general in the sense that it includes, as special cases, optimization problems, variational inequalities, minimax problems, Nash equilibrium problem in noncooperative games and others; see for instance, [14,16-19].
i.e., z is a solution of the variational inequality. Equilibrium problems have been studied extensively; see, for instance, [15,16]. The mixed equilibrium problem (1.8) is very general in the sense that it includes, as special cases, optimization problems, variational inequalities, minimax problems, Nash equilibrium problem in noncooperative games and others; see for instance, [14,16-19].
Combettes and Hirstoaga (see [15]) introduced an iterative scheme for finding the best approximation to the initial data when 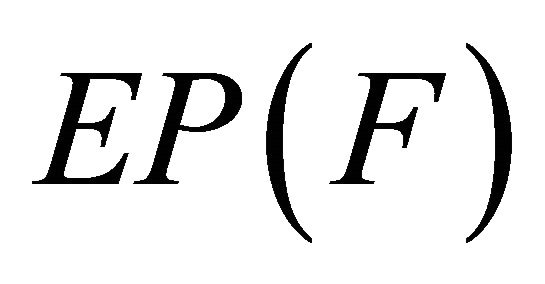 is nonempty and proved a strong convergence theorem. In 2007, S. Takahashi and W. Takahashi (see [20]) introduced an iterative scheme using the viscosity approximation method for finding a common element of the set of solutions of equilibrium problem (1.9) and the set of fixed points of a nonexpansive nonself-mapping in a Hilbert space. The scheme is defined as follows:
is nonempty and proved a strong convergence theorem. In 2007, S. Takahashi and W. Takahashi (see [20]) introduced an iterative scheme using the viscosity approximation method for finding a common element of the set of solutions of equilibrium problem (1.9) and the set of fixed points of a nonexpansive nonself-mapping in a Hilbert space. The scheme is defined as follows: 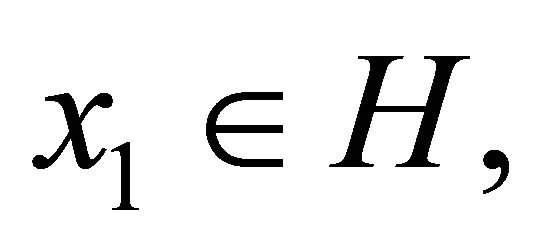
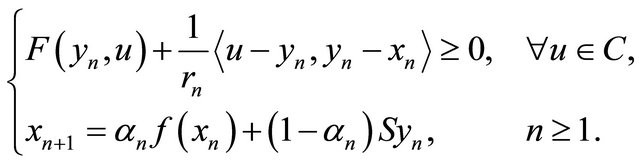 (1.10)
(1.10)
They proved that under certain appropriate conditions imposed on 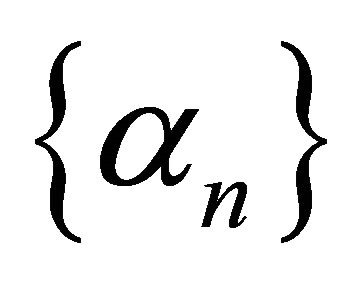 and
and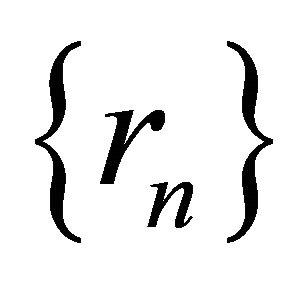 , the sequences
, the sequences 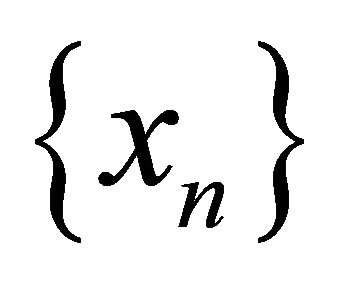 and
and 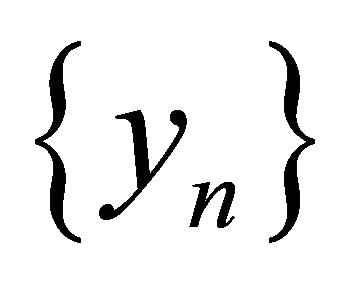 generated by (1.10) converge strongly to
generated by (1.10) converge strongly to 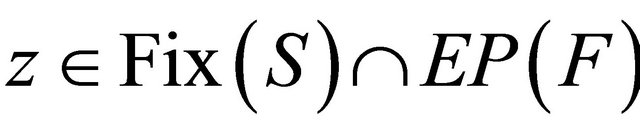 , where
, where 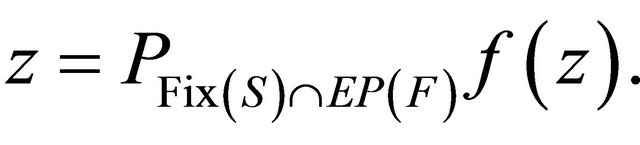 In the same year, Shang et al. (see [21]) introduced the following iterative scheme:
In the same year, Shang et al. (see [21]) introduced the following iterative scheme: 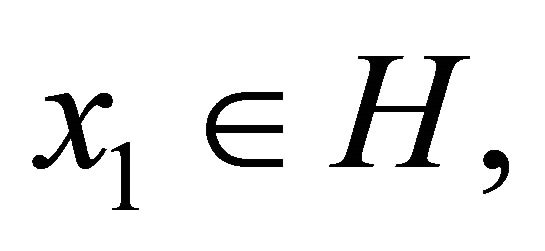
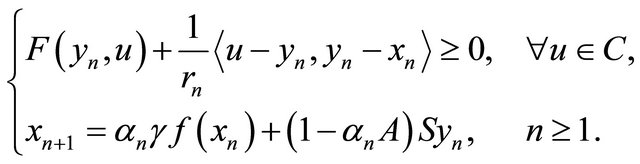 (1.11)
(1.11)
for finding a common element of the set of solutions of equilibrium problem (1.9) and the set of fixed points of a nonexpansive nonself-mapping in a Hilbert space. They proved that under some sufficient suitable conditions, the sequences 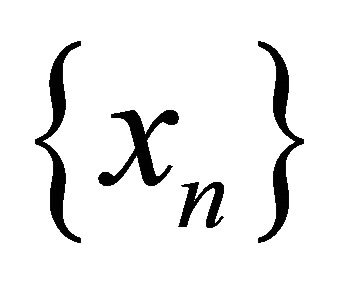 and
and 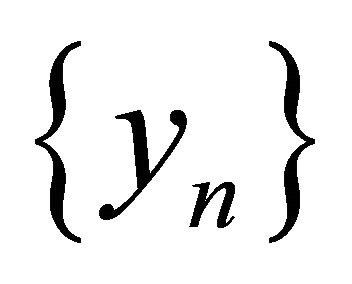 generated by (1.11) converge strongly to
generated by (1.11) converge strongly to
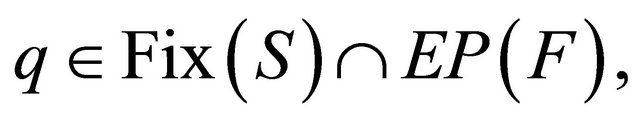
where
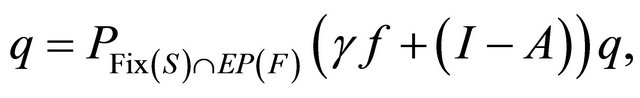
which is the unique solution of the variational inequality
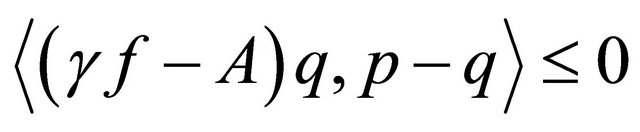
for all 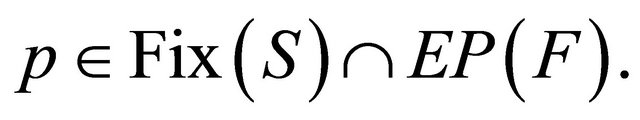
Let 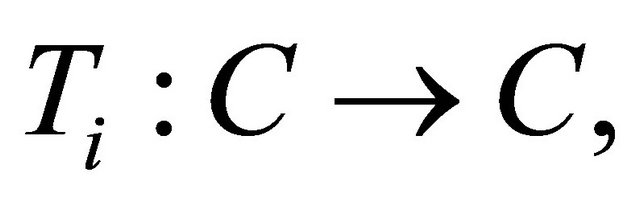 where
where 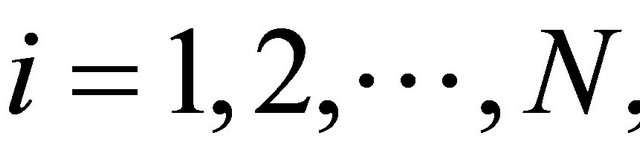 be a finite family of nonexpansive mappings. Finding an optimal point in the intersection
be a finite family of nonexpansive mappings. Finding an optimal point in the intersection 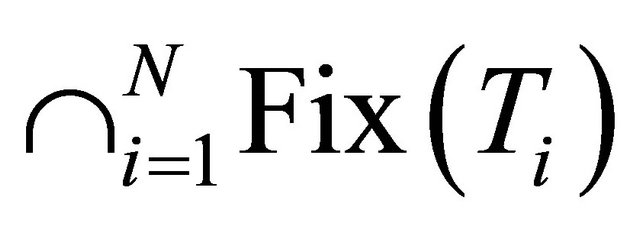 of the fixed points set of a finite family of nonexpansive mappings is a problem of interest in various branches of sciences; see [22-27] and also see [28] for solving the variational problems defined on the set of common fixed points of finitely many nonexpansive mappings. Atsushiba and Takahashi (see [29]), defined the mappings
of the fixed points set of a finite family of nonexpansive mappings is a problem of interest in various branches of sciences; see [22-27] and also see [28] for solving the variational problems defined on the set of common fixed points of finitely many nonexpansive mappings. Atsushiba and Takahashi (see [29]), defined the mappings
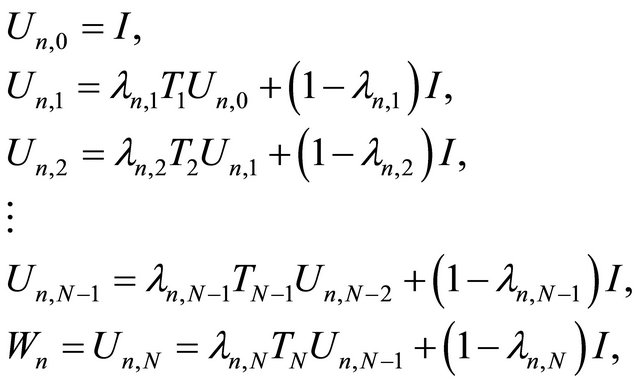 (1.12)
(1.12)
where 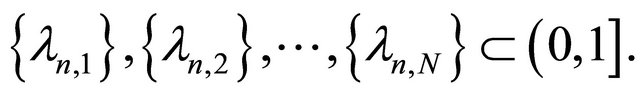 Such a mapping
Such a mapping 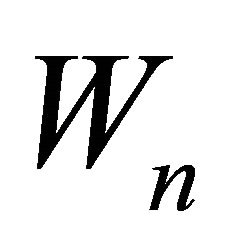 is called the W-mapping generated by
is called the W-mapping generated by 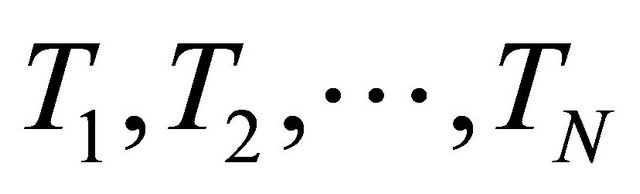 and
and 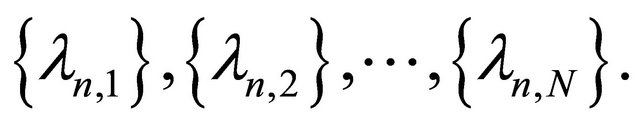 The concept of W-mappings was introduced in [30-33]. In 2008, Qin et al. (see [34]) introduced and studied the following iterative process:
The concept of W-mappings was introduced in [30-33]. In 2008, Qin et al. (see [34]) introduced and studied the following iterative process: 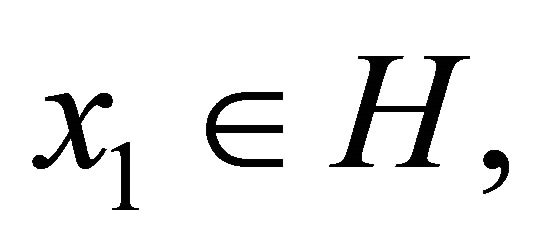
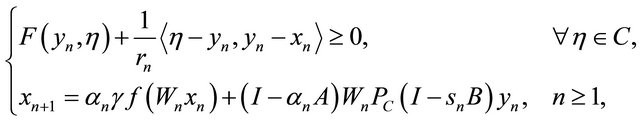 (1.13)
(1.13)
where 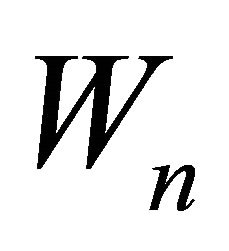 is defined by (1.12),
is defined by (1.12),  is a strongly linear bounded operator and B is
is a strongly linear bounded operator and B is 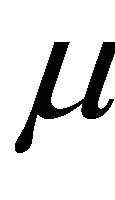 -Lipschitzian, relaxed
-Lipschitzian, relaxed 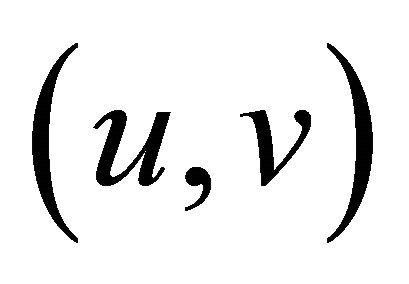 -cocoercive mapping of C into H. They proved that the sequences
-cocoercive mapping of C into H. They proved that the sequences 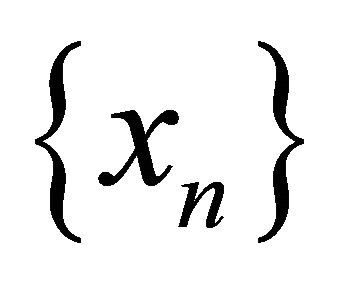 and
and 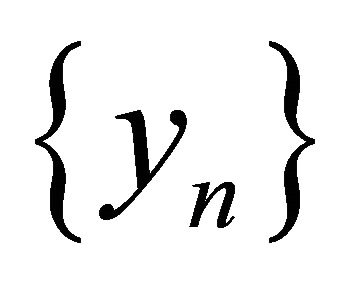 generated by the iterative scheme (1.13) converge strongly to
generated by the iterative scheme (1.13) converge strongly to
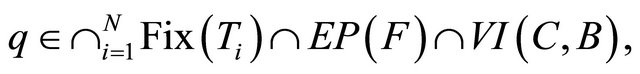
where
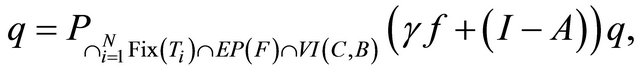
which is the unique solution of the variational inequality
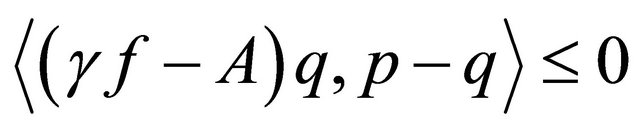
for all
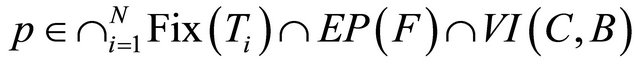 .
.
In the same year, Colao et al. (see [35]) introduced a new iterative scheme: 
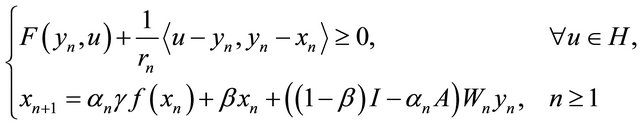 (1.14)
(1.14)
for approximating a common element of the set of solutions of equilibrium problem (1.9) and the set of common fixed points of a finite family of nonexpansive mappings and obtained a strong convergence theorem in a Hilbert space. In 2009, Yao et al. (see [36]) studied similar scheme as follows: 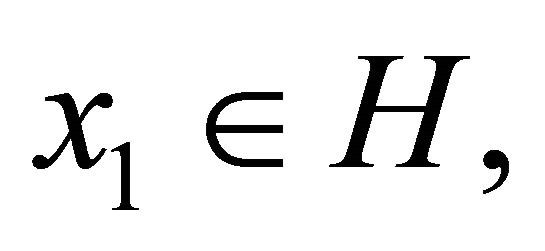
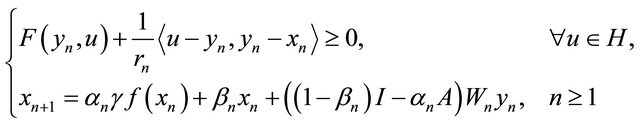 (1.15)
(1.15)
where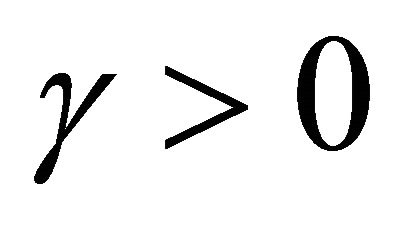 ,
, 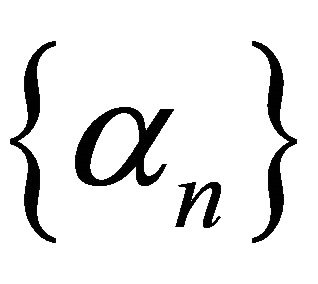 ,
, 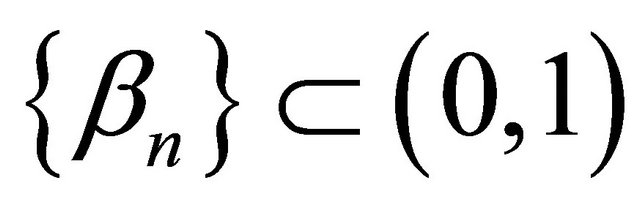 ,
, 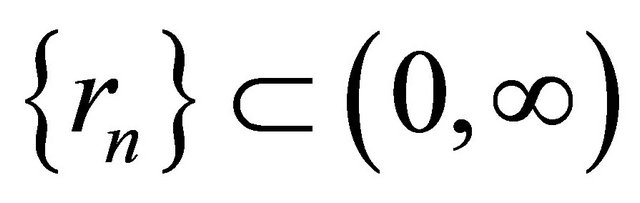 and
and 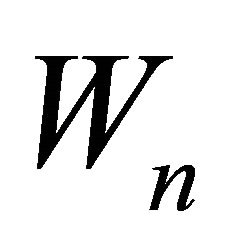 is the W-mapping defined by (1.12). They proved that under certain appropriate conditions imposed on
is the W-mapping defined by (1.12). They proved that under certain appropriate conditions imposed on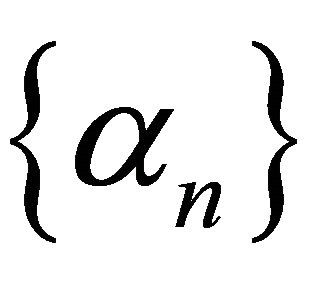 ,
, 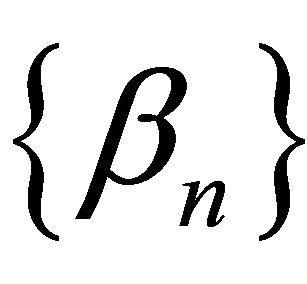 ,
, 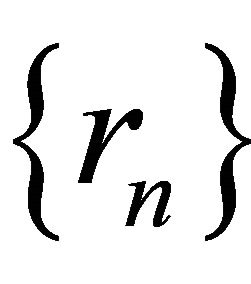 and
and 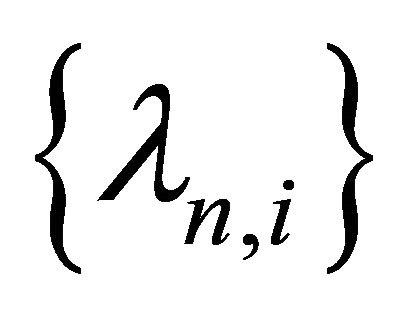
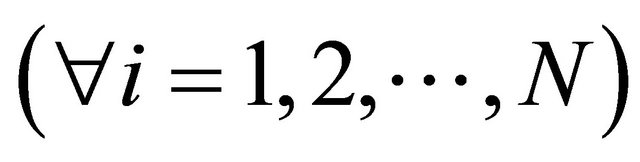 , the sequences
, the sequences 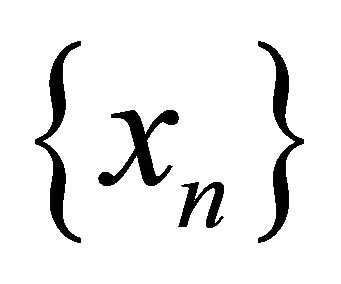 and
and 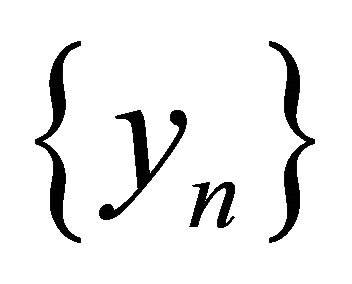 generated by (1.15) converge strongly to
generated by (1.15) converge strongly to
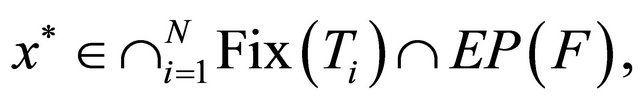
where
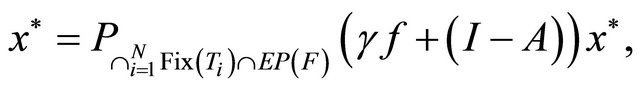
which is the unique solution of the variational inequality
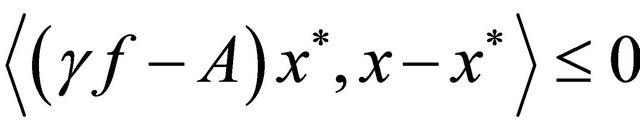 for all
for all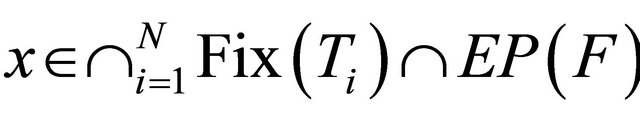 .
.
If 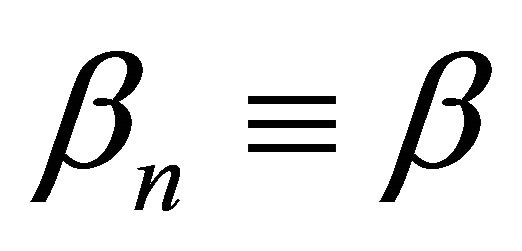 for some
for some 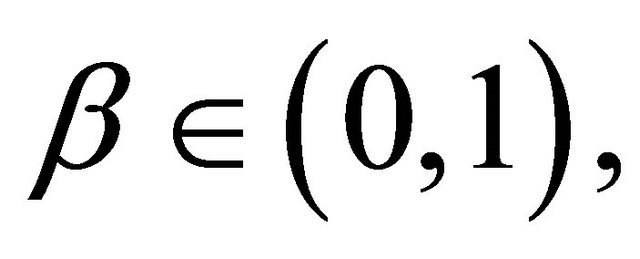 then (1.15) reduces to the iterative scheme (1.14). Very recently, Kangtunyakarn and Suantai (see [37]) defined the new mappings
then (1.15) reduces to the iterative scheme (1.14). Very recently, Kangtunyakarn and Suantai (see [37]) defined the new mappings
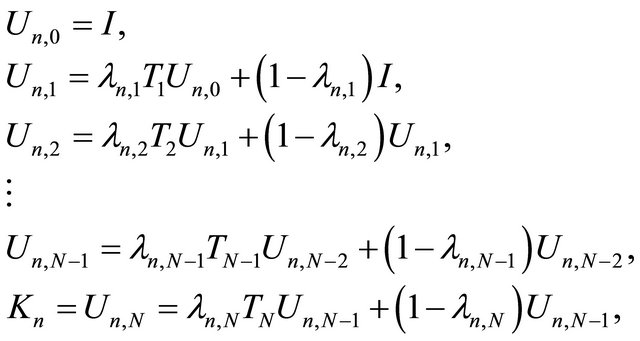 (1.16)
(1.16)
where 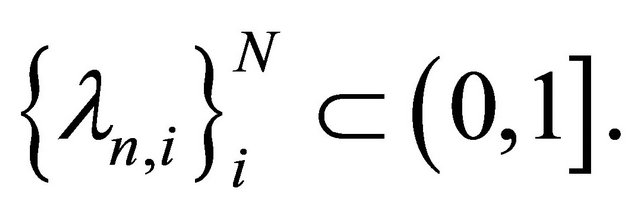 Such a mapping Kn is called the K-mapping generated by
Such a mapping Kn is called the K-mapping generated by 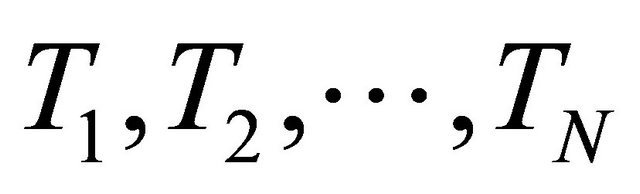 and
and 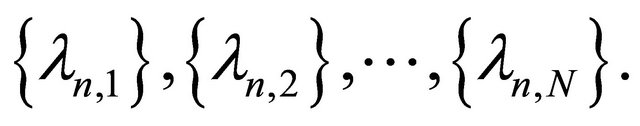 Nonexpansivity of each Ti ensures the nonexpansivity of Kn Also following they defined the new mappings
Nonexpansivity of each Ti ensures the nonexpansivity of Kn Also following they defined the new mappings
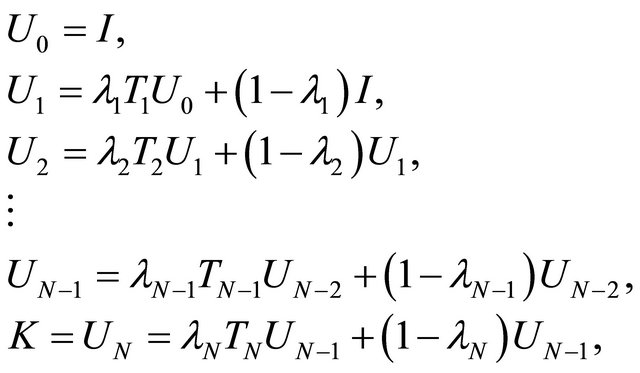 (1.17)
(1.17)
where 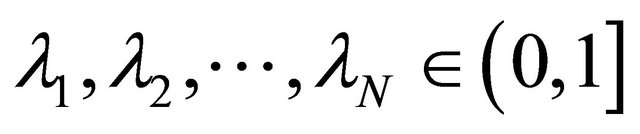 such that
such that 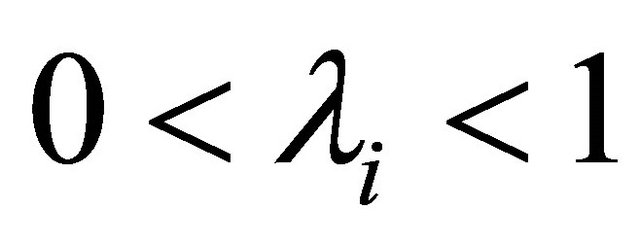 for all
for all 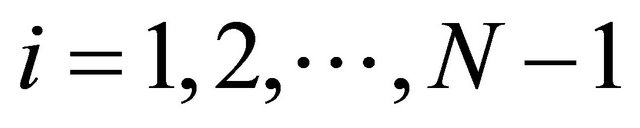 and
and 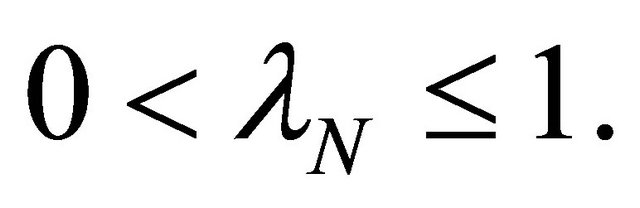 Such a mapping K is called the K-mapping generated by
Such a mapping K is called the K-mapping generated by 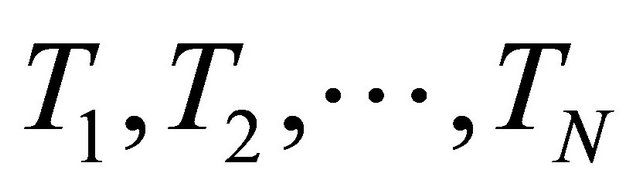 and
and 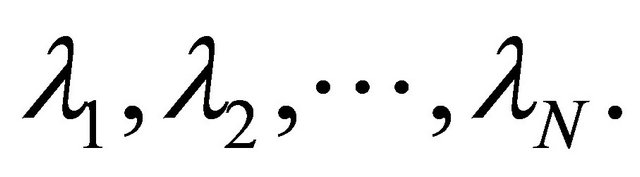 In [37], Lemma 2.9 and Lemma 2.10, its shown that
In [37], Lemma 2.9 and Lemma 2.10, its shown that
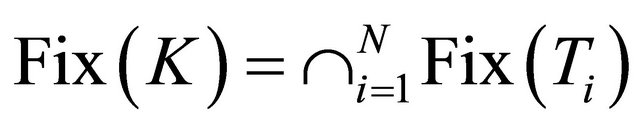
and 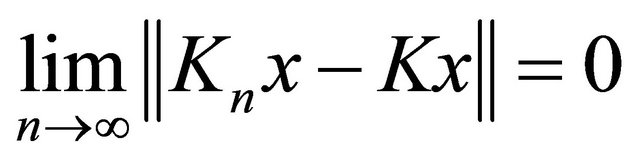 for all
for all 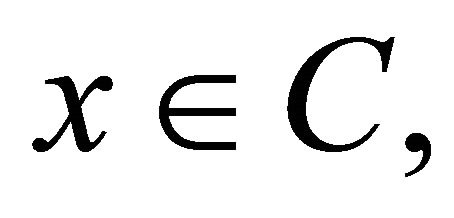 where Kn and K are the K-mappings defined by (1.16) and (1.17), respectively. Its important tool for the proof of the main results in this paper. Moreover, Kangtunyakarn and Suantai (see [37]) introduced a new iterative scheme:
where Kn and K are the K-mappings defined by (1.16) and (1.17), respectively. Its important tool for the proof of the main results in this paper. Moreover, Kangtunyakarn and Suantai (see [37]) introduced a new iterative scheme: 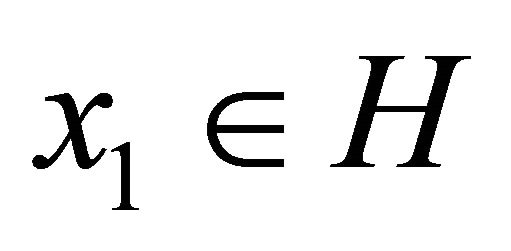 and
and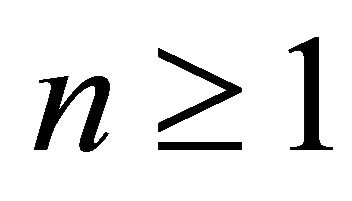 ,
,
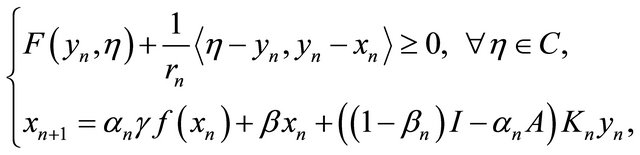 (1.18)
(1.18)
where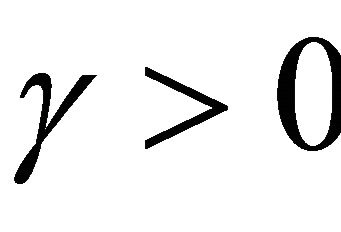 ,
, 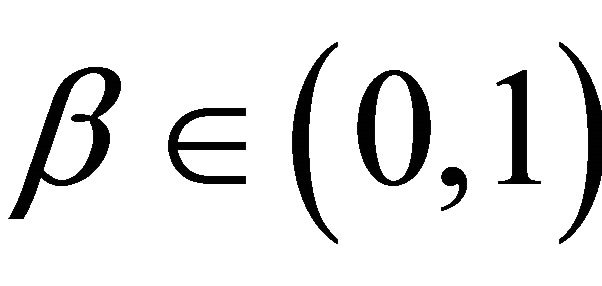 ,
, 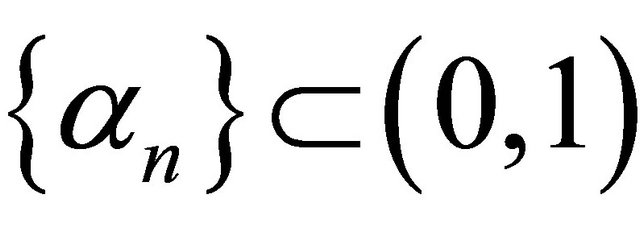 ,
, 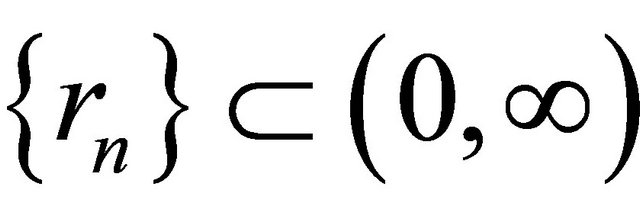 and Kn is the K-mapping defined by (1.16). They proved that under certain appropriate conditions imposed on
and Kn is the K-mapping defined by (1.16). They proved that under certain appropriate conditions imposed on ,
,  and
and 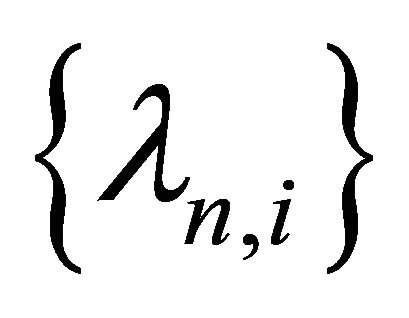
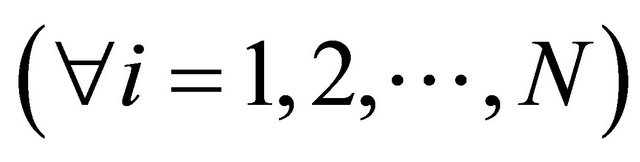 , the sequences
, the sequences 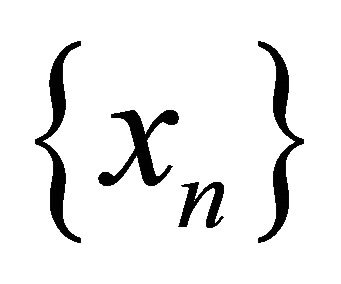 and
and 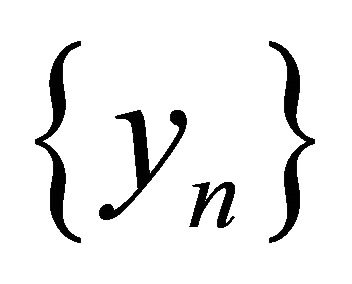 generated by (1.18) converge strongly to
generated by (1.18) converge strongly to
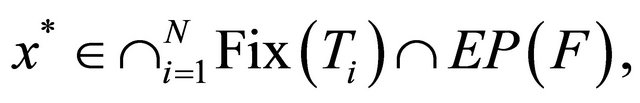
where
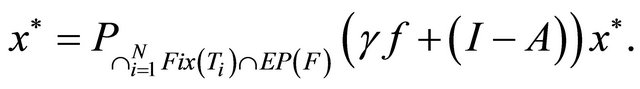
Motivated by the recent works, we introduce a more general iterative algorithm for finding a common element of the set of common fixed points of a finite family of nonexpansive mappings, the set of solutions of a mixed equilibrium problem, and the set of solutions of the variational inequality problem for a relaxed cocoercive mapping in a real Hilbert space. The scheme is defined as follows:  and
and 
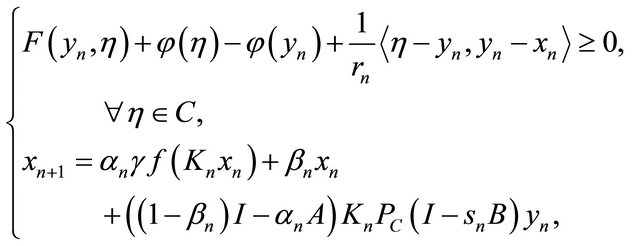 (1.19)
(1.19)
where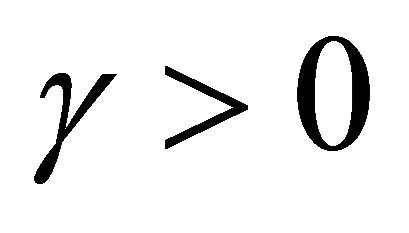 ,
, 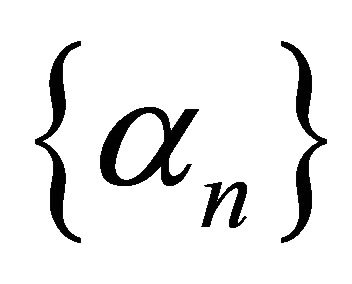 ,
, 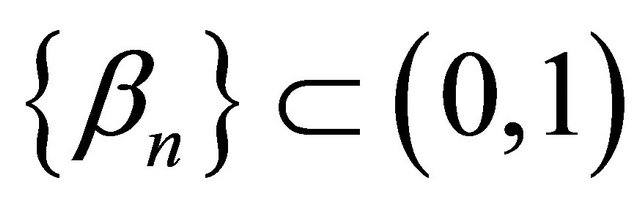 ,
, 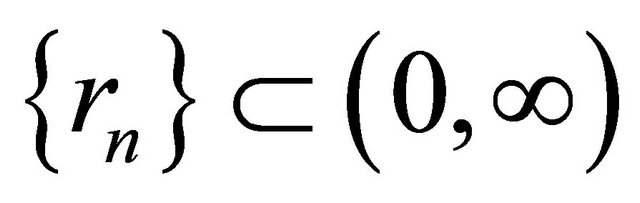 ,
, 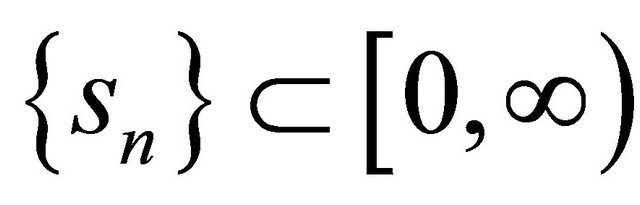 ,
, 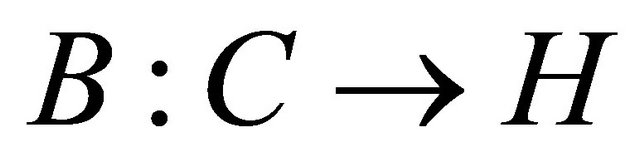 is a
is a 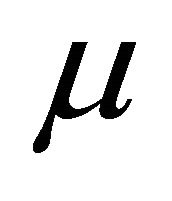 -Lipschitzian, relaxed
-Lipschitzian, relaxed 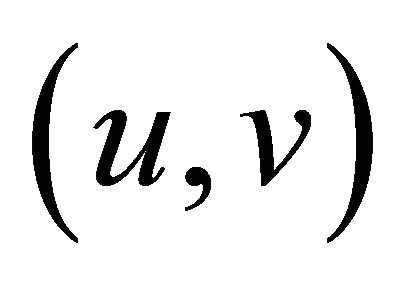 -cocoercive mapping, f is a contraction of H into itself with a coefficient
-cocoercive mapping, f is a contraction of H into itself with a coefficient 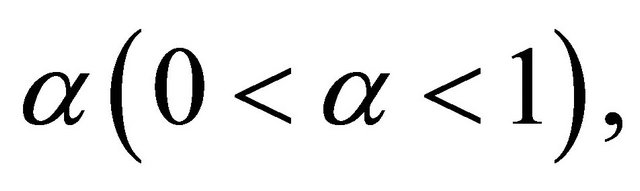
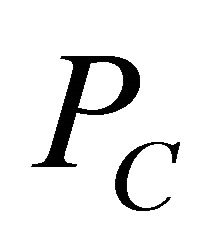 is a projection of H onto C, A is a strongly positive linear bounded operator on H, F is a mixed equilibrium bifunction,
is a projection of H onto C, A is a strongly positive linear bounded operator on H, F is a mixed equilibrium bifunction, 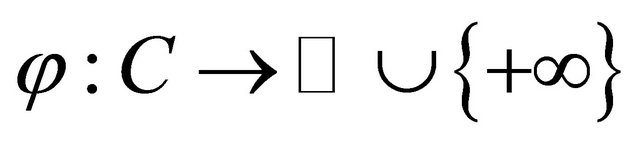 is a proper lower semicontinuous and convex function and Kn is the K-mapping generated by
is a proper lower semicontinuous and convex function and Kn is the K-mapping generated by 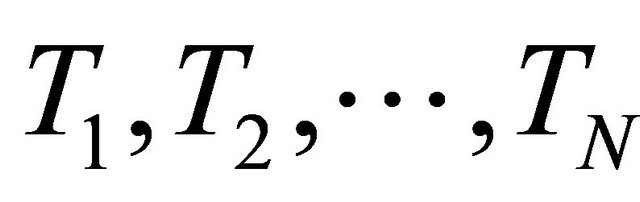 and
and 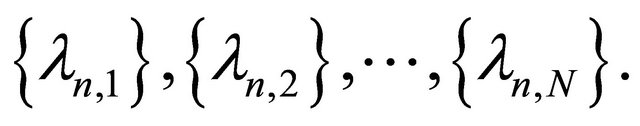 We prove that the sequences
We prove that the sequences 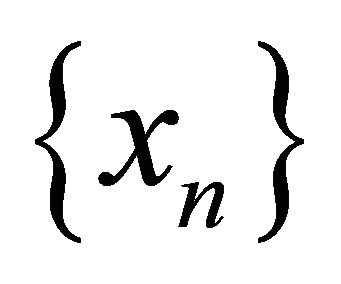 and
and 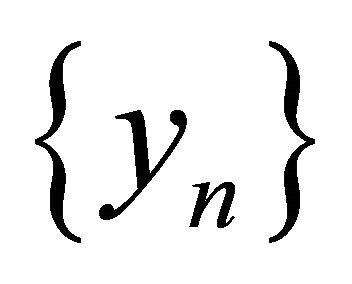 generated by the iterative scheme (1.19) converge strongly to
generated by the iterative scheme (1.19) converge strongly to
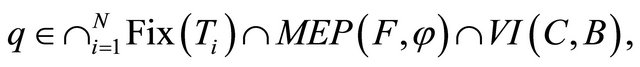
where
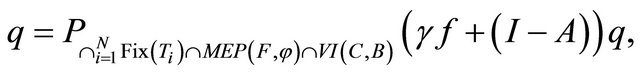
which is the unique solution of the variational inequality for all 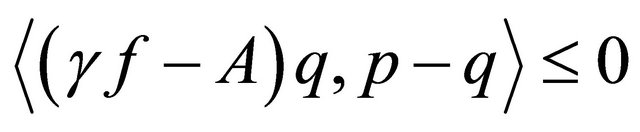
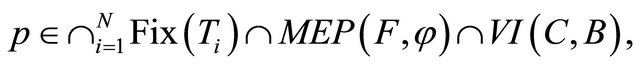
and is also the optimality condition for the minimization problem
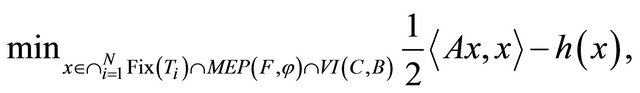
where h is a potential function for 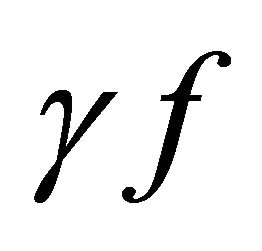 (i.e.,
(i.e., 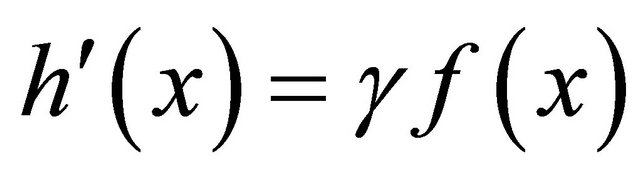 for
for ).
).
2. Preliminaries and Lemmas
In this section, we collect and give some useful lemmas that will be used for our main result in the next section.
A mapping B is called 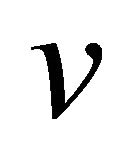 -strongly monotone, if each
-strongly monotone, if each 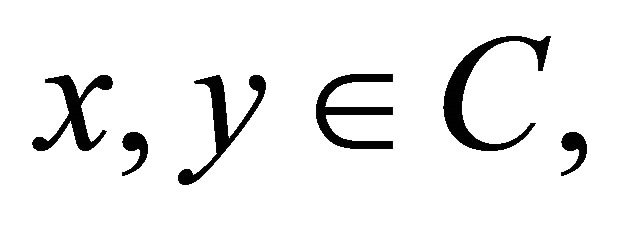 we have
we have
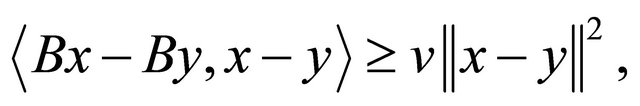
for a constant v > 0, which implies that 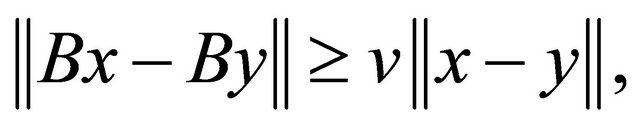 so that B is v-expansive and when v = 1, it is expansive. B is said to be v-cocoercive (see [8] and [9]), if for each
so that B is v-expansive and when v = 1, it is expansive. B is said to be v-cocoercive (see [8] and [9]), if for each 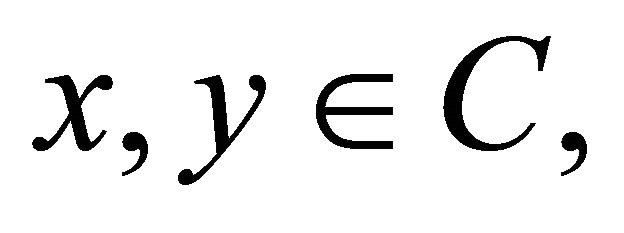 we have
we have
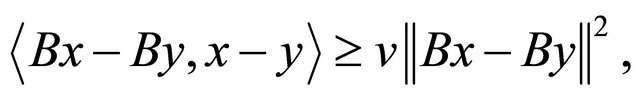
for a constant v > 0. Clearly, every v-cocoercive mapping B is  -Lipschitz continuous. B is called relaxed u-cocoercive, if there exists a constant u > 0 such that
-Lipschitz continuous. B is called relaxed u-cocoercive, if there exists a constant u > 0 such that
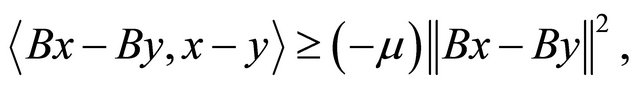
for all 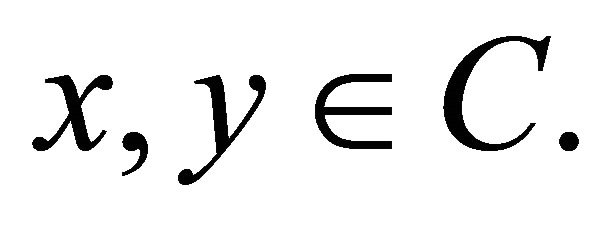 B is said to be relaxed
B is said to be relaxed 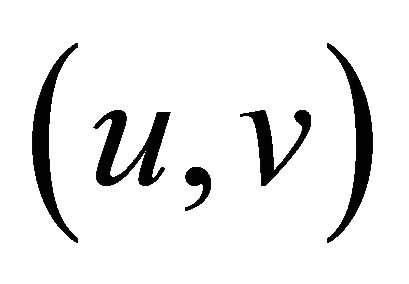 -cocoercive, if there exist two constants u, v > 0 such that
-cocoercive, if there exist two constants u, v > 0 such that
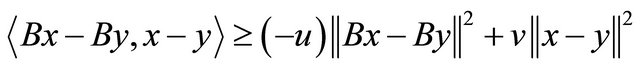
for all 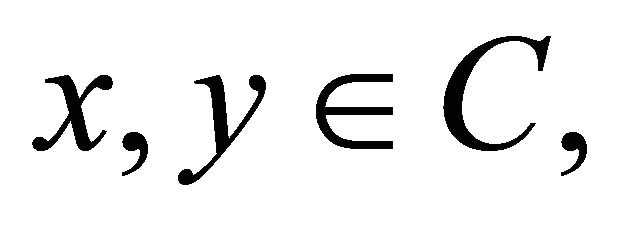 for
for 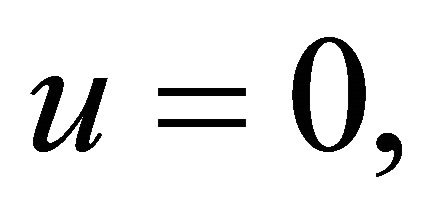 B is v-strongly monotone.
B is v-strongly monotone.
It is worth mentioning that the class of mappings which are relaxed 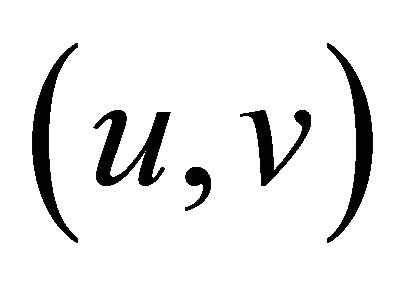 -cocoercive more general than the class of strongly monotone mappings. It is easy to see that if B is a v-strongly monotone mapping, then it is a relaxed
-cocoercive more general than the class of strongly monotone mappings. It is easy to see that if B is a v-strongly monotone mapping, then it is a relaxed 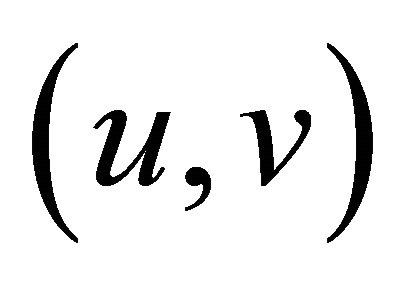 -cocoercive mapping (see [10]).
-cocoercive mapping (see [10]).
It is well known that for all 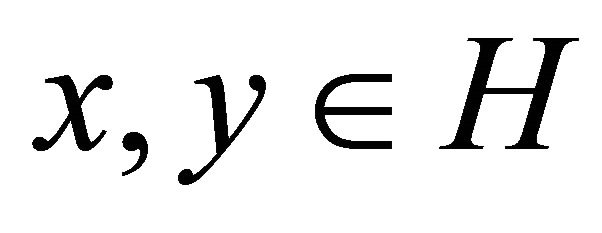 and
and 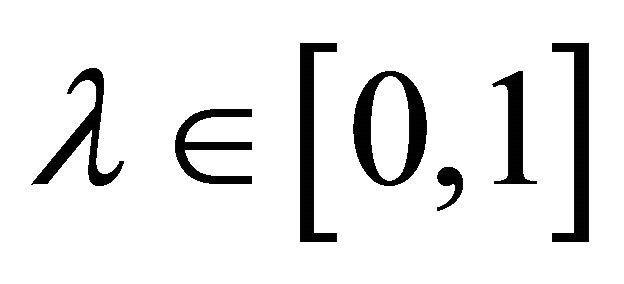 there holds
there holds
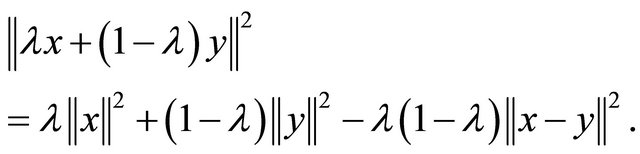
Recall that a space X is said to satisfy Opial’s condition (see [38]) if 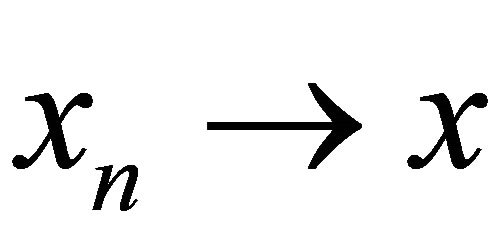 weakly as
weakly as  and
and 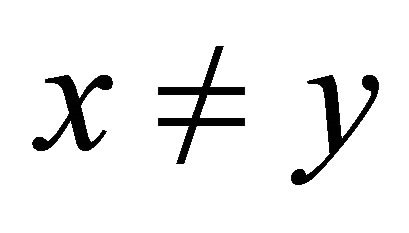 for all
for all 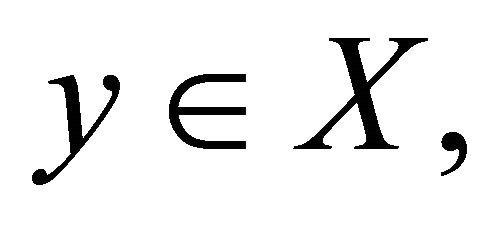 then
then
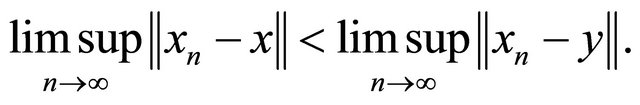
A set-valued mapping 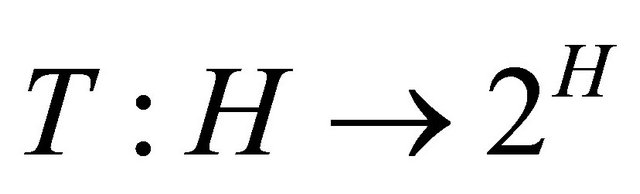 is called monotone if for all
is called monotone if for all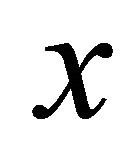 ,
, 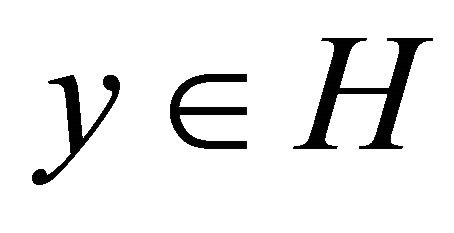 ,
, 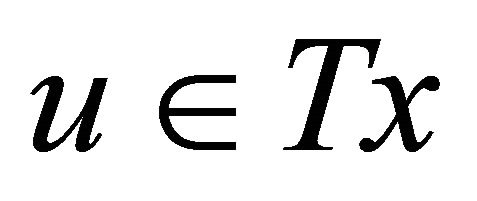 and
and 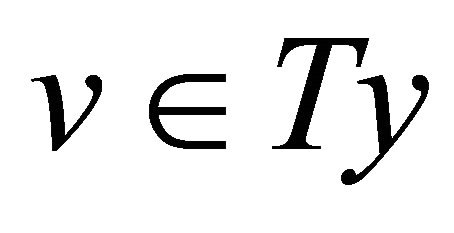 imply
imply 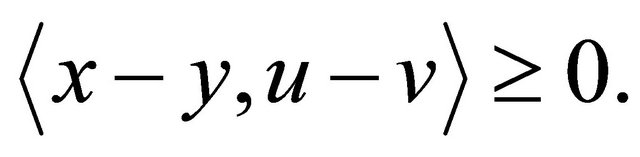
A monotone mapping 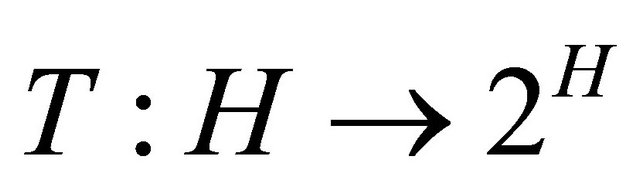 is maximal if graph
is maximal if graph 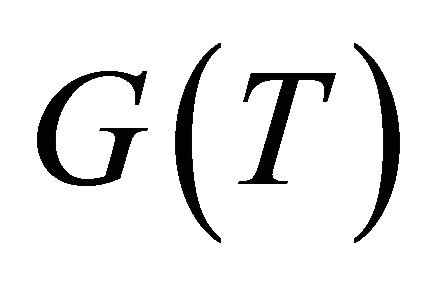 of T is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping T is maximal if and only if for
of T is not properly contained in the graph of any other monotone mapping. It is known that a monotone mapping T is maximal if and only if for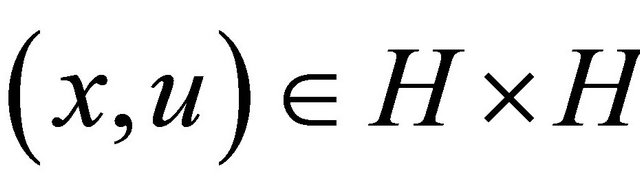 ,
, 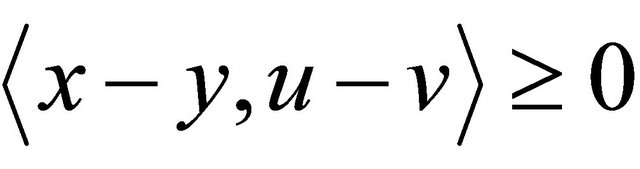 for every
for every 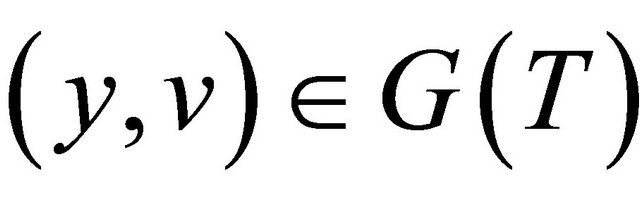 implies
implies 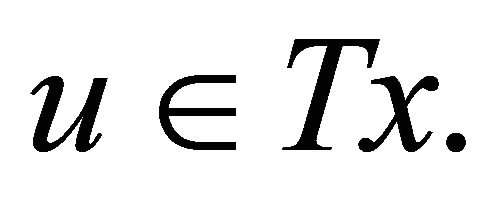 Let B be a monotone mapping of C into H and let
Let B be a monotone mapping of C into H and let 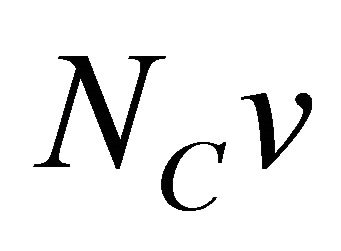 be normal cone to C at
be normal cone to C at 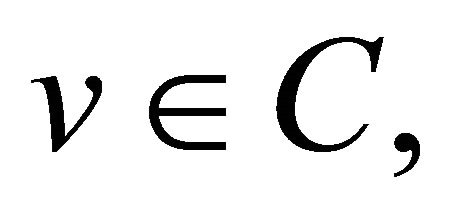 i.e.,
i.e.,
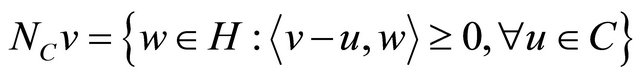
and define
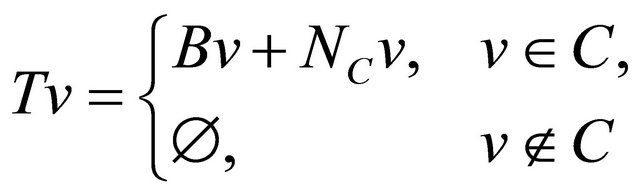
Then T is a maximal monotone and 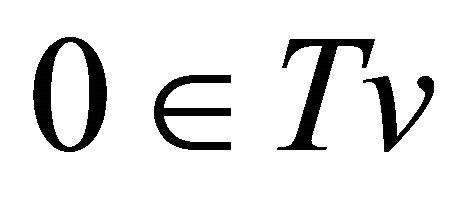 if and only if
if and only if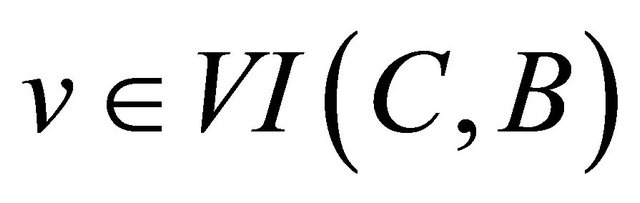 ; see [39].
; see [39].
In the sequel, the following lemmas are needed to prove our main results.
Lemma 2.1. (see [4,5]). Assume that 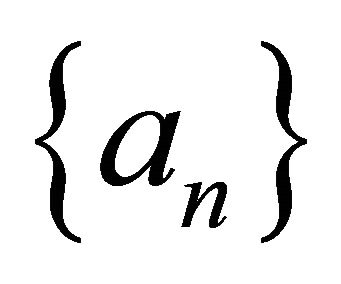 is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that
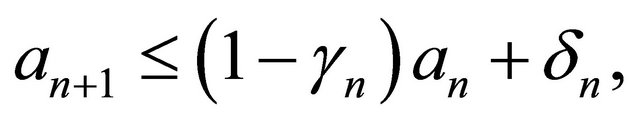
where 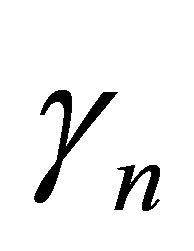 is a sequence in
is a sequence in 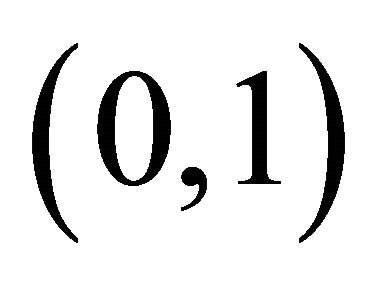 and
and 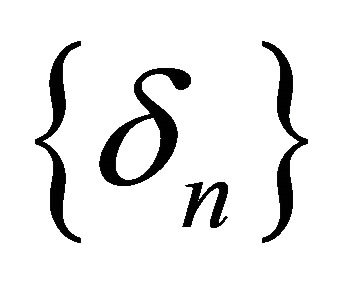 is a sequence such that 1)
is a sequence such that 1) 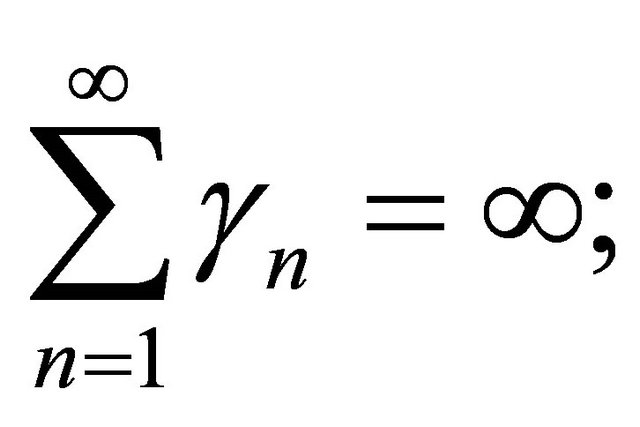
2) 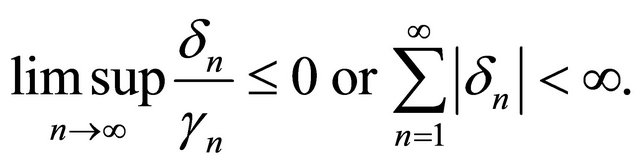 Then
Then 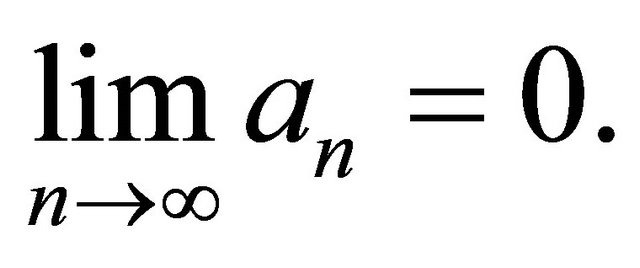
Lemma 2.2. (see [3]). Assume A is a strong positive linear bounded operator on a Hilbert space H with coefficient 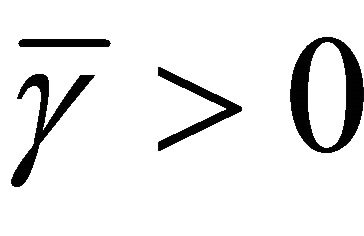 and
and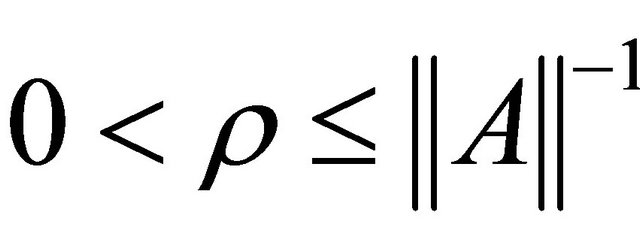 . Then
. Then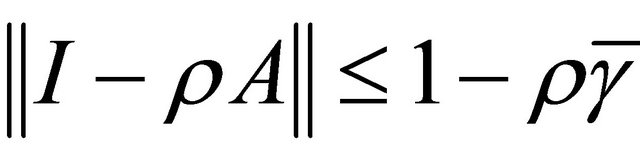 .
.
Lemma 2.3. (see [40]). Let 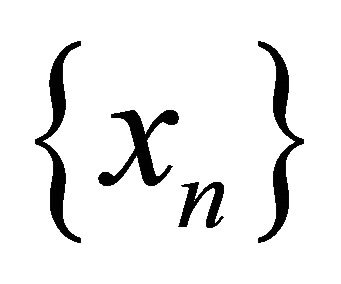 and
and 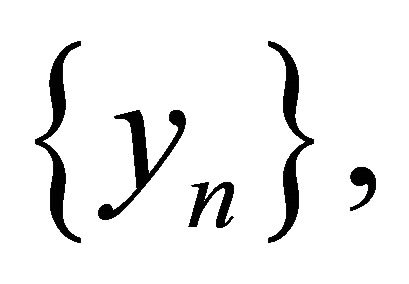 be bounded sequences in a Banach space
be bounded sequences in a Banach space 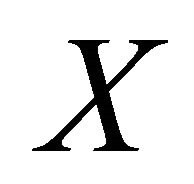 and let
and let 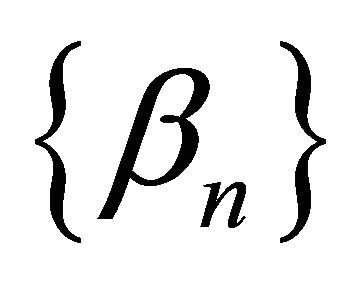 be a sequence in
be a sequence in 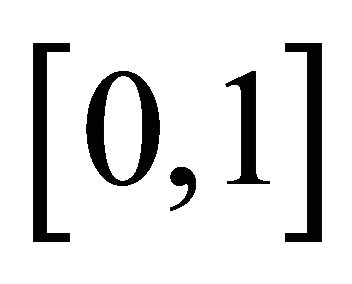 with
with
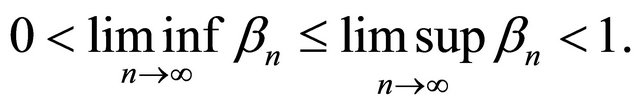
Suppose 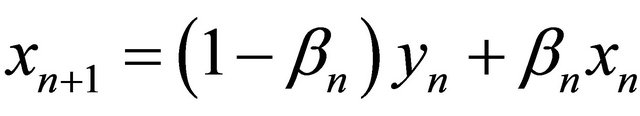 for all integers n ≥ 0 and
for all integers n ≥ 0 and 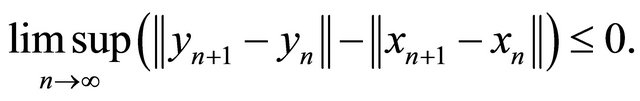
Then
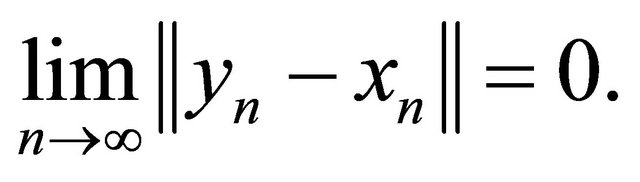
Lemma 2.4. (see [37]). Let C be a nonempty closed convex set of a strictly convex Banach space. Let 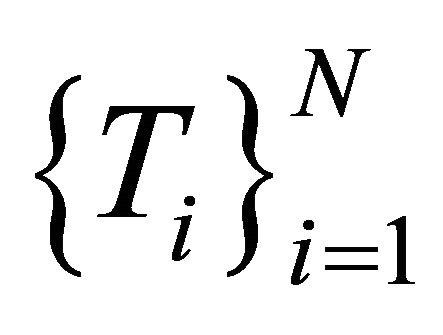 be a finite family of nonexpansive mappings of C into itself with
be a finite family of nonexpansive mappings of C into itself with 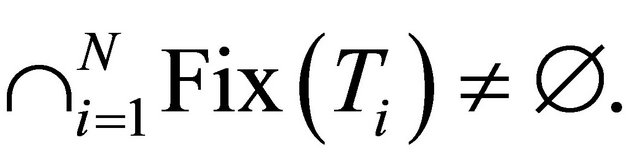 and let
and let 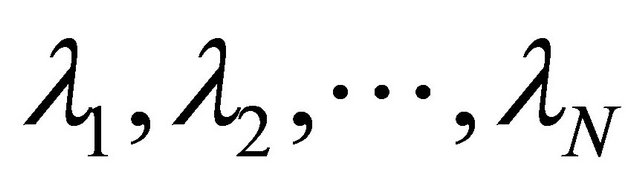 be real numbers such that
be real numbers such that 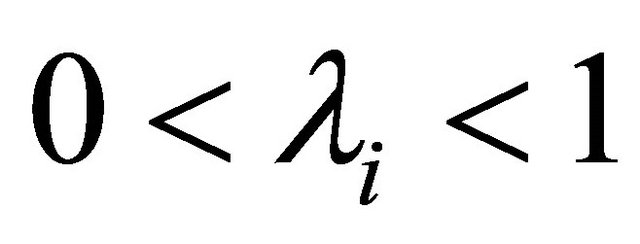 for every
for every 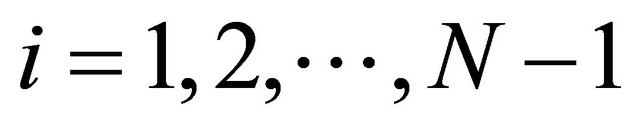 and
and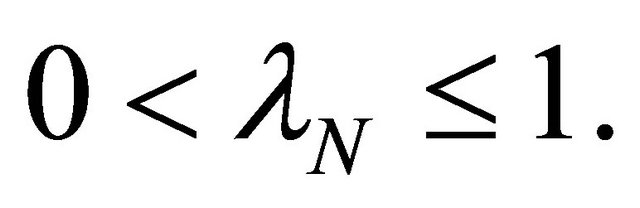 Let K be the K-mapping generated by
Let K be the K-mapping generated by 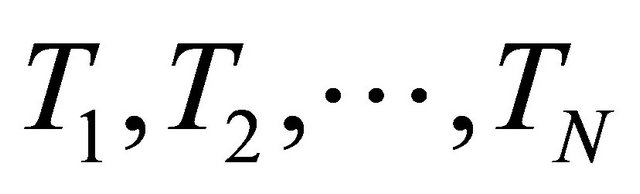 and
and  Then
Then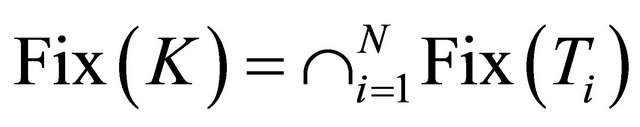 .
.
Lemma 2.5. (see [37]). Let C be a nonempty convex subset of a Banach space. Let 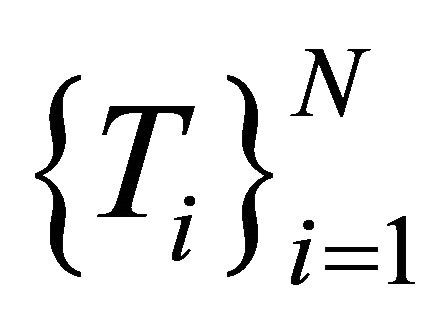 be a finite family of nonexpansive mappings of
be a finite family of nonexpansive mappings of 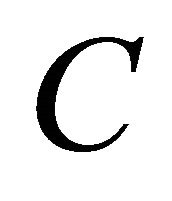 into itself and
into itself and 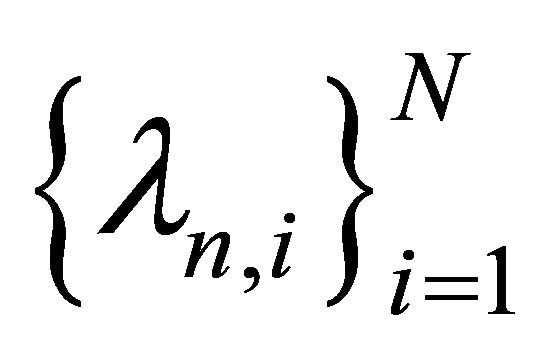
be sequences in 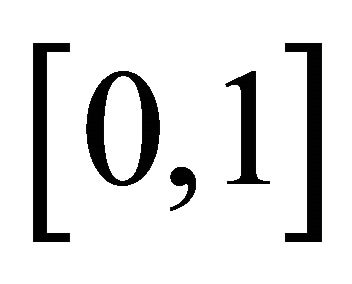 such that
such that 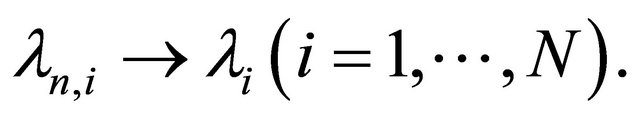 Moreover for every
Moreover for every 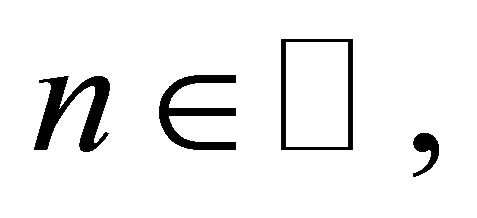 let K and
let K and 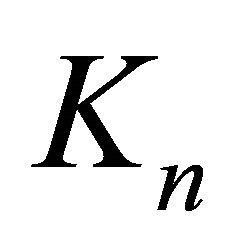 be the Kmappings generated by
be the Kmappings generated by  and
and 
and 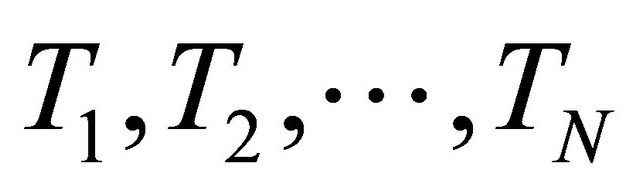 and
and 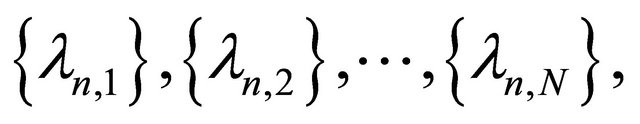 respectively. Then for every
respectively. Then for every 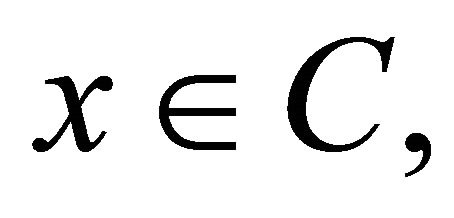 it follows that
it follows that
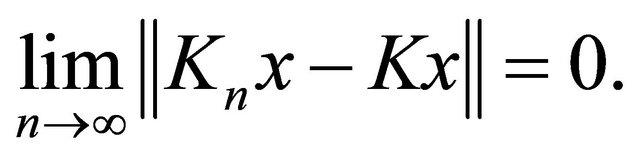
For solving the mixed equilibrium problem, let us give the following assumptions for a bifunction 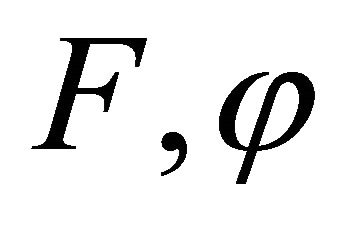 and the set C:
and the set C:
(A1) 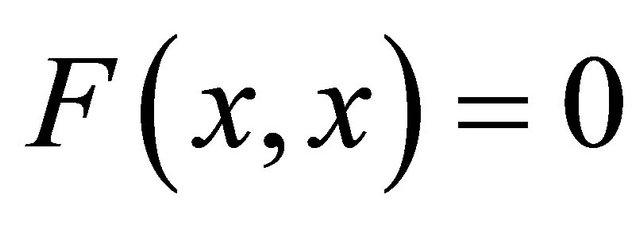 for all
for all 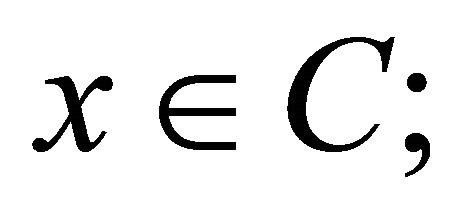
(A2) 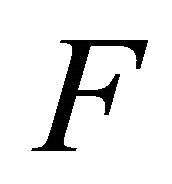 is monotone, i.e.,
is monotone, i.e., 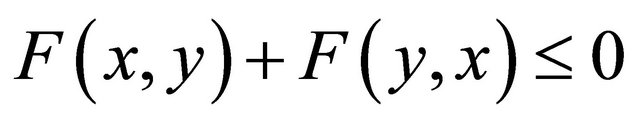 for all
for all 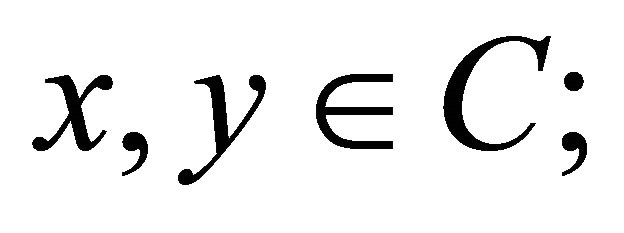
(A3) For each 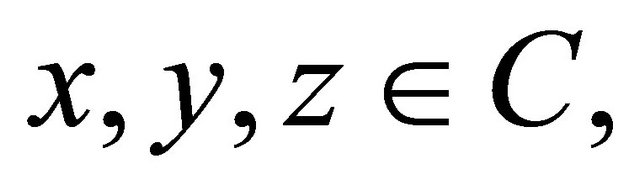
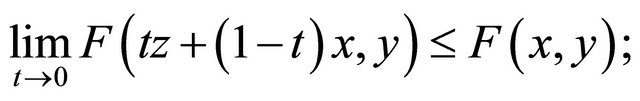
(A4) For each 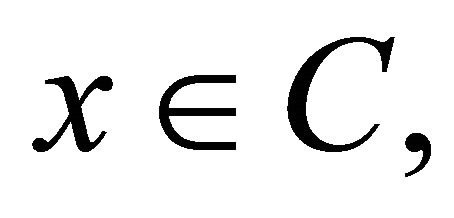
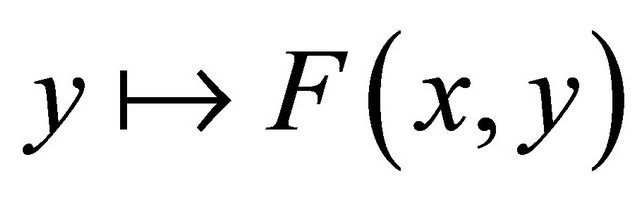 is convex and lower semicontinuous;
is convex and lower semicontinuous;
(B1) For each 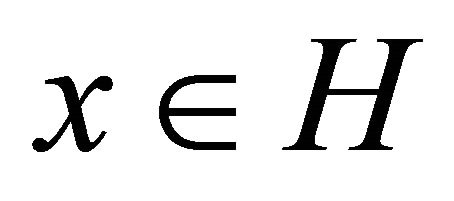 and
and 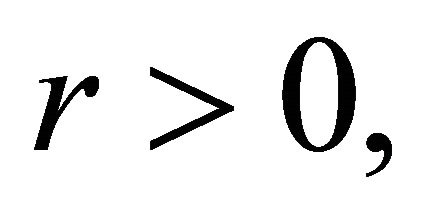 there exists a bounded subset
there exists a bounded subset 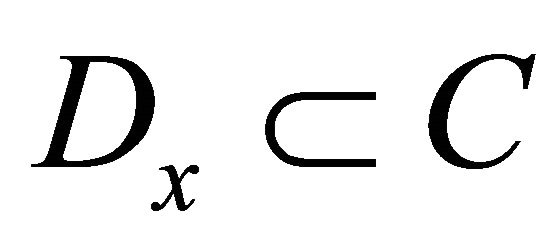 and
and 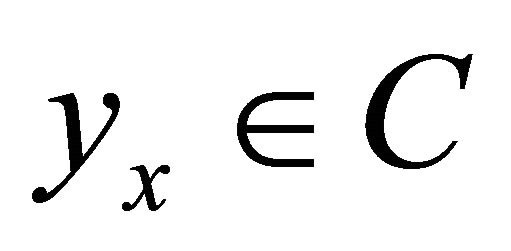 such that for any
such that for any 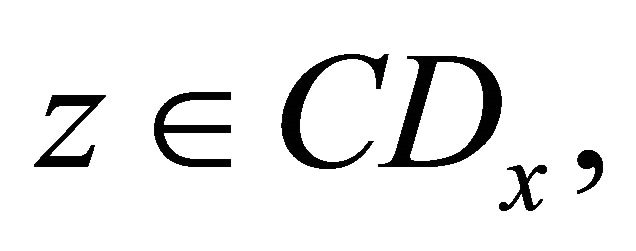
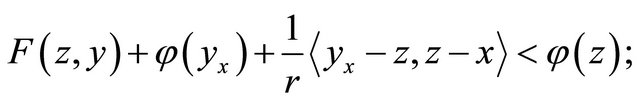
(B2) C is a bounded set.
By a similar argument as in the proof of Lemma 2.3 in [18], we have the following result.
Lemma 2.6. Let C be a nonempty closed convex subset of a Hilbert space H and let F be a mixed equilibrium bifunction of C × C into  satisfying conditions (A1)- (A4) and let
satisfying conditions (A1)- (A4) and let 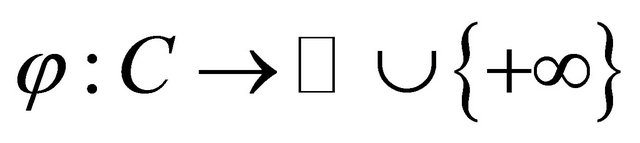 be a proper lower semicontinuous and convex function. Assume that either (B1) or (B2) holds. For
be a proper lower semicontinuous and convex function. Assume that either (B1) or (B2) holds. For  and
and 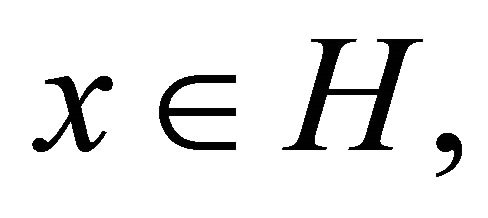 define a mapping
define a mapping 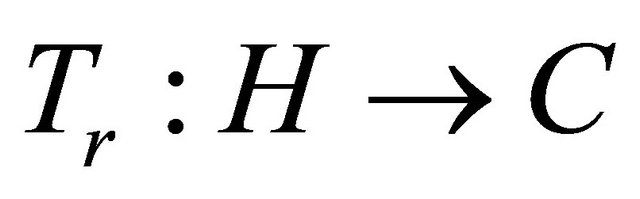 as follows:
as follows:
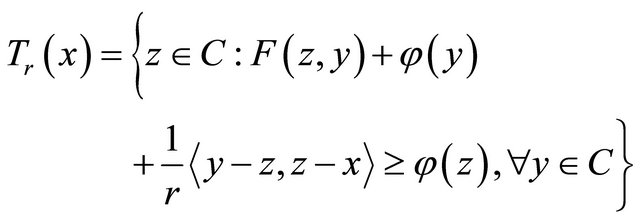
for all 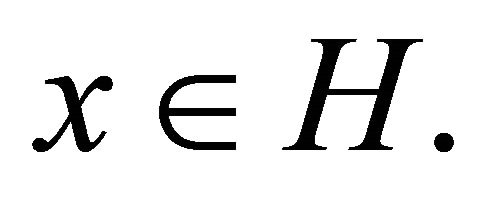 Then
Then 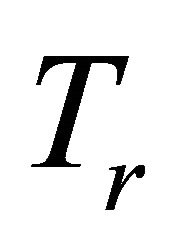 is well defined and the following hold:
is well defined and the following hold:
1) 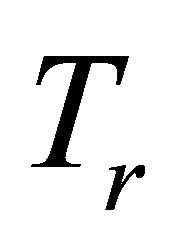 is single-valued;
is single-valued;
2) 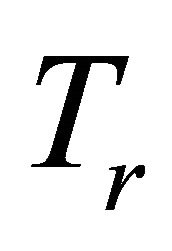 is firmly nonexpansive, i.e., for any
is firmly nonexpansive, i.e., for any 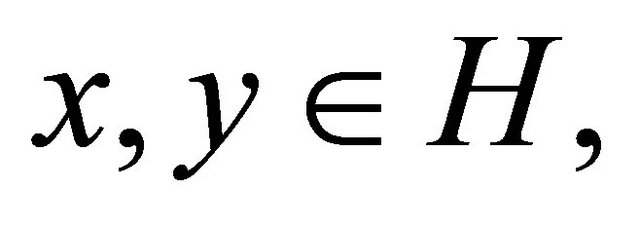
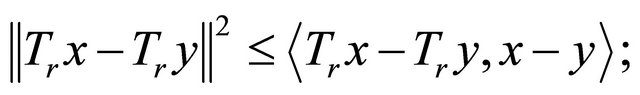
3)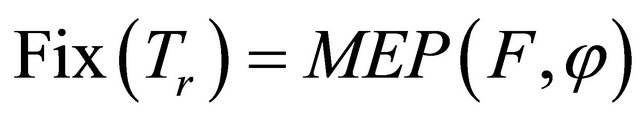 ;
;
4) 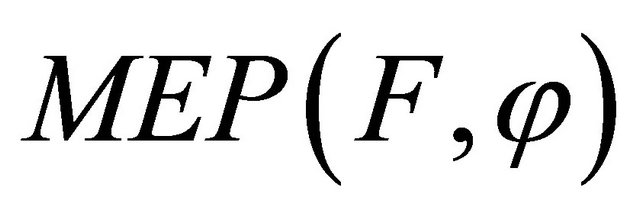 is closed and convex.
is closed and convex.
Remark 2.7. We remark that Lemma 1.6 is not a consequence of Lemma 3.1 in [14], because the condition of the sequential continuity from the weak topology to the strong topology for the derivative 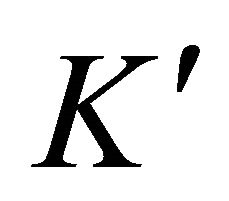 of the function
of the function 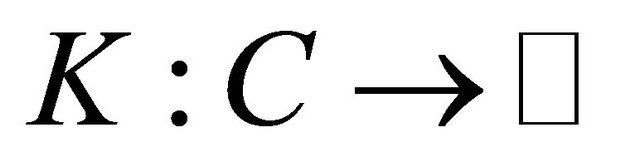 does not cover the case
does not cover the case
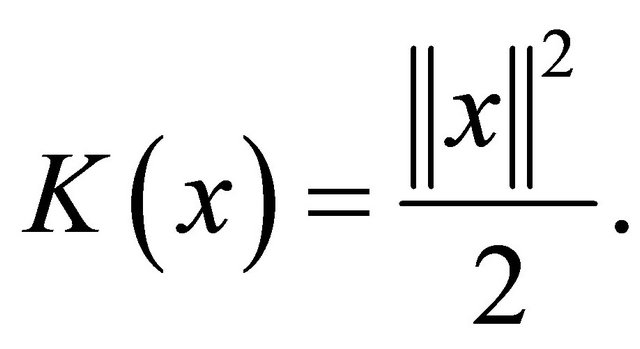
The following lemma is well known.
Lemma 2.8. In a real Hilbert space H, there holds the following inequality
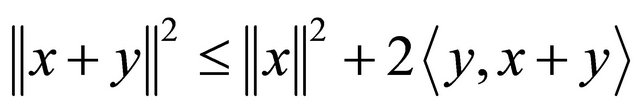
for all 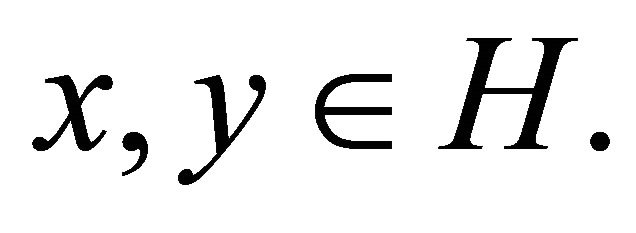
3. Main Results
Theorem 3.1. Let H be a real Hilbert space, C a nonempty closed convex subset of H, B a 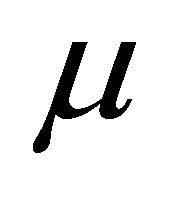 -Lipschitzian, relaxed
-Lipschitzian, relaxed  -cocoercive mapping of C into H, F a bifunction from C × C to
-cocoercive mapping of C into H, F a bifunction from C × C to  which satisfies (A1)-(A4),
which satisfies (A1)-(A4), 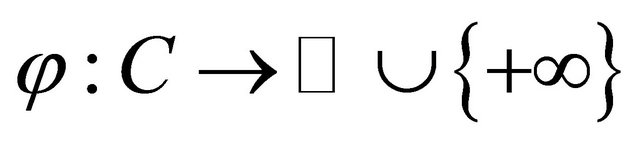 a proper lower semicontinuous and convex function and
a proper lower semicontinuous and convex function and 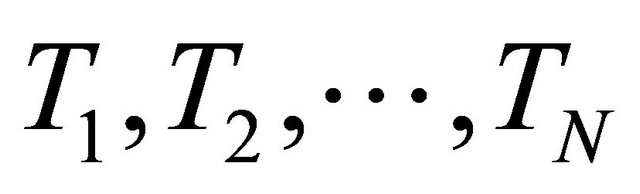 a finite family of nonexpansive mappings of C into H such that the common fixed points set
a finite family of nonexpansive mappings of C into H such that the common fixed points set
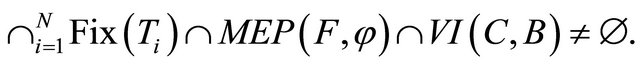
Let f be a contraction of H into itself with a coefficient 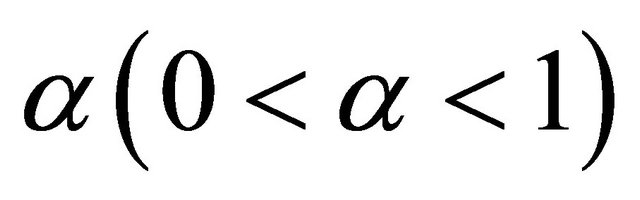 and A a strongly positive linear bounded operator on H with coefficient
and A a strongly positive linear bounded operator on H with coefficient 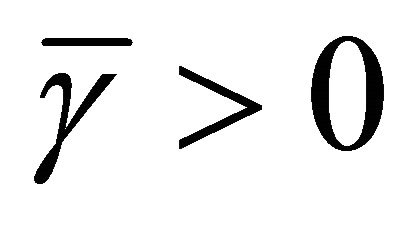 such that
such that 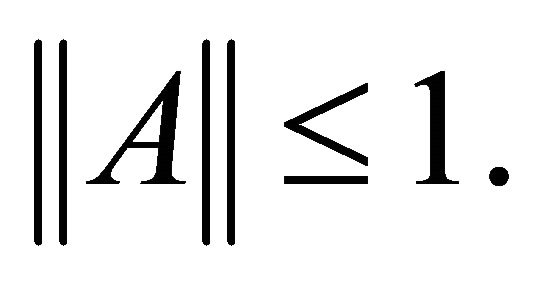
Assume that 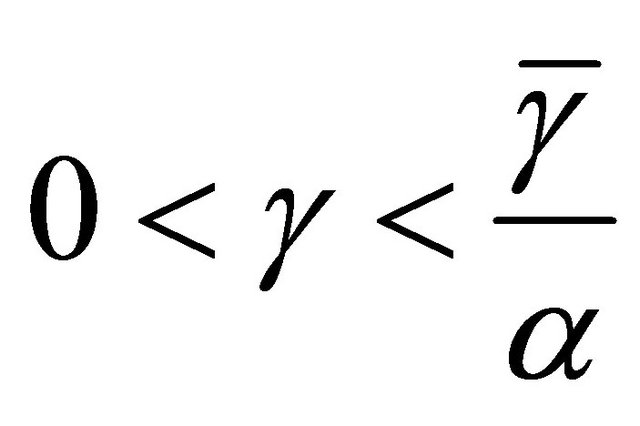 and either (B1) or (B2) holds.
and either (B1) or (B2) holds.
Let 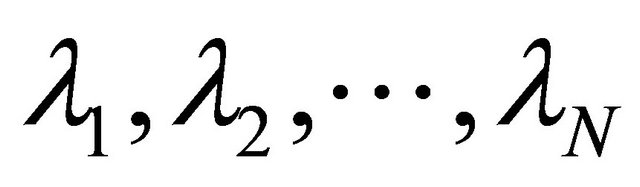 be real numbers such that
be real numbers such that 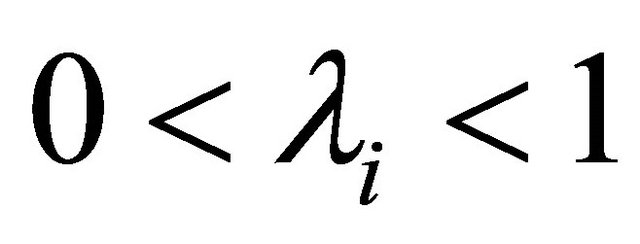 for every
for every 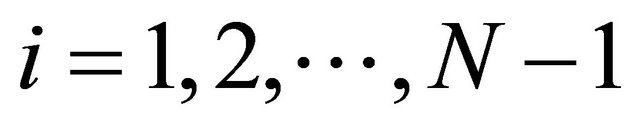 and
and 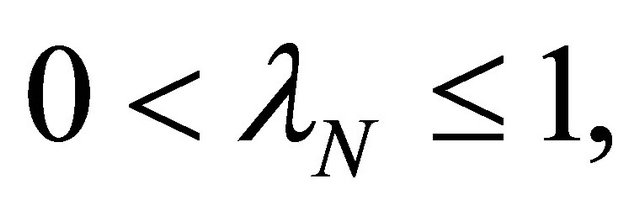
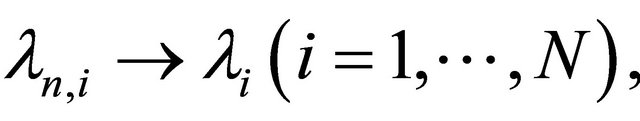
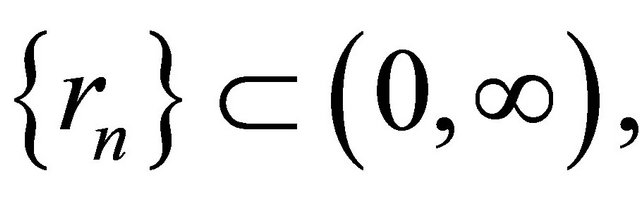
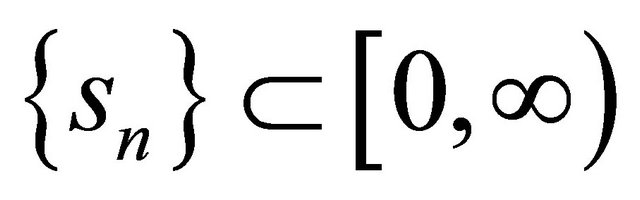 and
and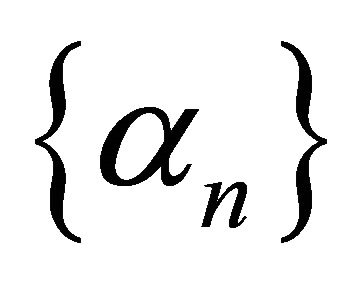 ,
, 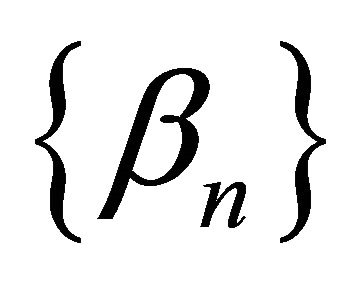 two real sequences in (0, 1) satisfying the following conditions:
two real sequences in (0, 1) satisfying the following conditions:
(C1) 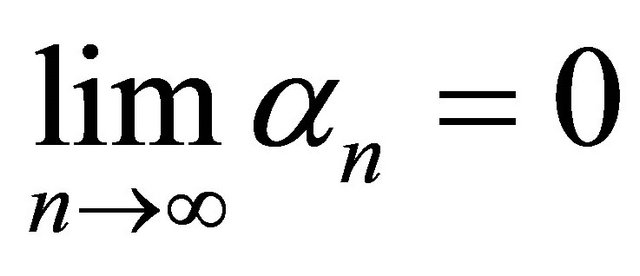 and
and 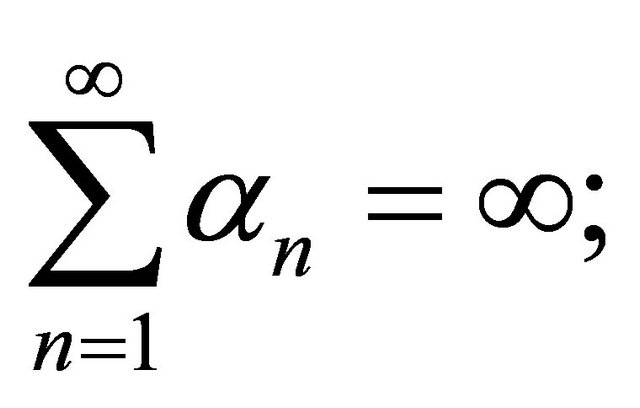
(C2) 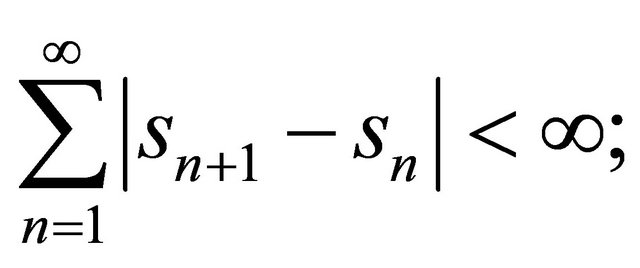
(C3) 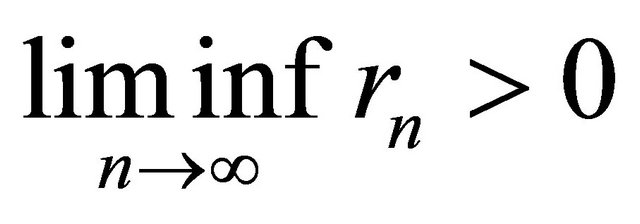 and
and 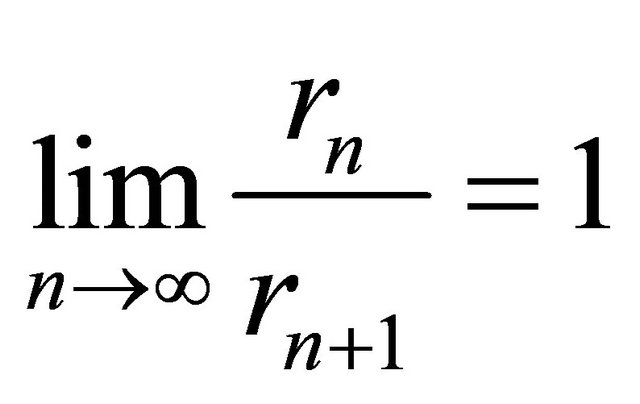 (this is weaker than the condition );
(this is weaker than the condition ); 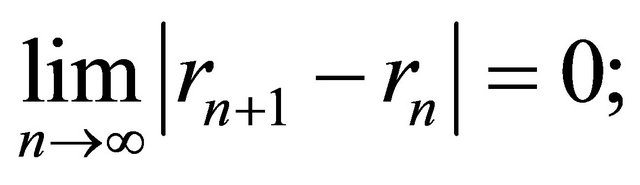
(C4) 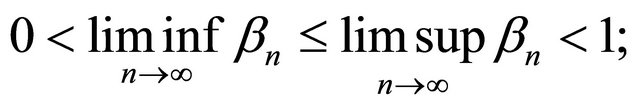
(C5) 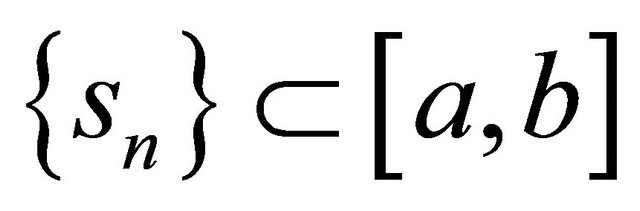 for some a, b with
for some a, b with
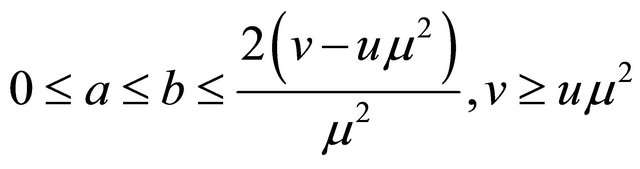 ;
;
(C6) 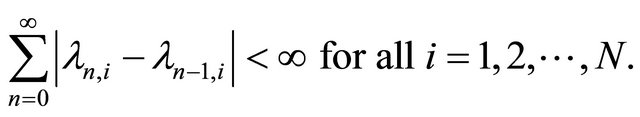
Then, the sequences 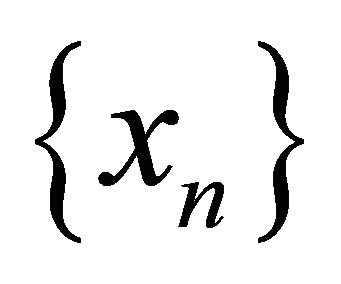 and
and 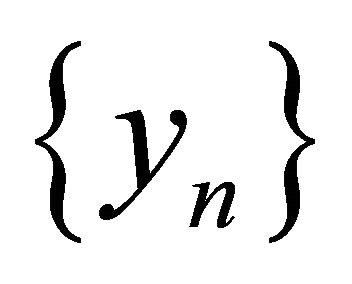 generated iteratively by (1.19) converge strongly to
generated iteratively by (1.19) converge strongly to
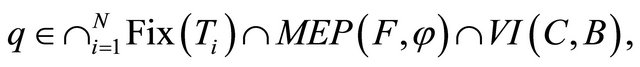
where
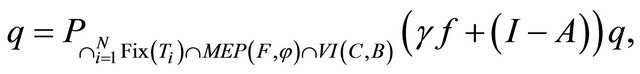
which solves the following variational inequality:
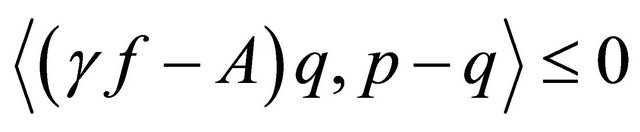
for all
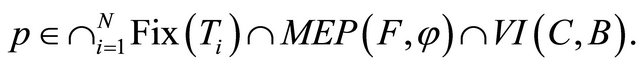
Proof Since 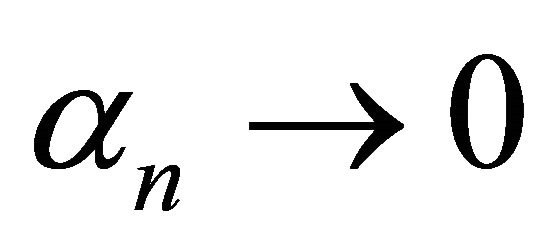 as
as  by the condition (C1), we may assume, without loss of generality, that
by the condition (C1), we may assume, without loss of generality, that
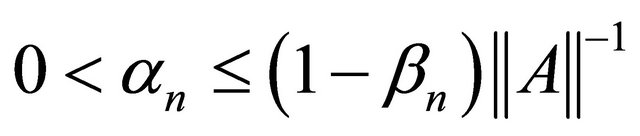
for all n. We also have 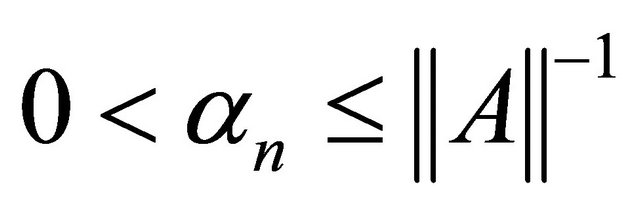 for all n. By using Lemma 2.2, we have
for all n. By using Lemma 2.2, we have
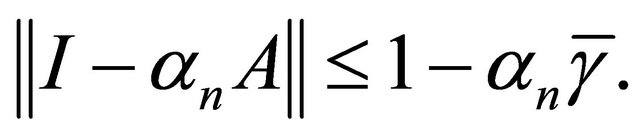
Since A is a strongly positive linear bounded operator on a Hilbert space H, we have
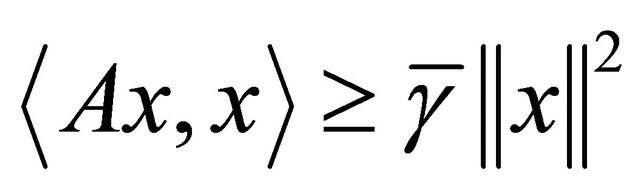
and
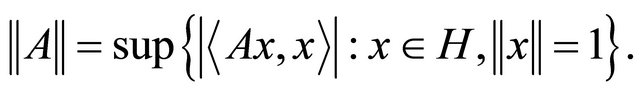
Observe that
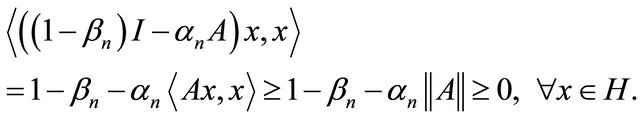
This shows that 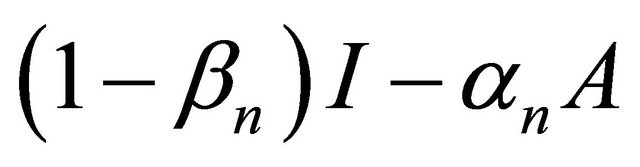 is positive. It follows that
is positive. It follows that
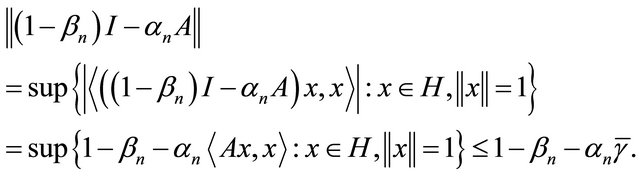
Next, we will assume that 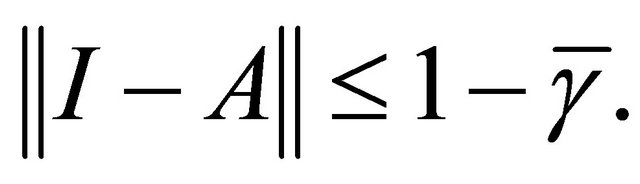 First, we show
First, we show 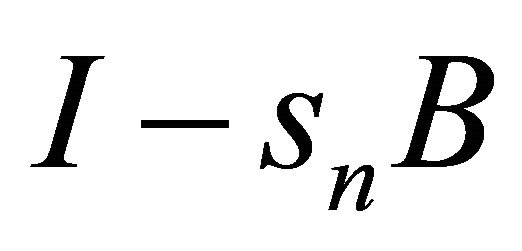 is nonexpansive. Indeed, from the relaxed
is nonexpansive. Indeed, from the relaxed  -cocoercive and
-cocoercive and 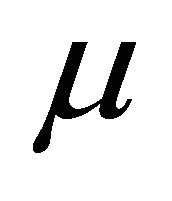 -Lipschitzian definition on B and condition (C5), we have which implies the mapping
-Lipschitzian definition on B and condition (C5), we have which implies the mapping 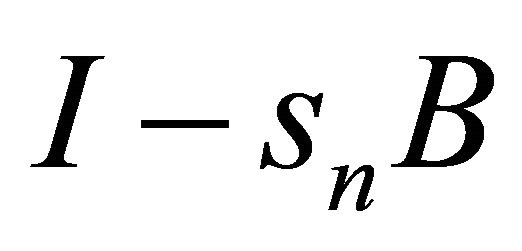 is nonexpansive.
is nonexpansive.
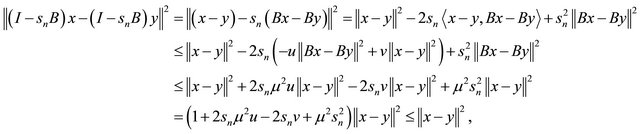
We shall divide our proof into 5 steps.
Step 1. We shall show that the sequence  is bounded. Let
is bounded. Let
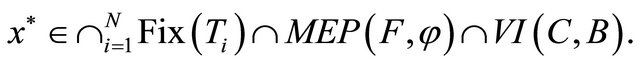
Since 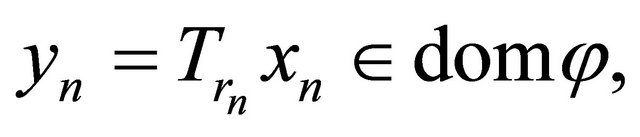 we have
we have
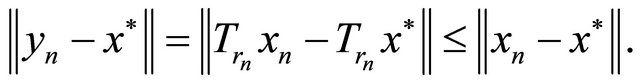 (3.1)
(3.1)
Putting 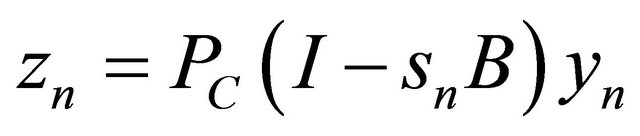 for all
for all  we have
we have
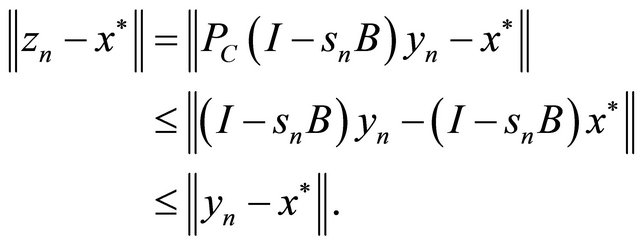
Using (1.19), (3.1) and (3.2), we have
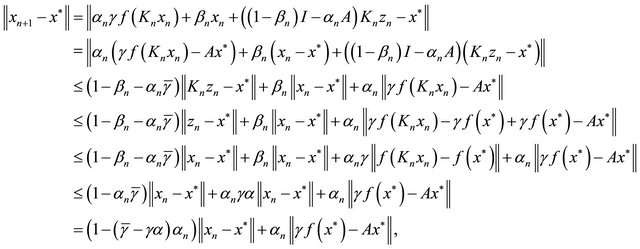
which gives that
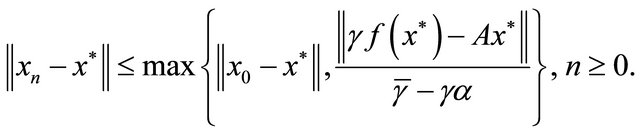
Hence  is bounded, so are
is bounded, so are 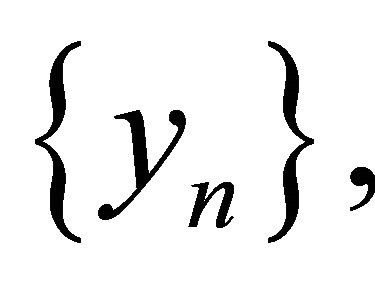
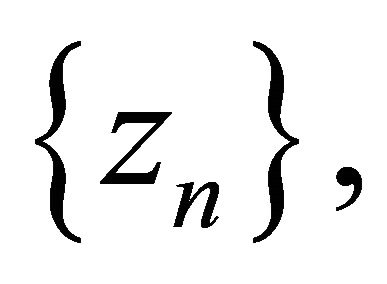
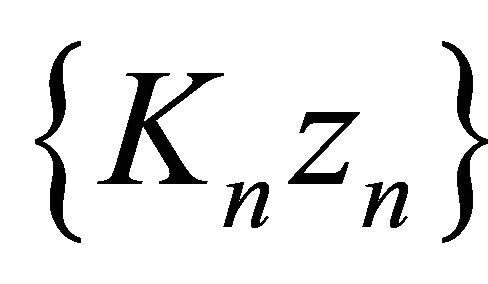 ,
,
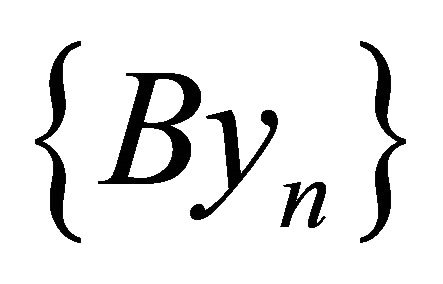 and
and 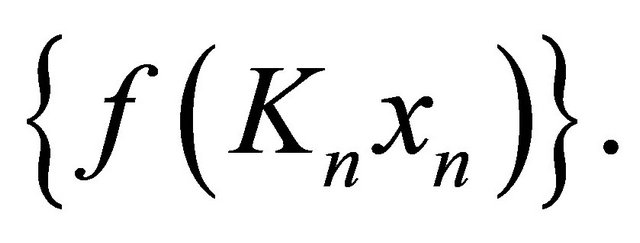
Step 2. We will show that
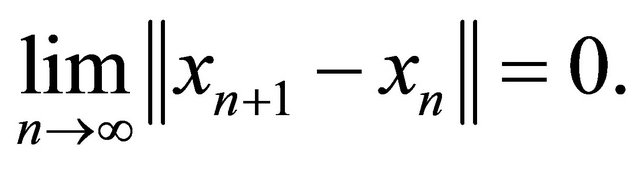
Observing that 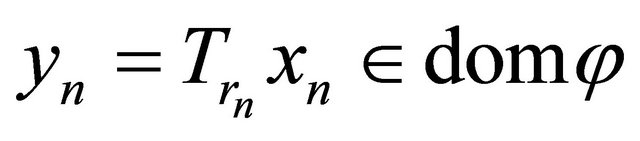 and
and 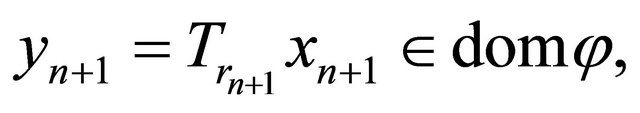 we have
we have
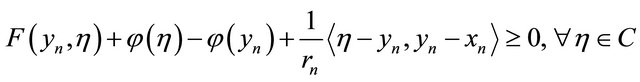 (3.3)
(3.3)
and
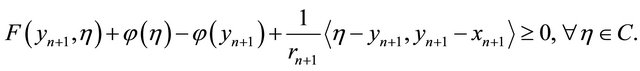 (3.4)
(3.4)
Putting 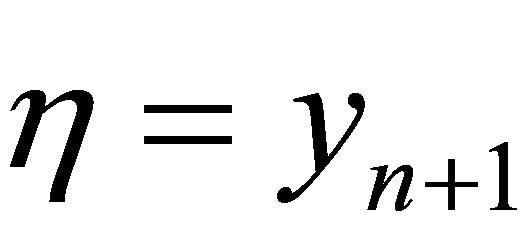 in (3.3) and
in (3.3) and 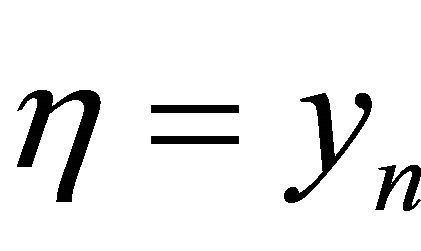 in (3.4), we have
in (3.4), we have
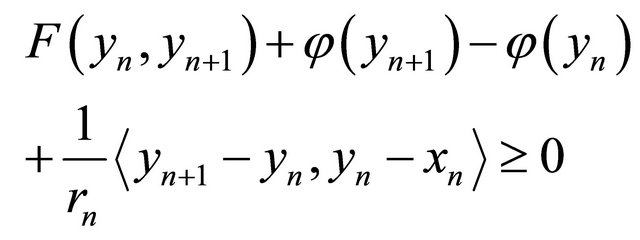
and
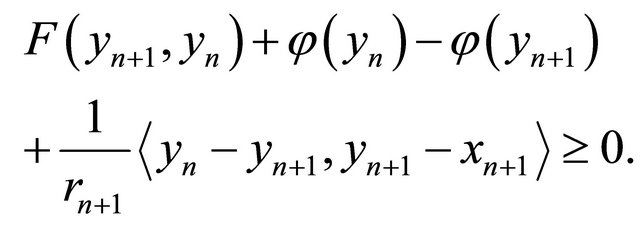
Summing up the last two inequalities and using Lemma 2.6 (A2), we obtain
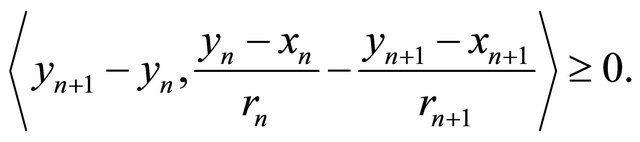
That is,
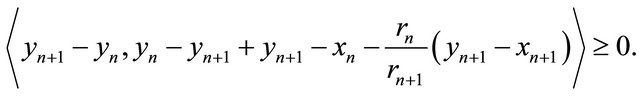
It then follows that
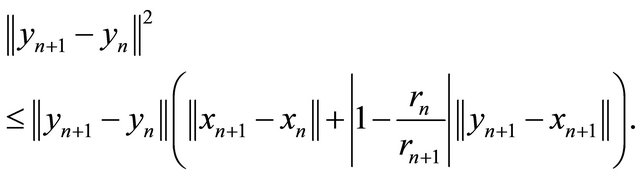
This implies that
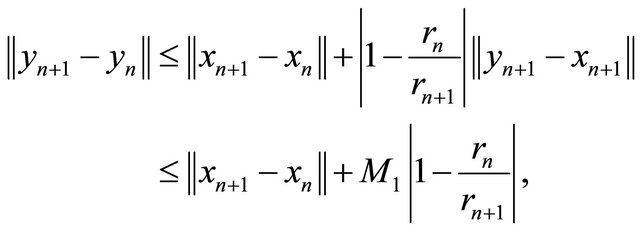
where M1 is an appropriate constant such that
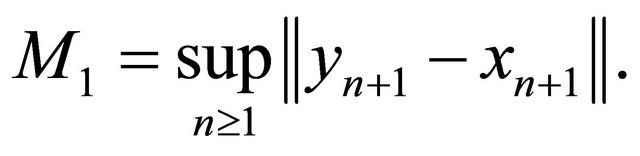
Since 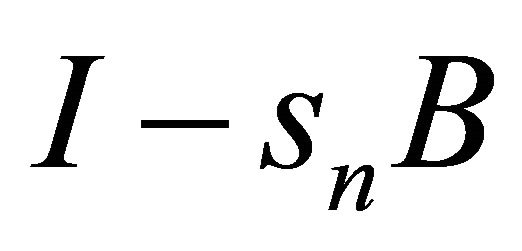 is nonexpansive and
is nonexpansive and 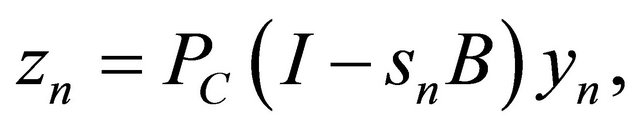 using (3.5), we also have
using (3.5), we also have
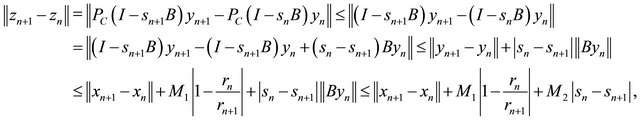
where M2 is an appropriate constant such that
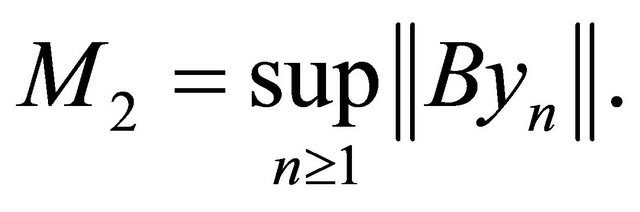
Define
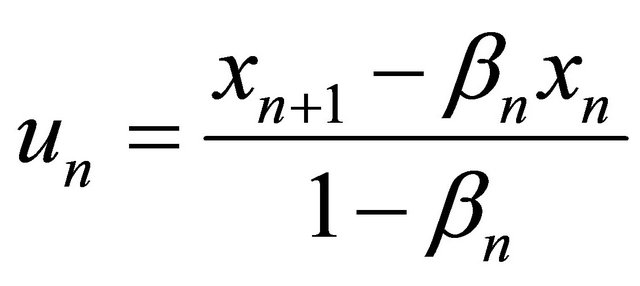
for all 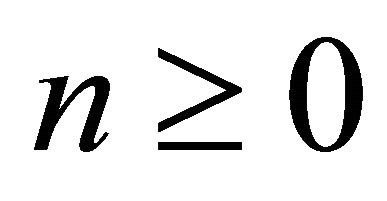 so that
so that
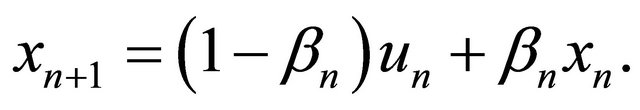
It follows that
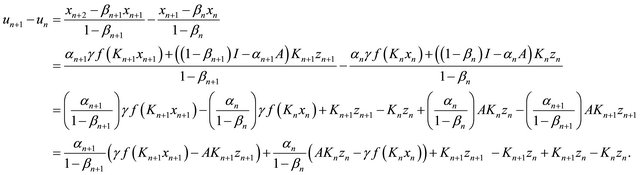
Observe that 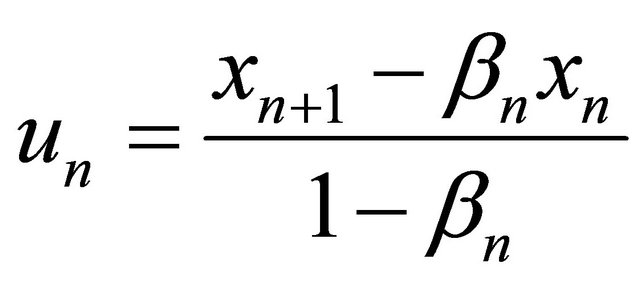 from (3.6), we obtain
from (3.6), we obtain
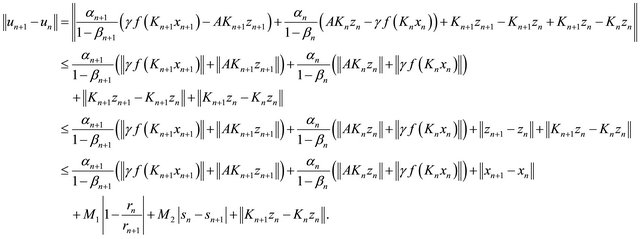 (3.7)
(3.7)
Next we estimate 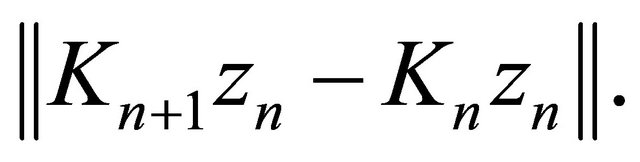
For  we have
we have
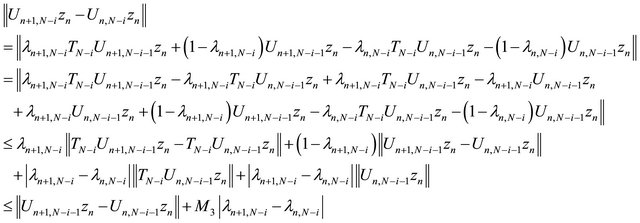 (3.8)
(3.8)
and
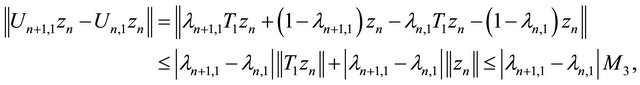 (3.9)
(3.9)
where
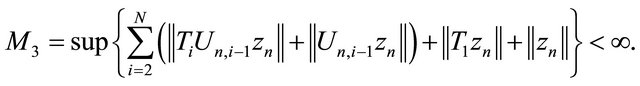
Using (3.8) and (3.9), we have
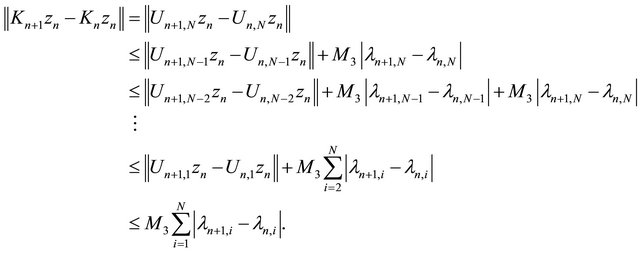 (3.10)
(3.10)
Substitute (3.10) into (3.7) yields that
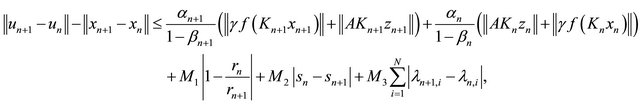
which implies that (noting that (C1), (C2), (C3), (C4) and (C6))
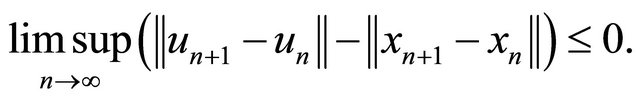
Hence by Lemma 2.3, we have
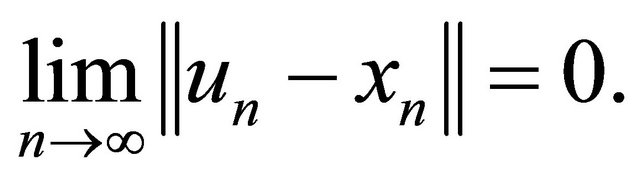 (3.11)
(3.11)
Using (3.11) and we have 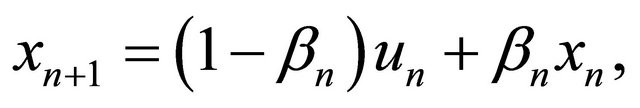
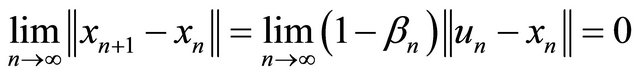 (3.12)
(3.12)
Step 3. We shall show that
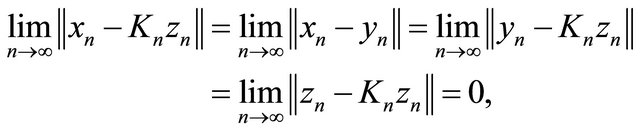
where 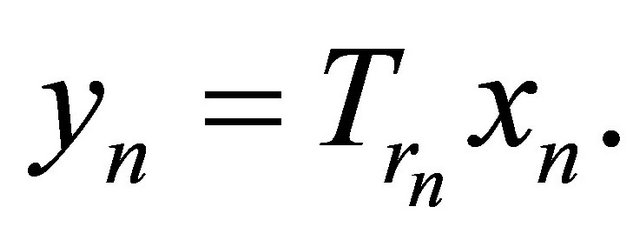
Note that
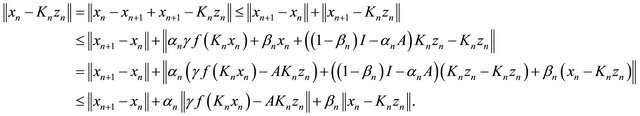
This implies
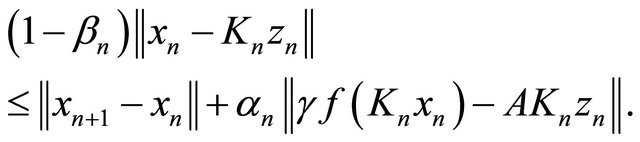
From condition (C1), (C4) and (3.12), we have
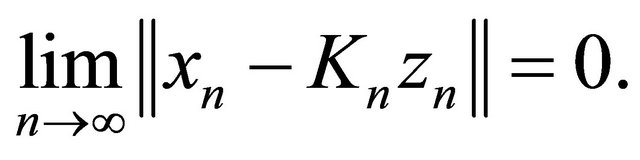 (3.13)
(3.13)
Next we prove that
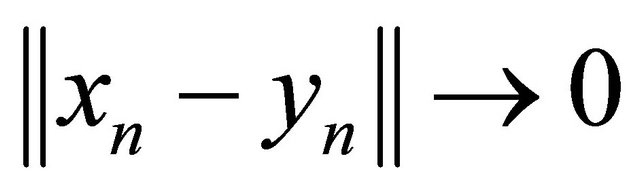
as 
Indeed, picking
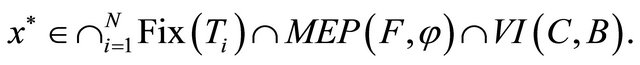
Since 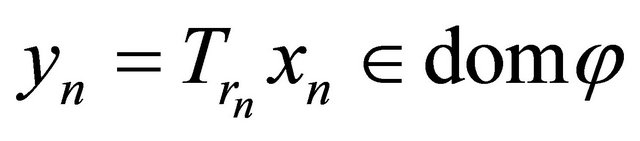 and Tr is firmly nonexpansive, we obtain and hence
and Tr is firmly nonexpansive, we obtain and hence
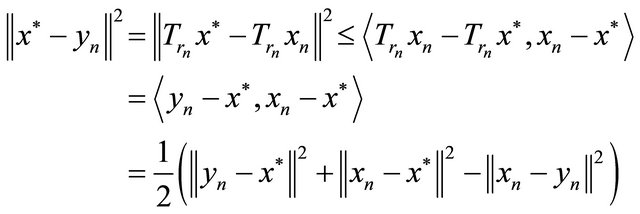 (3.14)
(3.14)
Set 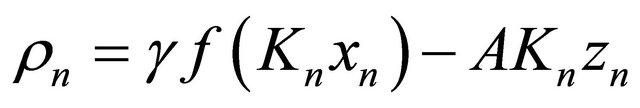 and let
and let 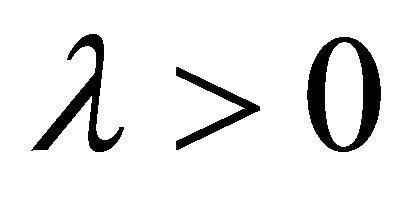 be an appropriate constant such that
be an appropriate constant such that
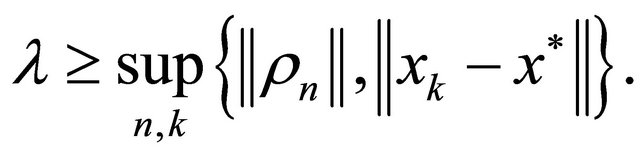
Therefore, from the convexity of 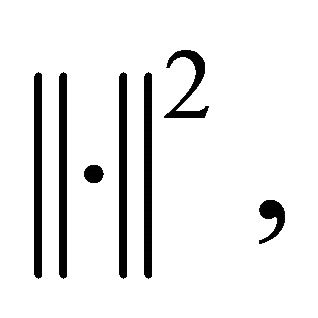 using (3.2), (3.14) and Lemma 2.8 we have
using (3.2), (3.14) and Lemma 2.8 we have
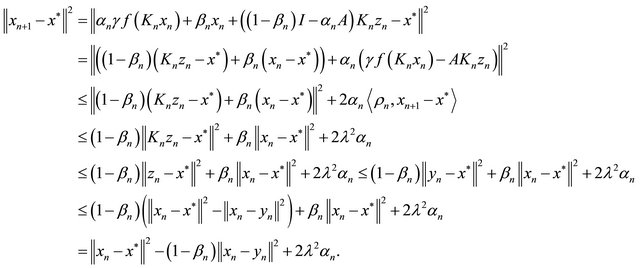
It follows that
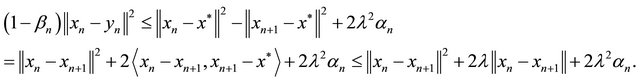
By using condition (C1), (C4) and (3.12), we have
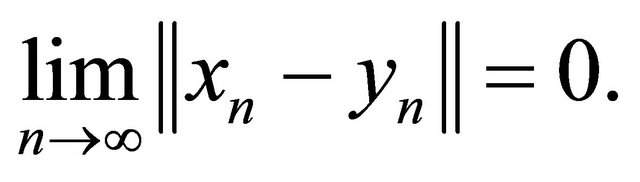 (3.15)
(3.15)
From (3.13) and (3.15), we obtain
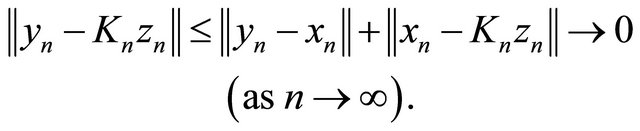 (3.16)
(3.16)
From (3.11) and (3.13), we also obtain
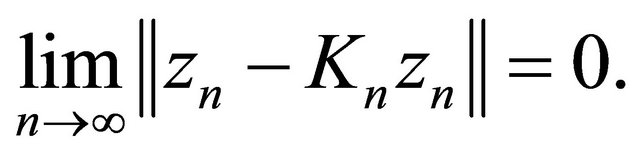 (3.17)
(3.17)
Step 4. We shall show that
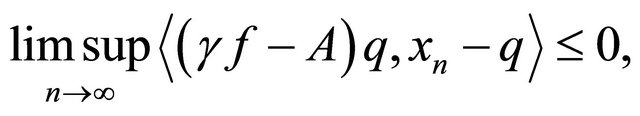
where q is the unique solution of the variational inequality 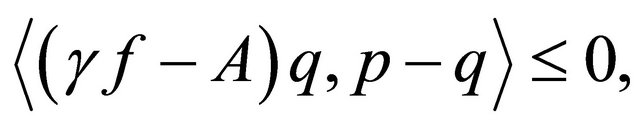

Let 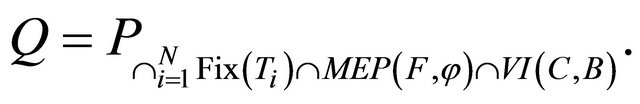 Observe that
Observe that
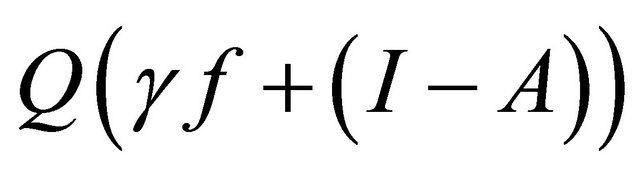 is a contraction. Indeed, for all
is a contraction. Indeed, for all ,
,  and
and 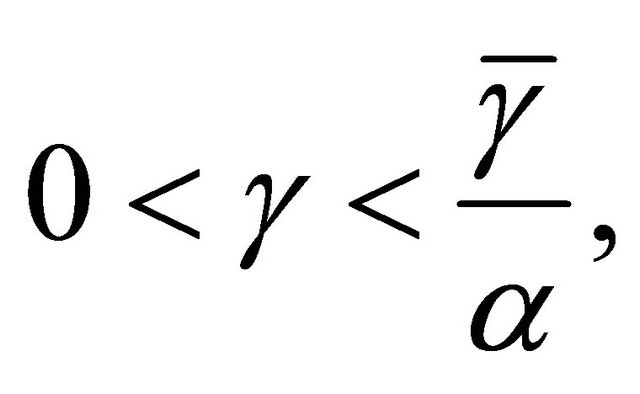 we have
we have
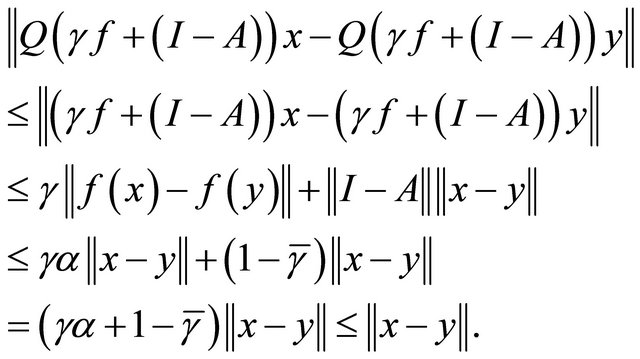
Banach’s Contraction Mapping Principle guarantees that 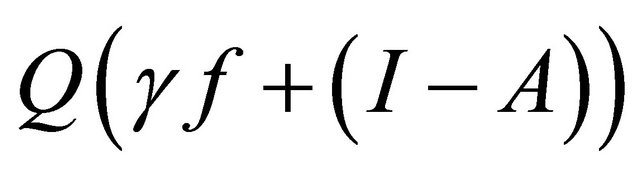 has a unique fixed point, say
has a unique fixed point, say  That is,
That is,
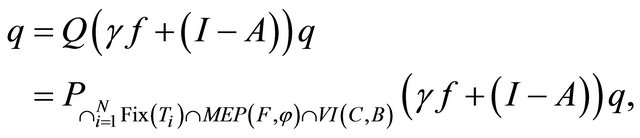
by (1.1) we obtain that 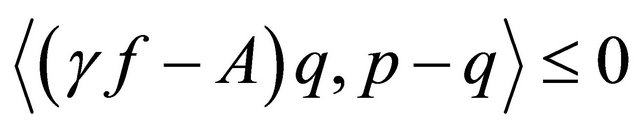 for all
for all
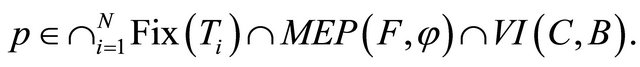
Next, we show that
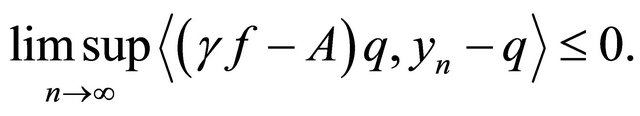
To see this, we choose a subsequence 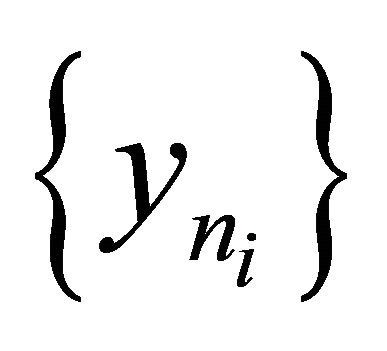 of
of 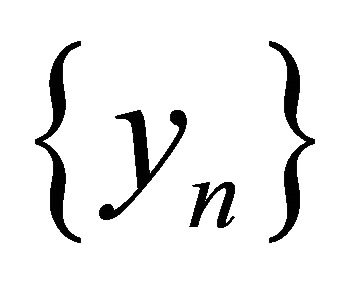 such that
such that
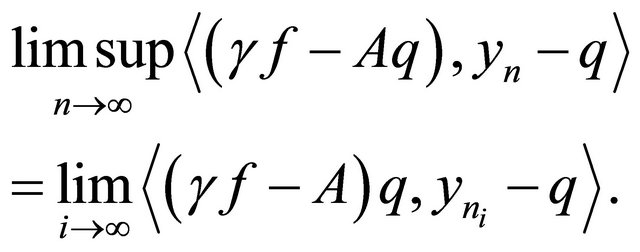
Since 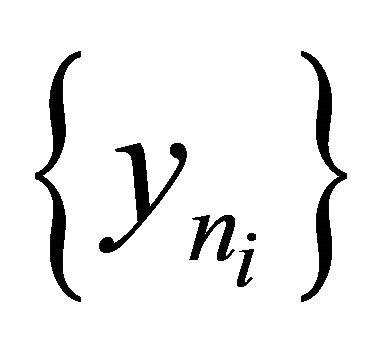 is bounded, there exists
is bounded, there exists 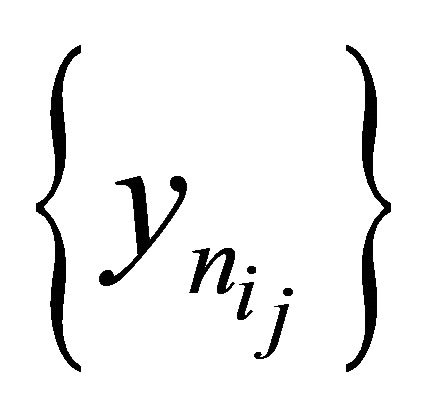 a subsequence of
a subsequence of 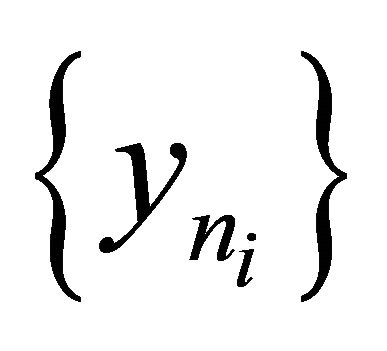 which converges weakly to p. Without loss of generality, we can assume that
which converges weakly to p. Without loss of generality, we can assume that 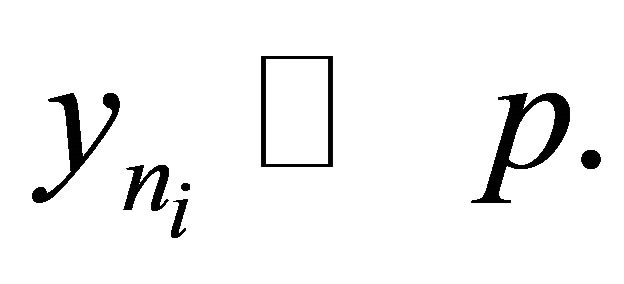 Claim that
Claim that
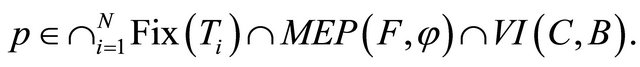
First, we prove .
.
Since 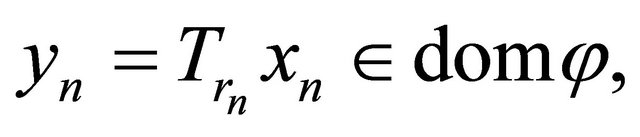 we have
we have
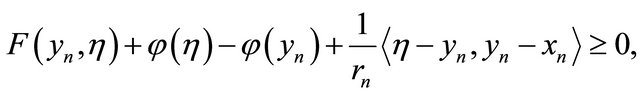
for all 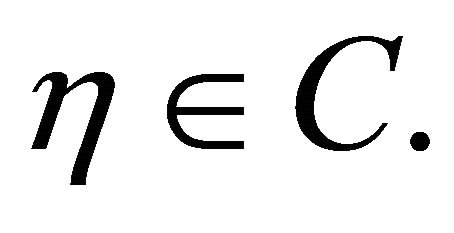 It follows from Lemma 2.6 (A2) that
It follows from Lemma 2.6 (A2) that
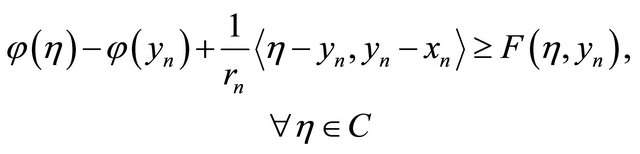
and hence
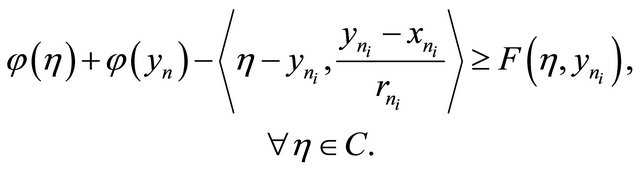
Since 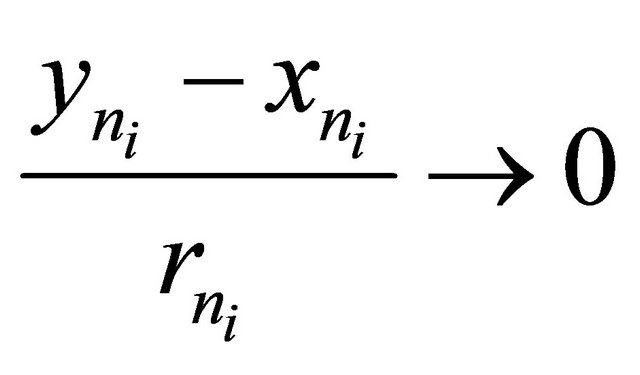 and
and 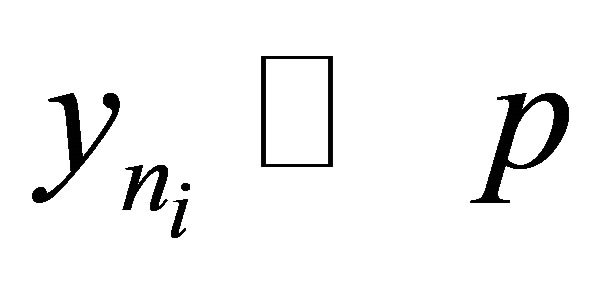 together with the lower semicontinuity of
together with the lower semicontinuity of  and Lemma 2.6 (A4), we have
and Lemma 2.6 (A4), we have 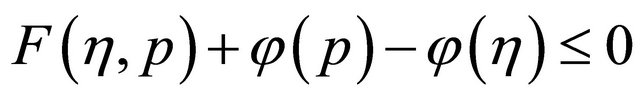 for all
for all 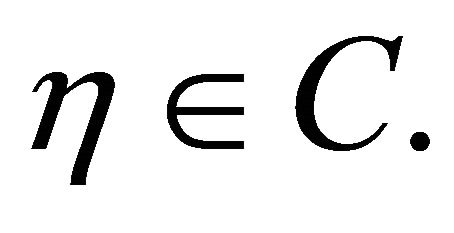 For t with
For t with 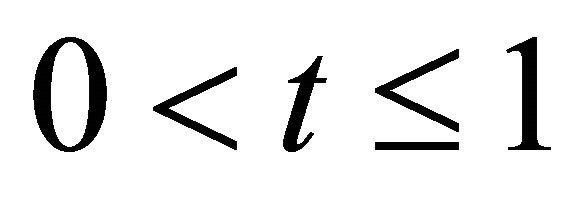 and
and 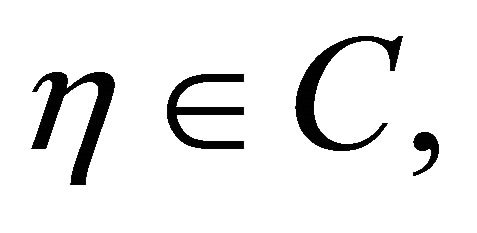 let
let 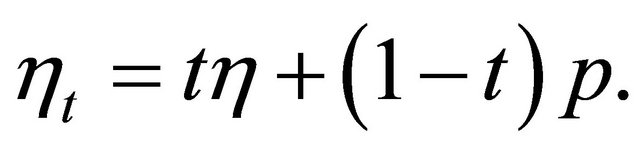 Since
Since 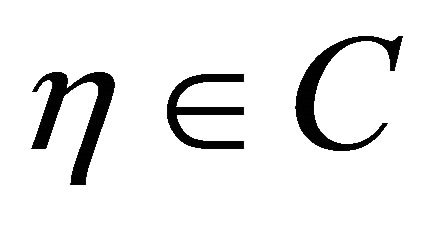 and
and 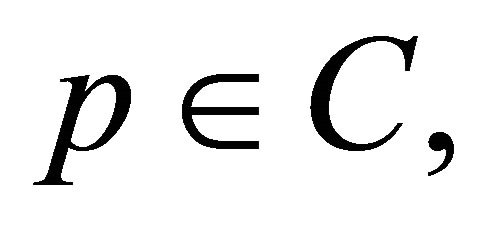 we have
we have 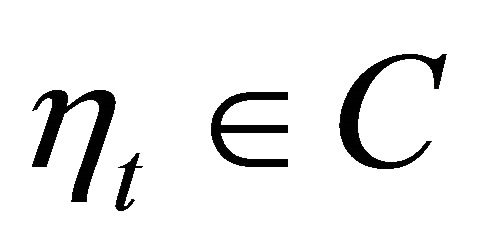 and hence
and hence
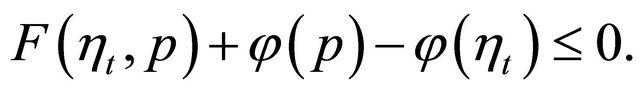 So, from Lemma 2.6 (A1), (A4) and the convexity of
So, from Lemma 2.6 (A1), (A4) and the convexity of  we have
we have
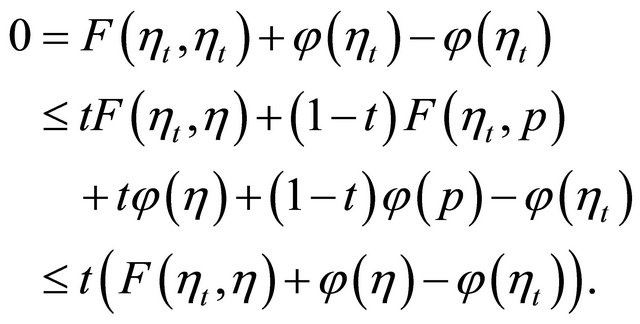
Dividing by t, we get 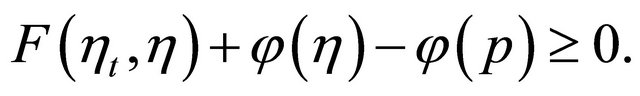
Letting 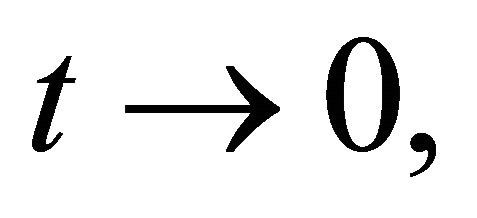 it follows from Lemma 2.6 (A3) and the lower semicontinuity of
it follows from Lemma 2.6 (A3) and the lower semicontinuity of  that
that 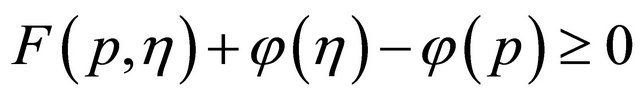 for all
for all 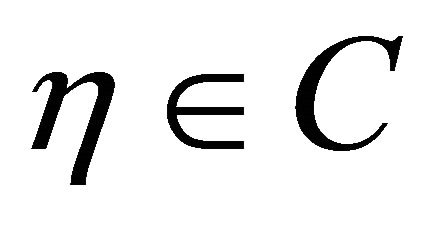 and hence
and hence  Next, we prove
Next, we prove 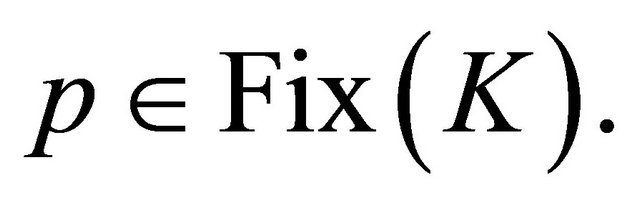 To see this, we observe that we may assume (by passing to a further subsequence if necessary)
To see this, we observe that we may assume (by passing to a further subsequence if necessary) 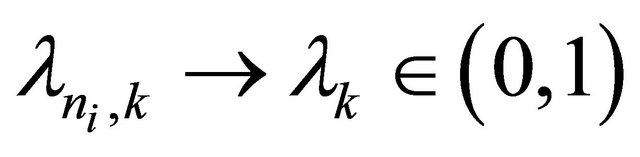
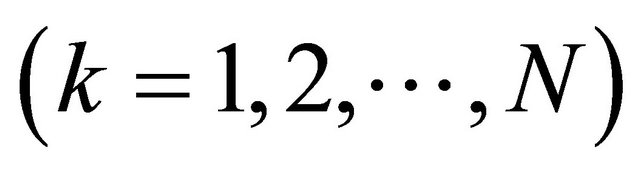 . Let K be the K-mapping generated by
. Let K be the K-mapping generated by 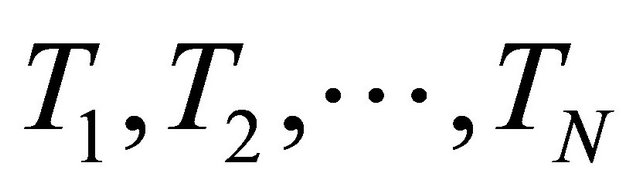 and
and 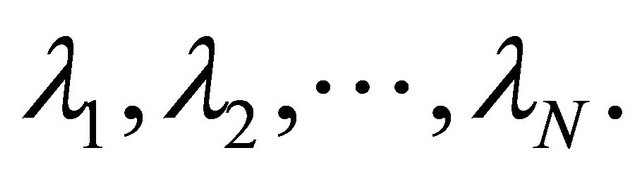 Then by Lemma 2.5, we have, for every
Then by Lemma 2.5, we have, for every 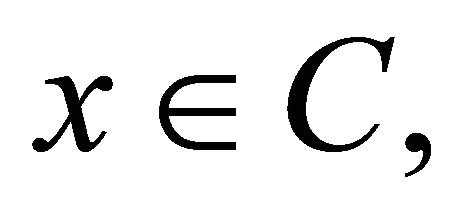
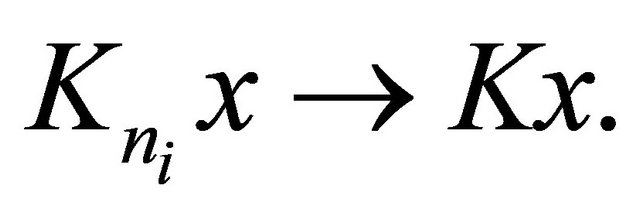 (3.18)
(3.18)
every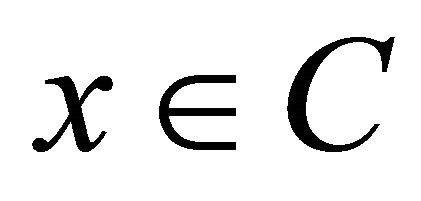 Moreover, from Lemma 2.4 it follows that
Moreover, from Lemma 2.4 it follows that
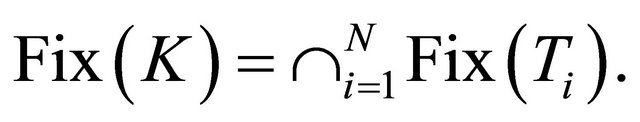
Suppose for contradiction . Then
. Then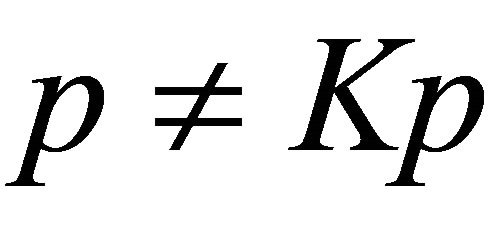 . Since Hilbert space are Opial’s spaces and
. Since Hilbert space are Opial’s spaces and
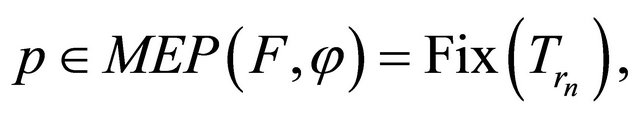
from (3.17) and (3.18), we have
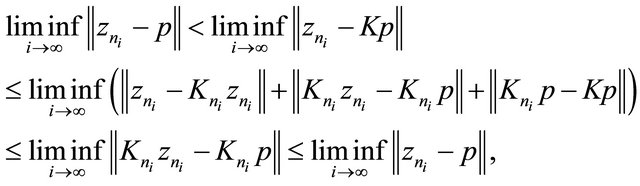
which derives a contradiction. Thus, we have 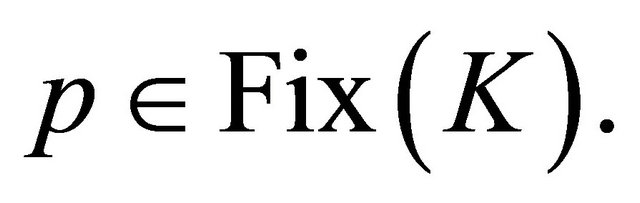 It follows from
It follows from
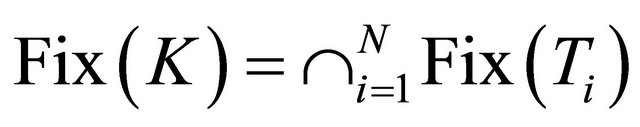
that
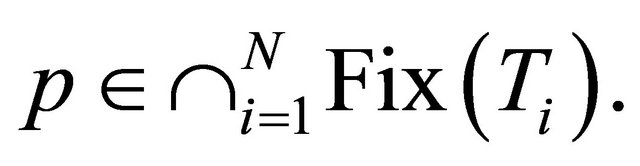
Next, we prove 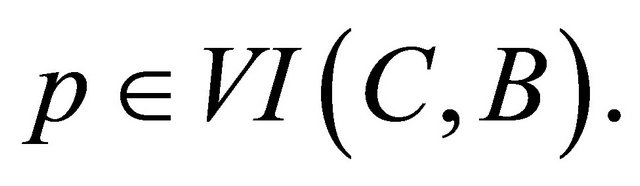 Put
Put
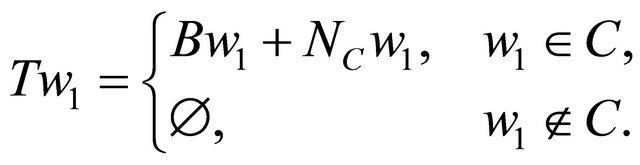
Since B is relaxed 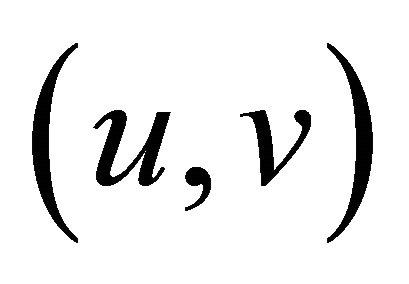 -cocoercive and condition (C5), we have
-cocoercive and condition (C5), we have
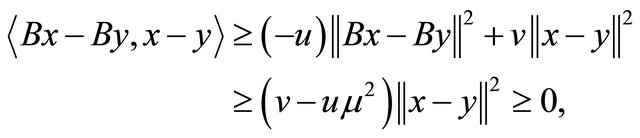
which yields that B is monotone. Thus T is maximal monotone. Let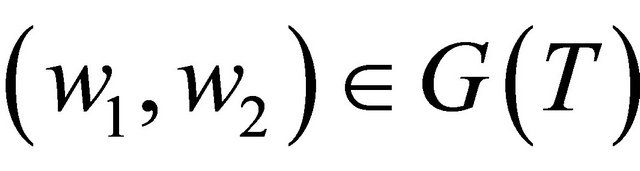 . Since
. Since 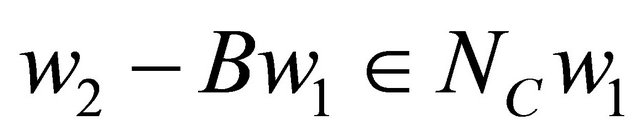 and
and 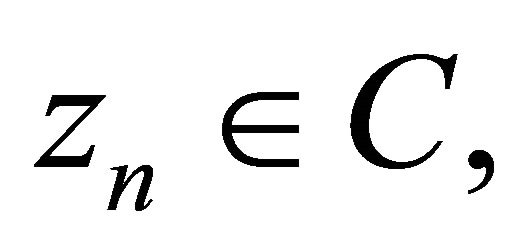 we have
we have
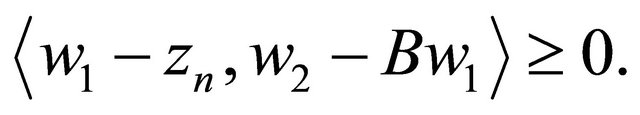
On the other hand, from 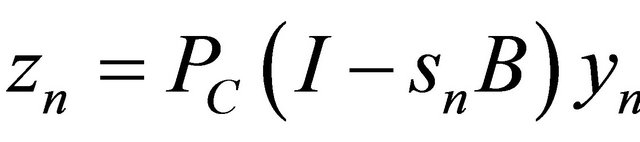 and (1.1), we have
and (1.1), we have
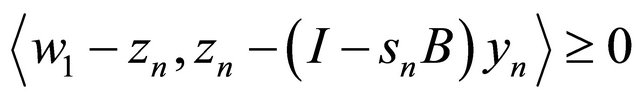
and hence
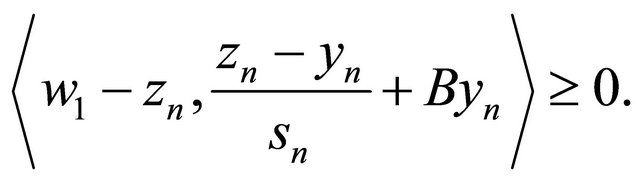
It follows that
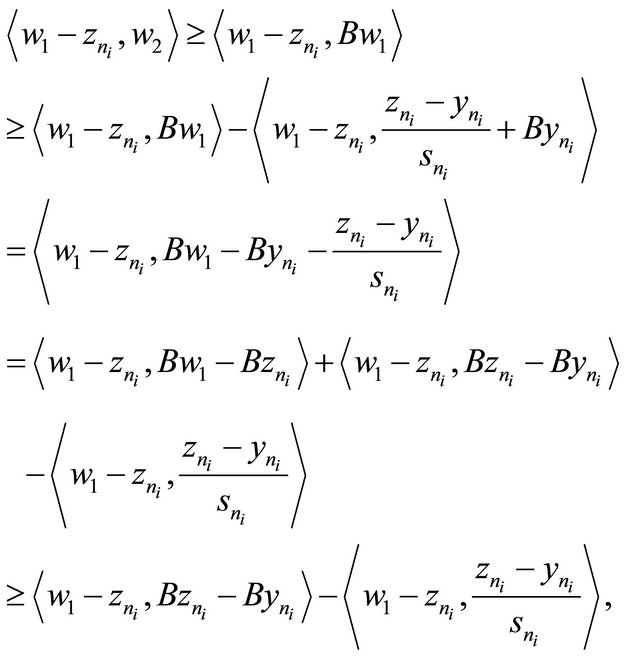
which together with (3.16), (3.17) and B is Lipschitz continuous implies that 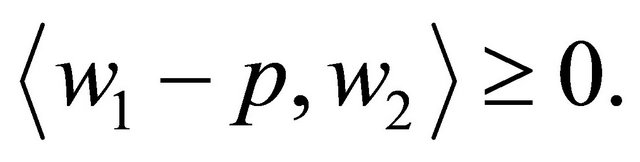 We have
We have 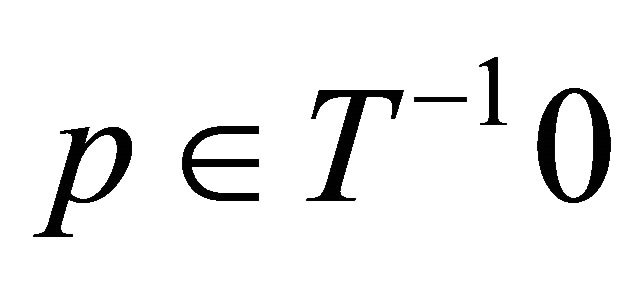 and hence
and hence 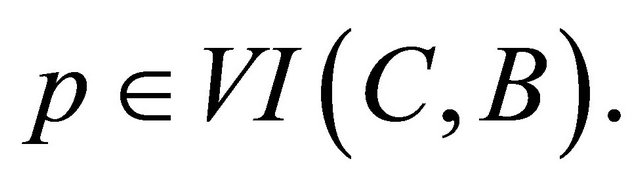 That is,
That is,
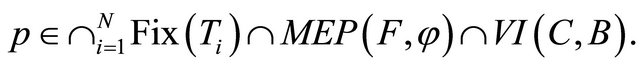
It follows from the variational inequality 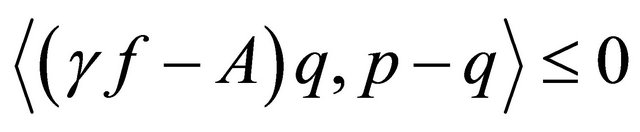 for all
for all
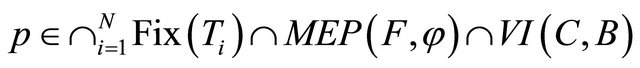
that
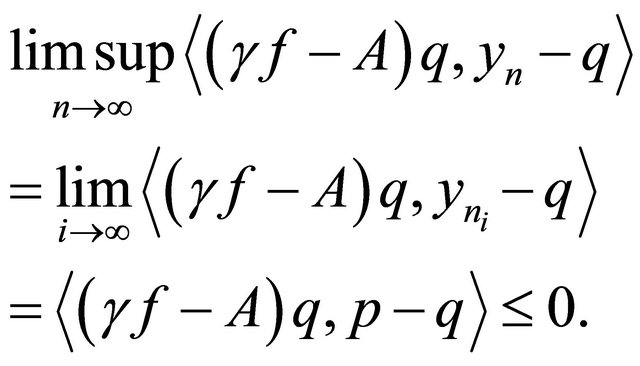 (3.19)
(3.19)
Using (3.16) and (3.19), we have
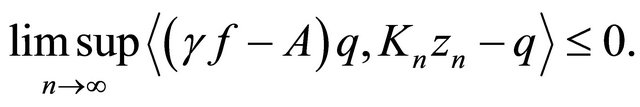 (3.20)
(3.20)
Moreover, from (3.15) and (3.19), we have
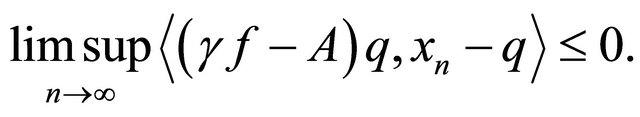 (3.21)
(3.21)
Step 5. Finally, we will show that the sequences 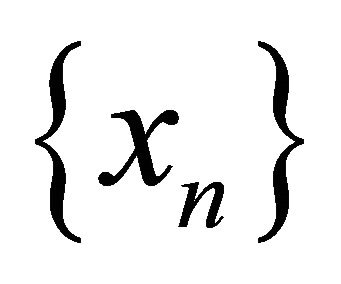 and
and 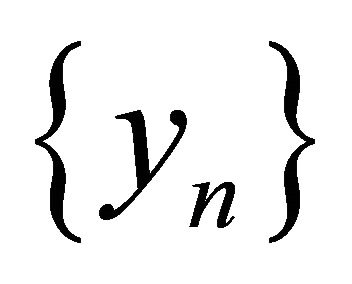 converge strongly to q.
converge strongly to q.
Since 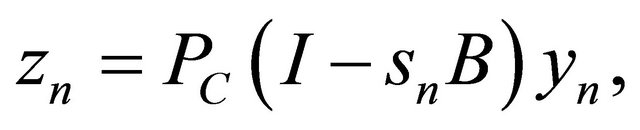 using (1.19), (3.1), (3.2) and Lemma 2.8, we have
using (1.19), (3.1), (3.2) and Lemma 2.8, we have
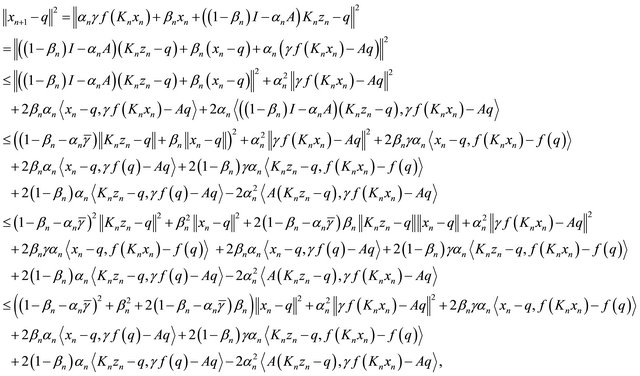
which implies that
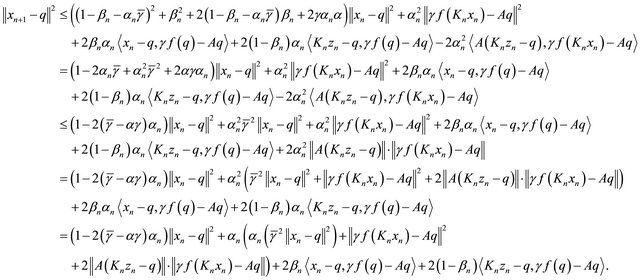
Since 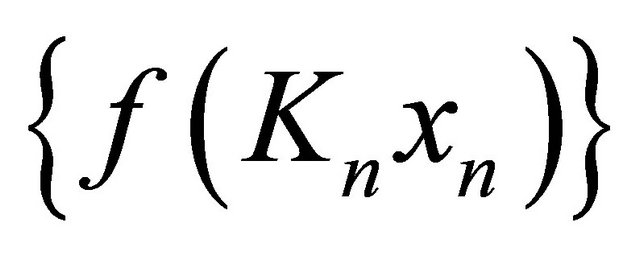
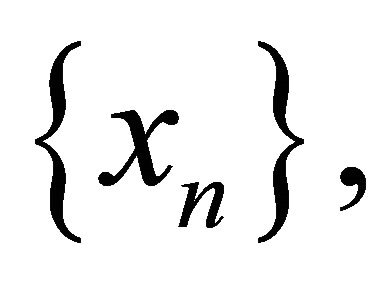 and
and 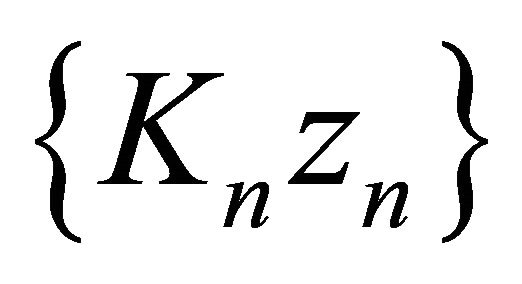 are bounded, we can take a constant
are bounded, we can take a constant 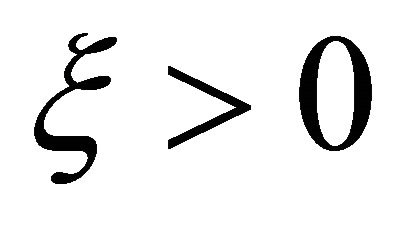 such that
such that
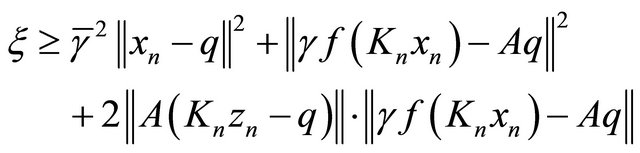
for all 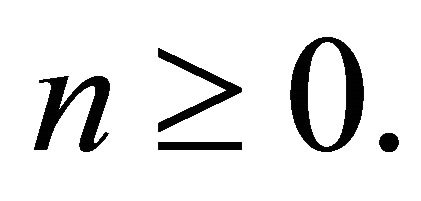 It then follows that
It then follows that
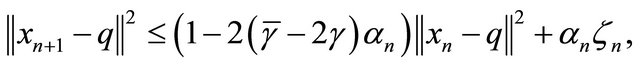 (3.22)
(3.22)
where
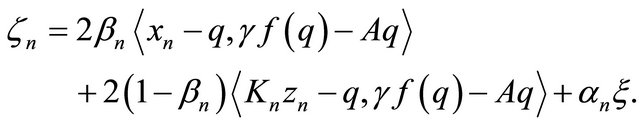
By using (3.20), (3.21) and condition (C1), we get
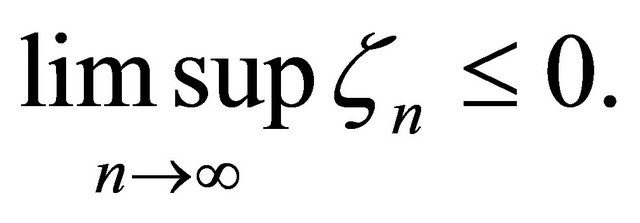
Now applying Lemma 2.1 to (3.22) concludes that 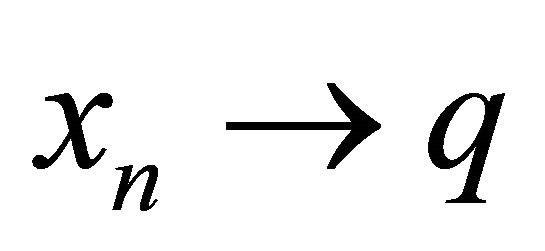 as
as  Finally, noticing
Finally, noticing
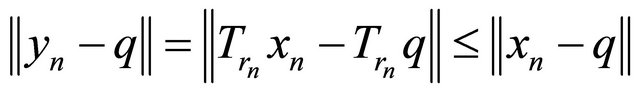
we also conclude that 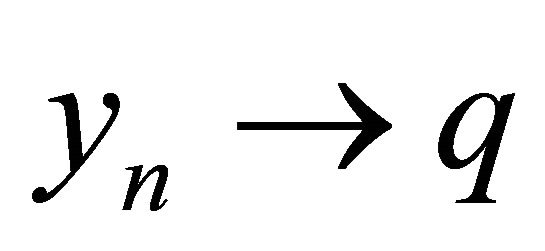 as
as  This completes the proof.
This completes the proof.
4. Applications
In this section, by Theorem 3.1, we can obtain some new and interesting strong convergence theorems. Now we give some examples as follows:
Let 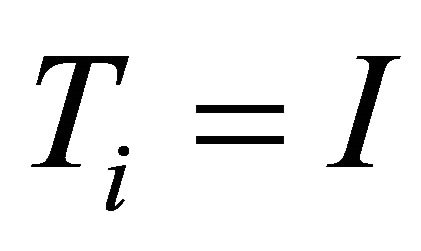 for all
for all 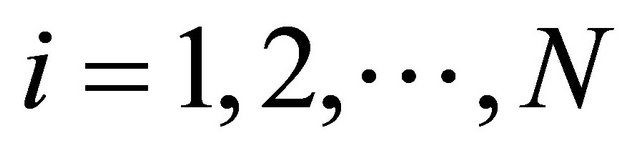 and setting
and setting 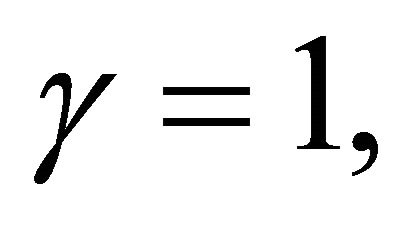
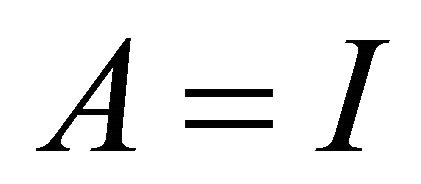 and
and 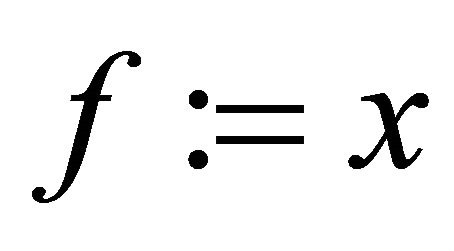 in Theorem 3.1, we obtain the following result.
in Theorem 3.1, we obtain the following result.
Corollary 4.1. Let H be a real Hilbert space, C a nonempty closed convex subset of H, F a bifunction from 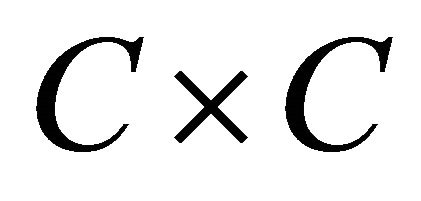 to
to  which satisfies (A1)-(A4),
which satisfies (A1)-(A4), 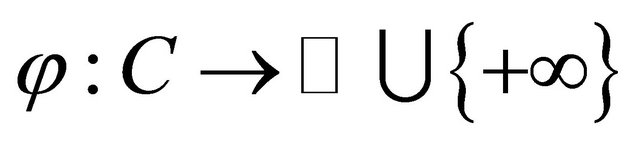 a proper lower semicontinuous and convex function and
a proper lower semicontinuous and convex function and 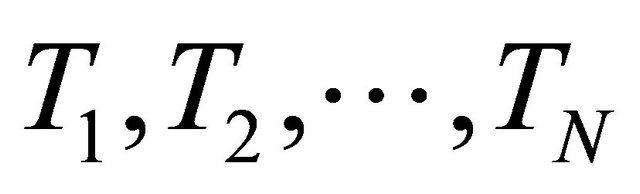 a finite family of nonexpansive mappings of C into H such that the common fixed points set
a finite family of nonexpansive mappings of C into H such that the common fixed points set 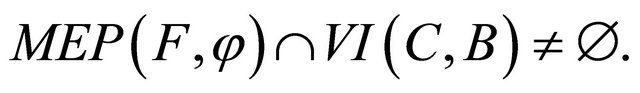 Assume that either (B1) or (B2) holds and
Assume that either (B1) or (B2) holds and 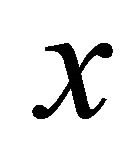 is an arbitrary point in C. Let
is an arbitrary point in C. Let 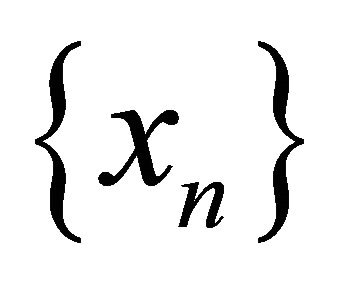 and
and 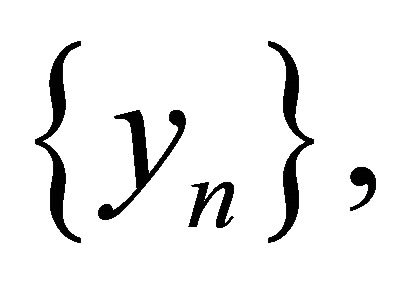 be sequences generated by
be sequences generated by 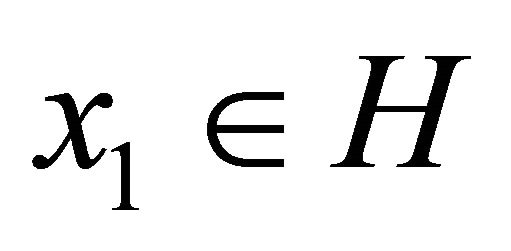 and
and 
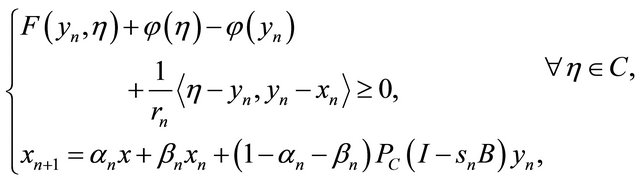
where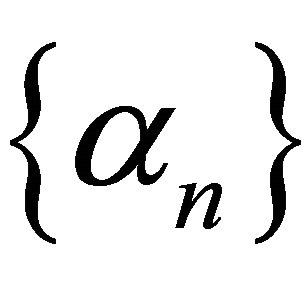 ,
, 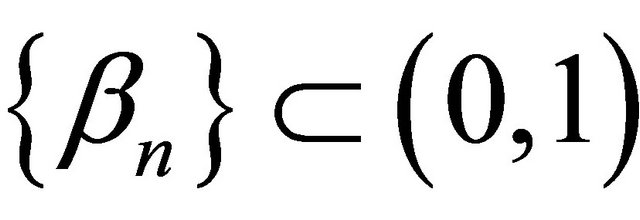 ,
, 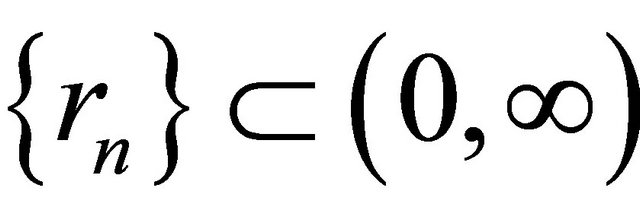 ,
, 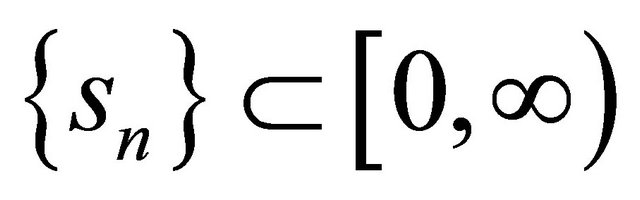 satisfying the conditions (C1)-(C5) in Theorem 3.1. Then,
satisfying the conditions (C1)-(C5) in Theorem 3.1. Then, 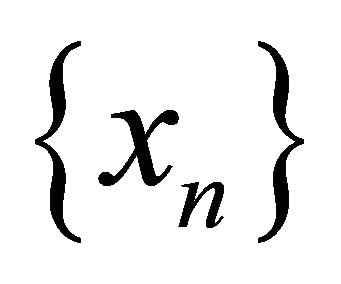 and
and 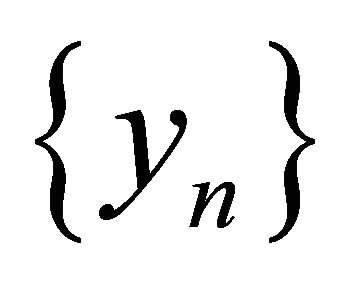 converge strongly to a point
converge strongly to a point
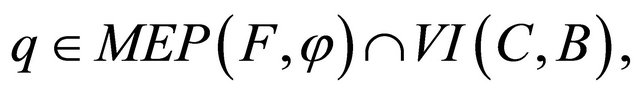
where
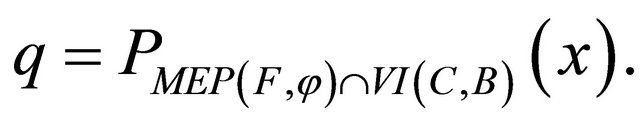
Setting 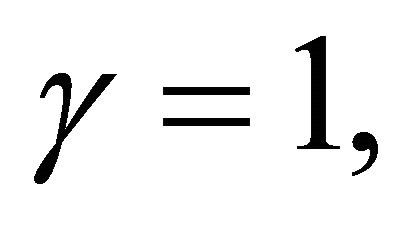
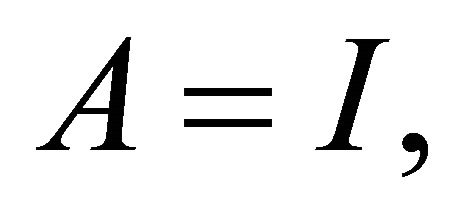
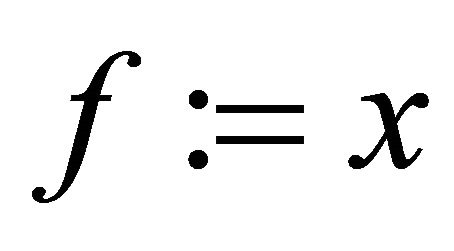 and
and 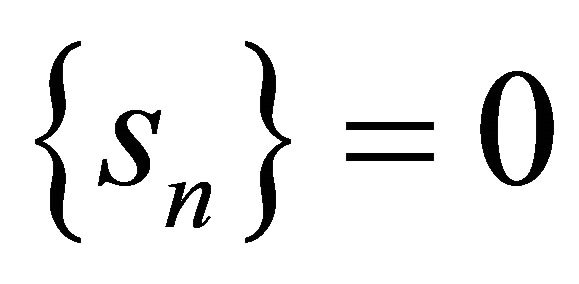 for all n in Theorem 3.1, we obtain the following result.
for all n in Theorem 3.1, we obtain the following result.
Corollary 4.2. Let H be a real Hilbert space, C a nonempty closed convex subset of H, F a bifunction from 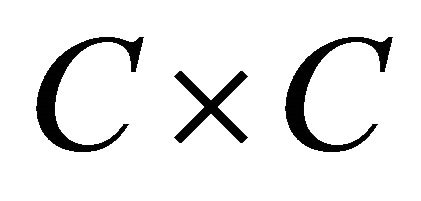 to
to  which satisfies (A1)-(A4),
which satisfies (A1)-(A4), 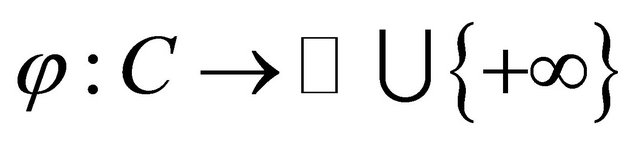 a proper lower semicontinuous and convex function and
a proper lower semicontinuous and convex function and 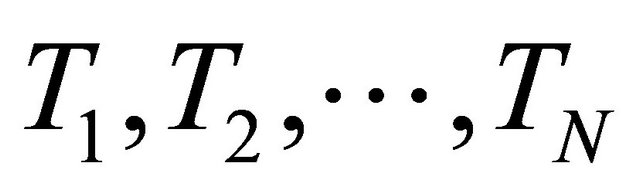 a finite family of nonexpansive mappings of C into H such that the common fixed points set
a finite family of nonexpansive mappings of C into H such that the common fixed points set 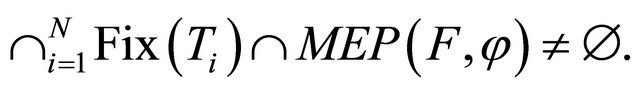 Let Kn and K be the K-mappings defined by (1.16) and (1.17), respectively. Assume that either (B1) or (B2) holds and x is an arbitrary point in C. Let
Let Kn and K be the K-mappings defined by (1.16) and (1.17), respectively. Assume that either (B1) or (B2) holds and x is an arbitrary point in C. Let 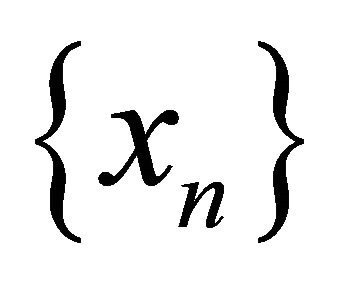 and
and 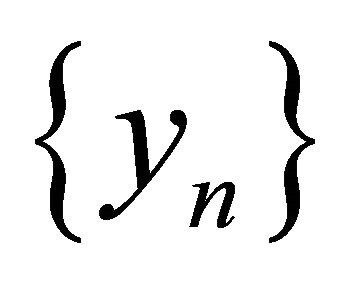 be sequences generated by
be sequences generated by 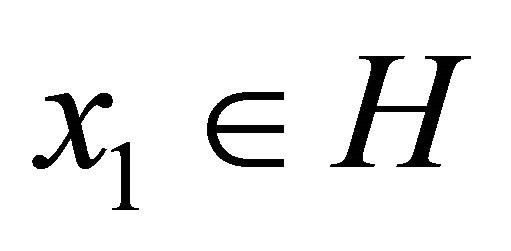 and
and 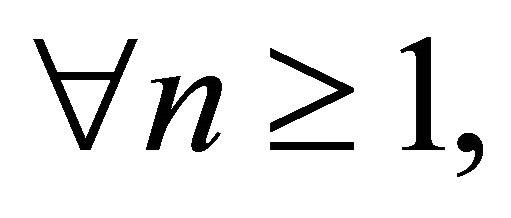
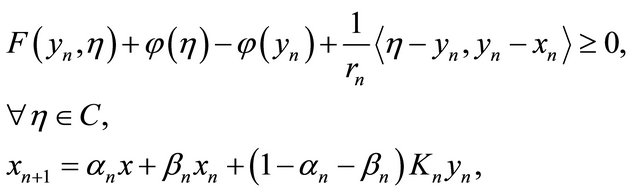
where 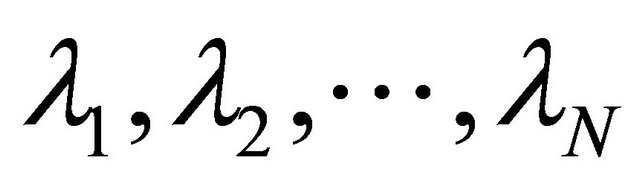 are real numbers such that
are real numbers such that 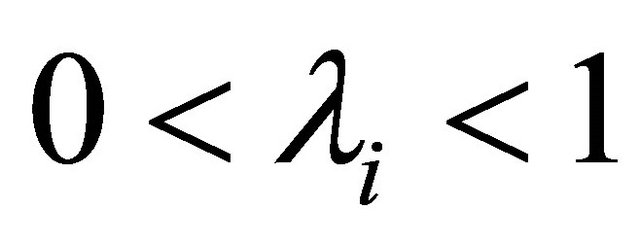 for every
for every 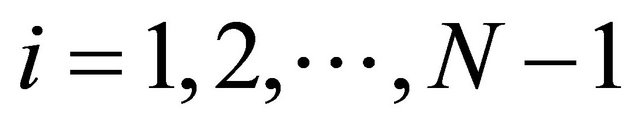 and
and
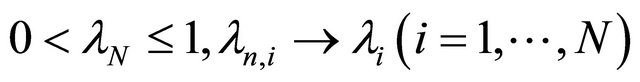 and
and ,
,  ,
, 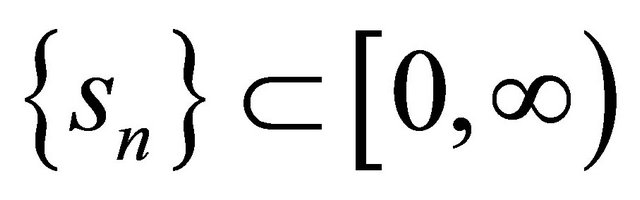
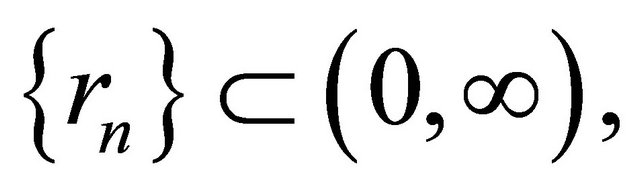 satisfying the conditions (C1), (C3), (C4) and (C6) in Theorem 3.1. Then,
satisfying the conditions (C1), (C3), (C4) and (C6) in Theorem 3.1. Then, 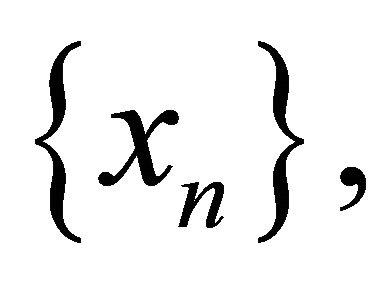 and
and 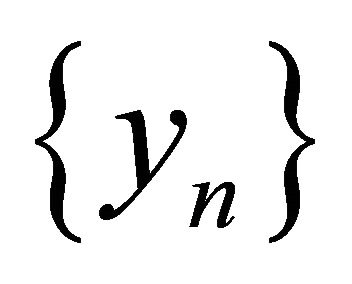 converge strongly to a point
converge strongly to a point
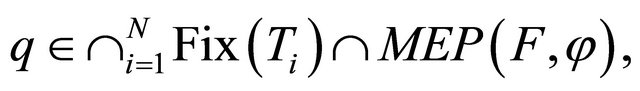
where
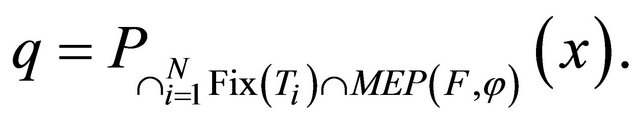
Finally as applications, we will utilize the results presented in this paper to study the following optimization problem:
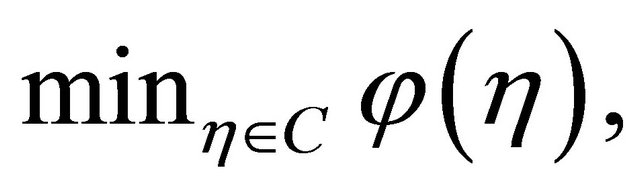 (4.1)
(4.1)
where C is a nonempty bounded closed convex subset of a Hilbert space and 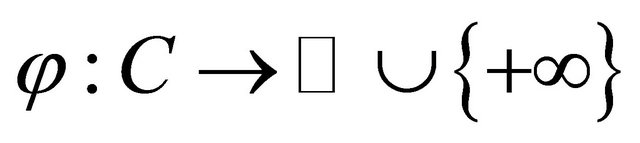 is a proper lower semicontinuous and convex function. We denote by
is a proper lower semicontinuous and convex function. We denote by 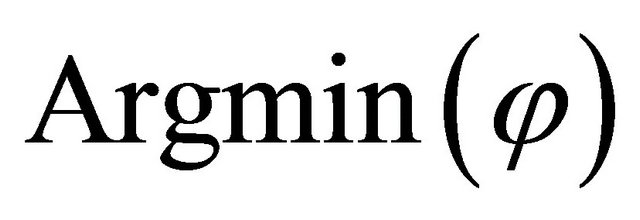 the set of solutions in (4.1). Let
the set of solutions in (4.1). Let 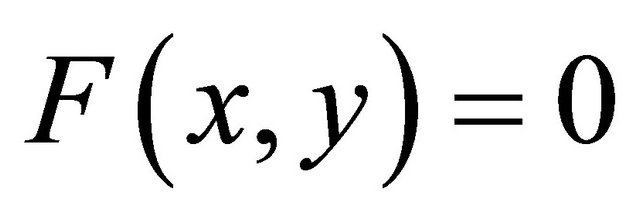 for all
for all 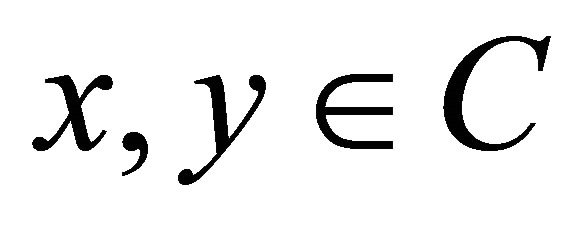 in Corollary 4.1, then
in Corollary 4.1, then
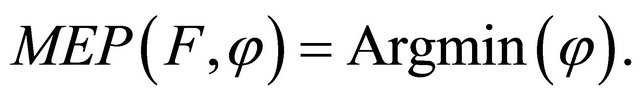
It follows from Corollary 4.1 that the sequence 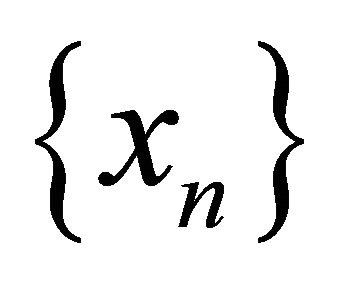 generated by
generated by 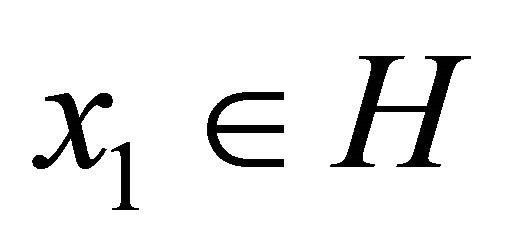 and
and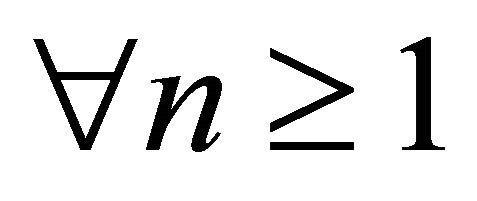 ,
,
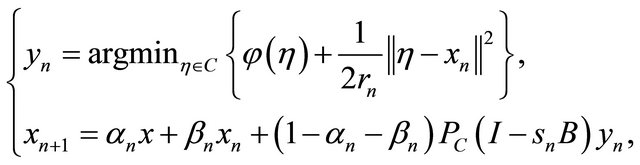 (4.2)
(4.2)
where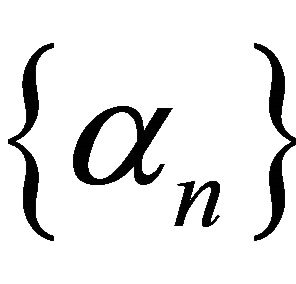 ,
, 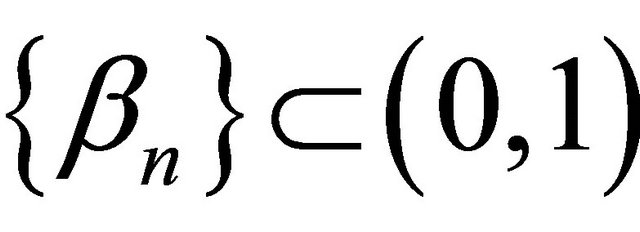 ,
, 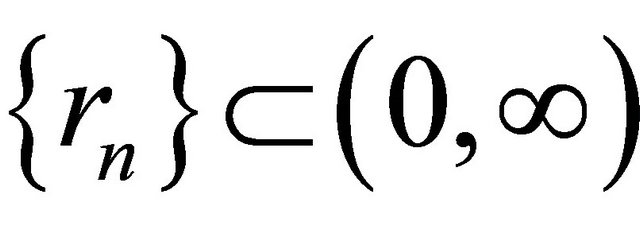 and
and 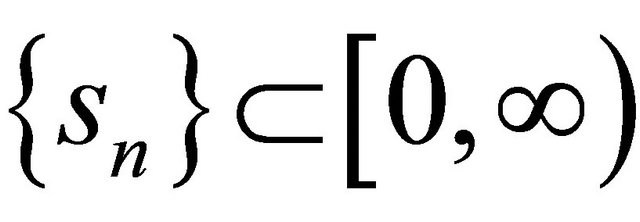 satisfying the conditions (C1)-(C5) in Theorem 3.1. Then the sequence
satisfying the conditions (C1)-(C5) in Theorem 3.1. Then the sequence 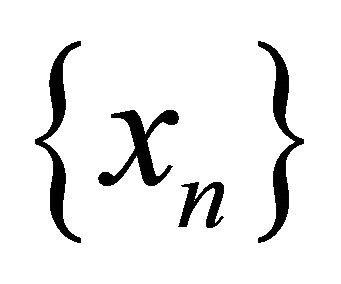 converges strongly to a point
converges strongly to a point
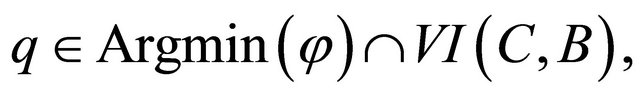
where
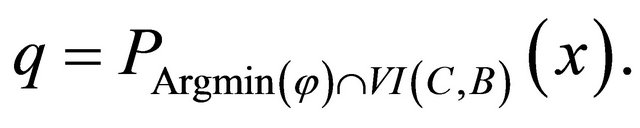
Let 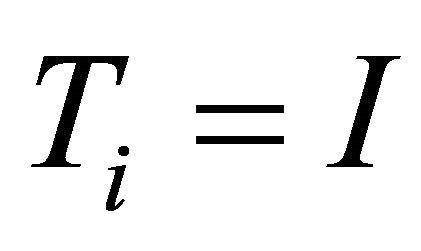 for all
for all 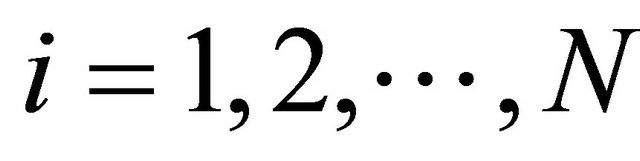 and
and 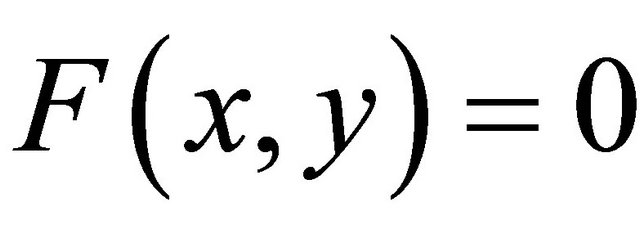 for all
for all 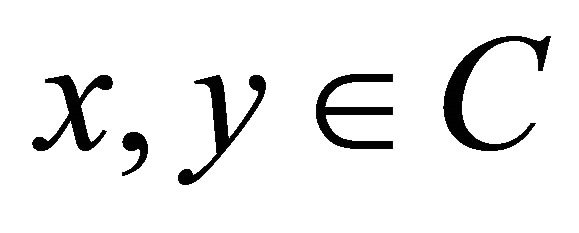 in Corollary 4.2, then
in Corollary 4.2, then 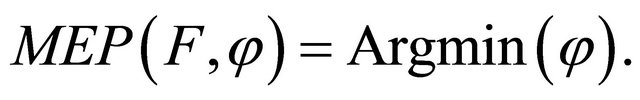 It follows from Corollary 4.2 that the iterative sequence
It follows from Corollary 4.2 that the iterative sequence 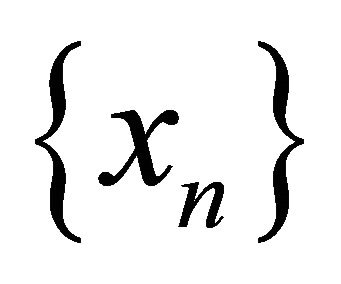 generated by
generated by 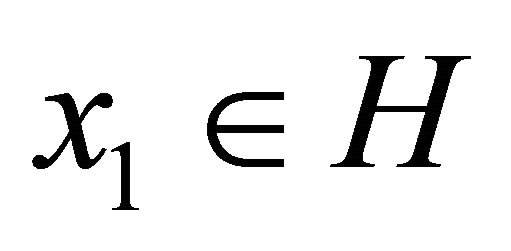 and
and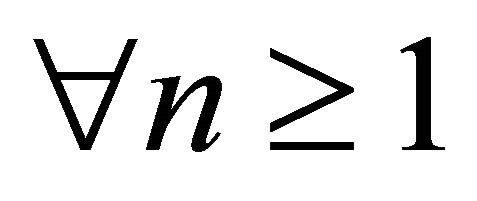 ,
,
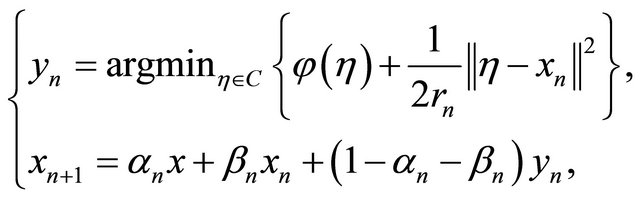 (4.3)
(4.3)
where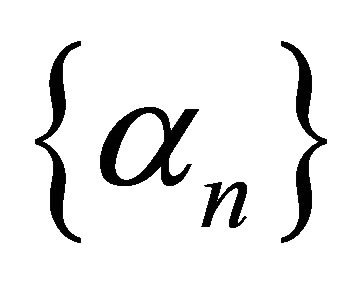 ,
, 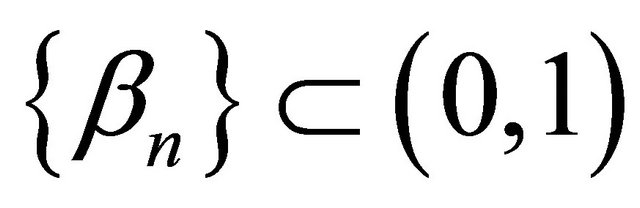 and
and 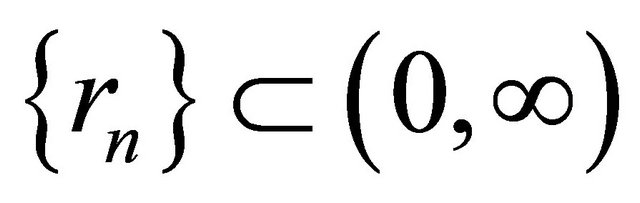 satisfying the conditions (C1), (C3) and (C4) in Theorem 3.1. Then the sequence
satisfying the conditions (C1), (C3) and (C4) in Theorem 3.1. Then the sequence 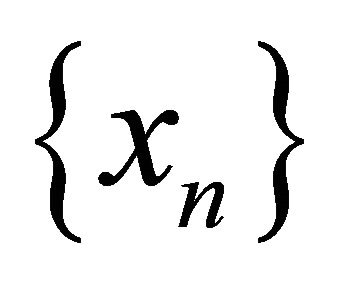 converges strongly to a point
converges strongly to a point 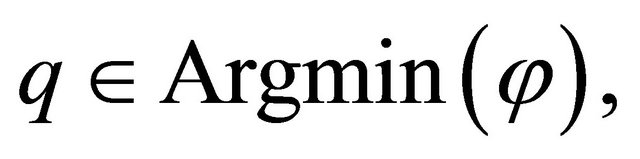 where
where 
Remark 4.3. The algorithms (4.2) and (4.3) are variants of the proximal method for optimization problems introduced and studied by Martinet [41], Rockafellar [42], Ferris [43] and many others.
5. Acknowledgements
This research is (partially) supported by the Centre of Excellence in Mathematics, the Commission on Higher Education, Thailand. The author is extremely grateful to the referees for useful suggestions that improved the contents of the paper.
REFERENCES
- W. Takahashi, “Nonlinear Functional Analysis: Fixed Point Theory and Its Applications,” Yokohama Publishers, Yokohama, 2000.
- F. Deutsch and I. Yamada, “Minimizing Certain Convex Functions over the Intersection of the Fixed Point Set of Nonexpansive Mappings,” Numerical Functional Analysis and Optimization, Vol. 19, No. 1-2, 1998, pp. 33-56. doi:10.1080/01630569808816813
- G. Marino and H. K. Xu, “A General Iterative Method for Nonexpansive Mappings in Hilbert Spaces,” Journal of Mathematical Analysis and Applications, Vol. 318, No. 1, 2006, pp. 43-52. doi:10.1016/j.jmaa.2005.05.028
- H. K. Xu, “Iterative Algorithms for Nonlinear Operators,” Journal London Mathematical Society, Vol. 66, No. 1, 2002, pp. 240-256. doi:10.1112/S0024610702003332
- H. K. Xu, “An Iterative Approach to Quadratic Optimization,” Journal of Optimization Theory and Applications, Vol. 116, 2003, pp. 659-678. doi:10.1023/A:1023073621589
- I. Yamada, “The Hybrid Steepest Descent Method for the Variational Inequality Problem of the Intersection of Fixed Point Sets of Nonexpansive Mappings,” In: D. Butnariu, Y. Censor and S. Reich, Eds., Inherently Parallel Algorithm for Feasibility and Optimization, Elsevier, Amsterdam, 2001, pp. 473-504. doi:10.1016/S1570-579X(01)80028-8
- A. Moudafi, “Viscosity Approximation Methods for Fixed Points Problems,” Journal of Mathematical Analysis and Applications, Vol. 241, No. 1, 2000, pp. 46-55. doi:10.1006/jmaa.1999.6615
- R. U. Verma, “Generalized System for Relaxed Cocoercive Variational Inequalities and Its Projection Methods,” Journal of Optimization Theory and Applications, Vol. 121, No. 1, 2004, pp. 203-210. doi:10.1023/B:JOTA.0000026271.19947.05
- R. U. Verma, “General Convergence Analysis for TwoStep Projection Methods and Application to Variational Problems,” Applied Mathematics Letters, Vol. 18, No. 2, 2005, pp. 1286-1292. doi:10.1016/j.aml.2005.02.026
- R. U. Verma, “Sensitivity Analysis for Relaxed Cocoercive Nonlinear Quasivariational Inclusions,” Journal of Applied Mathematics and Stochastic Analysis, No. 3, 2006, pp. 1-10. doi:10.1155/JAMSA/2006/52041
- W. Takahashi and M. Toyoda, “Weak Convergence Theorems for Nonexpansive Mappings and Monotone Mappings,” Journal of Optimization Theory and Applications, Vol. 118, No. 2, 2003, pp. 417-428. doi:10.1023/A:1025407607560
- H. Iiduka and W. Takahashi, “Strong Convergence Theorems for Nonexpansive Mappings and Inverse-Strongly Monotone Mappings,” Nonlinear Analysis, Vol. 61, No. 4, 2005, pp. 341-350. doi:10.1016/j.na.2003.07.023
- X. Qin, S. M. Kang and M. Shang, “Strong Convergence Theorems of k-Strict Pseudo-Contractions in Hilbert Spaces,” Czechoslovak Mathematical Journal, Vol. 59, No. 3, 2009, pp. 695-706. doi:10.1007/s10587-009-0041-3
- L. C. Ceng and J. C. Yao, “A Hybrid Iterative Scheme for Mixed Equilibrium Problems and Fixed Point Problems,” Journal of Computational and Applied Mathematics, Vol. 214, No. 1, 2008, pp. 186-201. doi:10.1016/j.cam.2007.02.022
- P. L. Combettes and S. A. Hirstoaga, “Equilibrium Programming in Hilbert Spaces,” Journal of Nonlinear and Convex Analysis, Vol. 6, No. 1, 2005, pp. 117-136.
- S. D. Flam and A. S. Antipin, “Equilibrium Programming Using Proximal-Like Algorithms,” Mathematical Programming, Vol. 78, No. 1, 1997, pp. 29-41. doi:10.1007/BF02614504
- E. Blum and W. Oettli, “From Optimization and Variational Inequalities to Equilibrium Problems,” Mathematics Student-India, Vol. 63, No. 1-4, 1994, pp. 123-145.
- J. W. Peng and J. C. Yao, “A New Hybrid-Extragradient Method for Generalized Mixed Equilibrium Problems and Fixed Point Problems and Variational Inequality Problems,” Taiwanese Journal of Mathematics, Vol. 12, No. 6, 2008, pp. 1401-1432.
- J. W. Peng and J. C. Yao, “Strong Convergence Theorems of Iterative Scheme Based on the Extragradient Method for Mixed Equilibrium Problems and Fixed Point Problems,” Mathematical and Computer Modelling, Vol. 49, No. 9-10, 2009, pp. 1816-1828. doi:10.1016/j.mcm.2008.11.014
- S. Takahashi and W. Takahashi, “Viscosity Approximation Methods for Equilibrium Problems and Fixed Point Problems in Hilbert Spaces,” Journal of Mathematical Analysis and Applications, Vol. 331, No. 1, 2007, pp. 506- 515. doi:10.1016/j.jmaa.2006.08.036
- M. Shang, Y. Su and X. Qin, “A General Iterative Method for Equilibrium Problems and Fixed Point Problems in Hilbert Spaces,” Fixed Point Theory and Applications, 2007, Article ID: 95412.
- H. H. Bauschke, “The Approximation of Fixed Points of Compositions of Nonexpansive Mappings in Hilbert Space,” Journal of Mathematical Analysis and Applications, Vol. 202, No. 1, 1996, pp. 150-159. doi:10.1006/jmaa.1996.0308
- H. H. Bauschke and J. M. Borwein, “On Projection Algorithms for Solving Convex Feasibility Problems,” SIAM: SIAM Review, Vol. 38, No. 3, 1996, pp. 367-426. doi:10.1137/S0036144593251710
- P. L. Combettes, “Constrained Image Recovery in a Product Space,” Proceedings of the IEEE International Conference on Image Processing, Washington DC, 23-26 October 1995, pp. 2025-2028. doi:10.1109/ICIP.1995.537406
- P. L. Combettes, “The Foundations of Set Theoretic Estimation,” Proceeding of the IEEE, Vol. 81, No. 2, 1993, 182-208. doi:10.1109/5.214546
- F. Deutsch and H. Hundal, “The Rate of Convergence of Dykstra’s Cyclic Projections Algorithm: The Polyhedral Case,” Numerical Functional Analysis and Optimization, Vol. 15, No. 5-6, 1994, pp. 537-565. doi:10.1080/01630569408816580
- D. C. Youla, “Mathematical Theory of Image Restoration by the Method of Convex Projections,” In: H. Stark, Ed., Image Recovery: Theory and Applications, Academic Press, Gainesville, 1987, pp. 29-77.
- I. Yamada and N. Ogura, “Hybrid Steepest Descent Method for the Variational Inequality Problem over the Fixed Point Set of Certain Quasi Nonexpansive Mappings,” Numerical Functional Analysis and Optimization, Vol. 25, No. 7-8, 2004, pp. 619-655. doi:10.1081/NFA-200045815
- S. Atsushiba and W. Takahashi, “Strong Convergence Theorems for a Finite Family of Nonexpansive Mappings and Applications,” Indian Journal of Mathematics, Vol. 41, No. 3, 1999, pp. 435-453.
- G. Emmanuele, “A Remark on a Paper: Common Fixed Points of Nonexpansive Mappings by Iteration by P. K. F. Kuhfittig,” Pacific Journal of Mathematics, Vol. 110, No. 2, 1984, pp. 283-285. doi:10.2140/pjm.1984.110.283
- P. K. F. Kuhfittig, “Common Fixed Points of Nonexpansive Mappings by Iteration,” Pacific Journal of Mathematics, Vol. 97, No. 1, 1981, pp. 137-139. doi:10.2140/pjm.1981.97.137
- W. Takahashi, “Weak and Strong Convergence Theorems for Families of Nonexpansive Mappings and Their Applications,” Annales Universitatis Mariae Curie-Sklodowska, Vol. 51, 1997, pp. 277-292.
- W. Takahashi and K. Shimoji, “Convergence Theorems for Nonexpansive Mappings and Feasibility Problems,” Mathematical and Compute Modelling, Vol. 32, No. 11, 2000, pp. 1463-1471. doi:10.1016/S0895-7177(00)00218-1
- X. Qin, M. Shang and Y. Su, “Strong Convergence of a General Iterative Algorithm for Equilibrium Problems and Variational Inequality Problems,” Mathematical and Compute Modelling, Vol. 48, No. 7-8, 2008, pp. 1033-1046. doi:10.1016/j.mcm.2007.12.008
- V. Colao, G. Marino and H. K. Xu, “An Iterative Method for Finding Common Solutions of Equilibrium and Fixed Point Problems,” Journal of Mathematical Analysis and Applications, Vol. 344, No. 1, 2008, pp. 340-352. doi:10.1016/j.jmaa.2008.02.041
- Y. Yao, M. A. Noor and Y. C. Liouc, “On Iterative Methods for Equilibrium Problems,” Nonlinear Analysis, Vol. 70, No. 9, 2009, pp. 497-509. doi:10.1016/j.na.2007.12.021
- A. Kangtunyakarn and S. Suantai, “A New Mapping for Finding Common Solutions of Equilibrium Problems and Fixed Point Problems of Finite Family of Nonexpansive Mappings,” Nonlinear Analysis, Vol. 71, No. 10, 2009, pp. 4448-4460. doi:10.1016/j.na.2009.03.003
- Z. Opial, “Weak Convergence of Successive Approximations for Nonexpansive Mappins,” Bulletin of the American Mathematical Society, Vol. 73, No. 4, 1967, pp. 591- 597. doi:10.1090/S0002-9904-1967-11761-0
- R. T. Rockafellar, “On the Maximality of Sums of Nonlinear Monotone Operators,” Transactions of the American Mathematical Society, Vol. 149, No. 1, 1970, pp. 75-88. doi:10.1090/S0002-9947-1970-0282272-5
- T. Suzuki, “Strong Convergence of Krasnoselskii and Mann’s Type Sequences for One-Parameter Nonexpansive Semigroups without Bochner Integrals,” Journal of Mathematical Analysis and Applications, Vol. 305, No. 1, 2005, pp. 227-239. doi:10.1016/j.jmaa.2004.11.017
- B. Martinet, “Perturbation Des Méthodes d’Optimisation,” AIRO Analyse Numérique, Vol. 12, No. 2, 1978, pp. 153-171.
- R. T. Rockafellar, “Monotone Operators and the Proximal Point Algorithm,” IAM: SIAM Journal on Control and Optimization, Vol. 14, No. 5, 1976, pp. 877-898. doi:10.1137/0314056
- M. C. Ferris, “Finite Termination of the Proximal Point Algorithm,” Mathematical Programming, Vol. 50, No. 1-3, 1991, pp. 359-366. doi:10.1007/BF01594944
NOTES
*This research is (partially) supported by the Centre of Excellence in Mathematics, the Commission on Higher Education, Thailand.

