ABSTRACT

Let 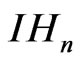be the 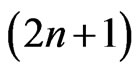-dimensional Heisenberg group and let 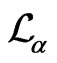and 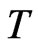be the sublaplacian and central element of the Lie algebra of 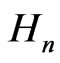respectively. For 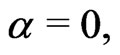denote by 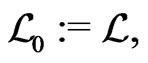the Heisenberg Laplacian and let be a compact subgroup of Automorphism of. In this paper, we give some properties of the Heisenberg Laplacian and prove that and 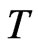generate the 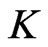-invariant universal enveloping algebra, 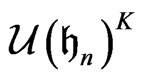of.

1. Preliminaries

The Heisenberg group (of order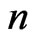), 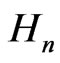is a noncommutative nilpotent Lie group whose underlying manifold is with coordinates 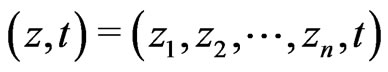and group law given by

Setting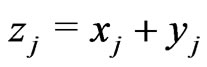, then 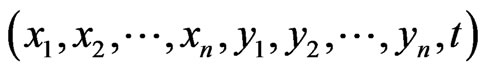forms a real coordinate system for. In this coordinate system, we define the following vector fields:

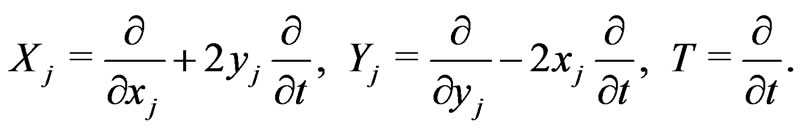
It is clear from [1] that is a basis for the left invariant vector fields on 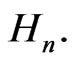These vector fields span the Lie algebra of and the following commutation relations hold:

Similarly, we obtain the complex vector fields by setting

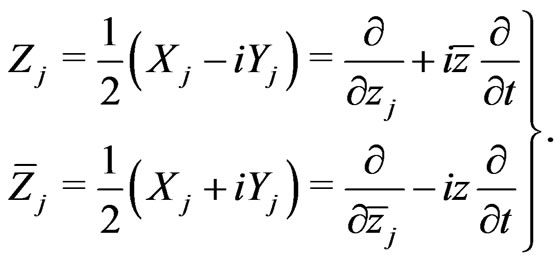(1)

In the complex coordinate, we also have the commutation relations

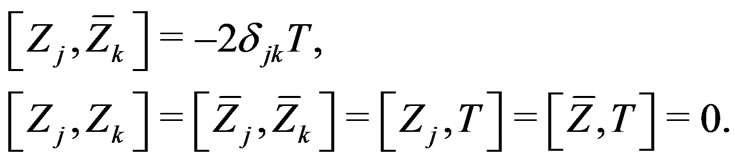
The Haar measure on 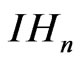is the Lebesgue measure on [2]. In particular, for, we obtain the 3-dimensional Heisenberg group 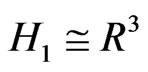(since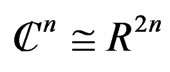). Hence 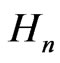may also be referred to as (2n + 1)-dimensional Heisenberg group.

One significant structure that accompanies the Heisenberg group is the family of dilations

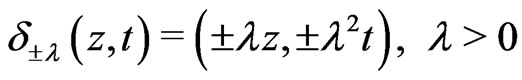
This family is an automorphism of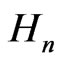. Now, if 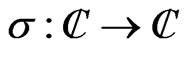is an automorphism, there exists an induced automorphism, such that

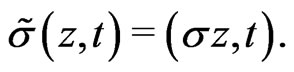
For simplicity, assume that 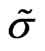and 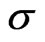coincide. Thus we may simply assume that if 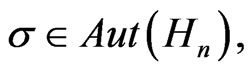we have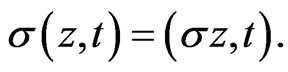

2. Heisenberg Laplacian

An operator that occurs as an analogue (for the Heisenberg group) of the Laplacian

on 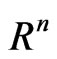is denoted by 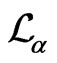where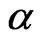

is a parameter and defined by

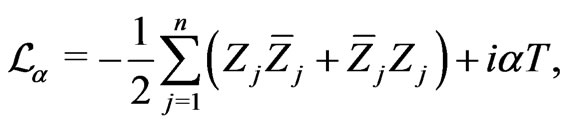
where 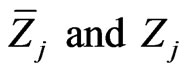are as defined in (1) so that 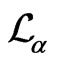can be written as

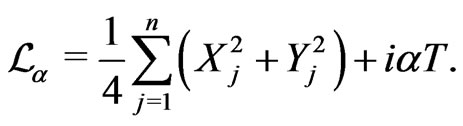(2)

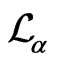is called the sublaplacian. satisfies symmetry properties analogous to those of 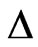on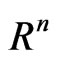. Indeed, we have that

1) is left-invariant on;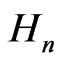

2) has degree 2 with respect to the dilation automorphism of and 3) is invariant under unitary rotations.

Several methods for the determination of solutions, fundamental solutions of (2) and conditions for local solvability are well known [3-5].

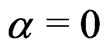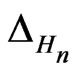The Heisenberg-Laplacian is a subelliptic differential operator defined for as on 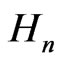and denoted by. It is obtained from the usual vector fields as

(3)

By a technique in [6], the operator is factorized into two quasi-linear first order operators on 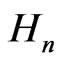as:

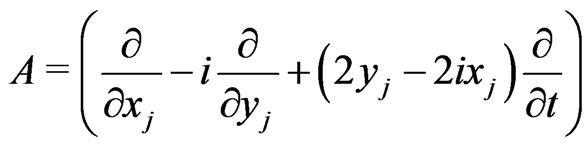
and

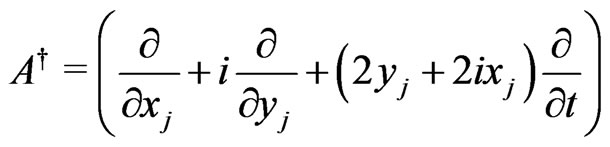
so that

Introducing the Lie algebra structure, we have

indicating that the Heisenberg algebra is noncommutative and is hypoelliptic [4]. We thus obtain an operator (which is a homogeneous element of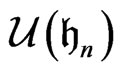, the universal enveloping algebra of the Heisenberg group when 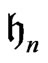is the Heisenberg algebra) [5] consistent with that of Hans Lewy [7]. In [2], it has been shown that none of the factors of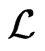, 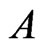or is solvable and as such, 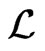is not solvable.

In this paper, we shall prove that 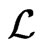only possesses a trivial group-invariant solution and for 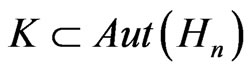a compact subgroup of 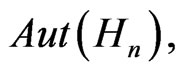we have that

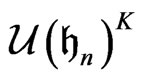the K-invariant universal enveloping algebra of the Heisenberg group is generated by 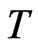and.

Now, by a solution of a factor say, we shall mean that if 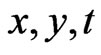are independent real variables, and 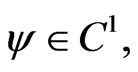such that 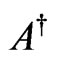has a solution in the neighbourhood 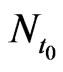of the point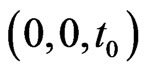, with 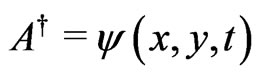then 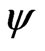is analytic at.

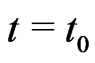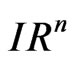Definition 2.0. Let be any open subset of, and 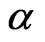a number such that A function on satisfying

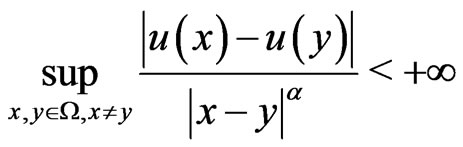
is said to be uniformly Holder continuous with Holder exponent 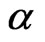if when 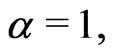they are called uniformly Lipschitz continuous. When 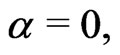they are simply continuous and bounded. A function is said to be in 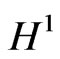-space if its first partial derivatives satisfy a Holder condition with positive exponent, provided the distance of the points involved does not exceed 1.

Theorem 2.1. Let 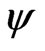be a periodic real -function which is analytic in no t-interval. Then there exists a -function 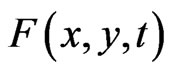determined by the derivative of 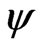such that

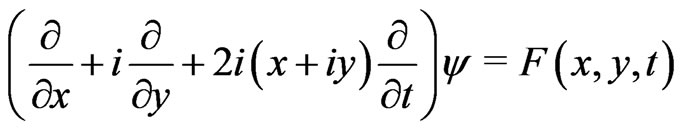
has no -solution,(no matter what open -set taken as domain of existence).

For Proof, see [8].

Theorem 2.2. The Heisenberg Laplacian, 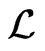defined in (3) has no non-trivial group invariant solution.

Proof. Let 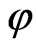be a group-invariant solution of (3). We wish to show that 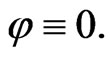To do this, let 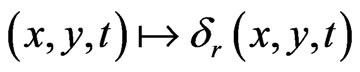be a map generated by the group of automorphisms, dilations 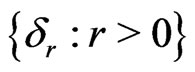where 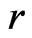determines the growth or decay rate. If 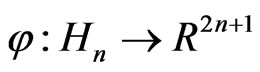is defined by

then obtaining the first and second order derivatives of with respect to the independent variables we have

Substituting these into (3), we obtain a trivial equation. But by Group-invariant method, we should obtain a system of ordinary differential equations of lower order (see [9] p. 185). Thus, there exists no non-trivial groupinvariant solution for. □

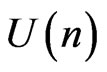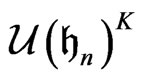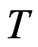Theorem 2.3. Let be a compact subgroup of, then the -invariant universal enveloping algebra of the Heisenberg group is generated by and.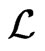

Proof. Let 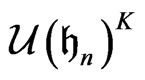be the algebra of 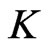-invariant differential operators on and let 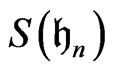be the symmetric algebra generated by the set

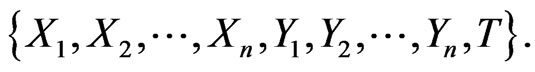
We note that the derived action of 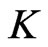on 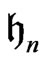is given by

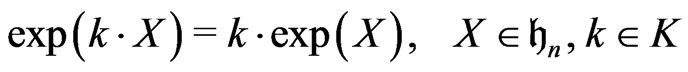
and 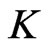acts on 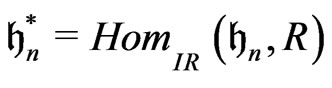via

and on the 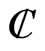-valued polynimial functions on 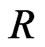-vector space 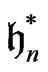via

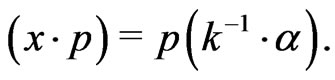
Now, if we identify with the complexified symmetric algebra then the symmetric product 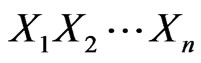of becomes the polynomial given by

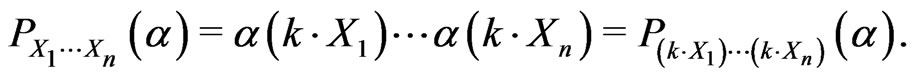
Now, define a symmetrization map by

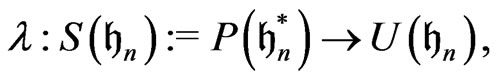
with

Now since 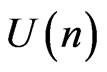acts on 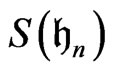and by automorphism and 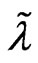defined by

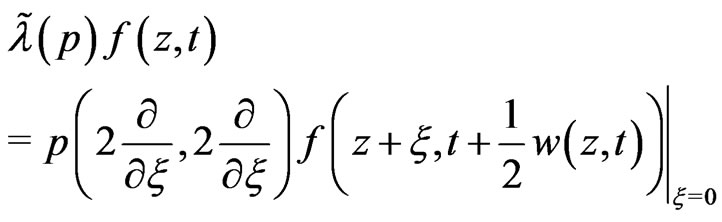
induces an algebra map on the associated graded algebras and by induction [10, p. 282] the eigenfunctions of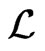

and 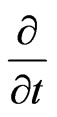are eigenfunctions of any element in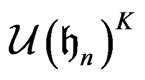

we have that the following diagram is commutative.

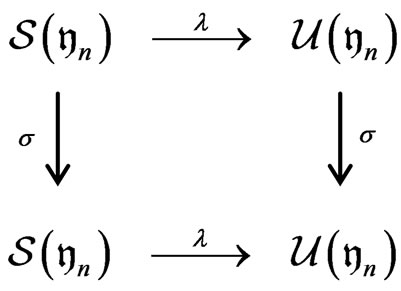
for 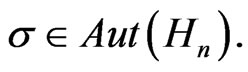Since 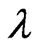is a linear isomorphismit maps 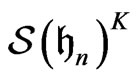onto 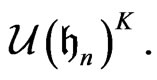Since the action of

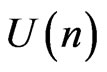preserves degree on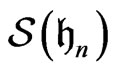, and by [11], if

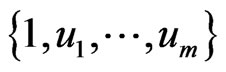generates 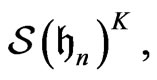then,

generates 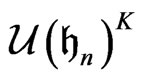If then

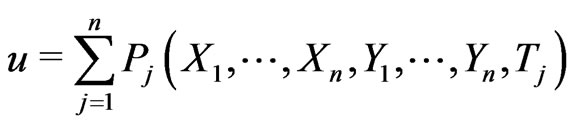
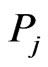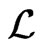where the sum is finite and each is a polynomial which is -invariant. Thus, the result follows by the fact that the eigenfunctions of and 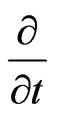are the eigenfunctions of [12]. □

REFERENCES