World Journal of Condensed Matter Physics
Vol.05 No.03(2015), Article ID:58949,11 pages
10.4236/wjcmp.2015.53023
Investigation of the Effect of Film Thickness and Heat Treatment on the Optical Properties of TeSeSn Thin Films
A. Elwhab B. Alwany1, O. M. Samir1, Mohammed A. Algradee1, M. M. Hafith2, M. A. Abdel-Rahim2
1Physics Department, Faculty of Science, Ibb University, Ibb, Yemen
2Physics Department, Faculty of Science, Assuit University, Assuit, Egypt
Email: abdualwhab@yahoo.com, algradi772001@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 June 2015; accepted 18 August 2015; published 21 August 2015
ABSTRACT
Glassy substrates TeSeSn thin films were thermally evaporated onto chemically cleaned glass. The as-deposited (as-prepared) and annealed thin films were characterized by scanning electron microscopy (SEM), X-ray diffraction (XRD) and optical transmission. The optical absorption of the as-prepared and annealed TeSeSn thin films is studied in the wavelength range of 300 nm - 900 nm. The direct optical energy gap (Eg) increases from 1.989 to 2.143 eV with increasing the thickness of the as-prepared films from 100 to 200 nm. The annealed TeSeSn films showed a decrease in the optical energy gap with increasing the annealing temperature. The effect of heat treatment on the lattice dielectric constant (εL) and carrier concentration (N) are also studied.
Keywords:
Thin Film, Film Thickness, Annealing Temperature, Optical Properties

1. Introduction
Chalcogenide glasses are used as photographic materials and have gained much importance recently. The shortcomings of pure glassy Se used for photographic drums are its short lifetime and low sensitivity [1] . Certain additives are used to improve these properties. Recently, new optimistic applications of chalcogenide alloys have occurred in the field of infrared spectroscopy, lasers and fiber techniques [2] [3] . There are promising applications in the field of laser surgery and radiometric low-temperature measurement. The transmission limits of selenium and tellurium glasses are now well known [4] . Selenium glasses exhibit a transmission range from 8 to 12 µm, but tellurium glasses offer the widest infrared transmission [5] . TeSeSn thin films have generated great interest because they are reported as reversible optical recording media [6] - [8] . The recording is carried out by making use of changes in the optical properties associated with improve of crystalline phase of these films resulting from annealing temperature. TeSeSn thin films have been prepared by various techniques such as thermal evaporation under vacuum [6] , radio frequency sputtering [8] and pulsed laser evaporation [9] . Among the various techniques, the vacuum thermal evaporation is very common due to its simplicity, low cost reproducibility and scalability deposit onto large area substrates. Moreover, the produced films with this method are highly adherent and uniform. On the other hand, the structural, electrical and optical properties of thin films are very sensitive to deposition conditions and post-deposition heat treatments [10] .
The present work deals with some experimental observation on the effect of heat treatment on structure and optical properties of TeSeSn films. Also, we report the study of the dependence of the optical properties of the TeSeSn thin films on annealing temperature.
2. Experimental Details
2.1. Preparation of Bulk
The bulk TeSeSn was prepared by the melt-quench technique. Materials (99.99% pure) Te, Se and Sn (from Aldrich, UK) were weighted (6 g total weight) according to their atomic percentage. The weighted elements were placed into a quartz glass ampoule and sealed under vacuum of 10 - 5 Torr. The sealed ampoule was heated in Heraus programmable tube furnace (type R 07115). The heating rate was approximately 4 K/m. The temperature was kept at 800˚C for 14 h and the ampoule was rocked during the melt process to ensure complete mixing and reaction. After that, the ampoule was quenched into ice-water mixture.
2.2. Thin Films Preparation
Thin films were prepared by thermal evaporation under vacuum of 10 - 5 Torr using the Edwards E-306 coating system. A constant evaporation rate (4 nm/sec) was used to deposit the films. The evaporation rates as well as the films thickness were controlled using a quartz crystal monitor (FTM5). TeSeSn films were annealed at different temperature (323 ≤ Tann ≤ 423 K) for one hour under gas Nitrogen. The morphology for as-deposited and annealed films were investigated using (SEM) type JEOL JSM-T200. The crystalline phases for as-prepared and annealed films were identified using a Philips diffractometer type 1710. The X-ray diffraction patterns were analysed using some software. Peakfit program was utilized to determine and identify the peaks of the patterns. These peaks were employed using Williamson-Hall method to estimate the crystallite size and lattice strain for the samples. Chekcell program was used to obtain and refine the cell parameters [11] . The optical transmittance (T) and reflectance (R) of the as-deposited and annealed TeSeSn films were measured at room temperature using a double-beam spectrophotometer (SHIMADZU UV-2101combined with a PC) in the wavelength 300 - 900 nm.
3. Results and Discussion
3.1. Surface Morphological (SEM Observations)
The morphology of the samples for as-prepared and after annealing temperature was examined using SEM. The samples were gold coated before SEM examination to study the surface morphology. The scanning micrograph specimens of as-prepared and annealed at 373 K for hour are shown in Figure 1(a) and Figure 1(b). The microstructure obtained for the as-prepared TeSeSn composition is shown in Figure 1(a), it is clear that the crystalline phase is embedded in the amorphous matrix. In general, after annealing to 373 K the system reveals that the amount of the transformed crystalline phase increases and the crystallized particles decreases in size as shown in Figure 1(b).
3.2. Assessment of Crystalline Phase
In order to determine the crystalline phases that appeared in SEM the X-ray diffraction pattern of films was analyzed. Figure 2 shows XRD pattern of the as-deposited and annealed TeSeSn films. The Williamson-Hall method relies on the principle that the approximate formulae for size broadening, βL, and strain broadening, βe,

Figure 1. The SEM patterns of the surface morphology of TeSeSn thin films (a) as-prepared and (b) annealing temperatures.
Figure 2. X-ray diffraction pattern of TeSeSn thin films for as-prepared and annealed.
vary quite differently with respect to Bragg angle, θ:
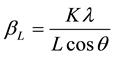 (1)
(1)
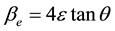 (2)
(2)
where K is the crystallite shape constant (≈0.89), ε lattice strain and L crystallite size. First contribution varies as 1/cosθ and the other as tanθ. The first contribution of crystallite size was measured by the Scherrer method as given in Equation (1) [12] . If both contributions are present then their combined effect should be determined by convolution. The simplification of Williamson and Hall is to assume the convolution is either a simple sum or sum of squares. Using the sum of these we get:
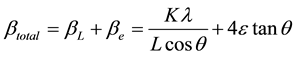 (3)
(3)
If we multiply this equation by cosθ we get:
 (4)
(4)
and comparing this to the standard equation for a straight line (m = slope; c = intercept). We see that by plotting βtotcosθ versus sinθ we obtain the strain component from the slope (4ε) and the size component from the intercept (Kλ/L). Such a plot is known as a Williamson-Hall plot [13] . The dislocation density (δ) is defined as the length of dislocation lines per unit volume of the crystal and is given by, δ =1/L2.
The deduced L, δ and ε are listed in Table 1. It is observed that the strain and crystal size decrease whereas dislocation density increases with increasing the annealing temperature. The calculated values of structure parameters of TeSeSn thin films for as-prepared and different annealing temperatures are listed in Table 2.
3.3. Effect of Thickness on Optical Properties
The spectral distribution of transmittance and reflectance for as-prepared at different thickness TeSeSn films are shown in Figure 3(a) and Figure 3(b). It could be noted that as the film thickness increased, transmittance decreased which was an indication of increase in light absorption by the films. The increase of reflectance with film thickness at specific wavelengths was due to the effect of decreased transmittance [14] . The optical absorption coefficient (α) was computed from the experimentally measured values of transmittance T(λ) and reflectance R(λ) according to the following relation [15] ,
Table 1. Structure parameters of TeSeSn thin films for as-prepared and different annealing temperatures.
Table 2. Structure parameters of TeSeSn thin films for as-prepared and different annealing temperatures.
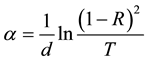 (5)
(5)
where d denotes the film thickness, R and T are the reflection and transmission coefficients, respectively.
Figure 4 shows the dependence of the absorption coefficient (α) on the incident photon energy (hν) for the as-prepared at different thickness TeSeSn films. It is observed that the values of the absorption coefficient increase with increasing both the photon energy and thickness.
According to Tauc [16] it is possible to separate three distinct regions in the absorption edge spectrum for amorphous semiconductor: the weak absorption tail which originates from defect and impurities, the exponential edge region which strongly related to the structural randomness of the system, and the high absorption region which determine the optical energy gap. In the high absorption region (α > 104 cm−1), the parabolic relation can be applied [10] [17] .
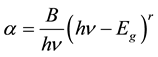 (6)
(6)
where B is a characteristic parameter (independent of photon energy) for respective transitions [18] , hν denotes photon energy, Eg is optical energy gap, and r is a number characterizing the transition process, having a value 1/2 for the direct allowed transition and value of 2 for the indirect transition. Figure 5 shows that the variation of (αhν)2 versus (hν) for as-prepared at different thickness films is linear at the absorption edge, which confirmed

Figure 3. (a) The spectral dependence of transmittance for as-prepared at different thickness TeSeSn films; (b) The spectral dependence of reflectance for as-prepared at different thickness TeSeSn films.
Figure 4. The spectral dependence of absorption coefficient for as-prepared at different thickness TeSeSn films.
Figure 5. The plots of (αhν)2 versus photon energy (hν) for the as-prepared at different thickness TeSeSn films.
direct band gap transition in TeSeSn films. The values of optical energy gap, Eg, have been determined by extrapolating the linear portions of the respective curves to (αhν)2 = 0. In the exponential edge region, the absorption coefficient is governed by the relation [19] ,
 (7)
(7)
where Ee is the band tail width and hν is the photon energy, therefore, plotting the dependence of (lnα) versus (hν) should give a straight line. The inverse of the slope gives the band tail width (Ee) of the localized states at the band gap as shown in Figure 6. The optical energy gap Eg increases with increasing the thickness and the band tail width Ee decreases with increasing the film thickness as shown in Figure 7.
The increase of energy gap (Eg) and the decrease of band tail width (Ee) may be explained in terms of unsaturated bonds present in amorphous materials. It is known that unsaturated bonds are produced as a result of an insufficient number of atoms deposited on the amorphous films [20] . These bonds are responsible for the formation of some defects in thin films which in turn produce localized states in the band gap of amorphous solids. Thicker films are greater characterized by homogeneous network, which minimizes the number of defects and the localized states thereby increasing the optical gap and decreasing the band tail width.
On the other hand, the values of refractive index (n) and extinction coefficient (k) have been calculated using the following relations [10] [21] .
 (8)
(8)

where α is absorption coefficient and R is reflectance, The spectral dependence of refractive index (n) and extinction coefficient (k) on the wavelength for as-prepared at different thickness TeSeSn thin films are shown in Figure 8 and Figure 9, respectively. Mostly, the value of n increased by increasing film thickness, also the value of k decreased. This decreasing indicates that the free carrier concentration changes. Hence, the disorder induced tailing decrease by increasing film thickness. This decrease is due to reducing the density of localized states near the mobility edges, and thereby reducing the extent tailing [22] .
Figure 6. Plots of ln(a) versus hν for as-prepared at different thickness samples for TeSeSn thin films.
Figure 7. The variation of the optical energy gap (Eg) and the width of tail states (Ee) at different thickness samples for TeSeSn thin films.
Figure 8. Refractive index (n) versus wavelength (λ) at different thickness for TeSeSn films.
3.4. Effect of Heat Treatment on Optical Properties
In order to deduce the optical properties as a function of the annealing temperature, an analysis of the transmittance and reflectance spectra was done. The absorption coefficient was plotted as (αhν)2 versus photon energy (hν) for TeSeSn films (100 nm thickness) at various annealing temperature ranges from (323 ≤ Tann. ≤ 423), see Figure 10 as a representing example. Figure 11 demonstrates that the exponential behavior of the absorption edge, via Equation (7) is satisfied in our glassy films, the calculated values of optical energy gap (Eg) and localized states tail (Ee) for TeSeSn films under investigation at different annealing temperature are listed in Table 3.
It is observed from Table 3 that, the values of (Eg) decreases with increasing the annealing temperature. The existence of tin means that the states defects increase in the amorphous selenium-tellurium glass. In addition to that the annealing process increases the defect states inside the samples, which reduces the optical band gap energy [14] . Also the effect of annealing temperature on Ee for TeSeSn thin films are shown in Table 3 it’s observed that Ee increases with increasing the annealing temperature. Also, the decrease of optical energy gap and increase of Ee with the annealing temperature can be interpreted according to the Davis and Mott model [23] for amor-
Figure 9. Extinction coefficient (k) versus wavelength (λ) at different thickness for TeSeSn films.
Figure 10. The plots of (αhν)2 versus photon energy (hν) for as-prepared and annealed samples for TeSeSn films.
Figure 11. Plots of ln(a) versus (hν) for as-prepared and annealed samples for TeSeSn films.
Table 3. Effect of annealing temperature on the values Eg, Ee, Eo, Ed, εL and N/m* of TeSeSn thin films.
phous materials, the width of the localized tail states near the mobility edges of the band gap depends on the degree of disorder and the density of defects present in the amorphous state. In particular, it is known that unsaturated bonds together with some saturated bonds, such as like dative bonds [24] , are produced as a result of an insufficient number of atoms deposited in the amorphous films [20] . Hesegawa et al. [25] showed that the unsaturated bonds are responsible for the formation of localized tail states in the band gap. The presence of a high concentration of these states is responsible for the decrease of Eg in the as-deposited films. Therefore, the drastic effect of crystalline phases on optical gap can be explained as a result of the production of surface dangling bonds around the crystallites [26] during the crystallization process. Further increase of annealing temperature results in the breaking up of the formed crystallites into smaller crystallites, thereby increasing the number of surface dangling bonds responsible for the formation of some types of defects. These defects lead to the decrease of the Eg. Wemple and Didomenico [27] [28] used a single oscillator description of the frequency-de- pendent dielectric constant to define the dispersion energy parameters Ed and Eo. The relation between the refractive index, n, and the single oscillator strength below the band gap is given by the expression [28] :

where Eo is the oscillator energy, Ed is the dispersion energy, which measures the average strength of the interband optical transition and E is the photon energy.
Figure 12 shows the relation between (n2 − 1)−1 and (E2) for as-prepared and after annealing. The values of Eo and Ed are directly determined from the slope, (Eo/Ed)−1 and the intercept, (Eo/Ed). The obtained values of Eo and Ed for the typical TeSeSn thin films are listed in Table 3. It is observed that the values of Eo decrease with increasing the annealing temperature but the values of Ed increase with increasing the annealing temperature. The decreasing Eo and increasing Ed with the annealing temperature could be attributed to increase the rate of diffusion of atoms of the films with increasing the annealing temperature. The increase in the diffusion rate with increasing temperature gives more number of atoms at interstitial sites, thereby leading to impurity type scattering centers [29] [30] . The obtained data of refractive index n can be analyzed to obtain the high frequency dielectric constant (εL). The following equation can be used to obtain (εL) [31] :

where ε1 is the real part of dielectric constant, εL is the lattice dielectric constant or (the high frequency dielectric constant), λ is the wavelength, N is the free charge carrier concentration, εo is the permittivity of free space (8.854 × 10−12 F/m), m* is the effective mass of the charge carrier and c is the velocity of light. The real part of dielectric constants ε1 = n2 was calculated at different values of λ. Then, the obtained values of ε1 are plotted as a function of λ2 as shown in Figure 13. It is observed that the dependence of ε1 on λ2 is linear at longer wavelengths.
Figure 12. Plots of (1/(n2 − 1) versus the photon energy (hν)2 for as-prepared and annealed samples for TeSeSn films.
Figure 13. Relative permittivity (er) versus wavelength (λ2) for as-prepared and annealed samples for TeSeSn films.
The high frequency dielectric constant εL and the ratio N/m* of the as-deposited and annealed films can be determined. The values of these two parameters with annealing temperature are given in Table 3. It can be seen that both the εL and the ratio N/m* increases with increasing the annealing temperature.
4. Conclusion
TeSeSn thin films were deposited onto glass substrates under a vacuum of 10−5 Torr using a vacuum evaporation technique. X-ray analyses showed that the average particle size decreased with the increase in annealing temperature. The optical absorption measurements indicate that the absorption mechanism is due to a direct forbidden transition. The optical energy gap (Eg) increases with the increase of the film thickness and decreases with the increase of the annealing temperature; the optical data may also be fitted to an exponential Urbach formula. The optical parameters, (Eg) and (Ee), are affected by both film thickness and annealing temperature; this confirms the effect of these two factors on the density of localised states. It was found that the dispersion of refractive index obeyed the single oscillator model. On the other hand, the high frequency dielectric constant (εL) and the ratio (N/m*) increase with increasing the annealing temperature.
Acknowledgements
The authors wish to thank the Ibb University for financial support. Assuit University (Department of Physics) has been thanked for availing the research equipment.
Cite this paper
A. Elwhab B.Alwany,O. M.Samir,Mohammed A.Algradee,M. M.Hafith,M. A.Abdel-Rahim, (2015) Investigation of the Effect of Film Thickness and Heat Treatment on the Optical Properties of TeSeSn Thin Films. World Journal of Condensed Matter Physics,05,220-231. doi: 10.4236/wjcmp.2015.53023
References
- 1. Pfister, G. (1979) Electronic Properties of Chalcogenide Glasses and Their Use in Xerography. Journal of Electronic Materials, 8, 789-837.
http://dx.doi.org/10.1007/BF02651186 - 2. Katsuyama, T., Satoh, S. and Matsumura, H. (1992) Scattering Loss Characteristics of Selenide-Based Chalcogenide Glass Optical Fibers. Journal of Applied Physics, 71, 4132.
http://dx.doi.org/10.1063/1.3 - 3. Kamaruizaman, B.M.Z., Juhasz, C. and Vaezi-Nejad, S.M. (1992) Application of Thermally Stimulated Discharge Techniques to a-Se: Te/Se Double-Layer Photoreceptors. Journal of Materials Science, 27, 4316-4322.
http://dx.doi.org/10.1007/BF00541559 - 4. Savage, J.A., Webber Webber, P.J. and Pitt, A.M. (1980) The Potential of Ge-As-Se-Te Glasses as 3 - 5 μm and 8 - 12 μm Infrared Optical Materials. Infrared Physics, 20, 313-320.
http://dx.doi.org/10.1016/0020-0891(80)90045-7 - 5. Reddy, K.V. and Bhatnagar, A.K. (1992) Electrical and Optical Studies on Amorphous Se-Te Alloys. Journal of Physics D: Applied Physics, 25, 1810.
http://dx.doi.org/10.1088/0022-3727/25/12/017 - 6. Terao, M., Nishida, T., Miyauchi, Y., Nakao, T., Kaku, T., Horigome, S., Ojima, M., Tsunoda, Y., Sugita, Y. and Ohta, Y. (1985) Sn-Te-Se Phase Change Recording Film For Optical Disks. SPIE Proceedings, 529, 46.
http://dx.doi.org/10.1117/12.946430 - 7. Terao, M., Nlshlda, T., Mlyauchl, Y., Kaku, T., Hongome, S. and Suglta, Y. (1989) Sn-Te-Se Films for Reversible Phase-Change Optical Recording. Japanese Journal of Applied Physics, 28, 804.
http://dx.doi.org/10.1143/JJAP.28.804 - 8. Hou, L.S., Gu, D.H. and Can, F.X. (1987) Thermal and Laser-Induced Phase Changes of Te-Se-M(M=In,Sn,Sb) Thin Films. Journal of Non-Crystalline Solids, 95-96, 525-532.
http://dx.doi.org/10.1016/S0022-3093(87)80153-9 - 9. Dimitrov, D.Z. and Kozhukharov, V.S. (1992) Laser-Deposited Thin TeSeSn Alloy Films. Thin Solid Films, 209, 80-83.
http://dx.doi.org/10.1016/0040-6090(92)90013-2 - 10. Abdel-Rahim, M.A., Hafiz, M.M., Elwhab, A. and Alwany, B. (2012) Influence of Annealing on the Structure and Optical Properties of Zn40Se60 Thin Films. Optics & Laser Technology, 44, 1116-1121.
http://dx.doi.org/10.1016/j.optlastec.2011.10.003 - 11. Laugier, J. and Bochu, B. (2004) Checkcell, LMGP-Suite of Programs for the Interpretation of X-Ray Experiments. Ensp/Laboratoire des Materiaux et du Genie, Physique, Saint Martin d’Heres.
http://www.ccp14.ac.in/tutorial/lmgp/ - 12. Scherrer, P. (1918) Bestimmung der Grösse und der Inneren Struktur von Kolloidteilchen Mittels Röntgenstrahlen, Nachrichten von der Gesellschaft der Wissenschaften, Göttingen. Mathematisch-Physikalische Klasse, 2, 98-100.
- 13. Williamson, G.K. and Hall, W.H. (1953) X-Ray Line Broadening from Filed Aluminium and Wolfram. Acta Metallurgica, 1, 22-31.
http://dx.doi.org/10.1016/0001-6160(53)90006-6 - 14. Mulama, A.A., Mwabora, J.M., Oduor, A.O., Muiva, C.M. and Muthoka, B. (2014) Investigation of the Effect of Film Thickness on the Optical Properties of Amorphous Se85-xTe15Sbx Thin Films. Africa Journal of Physical Sciences, 1, 38-42.
- 15. Rusu, G.I., Diciu, M., Pîrghie, C. and Popa, E.M. (2007) Structural Characterization and Optical Properties of ZnSe Thin Films. Applied Surface Science, 253, 9500-9505.
http://dx.doi.org/10.1016/j.apsusc.2007.06.009 - 16. Tauc, J. (1974) Amorphous and Liquid Semiconductor. Plenum, New York.
http://dx.doi.org/10.1007/978-1-4615-8705-7 - 17. Shamshad, A., Khan, M., Zulfequar, Z., Khan, H. and Husain, M. (2003) Effects of Annealing on the Optical Band Gap of Amorphous Ga5Se95-xSbx during Crystallization. Journal of Modern Optics, 50, 51-62.
- 18. Rusu, G.I., Ciupina, V., Popa, M.E., Prodan, G., Rusu, G.G. and Baban, C. (2006) Microstructural Characterization and Optical Properties of ZnSe Thin Films. Journal of Non-Crystalline Solids, 352, 1525-1528.
http://dx.doi.org/10.1016/j.jnoncrysol.2006.01.029 - 19. El-Wahabb, E.A., El-Samanoudy, M.M. and Fadel, M. (2001) Effect of Thickness and Heat Treatment on the Electrical and Optical Properties of (Ge2S3)1 (Sb2Se3)1 Thin Films. Applied Surface Science, 174, 106-117.
http://dx.doi.org/10.1016/S0169-4332(00)00911-9 - 20. Theye, M.L. (1974) Optical Properties of a-Ge, a-Si and a-III-V Compounds. Proceedings of the 5th International Conference on Amorphous and Liquid Semiconductors, Vol. 1, Garmisch-Partenkirchen, 3-8 September 1973, 479-498.
- 21. Gosain, D.P., Shimizu, T., Ohmura, M., Suzuki, M., Bando, T. and Okano, S. (1991) Some Properties of Sb2 Te3-x Sex for Nonvolatile Memory Based on Phase Transition. Journal of Materials Science, 26, 3271-3274.
http://dx.doi.org/10.1007/BF01124673 - 22. El-Sayed, S.M. (2002) Glass Formation and Local Arrangement of Chalcogenide of Ga40Se60 and Ga33Se60Te7. Materials Chemistry and Physics, 78, 262-270.
http://dx.doi.org/10.1016/S0254-0584(02)00345-0 - 23. Mott, N.F. and Davis, E.A. (1971) Electronic Processes in Non-Crystalline Materials. Clarenden, Oxford.
- 24. Ovshinsky, S.R. and Adler, D. (1978) Local Structure, Bonding, and Electronic Properties of Covalent Amorphous Semiconductors. Journal of Contemporary Physics, 19, 109-126.
http://dx.doi.org/10.1080/00107517808210876 - 25. Hasegawa, S., Yazaia, S. and Shimizu, T. (1978) Effects of Annealing on Gap States in Amorphous Si Films. Solid State Communications, 26, 407-410.
http://dx.doi.org/10.1016/0038-1098(78)90515-X - 26. Chaudhuri, S., Biswas, S.K., Choudhury, A. and Goswami, K. (1983) Variation of Optical Gap of Thick Amorphous Selenium Film on Heat Treatment. Journal of Non-Crystalline Solids, 54, 179-182.
http://dx.doi.org/10.1016/0022-3093(83)90092-3 - 27. Wemple, S.H. and DiDomenico Jr., M. (1971) Behavior of the Electronic Dielectric Constant in Covalent and Ionic Materials. Physical Review B, 3, 1338.
http://dx.doi.org/10.1103/PhysRevB.3.1338 - 28. Wemple, S.H. (1973) Refractive-Index Behavior of Amorphous Semiconductors and Glasses. Physical Review B, 7, 3767.
http://dx.doi.org/10.1103/PhysRevB.7.3767 - 29. Malik, M.M., Zulfequar, M., Kumar, A. and Husain, M. (1992) Effect of Indium Impurities on the Electrical Properties of Amorphous Ga30Se70. Journal of Physics: Condensed Matter, 4, 331-8338.
http://dx.doi.org/10.1088/0953-8984/4/43/008 - 30. Das, V.D. and Mallik, R.C. (2001) Study of Scattering of Charge Carriers in Thin Films of (Bi0.25Sb0.75)2Te3 Alloy with 2% Excess Te. Materials Research Bulletin, 37, 1961-1971.
- 31. Abdel-Aziz, M.M., Yahia, I.S., Wahab, L.A., Fadel, M. and Afifi, M.A. (2006) Determination and Analysis of Dispersive Optical Constant of TiO2 and Ti2O3 Thin Films. Applied Surface Science, 252, 8163-8170.
http://dx.doi.org/10.1016/j.apsusc.2005.10.040














