Atmospheric and Climate Sciences
Vol.04 No.05(2014), Article ID:52299,7 pages
10.4236/acs.2014.45079
Numerical Modeling of the Initial Formation of Cyclonic Vortices at Tropical Latitudes
Igor V. Mingalev1, Natalia M. Astafieva2, Konstantin G. Orlov1, Victor S. Mingalev1, Oleg V. Mingalev1, Valery M. Chechetkin3
1Polar Geophysical Institute, Kola Scientific Center of the Russian Academy of Sciences, Apatity, Russia
2Space Research Institute of the Russian Academy of Sciences, Moscow, Russia
3Keldysh Institute of Applied Mathematics of the Russian Academy of Sciences, Moscow, Russia
Email: mingalev@pgia.ru
Academic Editor: Mohammad Valipour, University of Tehran, Iran
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 October 2014; revised 20 November 2014; accepted 1 December 2014
ABSTRACT
To investigate the initial formation of large-scale vortices at tropical latitudes a regional non-hy- drostatic mathematical model of the wind system of the lower atmosphere, developed earlier in the Polar Geophysical Institute, is utilized. Three-dimensional distributions of the atmospheric parameters in the height range from 0 to 15 km over a limited region of the Earth’s surface are produced by the utilized model. Simulations are performed for the case when the limited three- dimensional simulation domain is intersected by an intertropical convergence zone in the west- east direction. Simulation results indicated that the origin of two convexities in the north direction in the configuration of the intertropical convergence zone can lead to the formation of three distinct tropical cyclones during the period of about four days.
Keywords:
Numerical Simulation, Air Flow, Lower Atmosphere, Tropical Cyclones

1. Introduction
Tremendous damage and numerous fatalities may be produced by severe tropical cyclonic storms and hurricanes. Therefore, prediction of tropical cyclone origin is very important problem. The physical theory of tropical cyc- lone origin is still far from completion despite of considerable efforts. Nevertheless, some aspects of tropical cyclogenesis are commonly understood, in particular, in the late stages of formation as well as in a fully developed stage (see [1] - [4] and references therein). Unfortunately, modern scientific facility does not allow some- body to measure detailed three-dimensional fields of thermodynamical and gas dynamical parameters of the lower atmosphere with sufficient accuracy to understand the physical mechanisms responsible for the initial formation of tropical cyclones. To investigate these physical mechanisms, not only the experimental and theo- retical but also computational studies may be applied. However, most of numerical studies of tropical cyclone genesis explore how a tropical cyclone forms from pre-existing large-scale disturbances of the troposphere, or from vortices, those are precursors to tropical cyclones (for example, see [5] - [12] ). Thus, many of the details of the initial stage of the formation of tropical cyclones are still unresolved.
In the present study, to investigate the initial stage of the origin of large-scale vortices at tropical latitudes a mathematical model of the wind system of the lower atmosphere, developed earlier in the Polar Geophysical Institute (PGI), is utilized. This mathematical model is the regional version of the non-hydrostatic mathematical model of the global wind system in the Earth’s atmosphere, developed earlier in the PGI [13] [14] and applied in order to investigate numerically how the horizontal non-uniformity of the atmospheric gas temperature affects the formation of the middle atmosphere global circulation for different geophysical conditions [15] - [18] .
The regional non-hydrostatic mathematical model of the wind system of the lower atmosphere, utilized in the present study, was earlier applied in order to investigate numerically the mechanisms responsible for the formation of large-scale vortices in the Earth’s lower atmosphere. In particular, this model was applied to investigate the formation mechanisms of a large-scale vortex over an ocean surface [19] [20] . This regional model was ap- plied to investigate the formation mechanism of polar lows [21] [22] , too. Also, this regional model was applied to verify the hypothesis of the influence of the shape of the intertropical convergence zone (ITCZ) on the pro- cess of the formation of tropical cyclones [23] [24] . In these investigations, it was shown that the origin of con- vexities in the form of the intertropical convergence zone, having the specific configurations, can lead to the formation of different large-scale vortices, in particular, a single cyclonic vortex, pair of cyclonic-anticyclonic vortices, and pair of cyclonic vortices, during the period not longer than three days.
The purpose of the present study is to continue these investigations and to study numerically, applying the regional mathematical model of the wind system of the lower atmosphere, the initial stage of the origin of large- scale vortexes in the vicinity of the intertropical convergence zone. Simulations are performed for the case when the limited three-dimensional simulation domain is intersected by an intertropical convergence zone in the west- east direction. It is supposed that, at the initial moment, the intertropical convergence zone contains two convexi- ties in the north direction. Time-dependent modeling is performed during the period of about four days.
2. Mathematical Model
The regional mathematical model of the wind system of the lower atmosphere, developed not long ago at the PGI, is utilized in the present study. The characteristic feature of the model is that it is non-hydrostatic, that is the model does not include the pressure coordinate equations of atmospheric dynamic meteorology, in particular, the hydrostatic equation. Instead, the vertical component of the air velocity is obtained by means of a numerical solution of the appropriate momentum equation, with whatever simplifications of this equation being absent. Thus, three components of the air velocity are obtained by means of a numerical solution of the generalized Navier- Stokes equation.
In the utilized model, the atmospheric gas is considered as a mixture of air and water vapor, in which two types of precipitating water (namely, water microdrops and ice microparticles) can exist. The model is based on the numerical solution of the system of transport equations containing the equations of continuity for air and for the total water content in all phase states, momentum equations for the zonal, meridional, and vertical compo- nents of the air velocity, and energy equation. In the momentum equations for all components of the air velocity, the effect of the turbulence on the mean flow is taken into account by using an empirical subgrid-scale parameterization similarly to the global circulation model of the Earth’s atmosphere developed earlier in the PGI [13] [14] .
Thus, the utilized mathematical model is based on numerical solving of non-simplified gas dynamic equations and produces three-dimensional time-dependent distributions of the wind components, temperature, air density, water vapor density, concentration of micro drops of water, and concentration of ice particles. The model takes into account heating/cooling of the air due to absorption/emission of infrared radiation, as well as due to phase transitions of water vapor to micro drops of water and ice particles, which play an important role in energetic balance. The finite-difference method and explicit scheme are applied for solving the system of governing equa- tions.
In the utilized model, the following variables are computed at each grid node: the temperature of the mixture of air and water vapor, ; densities of air and water vapor,
; densities of air and water vapor, 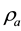 and
and , respectively; hydrodynamic velocity of the mixture (a 3D vector),
, respectively; hydrodynamic velocity of the mixture (a 3D vector),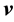 ; and the total mass of water microdrops and ice microparticles in a unit volume,
; and the total mass of water microdrops and ice microparticles in a unit volume, 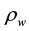 and
and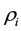 , respectively. The governing equations in vectorial form can be written as follows:
, respectively. The governing equations in vectorial form can be written as follows:
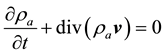 (1)
(1)
 (2)
(2)
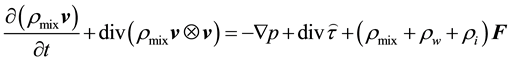 (3)
(3)
 (4)
(4)
where  and
and 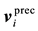 are the precipitation velocities of water microdrops and ice microparticles, respectively, conditioned by the presence of an external force field and determined from the Stokes relation with Cunningham’s correction;
are the precipitation velocities of water microdrops and ice microparticles, respectively, conditioned by the presence of an external force field and determined from the Stokes relation with Cunningham’s correction;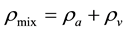 ;
;  is the pressure of the mixture defined as
is the pressure of the mixture defined as , where
, where 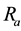 and
and 


where 


where 










It can be noted that the model assumes that the water microdrops can exist only in the presence of saturated water vapor on condition that


It is assumed that the three-dimensional simulation domain of the model is a part of a spherical layer stretch- ing from land and ocean surface up to the altitude of 15 km over a limited region of the Earth’s surface. In the present study, the dimensions of this region in longitudinal and latitudinal directions are 75˚ and 25˚, respectively. The calculated parameters are determined on a uniform grid. The latitude and longitude steps are equal to 0.08˚, and height step is equal to 200 m. As pointed out previously, the finite-difference method is applied for solving the system of equations. Complete details of the utilized finite-difference method and numerical schemes have been presented in the paper of Mingalev et al. [26] . More complete details of the applied regional mathematical model may be found in the studies of Belotserkovskii et al. [19] [20] and Mingalev et al. [23] .
3. Presentation and Discussion of Results
The present study is the continuation of the investigations of the initial stage of the origin of large-scale vortices in the vicinity of an intertropical convergence zone, fulfilled earlier [23] [24] . It is known that an intertropical convergence zone may be considered as a fluid stream, having enhanced zonal velocities, in the ambient atmospheric gas, with a zonal flow of air being westward. A meridional wind velocity directs towards the centerline of an intertropical convergence zone at levels less than approximately 3 km and directs from the centerline of an intertropical convergence zone at levels higher than approximately 3 km. A vertical wind velocity in an intertropical convergence zone is upward. Also, it is known that the form of an intertropical convergence zone may be different and, sometimes, can contain convexities with distinct shapes. The north-south position of the intertropical convergence zone responds to changes in interhemispheric temperature contrast. An asymmetry in air- sea interactions can play an important role in forming the configuration of the intertropical convergence zone [27] - [29] .
In the earlier study of Mingalev et al. [23] , the idea has been advanced that the transformation of the form of the intertropical convergence zone can influence the process of the formation of tropical cyclones. This idea has been confirmed with the help of mathematical modeling [23] [24] . In particular, it was shown that the origin of a convexity in the configuration of the intertropical convergence zone can lead to the formation of a single cyclonic vortex during the period of about one day, with the cyclonic center being close to the southern edge of the initial intertropical convergence zone [23] . Moreover, the results of mathematical modeling have indicated that the origin of a convexity of the intertropical convergence zone, having the specific forms, can lead to the formation of not only a single cyclonic vortex but also a cyclonic-anticyclonic pair [23] and pair of cyclonic vortices [24] , during the period not longer than three days. It can be noted that the results of observation of the Earth’s atmosphere indicated a simultaneous origin of twin tropical cyclones sometimes [30] .
In the present study, simulations are performed for the case when the three-dimensional simulation domain is intersected by an intertropical convergence zone in the west-east direction. It was supposed that, at the initial moment, the intertropical convergence zone contains two convexities in the north direction, with the deviations achieving a value of a few hundreds of kilometers. The initial form of the intertropical convergence zone may be easy seen from Figure 1, where it is like a light curved band. The time evolution of model parameters was nu- merically simulated using the mathematical model during the period of about four days. The results of time-depen- dent modeling are shown in Figures 2-4.
Figure 1. The distribution of horizontal component of the air velocity (m/s) at the altitude of 600 m , assigned at the initial moment. The degree of shadowing of the figure indicates the module of the velocity in m/s.
Figure 2. The distribution of horizontal component of the air velocity (m/s) at the altitude of 600 m , computed 20 hours after the beginning of calculations. The degree of shadowing of the figure indicates the module of the velocity in m/s.
Figure 3. The distribution of horizontal component of the air velocity (m/s) at the altitude of 600 m , computed 50 hours after the beginning of calculations. The degree of shadowing of the figure indicates the module of the velocity in m/s.
Figure 4. The distribution of horizontal component of the air velocity (m/s) at the altitude of 600 m , computed 90 hours after the beginning of calculations. The degree of shadowing of the figure indicates the module of the velocity in m/s.
The results of simulation indicate that, in the course of time, the initial distribution of horizontal component of the air velocity was considerably transformed. In a moment of 20 hours after the beginning of calculations, a pair of tropical cyclonic vortices arose. Their centers are close to the southern edge of the initial intertropical convergence zone. In a moment of 50 hours after the beginning of calculations, these cyclonic vortices have moved in the western direction for about 10 degrees. Simultaneously, the third cyclonic vortex arose, with its center being close to the southern edge of the initial intertropical convergence zone. All arisen cyclonic vortices have moved in the western direction. In a moment of 90 hours after the beginning of calculations, the displacement of third cyclonic vortex is about 6 degrees. The horizontal wind velocity in the cyclones can achieve values of 15 - 20 m/s in the course of time. The maximum wind velocities within the vortices are reached approximately 20 h after their origins, and then they begin to decrease slowly. The radii of these three cyclones are about 800 km.
The simulation results indicate that a key factor in the modeled formation of the triplet of tropical cyclonic vortices is the origin of convexities in the configuration of the intertropical convergence zone. The origin of these convexities leads to beginning of instability of stream air flow. This instability leads to considerable transformation of the wind field. As a consequence, the triplet of tropical cyclonic vortices arises in the lower atmosphere in the course of time. In addition to that, the initial intertropical convergence zone is broken down.
4. Summary and Concluding Remarks
In earlier studies by the authors of the present work, the idea has been advanced that the transformation of the shape of the intertropical convergence zone can influence the process of the formation of tropical cyclones [23] [24] . It was shown that the origin of a convexity of the intertropical convergence zone, having the specific forms, can lead to the formation of not only a single cyclonic vortex but also a pair of large-scale vortices.
The present work is the continuation of the investigation of the initial stage of the origin of large-scale vortices at tropical latitudes. For this investigation, a regional non-hydrostatic mathematical model of the wind system of the lower atmosphere, developed earlier in the Polar Geophysical Institute, is utilized. The model is based on the numerical solution of the system of transport equations containing the equations of continuity for air and for the total water content in all phase states, momentum equations for the zonal, meridional, and vertical components of the air velocity, and energy equation. The model produces three-dimensional distributions of the atmospheric parameters in the height range from 0 to 15 km over a limited region of the Earth's surface. Simulations are per- formed for the case when this region is intersected by the intertropical convergence zone having the specific configuration. It was supposed that, at the initial moment, the intertropical convergence zone contains two con- vexities, having the longitudinal dimension of about 1400 km and deviations in the north direction, achieving a value of a few hundreds of kilometers.
The simulation results indicated that the twin tropical cyclones were formed during the period of about 20 hours. Their centers are close to the southern edge of the initial intertropical convergence zone. Besides, in a moment of approximately 50 hours after the beginning of calculations, third tropical cyclone arose whose center is close to the southern edge of the initial intertropical convergence zone, too. The arisen triplet of tropical cyc- lonic vortices has moved in the western direction. The horizontal wind velocity in the cyclones can achieve val- ues of 15 - 20 m/s in the course of time. The radii of these three cyclones are about 800 km.
The simulation results have shown that the cause for the formation of tropical large-scale vortices in the vicinity of the intertropical convergence zone is a rise of instability of stream air flow present in this zone. The cause for the rise of this instability is the origin of the convexities in the configuration of the intertropical convergence zone. This instability leads to considerable transformation of the air flow. As a result, the intertropical convergence zone may be broken and tropical large-scale vortices can be formed in the vicinity of the initial position of the intertropical convergence zone in the course of time.
It may be expected that the simulation results of the present study, as well of studies by Mingalev et al. [23] [24] , will be useful for tropical cyclones forecasting. The origin of the convexities in the configuration of the intertropical convergence zone, which may be observed with the help of satellite monitoring of the Earth’s atmosphere, is a precursor of the formation of tropical cyclones. Incidentally, depending on the configurations of the convexities one can predict the number of tropical large-scale vortices and the regions of their appearance.
It can be noticed that, according to observations, not each cyclonic vortex, arisen in the lower atmosphere, has the potential to grow up to the long-live large-scale atmospheric vortex. It is known that, sometimes, a vortex, initially arisen in the lower atmosphere, can be attenuated in the course of time and will not achieve a status of the long-live large-scale atmospheric vortex. This peculiarity may take place for the large-scale vortices arisen in the calculations of the present study, with further transformation of the originated vortices depending on en- vironmental conditions, in particular, on the degree of saturation of air by water vapor.
Simulations of the present study were limited by the time interval of approximately four days. Unfortunately, more prolonged time intervals are impossible for the utilized mathematical model because of limited sizes of its simulation domain and owing to tendency of the modeled vortices to move and to abandon the simulation do- main in the course of time.
Acknowledgements
This work was partly supported by Grant No. 13-01-00063 from the Russian Foundation for Basic Research.
References
- Emanuel, K.A. (1986) An Air-Sea Interaction Theory for Tropical Cyclones. Part I: Steady-State Maintenance. Journal of Atmospheric Sciences, 43, 585-605. http://dx.doi.org/10.1175/1520-0469(1986)043<0585:AASITF>2.0.CO;2
- Montgomery, M.T. and Farrell, B.F. (1993) Tropical Cyclone Formation. Journal of Atmospheric Sciences, 50, 285- 310. http://dx.doi.org/10.1175/1520-0469(1993)050<0285:TCF>2.0.CO;2
- Kieu, C.Q. and Zhang, D.-L. (2008) Genesis of Tropical Storm Eugene (2005) from Merging Vortices Associated with ITCZ Breakdowns. Part I: Observational and Modeling Analyses. Journal of Atmospheric Sciences, 65, 3419-3439. http://dx.doi.org/10.1175/2008JAS2605.1
- Mao, J. and Wu, G. (2011) Barotropic Process Contributing to the Formation and Growth of Tropical Cyclone Nargis. Advances in Atmospheric Sciences, 28, 483-491. http://dx.doi.org/10.1007/s00376-010-9190-4
- Ooyama, K. (1969) Numerical Simulation of the Life Cycle of Tropical Cyclones. Journal of Atmospheric Sciences, 26, 3-40. http://dx.doi.org/10.1175/1520-0469(1969)026<0003:NSOTLC>2.0.CO;2
- Montgomery, M.T. and Enagonio, J. (1998) Tropical Cyclogenesis via Convectively Forced Vortex Rossby Waves in a Three-Dimensional Quasigeostrophic Model. Journal of Atmospheric Sciences, 55, 3176-3207. http://dx.doi.org/10.1175/1520-0469(1998)055<3176:TCVCFV>2.0.CO;2
- Li, T., Ge, X., Wang, B. and Zhu, Y. (2006) Tropical Cyclogenesis Associated with Rossby Wave Energy Dispersion of a Preesxisting Typhoon. Part II: Numerical Simulations. Journal of Atmospheric Sciences, 63, 1390-1409. http://dx.doi.org/10.1175/JAS3693.1
- Montgomery, M.T., Wang, Z. and Dunkerton, T.J. (2010) Coarse, Intermediate and High Resolution Numerical Simulation of the Transition of a Tropical Wave Critical Layer to a Tropical Storm. Atmospheric Chemistry and Physics, 10, 10803-10827. http://dx.doi.org/10.5194/acp-10-10803-2010
- Venkatesh, T.N. and Mathew, J. (2010) A Numerical Study of the Role of the Vertical Structure of Vorticity during Tropical Cyclone Genesis. Fluid Dynamics Research, 42, Article ID: 045506. http://dx.doi.org/10.1088/0169-5983/42/4/045506
- Reed, K.A. and Jablonowski, C. (2011) Impact of Physical Parameterizations on Idealized Tropical Cyclones in the Community Atmosphere Model. Geophysical Research Letters, 38, Article ID: L04805. http://dx.doi.org/10.1029/2010GL046297
- Abarca, S.F. and Corbosiero, K.L. (2011) Secondary Eyewall Formation in WRF Simulations of Hurricanes Rita and Katrina (2005). Geophysical Research Letters, 38, Article ID: L07802. http://dx.doi.org/10.1029/2011GL047015
- Xu, Y.M. (2011) The Genesis of Tropical Cyclone Bilis (2000) Associated with Cross-Equatorial Surges. Advances in Atmospheric Sciences, 28, 665-681. http://dx.doi.org/10.1007/s00376-010-9142-z
- Mingalev, I.V. and Mingalev, V.S. (2005) The Global Circulation Model of the Lower and Middle Atmosphere of the Earth with a Given Temperature Distribution. Mathematical Modeling, 17, 24-40. (In Russian)
- Mingalev, I.V., Mingalev, V.S. and Mingaleva, G.I. (2007) Numerical Simulation of Global Distributions of the Horizontal and Vertical Wind in the Middle Atmosphere Using a Given Neutral Gas Temperature Field. Journal of Atmospheric and Solar-Terrestrial Physics, 69, 552-568. http://dx.doi.org/10.1016/j.jastp.2006.10.005
- Mingalev, I.V., Mingalev, O.V. and Mingalev, V.S. (2008) Model Simulation of Global Circulation in the Middle Atmosphere for January Conditions. Advances in Geosciences, 15, 11-16. http://dx.doi.org/10.5194/adgeo-15-11-2008
- Mingalev, I.V., Mingalev, V.S. and Mingaleva, G.I. (2012) Numerical Simulation of the Global Neutral Wind System of the Earth’s Middle Atmosphere for Different Seasons. Atmosphere, 3, 213-228. http://dx.doi.org/10.3390/atmos3010213
- Mingalev, I.V. and Mingalev, V.S. (2012) Numerical Modeling of the Influence of Solar Activity on the Global Circulation in the Earth’s Mesosphere and Lower Thermosphere. International Journal of Geophysics, 2012, Article ID: 106035, 15 pages. http://dx.doi.org/10.1155/2012/106035
- Mingalev, I., Mingaleva, G. and Mingalev, V. (2013) A Simulation Study of the Effect of Geomagnetic Activity on the Global Circulation in the Earth’s Middle Atmosphere. Atmospheric and Climate Sciences, 3, 8-19. http://dx.doi.org/10.4236/acs.2013.33A002
- Belotserkovskii, O.M., Mingalev, I.V., Mingalev, V.S., Mingalev, O.V. and Oparin, A.M. (2006) Mechanism of the Appearance of a Large-Scale Vortex in the Troposphere above a Nonuniformly Heated Surface. Doklady Earth Sci- ences, 411, 1284-1288. http://dx.doi.org/10.1134/S1028334X06080277
- Belotserkovskii, O.M., Mingalev, I.V., Mingalev, V.S., Mingalev, O.V., Oparin, A.M. and Chechetkin, V.M. (2009) For- mation of Large-Scale Vortices in Shear Flow of the Lower Atmosphere of the Earth in the Region of Tropical Latitudes. Cosmic Research, 47, 466-479. http://dx.doi.org/10.1134/S0010952509060033
- Mingalev, I.V., Orlov, K.G. and Mingalev, V.S. (2012) A Mechanism of Formation of Polar Cyclones and Possibility of Their Prediction Using Satellite Observations. Cosmic Research, 50, 160-169. http://dx.doi.org/10.1134/S0010952512010066
- Mingalev, I.V., Orlov, K.G. and Mingalev, V.S. (2014) A Modeling Study of the Initial Formation of Polar Lows in the Vicinity of the Arctic Front. Advances in Meteorology, 2014, Article ID: 970547, 10 pages. http://dx.doi.org/10.1155/2014/970547
- Mingalev, I.V., Astafieva, N.M., Orlov, K.G., Chechetkin, V.M., Mingalev, V.S. and Mingalev, O.V. (2012) Numerical Simulation of Formation of Cyclone Vortex Flows in the Intertropical Zone of Convergence and Their Early Detection. Cosmic Research, 50, 233-248. http://dx.doi.org/10.1134/S0010952512020062
- Mingalev, I.V., Astafieva, N.M., Orlov, K.G., Mingalev, V.S., Mingalev, O.V. and Chechetkin, V.M. (2013) A Simulation Study of the Formation of Large-Scale Cyclonic and Anticyclonic Vortices in the Vicinity of the Intertropical Convergence Zone. ISRN Geophysics, 2013, Article ID: 215362, 12 pages. http://dx.doi.org/10.1155/2013/215362
- Mingalev, V.S. (1993) Transport Equations for the Upper Atmosphere in a Rotating Reference Frame. Geomagnetism and Aeronomy, 33, 106-112. (Russian Issue)
- Mingalev, V.S., Mingalev, I.V., Mingalev, O.V., Oparin, A.M. and Orlov, K.G. (2010) Generalization of the Hybrid Monotone Second-Order Finite Difference Scheme for Gas Dynamics Equations to the Case of Unstructured 3D Grid. Computational Mathematics and Mathematical Physics, 50, 877-889. http://dx.doi.org/10.1134/S0965542510050118
- Broccoli, A.J., Dahl, R.A. and Stouffer, R.J. (2006) Response of the ITCZ to Northern Hemisphere Cooling. Geophysical Research Letters, 33, Article ID: L01702. http://dx.doi.org/10.1029/2005GL024546
- Fedorov, A., Barreiro, M., Boccaletti, G., Pacanowski, R. and Philander, S.G. (2007) The Freshening of Surface Waters in High Latitudes: Effects on the Thermohaline and Wind-Driven Circulations. Journal of Physical Oceanography, 37, 896-907. http://dx.doi.org/10.1175/JPO3033.1
- Chiang, J.C.H. and Friedman, A.R. (2012) Extratropical Cooling, Interhemispheric Thermal Gradients, and Tropical Climate Change. Annual Review of Earth and Planetary Sciences, 40, 383-412. http://dx.doi.org/10.1146/annurev-earth-042711-105545
- Chen, T.C., Tsay, J.D., Yen, M.C. and Cayanan, E.O. (2010) Formation of the Philippine Twin Tropical Cyclones during the 2008 Summer Monsoon Onset. Weather and Forecasting, 25, 1317-1341. http://dx.doi.org/10.1175/2010WAF2222395.1







