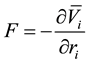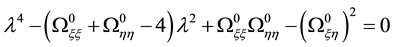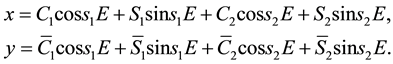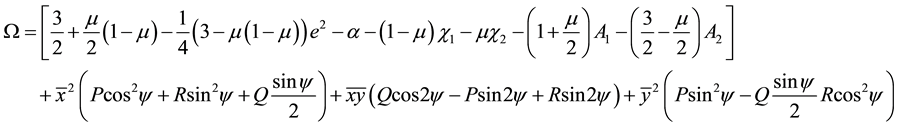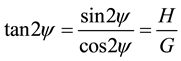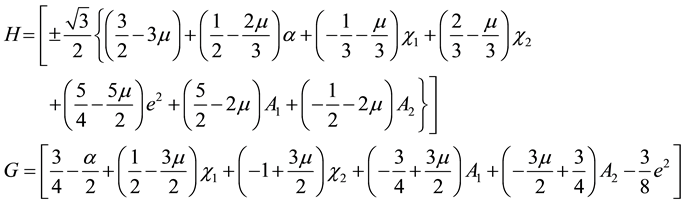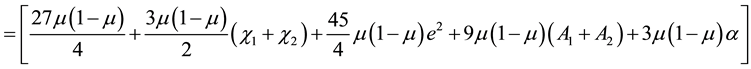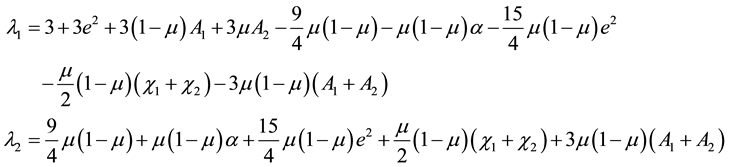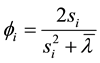International Journal of Astronomy and Astrophysics
Vol.04 No.04(2014), Article ID:52771,14 pages
10.4236/ijaa.2014.44061
Periods, Eccentricities and Axes around L4,5 in the ER3BP under Radiating and Oblate Primaries
Aishetu Umar, Jagadish Singh
Department of Mathematics, Faculty of Science, Ahmadu Bello University, Zaria, Nigeria
Email: umaraishetu33@yahoo.com, jgds2004@yahoo.com
Academic Editor: Luigi Maxmilian Caligiuri, University of Calabria, Italy
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 17 October 2014; revised 12 November 2014; accepted 7 December 2014
ABSTRACT
In the framework of the elliptic restricted three-body problem, using a semi-analytic approach, we investigate the effects of oblateness, radiation and eccentricity of both primaries on the periodic orbits around the triangular Lagrangian points of oblate and luminous binary systems. The frequencies of the long and short orbits of the periodic motion are affected by the oblateness and radiation of both primaries, so are their eccentricities, semi-major and semi-minor axes.
Keywords:
Celestial Mechanics, Periods, Eccentricities, Axes, Triangular Points

1. Introduction
There exist five co-planar equilibrium points in the restricted three-body problem (R3BP), three collinear with the primaries (collinear points) and two, form equilateral triangles with the line (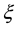 -axis) joining the primaries. The collinear points are generally unstable, while the triangular points are conditionally stable. As a result of rotational motion, long and short periodic orbits exist around these points. The shapes, orientation and sizes of the orbits are determined by the eccentricities, inclination and the semi-major axes of the orbits. Let us briefly recall that the R3BP consists of two massive bodies (primaries) moving in orbits (circular or elliptic) around their common barycenter and a third body of negligible mass being influenced, but not influencing them. A typical example of the ER3BP is the motion of an asteroid under the gravitational attraction of the Sun and Jupiter. The solution to this type of problem which has been developed over the centuries from [1] -[6] and others, forms the basis of the study of the dynamics of celestial bodies, from the computation of the ephemerides to the recent advances in flight dynamics.
-axis) joining the primaries. The collinear points are generally unstable, while the triangular points are conditionally stable. As a result of rotational motion, long and short periodic orbits exist around these points. The shapes, orientation and sizes of the orbits are determined by the eccentricities, inclination and the semi-major axes of the orbits. Let us briefly recall that the R3BP consists of two massive bodies (primaries) moving in orbits (circular or elliptic) around their common barycenter and a third body of negligible mass being influenced, but not influencing them. A typical example of the ER3BP is the motion of an asteroid under the gravitational attraction of the Sun and Jupiter. The solution to this type of problem which has been developed over the centuries from [1] -[6] and others, forms the basis of the study of the dynamics of celestial bodies, from the computation of the ephemerides to the recent advances in flight dynamics.
It is a well-known fact that when at least one of the primary bodies is a source of radiation, the classical restricted three-body problem fails to adequately discuss the motion of the infinitesimal body. Radzievsky [7] was the first to circumvent this inadequacy by formulating the photogravitational CR3BP in the cases of the Sun- Planet-Particle and Galaxy Kernel-Sun-Particle. The photogravitational restricted three-body problem models adequately, the motion of a particle of a gas-dust cloud which is in the field of two gravitating and radiating stars. The summary action of gravitational and light repulsive forces may be characterized by the mass reduction factor q. The effect of radiation pressure(s) has been the subject of many studies. The existence and stability of equilibrium points were studied by [8] and [9] in the case when only one body radiates, while [10] - [26] in the cases when both bodies are luminous. Also, Das et al. [10] examined numerically the effect of radiation on the stability of retrograde trajectories around Jupiter and the smaller of the primaries in RW-Monocerotis and Kruger- 60. They found a reduction of the size of the region of stability around the binaries due to third order resonances. The double stellar systems form a considerable part of all stellar systems; as a result, the motion of a particle in their neighborhood may be of particular interest. Lastly, [23] investigated the motion of a dust particle in orbit with a dark oblate, degenerate primary and a stellar secondary companion moving in elliptic orbits around their common centre of mass.
The classical restricted three-body problem considers the bodies to be strictly spherical, but in the solar (e.g., Earth, Jupiter and Saturn) and stellar (e.g., Achernar, Alfa Arae, Regulus, VFTS 102, Vega and Altair) systems, some planets and stars are sufficiently oblate to justify the inclusion of oblateness in the study of motion of celestial bodies. Therefore, [19] , [23] - [35] have included oblateness and/or radiation of one or both primaries in their communications. Taking account of the oblateness of the Earth, Ammar et al. [35] have conducted an analytic study of the motion of a satellite and solved the equations of the secular variations in a closed form, while Abouelmagd [34] analyzed the effect of oblateness of the more massive primary up to J4 in the planar CR3BP and proved that the positions and stability of the triangular points are affected by this perturbation.
The orbits of most celestial and stellar bodies are elliptic rather than circular; as a result, the study of the elliptic restricted three-body problem (ER3BP) can have significant effects. When the primaries’ orbit is elliptic, a nonuniformly rotating-pulsating coordinate system is commonly used. These new coordinates have the felicitous property that, the positions of the primaries are fixed; however, the Hamiltonian is explicitly time-dependent [5] . Such an oscillating coordinate system has been introduced by using the variable distance between the primaries as a unit of length of the system by which distances are divided. Several studies [23] - [26] , [36] - [42] and [43] have examined the influence of the eccentricity of the orbits of the primary bodies with or without radiation pressure(s). Zimovshchikov and Tkhai [39] established the conditions of stability of the collinear and triangular points for various values of the eccentricity of the Keplerian orbits and the mass ratio of the primary bodies. Finally, Singh and Umar [23] - [26] considering both luminous primaries to be oblate spheroids as well investigated the existence of triangular, collinear and the out of plane equilibrium points in the ER3BP respectively.
A vast number of researches [44] - [52] have been conducted on periodic orbits in the R3BP under various considerations. The consideration of the primaries as either point masses or spherical in shape may leave out a good number of practical problems. This is as a result of the fact that most celestial and stellar bodies are axisymmetric and their orbits are elliptic. The re-entry of artificial satellites and the minimization of station keeping have shown the importance of periodic orbits. The existence of two families of periodic motions near the Lagrangian solutions in the plane CR3BP was shown for arbitrary values of the parameter μ by Charlier [44] and Plummer [45] , while Sarris [36] studied the families of symmetric-periodic orbits in the three-dimensional elliptic problem with a variation of the mass ratio μ and the eccentricity e. Khanna and Bhatnagar [22] , [49] and [53] have studied the long and short periodic orbits around the Lagrangian point(s). Also, Mittal et al. [32] in examining periodic orbits, determined periodic orbits for different values of the mass parameter μ, energy constant h, and oblateness factor A. Beevi and Sharma [52] and Abdouelmagd and El-Shaboury [54] explored the effect of the oblateness of Saturn on the periodic orbits and the regions of quasi-periodic motion around both primaries in the Saturn-Titan system and combined effects of oblateness and radiation on periodic orbits in the circular framework of the restricted three-body problem respectively.
In this communication, we investigate in the elliptic framework the long and short periodic orbits around the triangular points when both primary bodies emit light energy simultaneously and are oblate spheroids as well. The analytic results obtained are applied to the binary systems of mass ratio 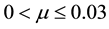 and to Algol.
and to Algol.
The paper is organized as follows: Section 2 provides the equations of motion for the system under investigation; Section 3 computes the long and short periodic orbits and Section 4 describes the eccentricities, semi-ma- jor and semi-minor axes; while Sections 5 & 6 are the numerical analysis and conclusion respectively.
2. Equations of Motion
2.1. Force Due to Radiation Pressure
The radiation pressure force 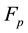 acts opposite to the gravitational attraction force
acts opposite to the gravitational attraction force 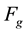 and changes with distance by the same law, this force tends to reduce the effective mass of a particle. The resulting force on the particle is given by
and changes with distance by the same law, this force tends to reduce the effective mass of a particle. The resulting force on the particle is given by
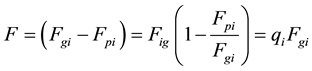
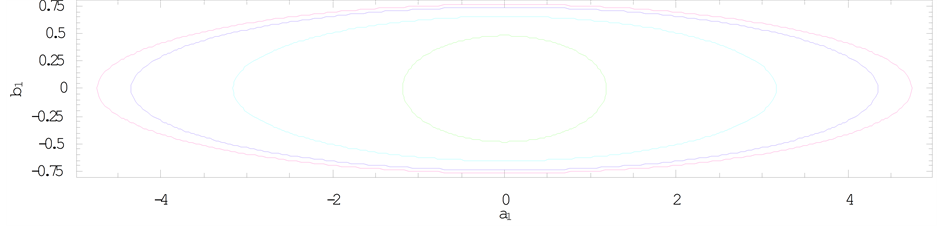
where , a constant for a given particle, is the mass reduction factor. We denote the radiation factors as
, a constant for a given particle, is the mass reduction factor. We denote the radiation factors as

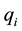 for the bigger and smaller primaries such that
for the bigger and smaller primaries such that . So that instead of mass
. So that instead of mass 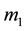 and
and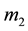 , we have
, we have 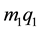 and
and 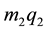 in the force function.
in the force function.
2.2. Force Due to Oblateness
The force due to oblateness of the primaries of masses 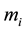
 is given by [55] as,
is given by [55] as,
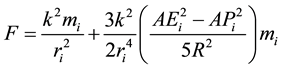 ,
,
where 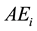

Let 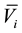
Equating their right hand sides, and then integrating with respect to 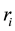

Thus, the equations of motion of the test particle are presented here in a dimensionless-rotating-pulsating coordinate system as:
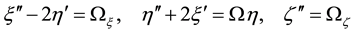
with the force function
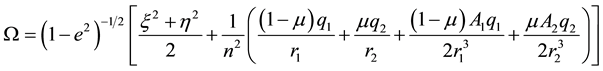
The mean motion, 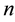
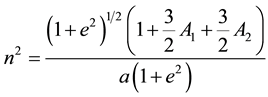
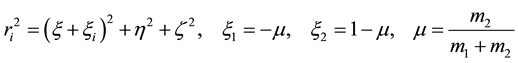
with, 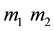
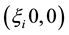
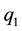
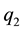
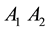
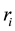

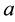
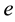
3. Periodic Orbits
The triangular Lagrangian points 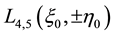

We give these points a small displacement 
The superscript 0 indicate that the partial derivatives are to be evaluated at the equilibrium points


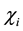
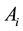
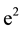
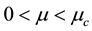
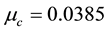
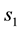

where
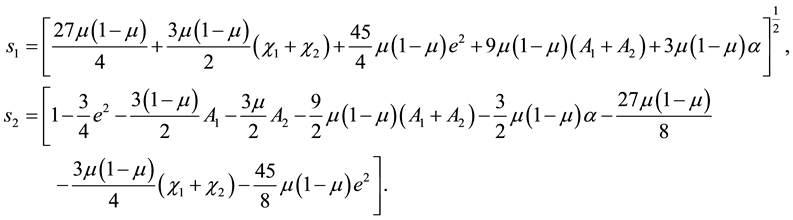
and
The terms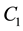
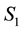
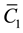
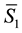
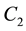
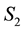
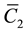
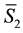


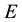
4. Elliptic Orbits
The function 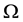
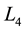
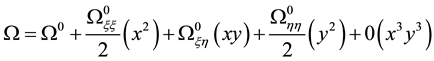
Which is a quadratic form in 
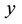

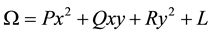
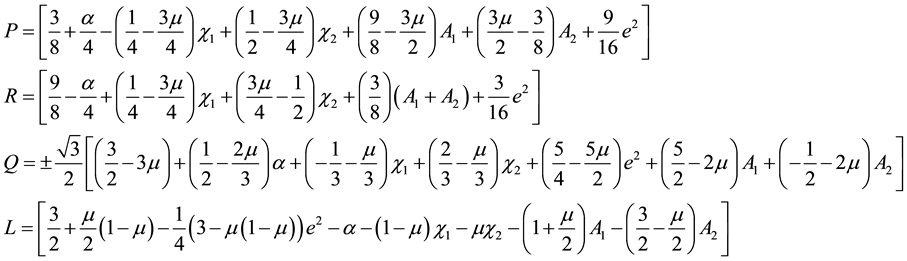
Using the transformation,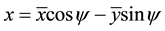
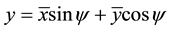
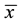
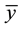
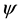
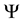
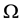
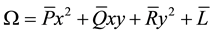
where

But
where
5. Eccentricities of the Ellipses
The function around the triangular point is given by Equation (7), but, 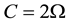
The determinant of which is
The characteristic equation of the associated matrix is thus
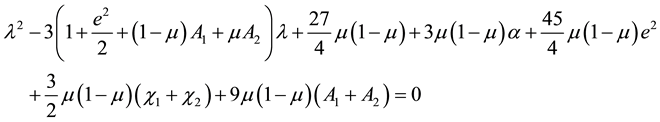
The roots are
The eccentricities of the ellipses are given by (Szebehely 1967)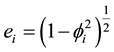
where 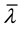
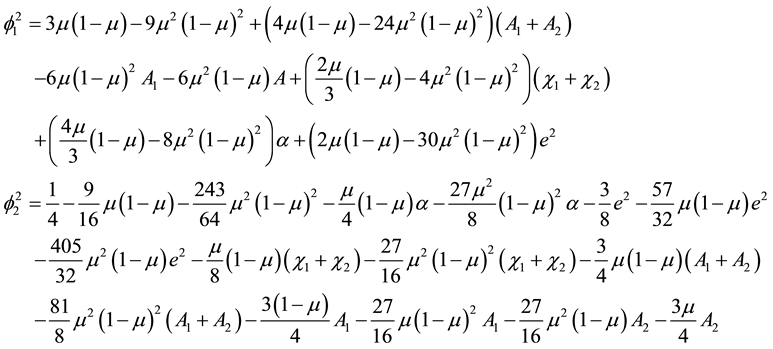
And therefore,
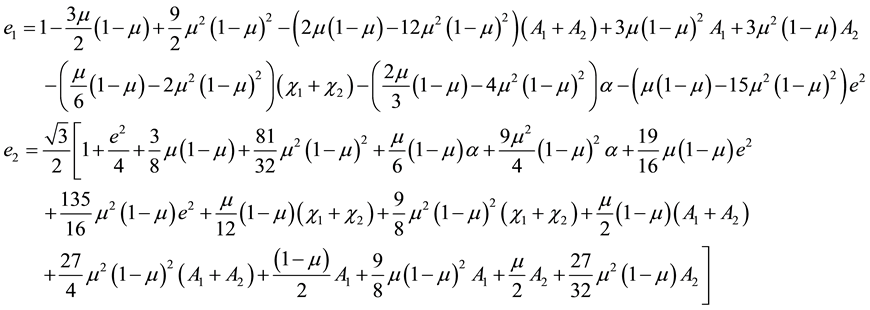
Semi-Major and Semi-Minor Axes
The semi-major and semi-minor axes of the periodic orbits are given by
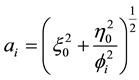


(13)
and

6. Numerical Analysis
Following Singh and Umar [24] , [in which the stability of triangular points for the problem under consideration was examined for the binary systems, Achird (eta Cassiopeia, Luyten 726-8, Alpha Centaurus AB, Kruger 60 1 and Xi Bootis] we compute the frequencies of the long and short periodic orbits, their eccentricities, semi-major and semi-minor axes using Equations (6), (12), (13) & (14) and present them in Table 1 for some assumed values of oblateness, radiation pressures, semi-major axis and eccentricities of the primaries for binary systems with mass ratio in the range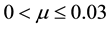
Table 1. Frequencies of the long and short periods, their eccentricities, semi-major and semi-minor axes for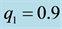
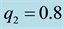
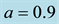
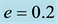
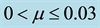
Table 2. Effect of the eccentricity of the primaries on the frequencies of the long and short periods, their eccentricities, semi- major and semi-minor axes and the roots of (10), for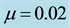
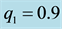
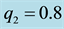
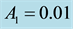
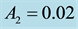
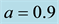
Table 3. Effect of semi-major axis of the primaries on the frequencies of the long and short periods, their eccentricities, semi-major and semi-minor axes for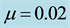
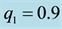
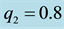
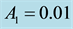
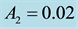
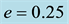
Table 4. Effect of radiation pressure of the bigger primary on the frequencies of the long and short periods, their eccentricities, semi-major and semi-minor axes for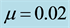
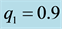

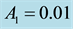
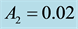
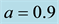
Table 5. Frequencies of the long and short periods, their eccentricities, semi-major and semi-minor axes of the binary System Algol, for assumed oblateness and a = 0.999; e = 0.2.
shown in Figures 1-9. Figures 1-8 show the effects of the semi-major axis of the elliptic orbits (Table 3), eccentricity (Table 2), oblateness and radiation pressures (Table 4) of the primaries on the long and short periods respectively, while the effect of mass ratio 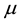
7. Discussion
Table 2 shows clearly the effect of oblateness of the primaries on the long and short periods. The frequency of the long period increases with increase in oblateness while that of the short period decreases. This agrees with [2] in the absence of small perturbations in the Coriolis and centrifugal forces in their case and with 
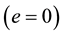
Equation (12) gives the eccentricities of the long and short periods, the eccentricity of the long period increases with oblateness, while that of the short period decreases (Table 2). The eccentricity of the orbits and the effect of oblateness are shown graphically in Figures 1-9 for mass ratio 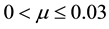
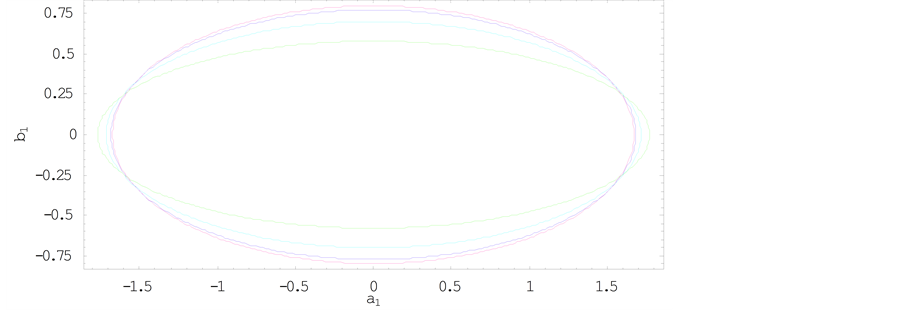
Figure 1. Effect of semi-major axis on the long periodic orbits for μ = 0.02; q1 = 0.9; q2 = 0.8; A1 = 0.01; A2 = 0.02 and e = 0.25.
Figure 2. Effect of semi-major axis on the short periodic orbits for μ = 0.02; q1 = 0.9; q2 = 0.8; A1 = 0.01; A2 = 0.02 and e = 0.25.
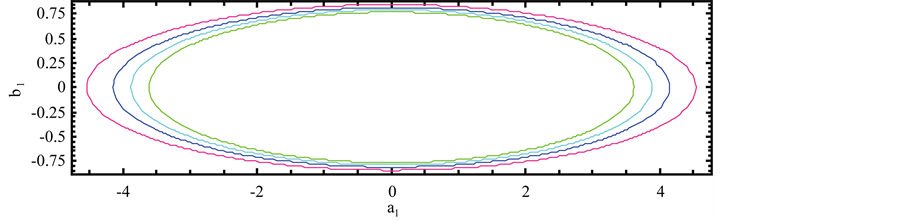
Figure 3. Effect of eccentricity on the long periodic orbits for μ = 0.02; q1 = 0.9; q2 = 0.8; A1 = 0.01; A2 = 0.02 and a = 0.9.
Figure 4. Effect of eccentricity on the short periodic orbits for μ = 0.02; q1 = 0.9; q2 = 0.8; A1 = 0.01; A2 = 0.02 and a = 0.9.
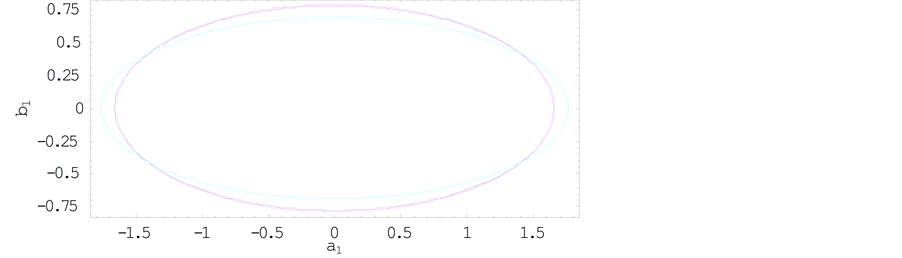
axis, eccentricity and radiation pressure while their sizes reduce with increase in oblateness parameters of both primaries.
Figure 5. Effect of radiation of the bigger primary on the long periodic orbits for μ = 0.03; q2 = 0.8; A1 = 0.01; A2 = 0.02; e = 0.35 and a = 1.2.
Figure 6. Effect of radiation of the bigger primary on the short periodic orbits for μ = 0.03; q2 = 0.8; A1 = 0.01; A2 = 0.02; e = 0.35 and a = 1.2.
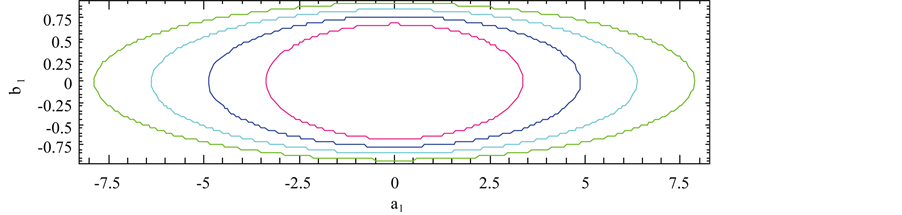
Figure 7. Effect of oblateness on the long periodic orbits for μ = 0.01; q1 = 0.9; q2 = 0.8; e = 0.2 and a = 0.9.
Figure 8. Effect of oblateness on the short periodic orbits for μ = 0.01; q1 = 0.9; q2 = 0.8; e = 0.2 and a = 0.9.
8. Conclusion
The expressions for the frequencies of the long and short periods around the triangular points with their orientations, eccentricities, semi-major and semi-minor axes has been obtained. They have been found to be influ-
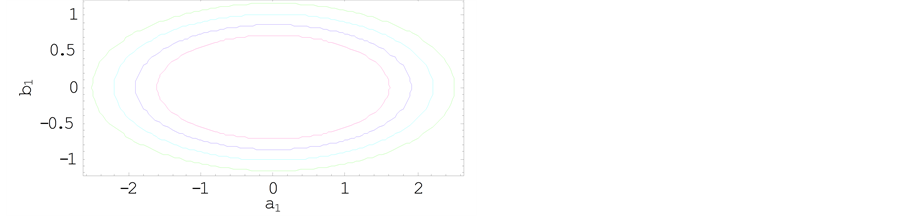
Figure 9. Effect of mass ratio μ in the absence of oblateness on the long periodic orbits for q1 = 0.9; q2 = 0.8; e = 0.2 and a = 0.9.
enced by the eccentricities of the orbits of the primaries, radiation pressures, semi-major axis and oblateness. In the absence of these perturbations, the results are in accordance with [5] .
References
- Lagrange (1772) Collected Works Paris, VI, 229.
- Laplace and Delaunay (1867) Memoire sur la theorie de la Lune, Mem. De l’des Science, 28 and 29.
- Poincare (1892) Les Methodes Nouevelles de la Mechanique ce’leste Guthier villars, Paris, Chap. V, 250. (Published in English in Three Volumes).
- Birkhoff (1927) Dynamical System. American Mathematical Society, New York.
- Szebehely, V.G. (1967) Theory of Orbits. Academic Press, New York.
- Danby, J.M.A. (1988) Fundamentals of Celestial Mechanics. 2nd Edition, Willmann-Bell, Inc., Virginia.
- Radzievskii, V.V. (1950) The Restricted Problem of Three Bodies Taking Account of Light Pressure. Astronomical Journal, 27, 249.
- Chernikov, Yu.A. (1970) The Photo Gravitational Restricted Three Body Problem. Soviet Astronomy―AJ, 14, 176- 181.
- Kunitsyn, A.L. and Perezhogin, A.A. (1978) On the Stability of Triangular Libration Points of the Photo Gravitational Circular Restricted Three-Body Problem. Celestial Mechanics and Dynamical Astronomy, 18, 395-408.
- Schuerman, D.W. (1980) The Restricted Three Body Problem including Radiation Pressure. The Astrophysical Journal, 238, 337-342. http://dx.doi.org/10.1086/157989
- Luk’yanov, L.G. (1984) Lagrangian Solutions in the Photogravitational Restricted Circular Three-Body Problem. Astronomicheskii Zhurnal, 789, 94; Soviet Astronomy, 28, 329-333.
- Luk’yanov, L.G. (1988) On the Family of Libration Points in the Restricted Three-Body Problem. Astronomicheskii Zhurnal, 65, 422, 432; Soviet Astronomy, 32, 6.
- Simmons, J.F.L., McDonald, A.J.C. and Brown, J.C. (1985) The Restricted 3-Body Problem with Radiation Pressure. Celestial Mechanics, 35, 145-187. http://dx.doi.org/10.1007/BF01227667
- Kunitsyn, A.L. and Tureshbaev, A.T. (1985) On the Collinear Libration Points of the Photogravitational Restricted Three-Body Problem. Celestial Mechanics, 35, 105, 112.
- Kunitsyn, A.L. (2000) The Stability of Triangular Libration Points in the Photogravitational Three-Body Problem. Journal of Applied Mathematics and Mechanics, 64, 757-763. http://dx.doi.org/10.1016/S0021-8928(00)00105-2
- Kunitsyn, A.L. (2001) The Stability of Collinear Libration Points in the Photogravitational Three-Body Problem. Journal of Applied Mathematics and Mechanics, 65, 703-706. http://dx.doi.org/10.1016/S0021-8928(01)00075-2
- AbdulRaheem, A. and Singh, J. (2006) Combined Effects of Perturbations, Radiation and Oblateness on the Stability of Equilibrium Points in the Restricted Three-Body Problem. Astronomical Journal, 131, 1880-1885.
- AbdulRaheem, A. and Singh, J. (2008) Combined Effects of Perturbations, Radiation and Oblateness on the Periodic Orbits in the Restricted Three-Body Problem. Astrophysics and Space Science, 317, 9-13. http://dx.doi.org/10.1007/s10509-008-9841-4
- Singh, J. and Ishwar, B. (1999) Stability of Collinear Equilibrium Points in the Generalized Photogravitational Elliptic Restricted Three-Body Problem. Bulletin of the Astronomical Society of India, 27, 415.
- Singh, J. and AbdulKarim, A. (2014) Instability of Triangular Libration Points in the Perturbed Photogravitational R3BP with Poynting-Robertson (P-R) Drag. Astrophysics and Space Science, 351, 473-482. http://dx.doi.org/10.1007/s10509-014-1862-6
- Shankaran, S.J.P. and Ishwar, B. (2011) Out-of-Plane Equilibrium Points and Stability in the Generalized Photogravitational Restricted Three-Body Problem. Astrophysics & Space Science, 332, 115.
- Sharma, R.K., Taqvi, Z.A. and Bhatnagar, K.B. (2001) Existence and Stability of Libration Points in the Restricted Three-Body Problem When the Primaries Are Triaxial Rigid Bodies. Celestial Mechanics and Dynamical Astronomy, 79, 119-133. http://dx.doi.org/10.1023/A:1011168605411
- Singh, J. and Umar, A. (2012) Motion in the Photogravitational Elliptic Restricted Three-Body Problem under an Oblate Primary. The Astronomical Journal, 143, 109-131. http://dx.doi.org/10.1088/0004-6256/143/5/109
- Singh, J. and Umar, A. (2012) On the Stability of Triangular Equilibrium Points in the Elliptic R3BP under Radiating and Oblate Primaries. Astrophysics and Space Science, 341, 349-358. http://dx.doi.org/10.1007/s10509-012-1109-3
- Singh, J. and Umar, A. (2013) On “out of Plane” Equilibrium Points in the Elliptic Restricted Three-Body Problem with Radiating and Oblate Primaries. Astrophysics and Space Science, 344, 13-19. http://dx.doi.org/10.1007/s10509-012-1292-2
- Singh, J. and Umar, A. (2013) Collinear Equilibrium Points in the Elliptic R3BP with Oblateness and Radiation. Advances in Space Research, 52, 1489-1496. http://dx.doi.org/10.1016/j.asr.2013.07.027
- Das, M.K., Narang, P., Mahajan, S. and Yuasa, M. (2009) Effect of Radiation on the Stability of a Retrograde Particle Orbit in Different Stellar Systems. Planetary and Space Science, 57, 836-845. http://dx.doi.org/10.1016/j.pss.2009.02.007
- Sharma, R.K. (1987) The Linear Stability of Libration Points of the Photogravitational Restricted Three-Body Problem When the Smaller Primary Is an Oblate Spheroid. Astrophysics and Space Science, 135, 271-281. http://dx.doi.org/10.1007/BF00641562
- Ishwar, B. and Kushvah, B.S. (2006) Linear Stability of Triangular Equilibrium Points in the Generalized Photogravitational Restricted Three Body Problem with Poynting_Robertson Drag. Journal of Dynamical Systems and Geometric Theories, 4, 79-86. http://dx.doi.org/10.1080/1726037X.2006.10698504
- Tsirogiannis, G.A., Douskos, C.N. and Perdios, E.A. (2006) Computation of the Liapunov Orbits in the Photogravitational RTBP with Oblateness. Astrophysics and Space Science, 305, 389-398. http://dx.doi.org/10.1007/s10509-006-9171-3
- Vishnu Namboori, N.I., Sudheer Reedy, D. and Sharma, R.K. (2008) Effect of Oblateness and Radiation Pressure on Angular Frequencies at Collinear Points. Astrophysics and Space Science, 318, 161-168. http://dx.doi.org/10.1007/s10509-008-9934-0
- Mital, A., Ahmad, I. and Bhatnagar, K.B. (2009) Periodic Orbits in the Photogravitational Restricted Problem with the Smaller Primary an Oblate Body. Astrophysics and Space Science, 323, 65-73. http://dx.doi.org/10.1007/s10509-009-0038-2
- Sahoo, S.K. and Ishwar, B. (2000) Stability of Collinear Equilibrium Points in the Generalized Photogravitational Elliptic Restricted Three-Body Problem. Bulletin of the Astronomical Society of India, 28, 579-586.
- Abouelmagd, E.I. (2012) Existence and Stability of Triangular Points in the Restricted Three-Body Problem with Numerical Applications. Astrophysics and Space Science, 342, 45-53.
- Singh, J. and Haruna, S. (2014) Periodic Orbits around Triangular Points in the Restricted Problem of Three Oblate Bodies. American Journal of Astronomy and Astrophysics, 2, 22-26.
- Sarris, E. (1989) Families of Symmetric-Periodic Orbits in the Elliptic Three-Dimensional Restricted Three-Body Problem. Astrophysics and Space Science, 162, 107-122. http://dx.doi.org/10.1007/BF00653348
- Kumar, V. and Choudry, R.K. (1990) Nonlinear Stability of the Triangular Libration Points for the Photo Gravitational Elliptic Restricted Problem of Three Bodies. Celestial Mechanics and Dynamical Astronomy, 48, 299-317. http://dx.doi.org/10.1007/BF00049387
- Markellos, V.V., Perdios, E. and Labropoulou, P. (1992) Linear Stability of the Triangular Equilibrium Points in the Photogravitational Elliptic Restricted Problem I. Astrophysics and Space Science, 194, 207-213. http://dx.doi.org/10.1007/BF00643991
- Zimovshchikov, A.S. and Tkhai, V.N. (2004) Instability of Libration Points and Resonance Phenomena in the Photogravitational Elliptic Restricted Three-Body Problem. Solar System Research, 38, 155-164. http://dx.doi.org/10.1023/B:SOLS.0000022826.31475.a7
- Ammar, M.K. (2008) The Effect of Solar Radiation Pressure on the Lagrangian Points in the Elliptic Restricted Three-body Problem. Astrophysics and Space Science, 313, 393-408. http://dx.doi.org/10.1007/s10509-007-9709-z
- Kumar, S. and Ishwar, B. (2009) Solutions of Generalized Photogravitational Elliptic Restricted Three-Body Problem. AIP Conference Proceedings, 1146, 456-460. http://dx.doi.org/10.1063/1.3183564
- Kumar, S. and Ishwar, B. (2011) Location of Collinear Equilibrium Points in the Generalized Photogravitational Elliptic Restricted Three-Body Problem. International Journal of Engineering, Science and Technology, 3, 157-162. http://dx.doi.org/10.4314/ijest.v3i2.68143
- Singh, J. and Umar, A. (2014) On Motion around the Collinear Libration Points in the Elliptic Restricted Three-Body Problem with a Bigger Triaxial Primary. New Astronomy, 29, 36-41. http://dx.doi.org/10.1016/j.newast.2013.11.003
- Charlier, C.I. (1899) Die Mechanik des Himmels. Walter de Gryter and Co., Berlin and Leipzig.
- Plummer, H.C. (1901) On Periodic Orbits in the Neighborhood of Centres of Liberation. Monthly Notices of the Royal Astronomical Society, 62, 6.
- Riabov, U.A. (1952) Preliminary Orbits Trojan Asteroids. Soviet Astronomy, 29, 5.
- Elipe, A. and Lara, M. (1997) Periodic Orbits in the Restricted Three-Body Problem with Radiation Pressure. Celestial Mechanics and Dynamical Astronomy, 68, 1-11. http://dx.doi.org/10.1023/A:1008233828923
- Hadjidemetriou, J.D. (1984) Periodic Orbits. Celestial Mechanics, 34, 379-393. http://dx.doi.org/10.1007/BF01235816
- Khanna, M. and Bhatnagar, K.B. (1999) Existence and Stability of Libration Points in the Restricted Three Body Problem When the Smaller Primary Is a Triaxial Rigid Body and the Bigger One an Oblate Spheroid. Indian Journal of Pure and Applied Mathematics, 30, 721-723.
- Perdios, E.A. (2003) Critical Symmetric Periodic Orbits in the Photogravitational Restricted Three-Body Problem. Astrophysics and Space Science, 286, 501-513. http://dx.doi.org/10.1023/A:1026328832021
- Kushvah, B.S., Kishor, R. and Dolas U. (2012) Existence of Equilibrium Points and Their Linear Stability in the Generalized Photogravitational Chermykh-Life Problem with Power-Law Profile. Astrophysics and Space Science, 337, 115-125. http://dx.doi.org/10.1007/s10509-011-0857-9
- Beevi, A. and Sharma, R.K. (2012) Oblateness Effect of Saturn on Periodic Orbits in Saturn-Titan Restricted Three-Body Problem. Astrophysics and Space Science, 340, 245-261. http://dx.doi.org/10.1007/s10509-012-1052-3
- Singh, J. and Begha, J.M. (2011) Stability of Equilibrium Points in the Generalized Perturbed Restricted Three-Body Problem. Astrophysics and Space Science, 331, 511-519. http://dx.doi.org/10.1007/s10509-010-0464-1
- Abouelmagd, E.I. and El-Shaboury, S.M. (2012) Periodic Orbits under Combined Effects of Oblateness and Radiation in the Restricted Problem of Three Bodies. Astrophysics and Space Science, 341, 331-341.
- McCuskey, S.W. (1963) Introduction to Celestial Mechanics. Addison-Wesley, New York.
- Ishwar, B. and Elipe, A. (2001) Secular Solutions at Triangular Equilibrium Point in the Generalized Photogravitational Restricted Three Body Problem. Astrophysics and Space Science, 277, 437-446. http://dx.doi.org/10.1023/A:1012528929233