International Journal of Astronomy and Astrophysics
Vol.4 No.2(2014), Article
ID:47120,5
pages
DOI:10.4236/ijaa.2014.42036
Mass Limit of Neutron Star
Jehangir Ahmad Dar
Inventor at Department of USIC/EDC, University of Kashmir, Hazratbal, Srinagar, India
Email: jahangirahmad63@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 April 2014; revised 15 May 2014; accepted 22 May 2014
ABSTRACT
The mass limit of neutron star has still remained a mystery. The existing Tolman-OppenheimerVolkoff (TOV) equation for calculating the limit always gives different values, by introducing different assumptions and having been predicted like 0.7 Mo, 3.2 Mo, 3.6 Mo, where Mo = 1.98 × 1030 Kg. There is a need of some better technique to adopt other than TOV relation to seek out the value. In this paper, a new relation between the mass 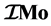 of the collapsing star and its average density ρ′ has been derived and used to calculate the limit of neutron star. The conditions in radii between Schwarz Child’s radius and the actual radius of the collapsing star have been introduced to calculate the mass of star above which it will transform into a black hole and below it to a neutron star. A new constant, JN = 8.53707554 × 1039 N−3/2s−3Kg3 has been proposed with which if we introduce the average density of the collapsing neutron star, its mass limit can be calculated very easily. By putting the most possible mass density, which is the minimum required density for a collapsing star to transform into the black hole, it has been found that the mass limit of neutron star is quite higher than it has been assumed. The definition for black hole has also been re-defined on the basis of said radii conditions.
of the collapsing star and its average density ρ′ has been derived and used to calculate the limit of neutron star. The conditions in radii between Schwarz Child’s radius and the actual radius of the collapsing star have been introduced to calculate the mass of star above which it will transform into a black hole and below it to a neutron star. A new constant, JN = 8.53707554 × 1039 N−3/2s−3Kg3 has been proposed with which if we introduce the average density of the collapsing neutron star, its mass limit can be calculated very easily. By putting the most possible mass density, which is the minimum required density for a collapsing star to transform into the black hole, it has been found that the mass limit of neutron star is quite higher than it has been assumed. The definition for black hole has also been re-defined on the basis of said radii conditions.
Keywords:Black Hole, Neutron Star, Schwarz Child’s Radius Relation, Degeneracy Pressure, Event Horizon, FCC and HCP Lattices and TOV Equation

1. Introduction
Chandra Shaker put an end to the maximum mass limit of white dwarf search and introduced the minimum limit for the neutron star as 1.4 Mo [1] [2] , usually called as Chandra Shaker limit, but what is the limit of neutron star? This is the question which has put all the astronomers and astrophysicists all over the world for the last centuries in a great trouble. The first attempt was put in 1939 by J. Robert Oppenheimer and George Volkoff by using the work of Richard Chace Tolmann, who considered the neutrons in the neutron star as a degenerate Fermi gas [1] [3] [4] . They derived an equation commonly called as the Tolman-Oppenheimer-Volkoff (TOV) equation for deriving the limit of neutron above which the neutron degeneracy fails to restrict the further collapsing of neutron star to form black hole like star [1] .
From the calculations taken by Oppenheimer and Volkoff, they found the mass limit for neutron star to be 0.7 Mo, where Mo is the solar mass [1] [3] [4] . But how is it possible that the white dwarfs has maximum mass limit than the neutron star which is 1.4 Mo? So due to its failure many other calculations were taken by many physicists by considering many another assumptions. One of well known limit yet known is 3.2 Mo, calculated by Rhoades and Remo Ruffini [4] . However, the highest value for the limit of neutron star has been calculated by Nauenberg and Chapline―they calculated it to be 3.6 Mo [1] . Since different assumptions provided different results, therefore, we can say that actual mass limit for neutron star is still a mystery [1] . Also neither the physics behind the neutron star nor the observations match mathematical calculations of assumptions physicists introduce. Really, there is a need of a more accurate calculation that is consistent with the observations. Yet we can only assume that the mass should be between 1.4 Mo to 6 Mo by including observations and the physics behind it as is proposed by some physicists [1] .
But I wonder if a technique fails then why not try for the other new methods and one of such new techniques has been attempted here.
The mathematical formulation of the TOV equation is as under
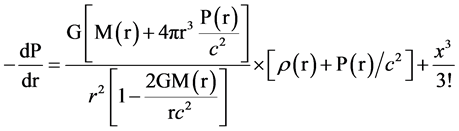
Which can be simply written in terms of Newtonian mechanics, where![]() , as
, as
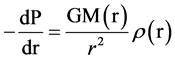
where ρ is mass-energy density, M is the gravitational mass of star, G is gravitational constant and P is pressure. It is clear in the relation that mass (limit) of the neutron star depends on three parameters: r, ρ and P. Different assumptions of these functions have led physicists to calculate different values of the mass limit for neutron star. Also, the neutrons in this TOV technique have been assumed as ideal Fermi gas [1] [3] [4] , as Chandra Shekhar assumed while calculating mass limit for white dwarf, but for neutrons, it is a very poor assumption and unfortunately this assumption has been taken as the heart for all calculations of neutron star limit. As long as we will try to solve the mystery about neutron star limit using the TOV equation, we will never conclude its actual value due to the imporoper assumptions used in its derivation. So there is a severe need of any other method to obtain to seek out the neutron star limit, otherwise waiting for observations [1] .
2. Formulation
We know it clearly that the neutron star is balanced by neutron degeneracy pressure [1] . However if the mass of neutron star is slightly increased such that the gravitational collapsing pressure becomes slightly higher than the neutron degeneracy pressure but lesser than the mass required to overcome the degeneracy pressure possessed by the constituents of neutrons called as quarks, having spin-1/2 implying that they are fermions according to spin-statistics theorem and therefore possess degeneracy pressure as another fermions do. So therefore at such instant of star, there are two possible lattice conditions which it should possess. The two conditions are described below and have been used to find the maximum mass limit of neutron stars.
2.1. Condition 1
The first probable condition is that the neutrons will form closely packed lattice structure. Such closely packed lattice condition was studied on similar sized cannonballs in 1606 for the first time by Thomas Harriot and Johannes Kepler [5] [6] . According to the work done on closely packing similar spheres, there are two simple regular lattices that cannonballs can achieve for very closely packing and to achieve highest average density. They are Face Centered Cubic (FCC) or Cubic Close Packed (CCP) and Hexagonal Close Packed (HCP).
It has been assumed that the neutrons are like cannon balls, so the star with slightly mass higher required to overcome the neutron degeneracy pressure, will have FCC or HCP lattice, such that the neutrons in it are closely packed.
Following are the two diagrams for the unit cells FCC and HCP


HCP unit cell FCC unit cell In both unit cells each sphere is surrounded by 6 other spheres and each with Atomic Packing Factor (APF) of 0.740480489 according to Kepler’s Conjecture Theorem [5] [6] .
The volume possessed by the HCP unit cell is given by the relation
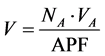
where NA is the number of neutrons present in the unit cell which is the 6 in the case, VA is the volume occupied by each cell?
The mass possessed by the unit cell is equal to the mass of 6 neutrons present in it, therefore the density ρ , of the unit cell which is equal to the average density of the star will be
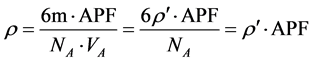
Now consider the star of mass 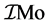 where
where 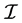 is the constant and Mo is the solar mass. The radius possessed by the star due to the relation
is the constant and Mo is the solar mass. The radius possessed by the star due to the relation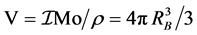 , is
, is
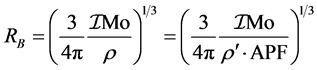 (1)
(1)
where ρ′ is the density of the neutron particle. This relation gives the radius of the star consisting of FCC and HCP lattice.
The boundary of black hole is called the event horizon from which the light rays just fall to escape to infinity or at which the escape velocity for any object gets equal to the speed of light [2] . According to Schwarz child’s relation the radius of event horizon for the black hole is given by
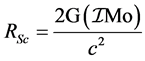 (2)
(2)
Form the definitions of black hole and neutron star we have the condition which states that the star is black hole if the radius of event horizon is equal or greater than its actual radius and it is neutron star if the radius of its event horizon is lesser than its actual radius.
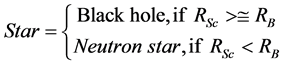
Now the minimum condition for the star, the mass of which is slightly higher to overcome the degeneracy pressure possessed by the neutrons, to be a black hole is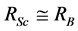 . Or the ratio between RSc and RB is nearly 1.
. Or the ratio between RSc and RB is nearly 1.
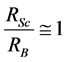
Putting the values from equation І and equation ІІ, we get
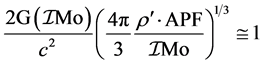
After expanding the relation we arrive on the result that
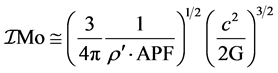 (3)
(3)
This relation gives the mass of the star above which if the mass is slightly increased it will become black hole and if mass is slightly decreased it will become neutron star, in a general term it is the maximum limit of neutron star and minimum limit of black hole.
After putting the constants their value the calculated limit 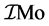 we obtained is 9.26761 Mo approximately. Where
we obtained is 9.26761 Mo approximately. Where 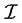 can be calculated as
can be calculated as
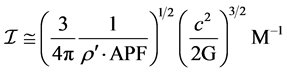
here APF = 0.740480489, c = 2.99792458 × 108 ms−1 and G = 6.67384 × 10−11 Nm2Kg−2. ρ′ is the average density of the unit cell of the star and in this above approximation its value is taken as 2.14450 × 1017 Kgm−3.
2.2. Condition 2
If the shape of neutrons will get deformed from spherical to another shape like cubic as suggested by two Spanish physicists J Lanes Estrada and Gasper Mareno Navarro, in 2011 [7] , such that there will be no voids in packing, then the unit of neutron star will be the neutron itself. Therefore the average density of such star will be equal to the average density of its constituents and the volume of its unit will be equal to the volume possessed by the neutron in its spherical condition.
i.e., ρ = ρ′ with APF = 1, since there are no voids.
Therefore, the equation ІІІ becomes,
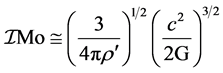 (4)
(4)
By putting the constants their values as before we will observe the mass limit 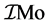 as 7.97488 Mo. Here the value of ρ′ is the density of the neutron particle itself which is 2.897986 × 1017 Kgm−3.
as 7.97488 Mo. Here the value of ρ′ is the density of the neutron particle itself which is 2.897986 × 1017 Kgm−3.
We have calculated two limits of neutron star mass but the actual value will be very near around 9.267 Mo (average density of the unit cell of the star is 2.14450 × 1017 Kgm−3) due to the reason that with increase in pressure it is possible that neutrons will get deform from their spherical shape to other cubic structure providing no voids between cells as suggested by work of J Lanes Estrada and Gasper Mareno Navarro, in 2011 [7] . Such condition is possible inside the core of neutron star. The density above it, i.e. 2.897986 × 1017 Kgm−3 will mean that neutron constituents get collapsed indicating a black hole is in the centre of neutron star, which is not possible! The 2nd condition has been implemented here only to show clear idea of general relation which we will discuss below.
The relation ІV is the general relation between the mass limit of neutron star and its average density ρ′. The equation can also be simply written as
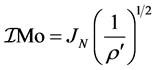 (5)
(5)
where JN is the constant and has value equal to 8.53707554 × 1039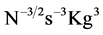 .
.
It has been derived by taking the quantity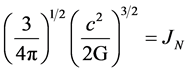 .
.
where the constants have same values as mentioned above. This constant JN is the theoretical discovery derived on the basis of equating actual radius and Schwarz Child’s radius for the star to be either black hole or neutron star. In TOV we were having necessity to include three functions r(R), ρ and P to include in equation to calculate the mass limit, however in the above derived general relation, indicated as equation V above, we have to consider only its density ρ′ and the constant JN include itself all the other information and this is the uniqueness of the derived general relation and the constant, JN.
The specialty about the method concluded in the general relation is that it uses more logical as well as scientific approach than the TOV which work on some inaccurate assumptions.
3. Conclusion
We have proposed a new approach to determine the upper mass limit of neutron star and lower limit of black hole. By introducing a new constant JN, together with the density of neutron star alone, we derived the limit to be 9.267 Mo.
References
- Srinivasan, G. (2002) The Maximum Mass of Neutron Stars. Bulletin of Astronomic Society of India, 30, 523-547.
- Brill, D. (2012) Black Hole Horizons and How They Begin. Astronomical Review.
- Oppenheimer, J.R. and Volkoff, G.M. (1939) Physical Review Letters, 55, 374.
- Rhoades, C.E. and Ruffini, J.R. (1974) Physical Review Letters, 32, 3240. http://dx.doi.org/10.1103/PhysRevLett.32.324
- Hales, T.C. The Kepler Conjecture. http://front.math.ucdavis.edu/math.MG/9811078
- Hales, T.C. (1992) The Spherical Packing Problem. Journal of Computing and Applied Mathematics, 44, 41-76. http://dx.doi.org/10.1016/0377-0427(92)90052-Y
- Llanes-Estrada, F.J. and Navarro, G.M. (2011) Cubic Neutrons.

