International Journal of Astronomy and Astrophysics
Vol.4 No.1(2014), Article ID:43535,9 pages DOI:10.4236/ijaa.2014.41011
Dust-Acoustic Solitary Waves in an Unmagnetized Dusty Plasma with Arbitrarily Charged Dust Fluid and Trapped ion Distribution
O. Rahman, M. D. I. Bhuyan, M. M. Haider, J. Islam
Department of Physics, Mawlana Bhashani Science and Technology University, Tangail, Bangladesh
Email: armanphy203@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 27 October 2013; revised 25 November 2013; accepted 4 December 2013
ABSTRACT
The nonlinear propagation of dust-acoustic (DA) solitary waves in three-component unmagnetized dusty plasma consisting of Maxwellian electrons, vortex-like (trapped) ions, and arbitrarily charged cold mobile dust grain has been investigated. It has been found that, owing to the departure from the Maxwellian ions distribution to a vortex-like one, the dynamics of small but finite amplitude DA waves is governed by a nonlinear equation of modified Korteweg-de Vries (mK-dV) type instead of K-dV. The reductive perturbation method has been employed to study the basic features (phase speed, amplitude, width, etc.) of DA solitary waves which are significantly modified by the presence of trapped ions. The implications of our results in space and laboratory plasmas are briefly discussed.
Keywords:Dust-Acoustic Solitary Waves; Vortex-Like Distribution; Unmagnetized Dusty Plasma

1. Introduction
It is well known from computer simulations [1] -[3] and experiments [4] [5] that plasmas, which are strongly excited by means of the injection of particle beams, are often found to evolve toward a coherent trapped particle state, instead of developing into a turbulent one. The nonlinear behavior of electrostatic waves in a plasma with this trapped state [6] [8] has received considerable attention and been studied by a number of authors in the last few years [6] -[11] . To the best knowledge of the authors, most of these studies [6] -[11] describe the electroacoustic or dust-ion-acoustic waves with static dust particles either negatively or positively charged. But in the case of laboratory experiments and space plasmas we have found both polarities (positive as well as negative charged) of dust particles at the same time. In dust-ion-acoustic waves, ion mass provide the inertia and the restoring force is provided by the pressure of the inertia less electrons. It is possible to move the dust particles with ion. However, Rao et al. [12] first theoretically predicted the existence of dust-acoustic waves (DAWs), in which the inertia is provided by the dust particle mass and the restoring force is provided by the pressures of the inertia less electrons and ions. This pioneering work of Rao et al. [12] initiated a number of laboratory experiments [13] -[15] , where DAWs are observed even with naked eyes because of their appearance on a very long time scale and a large number of theoretical investigations [11] [16] -[23] , which provide different linear and nonlinear features of the DAWs in an unmagnetized weakly coupled dusty plasma. Rao et al. [12] have studied the DA solitary waves in unmagnetized dusty plasma with cold mobile dust particles by using the reductive perturbation method. Motivated by the experimental observations [13] -[15] of such low phase velocity DA waves, Mamun et al. [23] have investigated nonlinear DA waves in a two component unmagnetized dusty plasma and they have considered negatively charged cold mobile dust fluid and Maxwellian distributed ions. Recently, K. Annou and R. Annou have studied the nonlinear propagation of DA solitary waves [24] , they have considered three component unmagnetized dusty plasma consisting inertial charged dust grains, Boltzmannian electrons and non-thermal ions and investigated large-amplitude solitary waves with finite dust temperature incorporating the effect of non-thermal ion distribution by using Sagdeev pseudopotential method [24] . Very recently, we have studied the nonlinear propagation of dust-acoustic solitary waves in an unmagnetized three component dusty plasma consisting of Maxwellian ions, vortex-like electron distribution and arbitrarily charged cold mobile dust [25] . Therefore, in our present work, we have studied the basic properties such as phase speed, amplitude, and width of DA solitary waves containing vortex-like ions, Maxwellian electrons, and arbitrarily charged cold mobile dust grain.
The manuscript is organized as follows. The basic equations governing the plasma system under consideration are presented in Section 2. The mK-dV equation is derived by employing the reductive perturbation method for trapped ion in Section 3. The solitary wave solution of this mK-dV equation is obtained and the properties of these DA solitary structures are discussed in Section 4. Finally, a brief discussion is presented in Section 5.
2. Governing Equation
We consider a three component duty plasma system which consists of Maxwellian electrons, trapped ions, and arbitrarily charged cold mobile dust grains. Thus, at equilibrium, we have , where
, where ,
, 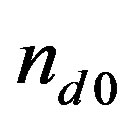 , and
, and 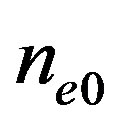 are the unperturbed ion, dust, and electron number densities, respectively,
are the unperturbed ion, dust, and electron number densities, respectively, 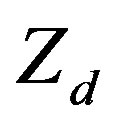 is the number of electrons residing on the dust grains, and j = +1 (–1) for positively (negatively) charged dust grains. The dynamics of such DA waves in one dimensional form whose phase speed is in between dust thermal speed, VTd and ion thermal speed, VTi, i.e.
is the number of electrons residing on the dust grains, and j = +1 (–1) for positively (negatively) charged dust grains. The dynamics of such DA waves in one dimensional form whose phase speed is in between dust thermal speed, VTd and ion thermal speed, VTi, i.e. 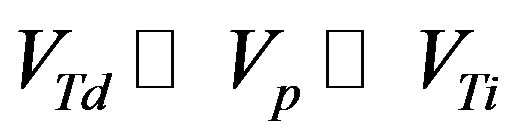 is governed by [23]
is governed by [23]
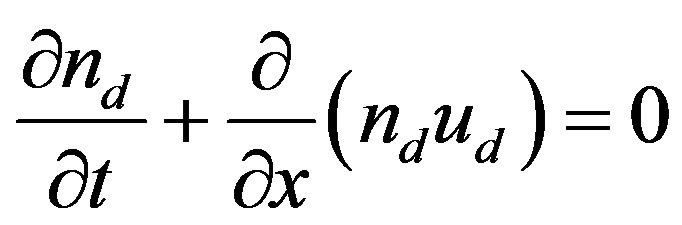 (1)
(1)
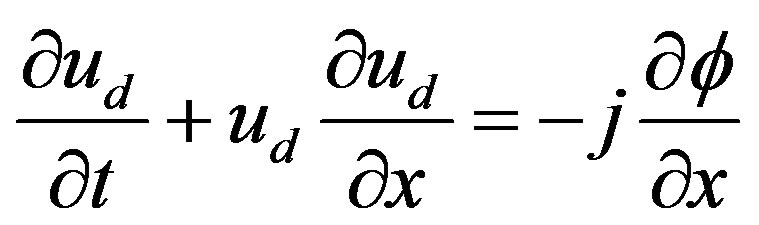 (2)
(2)
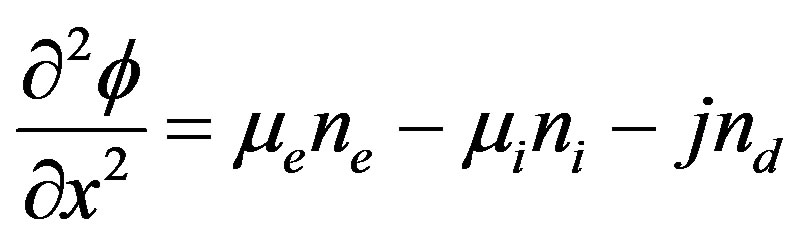 (3)
(3)
where 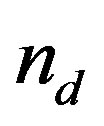 is the dust particle number density normalized to
is the dust particle number density normalized to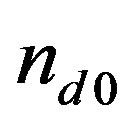 ,
, 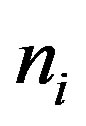 is the ion number density normalized to
is the ion number density normalized to ,
,  is the electron number density normalized to
is the electron number density normalized to ,
, 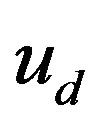 is the speed of dust particle normalized to
is the speed of dust particle normalized to , and
, and 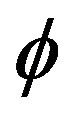 is the electrostatic wave potential normalized to
is the electrostatic wave potential normalized to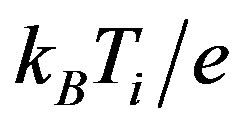 , where Ti is the ion temperature,
, where Ti is the ion temperature, 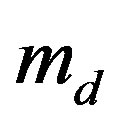 is the mass of arbitrarily charged dust particles, e is the magnitude of the electron charge,
is the mass of arbitrarily charged dust particles, e is the magnitude of the electron charge, 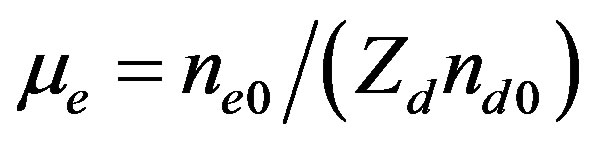 and
and  The time and space variables are in the units of the dust plasma period
The time and space variables are in the units of the dust plasma period 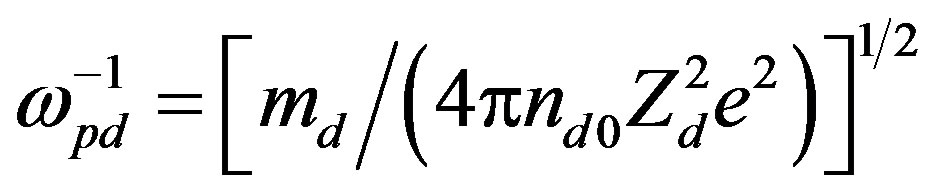 and the Debye length
and the Debye length 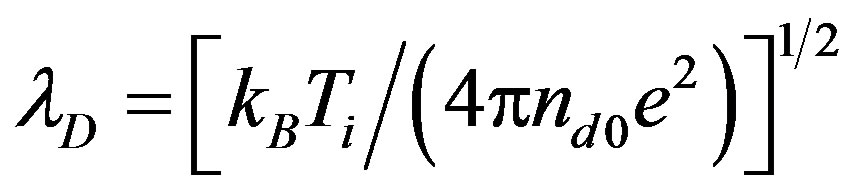 respectively.
respectively.
To model an ion distribution with trapped particles we employ the trapped ion distribution function of Schamel [6] [8] , which solves the ion Vlasov equation. Therefore, we have,
 (4a)
(4a)
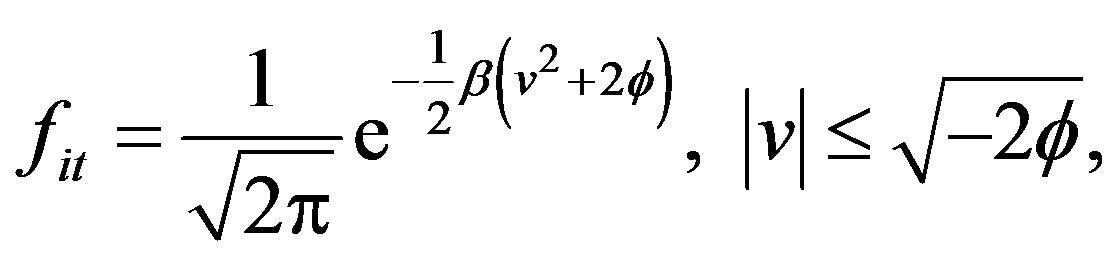 (4b)
(4b)
where  and
and  represents the free ion and trapped ion contribution respectively. It may be noted here that the distribution function, as presented above, is continuous in velocity space and satisfies the regularity requirements for an admissible BGK solution [6] . Here the velocity
represents the free ion and trapped ion contribution respectively. It may be noted here that the distribution function, as presented above, is continuous in velocity space and satisfies the regularity requirements for an admissible BGK solution [6] . Here the velocity  is normalized to the ion thermal velocity
is normalized to the ion thermal velocity 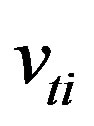 and
and , which is the ratio of free ion temperature Tif to trapped ion temperature Tit, is a parameter determining the number of trapped ions. It has been assumed that the velocity of nonlinear dust-acoustic waves is small in comparison with the ion thermal velocity.
, which is the ratio of free ion temperature Tif to trapped ion temperature Tit, is a parameter determining the number of trapped ions. It has been assumed that the velocity of nonlinear dust-acoustic waves is small in comparison with the ion thermal velocity.
The ion number density 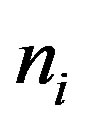 can be obtained by integrating the ion distribution functions over the velocity space. Therefore, we get
can be obtained by integrating the ion distribution functions over the velocity space. Therefore, we get
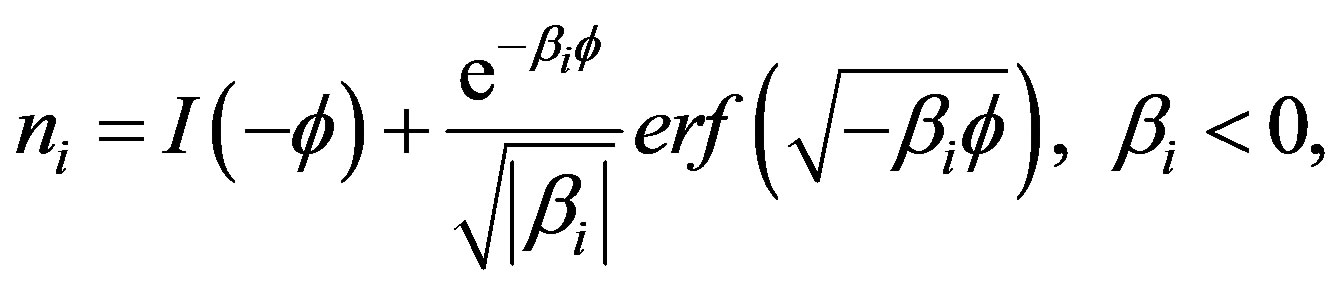 (5a)
(5a)
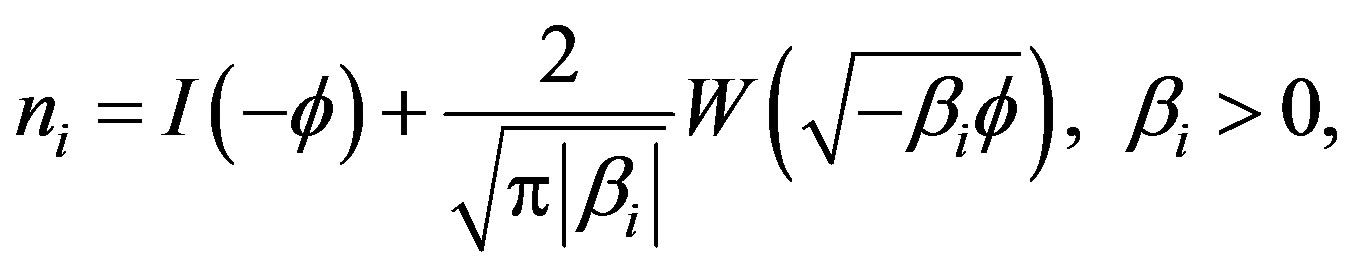 (5b)
(5b)
where,
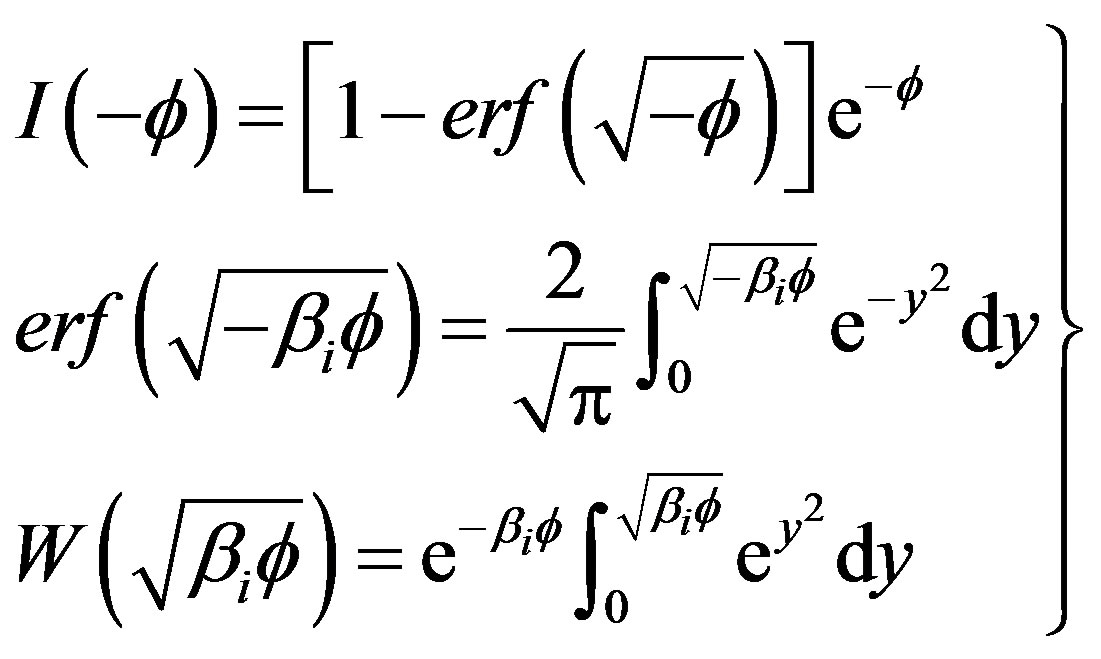 (6)
(6)
If we expand this 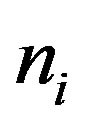 for the the small amplitude limit and keep the terms up to
for the the small amplitude limit and keep the terms up to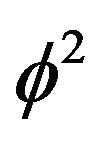 , we found that
, we found that 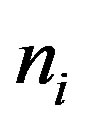 is the same for both βi > 0 and βi < 0 and is finally given by
is the same for both βi > 0 and βi < 0 and is finally given by
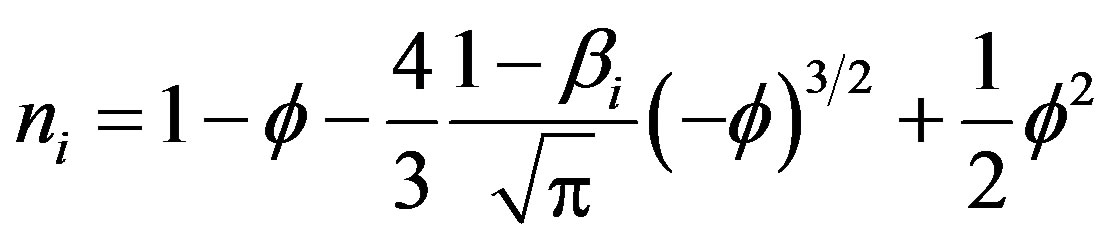 (7)
(7)
where  is a parameter which determines the number of trapped ions. When
is a parameter which determines the number of trapped ions. When 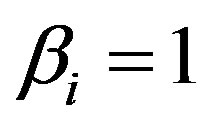 then it represents a Maxwellian distribution, when
then it represents a Maxwellian distribution, when 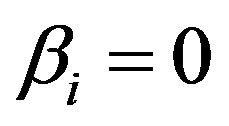 then it represents a flat-topped distribution, and when
then it represents a flat-topped distribution, and when 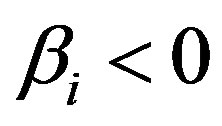 then it represents a trapped electron distribution. It has been assumed that the velocity of nonlinear DA waves is small in comparison with the ion thermal velocity.
then it represents a trapped electron distribution. It has been assumed that the velocity of nonlinear DA waves is small in comparison with the ion thermal velocity.
3. Modified K-dV Equation for Trapped Ions
We now follow the reductive perturbation technique [26] and construct a weakly nonlinear theory for the DA waves with small but finite amplitude, which leads to a scaling of the independent variables through the stretched coordinates [6] [8] as,
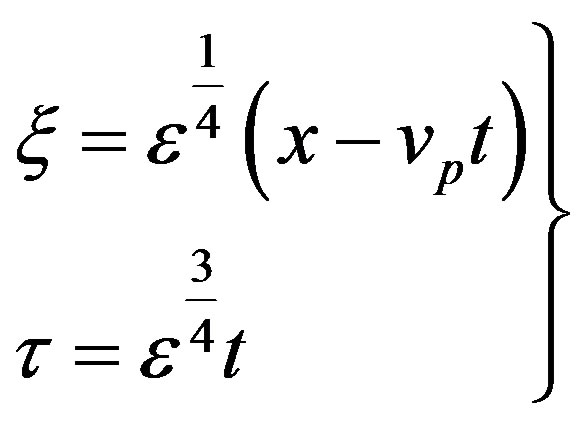 (8)
(8)
where  is a smallness parameter measuring the weakness of the dispersion, vp is the nonlinear wave phase velocity. We can expand the perturbed quantities
is a smallness parameter measuring the weakness of the dispersion, vp is the nonlinear wave phase velocity. We can expand the perturbed quantities 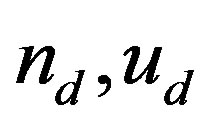 and
and  about their equilibrium values in powers of
about their equilibrium values in powers of , including terms
, including terms ,
,
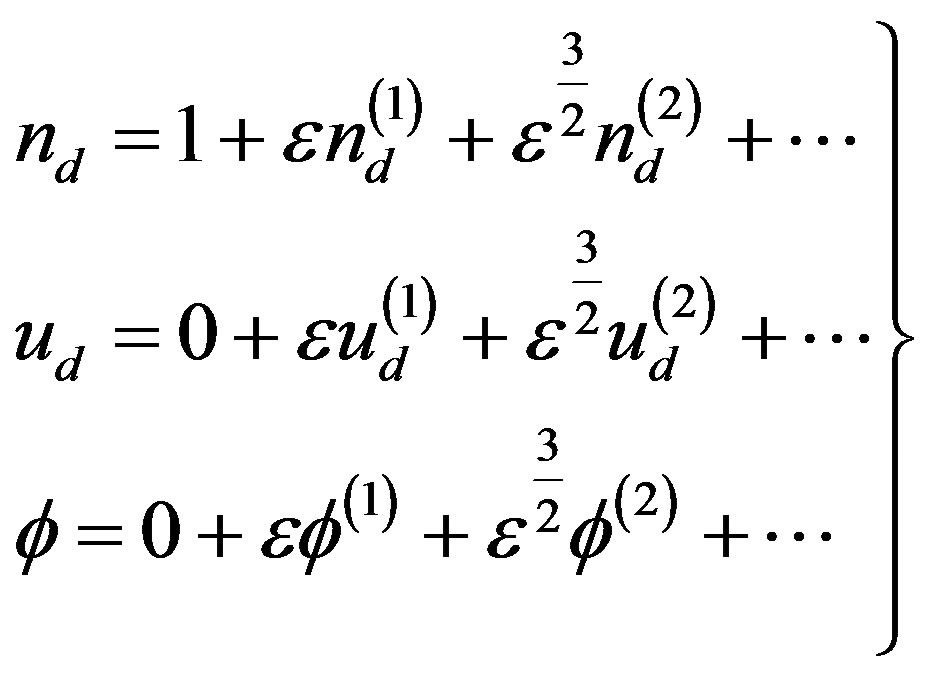 (9)
(9)
Now, substituting Equations (7) - (9) into Equations (1) - (3) one can obtain the lowest order continuity equation, momentum equation, and Poisson’s equation which in turn can be solved as,
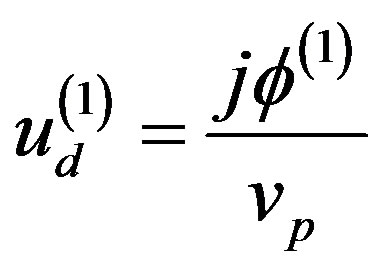 (10)
(10)
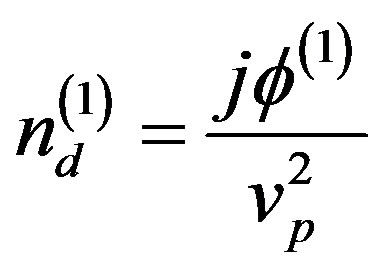 (11)
(11)
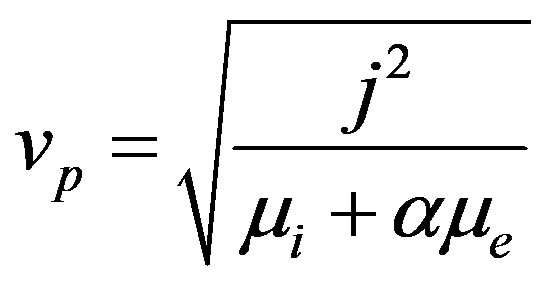 (12)
(12)
where α = Ti/Te i.e., is the ratio between the ion temperature (Ti) and electron temperature (Te.). Therefore, Equation (12) represents the linear dispersion relation for DA waves. It has been found that the phase speed (vp) of DA solitary waves is independent on the polarity of dust particles. Putting the values of Equations (7)-(12) into Equations (1)-(3), we obtain the next higher order equations,
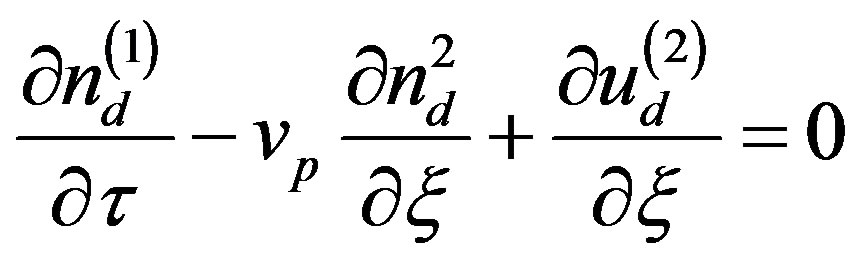 (13)
(13)
 (14)
(14)
 (15)
(15)
Now, using Equations (13)-(15) one can easily eliminate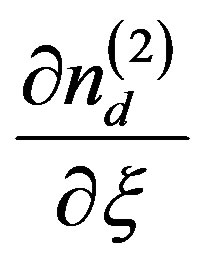 ,
,  and
and 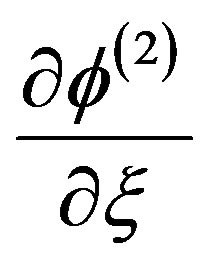 obtain
obtain
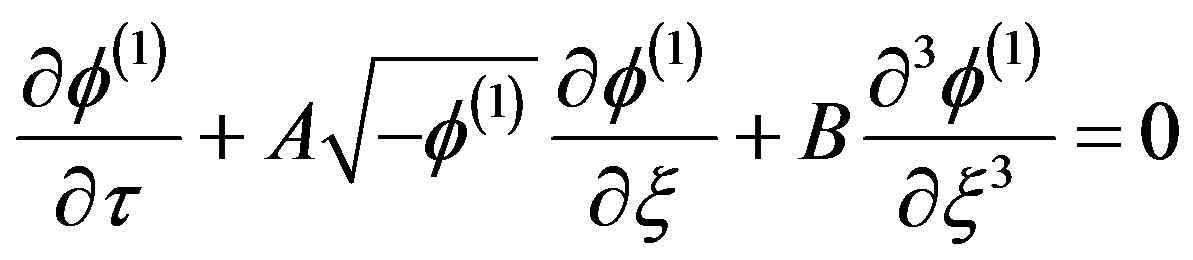 (16)
(16)
where,
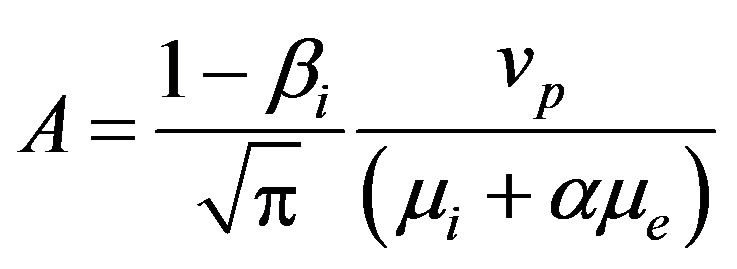 (17)
(17)
 (18)
(18)
Equation (16) is a mK-dV equation for trapped ions, exhibiting a stronger nonlinearity because of the term
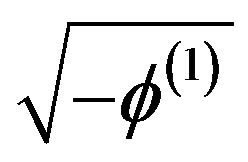 , which arises due to the vortex-like ion distribution.
, which arises due to the vortex-like ion distribution.
4. Solution of mK-dV Equation
The stationary solution of this mK-dV equation can be obtained by transforming the independent variables  and
and  to
to 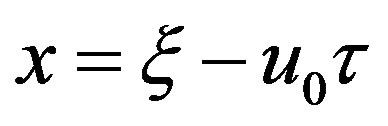 and
and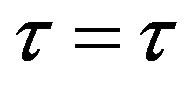 , where
, where 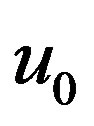 is a constant solitary wave velocity. Now using the appropriate boundary conditions for localized disturbances, viz.
is a constant solitary wave velocity. Now using the appropriate boundary conditions for localized disturbances, viz. 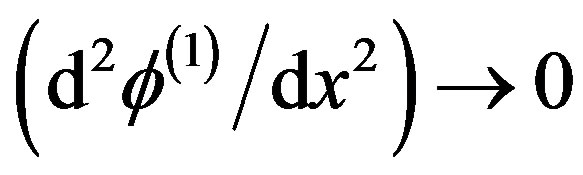
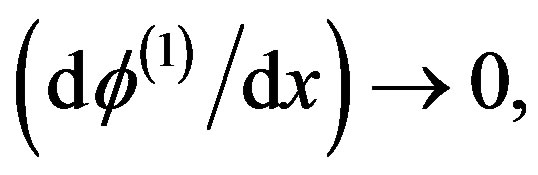
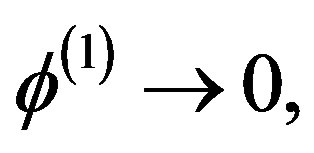 at
at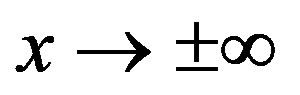 .
.
Thus, one can express the stationary solution of this mK-dV equation as
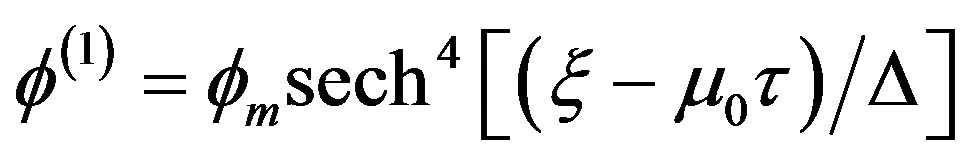 (19)
(19)
where 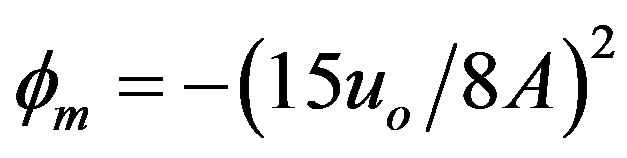 is the amplitude and
is the amplitude and 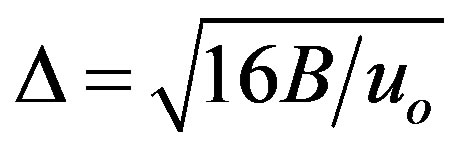 is the width of the solitary waves, respectively.
is the width of the solitary waves, respectively.
It is clear that the amplitude of the solitary waves does not depend on the sign of the constant A. This is due to the effect of the vortex-like ion distribution. Therefore, in the case of trapped ion distribution, the arbitrarily charged dust has no effects on the solitary waves and associated with negative potential only , whereas the width of the solitary waves will have positive value. It has been found that from eqn. (19) as
, whereas the width of the solitary waves will have positive value. It has been found that from eqn. (19) as 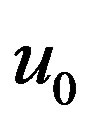 increases, the amplitude
increases, the amplitude  increases while the width (∆) decreases while as
increases while the width (∆) decreases while as  increases, the amplitude decreases for
increases, the amplitude decreases for  (a vortex-like excavated trapped ion distribution) [6] and increases for
(a vortex-like excavated trapped ion distribution) [6] and increases for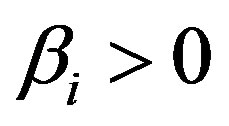 .
.
We have numerically shown how the phase speed (vp), amplitude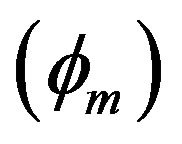 , and the width (∆) of the DA solitary waves changes with various parameters. These are shown in Figures 1-7. Figure 1, which shows the variation of the phase speed (vp) of the solitary waves with
, and the width (∆) of the DA solitary waves changes with various parameters. These are shown in Figures 1-7. Figure 1, which shows the variation of the phase speed (vp) of the solitary waves with 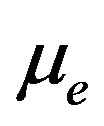 and
and 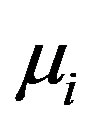 for
for 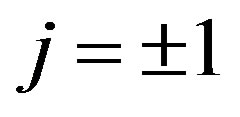 and
and . This figure shows
. This figure shows
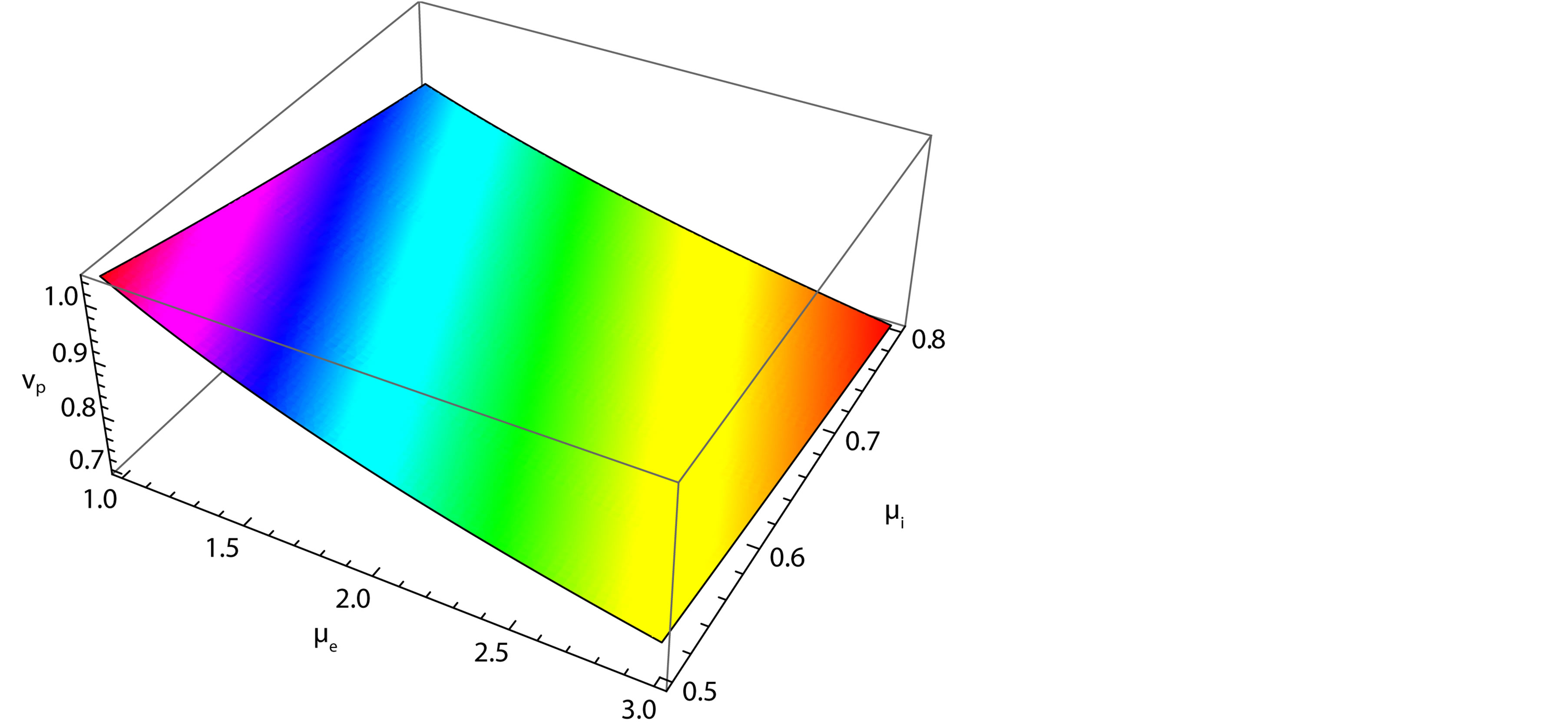
Figure 1. Showing the variation of the phase speed (vp) of solitary waves with μe and μi for j = ±1 and Te = 2.4 Ti.
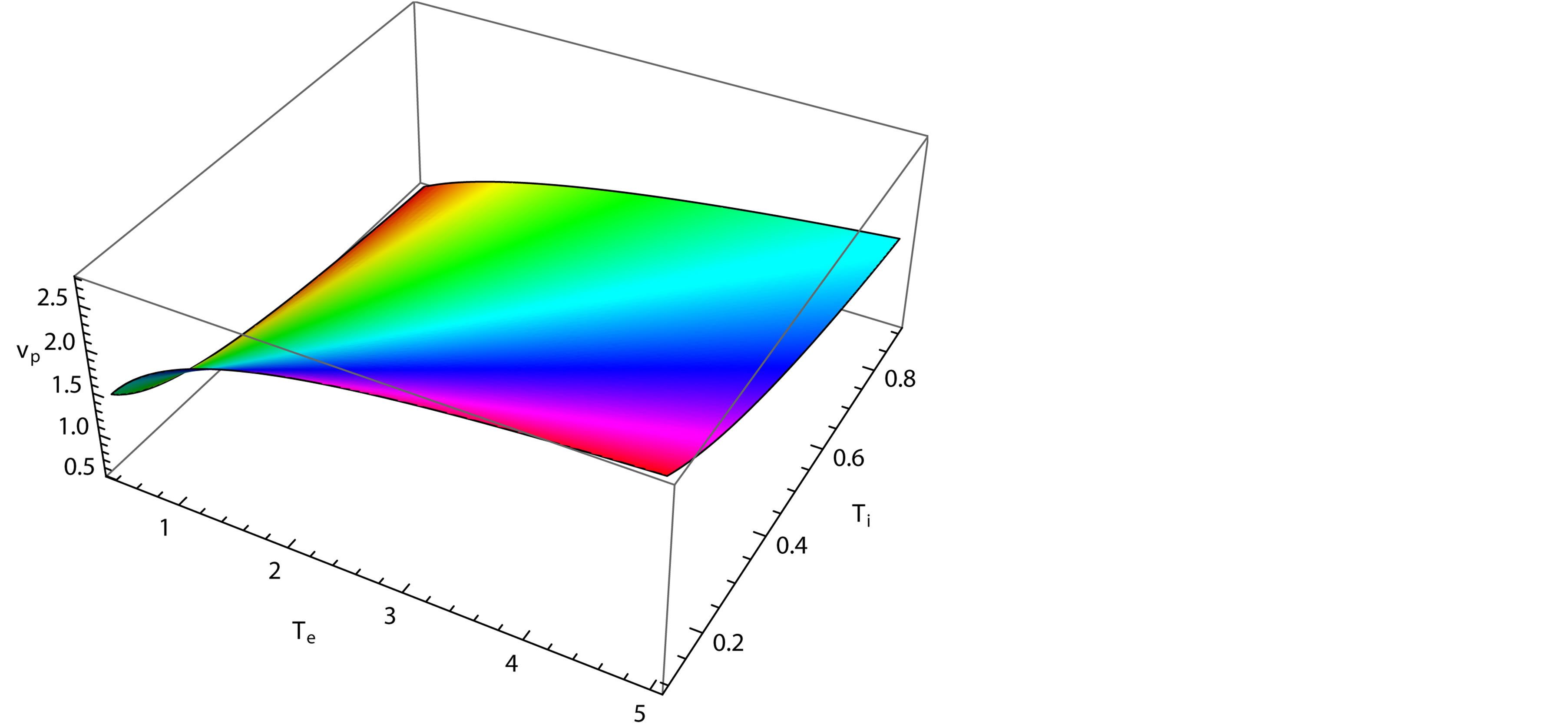
Figure 2. Showing the variation of the phase speed (vp) of solitary waves with Te and Ti for j = ±1 and μe = 15 μi.
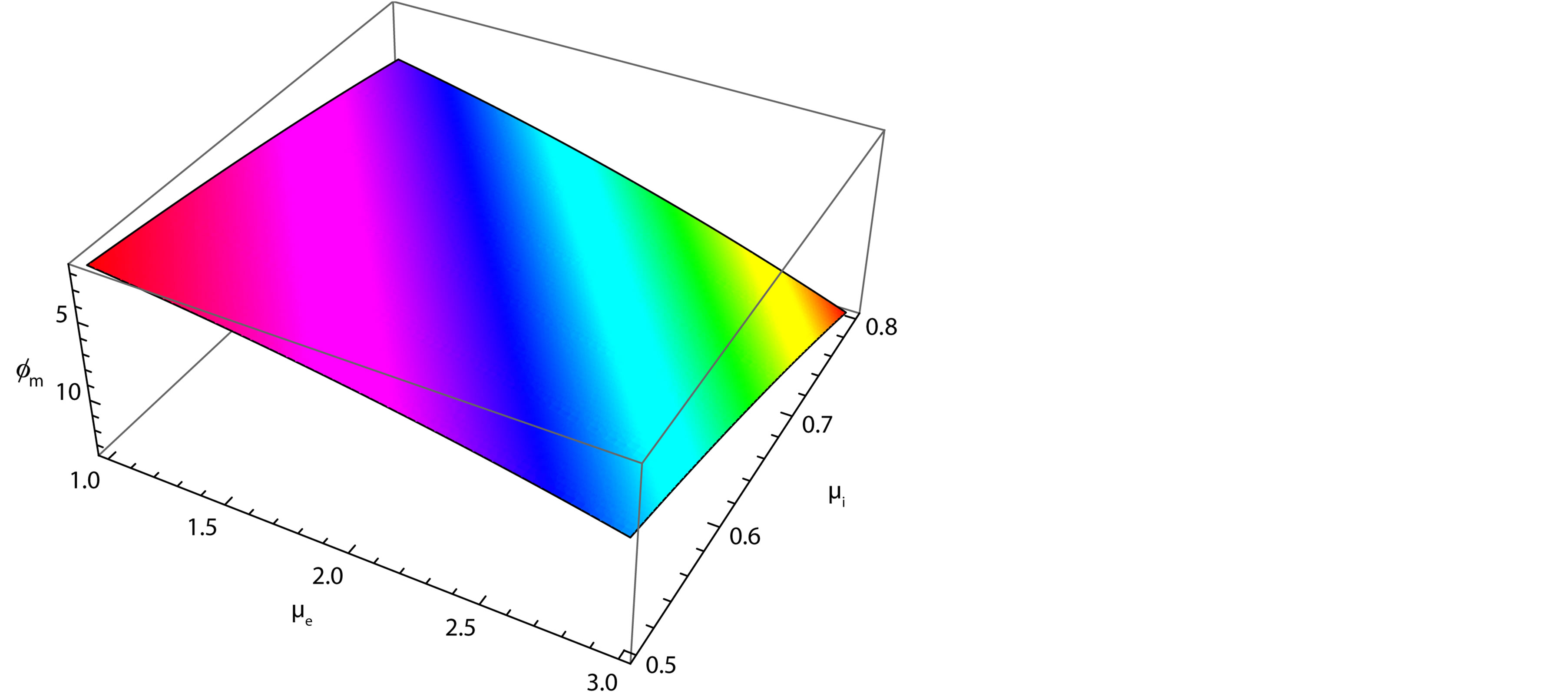
Figure 3. Showing the variation of the amplitude (ϕm) of solitary waves with μe and μi for u0 = 1, j = ±1, α = 0.2 and βi = −0.5.

Figure 4. Showing the variation of the amplitude (ϕm) of solitary waves with βi for u0 = 1, j = ±1, α = 0.5 and μe = 5μi.
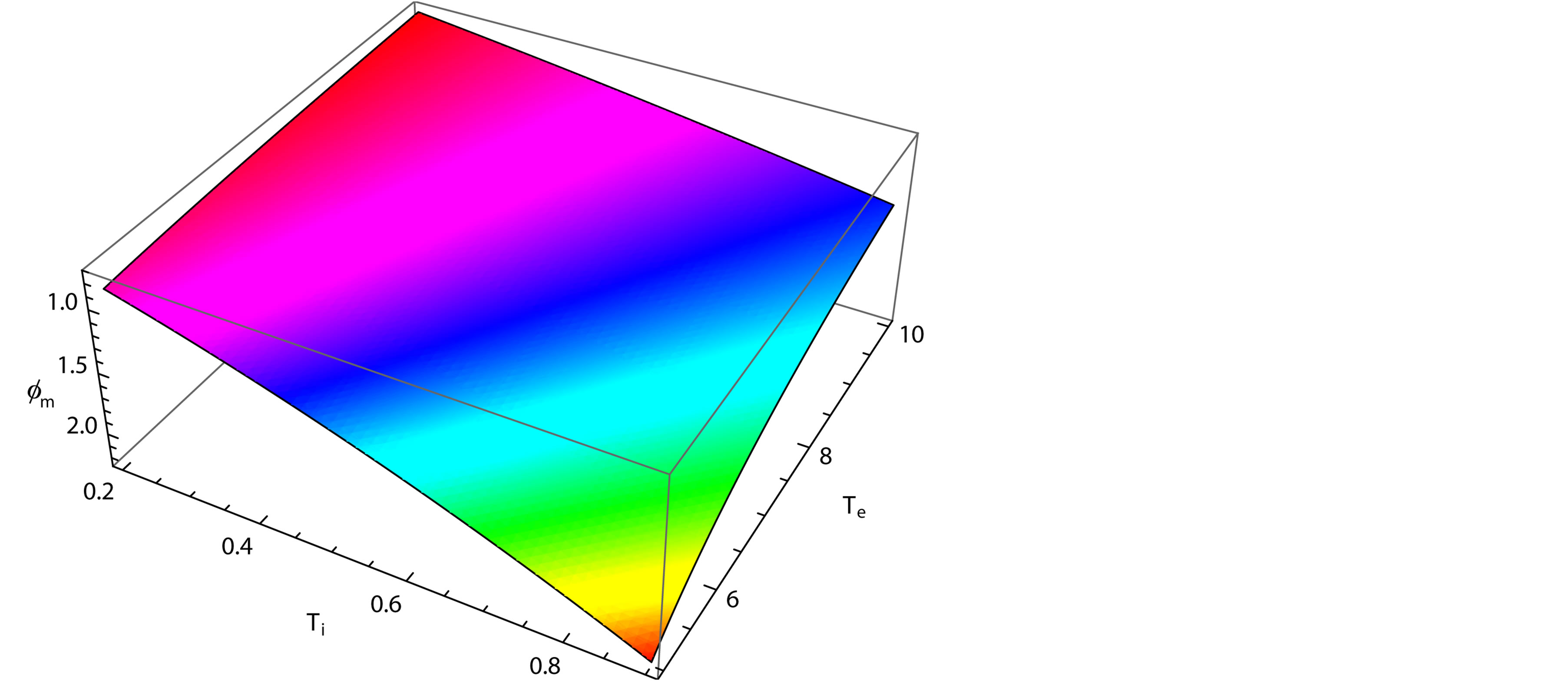
Figure 5. Showing the variation of the amplitude (ϕm) of solitary waves with Ti and Te for μ0 = 1, j = ±1, μe = 3μi and βi = −0.5.
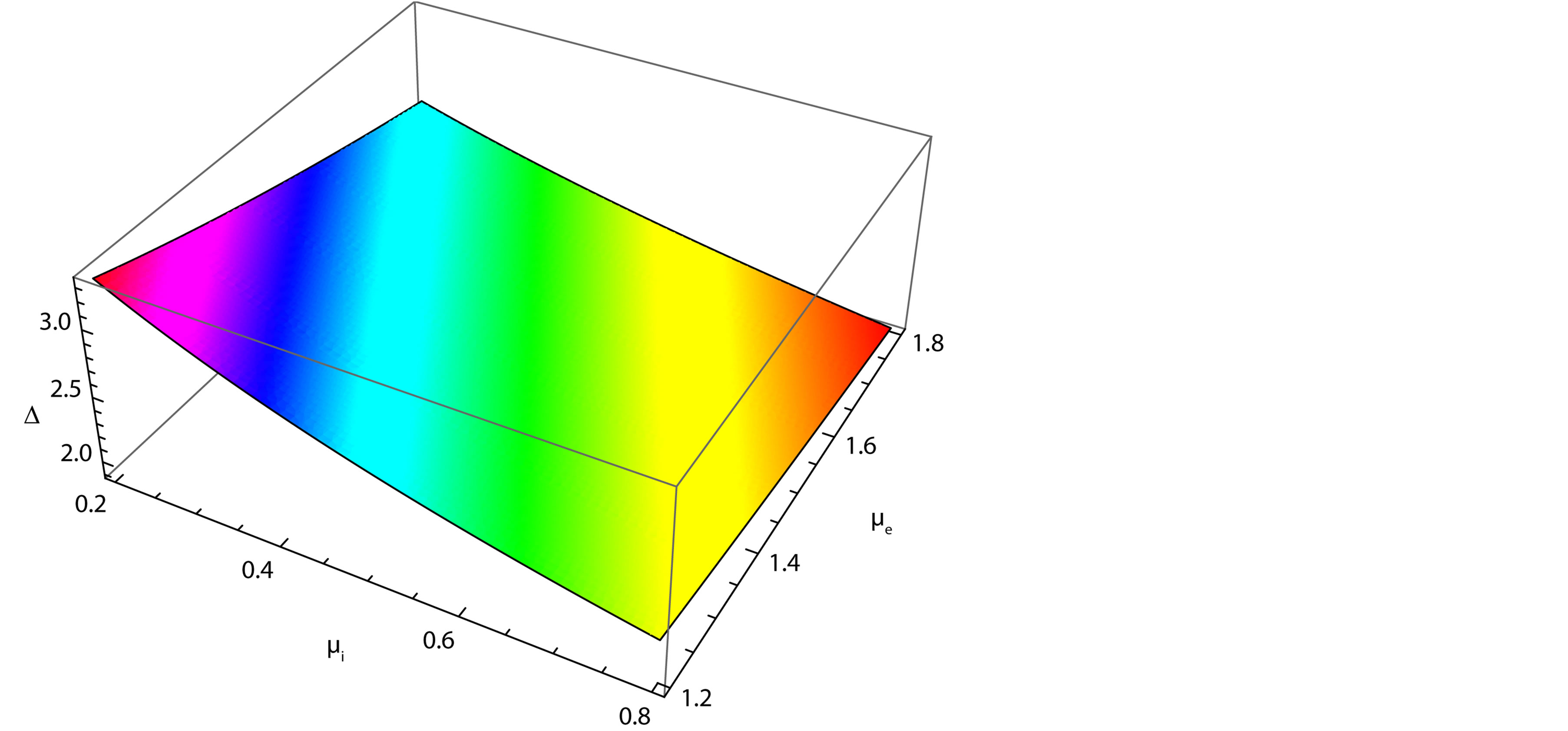
Figure 6. Showing the variation of the width (∆) of solitary waves with μi and μe for u0 = 1, j = ±1 and α = 0.5.
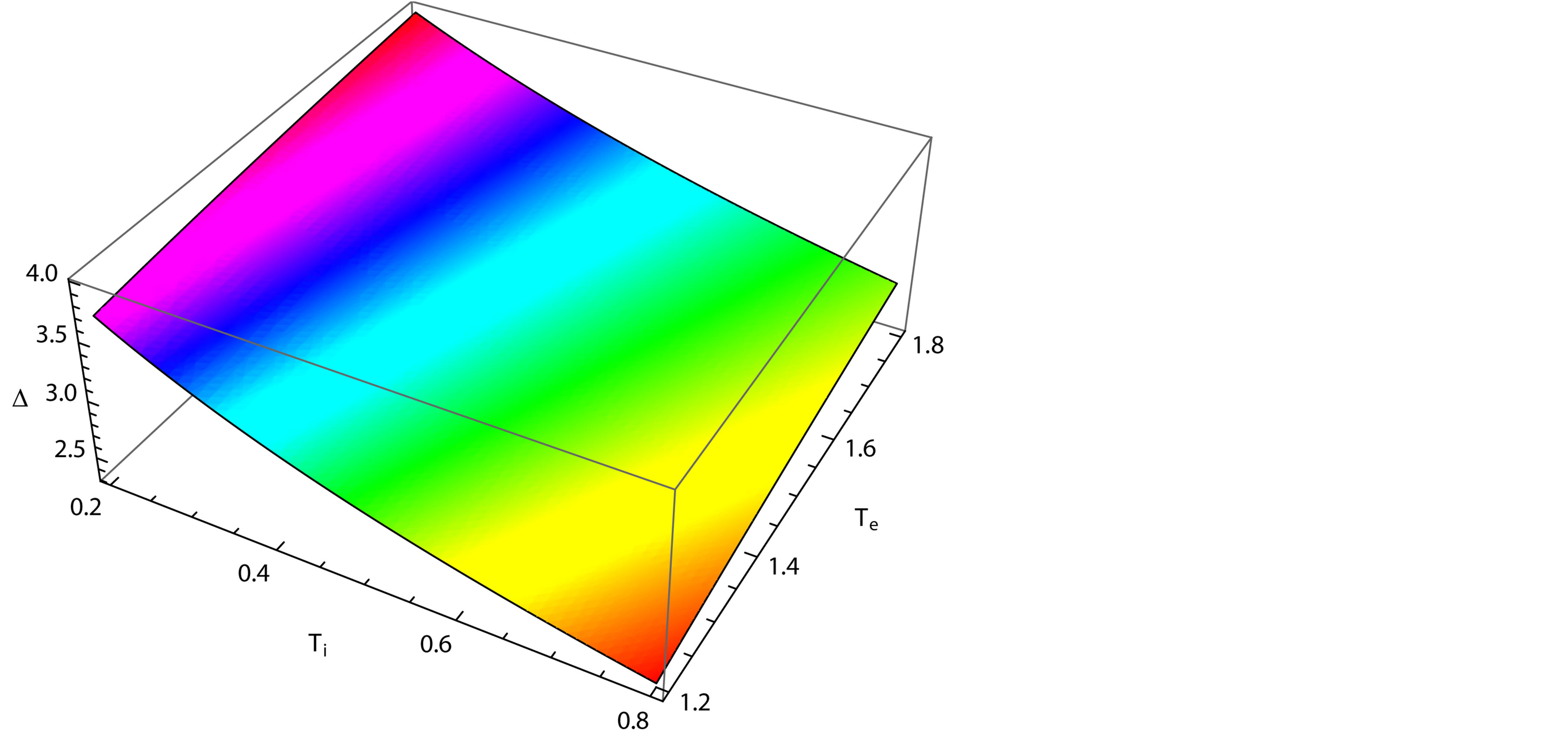
Figure 7. Showing the variation of the width (∆) of solitary waves with Ti and Te for μ0 = 1, j = ±1, and μe = 2.4 μi.
that the phase speed (vp) of the solitary waves decreases with the increasing 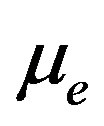 and
and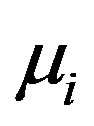 . But the phase velocity more decreases with respect to
. But the phase velocity more decreases with respect to 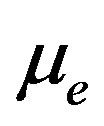 than that of
than that of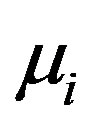 . Figure 2, which shows the variation of the phase speed (vp) of the solitary waves with
. Figure 2, which shows the variation of the phase speed (vp) of the solitary waves with 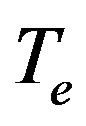 and
and 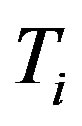 for
for 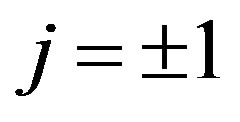 and
and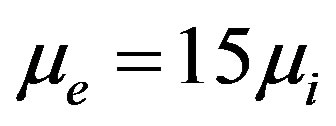 . From this figure we have found that the phase speed (vp) of the solitary waves increases with increasing the value of electron temperature
. From this figure we have found that the phase speed (vp) of the solitary waves increases with increasing the value of electron temperature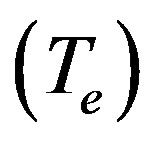 , on the other hand it decreases with increasing the value of ion temperature
, on the other hand it decreases with increasing the value of ion temperature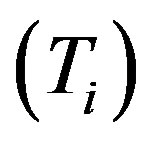 .
.
Figure 3, which shows the variation of the amplitude 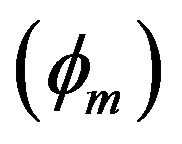 of the solitary waves with
of the solitary waves with 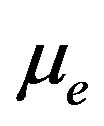 and
and 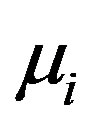 for
for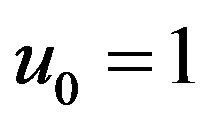 ,
, 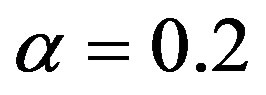
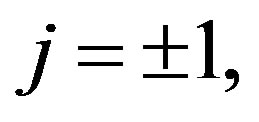 and
and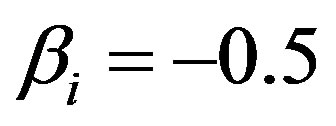 . This figure indicates that the amplitude
. This figure indicates that the amplitude 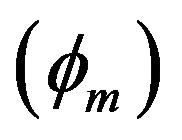 of the solitary waves decreases with the increasing the value of both
of the solitary waves decreases with the increasing the value of both  (slowly) and
(slowly) and 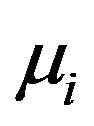 (rapidly). Figure 4, which shows the variation of the amplitude
(rapidly). Figure 4, which shows the variation of the amplitude 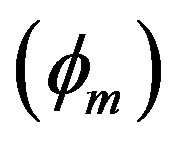 of the solitary waves with
of the solitary waves with 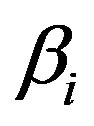 for
for 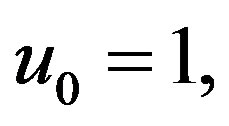
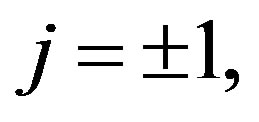
 and
and . This figure indicates that the amplitude
. This figure indicates that the amplitude 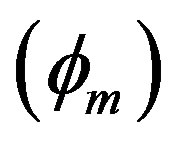 of the solitary waves decreases with the increasing the negative value of
of the solitary waves decreases with the increasing the negative value of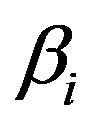 . The variation of the amplitude
. The variation of the amplitude 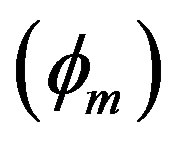 of the solitary waves with Ti and Te is shown in Figure 5, for
of the solitary waves with Ti and Te is shown in Figure 5, for 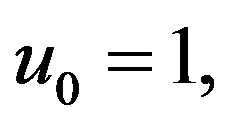
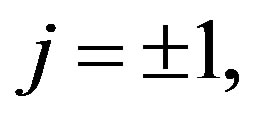
 and
and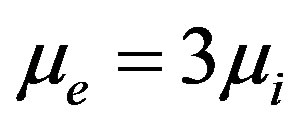 . From this figure we have seen that the amplitude
. From this figure we have seen that the amplitude 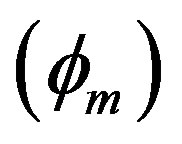 of the solitary waves decreases with the increasing the value of ion temperature (Ti) and it increases with increasing the value of electron temperature (Te). Figure 6, which shows the variation of the width (∆) of the solitary waves with
of the solitary waves decreases with the increasing the value of ion temperature (Ti) and it increases with increasing the value of electron temperature (Te). Figure 6, which shows the variation of the width (∆) of the solitary waves with  and
and 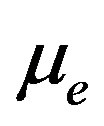 for
for 
 and
and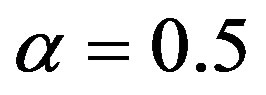 . This figure indicates that the width (∆) of the solitary waves decreases with the increasing
. This figure indicates that the width (∆) of the solitary waves decreases with the increasing  and
and . But the width more decreases with respect to
. But the width more decreases with respect to 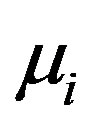 than that of
than that of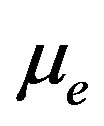 . Figure 7, which shows the variation of the width (∆) of the solitary waves with Ti and Te for
. Figure 7, which shows the variation of the width (∆) of the solitary waves with Ti and Te for 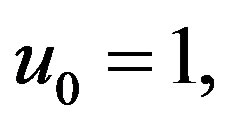
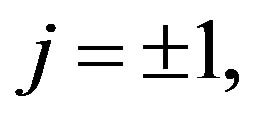 and
and 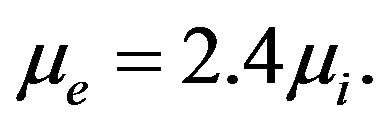 In that case the width (∆) of the solitary waves decreases with the increasing the value of ion temperature (Ti) rapidly but it increases with increasing the value of electron temperature (Te) slightly.
In that case the width (∆) of the solitary waves decreases with the increasing the value of ion temperature (Ti) rapidly but it increases with increasing the value of electron temperature (Te) slightly.
5. Discussion
A three component unmagnetized collision less dusty plasma system, consisting of extremely massive, micronsized, arbitrarily charged cold mobile dust grains, Maxwellian electrons, trapped (vortex-like) ions, has been considered and the properties of finite amplitude dust-acoustic potential, which has been found to exist in such a dusty plasma system, have been investigated by the reductive perturbation method. It has been found that the basic features of such DA solitary waves are significantly modified by the presence of trapped ions. It is also found that the DA solitary waves in our dusty plasma model differ from the usual K-dV equation by their polarity, width, speed, and the power of sech. The results, which have been obtained from this investigation, may be pointed out as follows:
1. Dusty plasma system, whose constituents are arbitrarily charged cold mobile dust grains, Maxwellian electrons, and trapped ions of different constant temperatures, is found to support solitary waves associated with the non-linear DA waves.
2. The presence of the vortex-like ions distribution, the dynamics of weakly dispersive non-linear DA waves is governed by the mK-dV equation instead of K-dV equation, the stationary solution of which is represented in the form of an inverted secant hyperbolic fourth profile. Thus, the potential polarity of the DA solitary waves in our dusty plasma is different from the usual IA solitary waves in an electron-ion plasma.
3. The dusty plasma system under consideration supports the DA solitary waves that are associated with negative potential only. The fixed polarity of the potential structures is due to the effect of vortex-like ion distribution.
4. It has been found that trapped ions are responsible for DA solitary waves which have smaller width, larger amplitude, and higher propagation velocity than that involving Maxwellian ions, and that they can be represented in the form sech4(z/∆), instead of sech2(z/∆) which is the stationary solution of the standard K-dV equation.
5. It has been found that as  increases, the amplitude
increases, the amplitude  increases while the width ∆ decreases while as
increases while the width ∆ decreases while as 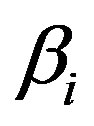 increases, the amplitude decreases for
increases, the amplitude decreases for 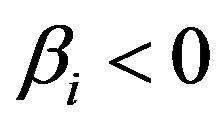 (a vortex-like excavated trapped ion distribution and increases for
(a vortex-like excavated trapped ion distribution and increases for .
.
6. The polarity of dust particles has no effect on the nonlinear propagation of DA solitary waves.
We hope that our present investigation should be helpful in understanding the basic features of localized electrostatic disturbances in space and laboratory devices, in which arbitrarily charged dust particulates, free electrons, and ions with trapped particles are the plasma species. The present work can also provide a guideline for interpreting the most numerical simulation results, which exhibit the simultaneous presence of non-thermal ion distributions and associated DA localized wave packets.
References
- Roberts, K.V. and Berk, H.L. (1967) Nonlinear Evolution of a Two-Stream Instabilit. Physical Review Letters, 19, 297-300. http://dx.doi.org/10.1103/PhysRevLett.19.297
- Morse, R.L. and Nielson, C.W. (1969) One-, Two-, and Three-Dimensional Numerical Simulation of Two-Beam Plasmas. Physical Review Letters, 23, 1087-1090. http://dx.doi.org/10.1103/PhysRevLett.23.1087
- Sakanaka, P.K. (1972) Beam-Generated Collisionless Ion—Acoustic Shocks. Physics of Fluids, 15, 1323. http://dx.doi.org/10.1063/1.1694084
- Saeki, K., et al. (1979) Formation and Coalescence of Electron Solitary Holes. Physical Review Letters, 42, 501-504. http://dx.doi.org/10.1103/PhysRevLett.42.501
- Lynov, J.P., et al. (1979) Observations of Solitary Structures in a Magnetized, Plasma Loaded Waveguide. Physica Scripta, 20, 328. http://dx.doi.org/10.1088/0031-8949/20/3-4/005
- Schamel, H. (972) Stationary Solitary, Snoidal and Sinusoidal Ion Acoustic Waves. Physics of Plasmas, 14, 905. http://dx.doi.org/10.1088/0032-1028/14/10/002
- Schamel, H. (1973) A Modified Korteweg-de Vries Equation for Ion Acoustic Waves Due to Resonant Electrons. Journal of Plasma Physics, 9, 377. http://dx.doi.org/10.1017/S002237780000756X
- Schamel, H. (1975) Analytic BGK Modes and Their Modulational Instability. Journal of Plasma Physics, 13, 139. http://dx.doi.org/10.1017/S0022377800025927
- Schamel, H. and Bujarbarua, S. (1980) Solitary Plasma Hole via Ion-Vortex Distribution. Physics of Fluids, 23, 2498. http://dx.doi.org/10.1063/1.862951
- Bujarbarua, S. and Schamel, H. (1981) Theory of Finite-Amplitude Electron and Ion Holes. Journal of Plasma Physics, 25, 515. http://dx.doi.org/10.1017/S0022377800026295
- Mamun, A.A., Shukla, P.K. and Cairns, R.A. (1996) Effects of Vortex-Like and Non-Thermal Ion Distributions on Non-Linear Dust-Acoustic Waves. Physics of Plasmas, 3, 2610. http://dx.doi.org/10.1063/1.871973
- Rao, N.N., Shukla, P.K. and Yu, M.Y. (1990) Dust-Acoustic Waves in Dusty Plasmas. Planetary and Space Science, 38, 543-546. http://dx.doi.org/10.1016/0032-0633(90)90147-I
- Barkan, A., Merlino, R.L. and D’Angelo, N. (1995) Laboratory Observation of the Dust-Acoustic Wave Mode. Physics of Plasmas, 2, 3563-3565. http://dx.doi.org/10.1063/1.871121
- D’Angelo, N. (1995) Coulomb solids and low-frequency fluctuations in RF dusty plasmas. Journal of Physics D: Applied Physics, 28, 1009. http://dx.doi.org/10.1088/0022-3727/28/5/024
- Thompson, C., Barkan, A. and Merlino, R.L. (1999) Video Imaging of Dust Acoustic Waves. IEEE Transactions on Plasma Science, 27, 146-147. http://dx.doi.org/10.1109/27.763096
- Rao, N.N. and Shukla, P.K. (1994) Nonlinear Dust-Acoustic Waves with Dust Charge Fluctuations. Planetary and Space Science, 42, 221-225. http://dx.doi.org/10.1016/0032-0633(94)90084-1
- Melands, F. and Shukla, P.K. (1995) Theory of Dust-Acoustic Shocks. Planetary and Space Science, 43, 635-648. http://dx.doi.org/10.1016/0032-0633(94)00200-B
- Mamun, A.A. (1999) Arbitrary Amplitude Dust-Acoustic Solitary Structures in a Three Component Dusty Plasma. Astrophysics and Space Science, 268, 443.
- Shukla, P.K. and Mamun, A.A. (2003) Solitons, Shock and Vortices in Dusty Plasmas. New Journal of Physics, 5, 17. http://dx.doi.org/10.1088/1367-2630/5/1/317
- Shukla, P.K. and Mamun, A.A. (2002) Introduction to Dusty Plasma Physics. Institute of Physics Publishing Publishing, Ltd., Britol.
- Ishihara, O. (1988) Physics of Dusty Plasmas. American Institute of Physics, New York.
- Moslem, W. M. (2006) Dust-ion-acoustic solitons and shocks in dusty plasmas. Chaos, Solitons Fractals, 28, 994. http://dx.doi.org/10.1016/j.chaos.2005.08.150
- Mamun, A.A. Shukla, P.K. and Cairns, R.A. (1996) Solitary Potentials in Dusty Plasmas. Physics of Plasmas, 3, 702. http://dx.doi.org/10.1063/1.871905
- Annou K. and Annou, R. (2012) Effect of Nonthermal Ion Distribution and Dust Temperature on Nonlinear DustAcoustic Solitary Waves. Pramana-Journal of Physics, 78, 121. http://dx.doi.org/10.1007/s12043-011-0203-3
- Rahman, O. and Mamun, A.A. (2013) Nonlinear Propagation of Dust-Acoustic Solitary Waves in a Dusty Plasma with Arbitrarily Charged Dust and Tapped Electrons. Pramana-Journal of Physics, 80, 1031. http://dx.doi.org/10.1007/s12043-013-0535-2
- Washimi, H. and Taniuti, T. (1966) Propagation of Ion-Acoustic Solitary Waves of Small Amplitude. Physical Review Letters, 17, 996-998. http://dx.doi.org/10.1103/PhysRevLett.17.996

