International Journal of Astronomy and Astrophysics
Vol.3 No.3(2013), Article ID:36517,6 pages DOI:10.4236/ijaa.2013.33034
The Cherenkov Radiation in the Galaxy’s Halo of Dark Matter
V. G. Fessenkov Astrophysical Institute, Almaty, Kamenskoye Plato, National Centre for the Space Researches and Technology, National Space Agency, Republic of Kazakhstan
Email: chechin-lm@mail.ru, leonid.chechin@gmail.com
Copyright © 2013 L. M. Chechin. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 14, 2013; revised May 16, 2013; accepted May 23, 2013
Keywords: Dark Matter Profile; The Cherenkov Radiation
ABSTRACT
The effect of light refraction in a galaxy’s halo of dark matter, described by profiles of Navarro-Frenk-White and Burkert, was considered. Powers of the Cherenkov radiation for the refractive indexes of gravitational fields with these profiles were calculated. It was shown that correspondent radiation temperature in the X-rays diapason have the magnitude about . It was also marked that its detection may be the criteria on choosing the preferable dark matter density distribution in a galaxy.
. It was also marked that its detection may be the criteria on choosing the preferable dark matter density distribution in a galaxy.
1. Introduction
The substance refracting index, as it well known, is the value that equals to ratio between phase velocities in vacuum and in a given media. However, if any charge particle whose group velocity  in a media is larger than the phase velocity in this substance
in a media is larger than the phase velocity in this substance , i.e.
, i.e. 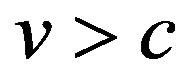 the specific electromagnetic radiation appears. The theory of such radiation—the Cherenkov radiation—was given in the references [1,2], for example.
the specific electromagnetic radiation appears. The theory of such radiation—the Cherenkov radiation—was given in the references [1,2], for example.
The generalization of Cherenkov radiation on a gravitational field presence was given in monograph [3]. For the Schwarzschild field this radiation characterizes by the upper boundary frequency
 .
.
Note that this effect is very small and may be detected in the very strong gravitational field. (It is necessary cite the article [4] where it was shown that if a charged particle will move in the external gravitational field along the geodesic line it creates the Cherenkov radiation also, but for the case of field’s nonzero Ricci tensor.)
By the way, the problems of searching the electromagnetic radiation’s and light rays’ behavior not only in the local weak gravitational fields but on the cosmological scales also, where got the essential development at last time. For this it is enough to mention the searching on the gravitational microlensing of stars’ halo of dark matter. In spite of the minuteness of angle images’ separation (about 0.001") it is possible to detect the stars’ brightness changing under the mutual movement of star, galaxy and observer at the microlensing process (see, for example [5]).
Another aspects of the dark matter searching on the cosmological scales based on the different radiation processes studying in it, including the dynamics of cosmic rays in dark matter, where done in articles [6-9]. Moreover, the searching of dark matter’s properties on the small space scales where done in articles [10,11].
For example, the dark matter density in the vicinity of Sun was discussed in [11]. In this article authors derived the value of the dark matter density at the Sun’s location without modeling the mass distribution in the Galaxy. For its deriving they based on the local equation of centrifugal equilibrium and took into account the shape of the dark matter density profile, knowledge of the rotation curve from the galaxy center out to the virial radius, and the uncertainties in the slope of the circular-velocity at the Sun location and the ratio between this radius and the length scale of the stellar exponential thin disk. Their result is
 .
.
The influence of dark matter on the light rays’ propagation in the Solar system was considered also. In fact, in article [12] the time delay effect (analog of the Shapiro effect) and the shift of light rays’ frequency effect in the spherical-symmetric dark matter distribution where considered. But the shape of dark matter profile has been chosen a priori as
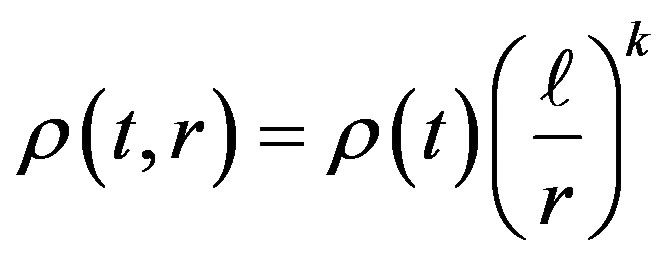 where
where .
.
Here  and
and  are some constant parameters with the initial distance and dark matter density physical essences. As for the index of dark matter density’s profile
are some constant parameters with the initial distance and dark matter density physical essences. As for the index of dark matter density’s profile 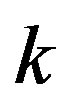 it was specified as –1, 0, and +1.
it was specified as –1, 0, and +1.
In spite of the numerical minuteness of these effects (for example,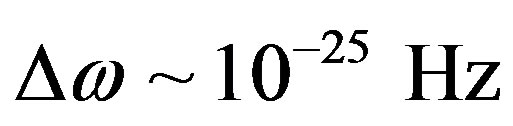 ) just at the upper magnitude of dark matter density
) just at the upper magnitude of dark matter density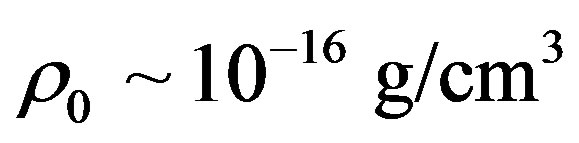 their possible physical application was aimed to improving the astronomical unit.
their possible physical application was aimed to improving the astronomical unit.
In our article the effect of light rays refraction in the dark matter’s halo for its some profiles is considered and the corresponding Cherenkov radiation is searched. In the conclusion the powers of such radiation for optical, ultraviolet and X-ray frequency diapasons were estimated and the possibility of their detecting is discussed also.
2. The Spherical-Symmetric Model of Dark Matter Halo
The basic morphological elements of a galaxy are the nucleus, bulge, gaseous-dust disk, clouds of neutral hydrogen, stars cluster and galactic halo. Later on we’ll focus our attention on the galactic halo only, because it contains the most part of galaxy’s mass and consists preferably of the dark matter [13,14]. Let’s consider the spherical-symmetric model of dark matter halo. The spherical-symmetric interval of the gravitational field we write down in the standard form [15]
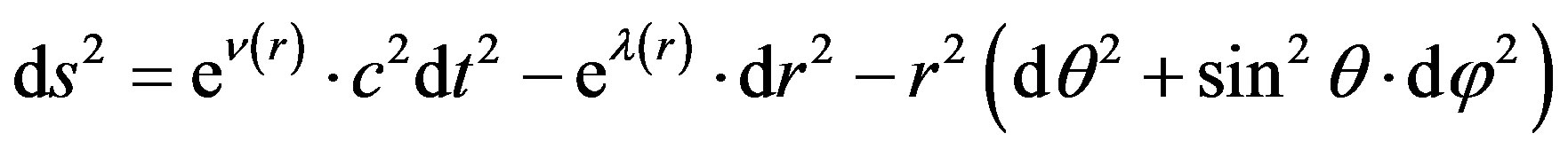 , (1)
, (1)
where
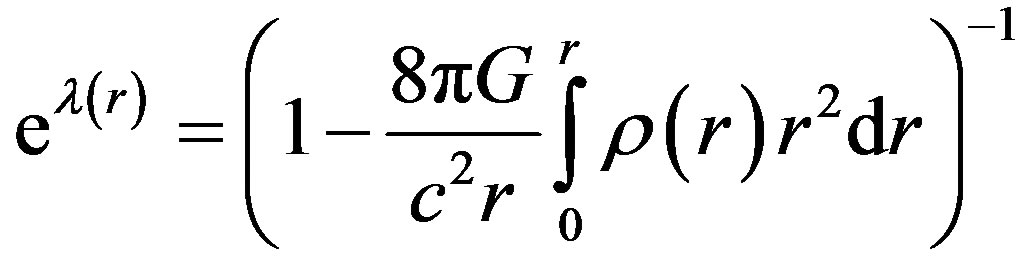 (2)
(2)
and
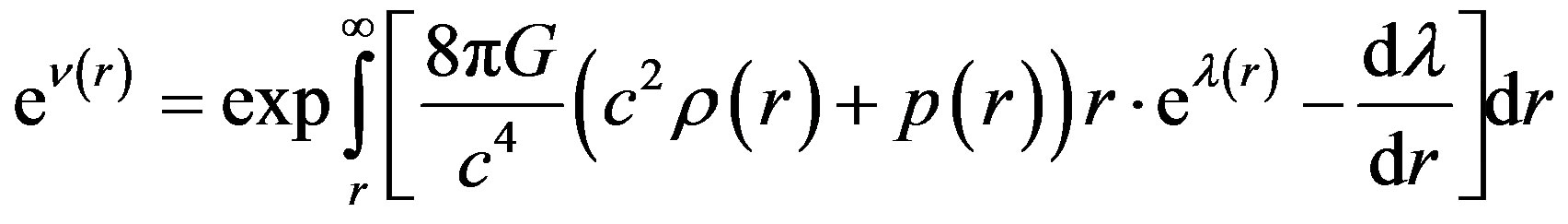 . (3)
. (3)
In expressions (2) and (3)  and
and 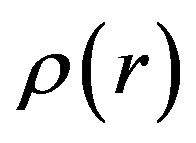 are the mass-energy density and pressure of dark matter, accordingly. The real expressions for mass-energy density and pressure are possible get by searching the rotational curves of galaxies. Meanwhile, the plausible space distribution for these expressions is possible get by the N-body simulation method. In fact, the profiles for dark matter energy [16], temperature profiles [17] and some other characteristics of dark matter have been got by this method. In following as the current variable
are the mass-energy density and pressure of dark matter, accordingly. The real expressions for mass-energy density and pressure are possible get by searching the rotational curves of galaxies. Meanwhile, the plausible space distribution for these expressions is possible get by the N-body simulation method. In fact, the profiles for dark matter energy [16], temperature profiles [17] and some other characteristics of dark matter have been got by this method. In following as the current variable 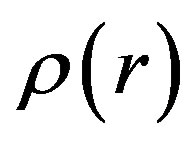 in (1)- (3), we’ll choose two profiles: Navarro-Frenk-White [18] and Burkert [19], only. Concerning for concretizetion the pressure we set
in (1)- (3), we’ll choose two profiles: Navarro-Frenk-White [18] and Burkert [19], only. Concerning for concretizetion the pressure we set  that relates to the well-known model of dark matter as ideal fluid (see, for example, [20]).
that relates to the well-known model of dark matter as ideal fluid (see, for example, [20]).
• Let’s write down the Navarro-Frenk-White profile
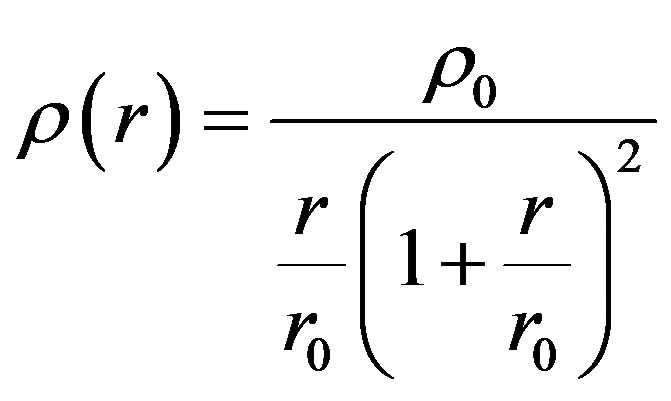 . (4)
. (4)
Assuming that  are the sizes of galaxy here, we may introduce the small parameter
are the sizes of galaxy here, we may introduce the small parameter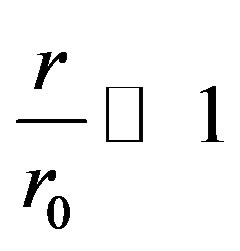 . Introducing (4) into (2) and (3) and take into account the terms up to the
. Introducing (4) into (2) and (3) and take into account the terms up to the 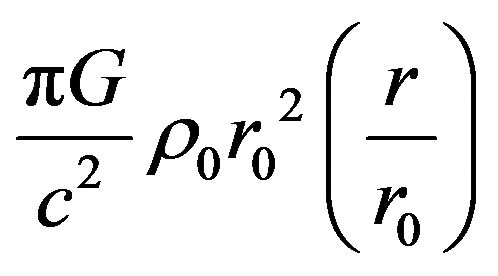 order of minuteness we get
order of minuteness we get
 , (5)
, (5)
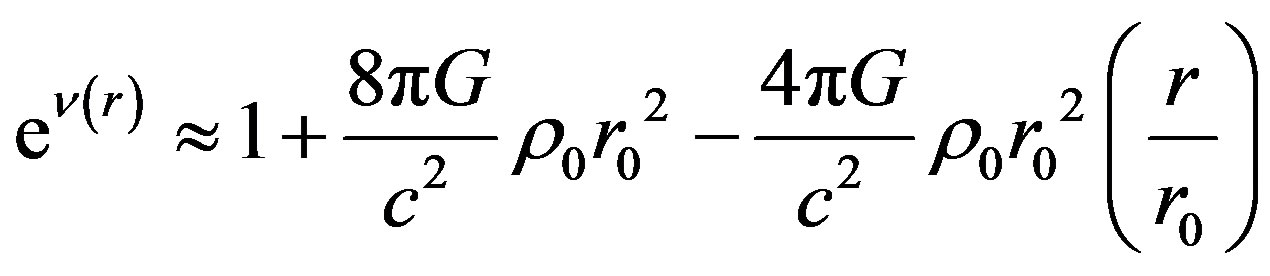 . (6)
. (6)
Putting that in (1) angle 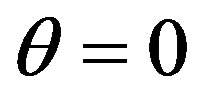 and passing in this plane to the Cartesian coordinates (
and passing in this plane to the Cartesian coordinates (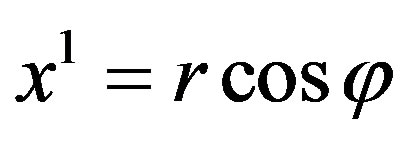 ,
,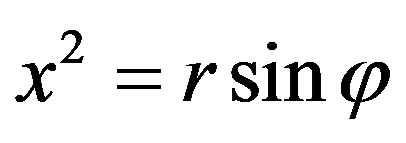 ), with the needed accuracy we get
), with the needed accuracy we get
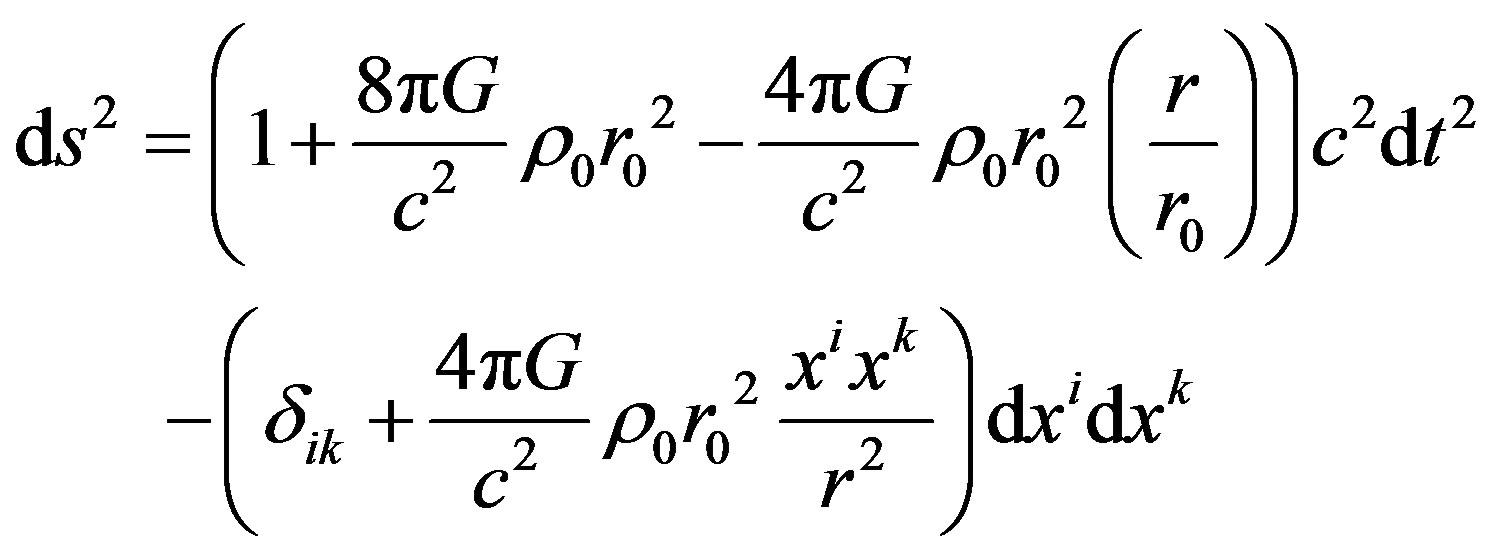 (7)
(7)
where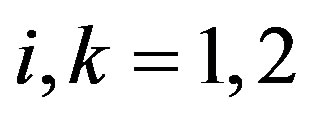 . As for the isotropic geodesic line the interval equals zero, it is easy find the gravitational field’s refractive index
. As for the isotropic geodesic line the interval equals zero, it is easy find the gravitational field’s refractive index
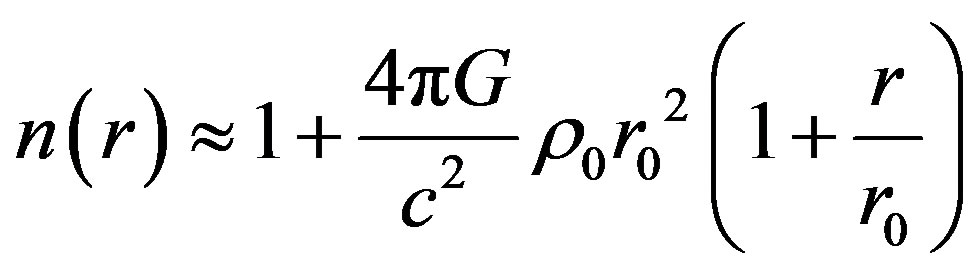 (8)
(8)
by introducing the speed of light in a media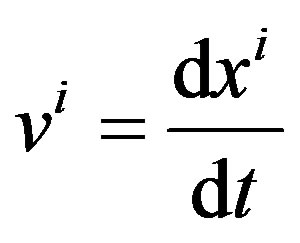 .
.
• The Burkert profile be written down in the same designations is
 . (9)
. (9)
In our next calculations, as in the previous subsectionwe’ll take into account terms of  order.
order.
Then with the needed accuracy we get
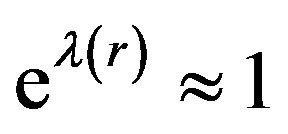 , (10)
, (10)
and
 . (11)
. (11)
According these coefficients the interval of spherecalsymmetric gravitational field, produces by the Burkert profile, takes on the for
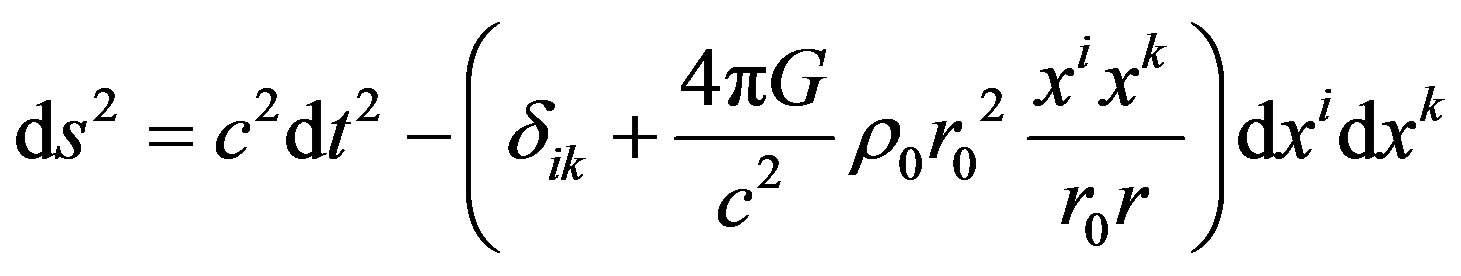 . (12)
. (12)
From (12) we get the final expression of refractive index for the corresponding gravitational field
 . (13)
. (13)
3. The Cherenkov Radiation in a Galaxy’s Halo of Dark Matter
The power of Cherenkov radiation at a frequency 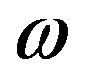 describes by expression [1,2]
describes by expression [1,2]
 , (14)
, (14)
where  is the dispersion refractive index,
is the dispersion refractive index,  the total charge of particles that moves with mean velocity
the total charge of particles that moves with mean velocity . As in our cases the refractive index depends on current coordinate
. As in our cases the refractive index depends on current coordinate , but not on a frequency (the dispersion absence) than expression (14) simplifies
, but not on a frequency (the dispersion absence) than expression (14) simplifies
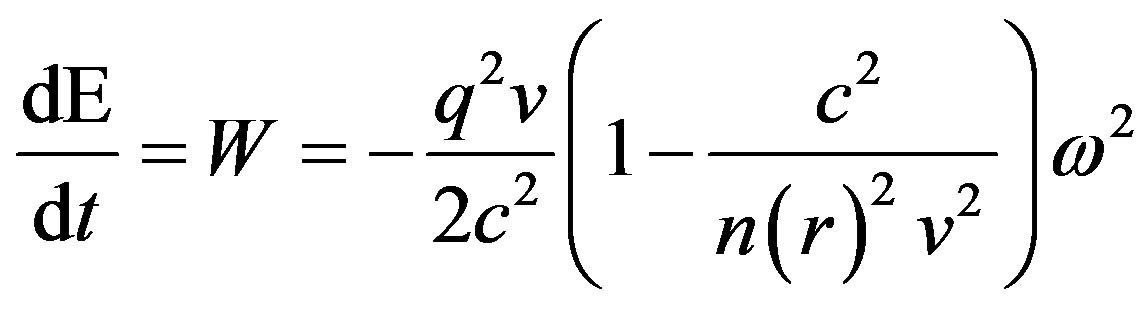 . (15)
. (15)
That is why the last expression be applied to (8) and (13) take on the forms
 (16)
(16)
 . (17)
. (17)
For the following analyses of the gravitational analog of Cherenkov radiation we have to attract the wellknown mechanisms of charged particle creation in a galaxy and to estimate the magnitude of probable charge that comes up to the Earth.
First of all consider the possibility of Sun radiation and radiation from Wolf-Rayet stars usage. It is known that sun wind—the flux of ionized particles (protons, electrons and  -particles)—flows from the solar corona. The slow sun wind have the velocity
-particles)—flows from the solar corona. The slow sun wind have the velocity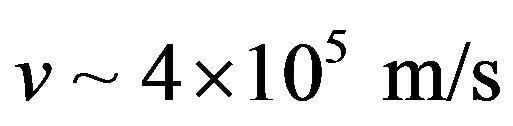 , while the velocity of fast sun wind is
, while the velocity of fast sun wind is .
.
The average Sun emits about 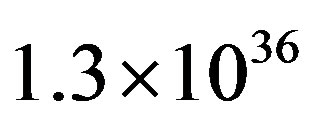 particles per second [21,22] due to the wind. In spite of the vast number particles, this type of radiation couldn’t be used for the estimation of Cherenkov radiation due to the fact that their velocities are radically smaller with respect to the speed of light and due to the minuteness of their flux.
particles per second [21,22] due to the wind. In spite of the vast number particles, this type of radiation couldn’t be used for the estimation of Cherenkov radiation due to the fact that their velocities are radically smaller with respect to the speed of light and due to the minuteness of their flux.
However, the energy diapason of the solar cosmic rays at Sun flare is about 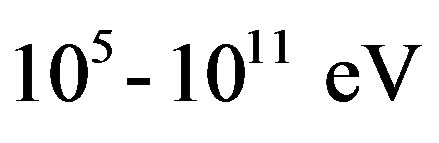 that corresponds to their maximal velocities order of
that corresponds to their maximal velocities order of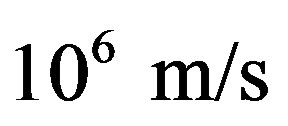 . Moreover, in this case the essentially stronger and the cosmic ray flux —its magnitude may be
. Moreover, in this case the essentially stronger and the cosmic ray flux —its magnitude may be 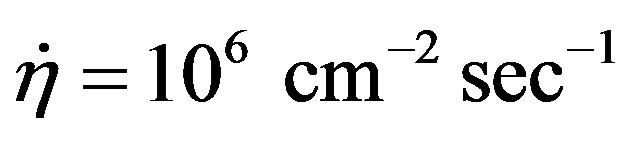 of order. But the dark matter does not influent practically on the cosmic rays propagation because the region of their movement is limiting by sizes of the Solar system, in particular.
of order. But the dark matter does not influent practically on the cosmic rays propagation because the region of their movement is limiting by sizes of the Solar system, in particular.
More active in the aspect of the star’s wind emission are the Wolf-Rayet stars. Their star’s wind emits about three Sun masses per one million years. Therefore the rate of substance loss for Wolf-Rayet stars is 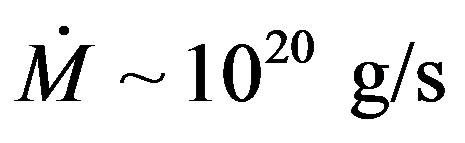 that at seven orders larger than the rate of a substance loss for the star’s wind. Beside, according to [23] the brightness for such type of stars at
that at seven orders larger than the rate of a substance loss for the star’s wind. Beside, according to [23] the brightness for such type of stars at 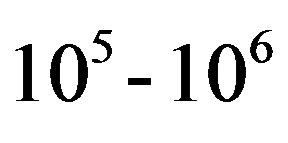 times larger than brightness of Sun. That is why the velocities of ionizing particles from these stars are essentially larger than from the quiet Sun and enrich magnitudes about
times larger than brightness of Sun. That is why the velocities of ionizing particles from these stars are essentially larger than from the quiet Sun and enrich magnitudes about .
.
Moreover, a particles in the galactic space be undergo the additional acceleration by shock waves acquire the high and ultrahigh energies 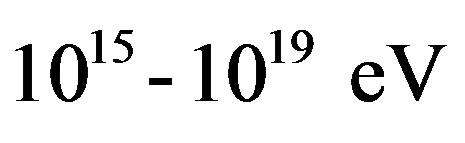 of order [24]. That is why their final velocities
of order [24]. That is why their final velocities 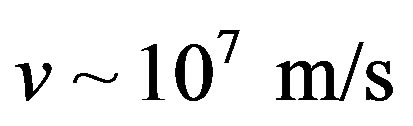 become are comparing with the speed of light, also. And though the number of such particles is highly small—one particle per meter squared during one year on the Earth— they may create the Cherenkov radiation at their traverse through the dark matter in principle.
become are comparing with the speed of light, also. And though the number of such particles is highly small—one particle per meter squared during one year on the Earth— they may create the Cherenkov radiation at their traverse through the dark matter in principle.
Examination of (16) and (17) leads to the significant conclusion that from physical viewpoint the most interesting is the first expression because it includes the largest term 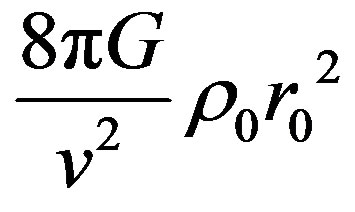 depending on the central magnitude of the dark matter density
depending on the central magnitude of the dark matter density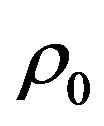 . That is why below we’ll focus our searching on this term in (8) and estimate the magnitude of it, only.
. That is why below we’ll focus our searching on this term in (8) and estimate the magnitude of it, only.
For doing this we must set the density 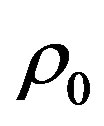 and take into account the following natural restriction
and take into account the following natural restriction .
.
Note that in article [12], mentioned above, the upper magnitude of cold dark matter’s density is about . But such magnitude seem is too large because from the restriction given above it must be
. But such magnitude seem is too large because from the restriction given above it must be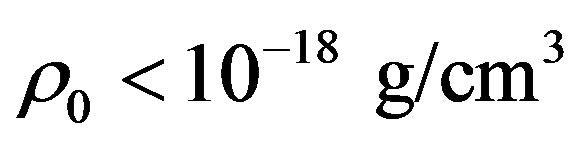 . Remember that mean magnitude of dark matter’s density in the Universe is
. Remember that mean magnitude of dark matter’s density in the Universe is  g/cm3. Hence, let the following interval for the dark matter’s density takes place
g/cm3. Hence, let the following interval for the dark matter’s density takes place
 . (18)
. (18)
As , the sizes of typical galaxy are
, the sizes of typical galaxy are
 , then setting
, then setting 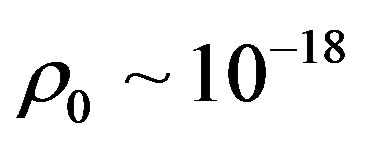 g/cm3 we get the following interval for the above mentioned term
g/cm3 we get the following interval for the above mentioned term
 . (19)
. (19)
Further from (8) it follows that velocity of charged particle has the expression
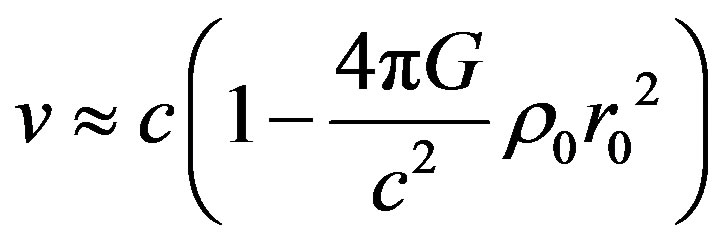 . (20)
. (20)
Hence the interval of its numerical magnitudes is
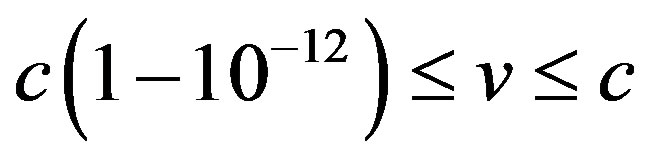 . (21)
. (21)
According to argumentation mentioned above, we put that in halo of dark matter the charged particles can be accelerated up to the velocities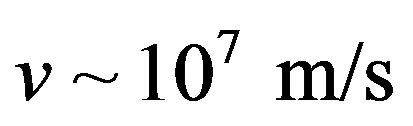 , too. Thus they will correspond to velocities of ionized particles from the Wolf-Rayet stars and satisfy the relation
, too. Thus they will correspond to velocities of ionized particles from the Wolf-Rayet stars and satisfy the relation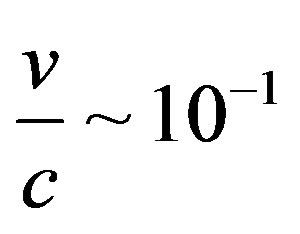 .
.
From these statements we get the magnitude of the dark matter’s density central part
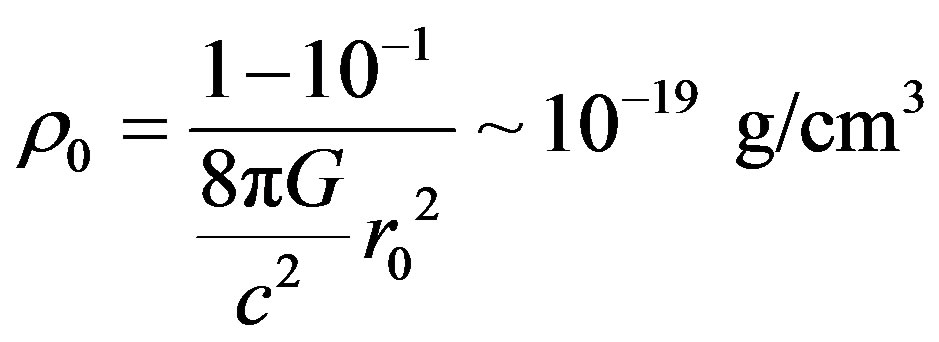 . (22)
. (22)
This estimation is at three orders smaller then the corresponding value argued in [12]. But last value, as it seems, is overvalued because the charged particle’s velocity will tent to the speed of light at the density . According this cause is overvaluing and magnitude of the dark matter’s density central part
. According this cause is overvaluing and magnitude of the dark matter’s density central part  that was argued in [25]. (Here we are not concerning the ultra light particles existence [2] and the results of novel experiment on their detection [26].)
that was argued in [25]. (Here we are not concerning the ultra light particles existence [2] and the results of novel experiment on their detection [26].)
Now basing on these data we can estimate the possible magnitude of the Cherenkov radiation in the halo of dark matter for the different (visible, ultraviolet and X-rays) frequency diapasons.
Putting that the flux of high energy charged particles is uniform and isotropic it is possible to estimate the charge’s quantity that falls down on the Earth during one year. Setting that Earth’s radius is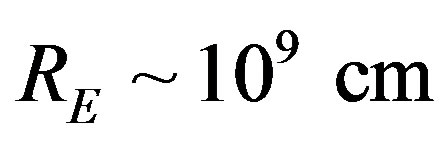 , area of its hemisphere is
, area of its hemisphere is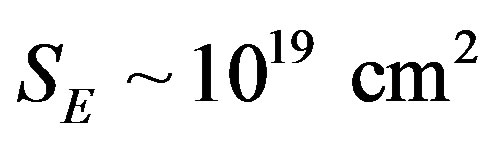 , than rate of particles changing is
, than rate of particles changing is . Next, a charge particle moving with the velocity
. Next, a charge particle moving with the velocity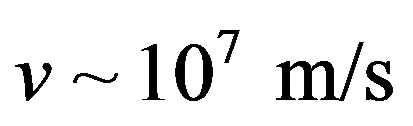 , that is closed to the speed of light, will cross a galaxy during
, that is closed to the speed of light, will cross a galaxy during
 . Hence, the number of upcoming charge particles will be
. Hence, the number of upcoming charge particles will be 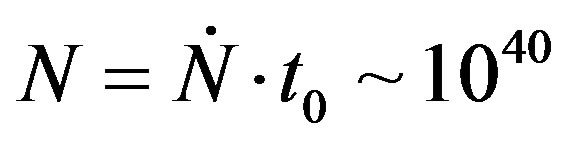 and the corresponding them entirety charge equals
and the corresponding them entirety charge equals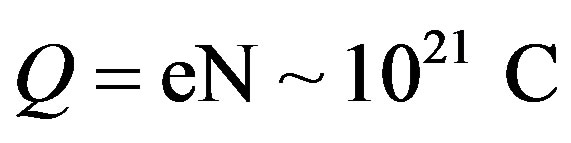 .
.
After that, assuming that area of a Cherenkov telescope mirrors lies in the limits 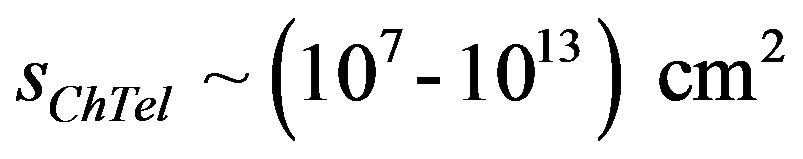 (that is identical to increasing such telescope’s sensitivity [27]), it possible detect charge magnitude about
(that is identical to increasing such telescope’s sensitivity [27]), it possible detect charge magnitude about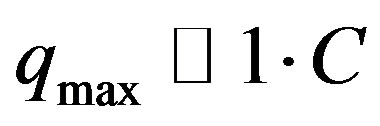 .
.
As we are interesting the dark matter influence on the Cherenkov radiation then sum of two first terms in (17) at velocities closed to the speed of light will tend to zero. Hence, the looking for power radiation is
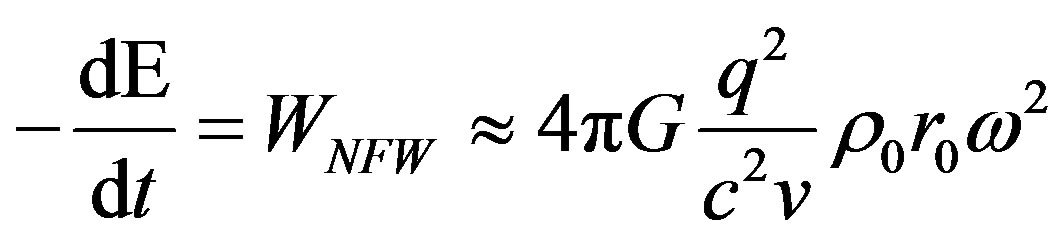 . (23)
. (23)
Putting here the orders of frequencies that relate to the visible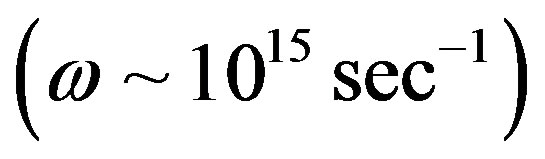 , the ultraviolet
, the ultraviolet 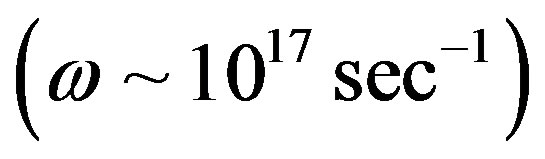 and the X-ray
and the X-ray 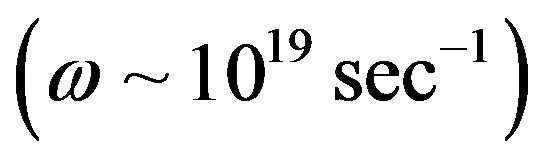 diapasons we get the following set of power estimations
diapasons we get the following set of power estimations

for the one coulomb charge
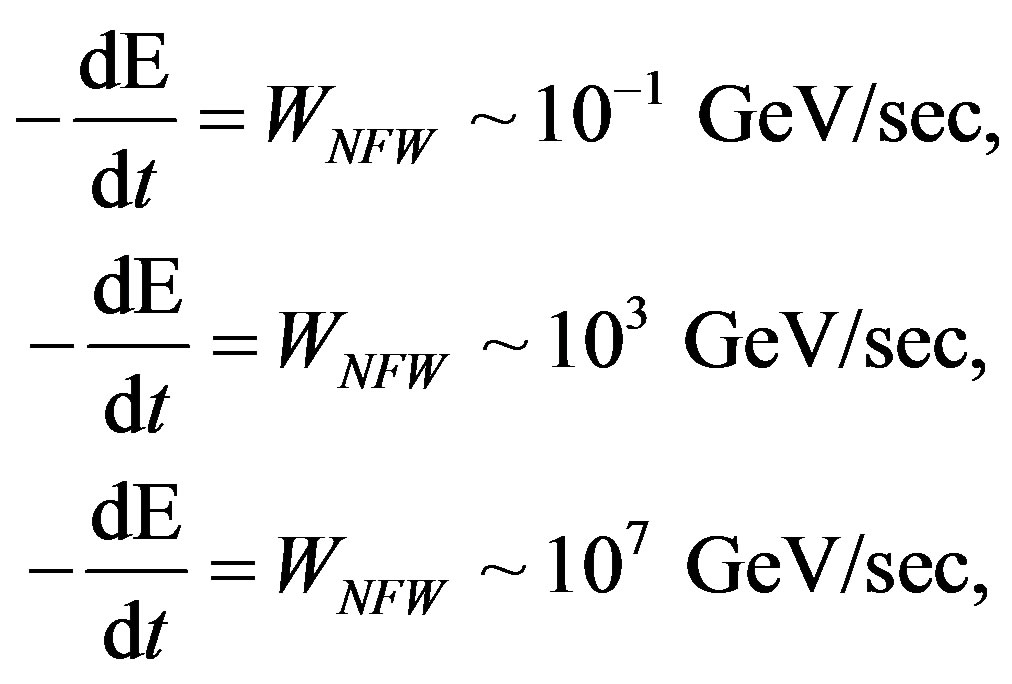 (24)
(24)
accordingly.
As it seems the largest power of the Cherenkov radiation is for the X-rays diapason. That is why the energy order of 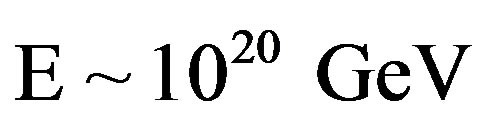 will emit during the particles’ time crossing a galaxy
will emit during the particles’ time crossing a galaxy .
.
Hence, the corresponding energy density in a halo will be
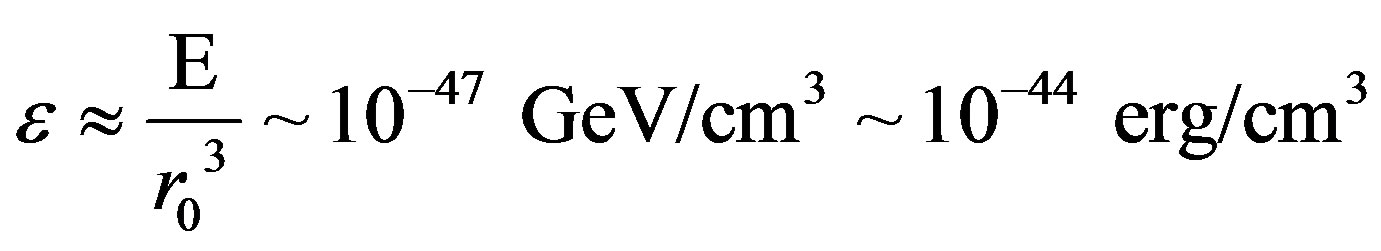 .
.
Finally, basing on the Stephan—Boltzmann law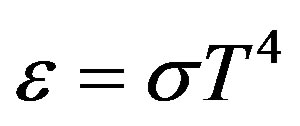 , where
, where  [28], it is possible estimate the temperature of Cherenkov radiation. It largest order (X-ray diapason) is about
[28], it is possible estimate the temperature of Cherenkov radiation. It largest order (X-ray diapason) is about  that is closed to the temperature fluctuations of cosmic background radiation
that is closed to the temperature fluctuations of cosmic background radiation 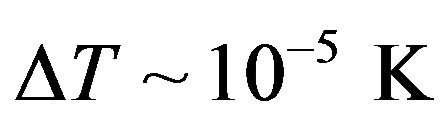 [29]. Hence, it lies on the threshold of modern astrophysical measurements.
[29]. Hence, it lies on the threshold of modern astrophysical measurements.
4. Conclusions
What is the physical essence have this type of radiation? Firstly, its detecting may be the criterion of choosing the preferable dark matter distribution in a galaxy. In fact, now there is number of other, except citing above, types of dark matter profiles. They were searched in many articles, for example in [30-35], etc. Though all of them are describing the structure of dark matter distribution in a galaxy—in dependence of its redshift, mass, sizes, and character of the evolution—it is desirable to have the general shape of such distribution. It is exactly giving the possibility of understanding the universal properties of the dark matter.
Secondly, in [36] it was shown that refracting index for the Einasto [30] dark matter profile is smaller then one. This fact is possible to interpret, probably, as the Cherenkov absorption in the dark matter. Hence, we get the additional perspectives for the dark matter searching because up to the present time it is considered that dark matter affects only gravitationally, and absorption processes in it was searched for the neutrino [37], only.
Concerning the above type of radiation it is necessary to mention and some other articles.
So, in article [38] it was shown that high energy particles are traversing the Universe through the cosmic microwave background radiation can, in principle, emit the Cherenkov radiation. It was shown that the energy threshold for this radiation is extremely high and its intensity would be too low due to the low density of the “relic photons gas” and very weak interaction of two photons.
In articles [39], this effect was also searched in the relic radiation field. For this media the refracting index was calculated in the framework of quantum electrodynamics. Its difference from the vacuum refracting index  was about
was about 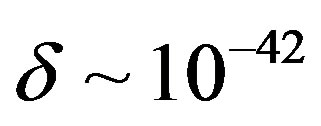 and is drastically smaller than in our case
and is drastically smaller than in our case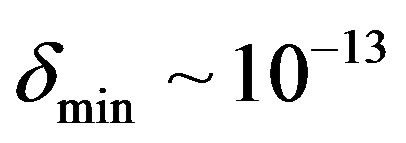 .
.
So, the Cherenkov radiation at the cosmological scales is preferable to search in the galaxy’s dark matter halo, namely.
The possibility of searching dark matter properties by the Cherenkov telescopes usage have been discussed in the recent article [40].
And last, the electronic publication of this article matter has been done in Reference [41].
5. Acknowledgements
The author is grateful to the National Space Agency Republic of Kazakhstan for supports this searching in the framework of state program 002—Space Researches of the Republic of Kazakhstan.
Also many thanks to the director of Virtual Institute of Astroparticle physics (VIA) professor M. Yu. Khlopov for the interest to this paper and the attraction my attention to some of his prior articles [42-46] in the considering subject matter.
REFERENCES
- B. M. Bolotovskij, “Theoriya Effekta Vaviliova—Cherenkova,” Uspekhi Fizicheskikh Nauk, Vol. 62, No. 7, 1957, pp. 201-246.
- V. L. Ginzburg, “Teoreticheskaya Fizika i Astrofizika,” Nauka, Moscow, 1975.
- O. S. Ivanitzkaya, “Lorentzev Bazis i Gravitatzionnuye Effektu v Einshtejnovoj Teorii Tyagoteniya,” Nauka i Tekhnika, Minsk, 1979.
- A. Gupta, S. Mohanty and M. K. Sama, “Cherenkov Radiation Emitted by Charged Particles in a Gravitational Field,” Classical and Quantum Gravity, Vol. 16, No. 1, 1999, pp. 291-298. doi:10.1088/0264-9381/16/1/021
- B. Paczyński, “Gravitational Microlensing in the Local Group,” Annual Review of Astronomy and Astrophysics, Vol. 34, 1996, pp. 419-459. doi:10.1146/annurev.astro.34.1.419
- P. Sizun, M. Cassé and S. Schanne, “Continuum GammaRay Emission from Light Dark Matter Positrons and Electrons,” Physical Review D, Vol. 74, No. 6, 2006, Artical ID: 063514. doi:10.1103/PhysRevD.74.063514
- P. Premadi, H. Martel, R. Matzner, et al., “Light Propagation in Inhomogeneous Universes II. Cosmological Parameter Survey,” The Astrophysical Journal Supplement Series, Vol. 135, No. 1, 2001, p. 135. doi:10.1086/321776
- A. Moiseev and S. Proumo, “Sources and Detection of Dark Matter and Dark Energy in the Universe,” Proceedings of the 8th UCLA Symposium. AIP Conference Proceedings, Vol. 1166, p. 151.
- W. de Boer, “Indirect Dark Matter Searches in the Light of ATIC, FERMI, EGRET and PAMELA,” Northeastern University, Boston, 2009.
- G. Gilmore, M. I. Wilkinson, R. F. G. Wyse, et al., “The Observed Properties of Dark Matter on Small Spatial Scales,” The Astrophysical Journal, Vol. 663, No. 2, 2007, p. 948. doi:10.1086/518025
- P. Salucci, F. Nesti, G. Gentile, et al., “The Dark Matter Density at the Sun’s Location,” Astronomy & Astrophysics, Vol. 523, 2010, Article ID: A83. doi:10.1051/0004-6361/201014385
- H. Arakida, “Influence of Dark Matter on Light Propagation in Solar System,” Advances in Space Research, Vol. 45, No. 8, 2010, pp. 1007-1014. doi:10.1016/j.asr.2009.11.012
- D. Clowe, M. Bradaĉ, A. Gonzalez, et al., “A Direct Empirical Proof of the Existence of Dark Matter,” The Astrophysical Journal Letters, Vol. 648, No. 2, 2006, Article ID: L109. doi:10.1086/508162
- L. Strigari, S. Koushiappas, J. Bullok, et al., “The Most Dark-Matter-Dominated Galaxies: Predicted Gamma-Ray Signals from the Faintest Milky Way Dwarfs,” The Astrophysical Journal, Vol. 678, No. 2, 2008, p. 614. doi:10.1086/529488
- Ya. B. Zel’dovich and I. D. Novokov, “Teoriya Tyagoteniya i Evolutziya Zvezd,” Nauka, Moscow, 1971.
- E. Rasia, G. Tormen and L. Moscardini, “A Dynamical Model for the Distribution of Dark Matter and Gas in Galaxy Clusters,” MNRAS, Vol. 351, No. 1, 2004, pp. 237-252. doi:10.1111/j.1365-2966.2004.07775.x
- M. Markevitch, W. R. Forman, C. L. Sarazin, et al., “The Temperature Structure of 30 Nearby Clusters Observed with ASCA. Similarity of Temperature Profiles,” The Astrophysical Journal, Vol. 503, No. 1, 1998, p. 77. doi:10.1086/305976
- J. F. Navarro, C. S. Frenk and D. M. White, “The Structure of Cold Dark Matter Halos,” The Astrophysical Journal, Vol. 462, 1996, pp. 563-578. doi:10.1086/177173
- A. Burkert, “The Structure of Dark Matter Haloes in Dwarf Galaxies,” The Astrophysical Journal Letters, Vol. 447, No. 1, 1995, Article ID: L25. doi:10.1086/309560
- C. G. Boehmer and T. Harko, “On Einstein Clusters as Galactic Dark Matter Halos,” MNRAS, Vol. 379, No. 1, 2007, pp. 393-398. doi:10.1111/j.1365-2966.2007.11977.x
- M.-B. Kallenrod, “Space Physics. An Introduction to Plasmas and Particles in the Heliosphere and Magnetosphere,” Springer, Berlin, 2004.
- B. W. Carroll, “An Introduction to Modern Astrophysics,” 2nd Edition, Benjamin Cummings, San Francisco, 1995.
- M. J. Barlow, L. J. Smith and A. J. Willis, “Wolf-Rayet Stars and Binarity,” MNRAS, Vol. 196, 1981, pp. 101- 110.
- R. Aloisio, V. Beresinsky and A. Gazizov, “Ultra High Energy Cosmic Rays: The Disappointing Model,” Astroparticle Physics, Vol. 34, No. 8, 2011, pp. 620-626. doi:10.1016/j.astropartphys.2010.12.008
- E. Vasiliev and M. Zelnikov, “Dark Matter Dynamics in the Galactic Center,” Physical Review D, Vol. 78, 2008, Article ID: 083506. doi:10.1103/PhysRevD.78.083506
- Opera Collaboration, “Measurement of the Neutrino Velocity with the OPERA Detector in the CNGS Beam,” 2012. arXiv:1109.4897v4 [hep-ex]
- M. Actis, G. Agnetta, F. Aharonian, et al. “Design Concepts for the Cherenkov Telescope Array,” Experimental Astronomy, Vol. 32, No. 3, 2011, pp. 193-316. doi:10.1007/s10686-011-9247-0
- L. E. Gurevitch and A. D. Chernin, “Vvedeniye v Kosmogoniyu,” Nauka, Moscow, 1978.
- G. F. Smoot and D. Scott, “The Cosmic Background Radiation,” 1996. astro-ph/9603157
- J. Einasto, “Dark Matter and Large Scale Structure,” 2000. astro-ph/0012161v1
- A. A. Klypin, A. V. Kravtsov, J. Bullok, et al. “Resolving the Structure of Cold Dark Matter Halos II,” The Astrophysical Journal, Vol. 554, No. 2, 2001, p. 903. doi:10.1086/321400
- T. Treu and V. E. Koopmans, “Massive Dark-Matter Halos and Evolution of Early-Type Galaxies to z = 1,” The Astrophysical Journal, Vol. 611, No. 2, 2004, p. 739. doi:10.1086/422245
- M. Weber and W. de Boer, “Determination of the Local Dark Matter Density in our Galaxy,” Astronomy & Astrophysics, Vol. 509, 2010, Article ID: A25. doi:10.1051/0004-6361/200913381
- S. Kazantzidis, L. Mayer, C. Mastropietro, et al. “Density Profiles of Cold Dark Matter Substructure: Implications for the Missing Satellites Problem,” The Astrophysical Journal, Vol. 608, No. 2, 2004, p. 663. doi:10.1086/420840
- R. Catena and P. Ullio, “A Novel Determination of the Local Dark Matter Density,” 2009. astro-phCO/0907.0018v2
- L. M. Chechin, G. Avkhynbayeva, E. Aimuratov and A. Umiraliyeva, “Deviation of Light Rays in Galaxy DarkMatter Halos,” Russian Physics Journal, Vol. 55, No. 6, 2012, pp. 86-92.
- R. Esteban, “Ultrahigh Energy Neutrino Absorption by Neutrino Dark Matter,” Physical Review D, Vol. 47, 1993, pp. 5247-5251.
- M. Marklund, G. Brodin, L. Stenflo, et al. “Cherenkov Radiation in a Photon Gas,” New Journal of Physics, Vol. 7, No. 70, 2005, p. 70. doi:10.1088/1367-2630/7/1/070
- S. G. Chefranov, “The Vavilov-Cherenkov Radiation by Relict Photon Gas,” 2010. astro-ph/1009.0594v1
- M. A. Sánchez-Conde, M. Cannoni, F. Zandanel, et al. “Dark Matter Searches with Cherenkov Telescopes: Nearby Dwarf Galaxies or Local Galaxy Clusters?” JCAP, No. 12, 2011, Article ID: 011.
- L. M. Chechin, “The Cherenkov Radiation in the Galaxy Halo of Dark Matter,” 2013. arXiv1302.3683v1[astro-ph.CO]
- Ya. B. Zeldovich, A. A. Klypin, M. Yu. Khlopov, et al. “Astrophysical Bounds on the Mass of Heavy Stable Neutral Leptons,” Soviet Journal of Nuclear Physics, Vol. 31, No. 5, 1980, pp. 664-669.
- R. V. Konoplich and M. Yu. Khlopov, “Astrophysical Constraints on Mass of Very Heavy Stable Neutrino,” Yadernaya Fizika, Vol. 57, 1994, pp. 452-458.
- D. Fargion, M. Yu. Khlopov, R. V. Konoplich and R. Mignani, “Is Stable Tau-Neutrino Really an Allowable Cold Dark Matter Candidate?” Physical Letter, Vol. B375, No. 1-4, 1996, pp. 223-228.
- D. Fargion, M. Yu. Khlopov, R. V. Konoplich and R. Mignani, “Bounds on Very Heavy Relic Neutrinos by their Annihilation in the Galactic Halo,” Physical Review, Vol. D52, No. 4, 1995, pp. 1828-1836.
- K. M. Belotsky and M. Yu. Khlopov, “On the Distribution of Collisionless Particles in Local Potential Well,” Gravitation & Cosmology, Vol. 11, No. 3, 2005, pp. 220- 222.

