Applied Mathematics
Vol. 3 No. 7 (2012) , Article ID: 19866 , 5 pages DOI:10.4236/am.2012.37111
A Hybrid Genetic Scheduling Algorithm to Heterogeneous Distributed System
1Department of Software Engineering, Yunnan University, Kunming, China
2Department of Computer Science, Xiamen University, Xiamen, China
Email: kangyan@ynu.edu.cn
Received April 25, 2012; revised May 29, 2012; accepted June 6, 2012
Keywords: Scheduling; Genetic Algorithm; Heterogeneous; Distributed System
ABSTRACT
In parallel and distributed computing, development of an efficient static task scheduling algorithm for directed acyclic graph (DAG) applications is an important problem. The static task scheduling problem is NP-complete in its general form. The complexity of the problem increases when task scheduling is to be done in a heterogeneous environment, consisting of processors with varying processing capabilities and network links with varying bandwidths. List scheduling algorithms are generally preferred since they generate good quality schedules with less complexity. But these list algorithms leave a lot of room for improvement, especially when these algorithms are used in specialized heterogeneous environments This paper presents an hybrid genetic task scheduling algorithm for the tasks run on the network of heterogeneous systems and represented by Directed Acyclic Graphs (DAGs). First, the algorithm assigns a coupling factor to each task to present the tasks should be scheduled onto the same processor by avoiding the large communication time. Second, the algorithm generate some high quality initial solution by scheduling the tasks which are strongly coupled with each other onto the same processor, and improve the quality of the solution by using coupling initial solutions, random solution, near optimal solutions obtained by the list scheduling algorithm in the crossover and mutation operator. The performance of the algorithm is illustrated by comparing with the existing effectively scheduling algorithms.
1. Introduction
Optimal scheduling of parallel tasks with precedence is critical for achieving high performance in heterogeneous computing system. The application scheduling is known to be NP-complete in general cases [1]. Although optimal solutions are known for restricted cases of this problem, such restrictions prevent the static task scheduling problem from being applicable to general computing environments. The search space of task scheduling solutions becomes extremely large and the task scheduling problem becomes more complicated for the system which has both processor heterogeneity and network heterogeneity. For this reason, there has been considerable research into heuristic static task scheduling algorithms [2]. These heuristics are classified into a variety of categories such as list scheduling algorithms [3-5], clustering algorithms [6], task duplication based algorithms [7-8] and Genetic algorithms [9-12].
The list-based heuristics are widely used due to their high performance and low time complexity. But there is always room for improvement, especially when they are used in heterogeneous environments. GA generally starts with a randomly generated initial population, which contains all individuals (chromosomes also called feasible solutions). Through a pre-specified generation number, quality of the solutions is augmented by the crossover and mutation operators designed to mimic the evolutionary theory. Algorithm aims at keeping the fittest solutions at the end of each generation. GAs have been applied to the task scheduling problem in a number of ways. The two main approaches appear to be: methods that use a GA in combination with other list scheduling techniques and methods that use a GA to evolve the actual assignment and order of tasks into processors.
We introduce a hybrid genetic (HG) algorithm to the problem of heterogeneous multiprocessor task scheduling. Two unique features distinguish this GA from a traditional GA algorithm. First, a coupling factor is assigned to each task to show the relation among the tasks. List scheduling algorithm is incorporated in the generation of the initial population of a GA to represent feasible high quality operation sequences and diminish coding space when compared to permutation representation. Second, high quality initial solutions are generated by scheduling the highly coupled task onto the same processor, which can largely decrease the communication cost among the heterogeneous environment.
2. Task Scheduling Problem
The general task scheduling problem includes the problem of assigning the tasks with required precedence relationship to suitable processors and the problem of ordering task executions on each resources. The characteristics of the application program is represented by a Directed Acyclic Graph (DAG), G = (V, E), where V is the set of v tasks nodes, and E is the set of e directed communication edges between the tasks. Each edge ei,j represents the precedence constraint that vj cannot be scheduled until task vi has been completed, hence vi is a predecessor of vj and vj is a successor of vi. Without loss of generality, it is assumed that there is one entry task to the DAG and one exit task from the DAG. A heterogeneous computing system P consists of a set of p independent different types of processors which are assumed to be fully interconnected by an arbitrary network. The estimated execution cost time wi,j to complete task vi on processor pi may be different on different processor depending on the processors computational capability.
D is a n × n matrix of communication data, where di,j is the amount of data required to be transmitted from task vi to task vj. The communication cost of edge ei,k which is for transferring data from task vi (scheduled on processor pm) to task vk (scheduled on processor pn) is
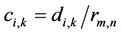 (1)
(1)
where rm,n is the link communication speed between two processors pm and processor pn. In this study, the channel initialization time is assumed to be negligible. Otherwise, di,k = 0 when both the tasks vi and vk are scheduled on the same processor. Further, for illustration, we assumed that the data transfer rate for each link is 1.0 and hence communication cost and amount of data to be transferred will be the same.
EST(vi, pj) and EFT(vi, pj) are the Earliest Start Time and Earliest Finish Time of task vi, on pj, respectively. For the entry task v0, EST(v0, pj) = 0 and for the other tasks in the graph, the EST and EFT values are computed recursively, starting from the entry task, as shown in (2) and (3). In order to compute the EFT and EST of a task vi, all immediate predecessor tasks of vi must have been scheduled.
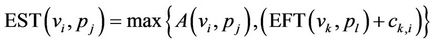 (2)
(2)
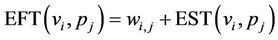 (3)
(3)
where vk is the immediate predecessor tasks of task vi and A(vi, pj) is the earliest time that processor pj completed the execution of the last assigned task, or the idle slot between the assigned tasks with an insertion-based scheduling policy.
The objective of task scheduling is to assign tasks to available processors such that precedence requirements between tasks are satisfied and the overall length of time required to execute the entire program, the schedule length or makespan, is minimized.
3. Hybrid Genetic Scheduling Algorithm
3.1. The Problem and Related Work
In list scheduling algorithms, the tasks in a list are assumed priorities and are assigned to the different processors based on descending order of priorities. List scheduling algorithms are generally preferred since they generate good quality schedules with less complexity. Several variant list scheduling algorithms have been proposed to deal with heterogeneous system, for example Mapping Heuristic (MH) [3], Levelized-MinTime (LMT) [4], Dynamic-Level Scheduling (DLS), Heterogeneous Earliest Finish Time (HEFT) [5] and Critical Path On a processor (CPOP). The HEFT algorithm significantly outperforms the DLS algorithm, MH, LMT and CPOP algorithm in terms of average schedule length ratio, speedup, etc. The HEFT algorithm selects the task with the so-called highest upward rank value at each step and assigns the selected task to the processor which minimizes its earliest finish time with an insert-based policy.
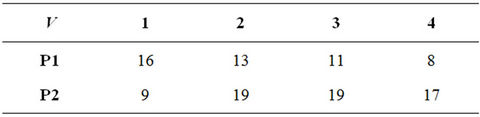
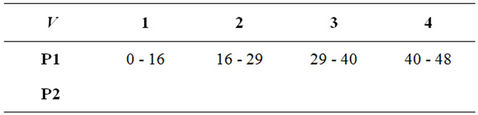
We noted that the list scheduling algorithms just consider the local optimal solution by scheduling the current task onto processor that gives the earliest finish time for the current task. In this way, the list scheduling algorithm cannot obtain the optimal solution for the scheduling problem. Figure 1 shows a DAG with four tasks and 4 edges. There are two processors available in the heterogeneous computing system. Table 1 shows the computation time of each task on every processor. For simplicity, we assume homogeneous communication and the communication times are as labeled on the edges in Figure 1. Table 2 shows the start time and finish time of all the tasks that are obtained by the HEFT algorithm. The optimal schedule length showed in Table 3 is 48 which is less than the schedule length obtained by HEFT algorithm is 59. And the optimal schedule length cannot be obtained by changing the order of the tasks.
The global minimum schedule length cannot be obtained by the above list scheduling algorithms since these methods were developed for fast execution on general heterogeneous environments. These list algorithms leave a lot of room for improvement, especially when these algorithms are used in specialized heterogeneous environments.
Genetic algorithms (GAs) are known as the most popular and widely used random guided search technique
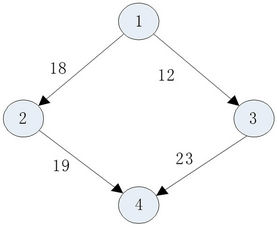
Figure 1. A sample task graph with 4 tasks.
for many types of combinatorial problems. One problem with the random guided search strategy is that this “randomness” prevents the search from proceeding in the proper search direction quickly. The optimal solution for the scheduling problem described in Figure 1 is obtained by the general genetic algorithm after 20 iterative of 50 individuals. Thus, we combine the genetic and the HEFT algorithm to improve the efficiency of the algorithm. And we improve the solution quality by scheduling the task onto the processor by using the coupling factor.
3.2. Coupling Factor
If a task has more than one predecessor and the communication cost between the task and its predecessors is relatively larger, we think that the tasks are coupled with each other strongly.
The coupling factor is given as:
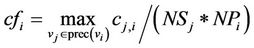 (4)
(4)
where prec (vi) is the set of immediate predecessors of task vi, NSi is the number of the successors of task vj, and NPi is the number of the predecessors of the task vi.
Obviously, if two tasks with high coupling factor are scheduled onto different processors, the communication cost is large and influence the quality of the solution.
3.3. Initial Population
Task scheduling problem actually is a combination of machine assignment and operation scheduling decisions, so any solution can be defined by the assignment of operations on machines and processing sequence of operations on the machines. Thus, a chromosome is composed of two parts: 1) machine assignment vector (called here V1) and 2) operation sequence vector (called here V2). Both V1 and V2 are vectors of length n where n is the number of tasks to be scheduled. The elements of a vector V1 represent the tasks themselves and the order of the tasks gives the relative task priorities. A specific number of initial solutions are generated at random by sticking to two vector representation.
For avoiding generate infeasible solutions and improve the quality of the solution, we generate the initial solutions by using two different ways.
First, we use the strategy of HEFT algorithm, an effective list scheduling algorithm to generate feasible random initial population effectively. The HEFT algorithm selects the task with the so-called highest upward rank value at each step and assigns the selected task to the processor which minimizes its earliest finish time with an insert-based policy. We firstly assign a random execution time to each task and assume the communication time is zero, and then use the task-prioritizing phase of the HEFT algorithm to assign the priority to all tasks, i.e., generate V1, based on upward rank priority. To assign priority, the upward rank of each task is computed. The upward rank of a task is computed as the critical path of that task, which is the highest sum of execution time starting from that task to exit task. The priority of task vi is
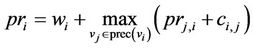 (5)
(5)
where succ(vi) is the set of immediate successors of task vi, wi is the average execution time of task vi
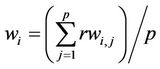 (6)
(6)
where rwi is the random execution time of task vi.
V2 is generated by randomly select the processor from the processors. Based on upward rank priority will be assigned to each task, we randomly schedule the task vi in V1 onto processor pj in V2 according to the same order, and obtains the earliest finish time for the task vi on processor pj. It uses an insertion based policy which considers the possible insertion of task vi in an earliest idle time slot between the already scheduled tasks on the same processor pj, if it satisfies the precedence restriction.
Second, we generate coupling initial solution. V1 is generated by assigning the priority to all tasks based on strategy described above which now uses the average execution time and actual communication time. We randomly schedule the task vi in V1 onto processor pj in V2, or schedule the task vi in V1 onto processor where is scheduled the task vj which is strong coupled with task vi, and obtains the earliest finish time for the task vi on processor pj. In this way, the strongly coupled tasks are scheduled onto the same processor in a high probability.
3.4. Crossover Operator
In the paper, GA has been used to directly evolve task assignment and order in processors. We use a GA to evolve individuals consisting of multiple lists, with list representing each task’s priority and the assigned processor. Crossover exchanges tasks between corresponding processors from two different individuals. Individuals are again vectors of length n, where n is the number of tasks to be scheduled. We select the crossover point based on the random probability.
For completing the unassigned positions on the operation sequence of the offspring, check all the operations of second parent from left to right. If corresponding operation is already assigned in the substring from first parent, skip to the next operation in operation sequence of second parent. Otherwise, place corresponding operation of the second parent for the position in offspring. The operations taken from second parent are the ones that protochild needs.
3.5. Mutation Operator
For machine assignment vectors, activity-based mutation randomly decides whether a task (1 ∙∙∙ n) should be selected for mutation in a certain probability.
3.6. Selection
In the proposed GA approach, selection process is performed on an enlarged sampling space, where both parents and offsprings have the same chance of competing for survival. In order to cope with the scaling problem of the direct fitness-based approach, ranking selection is introduced. The idea is simple: sort solutions in the population from the best to the worst according to their performance on the scheduling length, and assign the selection probability based on the ranking. And the second generation is generated by selecting the solution separately from the solutions obtained by HEFT algorithm, random initial solution, and coupling initial solution.
The proposed framework of the GA is shown as follows.
procedure: Hybrid Genetic algorithm input: Problems dataset, GA parameters output: a near-optimal schedule
begin
t = 0, assign the coupling factors to all tasks;
generate initialize P(t) which includes random initial solutions, coupling initial solution;
represent initialize P(t) with two vectors;
obtain fitness (P(t)) by the decoding method;
while (not termination condition) do crossover P(t) to yield C(t) by crossover operator;
mutation P(t) to yield C(t) by mutation;
obtain fitness (P(t), C(t)) by the decoding method;
select P(t + 1)from P(t) and C(t) by scheduling length;
t < −t + 1;
end while
output a near-optimal schedule;
end
4. Performance Analyses and Discussion
We have used Intel Xeon processors with 1 GHz speed for our experiments. We present the comparative evaluation of HG algorithm and the existing algorithms for heterogeneous system such as HEFT and GA algorithm [12] for DAGs with various characteristics by simulation. For our experiments, a variety of synthetic DAGs and heterogeneous systems were generated using a random graph generator and a random heterogeneous system generator. The generation of a random DAG requires five parameter inputs: the number of tasks, out-degree of a task, shape, deviation of task size and data size. The task size was randomly selected from the values between 1 and 100 and the data size was randomly set to a value between 1 and 100. The random heterogeneous generator produces a random computing environment based on two parameters: network heterogeneity, and processor heterogeneity.
The performances and cost of the algorithms were compared with respect to set of experiments with various graph characteristics. We investigate how the various parameters of the algorithm will impact the degree to which the schedules are improved through HG algorithm.
The experiments show that our GA exhibits the best performance on these problems. The results show that the HG algorithm is more effective when communication cost over execution time ratio is large.
5. Conclusion
In this paper the hybrid genetic algorithm for the heterogeneous distributed computing systems is proposed and studied. We use the coupling factor and assigning policy to schedule the tasks which are strongly coupled onto the same processor. The hybrid genetic algorithm generates high quality initial solution by using the strategy of the HEFT algorithm. The hybrid genetic algorithm can produce shorter schedule length than HEFT and genetic based on obtained schedule. We observe the percentage of cases that result in an improved final schedule and the average improvement ratio with randomly generated task graphs under various parameters and two real applications. It is observed that when the communication cost over execution time ratio is small, the hybrid genetic algorithm does not perform well; but when communication cost over execution time ratio is greater than some value, an improvement in the final schedule is obtained in most cases that were simulated. And it is also observed that the percentage of final schedule length is less than the initial one and the average improvement ratio are both sensitive to the graph structure and the initial one. Generally, hybrid genetic algorithm makes larger improvements on the problem with long communication cost, and the algorithm is more effectively with the graph structure is more flexible.
6. Acknowledgements
This work has been supported by the Open Foundation of Key Laboratory in Software Engineering of Yunnan Province under Grant No. 2011SE03, National Natural Science Foundation of China (Grant No. 60763008), “CDIObased software system modeling and design research and implementation” (Grant No. Rj14).
REFERENCES
- R. L. Graham, L. E. Lawler, J. K. Lenstra and A. H. Kan, “Optimization and Approximation in Deterministic Sequencing and Scheduling: A Survey,” Annals of Discrete Mathematics, Vol. 5, 1979, pp. 287-326.
- H. Topcuoglu, S. Harir and M.-Y. Wu, “Performance Effective and Low-Complexity Task Scheduling for Heterogeneous Computing,” IEEE Transactions on Parallel and Distributed Systems, Vol. 13, No. 3, 2002, pp. 260- 274. doi:10.1109/71.993206
- H. EI-Rewini and T. G. Lewis, “Scheduling Parallel Program Tasks onto Arbitrary Target Machines,” Journal of Parallel and Distributed Computing, Vol. 9, No. 2, 1990, pp. 138-153. doi:10.1016/0743-7315(90)90042-N
- M. Iverson, F. Ozguner and G. Follen, “Parallelizing Existing Applications in a Distributed Heterogeneous Environments,” Proceedings of the Heterogeneous Computing Workshop, 1995, pp. 93-100.
- H. Topcuoglu, S. Hariri and M. Y. Wu, “Performance Effective and Low-Complexity Task Scheduling for Heterogeneous Computing,” IEEE Transactions on Parallel and Distributed Systems, Vol. 13, No. 3, 2002, pp. 260- 274.
- C. Boeres, J. V. Filho and V. E. F. Rebello, “A ClusterBased Strategy for Scheduling Task on Heterogeneous Processors,” Proceedings of the 16th Symposium on Computer Architecture and High Performance Computing (SBAC-PAD), Brazil, October 2004.
- S. Basker and P. C. SaiRanga, “Scheduling Directed A-Cyclic Task Graphs on Heterogeneous Network of Workstations to Minimize Schedule Length,” Proceedings of the ICPPW, Taiwan, October 2003.
- R. Bajaj and D. P. Agrawal, “Improving Scheduling of Tasks in a Heterogeneous Environments,” IEEE Transactions on Parallel and Distributed Systems, Vol. 15, No. 2, 2004, pp. 107-118. doi:10.1109/TPDS.2004.1264795
- L. Wang, H. J. Siegel, V. P. Rowchoudhry and A. A. Maciejewski, “Task Matching and Scheduling in Heterogeneous Computing Environments Using a Genetic Algorithm-Based Approach,” Journal of Parallel and Distributed Computing, Vol. 47, No. 1, 1997, pp. 8-22. doi:10.1006/jpdc.1997.1392
- M. K. Dhodhi, I. Ahmad and A. Yatama, “An Integrated Technique for Task Matching and Scheduling onto Distributed Heterogeneous Computing Systems,” Journal of Parallel and Distributed Computing, Vol. 62, No. 9, 2002, pp. 1338-1361. doi:10.1006/jpdc.2002.1850
- S. C. Kim and S. Lee, “Push-Pull: Guided Search DAG Scheduling for Heterogeneous Clusters,” Proceedings of the International Conference on Parallel Processing, Oslo, June 2005.
- S. W. Annie, H. Yu, S. Jin and K.-C. Lin, “An Incremental Genetic Algorithm Approach to Multiprocessor Scheduling,” IEEE Transactions on Parallel and Distributed Systems, Vol. 15, No. 9, 2004, pp. 824-834. doi:10.1109/TPDS.2004.38