International Journal of Geosciences
Vol.4 No.3(2013), Article ID:31782,7 pages DOI:10.4236/ijg.2013.43058
Studying Relationships between the Fractal Dimension of the Drainage Basins and Some of Their Geomorphological Characteristics
1Kharazmi University of Tehran, Tehran, Iran
2Watershed Management Sciences and Engineering, Natural Resources Faculty, Tehran University, Tehran, Iran
Email: zkhanbabaei@yahoo.com
Copyright © 2013 Zahra Khanbabaei et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 13, 2012; revised January 16, 2013; accepted February 15, 2013
Keywords: Fractal Geometry; Fractal Dimension; Drainage Networks; Horton-Strahler
ABSTRACT
Complex nonlinear dynamic systems are ubiquitous in the landscapes and phenomena studied by earth sciences in general and by geomorphology in particular. Many natural landscape features have an aspect such as fractals. In the many geomorphologic phenomena such as river networks and coast lines this is visible. In recent years fractal geometry offers as an option for modeling river geometry and physical processes of rivers. The fractal dimension is a statistical quantity that indicates how a fractal scales with the shrink, the space occupied. This theory has the mathematical basis but also applied in geomorphology and also shown great success. Physical behavior of many natural processes as well as using fractal geometry is predictable relations. Behavior of complex natural phenomena as rivers has always been of interest to researchers. In this study using data basic maps, drainage networks map and Digital Elevation Model of the ground was prepared. Then applying the rules Horton-Strahler river network, fractal dimensions were calculated to examine the relationship between fractal dimension and some rivers geomorphic features were investigated. Results showed fractal dimension of watersheds have meaningful relations with factors such as shape form, area, bifurcation ratio and length ratio in the watersheds.
1. Introduction
Mandelbrot [1] introduced the concept of fractals in terms of the length of the west coast of Great Britain. Geomorphology introduces a transparent approach to the application of Chaos Theory, Fractals and the concept of Selforganized. The natural phenomena commonly enjoy a kind of order, if the usual conditions changes for any reason, disorder and chaos will occur. However, the natural systems usually achieve a kind of self regulation, reordering, and self organization. Geomorphology deals with natural processes and forms, and the geomorphologists are interested in exploring the application and utility of the ideas and methods of the Chaos Theory in geomorphology. These methods and ideas show the non linearity of the natural processes. In addition to that, most of the natural characteristics of the perspective enjoy a Fractal-like appearance, which means with different scales they show the same details (for example, a conifer or the trees’ stems). In many geomorphologic phenomena as river networks and shorelines, this fractal self-similarity could be observed. Introducing Fractal geometry as the natural geometry, Mandelbrot, the French mathematician, focused the attention of many scholars in the fields of basic sciences, engineering and geology to this new geometry. Since that time, the scholars, using this geometry, could model the geometry of these natural complicated phenomena well. Before the 20th century, the Euclid geometry was responsive to most of the questions about the natural and unnatural phenomena and all the phenomena could be explained and defined by Euclid geometry. But this branch of mathematics was and is still applicable for regular phenomena which have true dimensions. At the end of the 20th century, Hausdorff and Byskvych studied some of the basic specialties of the phenomena possessing unusual dimensions. Mandelbrot also studied in detail the importance of and the relationships between the Fractals and the physical phenomena and other sciences in his book named “the fractal geometry in the nature” [2,3].
The subjective literature of the Chaos Theory, Fractal Theory and their related concepts in geomorphology is rather new. For example, Huggett [4] expressed the application of Chaos Theory in geomorphology. Malanson et al. [5] evaluated the Chaos Theory in natural geography. Phillips [6] studied the effect of water rising on the coasts and its influences on the geomorphic system of the moist lands. Rodrigues-Iturbe & Rinaldo [7] evaluated the fractal and self-organization problems in river basins. Phillips [8] in a series of articles in his book named “the ground surface systems” studied the existence of chaos in the surface streaming waters, completing the skirts, the moist coastal lands, and soil systems. Baas [9] studied the chaos, fractals, and self-organization in the coastal geomorphology. Qin, et al. [10] studied the chaotic behavior in the system of the mass movements. Fonstad & Marcus [11] dealt with studying the self-organization in the systems of river coast and Pelletier [12] studied the fractal behavior in the flowing landforms.
In Iran, the Chaos Theory and the related concepts in geomorphology were first set forth by Ramesht and then they were thoroughly developed in an article called “the Chaos Theory and its application in geomorphology” by him. Besides describing the theory in that article, Ramesht mentioned its placement and application in geomorphology and provided some examples of chaos into consideration in Hanjan and Tameh valleys in Kashan [13].
Karam [14] in an article called “the Chaos Theory, fractal and non linear systems in geomorphology” pointed to the chaotic behaviors seen in most of the geomorphic and natural complicated dynamic systems including the surface streams, mass movements, soil systems, and etc. and added that the new viewpoints in morphology tried to analyze and determine the complicated chaotic behavior in the aforementioned systems through the Chaos Theory and the related concepts.
The river engineering scholars have always been in need of a proper model for expressing, justifying and predicting the rivers’ behavior during the time, and fractal geometry as an appropriate option for modeling the rivers’ geometry and also for evaluating the physical processes through the rivers have been posed in recent years. Since no study regarding the fractal geometry of rivers has been done in Iran, especially in geomorphology, such evaluations apparently seem required. The objective of the present paper is calculating the fractal dimension of the drainage networks and comparing it with some of the quantitative particularities of a drainage network. For that aim, three drainage basins in Zagross mountain chain were selected and some of the quantitative particularities of their drainage system and fractal dimensions were computed in terms of the existing relationships.
2. Methodology
2.1. Introducing the Studied Basins
In this study, three water-shed basins were evaluated including: Sarkhoun and Sabzkouh basins (some secondary sub-basins of Karoun watershed in the mountainous district of Zagross and Chaharmahale Bakhtyari Province), Rahdar basin in northwest of Shiraz in the heights of Ghalaat in Zagross chains. Figure 1 shows the position of these minor basins.
Sarkhoun watershed is a secondary basin of a bigger watershed basin in Karoun River which is located in the mountainous district of Zagross and Chaharmahale Bakhtyari Province. The following coordinates belong to that region: 31˚38' to 31˚52' of northern latitude and 50˚25' to 50˚43' of eastern longitude. Sarkhoun basin involves an area around 325 km2 and a perimeter about 95.5 km. This basin has a long northwest-southeast form. The exiting way of the basin is southeastern and Sarkhoun River’s water in that area goes directly into Karoun River. The maximum northwest altitude of the basin in Gareh mount is 3307 m and the least altitude in the exiting way is around 1000 m. The studied basin is located in an earth composed unit of the wrinkled Zagros. Petrologically speaking, although the age of the oldest sediments existing in this region and Zagros refers to the Cambrian and Precambrian eras, the oldest sediments in the studied basin involve Dolomite and the Jurassic Dolomitic limestone belonging to Sormeh composition. The earthquakes in the region are active and the seismicity of this region is critical. The basin’s topography is a mountain with various valleys and miscellaneous flood channels and stony outcrops and slope skirts [15].
Sabzkouh Basin is located in Naghan region (Kyar County) in Chaharmahale Bakhtyari province with these coordinates: 31˚25' to 31˚35' of north latitude and 50˚30' to 50˚40' of east longitude, involving an area around 175 km2. The general direction of the altitude in this basin is from northwest to southeast. The main river in the region is Sabzkouh streaming from southeast to the northwest in the area which receives some branches in the heights. A considerable point here is the deep cut of most of the river branches which suggests severe erosion and most probably, falling the base level of the river. The maximum altitude in this basin reaches to 2660 m the minimum of which is 1624 m. The age of the most ancient composition and sediments in the studied region which mainly involves the lime stones and Chill refers to the Paleozoic and the upper Cambrian and Milad composition. The newest sediments are related to Quaterner involving high and young cones, Marin, and the river channels’ alluvium. Regarding the main and reversed earthquakes, this region, because of its earth composition, is severely

Figure 1. The position of the three studied basins in Zagross.
critical. However, the earthquakes in the region enjoy a relatively low magnitude and their return era is short [16].
Rahdar Basin is located in northwestern Shiraz in the heights of Ghalaat. The streaming water of the basin pours into the Mahaarlou Lake. This basin involves an area about 100 km2 with the maximum altitude of 2641 m and the minimum altitude of 2200 m. Regarding the geological facts, the studied area is a part of the wrinkled zone of Zagros in the mountainous belt of Alp-Himalayas; of its geological airs are wide and unique anticline constructions and some synclinals with an east to west pivotal line. Lithologically speaking, the studied basin involves a random of moderate to highly thick layers of Marin, Grits, and Conglomerate with some effects of petty gyps and Enidrate. Its geological time of the stony outcrops which includes the mountainous parts of the region is from the Precambrian to the underneath Pleistocene; these stony units in the low regions are covered by sediments of the upper Pleistocene and Holocene. This region enjoys a high and continuous talent of seismicity [17].
2.2. Method and Data
In addition to the library studies, the used resources in the present paper are: 1) topography map with such coordinates: 1:50,000 geology map of 1:100,000 for Sarkhoun basin; 2) topography map of 1:25,000 and geology map of 1:100,000 for Sabzkouh basin and 3) topography map of 1:25,000 and geology map of 1:250,000 for Rahdar basin. In order to prepare the regarded map of drainage networks, at first, the floodways were extracted from the topography maps, the rivers’ amendments as connecting the floodways together were done in the place of breakings in the rivers and the topology was made in Cad Map environment, and by changing the map format to Shape, all the maps were transferred to Arc GIS environment. The grade and length of each floodway was calculated in the geographical informative system and at the end, the fractal dimension of the river networks was computed using particular relationships. Various methods were used in determining the fractal dimension of the drainage basins. Since at the beginning, most of the progresses in these studies were made through Horton ratio and developing it, here the counting system and Horton coefficient were used for the drainage system and then, the fractal dimensions would be calculated.
2.3. The Chaos and Fractal Theories
Concepts of chaos, fractals and self-organization, originating from research in nonlinear dynamics, have proven to be powerful approaches to understanding and modeling the evolution and characteristics of a wide variety of landscapes and bedforms [9]. The denotative meaning of chaos is muddling, confusion, and disorder and its equivalent in mechanic is turbulence. The vocabulary itself gives the meaning of a lack of any structure or order and in daily conversations, chaos and confusion are usually signs of disorderliness or disorganization, although in the new vision which has clarified its scientific and theoretical dimensions, disorder and confusion no longer mean disorganization, non efficiency and muddling, yet disorder is the existence of unpredictable issues in the dynamic phenomena, which has its special characteristics. Chaos is a kind of disorderly order or an orderly disorder. It is disorderly since its results are unpredictable and orderly because it enjoys a kind of certainty. Scientifically speaking, disorder is a mathematical concept which could not be defined exactly, but could be called a kind of certain happening. The Chaos Theory deals with studying the chaotic dynamic systems. The chaotic systems are some Nonlinear Dynamic Systems which are highly sensitive to their primary conditions. A minor change in the primary conditions of such systems leads to major changes in future. This phenomenon is known as the Butterfly effect. The chaotic behavior is shown by a phase diagram. The phase diagrams are some chaotic systems which are monitored by strange (heterogeneous) attractors (some complicated two-fork models which show the probable manners of a system during time). Strange attractors are in fact the same fractals. The chaotic systems are randomly formed and are ordered through time and will reach a form like strange attractor and fractal [14].
Fractal is derived from the Latin word Fractus (meaning a stone broken into pieces irregularly), it also means “torn into pieces” and “taken into parts”.
In 1982, Mandelbrot introduced the Fractal Theory for the first time. In that theory which versus the Euclid geometry, the geometry dimensions are not integers and are defined as decimals. Additionally, the objects are not symmetrical but self-similar. Many of the happenings and phenomena in nature have fractal behaviors [18]. The fractals are some forms which, in comparison with the Euclid geometry figures, are not orderly at all. These forms are firstly disordered wholly, and secondly, that disorder is the same by every scale [19].
The best way for defining a fractal is paying attention to its adjectives and signs. A fractal is “irregular” meaning no part of which is smooth. A Fractal is “self-similar” which means its parts are similar to the whole. The fractals are developed through “repetition” meaning that the transformation occurs repeatedly and depends on the start position. Its other characteristic is that it is “combined”. However, it could be shown by simple algorithms, therefore it is quite usual that beyond the disorderly natural elements there are a series of rules.
2.4. Fractal Dimension
The fractal dimension is a concept for measuring the roughness in the fractal curve which shows the degree of complicatedness of the system. In fact, the fractal dimension is a statistical quantity showing how a fractal occupies the space when the scale lessens [20]. This characteristic of the fractals is firm without regarding the increase in growth of the fractal or the change or not change in point of view. Fractal dimension, unlike the Euclid changes, is mainly expressed by a non integer or decimal number. If the Euclid dimension of line is one, and the dimension of the sheet will be two, the fractal dimension of a picture which is located in the sheet will be a decimal number between one and two [21].
There are various definitions for fractal dimension. Regarding the linear size of an item and decreasing it in any space direction to ε, then N(ε) self-similar items could be seen which would cover the entire primary item; this means that N(ε) number of the self-similar structures with a linear size of ε which cover the whole structure. This definition is the commonest for the fractal dimension, the so called Hausdorff dimension which is attained through the following ratio:
 (1)
(1)
In this dimension, unlike the Euclid figures, the length of the fractals depends on the length of the used scale for measuring [22].
One of the applications of the fractal geometry is studying the relationship between fractal dimension and the particularities of the considered phenomena. The fractal dimension of the drainage networks is calculated through Horton’s draining calculations. Horton introduced the following ratio for studying the river networks:
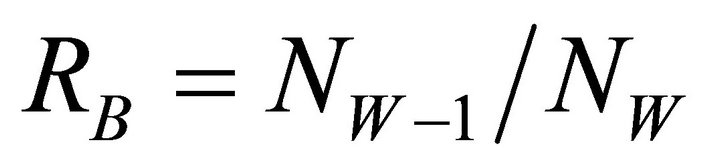 (2)
(2)
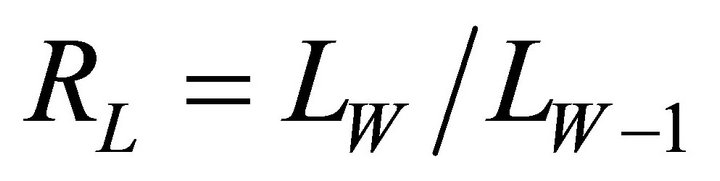 (3)
(3)
 (4)
(4)
In ratio 2 to 4, RB, RL, and RA are Horton’s coefficients for the number of branches, the length of branches, and the area of a river network, respectively. NW, LW, and AW are the number of branches, the length of branches, and the area of a river network, respectively; regarding the aforementioned ratio, the fractal and area dimensions and the river branches are achieved through Ratios 5 and 6 [23].
 (5)
(5)
 (6)
(6)
In these ratios, Da and Db are the fractal dimensions of the area and the river branches respectively [23].
3. Finding
For studying the altitudinal distribution of the basins, first of all, the topographical map of every basin became numeric in the environment of software CAD MAP, and then it was changed into shape file, it was transferred to GIS software environment. Changing the data to invaluable data, firstly the digital altitudinal model of the basins (DEM) and then the altitudinal distribution map of each basin were prepared (Figure 2).
Quantification of drainage networks resulted in the Horton-Strahler ordering and power-law scaling. Mandelbrot [24] pointed out that this power-law scaling is fractal. It is a standard practice to use the Strahler ordering system. When two like-order streams meet they form a stream with one higher order than the original. Thus, two first-order streams combine to form a second order stream, two second-order streams combine to form a thirdorder stream, and so forth [25]. The bifurcation ratio RB is defined by
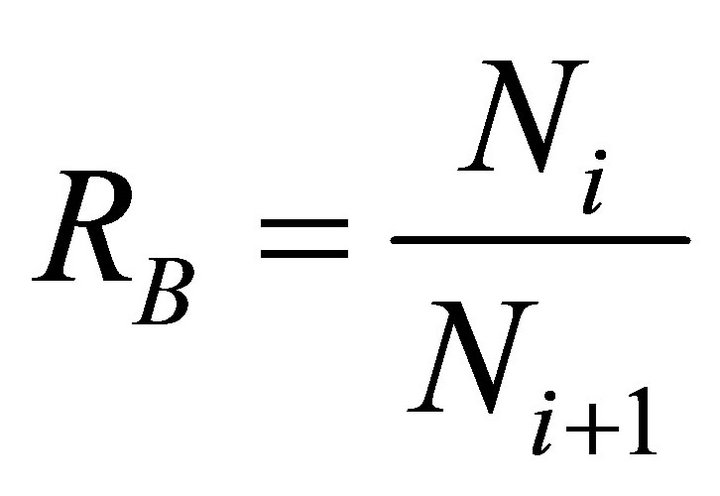 (7)
(7)
where Ni is the number of streams of order i. The lengthorder ratio Rr is defined by
 (8)
(8)
where ri is the length of streams of order i; RB and Rr are found to be nearly constant for a range of stream orders in a drainage basin. From Equation (5) the fractal dimen sion of a drainage network is:
 (9)
(9)
Unlike the geometrical dimension, the fractal dimension of the aquiferous basins is suggestive of their geomorphologic particularities and the details of the figures and the existing complications would be attained through calculating that dimension [26]. In order to study the relationship between the fractal dimension and the shape factor, the shape factor (SF) was also calculated. According to the American Army’s counseling engineers, the shape factor is the ratio between the shape length (L2) and its area (A) which is shown by SF [27].
 (10)
(10)
In that ratio, L is the shape length (the distance of the exiting points to the farthest part of the shape) in terms of kilometer and A is the area of the shape based on square kilometer. Applying the aforementioned ratio, the branch ratio, the longitudinal ratio of the river, and the fractal dimensions were attained for the three basins according to Table 1.
4. Discussions and Results
The computed results show that the fractal dimension of the drainage network in the studied basin equals 1.94, 1.54, and 1.25 respectively for Sarkhoun, Sabzkouh, and Rahdar basins. Evaluating the relationships between some morphometric characteristics of the basins and the fractal dimensions of the drainage network shows that there are some meaningful relationships between them in that studied region.
The fractal dimension suggests a positive relationship with the basin’s area, so that Sarkhoun basin with the largest area possesses the biggest fractal dimension (1.94) and Rahdar basin with the least area has the smallest fractal

Figure 2. The elevation categories of the three studied basins in Zagross.

Table 1. The comparison between calculated fractal dimensions of basins and their geomorphologic characteristics.
dimension (1.25). The shape factor has also a positive relationship with the fractal dimension of the drainage network. The correlation between these two factors shows an R2 equaling 0.97. In other words, the longer the shape forms, the bigger the fractal dimension of the drainage network, and the more circular the shape forms, the smalller the fractal dimension of the drainage network. The ratio of the drainage network’s branches, which shows the number of the river branches with various ranges in Sarkhoun basin, is more than the rests, suggesting the densest drainage in the whole basin. This can be derived from the petrological or regional conditions of the area. The least ratio numbers could be seen in Rahdar basin. Regardless of the lithological conditions, Rahdar basin in Shiraz enjoys a more arid region in comparison with the two other basins in Chaharmahale Bakhtyari Province. So the branch ratio of that region is the least. The branch ratio in the studied basins has a direct and positive relationship with the fractal dimension of the drainage network for which R2 equals 0.94, which means the fractal dimension would increase as the branch ratio increases.
The drainage network’s length, which is the length of the floodways with different ranges, has a converse ratio with the fractal dimension, meaning that the fractal dimension of the drainage network decreases as the total length increases. For example, the biggest longitudinal ratio of the floodways in Rahdar basin equals 2.79 while the fractal dimension of that basin equals 1.25, which is the least number.
In addition to identifying the morphometric particularities of the natural phenomena, the fractal dimension makes modeling and predicting their future behaviors possible. The chaos theory and its related concepts intend to provide a device for solving and understanding the complicated problems for human beings. The fractals are the basic elements of the methods which are required in geomorphology for analysis or modeling such non linear and complicated events and systems. In fact, the interest to and the application of fractal issues in geomorphology is because of the fact that many of geomorphologic landforms are fractal, and the formation and transformation of the fractals could be determined by mathematical ratios. In this way, the transformation and evolution of the fractal landforms could be modeled, as Pelletier showed that the fractal and chaotic structures are inborn evolutionary structures in the flowing landforms.
5. Conclusion
Chaos, fractal, non linear and self organized systems are all depended on and related to each other, some concepts which are present in the natural and humanistic complicated systems. The fractal geometry could be regarded as an appropriate device in studying the rivers’ geomorphology. The fractal dimension of the river networks in the aquiferous basins suggests the degree of geomorphologic and hydrological similarity in them, such parameters as the longitudinal ratio of the floodways, branch ratio, their curvature and abundance, form and width of the directions, and the topographic particularities of the region are considered important in determining the fractal dimension. Mathematically speaking, the basins whose fractal dimensions are the same would be metric equivalents of each other and there would be lots of similarity between the geomorphologic and hydrological characteristics of the basins. The branch number of a river from various ranges, and also the level and length of these branches derive from the fractal and power ratios. These ratios could be used for studying the branch changes in the rivers and their basins through the time as well.
REFERENCES
- B. B. Mandelbrot, “How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension,” Science, New Series, Vol. 156, No. 3775, 1967, pp. 636-638.
- M. F. Barensley, “Fractals Everywhere,” Academic Press Professional, New York, 1993.
- G. Cherbit, “Fractals-Non-In Integral Dimensions and Applacation,” Masson, Paris, 1993.
- R. J. Huggett, “Dissipative System: Implications for Geomorphology,” Earth Surface Processes and Landforms, Vol. 13, No. 1, 1988, pp. 45-49.
- G. P. Malanson, D. R. Butler and S. J. Walsh, “Chaos Theory in Physical Geography,” Physical Geography, Vol. 11, No. 4, 1990, pp. 293-304.
- J. D. Phillips, “Earth Surface Systems: Complexity, Order and Scale,” Blackwell, Oxford, 1992.
- I. Rodriguez and A. Rinaldo, “Fractal River Basins (Chance and Self-Organization),” Cambridge University Press, Cambridge, 1997.
- J. D. Phillips, “Earth Surface Systems: Complexity, Order and Scale,” Blackwell, Oxford, 1999.
- A. C. W. Baas, “Chaos, Fractals and Self-Organization in Coastal Geomorphology: Simulating Dune Landscapes in Vegetated Environments,” Geomorphology, Vol. 48, No. 2, 2002, pp. 309-328. doi:10.1016/S0169-555X(02)00187-3
- S. Qin, et al., “A Nonlinear Dynamical Model of Landslide Evolution,” Geomorphology, Vol. 43, No. 1, 2002, pp. 77-87.
- M. A. Fonstad and M. Marcus, “Self-Organized Criticality in Riverbank Systems,” Annals of Association of American Geographers, Vol. 93, No. 2, 2003, pp. 281-296.
- J. D. Pelletier, “Qualitative Chaos in Geomorphic Systems, with an Example from Wetland Response to Sea Level Rise,” Journal of Geology, Vol. 100, No. 3, 2007, pp. 365-374.
- M. H. Ramesht, “The Chaos Theory in Geomorphology,” 1382.
- A. Karam, “The Chaos Theory, Fractal and Non Linear Systems in Geomorphology,” The Natural Geography Quarterly, Vol. 3, No. 8, 1389, 17 p.
- A. Karam, “Quantitative Modeling and Danger Zonation of Earthquake in the WRINKLED ZAgross,” Ph.D. Thesis, Geographical Sciences and Remote Testing Department of Tarbiat Modarres University of Tehran, Tehran, 1381, 360 p.
- A. Karam, “Analysis and Zonation of the Risks in Naghan and Its Surrounding Using AHP and Geographical Informative System,” The Scientific Pole of the Space Analysis of the Dangers in Tarbiat Moallem University, Tehran, 1388, 12 p.
- Geological Survey of Iran.
- M. G. Moghaddam, “A Dynamic Study of the Water and Fog Production Viewing the Fractal Theory,” Aab and Khak Leaflet of Ferdousi University of Mashhad, 1389, Mashhad.
- M. Khakzand, “A Short Look at the Interaction between Nature and Architecture,” Baghe Nazar Magazine, Vol. 8, No. 3, 1386, 11 p.
- T. Tekyeh, “Studying the Effects of Viscosity and Solution Trembling in the Fusion of Liquid-Gel of Laponite Nano Particles through Dispersing Light,” MS Thesis, the Department of Basic Sciences of Tarbiat Moddares University of Tehran, Tehran, 1387, 145 p.
- A. Andalib, “Compressing the Figures by Waves and Fractals Theory,” MS Thesis, Engineering Department of Tarbiat Modarres University of Tehran, Tehran, 1381, 267 p.
- A. M. Tayefeh, “Analyzing and Designing the Fractal Micro Strip Aerial with Wireless Dispatching Application,” MS Thesis, Engineering Department of Tarbiat Moddares University of Tehran, Tehran, 1383, 207 p.
- A. Nikouee, “Fractal Geometry in River Engineering: Ideas, Basic Concepts, and the Achievements,” The 4th National Conference of Reconstruction Engineering, Tehran University, Tehran, 1387, 451 p.
- B. B. Mandelbrot, “Fractal Geometry of Nature,” Freeman, San Francisco, 1982.
- D. L. Turcotte, “Self-Organized Complexity in Geomorphology: Observations and Models,” Geomorphology, Vol. 91, No. 3-4, 2007, pp. 302-310. doi:10.1016/j.geomorph.2007.04.016
- A. Adl, “The Fractal Dimension and the Hydrological Particularities of the Aquiferous Basins,” The 1st National Engineering Congress of Reconstruction, Sharif Industrial University, Sharif, 1383, 575 p.
- A. Alizadeh, “The Rules of Applicable Hydrology,” Astane Ghodse Razavi Publications, Mashhad, 1389, 652 p.

